KSEEB Solutions Class 8 Science Chapter 6 Conservation Of Plants And Animals Points To Remember
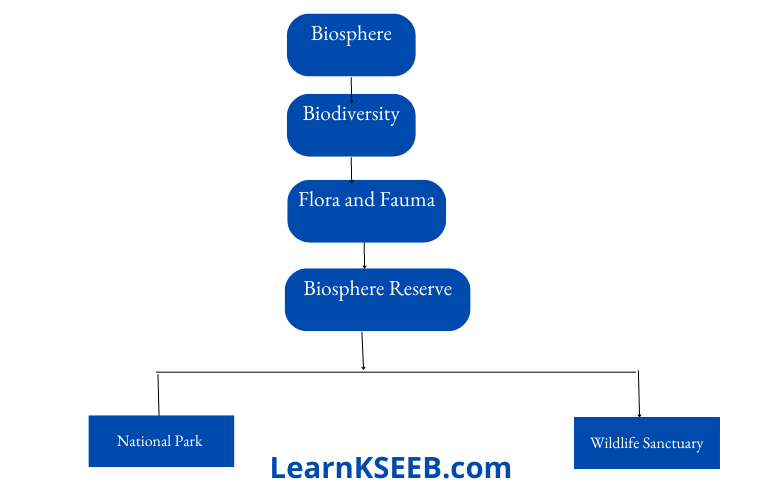
Biodiversity:
Occurrence of an innumerable number of different types of organisms and the whole range of their varieties (biotypes) adapted to different climates, environments and areas.
Wildlife sanctuary, national park, and biosphere reserve are names given to the areas meant for the conservation and preservation of forests and wild animals.
Biodiversity refers to the variety of living organisms in a specific area.
Plants and animals of a particular area are known as the flora and fauna of that area.
Endemic species are found only in a particular area.
Endangered species are those which are facing the danger of extinction.
Red Data Book contains a record of endangered species.
Migration is the phenomenon of the movement of a species from its own habitat to some other habitat for a particular time period every year for a specific purpose like breeding.
We should save, reuse and recycle paper to save trees, energy, and water.
Reforestation is the restocking of destroyed forests by planting new trees.
Flora: Different types of plants belonging to an area. Example: Silver Ferns, Sal, Teak, Mango, etc.
Fauna: Animals found in an area- Example: Dog, Frog, Insects, Bull Jackal, etc.
Endemic Species: Species of plants and animals found exclusively in a particular area. These are not naturally found anywhere else.
Extinct Species: Species of plants and animals which have already been lost. Examples: Dodo, Indian Cheetah, Pink-headed Duck, etc.
Threatened Species: Species that are liable to become extinct if it is not allowed to realize their full biotic potential by removing the cause of the threat.
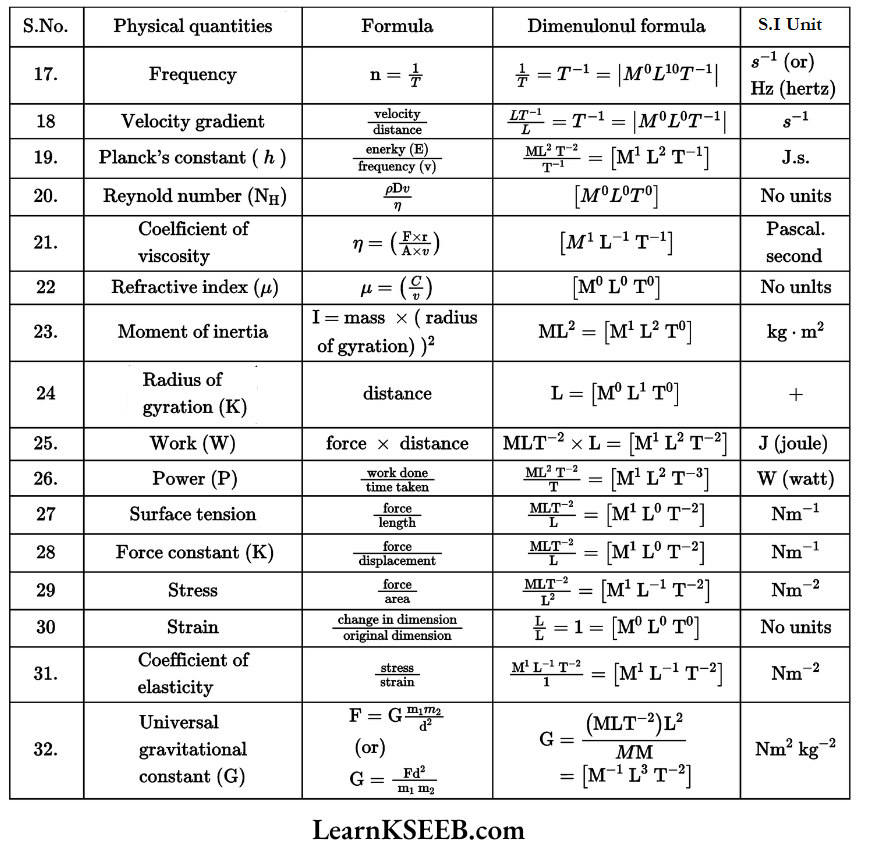
Type of Threatened Species:
1. Endangered Species: A species of animal or plant that is seriously at risk of extinction. Example: Indian rhinoceros, Asiatic ion, Asiatic wild ass, etc
2. Vulnerable Species: A vulnerable species is a species of animals or plants which are likely to become endangered unless something changes.
Example: Chinkara deer and Black buck, Golden Langur, etc
3. Rare Species: Species whose populations are originally scarce and scattered in the world.
4. National Parks: Protective areas reserved exclusively for the betterment of wildlife. These are established with the approval of the legislature.
Examples: Hazaribagh National Park in Jharkhand, Desert National Park in Rajasthan, etc
5. Sanctuaries: Hunting prohibited areas set up by the government are known as sanctuaries. These are only for the protection of wild animals. Example: Jaldapara in Madarihat, West Bengal), Keoladeo Ghana in Bharatpur (Rajasthan)
6. Migration: The regular, periodic, two-way movements of birds and some animals from their place of residence to some other place along well-defined routes. It is linked to seasonal factors, breeding, shortage of foods, etc. The Bharatpur Bird Sanctuary is known for its migratory birds.

Class 8 Science Conservation of Plants And Animals KSEEB Questions
Conservation Of Plants And Animals Ncert Textbook Exercises
Question 1. Fill in the blanks :
1. A place where animals are protected in their natural habitats is called a wildlife sanctuary.
2. Species found only m a particular area is known as biodiversity.
3. Migratory birds fly to faraway places because of climate changes.
Question 2. Differentiate between the following.
1. Wildlife Sanctuary and Biosphere reserve
2. Zoo and Wildlife sanctuary
3. Endangered and Extinct Species
4. Flora and Fauna
Answer:
1. Wildlife Sanctuary
- This is an area where wild animals are protected and preserved.
- It is a place found in
Biosphere reserves
- It helps to maintain the biodiversity and culture of the area.
- Abiosphere reserves may also d areas of other protected Wildlife Sanctuary
2. Zoo
- It is a place where we protect animals.
- Here artificial surroundings are made for
- Here animals are supplied with prepared food.
Wildlife Sanctuary
- Here, too, wild animals are protected and preserved.
- They live in their natural habitat or environment.
- They get their food from forests themselves.
3. Endangered Species
- These are those species that are facing the danger of extinction.
- Tiger is an example of an endangered species.
Extinct Species
- They are the species that have already vanished from the earth.
- Dinosaur is an example of extinct species.
4. Flora
- Flora Flora is a plant found in a particular region.
- Sal, mango, Jamun, etc. are examples of flora. Biosphere Reserves 121/105
Fauna
- Fauna is the animals found in a particular region.
- Chinkara, blue-bell, deer, cheetah, etc. are examples of fauna.
Question 3. Discuss the effects of deforestation on the | 5. following.
1. Wild animals
2. Environment
3. Villages (rural areas)
4. Cities
5. Earth
6. The next generation
Answer:
1. Wild animals: They won’t get their natural habitat and surroundings as well as food. They will migrate to another forest.
2. Environment: Climate changes disturb the environment. Global warming is caused due to accumulation of carbon dioxide.
3. Villages: Villagers cannot grow food because of no rain. So, drought situations will prevail. Villagers will move towns and cities.
4. Cities: Cities flooded with drought-affected villagers, will affect the environment. Food grains will either not be available or if available, they will be costlier.
5. Deforestation leads to changes in soil properties. The physical properties of the soil will get affected badly. The lands will be gradually converted into deserts.
Question 4. What will happen if
1. We co on cutting trees.
2. The habitat of an animal is disturbed
3. The top layer of soil is exposed
Answer:
1. If we go on cutting trees, then the following situation will arrive Climate change will affect the environment due to global warming and there will be no rain. The soil will become unfertile due to regular flooding of the topsoil.
2. If the habitat of an animal is disturbed, the animal may not be in a position of getting its natural habitat as well as food.
3. Removal of the top layer of soil by floods and heavy winds will expose the lower hard and rocky layers. This soil has less humus and less fertility.
Question 5.Answer in brief
1. Why should we conserve biodiversity?
2. Protected forests are also not completely safe for wild animals. Why?
3. Some tribes depend on the jungle. How?
4. What are the causes and consequences of deforestation?
5. What is Red Data Book?
6. What do you understand by the term migration?
Answer:
1. If biodiversity is not conserved, the life existing on earth, its interrelationships, and its relationship with the environment will be disturbed.
2. It is because despite all these the poachers keep killing or capturing the animals in these forests. That is why protected forests are also not completely safe for animals.
3. Some tribal life in the jungle. The jungle provides them with food and protection. That is why: they are fully dependent upon the forests.
Causes of deforestation:
- Procuring land for cultivation.
- Building houses and factories.
- Natural Calamities like floods, drought,s and forest fires.
- Consequence of deforestation
- Global warming.
- Soil erosion
- Melting ice on poles.
- Red Data Book is a book that keeps a record of all endangered animals and plants.
- Migration is the phenomenon of movements of species from its own habitat to some other habitat for a particular time period every year for a change of climate and for the purpose of breeding.
KSEEB Science Class 8 Chapter 6 Guide
Question 6. In order to meet the ever-increasing demand in factories and for shelter, trees are being continually cut Is it justified to cut trees for such projects?
Answer: Of course, to meet the ever-increasing demand in factories and for shelter, trees are being continually cut, which is not justified at all. fone tree is cut, a least five trees should be grown so that the reforestation process will remain continuous. But if trees are cut blindly and no trees are planted then the earth will face global warming, no rainfall, climate change, soil erosion, and deforestation. So, cutting trees for any reason at all is not justified.
Question 7. How can you contribute to the maintenance of the green wealth of your locality? Make a list of actions to be taken by you.
Answer: For the maintenance of the green wealth of my locality. I will prefer reforestation in the locality. I shall start a campaign, along with my friends, to make the people of the locality aware of the importance of trees. Once people become conscious of the importance of plants they will be requested to do the following-
Each family should plant at least one tree in the monsoon month.
During summer, they should assure the watering of the plants every day.
On the occasion of birthdays, marriage ceremonies, and other happy occasions, they should gift their friends and relatives.
Question 8. Explain how deforestation leads to reduced rainfall
Answer: Deforestation leads to the accumulation of CO, in the atmosphere which results in global warming as CO, traps the heat of the sun’s rays. The increase in the temperature of the earth will disturb the water cycle and reduce rainfall causing drought in the region.
Question 9. Find out about national parks in your state. Identify and show their location on the outline map of India.
Answer: There is not any national park in my native state but near national parks around my locality are Ranthambore, Bharatpur, and Sarika of
the nearby state of Rajasthan.
Question 10. Why should the paper be saved? Prepare a list of ways by which you can save paper.
Answer: The manufacturing of paper needs trees. By cutting trees, deforestation is caused. If the paper is saved or recycled, so many trees can be saved. To make one ton of paper17 full-grown trees are to be cut. Therefore, to stop deforestation, we should save paper. It can be saved by recycling. Paper can be recycled 5-7 times and can be used. If everyone who uses paper could save at least one sheet of paper in a day, we can save many trees in a year.
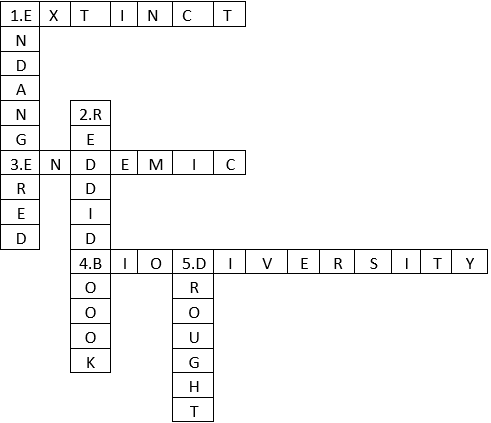
Question 11. Complete the word puzzle.
Down
1. Species on the verge of extinction.
2. A book carrying information about endangered species.
5. Consequence of deforestation.
Across
1. Species that have vanished.
3. Species found only in a particular habitat.
4. Variety of plants, animals, and microorganisms found in an area.

Conservation Of Plants And Animals Activities
Question 1. Add more causes of deforestation to your list and classify them into natural and man-made.
Answer:
Natural causes of deforestation:
1. Forest fires
2. Severe drought
Man-made causes of deforestation:
1. Wood for the manufacturing of paper.
2. Wood for fuel and the making of houses.
Question 2. Animal life is also affected by deforestation. How? List the points and discuss them in your class.
Answer:
- Due to deforestation, a great disturbance is caused in the food chain.
- Deforestation makes the animals homeless.
- Due to deforestation, animals become easy prey for hunters.
- Herbivorous animals face the scarcity of food due to deforestation.
- Animals face the bad effects of natural calamities.
Question 3. List the factors disturbing the biodiversity of your area. Some of these factors and human activities may disturb biodiversity unknowingly. List these human activities. How can these be checked? Discuss in your class and write a brief report in your notebook.
Answer: Cutting of trees, rising air, water, and land pollution, excessive construction, and using more resources or their products affect the biodiversity harshly.
Important Questions On Conservation Of Plants And Animals Class 8 KSEEB
Question 4. Try to identify the flora and fauna of your area and list them.
Answer:
Flora (trees and plants): Pipal, sal, teak, Kadam, babool, mango, guava, ferns, Arjun, Kelkar, etc., are flora present in our locality.
Fauna (animals): Blue-bull, chinkara, cheetah, deer, leopard, wolf, wild dog, etc., are the fauna present in our locality.
Question 5. Find out the endemic plants and animals of the region where you live.
Answer:
- Endemic plants: Mahua, wild mango, sal, Jamun, etc.
- Endemic animals: Bison, Indian giant squirrel, etc.
Question 6. Visit a nearby zoo. Observe the conditions provided to the animals. Were they suitable for animals? Can animals live in an artificial setting instead of their natural habitat? In your opinion, will the animals be comfortable in a zoo or in their natural habitat?
Answer:
- A zoo tends to provide suitable conditions for the animals to live in, similar to their natural habitat.
- Yes, animals can live in an artificial setting instead of their natural habitat, as they live in the natural environment and stay protected from people.
- In my opinion, animals are safer in the zoo in comparison with their natural environment, because special care is taken for the animals in the zoo. But I think animals feel more comfortable living in their natural habitat as no one wants to live in prison.
Conservation Of Plants And Animals Additional Questions
Question 1. What is sanctuary?
Answer: An area where animals are protected from any disturbance to them and their habitat is called a sanctuary.
Question 2. Write the names of some parks and sanctuaries.
Answer: Dudhwa National Park, Bharatpur Bird Sanctuary, Kaziranga National Park, Nelapattu Bird Sanctuary, etc.
Question 3. Give examples of flora.
Answer: Teak, sal, mango, Jamun, Arjun, etc.
Question 4. Give examples of fauna.
Answer: Elephant, tiger, wild bear, etc.
Question 5. Name two endemic fauna.
Answer: Giant squirrel, bison.
Question 6. Name the first Reserve Forest of India.
Answer: Satpura National Park.
Question 7. What is the name of the reserved land used to protect biodiversity?
Answer: Biosphere Reserve.
Question 8. List the names of some migratory birds.
Answer: Siberian crane
- Bar-headed goose
- Arctic tern
- Surkhab
Question 9. Write the names of some extinct animals.
Answer: Dodo, dinosaurs, mammoth, etc.
Question 10. What do you mean by deforestation?
Answer: The cutting of trees on a large scale is called deforestation.
Question 11. Mention the causes of deforestation.
Answer: The cause of deforestation could be:
- Forest fires
- Building houses, factories
- Severe droughts
- Using wood for some purposes
- Human encroachment and procuring land for cultivation
Question 12. How does deforestation lead to frequent floods and droughts?
Answer: Deforestation results in the decreased water-holding capacity of the soil. This reduces the infiltration of water into the ground which causes floods. On the other hand, deforestation leads to a higher level of carbon dioxide in the atmosphere which causes global warming. The scarcity of trees disturbs the water cycle and may reduce rainfall leading to droughts.
Question 13. How can we protect wildlife?
Answer: Wildlife plays a significant role in maintaining a balance in the environment. They can be protected by establishing secured and protected areas, which are restricted for human activities that are against the protection of wildlife. Cutting trees hunting, and poaching are strictly banned there. Many of these areas are national parks and wildlife sanctuaries.
Question 14. Why is the conservation of biodiversity important?
Answer: Because of the following reasons, the conservation of biodiversity is important:
- It boosts tourism and thus, plays a significant role in enhancing the economy of the country.
- It maintains the fertility of the soil.
- It helps in maintaining the ecological balance on the earth.
- Biodiversity is a rich source for the study of genetics and evolution.
- It helps in maintaining the weather by regulating climatic changes, rainfall, etc.
Question 15. What are ‘rare species? Give examples.
Answer: Rare species are uncommon and scarce, that is to say, their population is very small. Major steps are to be taken for their conservation and protection so that they may not fall under the category of endangered or extinct species. Examples: wild buffalo, Bengal fox, gaur, marbled cat, etc.
Question 16. For centuries human activities such as hunting and encroachment have led to the degradation of forests and the extinction of many species of plants and animals. The government of India has taken many steps to conserve forests and wildlife. But this movement will not be a success without the involvement of all of us.
1. What products are obtained from forests and wildlife?
2. How can we help in conserving forests and wildlife?
3. Can you name some organisations that are working against the killing or poaching of animals?
4. What values of humans are shown here towards nature?
Answer:
1. From forests: Wood for fire, timber furniture, medicines, forage for livestock, gums, raisins, papers, etc. From wildlife: Horns, skin, leather, fur, ivory, meat, fin, etc.
2. By saying No’ to animal products we can at least reduce their hunting and poaching.
- By not cutting the trees and planting more saplings we can help in restoring the natural habitat of wild animals.
- By creating awareness among people about the importance of forests and wildlife.
3. World Wide Fund for Nature (WWF), International Fund for Animal Welfare (IFAW), World Society for the Protection of Animals (WSPA)), etc.
4. They are cruel, money-minded, selfish, reckless, etc.
KSEEB Class 8 Conservation of Plants And Animals Exercise Solutions Multiple Choice Questions
Question 17. Wild buffalo is an endangered species because
1. Its population is diminishing
2. It has become extinct
3. It is found exclusively in a particular area
4. Its poaching is strictly prohibited
Answer: 1. Its population is diminishing
Question 18. Which one of the following changes may occur due to desertification?
1. Increased chances of floods.
2. Conversion of fertile land into a desert.
3. The decrease in atmospheric temperature.
4. Increase in water holding capacity of Bihar. soil
Answer: 2. Conversion of fertile land into a desert
Explanation: Soil is carried away by the wind there are no trees as there will be no roots to hold onto the soil. Thus topsoil erodes which will turn the land into a desert.
Question 19. Which one of the following statements is true about a Biosphere Reserve?
1. It is a protected area where only endemic species live.
2. It is meant only for the conservation of
3. It is meant to conserve both, the biodiversity and the culture of that area.
4. There are no other protected areas within its limits.
Answer:3.It is meant to conserve both, the biodiversity and the culture of that area.
Explanation: The biosphere reserve is the protected part of the land covered with forests. It is meant for the conservation of wildlife, biodiversity, and the traditional lifestyle of tribals.
Question 20. The place meant for the conservation of biodiversity in their natural habitat are
1. Zoological garden
2. Botanical garden
3. Wildlife sanctuary
4. National park
Answer: 3. Wildlife sanctuary, 4.National park
Explanation: In botanical gardens and zoological parks species are protected outside their natural habitat and ex-situ conservation. On the other hand, Wildlife sanctuaries and National parks are in-situ conservation where the conservation of biodiversity occurs in their natural habitat.
Question 21. Which one of the following statements is true about endemic species?
1. They are found exclusively in a specific habitat.
2. Endemic species can never become endangered.
3. They are found only in zoos and botanical gardens.
4. They are not affected by the destruction of their habitat.
Answer: 1. They are found exclusively in a specific habitat.
Explanation: Endemic species are those which are found exclusively in specific habitats. Endemic species get extinct when their habitat is destroyed by human activities or by the introduction of new species are introduced to the habitat.
Question 22. Which of the following feature is correct for a wildlife sanctuary?
1. It is an artificially created protected area for animals.
2. It is a protected area for threatened and endangered wild animals.
3. It is meant for the conservation of only plant species.
4. Capturing and poaching of animals is strictly prohibited here.
Answer: 1. It is an artificially created protected area for animals.
Explanation: The wildlife sanctuary is an artificially created protected area for animals.
- Hence option 3. is wrong. Wildlife sanctuaries are not specific for threatened and endangered wild animals.
- Hence answer 2. is wrong. Capturing and poaching animals is strictly prohibited everywhere.
- Hence option 4. is not appropriate.
Question 23. Which statement is incorrect about endangered species?
1. Their number has decreased drastically.
2. They might become extinct in the near future.
3. They pose a danger to other animals.
4. Their natural habitat needs to be protected
Answer: 3. They pose a danger to other animals.
Question 24. What do blackbuck, elephant, python, and golden cat together represent in a forest?
1. Fauna
2. Flora
3. Ecosystem
4. Species
Answer: 1. Fauna
Explanation: Fauna is the animal’s in a particular area. Flora is a plant species in a particular area. The ecosystem includes the physical environment along with plants and animals of a particular area. A species is a group of inbreeding populations.
Question 25. The Red Data Book keeps a record of all the
1. Endemic species.
2. Extinct species.
3. Endangered plants
4. Endangered animals.
Answer: 1. Endemic species,2. Extinct species.
Explanation: Red Data book keeps a record of endangered animals and endangered plants. Different books are maintained for different species including plants, animals, and other species.
Question 26. Migratory birds fly to faraway areas during a particular time of the year. Which of the following conditions present in their habitat
during that time are responsible for this behavior?
1. Unavailability of food.
2. Extreme weather conditions.
3. Overcrowding.
4. Lack of nesting areas.
Answer: 1. Unavailability of food, 2.Extreme weather conditions.
Explanation: The migration of birds is a process of moving to different habitats due to adverse climatic conditions. Because of extreme weather
conditions, birds fail to gather food and they cannot lay their eggs.
Question 27. In our country, large patches of forests are being cleared for the cultivation of crops. The environmental impact of such a practice will lead to
1. Soil erosion
2. Soil conservation
3. Soil pollution
4. Soil fertility
Answer: 1. soil erosion
Explanation: Due to the cutting of trees, there will no roots to hold the soil, and because of this topsoil erodes by the action of wind.
Question 28. Why is it important to conserve forests?
Answer: Forest should be conserved for balance in nature and to conserve the ecosystem.
Question 29. Mention any one action that you have undertaken to conserve trees.
Answer: Donating old books and spreading awareness about deforestation.
Question 30. State whether the following statements are True or False. Correct the false statements.
1. There can be a wildlife sanctuary within a biosphere reserve.
2. Plants of a particular area are collectively termed fauna.
3. Deforestation leads to an increase in the water-holding capacity of the soil.
4. Bison is an endemic fauna of the Pachmarhi Biosphere Reserve.
Answer:
1. True.
2. False- Plants of a particular area are collectively termed flora.
3. False- Deforestation leads to a decrease in the water-holding capacity of the soil.
4. True.
Question 31. Can a forest regenerate naturally in a short period of time?
Answer: It takes a long period of time to regenerate the forest naturally.
Question 32. Name the first Reserve Forest of India.
Answer: Satpura National Park.
Question 33. Why are wildlife sanctuaries important for the conservation of plants and animals?
Answer: Wildlife sanctuaries are important for the conservation of plants and animals because in these areas poaching or killing animals, and disturbing animals by any means of human activity are prohibited. Moreover, in wildlife sanctuaries animals can live in their natural environment. This promotes their breeding and population increase.
Question 34. Why are endemic organisms in greater danger of becoming extinct?
Answer: Endemic organisms are those which can live in a particular geographical location. Any disturbance to their natural habitat will affect the endemic animals adversely hence they are in great danger of becoming extinct.
Question 35. How are even small animals important in an ecosystem?
Answer: Every organism forms a part of the food chain and ecosystem. Hence every organism is important to balance the ecosystem.
Question 36. A new species X is introduced in a forest. How is it likely to affect the local species of that area?
Answer: Introduction of new species in a forest leads to competition for food and place. Hence it will affect the native species present in the forest.
Question 37. Does soil erosion affect the fertility of soil? How?
Answer: Soil erosion leads to the washing out of soil fertile layer of soil. This leads to the desertification of land due to a lack of fertile soil.
Question 38. What is the unique feature of the biodiversity found in the Panchmarhi Biosphere Reserve?
Answer: The biodiversity found in Panchmarhi Biosphere Reserve is similar to that found in the upper Himalayan peaks and lower Western Ghats.
Question 39. Mention the aim of the Forest (Conservation) Act.
Answer: Aim of the Forest (Conservation) Act are as follows
To conserve natural forests and the animals present in the forest.
To meet the basic needs of the people living in the forest.
Question 40. What is biodiversity?
Answer: Biodiversity refers to the variety of plants and animals present in a particular habitat.
Karnataka State Board Syllabus for Class 8 Textbooks Solutions
- Chapter 1 Crop Production and Management
- Chapter 2 Microorganisms: Friend and Foe
- Chapter 3 Synthetic Fibres and Plastics
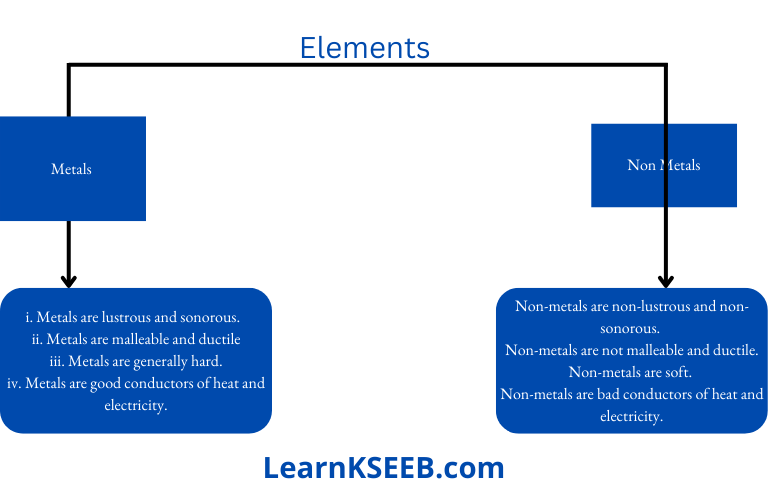
- Chapter 4 Materials: metals and Non-Metals
- Chapter 5 Coal and Petroleum
- Chapter 6 Conservation of Plants and Animals
- Chapter 7 Force and Pressure
- Chapter 8 Friction
- Chapter 9 Sound
- Chapter 10 Combustion and Flame
- Chapter 11 Cell Structure and Functions
- Chapter 12 Reproduction in Animals
- Chapter 13 Reaching the age of Adolescence
- Chapter 14 Chemical Effects of Electric Current
- Chapter 15 Some Natural Phenomena
- Chapter 16 Light
- Chapter 17 Stars and the Solar System
- Chapter 18 Pollution of Air and Water


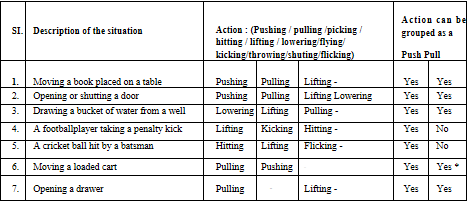



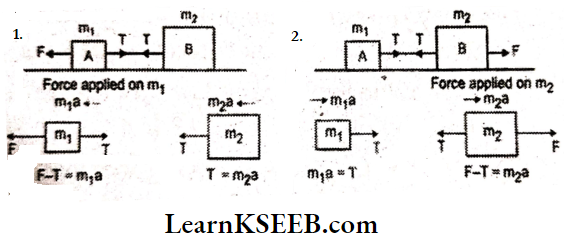
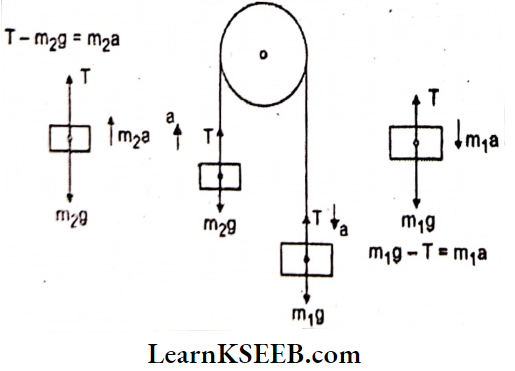
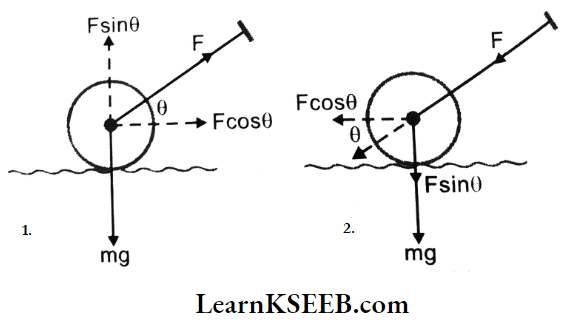
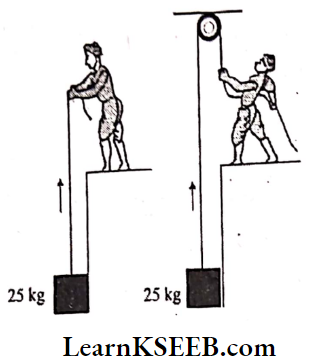
 Answer: From the above actions, we can conclude that force can change the shape of an object.
Answer: From the above actions, we can conclude that force can change the shape of an object. Answer: When unlike poles of the magnet are brought near the other magnet, they attract each other and move in the direction of another magnet. When like poles of a magnet are brought near to the other magnet, they repel each other and move in the direction away from the other magnet. Thus, the force exerted by a magnet on another magnet is a type of non-contact force.
Answer: When unlike poles of the magnet are brought near the other magnet, they attract each other and move in the direction of another magnet. When like poles of a magnet are brought near to the other magnet, they repel each other and move in the direction away from the other magnet. Thus, the force exerted by a magnet on another magnet is a type of non-contact force. Question 8. Take a transparent glass tube or a plastic pipe. The length of the pipe/tube should be about 15 cm and its diameter should be 5-7.5 cm. Also, take a piece of a thin sheet of good quality rubber, say, a rubber balloon. Stretch the rubber sheet tightly over one end of the pipe. Hold the pipe in the middle, keeping it in a vertical position. Ask one of your friends to pour some water into the pipe. Does the rubber sheet bulge out? Note also the height of the water column in the pipe. Pour some more water. Observe again the bulge in the rubber sheet and the height of the water column in the pipe. Repeat this process a few more times. Can you see any relation between the amount of the bulge in the rubber sheet and the height of the water column in the pipe?
Question 8. Take a transparent glass tube or a plastic pipe. The length of the pipe/tube should be about 15 cm and its diameter should be 5-7.5 cm. Also, take a piece of a thin sheet of good quality rubber, say, a rubber balloon. Stretch the rubber sheet tightly over one end of the pipe. Hold the pipe in the middle, keeping it in a vertical position. Ask one of your friends to pour some water into the pipe. Does the rubber sheet bulge out? Note also the height of the water column in the pipe. Pour some more water. Observe again the bulge in the rubber sheet and the height of the water column in the pipe. Repeat this process a few more times. Can you see any relation between the amount of the bulge in the rubber sheet and the height of the water column in the pipe?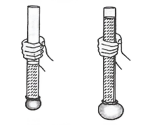 Answer:
Answer: Answer: Yes, the rubber tube bulge out, and the bulging increases with the amount of water in the bottle. Thus, liquid exerts pressure on the walls of the container.
Answer: Yes, the rubber tube bulge out, and the bulging increases with the amount of water in the bottle. Thus, liquid exerts pressure on the walls of the container.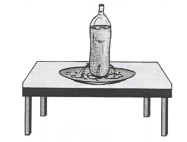 Answer: We observed different streams of a waterfall at the same distance from the bottle. Thus, it indicates that liquids exert equal pressure at the same depth.
Answer: We observed different streams of a waterfall at the same distance from the bottle. Thus, it indicates that liquids exert equal pressure at the same depth.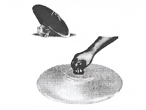 Answer: When we press the sucker, most of the air between its cup and the surface escapes. The sucker sticks to the surface because the pressure of the atmosphere acts on it. To pull the sucker off the surface, the applied force should be large enough to overcome the atmospheric pressure. Thus, this activity gives us an idea about the magnitude of atmospheric
Answer: When we press the sucker, most of the air between its cup and the surface escapes. The sucker sticks to the surface because the pressure of the atmosphere acts on it. To pull the sucker off the surface, the applied force should be large enough to overcome the atmospheric pressure. Thus, this activity gives us an idea about the magnitude of atmospheric Question 2. Make a 50cm x 50cm bed of dry sand about 10cm in thickness. Make sure that its top surface is leveled. Take a wooden or a plastic stool. Cut two strips of graph paper each with a width of 1 cm. Paste them vertically on any leg of the stool—one at the bottom and the other from the top. Now gently put the stool on the sand bed with its legs resting on the sand. Increase the size of the sand bed if required. Now put a load, say a school bag full of books, on the seat of the stool. Mark the level of sand on the graph strip. This would give you the depth, if any, to which the legs of the stool sink in the sand. Next, turn the stool upside down so that now it rests on its seat on the sand bed. Note the depth to which the stool sinks now. Next, put the same load on the stool and note the depth to which it sinks in the sand. Compare the pressure exerted by the stool in the two situations.
Question 2. Make a 50cm x 50cm bed of dry sand about 10cm in thickness. Make sure that its top surface is leveled. Take a wooden or a plastic stool. Cut two strips of graph paper each with a width of 1 cm. Paste them vertically on any leg of the stool—one at the bottom and the other from the top. Now gently put the stool on the sand bed with its legs resting on the sand. Increase the size of the sand bed if required. Now put a load, say a school bag full of books, on the seat of the stool. Mark the level of sand on the graph strip. This would give you the depth, if any, to which the legs of the stool sink in the sand. Next, turn the stool upside down so that now it rests on its seat on the sand bed. Note the depth to which the stool sinks now. Next, put the same load on the stool and note the depth to which it sinks in the sand. Compare the pressure exerted by the stool in the two situations.

 1. The pressure at A> Pressure at B > Pressure at C.
1. The pressure at A> Pressure at B > Pressure at C. Answer: 1. B and C
Answer: 1. B and C Answer: Magnetic force.
Answer: Magnetic force. Answer:
Answer:












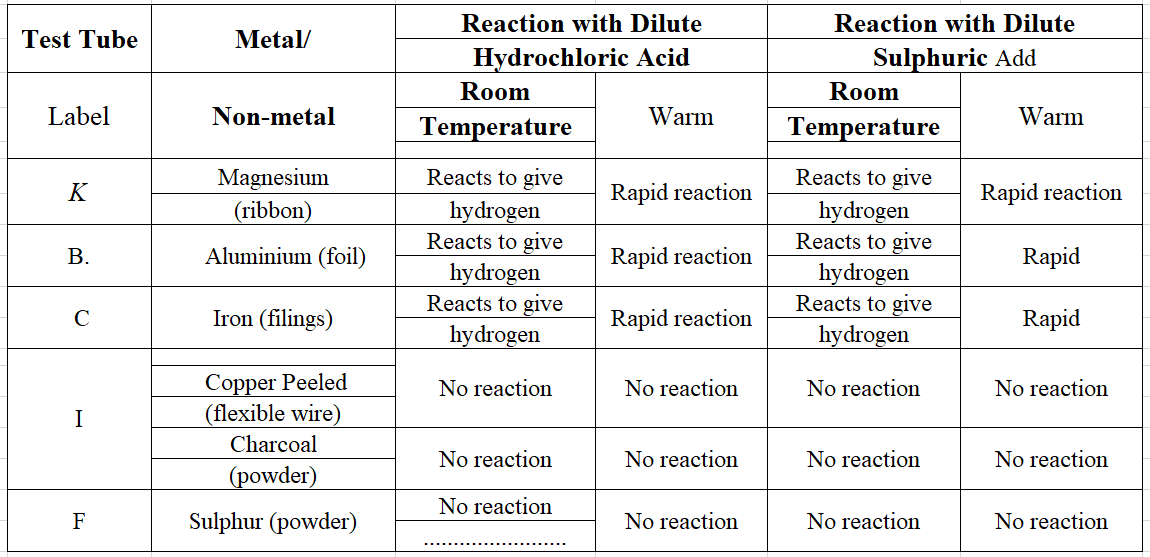
 (But take care that you don’t hurt yourself in the process). Try to hit hard. Hit hard the aluminium wire also. Then repeat the same kind of treatment on the coal piece and pencil lead. Record your observations Malleability of Materials
(But take care that you don’t hurt yourself in the process). Try to hit hard. Hit hard the aluminium wire also. Then repeat the same kind of treatment on the coal piece and pencil lead. Record your observations Malleability of Materials You might have performed the activity with various objects in Class VI. Now, repeat the activity with the materials mentioned Observe and group these materials into good conductors and poor conductors.
You might have performed the activity with various objects in Class VI. Now, repeat the activity with the materials mentioned Observe and group these materials into good conductors and poor conductors. Answer: We observed that the red litmus paper turns blue which shows that the injury of rust is basic. Blue litmus paper does not show any colour change with the solution.
Answer: We observed that the red litmus paper turns blue which shows that the injury of rust is basic. Blue litmus paper does not show any colour change with the solution. As soon as sulphur start burning, introduce the spoon into a gas jar/glass tumbler. Cover the tumbler with a lid to ensure that the gas produced does not escape. Remove the spoon after some time. Add a small quantity of water into the tumbler and quickly of water into the tumbler and quickly replace the lid. Shake the tumbler well. Check the solution with red and blue litmus papers.
As soon as sulphur start burning, introduce the spoon into a gas jar/glass tumbler. Cover the tumbler with a lid to ensure that the gas produced does not escape. Remove the spoon after some time. Add a small quantity of water into the tumbler and quickly of water into the tumbler and quickly replace the lid. Shake the tumbler well. Check the solution with red and blue litmus papers. Answer: We observed that the solution of oxide turns the blue litmus red which shows that the solution is acidic in nature. This also shows that the oxide of non-metals is acidic in nature.
Answer: We observed that the solution of oxide turns the blue litmus red which shows that the solution is acidic in nature. This also shows that the oxide of non-metals is acidic in nature. Answer: On touching the beaker, it felt hot. The solution turns the red litmus paper to blue which shows it is basic in nature. Blue litmus paper does not show any colour change with the solution.
Answer: On touching the beaker, it felt hot. The solution turns the red litmus paper to blue which shows it is basic in nature. Blue litmus paper does not show any colour change with the solution.