KSEEB Solutions For Class 9 Maths Chapter 6 Lines and Angles

KSEEB Solutions For Class 9 Maths Chapter 6 Lines and Angles Points to Remember

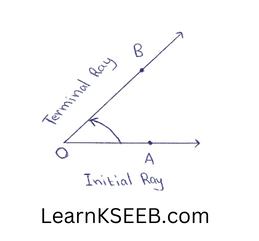
Ray : A line segment AB when extended indefinitely in one direction is called a ray \(\overrightarrow{\mathrm{AB}}\)
If has one endpoint A. A ray has no definite
length

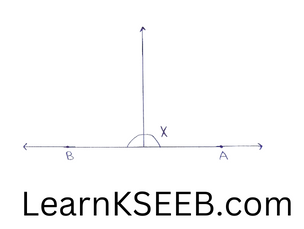
Angle: When an initial ray OA is rotated along its end point O & reach the terminal position ray OB than the measure of rotation is known as Angle.

 

Class 9 Social Science

Class 9 Science

Class 9 Maths

 

Different types of angles
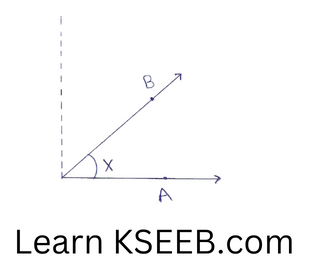
1)cute angle:
An angle whose measure is more than o° but less than 90° is called an actute angle, (0° < x < 90°)

Read and Learn More KSEEB Solutions for Class 9 Maths 

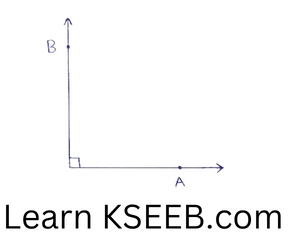
2) Right angle:
An angle whose measure is 90° is called a right angle.

KSEEB Class 9 Maths Chapter 6 Solutions PDF

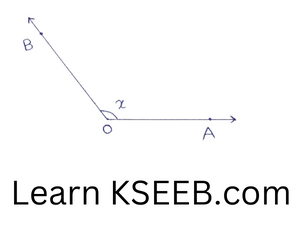
3) obtuse angle : (90° < x< 180°)

An angle whose measure is more than 90° but less than 180° is called an obtuse angle.

 

4) straight angle : x= 180°

An angle whose measure is 180° is called a straight angle.

5) Reflex angle : 180° <x< 360°.
An angle whose measure is more than 180° but less than 360° is called as reflex angle.

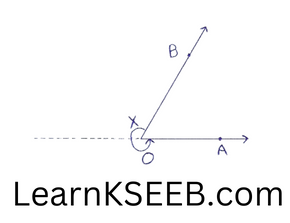
6) Complete angle : x= 360°.
An angle whose measure is 360° is called a complete angle.

Complementary Angles: Two angles whose sum is 90° are called complementary angles.
Eg:- Complement of20° angle is 70° angle.

Supplementary angles:
Two angles whose sum is 180° are called supplementary angles.
Eg: Supplment of 60° angle is 120° angle.

Adjacent angles:
Two angles are called adjacent angles, if
1)They have the same vertex.
2) They have a common arm &
3) On common arms on either side of the common arm

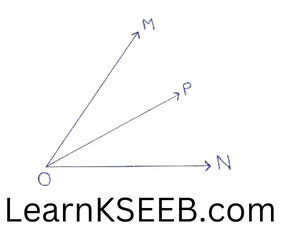
In the figure, \(\lfloor\mathrm{NOP} \&\lfloor\mathrm{MOP}\) are adjecent angles.

Vertically opposite angles:

 

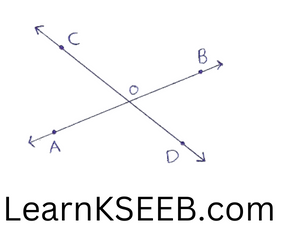
A pair of angle formed by two pair of opposite rays are called vertically opposite angles. In fig, \(\lfloor\mathrm{AOC} \&\lfloor\mathrm{BOD}\) are vertically opposite angles & \(\lfloor\mathrm{AOD} \&\lfloor\mathrm{BOD}\) are also vertically opposite angles.
Vertically opposite angles are always equal.

Karnataka 9th Standard Maths Chapter 6 Notes

Linear pair of Angles

Two adjacent angles are said to form a linear pair of angles, if their non common arms are two opposite rays
(or)
When the sum of two adjacent angles is 180°, then

In figure, |AOC & |BOC form a linear pair of angles.

Transversal line

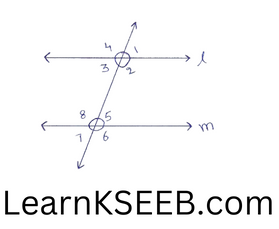
A straight line which intersects two or more given lines at distinct points is called a tranversal of the given lines.

In figure, straight lines l& m are cut by transversal n.

• Exterior Angles:
  \(\lfloor 1,\lfloor 4,\lfloor 6, \&\lfloor 7\)
•  Interior Angles:
  \(\lfloor 2,\lfloor 3,\lfloor 5, \&\lfloor 8\)
• Corresponding angles:
  Two angles on the same side of a tranversal are known as corresponding angles if both lie either above the lines or below the lines.
  In figure, \(\lfloor 1 \&\lfloor 5\), \(\lfloor 2 \&\lfloor 6\),\(\lfloor 3 \&\lfloor 7\), \(\lfloor 4 \&\lfloor 8\), are the pairs of corresponding angles.
•  Alternate Interior angles:
  \(\lfloor 2 \&\lfloor 8\), \(\lfloor 3 \&\lfloor 5\), are the pairs of alternate interior angles.
• Alternate exterior angles:
  \(\lfloor 1 \&\lfloor 7\), \(\lfloor 4 \&\lfloor 6\), are the pairs of alternate exterior angles.
• Consecutive Interior angles:
  The pair of two interior angles on the same side of the transversal are called the pairs of consecutive interior angles.
  In figure, \(\lfloor 2 \&\lfloor 5\), \(\lfloor 3 \&\lfloor 8\), are the pairs of consecutive interior angles.
• If a transversal intersects two parallel lines, then:
  1) each pair of corresponding angles is equal.
  2) each pair of alternate interior angles is equal.
  3) each pair of interior angles on the same side of the transversal is supplementary.
• If a transversal intersects two lines such that, either:
  1) any one pair of corresponding angles is equal, or
  2) any one pair of alternate interior angles is equal,
  or
  3) any one pair of co-interior angles is supplementary, then the lines are parallel.
•  Lines which are parallel to a given line are parallel to each other.
  Angle sum property of a triangle.
  1) The sum of angles of a straight angle is 180°.
  ∴ In ABC
  \(\left\lfloor\mathrm{A}+\left\lfloor\mathrm{B}+\left\lfloor\mathrm{C}=180^{\circ}\right.\right.\right.\)

2) If a side of a triangle is produced, the exterior angle so formed is equal to the sum of the two interior opposite angles. In ΔABC \(\lfloor\mathrm{ACD}=\lfloor\mathrm{A}+\lfloor\mathrm{B}\)

3) Sum of all the exterior angles formed by producing the sides of the polygon is 360°.

Lines and Angles Exercise 6.1

1. In figure, lines AB & CD intersect at O. If \(\left\lfloor\mathrm{AOC}+\left\lfloor\mathrm{BOE}=70^{\circ}\right.\right.\) & \(\lfloor\mathrm{BOE}=40^0{\circ}\) find \(\lfloor\mathrm{BOE}\) & reflex \(\lfloor\mathrm{BOE}\)

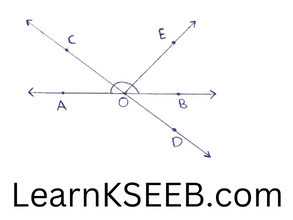
Solution:

Lines AB & CD intersect at O

∴ \(\lfloor\mathrm{AOC}=\lfloor\mathrm{BOD}\)  ( Y vertically opposite angles)

but \(\lfloor\mathrm{BOD}=40^{\circ}\)………. (1)

∴ \(\lfloor\mathrm{AOC}=40^{\circ}\) …………(2)

Given \(\lfloor\mathrm{AOC}\)+ \(\lfloor\mathrm{BOE}\) = 70°

40° + \(\lfloor\mathrm{BOE}\) = 70° (using (2))

=> \(\lfloor\mathrm{BOE}\) = 70°-40°

\(\lfloor\mathrm{BOE}\) =30° (3)

Reflex \(\lfloor\mathrm{COE}\) = \(\lfloor\mathrm{COD}\) + \(\lfloor\mathrm{BOD}\)+ \(\lfloor\mathrm{BOE}\)

= 180° + 40° + 30° (using (1) & (3))

= 250°

∴ \(\lfloor\mathrm{BOE}\) = 30°

reflex  \(\lfloor\mathrm{COE}\) = 250°

KSEEB Class 9 Maths Lines and Angles Solutions

2. In figure, lines XY & MN intersect at o, if \(\left\lfloor\mathrm{POY}=90^{\circ}\right.\) a:b=2:3 find c.

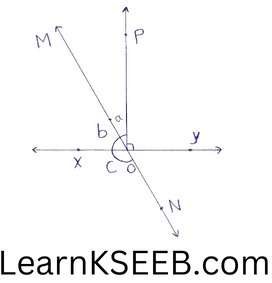
Ray OP stands on fine XY.

Solution:

Ray OP stands on line XY.

∴ \(\left\lfloor\mathrm{POX}+\left\lfloor\mathrm{POY}=180^{\circ}\right.\right.\)

(linear pair Axiom)

\(\Rightarrow\lfloor\mathrm{POX}=180-\lfloor\mathrm{POY}\)

=180-\(90^{\circ}\)

(∴ Given \(\left\lfloor\mathrm{POY}=90^{\circ}\right.\))

=\(90^{\circ}\)

=>\(\left\lfloor\mathrm{POM}+\left\lfloor\mathrm{XOM}=90^{\circ}\right.\right.\)

=> a + b=\(90^{\circ}\)

Given a:b=2:3

ie \(\begin{aligned}
a & =\frac{2}{5} \times 90^{\circ} \\
& =2 \times 18
\end{aligned}\)

∴ a=\(36^{\circ}\)…………(1)

\(\mathrm{b}=\frac{3}{5} \times 90^{\circ}\)

=3 x 18

=\(54^{\circ}\)…………(2)

Ray OX stands on MN

∴ \(\left\lfloor\mathrm{POX}+\left\lfloor\mathrm{POY}=180^{\circ}\right.\right.\)

ie b + c = \(180^{\circ}\)

=> \(54^{\circ}\) + c = \(180^{\circ}\)

(Using (2))

=> c = \(180^{\circ}\) – \(54^{\circ}\)

∴ c= \(126^{\circ}\)

∴ a = \(36^{\circ}\) ,b = \(54^{\circ}\) & c = \(126^{\circ}\)

3. In figure\(\left\lfloor\mathrm{PQR}=\left\lfloor\mathrm{PRQ}\right.\right.\), then prove that \(\left\lfloor\mathrm{PQR}=\left\lfloor\mathrm{PRQ}\right.\right.\)

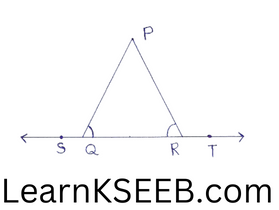
Solution:

Ray QP stands on line ST

\(\left\lfloor\mathrm{PQS}+\left\lfloor\mathrm{PQR}\right.\right.\) = 180° (linear pair)

Ray RP stands on line ST

\(\left\lfloor\mathrm{PRQ}+\left\lfloor\mathrm{PRT}\right.\right.\) = 180° ………..(2) (linear pair)

from (1) & (2) we get

\(\left\lfloor\mathrm{PQS}+\left\lfloor\mathrm{PQR}\right.\right.\) =\(\left\lfloor\mathrm{PRQ}+\left\lfloor\mathrm{PRT}\right.\right.\)

=> \(\left\lfloor\mathrm{PQR}=\left\lfloor\mathrm{PRQ}\right.\right.\)

(∵ Given \(\left\lfloor\mathrm{PQR}=\left\lfloor\mathrm{PRQ}\right.\right.\))

Hence proved.

4. In the figure, if x+y= w+z then prove that AOB is a line.

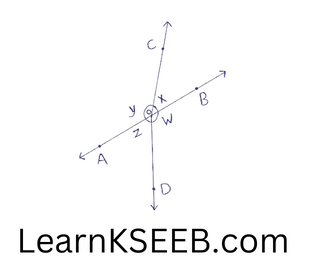
Solution:

Given: x+ y = w+ z………… (1)

The sum of all the angles round a point equal to 360°.

ie  x+y+w+z = 360°

=> x+ y+ x+ y= 360°

=> 2(x+y) = 360°

=>(x + y) = 360°/2

=> x+ y= 180°

∴  AOB is a line.

(If the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line)

KSEEB 9th Standard Maths Chapter 6 Important Questions

5. In the figure, POQ is a line, Ray OR is perpendicular to line PQ, OS is another ray lying between rays OP & OR. Prove that \(\lfloor\mathrm{ROS}\) = \(\frac{1}{2}(\lfloor\mathrm{QOS}-\lfloor\mathrm{POS})\)

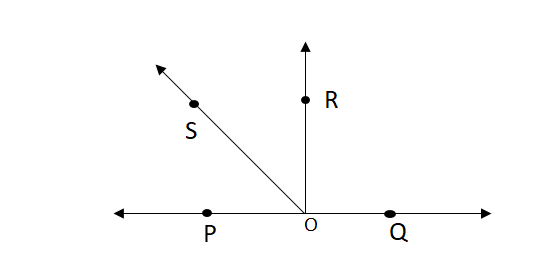
Solution:

Ray OR is perpendicular to line PQ

∴ \(\left\lfloor\mathrm{QOR}=\left\lfloor\mathrm{POR}=90^{\circ}\right.\right.\)…………..(1)

\(\left\lfloor\mathrm{QOR}=\left\lfloor\mathrm{POR}\right.\right.\) + \(\left\lfloor\mathrm{ROS}\right.\)…………..(2)

\(\left\lfloor\mathrm{POS}=\left\lfloor\mathrm{POR}\right.\right.\) – \(\left\lfloor\mathrm{ROS}\right.\)…………(3)

from (1) & (2)

\(\left\lfloor\mathrm{QOS}\right.\) – \(\left\lfloor\mathrm{POS}\right.\) = \(\left\lfloor\mathrm{QOR}\right.\) – \(\left\lfloor\mathrm{POR}\right.\) + \(\left\lfloor\mathrm{ROS}\right.\) – \(\left\lfloor\mathrm{ROS}\right.\)

= (\(\left\lfloor\mathrm{QOR}\right.\) – \(\left\lfloor\mathrm{POR}\right.\)) + 2 \(\left\lfloor\mathrm{ROS}\right.\)

\(\left\lfloor\mathrm{QOS}\right.\) – \(\left\lfloor\mathrm{POS}\right.\) =  2 \(\left\lfloor\mathrm{ROS}\right.\)

=> \(\left\lfloor\mathrm{ROS}\right.\) = 1/2 (\(\left\lfloor\mathrm{QOS}\right.\) – \(\left\lfloor\mathrm{POS}\right.\))

Hence proved.

6. It is given that \(\left\lfloor\mathrm{XYZ}\right.\)) = 64° & xy is produced to point P. Draw a figure from the given information. If ray YQ bisects \(\left\lfloor\mathrm{ZYP}\right.\)), find \(\left\lfloor\mathrm{XYQ}\right.\)) & reflex \(\left\lfloor\mathrm{QYP}\right.\))

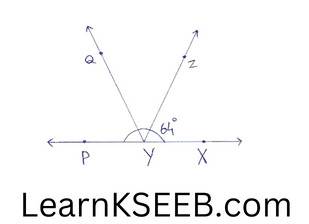
Solution:

Ray YZ stands on line PX

∴ \(\left\lfloor\mathrm{XYZ}+\left\lfloor\mathrm{ZYP}\right.\right.\) = 180° (linear pair)

=> 64 +\(\left\lfloor\mathrm{ZYP}\right.\) = 180° (∵ \(\left\lfloor\mathrm{ZYP}\right.\) = 64°)

=> \(\left\lfloor\mathrm{ZYP}\right.\) = 116°…………. (1)

Ray YQ bisects \(\left\lfloor\mathrm{ZYP}\right.\)

∴ \(\left\lfloor\mathrm{PYQ}\right.\)= \(\left\lfloor\mathrm{ZYQ}\right.\) =1/2 \(\left\lfloor\mathrm{ZYP}\right.\) = 1/2(116°) using (1)

=>  = 58° using (2)

Reflex \(\left\lfloor\mathrm{QYP}\right.\) = 360° – 58° = 302°

(The sum of all the angles round a point is equal to 360°)

again, \(\left\lfloor\mathrm{XYQ}\right.\) = \(\left\lfloor\mathrm{XYZ}\right.\) +\(\left\lfloor\mathrm{ZYQ}\right.\)

= 64° + 58°

=122°

(∵ \(\left\lfloor\mathrm{XYZ}\right.\) = 64° &  \(\left\lfloor\mathrm{ZYQ}\right.\) = 58°)

Hence, \(\left\lfloor\mathrm{XYQ}\right.\) = 122°   & reflex   \(\left\lfloor\mathrm{QYP}\right.\) = 302°

Lines and Angles Exercise 6.2

1. In figure, find the values of x&y then show that AB || CD

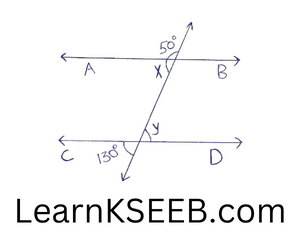
Solution:

Ray AE stands on line GH

∴ \(\left\lfloor\mathrm{AEG}+\left\lfloor\mathrm{AEH}\right.\right.\) = 180° (linear pair)

=> 50° + x =180°

=> x = 180° – 50°

=> x = 130°………………..(1)

=> y = 130°   (vertically opposite angle)

from (1) & (2) we conclude that

But these are alternate interior angles & they are equal

So, we can say that AB || CD

2. I figure, if AB || CD, CD || EF & Y : Z = 3: 7 find x.

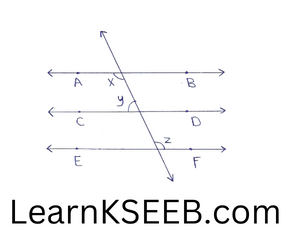
Solution:

AB || CD & CD || EF

∴ AB || EF

(lines parallel to the same line are parallel to each other)

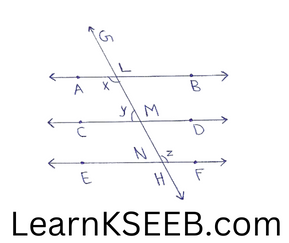
∴ x = z ………………..(1)

(Alternate interior angles)

x + y= 180 ………………..(2)

(consecutive interior angles on the same side of the transversal GH to parallel lines AB & CD) from(l)&(2)

z + y = 180

y: z = 3 : 7

sum of the ratios = 3 + 7=10

∴  y = 3/10xl80 = 54°

z = 7/10 x 180 = 126°

∴ x=z = 126°

3. In figure, if AB||CD, EF ⊥ CD & \(\left\lfloor\mathrm{GED}\right.\) = 126° find \(\left\lfloor\mathrm{AGE}\right.\), \(\left\lfloor\mathrm{GEF}\right.\), \(\left\lfloor\mathrm{FGE}\right.\)

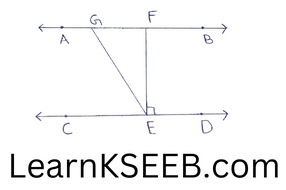
Solution:

1) \(\left\lfloor\mathrm{AGE}\right.\) = \(\left\lfloor\mathrm{GED}\right.\) = 126° (alternate interir angle)

2) \(\left\lfloor\mathrm{AGE}\right.\) = 126°

=> \(\left\lfloor\mathrm{GEF}\right.\) + \(\left\lfloor\mathrm{FED}\right.\) = 126°

=> \(\left\lfloor\mathrm{GEF}\right.\) + 90° = 126° (∵ EF ⊥ CD, \(\left\lfloor\mathrm{FED}\right.\) = 90°)

=> \(\left\lfloor\mathrm{GEF}\right.\) = 126° – 90° = 36°

3) \(\left\lfloor\mathrm{GEC}\right.\) + \(\left\lfloor\mathrm{GEF}\right.\) + \(\left\lfloor\mathrm{FED}\right.\) = 180°

(∵ CD is a line)

=> \(\left\lfloor\mathrm{GEC}\right.\) + 360° + 90°= 180°

=> \(\left\lfloor\mathrm{GEC}\right.\) + 126° = 180°

=> \(\left\lfloor\mathrm{GEC}\right.\) = 180° – 126° = 54°

\(\left\lfloor\mathrm{FGE}\right.\) = \(\left\lfloor\mathrm{GEC}\right.\) = 54° (alternate interior angle)

\(\left\lfloor\mathrm{AGE}\right.\) = 126°, \(\left\lfloor\mathrm{GEF}\right.\) =36°& \(\left\lfloor\mathrm{FGE}\right.\) = 54°

 

Class 9 Maths KSEEB Chapter 6 Lines and Angles Examples 

4. In figure, if PQ||ST, \(\left\lfloor\mathrm{PQR}\right.\) = 110° &
\(\left\lfloor\mathrm{RST}\right.\) = 130° find \(\left\lfloor\mathrm{QRS}\right.\) (Hint: Draw a line par¬allel to ST through point R)

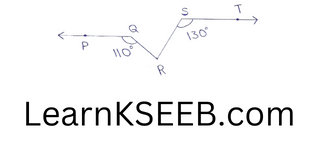
Solution :

Construction: Draw a line RU parallel to ST through point R.

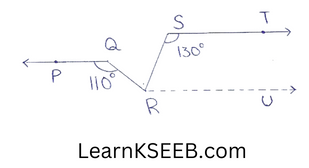
\(\left\lfloor\mathrm{RST}\right.\) + \(\left\lfloor\mathrm{SRU}\right.\) = 180° (sum of the consecutive interior angles on the same side of the transversal is 180°)

=>130°+\(\left\lfloor\mathrm{SRU}\right.\) = 180°

=> \(\left\lfloor\mathrm{SRU}\right.\) = 180°-130° = 50° (1)

=> \(\left\lfloor\mathrm{QRU}\right.\) = \(\left\lfloor\mathrm{PQR}\right.\) =110° (alternate interior angles)

=> \(\left\lfloor\mathrm{QRS}\right.\) + \(\left\lfloor\mathrm{SRU}\right.\) = 110°

=> \(\left\lfloor\mathrm{QRS}\right.\)+ 50° = 110°

=> \(\left\lfloor\mathrm{QRS}\right.\) = 110-50 = 60°

5. In figure, if AB||CD, \(\left\lfloor\mathrm{APQ}\right.\) = 50° & \(\left\lfloor\mathrm{PRD}\right.\) = 127° find x&y.

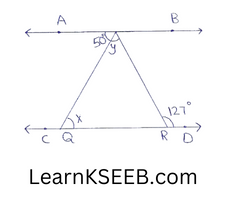
Solution:

x = \(\left\lfloor\mathrm{APQ}\right.\) = 50° (alternate interior angles)

\(\left\lfloor\mathrm{APQ}\right.\) + y= \(\left\lfloor\mathrm{PRD}\right.\) = 127

50° + y = 127°

y = 127°-50°

y = 77°

*=50° & y = 77°

6. In figure, PQ & RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC & strikes the mirror RS at C and again reflects back along CD. Prove that AB II CD.

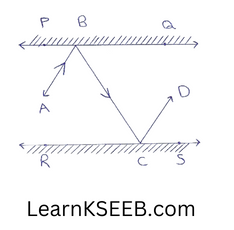(Hint: Draw perpendicular (normals) at B & C to the two plane mirrors. Recall that angle of incidence is equal to angle of reflection)

Solution:

Construction: Draw ray BL ⊥ PQ & ray

CM ⊥ RS

Proof: BL ⊥ PQ, CM ⊥ RS & PQ || RS

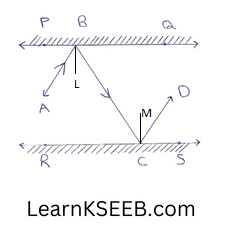
∴ BL || CM

\(\left\lfloor\mathrm{LBC}\right.\) = \(\left\lfloor\mathrm{MCB}\right.\) …………..(1) (alternate interior angles)

\(\left\lfloor\mathrm{ABL}\right.\) = \(\left\lfloor\mathrm{MCD}\right.\) ………..(2)(∵ Angle of incidence = angle of reflection)

\(\left\lfloor\mathrm{MCB}\right.\) = \(\left\lfloor\mathrm{MCD}\right.\) ……….(3) (∵ Angle of incidence = angle of reflection)

from (1), (2) & (3) we get

\(\left\lfloor\mathrm{ABL}\right.\) = \(\left\lfloor\mathrm{MCD}\right.\) ………(4)

adding (1) & (4), we get

\(\left\lfloor\mathrm{LBC}\right.\) +\(\left\lfloor\mathrm{ABL}\right.\) = \(\left\lfloor\mathrm{MCB}\right.\) +\(\left\lfloor\mathrm{MCD}\right.\)

\(\left\lfloor\mathrm{ACB}\right.\) – \(\left\lfloor\mathrm{BCD}\right.\)

But these are alternate interior angles & they are equal.

So, AB || CD

Lines and Angles Exercise 6.3

1. In figure, sides QP & RQ of ΔPQR are produced to points S & T respectively, if \(\left\lfloor\mathrm{SPR}\right.\) = 135 & \(\left\lfloor\mathrm{PQT}\right.\) = 110°, find \(\left\lfloor\mathrm{PRQ}\right.\)

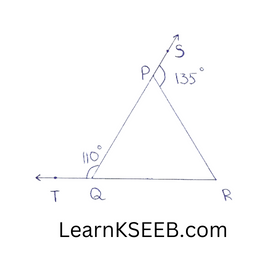
Solution:

TR is a line

\(\left\lfloor\mathrm{PQT}\right.\) + \(\left\lfloor\mathrm{PQR}\right.\) – 180°.

=> 110° + \(\left\lfloor\mathrm{PQR}\right.\) = 180°

=> \(\left\lfloor\mathrm{PQR}\right.\) = 180° -110°= 70° …………..(1)

QS is a line

∴ \(\left\lfloor\mathrm{SPR}\right.\) + \(\left\lfloor\mathrm{QPR}\right.\) = 180°

=> 135 + \(\left\lfloor\mathrm{QPR}\right.\) =180°

=> \(\left\lfloor\mathrm{QPR}\right.\) = 180°-135° = 45°

In APQR,

\(\left\lfloor\mathrm{PQR}\right.\) + \(\left\lfloor\mathrm{QPR}\right.\) + \(\left\lfloor\mathrm{PRQ}\right.\) = 180°

(The sum of all the angles of a triangle is 180°)

=> 70° + 45° + \(\left\lfloor\mathrm{PRQ}\right.\) =180° (using (1) & (2))

=> \(\left\lfloor\mathrm{PRQ}\right.\) = 180°-115°

∴ \(\left\lfloor\mathrm{PRQ}\right.\) = 65°

2. In figure\(\left\lfloor\mathrm{x}\right.\) – 62°, \(\left\lfloor\mathrm{xyz}\right.\) = 54° If YO & ZO are the bisectors of \(\left\lfloor\mathrm{xyz}\right.\) & \(\left\lfloor\mathrm{xzy}\right.\) respectively of Δxyz, find \(\left\lfloor\mathrm{ozy}\right.\) & \(\left\lfloor\mathrm{yoz}\right.\)

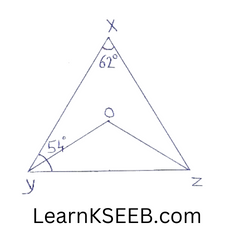
Solution:

In Δxyz

\(\left\lfloor\mathrm{xyz}\right.\) + \(\left\lfloor\mathrm{yzx}\right.\) + \(\left\lfloor\mathrm{zxy}\right.\) = 180°

(The sum of all the angles of a triangle is 180°)

=> 54° + \(\left\lfloor\mathrm{yzx}\right.\)+ 62°= 180°

=> \(\left\lfloor\mathrm{yzx}\right.\) = 180° -116 = 64° ………….(l)

YO is the bisector of \(\left\lfloor\mathrm{xyz}\right.\)

\(\left\lfloor\mathrm{xyo}\right.\) = \(\left\lfloor\mathrm{yoz}\right.\) =1/2 \(\left\lfloor\mathrm{xyz}\right.\)

= 1/2×54 2

= 27° ………………(2)

ZO is the bisector of \(\left\lfloor\mathrm{yzx}\right.\)

\(\left\lfloor\mathrm{xzo}\right.\) = \(\left\lfloor\mathrm{ozy}\right.\) = 1/2 \(\left\lfloor\mathrm{yzx}\right.\)

= -x64 using (1)

= 32° ………………..(3)

In Δoyz

\(\left\lfloor\mathrm{oyz}\right.\) + \(\left\lfloor\mathrm{ozy}\right.\) + \(\left\lfloor\mathrm{yoz}\right.\) = 180°

( ∵ The sum of alll the angles of a A/e is 180°)

=> 27° + 32° + \(\left\lfloor\mathrm{yzx}\right.\) = 180° [ using (2) & (3)]

=> \(\left\lfloor\mathrm{yzx}\right.\) = 180°-59 = 121°

\(\left\lfloor\mathrm{ozy}\right.\) = 32° & \(\left\lfloor\mathrm{yzx}\right.\) = 121°

3. In figure, if AB || DE, \(\left\lfloor\mathrm{BAC}\right.\) = 35° & \(\left\lfloor\mathrm{CDE}\right.\) = 53° find \(\left\lfloor\mathrm{DCE}\right.\).

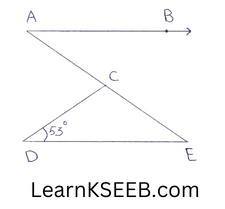
Solution:

Given: \(\left\lfloor\mathrm{CDE}\right.\) = 53° …………….(1)

\(\left\lfloor\mathrm{BAC}\right.\) = \(\left\lfloor\mathrm{DEC}\right.\) = 35° ……………….(2)

(alternate interior angles)

In ΔCDE

\(\left\lfloor\mathrm{CDE}\right.\) + \(\left\lfloor\mathrm{DEC}\right.\) + \(\left\lfloor\mathrm{DCE}\right.\) = 180°

(∵The sum of all the angles of a Δle is 180°)

=> 53° + 35° + \(\left\lfloor\mathrm{DCE}\right.\) = 180°(using 1 &2)

=> \(\left\lfloor\mathrm{DCE}\right.\) = 180°-88°

∴ \(\left\lfloor\mathrm{DCE}\right.\) = 92°

4. In figure, if lines PQ & RS intersect at point T, such that \(\left\lfloor\mathrm{PRT}\right.\) = 40°, \(\left\lfloor\mathrm{RPT}\right.\) = 95° & \(\left\lfloor\mathrm{TSQ}\right.\) = 75°find \(\left\lfloor\mathrm{SQT}\right.\).

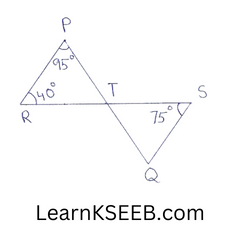
Solution:

In ΔPRT

\(\left\lfloor\mathrm{PTR}\right.\) + \(\left\lfloor\mathrm{PRT}\right.\) + \(\left\lfloor\mathrm{RPT}\right.\) =180°

(The sum of all the angles of a Δle is 180°)

=> \(\left\lfloor\mathrm{PTR}\right.\) + 40° + 95° = 180° (given)

=> \(\left\lfloor\mathrm{PTR}\right.\) = 180° -135°

\(\left\lfloor\mathrm{PTR}\right.\) = 45°

\(\left\lfloor\mathrm{QTS}\right.\) = \(\left\lfloor\mathrm{PTR}\right.\) = 45°

(vertically opposite angles)

In ΔSQT

\(\left\lfloor\mathrm{QTS}\right.\) +\(\left\lfloor\mathrm{TSQ}\right.\) + \(\left\lfloor\mathrm{SQT}\right.\) = 180°

(The sum of all the angles of a Δle is 180°)

=> 45°+75°+ \(\left\lfloor\mathrm{SQT}\right.\) =180°

=> \(\left\lfloor\mathrm{SQT}\right.\) = 180° -120°

∴ \(\left\lfloor\mathrm{SQT}\right.\) = 60°

5. In figure, if PQ ⊥ PS, PQ || SR, \(\left\lfloor\mathrm{SQR}\right.\) = 28⁰ & \(\left\lfloor\mathrm{QRT}\right.\) = 65° then find the values of x & y.

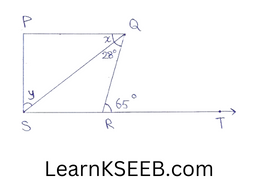
Solution:

\(\left\lfloor\mathrm{QRT}\right.\) = \(\left\lfloor\mathrm{RQS}\right.\) + \(\left\lfloor\mathrm{QSR}\right.\)

(∵ The exterior angle is equal to the sum of the two interior opposite angles)

=> 65° = 28° + \(\left\lfloor\mathrm{QSR}\right.\)

=> \(\left\lfloor\mathrm{QSR}\right.\) – 65° – 28° = 37°

PQ ⊥ SP

\(\left\lfloor\mathrm{QPS}\right.\) = \(\left\lfloor\mathrm{PSR}\right.\) = 90°

\(\left\lfloor\mathrm{PSQ}\right.\) + \(\left\lfloor\mathrm{QSR}\right.\) = \(\left\lfloor\mathrm{PSR}\right.\)

=> y+37° = 90°

=> y= 90-37

=> y= 53°

In ΔPQS

\(\left\lfloor\mathrm{PQR}\right.\) + \(\left\lfloor\mathrm{QSP}\right.\) + \(\left\lfloor\mathrm{QPS}\right.\) = 180°

(The sum of all the angles of a Δle is 180°)

=> x+ y+90° = 180°

=> x+53 + 90 = 180°

=> x= 180°-143°

=> x = 37°

∴  x=31° & y – 53°

6. In figure, the side QR of ΔPQR is produced to a point. If the bisectors of \(\left\lfloor\mathrm{PQR}\right.\) & \(\left\lfloor\mathrm{PRS}\right.\) meet at point T. Then prove that \(\left\lfloor\mathrm{QTR}\right.\)=1/2\(\left\lfloor\mathrm{QPR}\right.\)

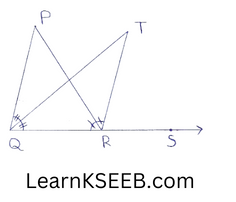
Solution:

\(\left\lfloor\mathrm{TRS}\right.\) is an exterior angle of ΔTQR \(\left\lfloor\mathrm{TRS}\right.\) = \(\left\lfloor\mathrm{TQR}\right.\) +

\(\left\lfloor\mathrm{QTR}\right.\) ……………..(1)

(∵ The exterior angle is equal to sum of its two interior opposite angles)

\(\left\lfloor\mathrm{PRS}\right.\) is an exterior angle of ΔPQR

∴  \(\left\lfloor\mathrm{PRS}\right.\) = \(\left\lfloor\mathrm{PQR}\right.\)+ \(\left\lfloor\mathrm{QPR}\right.\) ……………..(2)

(∴ The exterior angle is equal to sum of its two interior opposite angles)

=> 2\(\left\lfloor\mathrm{TRS}\right.\) = 2\(\left\lfloor\mathrm{TQR}\right.\) + \(\left\lfloor\mathrm{QPR}\right.\)

(∵ QT is the bisector of \(\left\lfloor\mathrm{PQR}\right.\) & RT is the

bisector of \(\left\lfloor\mathrm{PRs}\right.\))

=> 2\(\left\lfloor\mathrm{TRS}\right.\) – 2\(\left\lfloor\mathrm{TQR}\right.\) = \(\left\lfloor\mathrm{QPR}\right.\)

=> 2(\(\left\lfloor\mathrm{TRS}\right.\) – \(\left\lfloor\mathrm{TQR}\right.\) ) – \(\left\lfloor\mathrm{QPR}\right.\) ………………(3)

from(1) \(\left\lfloor\mathrm{TRS}\right.\) –\(\left\lfloor\mathrm{TQR}\right.\) –\(\left\lfloor\mathrm{QTR}\right.\) …………………(4)

from (3) & (4), we get

2\(\left\lfloor\mathrm{QTR}\right.\) = \(\left\lfloor\mathrm{QPR}\right.\)

=> \(\left\lfloor\mathrm{QTR}\right.\) = 1/2\(\left\lfloor\mathrm{QPR}\right.\) Hence proved.

Additional Problems

1. Given \(\left\lfloor\mathrm{POR}\right.\) = 3x &\(\left\lfloor\mathrm{QOR}\right.\) = 2x+10°. If POQ is a straight line, then the value of xis _

1. 34°
2. 35°
3. 30°
4. None of these

Solution: 1) 34°

2. In fig, AOB is a straight line, If
\(\left\lfloor\mathrm{AOC}\right.\) +\(\left\lfloor\mathrm{BOD}\right.\) = 85°, then \(\left\lfloor\mathrm{COD}\right.\) = 

1. 90°
2. 100°
3. 95°
4. 85°

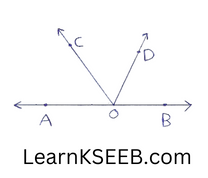
Solution : 3) 95°

3. In fig, if AB || CD, then the value of x is

1. 45°
2. 30°
3. 60°
4. 20°

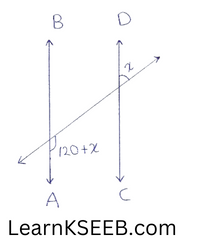
Solution:  2) 30°

4. In fig, AB || CD, then x = 

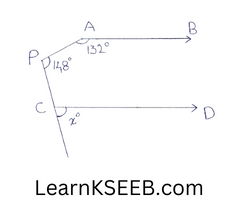
1. 100°
2. 105°
3. 100°
4. 115°
   

Solution: 3) 100°

5. In fig, if line segment AB is parallel to the line segment CD, what is the value of y?

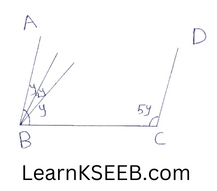
1. 12°
2. 18°
3. 15°
4. 20°

Solution: 4) 20°

6. In the given figure, the measure of \(\left\lfloor\mathrm{ABC}\right.\) is

1. 80°
2. 20°
3. 100°
4. 60°

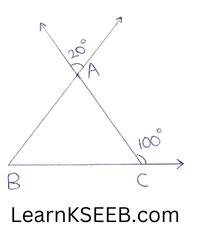
Solution: 1) 80°

7. Two angles measure (30-a)° & (125 + 2a)°. If each one is the supplement of the other, then the value of a is

1. 45°
2. 35°
3. 25°
4. 65°

Solution:  2) 35°

8. In figure if, PQ || RS then the measure of Q m is

1. 110°
2. 100°
3. 90°
4. 133°

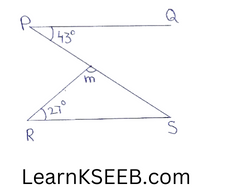
Solution: 1) 110°

9. In figure, the value of angle q is 

1. 60°
2. 90°
3. 50°
4. 40°

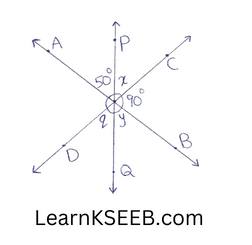
Solution: 4) 40°

10. Find the angle which is equal to if supplementary angle.

1. 30°
2. 60°
3. 45°
4. 90°

Solution: 4) 90°

One Mark Questions

1. Write the angle which is one fifth of its complement.
Solution:

Let the angle be x, then.

by given condition, x = 1/5(90° – x)

=> 6x = 90°

=> x = 15°

2. In the given figure, what is the value x.

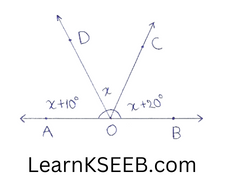
Solution:

Here, x+10° + *x+ 20° = 180°

=> 3x=180°-30°

=> 3x = 150 .

=> *=150/3

=> x=50°

Karnataka Board Class 9 Maths Chapter 6 MCQs

3. In the given figure, AB || CD & ‘l’is transversal, then calculate the value of ‘x’.

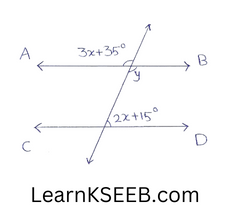
Solution:

y = 3x+ 3 5° (vertically opposite angle)

y+ 2x+15° = 180° (corresponding interior angle)

3x+35 + 2x+15 = 180°

5x+50 = 180

5x = 180-50

x=130/5

x= 26

4. In fig, PQ || RS, \(\left\lfloor\mathrm{QPR}\right.\) = 70°, \(\left\lfloor\mathrm{ROT}\right.\) = 20°, find the value of x.

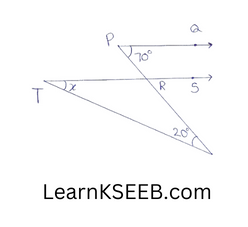
Solution:

70° + \(\left\lfloor\mathrm{PRS}\right.\) = 180°

\(\left\lfloor\mathrm{PRS}\right.\) = 110° = \(\left\lfloor\mathrm{TRO}\right.\) (vertically opposite angles)

In ΔTRO

x+110°+20° = 180°

x=50°

5. In the given figure, PQ || RS & EF || QS. If \(\left\lfloor\mathrm{PQS}\right.\) = 60° then what will be the measure of \(\left\lfloor\mathrm{RFE}\right.\)?

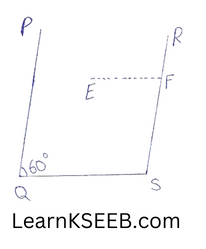
Solution:

\(\left\lfloor\mathrm{PQS}\right.\) + \(\left\lfloor\mathrm{QSF}\right.\) =180° (angles on the same side of transversal)

\(\left\lfloor\mathrm{PQS}\right.\) + \(\left\lfloor\mathrm{RFE}\right.\) = 180° as \(\left\lfloor\mathrm{QSF}\right.\)–\(\left\lfloor\mathrm{EFR}\right.\)

=>60° +\(\left\lfloor\mathrm{RFE}\right.\) -180°

=>\(\left\lfloor\mathrm{RFE}\right.\) = 180°-60°

=> \(\left\lfloor\mathrm{RFE}\right.\) = 120°

6. In the figure below, if \(\lfloor A+\lfloor B+\lfloor C+\lfloor D+\lfloor E+\lfloor F=K\) right angles, then what is the g value of k?

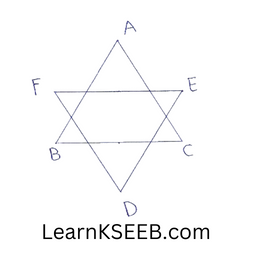
Solution:

In AABC

\(\lfloor A+\lfloor B+\lfloor C\) =180°

Also, in ΔDEF,

\(\lfloor D+\lfloor E+\lfloor F\) = 180°

∴ \(\lfloor A+\lfloor B+\lfloor C+\lfloor D+\lfloor E+\lfloor F\) = 360°

= 4×90°

Hence k = 4

7. In the fig, below in AABC? AB = AC? then calculate the value of x. 

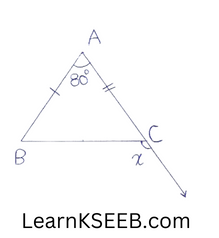
Solution:

AB = AC

\(\left\lfloor\mathrm{ACB}\right.\) = \(\lfloor B\)

In Δ ABC,

80° + \(\left\lfloor\mathrm{ACB}\right.\) = \(lfloor B\) = 180°

2\(\left\lfloor\mathrm{ACB}\right.\) = 180°-80°

2\(\left\lfloor\mathrm{ACB}\right.\) = 100°

\(\left\lfloor\mathrm{ACB}\right.\) = 50°

again,

\(\left\lfloor\mathrm{ACB}\right.\)+ x= 180°

50+x=180°

x = 180-50

x = 130°

8. In ΔABC, \(\lfloor A\) = \(\lfloor B\)/2 = \(\lfloor C\)/6, then what will be the measure of \(\lfloor A\)?

Solution:

In AABC

\(\lfloor A\)+ \(\lfloor B\) + \(\lfloor C\) = 180°

\(\lfloor A\) + 2\(\lfloor A\) + 6\(\lfloor A\) = 180°

9\(\lfloor A\) = 180°

\(\lfloor A\) = 20°

Two Mark Questions

1. Ray OE bisects \(\left\lfloor\mathrm{AOB}\right.\) & OF is the ray opposite to OE. Show that \(\left\lfloor\mathrm{FOB}\right.\) = \(\left\lfloor\mathrm{FOA}\right.\)

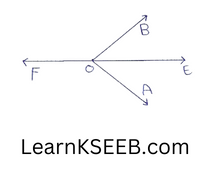
Solution:

\(\left\lfloor\mathrm{FOB}\right.\) + \(\left\lfloor\mathrm{BOE}\right.\) = 180° ………..(1)(linear pair)

\(\left\lfloor\mathrm{FOA}\right.\)+\(\left\lfloor\mathrm{AOE}\right.\) = 180° …………(2) (linear pair)

from(l) & (2)

\(\left\lfloor\mathrm{FOB}\right.\) + \(\left\lfloor\mathrm{BOE}\right.\) – \(\left\lfloor\mathrm{FOA}\right.\) + \(\left\lfloor\mathrm{AOE}\right.\) ……………(3)

but \(\left\lfloor\mathrm{BOE}\right.\) = \(\left\lfloor\mathrm{AOE}\right.\) (∵ Ray OE bisects \(\left\lfloor\mathrm{AOB}\right.\))

=> \(\left\lfloor\mathrm{FOB}\right.\) = \(\left\lfloor\mathrm{FOA}\right.\)

2. In figure, EF is a transversal to two parallel lines AB & CD, GM & HL are the bisectors of the corresponding angles EGB & EHD. Prove that GM || HL (Hint: first prove that \(\left\lfloor\mathrm{EGM}\right.\) = \(\left\lfloor\mathrm{GHL}\right.\) )

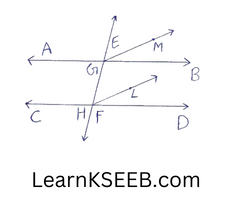
Solution:

AB || CD

& a transversal EF intersects then

\(\left\lfloor\mathrm{EGM}\right.\) = \(\left\lfloor\mathrm{GHD}\right.\) (corresponding angles)

=> 2\(\left\lfloor\mathrm{EGM}\right.\) = 2\(\left\lfloor\mathrm{GHL}\right.\) (∵ GM&HL are the bisectors of \(\left\lfloor\mathrm{EGB}\right.\) &

\(\left\lfloor\mathrm{EHD}\right.\) respectively

=> \(\left\lfloor\mathrm{EGM}\right.\) = \(\left\lfloor\mathrm{GHL}\right.\)

But these angles form a pair of equal corresponding angles for lines GM & HL & transversal EF.

∴ GM || HL

3. In the figure below, l1.11l2,& a1.11a2 find the value of x.

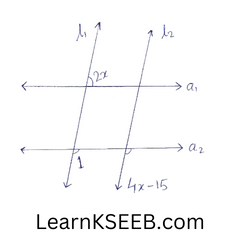
Solution:

\(\lfloor 1\)= 4x-15

(corresponding angles)

4x-15 + 2x=180° (linear pair)

6x= 195

195

x =195/6

x= 32.5

4. Prove that if one angle of a triangle equal to the sum of the other two angles, the triangle right angled.

Solution:

Let in ΔABC

\(\lfloor A\) = \(\lfloor B\) + \(\lfloor C\) …………………(1)

We know that \(\lfloor A\)+\(\lfloor B\)+\(\lfloor C\) = 180°

(v The sura ofthe three angles of a Δle is 180°)

=> \(\lfloor A\)+\(\lfloor A\) = 180° (from(l))

=> 2\(\lfloor A\) = 180°

=> \(\lfloor A\) = 180/2

=> \(\lfloor A\) = 90°

Hence triangle ABC is right angled triangled.

5. In the figure, a is greater than b, by 1/6of a straight angle. Find the values of a & b.

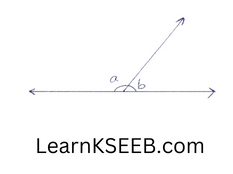
Solution:

Given, a-b = 1/6x 180°

=> a-b = 30°……………(1)

a+b = 180° (linear pair) ……………(2)

adding (l)&(2)we get

2a = 210

a = 105°

=> b = 180- a

= 180- 105°

=> b = 75°

∴ a= 105 & b=75°

6. Find the supplement of 4/3 of a right angle

Solution:

4/3 of a right angle = 4/3 x90° = 120°

(sum of supplementary angles is 180°)

supplement of 120° =180°- 120° = 60°

7. In figure if AB || CD || EF & x : y= 3:2. find z

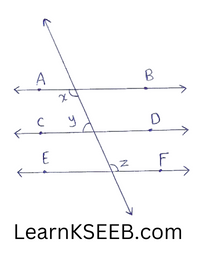
Solution:

Let x=3k,

y = 2k

Then x+ y = 3k + 2k = 180°

(Angles on the same side of transversal)

=> 5 k = 180°

=> k = 36°

∴ x= 3k = 3×36 = 108°

y= 2k = 2×36 = 72°

Thus \(\lfloor z\) = \(\lfloor x\) = 108° (alternate interior angles)

8. In figure, if AB || CD,
\(\left\lfloor\mathrm{APQ}\right.\) = 40° & \(\left\lfloor\mathrm{PRD}\right.\) =118° find x&y.

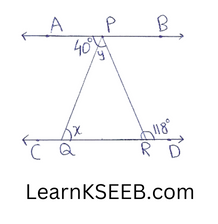
Solution:

x = \(\left\lfloor\mathrm{APQ}\right.\) = 40° (alternate angles)

(x + y)= 118° (Exterior angle is the sum of the two opposite interior angles)

9. Find the value of x in the given figure, where \(\lfloor A\)= 60° & \(\left\lfloor\mathrm{BED}\right.\) = 120°

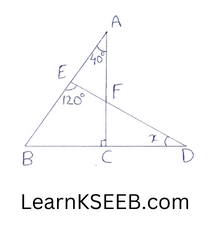
Solution:

In ΔACB,

\(\lfloor B\) = 180° – 90 – 40

=50

In ΔBED,

x= 180-120-50°

=> x=10°

10. Prove that if in a triangle, its sides are produced in order then the sum of the exterior angle so formed is 360°.

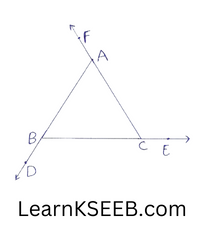
Solution:

To prove: \(\left\lfloor\mathrm{BAF}\right.\) + \(\left\lfloor\mathrm{ACE}\right.\) + \(\left\lfloor\mathrm{CBD}\right.\) = 360°

consider, \(\left\lfloor\mathrm{BAF}\right.\) = 180°-\(\left\lfloor\mathrm{BAC}\right.\) ……………..(1)

\(\left\lfloor\mathrm{ACE}\right.\) -180° –\(\left\lfloor\mathrm{ACB}\right.\) ……………(2)

\(\left\lfloor\mathrm{CBD}\right.\) = 180°-\(\left\lfloor\mathrm{ABC}\right.\) ……………(3)

adding (1), (2) & (3) we get

\(\left\lfloor\mathrm{BAF}\right.\) +\(\left\lfloor\mathrm{ACE}\right.\) + \(\left\lfloor\mathrm{CBD}\right.\) = 540°
-(\(\left\lfloor\mathrm{BAC}\right.\) +\(\left\lfloor\mathrm{ACB}\right.\) + \(\left\lfloor\mathrm{ABC}\right.\) )

= 540- 180°

(∵ sum of angles of A/e is 180°) = 360°

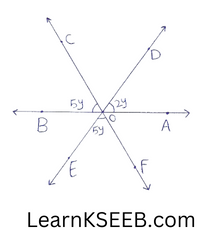
11. In given figure below, determine the value of y.

Solution:

Since \(\left\lfloor\mathrm{COD}\right.\) & \(\left\lfloor\mathrm{EOF}\right.\) are vertically opposite angles.

∴ \(\left\lfloor\mathrm{COD}\right.\) = \(\left\lfloor\mathrm{EOF}\right.\)

=> \(\left\lfloor\mathrm{COD}\right.\) = 5 y

(∵ \(\left\lfloor\mathrm{EOF}\right.\) = 5y)

Now OA & OB are opposite ray.

∴ \(\left\lfloor\mathrm{AOD}\right.\) + \(\left\lfloor\mathrm{DOC}\right.\) + \(\left\lfloor\mathrm{COB}\right.\) = 180°

=> 2y+5y+5y=180°

=> 12y = 180°

=> y=180/12=15

Hence y =15

Class 9 Maths Lines and Angles KSEEB Guide

12. In figure given below, AB || CD, determine x.

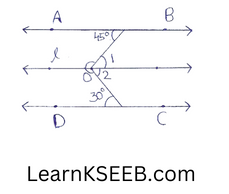
Solution:

Through O, draw a line l parallel to both AB & CD, then.

\(\lfloor 1\) = 45° (alternate angle)

& \(\lfloor 2\) = 30°  (alternate angle)

∴ \(\left\lfloor\mathrm{BOC}\right.\) = \(\lfloor 1\) + \(\lfloor 2\)

=>\(\left\lfloor\mathrm{AOD}\right.\) = 45° +30° = 75°

So   x= 360° – \(\left\lfloor\mathrm{BOC}\right.\)

=360°-75°

=285°

Hence x= 285°

Three Mark Questions

1. Prove that if two lines intersect each other, then the bisectors of vertically opposite angles are in the same line.

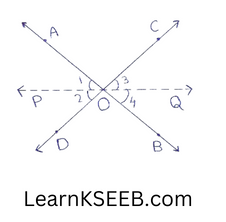
Solution:

OP &OQ are bisectors of \(\left\lfloor\mathrm{AOD}\right.\) = \(\left\lfloor\mathrm{BOC}\right.\)

\(\lfloor 1\) = \(\lfloor 2\) & \(\lfloor 3\)=\(\lfloor 4\)

\(\left\lfloor\mathrm{AOC}\right.\) = \(\left\lfloor\mathrm{BOD}\right.\)(vertically opposite angles)

∴ \(\lfloor 1\)+\(\left\lfloor\mathrm{AOC}\right.\) + \(\lfloor 3\) = \(\lfloor 2\)+\(\left\lfloor\mathrm{BOD}\right.\)+\(\lfloor 4\)

but \(\lfloor 1\) +\(\left\lfloor\mathrm{AOC}\right.\) +\(\lfloor 3\) +\(\lfloor 2\) + \(\left\lfloor\mathrm{BOD}\right.\) +\(\lfloor 4\) = 360°

∴ \(\lfloor 1\) +\(\left\lfloor\mathrm{AOC}\right.\)+ \(\lfloor 3\) = \(\lfloor 2\) + \(\left\lfloor\mathrm{BOD}\right.\) +\(\lfloor 4\)= 180°

OP & OQ are in the same line.

2. In the given figure, two straight lines PQ & RS intersect each other at O. If \(\left\lfloor\mathrm{POT}\right.\) = 75°, find the values of a, b, c.

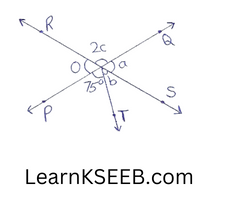
Solution:

4b + 75° + b = 180°    (linear pair)

=> 5b = 180-75°

=> 5b = 105/5

=> b = 21°

4b = 4 x 21 = 84°

∴ a = 4b (vertically opposite angles)

∴ a = 84°

2c+a = 180°

2c = 180 -a

=> 2c = 180-84

=> 2c = 96°

2C==96/2= 48°

∴ a = 84°, b = 21° & c = 48°

3. If two parallel lines are intersected by a transversal prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.

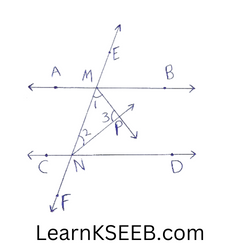
Solution:

\(\left\lfloor\mathrm{BMN}\right.\) + \(\left\lfloor\mathrm{BMN}\right.\) = 180°    (Interior angles)

=>\(\left\lfloor\mathrm{BMN/2}\right.\) + \(\left\lfloor\mathrm{DNM/2}\right.\) = 180°/2

\(\lfloor 1\) + \(\lfloor 2\) = 90° ……………..(1)

\(\lfloor 1\)+\(\lfloor 2\) + \(\lfloor 3\) = 180° (angle sum property of Δle)

90°+\(\lfloor 3\) = 180°

∴ \(\lfloor 3\) = 180-90 = 90°

∴ PM & PN intersect at right angle.

4. In the given figure l || m || n. From the figure find the ratio of (x + y): (y- x)

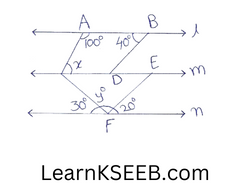
Solution:

y= 180 -(30 + 20)

= 180-50

= 130°

l || m

x+100°=100°

x=180-100

x=80°

x+y=130 + 80

= 210

x- y= 130-80

= 50°

∴ (x+ y): (x- y) = 210:50

=21:5

5. In the given figure, QT ⊥ PR, \(\left\lfloor\mathrm{TQR}\right.\) = 40° &\(\left\lfloor\mathrm{SPR}\right.\) =30° find x & y

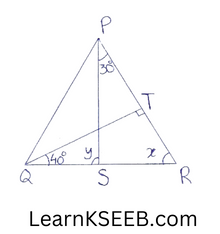
Solution:

In ΔQTR

\(\left\lfloor\mathrm{TQR}\right.\) + \(\left\lfloor\mathrm{QTR}\right.\)+ \(\left\lfloor\mathrm{QTR}\right.\) = 180°

(angle sum property of Δle)

40° +90° + \(\left\lfloor\mathrm{TRQ}\right.\) = 180°

=> \(\left\lfloor\mathrm{TRQ}\right.\) = 180°-130°

=> x=50°

y = \(\left\lfloor\mathrm{SPR}\right.\) + x (By exterior property of Δle)

= 30°+50°

y = 80°

∴ x=50° & y=80°

6. In AABC, AD & CE A are the bisectors of\(\lfloor A\) & \(\lfloor C\) respectively. If E\(\left\lfloor\mathrm{ABC}\right.\) = 90° then find \(\left\lfloor\mathrm{AOC}\right.\).

Solution:

In ΔABC

\(\lfloor A\)+ \(\lfloor B\) + \(\lfloor C\) = 180°

=> \(\lfloor A\) + \(\lfloor C\)= 180 – 90° (∵ \(\lfloor B\) = 90°)

=>\(\lfloor A\) + \(\lfloor C\) = 90°

1/2(\(\lfloor A\) + \(\lfloor C\)) = 45° …………..(1)

In ΔAOC

1/2\(\lfloor A\) + 1/2\(\lfloor C\)+ \(\left\lfloor\mathrm{AOC}\right.\) = 180°

1/2(\(\lfloor A\) + \(\lfloor C\)) + \(\left\lfloor\mathrm{AOC}\right.\) = 180°

45°+\(\left\lfloor\mathrm{AOC}\right.\) = 180°(from (1))

=> \(\left\lfloor\mathrm{AOC}\right.\) = 180°-45°

∴ \(\left\lfloor\mathrm{AOC}\right.\) = 135°

7. Prove that the sum of angles of a triangle is 180°

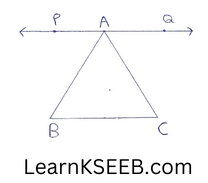
Solution:

Through vertex A,draw PAQ || BC

∴ \(\left\lfloor\mathrm{PAB}\right.\) = \(\left\lfloor\mathrm{ABC}\right.\) ……………..(1)      (alternate angles)

\(\left\lfloor\mathrm{QAC}\right.\) = \(\left\lfloor\mathrm{ACB}\right.\) …………….(2 (altrenate angles)

adding (1) & (2) we get

\(\left\lfloor\mathrm{PAB}\right.\) + \(\left\lfloor\mathrm{QAC}\right.\) = \(\left\lfloor\mathrm{ABC}\right.\) + \(\left\lfloor\mathrm{ACB}\right.\)

adding \(\left\lfloor\mathrm{BAC}\right.\) to both sides we get

\(\left\lfloor\mathrm{PAB}\right.\) + \(\left\lfloor\mathrm{QAC}\right.\) + \(\left\lfloor\mathrm{BAC}\right.\) = \(\left\lfloor\mathrm{ABC}\right.\)

+ \(\left\lfloor\mathrm{ACB}\right.\) + \(\left\lfloor\mathrm{BAC}\right.\)

=> 180° = \(\left\lfloor\mathrm{ABC}\right.\) + \(\left\lfloor\mathrm{ACB}\right.\) + \(\left\lfloor\mathrm{ABC}\right.\)

=> \(\left\lfloor\mathrm{ABC}\right.\) + \(\left\lfloor\mathrm{ACB}\right.\) + \(\left\lfloor\mathrm{BAC}\right.\) = 180°

Hence it is proved that the sum of angles of a triangle is 180°.

KSEEB Class 9 Maths Chapter 6 Exercise Solutions

8. In the given figure, AP & DP are bisectors of \(\lfloor A\) & \(\lfloor D\) prove that 2\(\left\lfloor\mathrm{APD}\right.\) = \(\lfloor B\) + \(\lfloor C\)

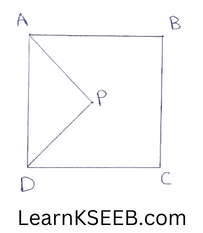
Solution:

In ΔAPD,

\(\left\lfloor\mathrm{APD}\right.\) + \(\left\lfloor\mathrm{DAP}\right.\) + \(\left\lfloor\mathrm{ADP}\right.\) = 180° (Angle sum property)

\(\left\lfloor\mathrm{APD}\right.\)+\(\lfloor A\)/2 + \(\lfloor D\)/2 = 180°

Given \(\left\lfloor\mathrm{DAP}\right.\) = 1/2\(\lfloor A\)&\(\left\lfloor\mathrm{ADP}\right.\) = 1/2\(\lfloor D\).

multiply eqn (1) by 2 we get

=> 2\(\left\lfloor\mathrm{APD}\right.\) + \(\lfloor A\) + \(\lfloor D\) = 360°

2\(\left\lfloor\mathrm{APD}\right.\) = 360°- (\(\lfloor A\)+ \(\lfloor D\)) …………………(2)

By angle sum property

\(\lfloor B\) + \(\lfloor C\) = 360°-\(\lfloor A\)+ \(\lfloor D\) ………………….(3)

on comparing (2) & (3) we get

2\(\left\lfloor\mathrm{APD}\right.\) = \(\lfloor B\) + \(\lfloor C\) Hence proved.

Four Mark Questions

1. In the given figure, AB || DC, \(\left\lfloor\mathrm{ABDC}\right.\)= 35° & \(\left\lfloor\mathrm{BAD}\right.\) = 80° find x,y,z

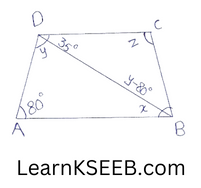
Solution: AB II DC

\(\left\lfloor\mathrm{CDB}\right.\) = \(\left\lfloor\mathrm{ABD}\right.\)=35°= x  (alternateangle)

x+ y+ 80 = 180° (angle sum property)

35° + 80 + y= 180°

=> y= 180-115

=> \(\left\lfloor\mathrm{ADB}\right.\) = 65° = y

\(\left\lfloor\mathrm{DCB}\right.\) = Z = 180-(35 + 35)

= 180-70

= 110°

∴ x=35°,y=65° & z = 110°

2. In the above figure ABCD is a quadrilateral in which \(\left\lfloor\mathrm{ABC}\right.\) = 73°, \(\lfloor C\) =97° & \(\lfloor D\) = 110° , if AE || DC & BE || AD & AE intersects BC at F, find the measure of \(\left\lfloor\mathrm{EBF}\right.\). 

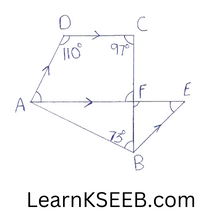
Solution:

Since AE || DC

\(\lfloor D\) + \(\lfloor 1\) =180°

(angle on the same side of transversal)

\(\lfloor 1\) = 180° –\(\lfloor D\) = 180-110°

=>\(\lfloor 1\) = 70°

\(\lfloor 4\) = \(\lfloor 1\) = 70° (alternate angles)

97° + \(\lfloor 2\) = 180°

(angle on the same side of transversal)

\(\lfloor 2\)= 180-97°

= 83°

\(\lfloor 2\) = \(\lfloor 3\) = 83° (vertically opp. angles)

In ΔBEF

\(\lfloor 3\) +\(\lfloor 4\) +\(\left\lfloor\mathrm{EBF}\right.\) = 180°

83° + 70° +\(\left\lfloor\mathrm{EBF}\right.\) = 180°

\(\left\lfloor\mathrm{EBF}\right.\) = 180°-153°

∴ \(\left\lfloor\mathrm{EBF}\right.\) = 27°

3. The sides AB & AC & ΔABC are produced to points P &Q respectively. If bisectors BO &
CO of \(\left\lfloor\mathrm{CBP}\right.\) & \(\left\lfloor\mathrm{BCQ}\right.\) respectively meet at point O, then prove that \(\left\lfloor\mathrm{BOC}\right.\) = 90°-1/2x

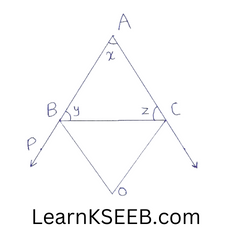
Solution:

\(\left\lfloor\mathrm{PBC}\right.\) = x + z

2\(\left\lfloor\mathrm{OBC}\right.\) = x + z …………….(1)

\(\left\lfloor\mathrm{QCB}\right.\) = x + y

2\(\left\lfloor\mathrm{OCB}\right.\) = x + y ………………(2)

In ABOC

\(\left\lfloor\mathrm{BOC}\right.\) + \(\left\lfloor\mathrm{OCB}\right.\) + \(\left\lfloor\mathrm{OBC}\right.\) =

(angle sum property) multiply by 2 we get

2\(\left\lfloor\mathrm{BOC}\right.\) + 2\(\left\lfloor\mathrm{OCB}\right.\) + 2\(\left\lfloor\mathrm{OBC}\right.\) = 360°

2\(\left\lfloor\mathrm{BOC}\right.\) + x+ y+x+z= 360°

2\(\left\lfloor\mathrm{BOC}\right.\) + x+ y+ z+ x=360°

2\(\left\lfloor\mathrm{BOC}\right.\) +180° + x = 360°

2\(\left\lfloor\mathrm{BOC}\right.\) + x = 360° – 180°

2\(\left\lfloor\mathrm{BOC}\right.\) = 180° – x

\(\left\lfloor\mathrm{BOC}\right.\) = (180° – x)/2

=> \(\left\lfloor\mathrm{BOC}\right.\) = 90° – 1/2 x

Hence proved.

4. Students in a school are preparing flags as shown below for a rally to make people aware of saving water. In the diagram below ΔABC is shown with AC extended through point D.

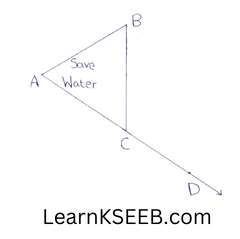
1) If \(\left\lfloor\mathrm{BCD}\right.\) = 6x+2, \(\left\lfloor\mathrm{BAC}\right.\) = 3x+15, & \(\left\lfloor\mathrm{ABC}\right.\) = 2x-1 What is the value of x ?
2) What value are they exhibiting by doing so?
3) State the property used to solve this problem?

Solution:

In ΔABC

\(\left\lfloor\mathrm{BCD}\right.\) = \(\left\lfloor\mathrm{BAC}\right.\) + \(\left\lfloor\mathrm{ABC}\right.\)

(exterior angle equal to the sum of opposite two interior angles).

6x+2 = 3x+15 + 2x-1

6x+2 = 5x+14

6x-5x= 14-2

∴  x= 12

2) By doing so, students exhibit the importance of water.

3) Exterior angle property of a triangle is used in the above problem.