KSEEB Solutions For Class 9 Maths Chapter 4 Linear Equations in Two Variables

KSEEB Solutions For Class 9 Maths Chapter 4 Linear Equations in Two Variables

Linear Equations in Two Variables Points to Remember

• The standard form of a linear equation in two variables x & y is ax+ by+c = 0, where a, b & c are real numbers & a ≠ 0, b ≠ 0

Solution of a linear equation

• Infinitely many solutions of a linear equation in two variables can be obtained.
• To find a solution of a linear equation in two variables easily, we put X- 0 in the equation & find the corresponding value of y, we can also put y = 0, & find the corresponding value of x
• Every point on the graph of a linear equation in two variables represents a solution of the linear equation. Also, every solution of the linear equation represents a point on the graph of the linear equation.

Class 9 Social Science

Class 9 Science

Class 9 Maths

 

Graph of a linear equation in 2 variables

• We find two convenient solutions of a linear equa¬tion in two variables & plot them on a graph paper. Then we join these points by a ruler to get the line which represents the graph of the given linear equation in two variables.
  Equations of lines parallel to the x- axis & y- axis.
•  x= a represents a straight line parallel to y – axis at a distance of | a | units from 0 to be right or left of 0 according as a is +ve or -ve. Similarly y= a represents a straight line parallel to x – axis at a distance of | a | units from 0 above or below 0. According as a is +ve or -ve.
•  The equation of the form y= mx represents a line passing through the origin.

Read and Learn More KSEEB Solutions for Class 9 Maths 

Linear Equations in Two Variables Exercise 4.1

1.  The cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement.

Solution: Let the cost of a notebook be  x & the cost of a pen by  y

Then, according to the given condition of the question,

x=2y

=> x-2y=0

This is the required linear equation in two variables x&y.

2. Express the following linear equations in the form ax+ by+c= 0 & indicate the values of a, b & c in each case.
1) 2x+3y = 9.35
2)\(2 x+3 y=9.3 \overline{5}\)
3) -2x+3y=6
4) x=3y
5)2x = -5y
6) 3x+ 2 = 0
7) y- 2 = 0
8) 5 = 2x

KSEEB Class 9 Maths Chapter 4 Solutions PDF

Solution: 1) \(2 x+3 y=9.3 \overline{5}\)
\(\begin{gathered}
\Rightarrow \quad 2 x+3 y-9.3 \overline{5}=0 \\
a=2, \quad b=3, \quad c=9.3 \overline{5}
\end{gathered}\)

2) \(x-\frac{y}{5}-10=0\)
\(a=1 \quad b=\frac{-1}{5} \quad c=-10\)

3) \(-2 x+3 y=6\)
\(\begin{aligned}
& \Rightarrow \quad-2 x+3 y-6=0 \\
& a=-2 \quad b=3 \quad c=-6
\end{aligned}\)

4) \(x=3 \mathrm{y}\)
\(\begin{aligned}
& \Rightarrow \quad x-3 y=0 \\
& a=1 \quad b=-3 \quad \mathrm{c}=0
\end{aligned}\)

5) \(2 x=-5 y\)
\(\Rightarrow \quad 2 x+5 y=0\)
\(a=2 \quad b=5 \quad c=0\)

6) \(3 x+2=0\)
\(\begin{aligned}
& \Rightarrow \quad 3 x+o y+2=0 \\
& a=3 \quad b=0 \quad c=2 \\
&
\end{aligned}\)

7) \(y-2=0\)
\(\begin{aligned}
& \Rightarrow \quad 0 x+y-2=0 \\
& \begin{array}{lll}
a=0 & b=1 & c=-2
\end{array} \\
&
\end{aligned}\)

8) \(5=2 x\)
\(\begin{aligned}
& \Rightarrow \quad-2 x+o y+5=0 \\
& a=-2 \quad b=0 \quad c=5
\end{aligned}\)

Linear Equations in Two Variables Exercise 4.2

1. Which one of the following options is true & why? y = 3x+5 has
1) a unique solution
2) only two solutions,
3) infinitely many solutions

Solution: The true option is (3)

y = 3 x+ 5 has infinitely many solutions.

Reason: For every value of x, there is a corresponding value of y & vice versa

2. Write four solutions for each of the following equations.

1) 2x+y=7

Solution:

\(\begin{aligned}
& 2 x+y=7 \\
& \Rightarrow \quad y=7-2 x \\
& \text { when } \quad x=0, \quad y=7-2(0)=7-0=7
\end{aligned}\) \(\begin{array}{ll}
x=1, & y=7-2(1)=7-2=5 \\
x=-1, & y=7-2(-1)=7+2=9 \\
x=2, & y=7-2(2)=7-4=3
\end{array}\)

four solutions are (0,7) (1, 5) (-1, 9) & (2,3)

2) πx+y=9

y=9-πx

When

\(\begin{aligned}
& x=0, \quad y=9-\pi(0)=9-0=9 \\
& x=1, \quad y=9-\pi(1)=9-\pi \\
& x=-10, y=9-\pi(-1)=9+\pi \\
& x=2, \quad y=9-\pi(2)=9-2 \pi
\end{aligned}\)

four solutions are (0,9), (1,9-π ),

(-1,9+π), (2, 9-2π)

3) x=4y

Solution: x=4y

when

\(\begin{aligned}
& y=0, \quad x=4(0)=0 \\
& y=1, \quad x=4(1)=4 \\
& y=-1, \quad x=4(-1)=-4 \\
& y=2, \quad x=4(2)=8 \\
&
\end{aligned}\)

∴ four solutions are (0, 0), (4,1) (-4, -1) & (8,2)

Karnataka 9th Standard Maths Chapter 4 Notes

3.  Check which of the following are solutions of the equation x-2y=4 & which are not

1) (0,2)

Solution: Consider the given equation: x-2y= 4……….(1)

i) (0,2)

Put x=0, y= 2 in (1) we get

x-2y=4

0 – 2(2) = 4

-4 ≠4

∴ (0,2) is not a solution of (1)

2) (2,0)

Solution: (2, 0)

put x=2, y=0 in(1) we get

x—2y=4

2-2(0) = 4

2-0 = 4

2≠4

∴ (2,0) is not a solution of (1)

3) (4,0)

Solution: (4,0)

put x = 4, y= 0 in(1) we get

x-2y=4

4 – 2 (0) = 4

4 = 4

∴ (4,0) is a solution of (1)

4) \((\sqrt{2}, 4 \sqrt{2})\)

Solution:

\((\sqrt{2}, 4 \sqrt{2})\) \(\begin{aligned}
& \text { put } x=\sqrt{2}, \quad y=4 \sqrt{2} \text { in (1) } \\
& x-2 y=4 \\
& \sqrt{2}-2(4 \sqrt{2}))=4 \\
& \sqrt{2}-8 \sqrt{2}=4 \\
& -7 \sqrt{2} \neq 4
\end{aligned}\)

∴ \((\sqrt{2}, 4 \sqrt{2})\) is not a solution of (1)

5) (1, 1)

Solution:

(1, 1)

\(\begin{aligned}
& \text { put } x=1, \quad y=1 \text { in }(1) \\
& x-2 y=4 \\
& 1-2(1)=4 \\
& 1-2=4 \\
& -1 \neq 4
\end{aligned}\)

∴ (1,1) is not a solution of (1)

4.  Find the value of k, if x= 2, y= 1 is a solution of the equation 2x+ 3y= k

Solution : If x=2, y= 1 is a solution of the equation 2x+ 3y=k. Then these values will satisfy the equation.

So putting x= 2 & y= 1 in the equation, we get

2(2) + 3(1) = k

=> 4 + 3-k

=> 7 = k

Linear Equations in Two Variables Exercise 4.3

1. Draw the graph of each of the following linear equations in two variables
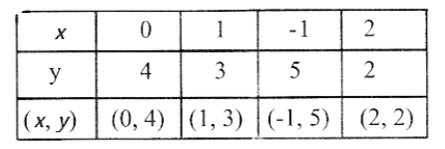
1) x+y=4
Solution; x + y =4
y= 4-x

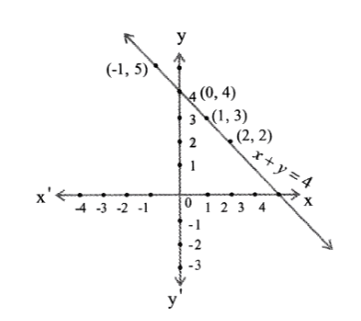
2) x-y = 2
Solution: x – y = 2
=> y = x – 2

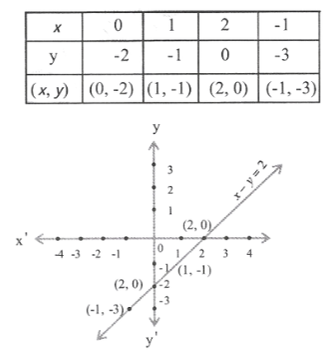
3) y = 3x

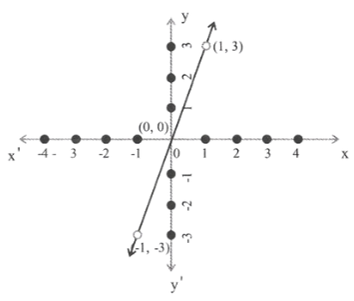
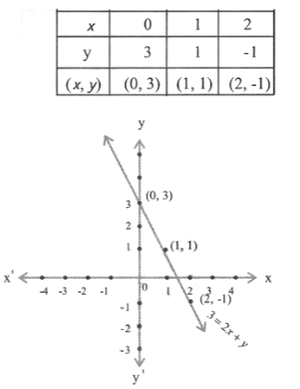
4) 3 = 2x + y
Solution: 3 = 2x + y
=> y = 3 – 2x

 

2. Give the equations of two lines passing through (2,14). How many more such lines are there and why?

Solution: The equations of two lines passing through (2, 14) can be taken as x+y- 16 & 7x-y-0

There are infinitely many such lines because through a point an infinite number of lines can be drawn.

3. If the point (3,4) lies on the graph of the equation 3y= ax+7, find the value of a.

Solution: If the point (3,4) lies on the graph of the equation 3y= ax+ 7, then

=> 3(4) = a(3) + 7

=> 12 = 3a + 7

=> 12- 7 = 3a

=> 5 = 3a

=> 3a = 5

=> a =\(5 / 3\)

4. The taxi fare in a city is as follows: For the 1st kilometer, the fare is ₹8 & for the subsequent distance. It is ₹5 per km. Taking the distance covered as x km & total fare as y, write a linear equation for this information & draw its graph.

Solution: Total distance covered = x km

Total fare = ₹y

Fare for the 1 st km = ₹8

Subsequent distance = (x-1) km

Fare for the subsequent distance = ₹ 5(x- 1)

According to the question

y= 8 + 5(x— 1)

=> y=8 + 5x-5

=> y= 5x+3

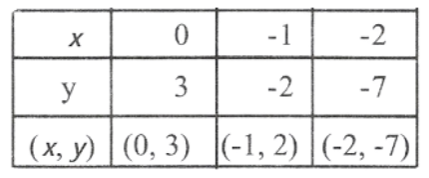
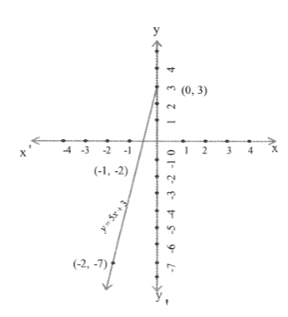
5. From the choices given below choose the equation whose graphs are given in fig (1) & fig(2)
For fig (1) For fig (2)
1) y = x 
2)x+y=0 
3) y=2x 
4) 2 + 2y =1 x

For fig (2)
1) y= x+2
2)y=x-2
3) y= x+2
4) x+2y=6

Solution: For fig (1)

The correct equation is (2) x+ y = 0

For fig (2)

The correct equation is (3) y=-x+2

KSEEB Class 9 Maths Linear Equations in Two Variables Solutions

6. If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables & draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance traveled by the body is (1) 2 units (2) 0 units.

Solution: Let the work done by the constant force be y units & the distance traveled by the body be x units.

constant force = 5 units.

W.K.T.

work done = Force x Displacement

=> y= 5x

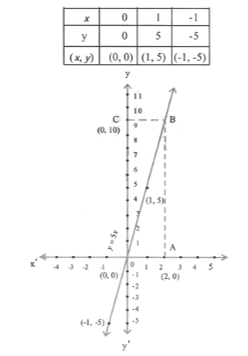
1) Let A —>(2,0) through A, draw a line parallel to OY to intersect the graph of the equation

y = 5 x at B. Through B draw a line parallel to OX to intersect OY at C. Then, C —> (0,10)

work done when the distance travelled by the body is 2 units =10 units.

2) Clearly y = 0 when x = 0, so, the work done when the distance travelled by the body is 0 unit is 0 units.

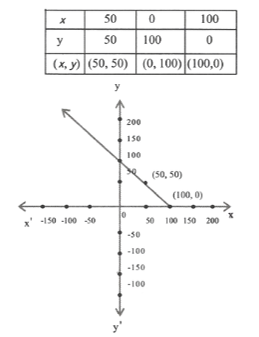
7. Yamini & Fatima two students of class IX of a school together contributed ? 100 towards the Prime minister’s Relief Fund to help the earthquake victims. Write a linear equation which satisfied this data. (You may take their contributions as ₹x, ₹ y) Draw the graph of the same.

Solution:

Let the contributions of yamini & Fatima be ₹ x & ₹ y respectively.

Then according to the question

x+y=100

=> y =100-x

8. In countries like USA & Canada temperature is measured in Fahrenheit, where as in countries like India, it is measured in Celsius. Here is a linear equation Fahrenheit to Celsius:
\(\mathrm{F}=\left(\frac{9}{5}\right) \mathrm{C}+32\)
1) Draw the graph of the linear equation above using Celsius for x- axis & Fahrenheit for y- axis.
2) If the temperature is 30°C, what is the temperature in Fahrenheit?
3) If the temperature is 95°F, what is the tem¬perature in Celsius?
4) If the temperature is 0°C, what is the tem-perature in Fahrenheit & if the temperature is 0°F, what is the temperature in Celsius?
5) Is there a temperature which is numerically the same in both Fahrenheit & Celsius? If yes, find it.

Solution:

\(\mathrm{F}=\frac{9}{5} \mathrm{C}+32\)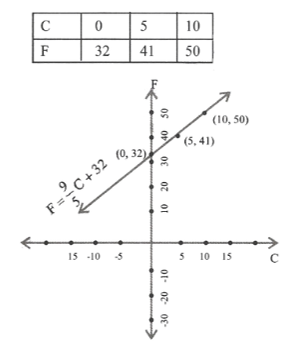

2) When C=30

Then

\(\mathrm{F}=\frac{9}{5} \mathrm{C}+32\) \(\mathrm{}=\frac{9}{5} \mathrm{x30}+32\)

=9×6+32

= 54 + 32

F = 86

∴ Required temperature is 86°F

3) When F = 95° then \(\mathrm{F}=\frac{9}{5} \mathrm{C}+32\)

=> 95 = 9/5 C+32

95-32 = 9/5C

63 = 9/5C

(63 x 5)/9=C

C=35

∴ Required temperature =35°C

4.)  When C = 0

Then F = 9/5C + 32

=(9/5) x 0 +32

= 32°F

When F=0, then

\(\begin{aligned}
& \mathrm{F}=\frac{9}{5} \mathrm{C}+32 \\
\Rightarrow & 0=\frac{9}{5} C+32 \\
\Rightarrow & 0-32=\frac{9}{5} C \\
\Rightarrow & \frac{-32 \times 5}{9}=C \\
\Rightarrow & C=\frac{-160}{0}
\end{aligned}\)

5) Let the temperature be x numerically then

\(\begin{aligned}
& \mathrm{F}=\frac{9}{5} \mathrm{C}+32 \\
& \Rightarrow \quad x=\frac{9}{5} x+32 \\
& x-\frac{9}{5} x=32 \\
& x\left(1-\frac{9}{5}\right)=32 \\
& x\left(\frac{5-9}{5}\right)=32
\end{aligned}\) \(\begin{aligned}
& x\left(\frac{-4}{5}\right)=32 \\
& x=\frac{32 \times 5}{-4} \\
& \Rightarrow \quad x=-40
\end{aligned}\)

∴ Numerical value of required temperature is – 40°

KSEEB 9th Standard Maths Chapter 4 Important Questions

Linear Equations in Two Variables Exercise 4.4

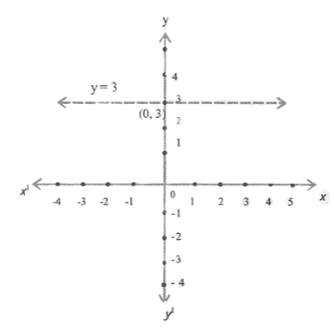
1. Give geometric representations of y= 3 as an equation.

1) in one variable

Solution: In one variable

The representation of y = 3 on the number line is as shown below.

2) in two variable

Solution: In two variables

y=3

=>0 x X+1 x Y =3

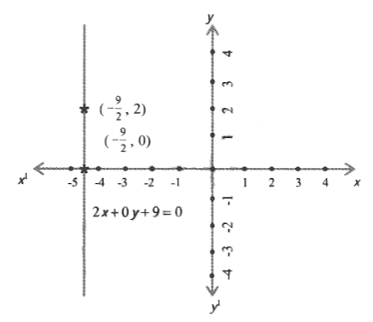
2. Give the geometric representations of 2x+ 9 = 0 as an equation.

1) in one variable

Solution: In one variable

2x+9 = 0

=> 2x= -9

=>x=(-9/2)

=>x=-4.5

2) in one variables

Solution: In two variables

2x + 9=0

=> 2x + 0 x y =0

ie   x=-9/2,    y=0

& x=-9/2,     y=0

Additional Problems

1. The standard form of a linear equation in two variables x& y is

1. ax+ by + c= 0
2. ax = c
3. by=c
4. x+y+c=0

Solution: 1) ax+ by + c= 0

2. The equation 3x+4y = 12 has

1. a unique solution
2. no solution
3. two solutions
4. Infinitely many solutions

Solution: 4) Infinitely many solutions

3. How many lines pass through O?

1. 1
2. 2
3. 4
4. Infinitely many

Solution: 4) Infinitely many

4. The force applied on a body is directly proportional to the acceleration produced in the body. Express this in the form of a linear equation in two variables.

1. y= x
2. y+x=0
3. y=kx
4. none of these

Solution: 3) y= kx

5. Where does the line 2x+ 3 y=6 cut the x-axis?

1. at (3,0)
2. at (0,3)
3. at (0,0)
4. at (3,3)

Solution: 1) at (3,0)

6. Which of the following is a solution of the equation x-y= -1?

1. (0,1)
2. (1, 0)
3. (1,1)
4. (2,1)

Solution: 1) (0,1)

7. x= 4 is a line

1. parallel to y= -4
2. parallel to x- axis
3. passing through the origin
4. parallel to x= -4

Solution: 4) parallel to x= -4

8. The point of intersection of the lines intersecting the equation 3x = 2y+1 & 2x=3y-1 is

1. (2,3)
2. (3,2)
3. (1,1)
4. (0, 0)

Solution : 3) (1,1)

Karnataka Board Class 9 Maths Chapter 4 MCQs

9. The equation of a line parallel to y-axis is

1. x=l
2. x+ y= 0
3. y=0
4. y= 1

Solution: 1) x= 1

10. If x= 3 & y= -2 is a solution of the equation 4px- 3y= 12, then the value of p is

1.  0
2. 1/2
3.  2
4. 3

Solution: 2) 1/2

Solve

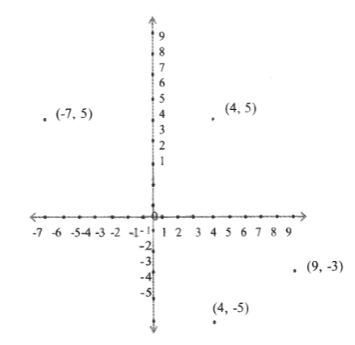
1. Plot the following points in a rectangular co-ordinates system. In which quadrant do they lie?
i) (4,5)
ii) (4, -5)
iii) (-7, 5)
iv)(9,-3)

Solution:

i) I quadrant

ii) IV quadrant

iii) II quadrant

iv) IV quadrant

2. Plot the points (-1,0), (1,0), (1,1), (0,2) (-1, 1) & join them in order. What figure do you get?
Solution:

The figure we got is pentagon.

3. In which quadrant will the point lie, if
1) The ordinate is 3 & the abscissa is -4?
2) The abscissa is -5 & the ordinate is – 3?
3) The ordinate is 4 & the abscissa is 5
4) The ordinate is 4 & The abscissa is – 4?

Solution:

1) The point whose ordinate is 3 & The abscissa is -4 lies in II Quadrant.

2) The point whose abscissa is -5 & The ordi¬nate is -3 lies in III Quadrant.

3) The point whose ordinate is 4 & The abscissa is 5 lies in I Quadrant.

4) The point whose ordinate is 4 & The abscissa is -4 lies in II Quadrant.

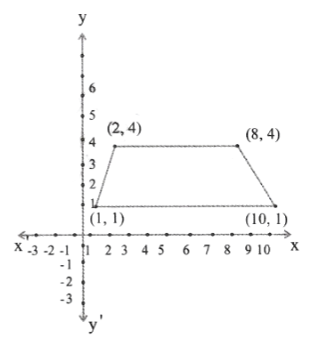
4. Draw the quadrilateral whose vertices are
1) (1,1), (2,4), (8, 4) & (10,1)
Solution:

2)(-2,2), (-4,2), (-6, -2) & (-4, -6)
Name the type of quadrilateral so formed in each case.
Solution:

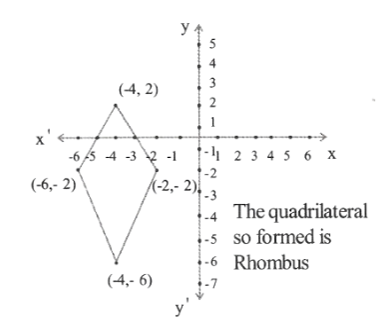
The quadrilateral so formed is a trapezium .

5. Express the linear equation 7 = 2jrin the form ax+ by+ c= 0 & also write the values of a, b & c.

Solution:

7 = 2x

=> 2x-7 = 0

=> 2x+ oy-1 = 0

comparing with ax+by+c= 0

we get a = 2, b = 0, c = -7

6. Find at least 3 solutions for the following lin¬ear equation in two variables 2x+5y= 13

Solution:

2x+5y= 13

=> 5y=13-2x

\(y=\frac{13-2 x}{5}\)

put x=0,

\(y=\frac{13-2(0)}{5}=\frac{13}{5}\)

put x=1,

\(y=\frac{13-2(1)}{5}=\frac{13-2}{5}=\frac{11}{5}\)

put x=-1,

\(y=\frac{13-2(-1)}{5}=\frac{13+2}{5}=\frac{15}{5}=3\)

∴ The three solutions are (0,13/5), (1,11/5)

(-1,3)

7. If x = -2, y = 6 is a solution of equation 3ax+ 2by = 6, then find the value of b from 2(a-1) + 2 (3b- 4) = 4

Solution:

If x= -2, y= 6 is a solution of  equation

3ax+2by= 6, then

3a(-2) + 2b(6) = 6

-6 a +12b = 6

÷ 6     -3+2b=1…………….. (1)

also    2(a-1) + 2(3b-4) = 4

=> 2a-2 + 6b-8 = 4

=> 2a + 6b-10-4 = 0

=> 2a + 6b-14 = 0

=> 2a + 6b = 14

÷ 2        => a + 3b = 7……………..(2)

adding Eqn (1) & (2) we get

\(\begin{array}{r}
-a+2 b=1 \\
a+3 b=7 \\
\hline 5 b=8 \\
b=8 / 5
\end{array}\)

putting b = 8/5 in (1) we get

\(\begin{gathered}
-a+2 \times \frac{8}{5}=1 \\
-a+\frac{16}{5}=1 \\
-a=1-\frac{16}{5} \\
=\frac{5-16}{5} \\
-a=\frac{-11}{5}
\end{gathered}\)

∴ a=11/5

Hence a=11/5 & b=8/5

8. Find the coordinates of the points where the line representing the equation \(\frac{x}{4}=1-\frac{y}{6}\) cuts the x-axis & the y-axis

Solution:

\(\frac{x}{4}=1-\frac{y}{6}\)

For intersection with x-axis, put y= 0

∴ \(\frac{x}{4}=1-\frac{0}{6}\)

=> x/4=1

=> x=4

∴ The point of intersection with x – axis is (4,0) For intersection with y – axis, put x=0, then

\(\frac{0}{4}=1-\frac{y}{6}\)

=> 1-y/6=0

=> y/6=1

=> y=6

Hence the point of intersection with y – axis is (0,6).

9. Determine the point on the graph of equation 2x+5y= 20 where x- co-ordinate is 5/2 times its ordinate.

Solution:

2x+5y= 20

x – coordinate is 5/2 times its ordinate

ie  x=5/2y

∴ \(2\left(\frac{5}{2} y\right)+5 y=20\)

5y+5y=10

10y=20

y=20/10=2

∴ \(x=\frac{5}{2} \times 2=5\)

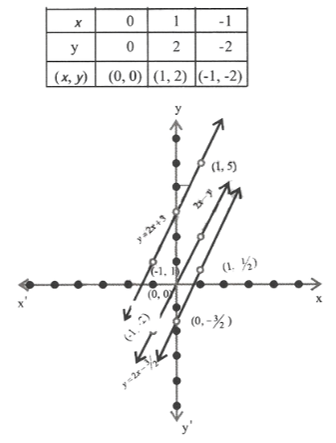
Hence the required point is (5,2)

10. Plot the graph of equations using the same pair of axes;
1) y=2x+3
Solution:

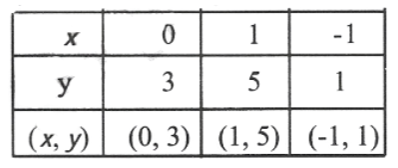
2) y=2x-3/2
Solution:

3) 2 x- y = 0 are these lines parallel?

Solution:

2x-y=0

=> y=2x

11. Shade the triangle formed by the graph of 2x-y=4, x+y= 2 & the axis. Write the coordinates of the vertices of the triangle.

Solution:

2x-y=4

=> y= 2x-4

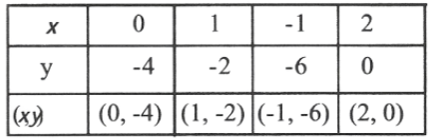
x+y=2
=> y=2-x

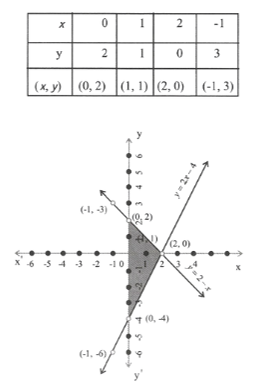
From the graph, we see that the co-ordinates of the verti¬ces of the triangle are (2,0), (0,2) & (0, -4)
The triangle has been shaded.

Class 9 Maths Linear Equations in Two Variables KSEEB Guide

12. Solve for: \(x: 3 x-12+\frac{3}{7} x=2(x-1)\) What type of graph is it in two dimensions?

Solution:

\(3 x-12+\frac{3}{7} x=2(x-1)\) \(\begin{aligned}
& 3 x+\frac{3}{7} x-2 x=-2+12 \\
& \frac{3 x}{7}+x=10 \\
& \frac{3 x+7 x}{7}=10 \\
& 10 x=70
\end{aligned}\)

x=70/10

x=7

The graph of this equation is a line parallel to y-axis at a distance of 7 units to the right of origin O.

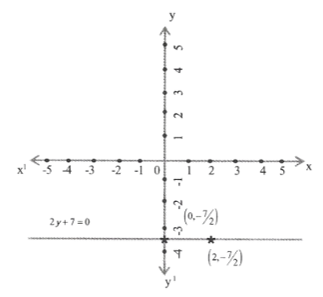
13. Given the geometrical representation of 2y+ 7 as equation in
1) one variable

Solution:

one variable

2y+7 = 0

=> 2y= -7

y=-7/2

2)  two variables

Solution:

In two variables

2y+7=0

=> 0 . x+2y+ 7 = 0

If x=0, y=-7/2

14. 1f the point (3,4) lies on the graph of the equation 3 y = ax+ 7, find the value of a.

Solution:

Since every point on the graph of a linear equation is a solution of the equation.

x = 3 & y= 4 is a solution of the equation 3 y= ax+1

3×4 = ax3 + 7

12 = 3a+7

3a=5

=> a =5/3

KSEEB Maths Chapter 4 Linear Equations In Two Variables Free Solutions 

15. Give the equations of two lines passing through (2,14). How many more such lines are there & why?

Solution:

We observe that x= 2 & y= 14 is a solution of each of the equations.

1) 1x- y= 0

2) 3x-y+8 = 0

3) x-y+12 = 0 etc.

We know that passing through a given point infinitely many lines can be drawn. So, there are infinitely many lines passing through (2,14)

16. Draw the graphs of 2x+y=6 & 2x- y+ 2 = 0 shade the region bounded by these lines & x – axis. Find the area of the shaded region.

Solution:

We have

2 x+y=6  &  2x-y+2 = 0

2x+ y=6

=> y = 6-2x

2x- y+2 = 0

=> 2x+2-y

=> y= 2x+ 2

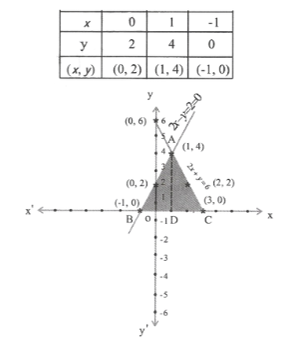
Area of the shaded region = Area of Δ ABC

= 1/2x Base x height

=1/2xBCxAD

=1/2x4x=8

Area of the shaded region = 8 sq. units

KSEEB Class 9 Maths Chapter 4 Exercise Solutions

17. Find out which of the following equations have x = 2, y= 1 as a solution.
1) 2x+5y=9
2) 5x+3y=14
3) 2x+3y= 7

Solution:

1) 2x+ 5y = 9

put x= 2 & y = 1

LHS = 2 (2) +5(1)

= 4+5

= 9

= RHS,

∴  x=2 & y = 1 is a solution of the given equation

2) 5x+3y-14

LHS = 5x+3y

= 5 (2) + 3 (1)

= 10 + 3

= 13

≠14

≠ RHS

∴ x=2 S& y= 1 is not a solution of the given equation.

3) 2x+3y=7

LHS = 2x+3y=7

= 2 (2)+ 3(1)

= 4 + 3

= 7

= RHS

x=2 & y= 1 is a solution of the given equation.