KSEEB Solutions For Class 9 Maths Chapter 3 Coordinate Geometry Points to Remember
- The system by which we can describe the position of a point in a plane is called cartesian system.
- In cartesian system, there are two perpendicular lines (one horizontal & other vertical) are required to locate the position of a point or an object.
- The plane is called the cartesian or coordinate plane & the lines.
- The horizontal line xx’ is called the x-axis & vertical line yy’ is called the y-axis.
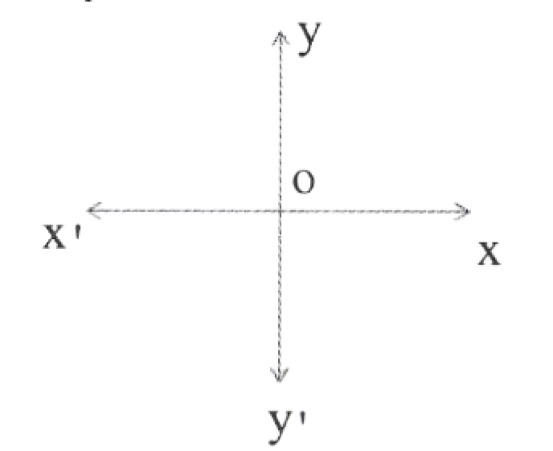
- The point where xx’ & yy’ cross is called the origin & is denoted by O.
- The co-ordinate axis divide the plane into four parts called quadrants (one-fourth part) numbered I, II, III
& IV

- x – co-ordinate (or absicca)= perpendicular distance of a point from y-axis.
- y co-ordinate (or ordinates) = perpendicular distance of a point from x-axis.
- If abscissa of a point is x & ordinate is y,then the coordinates of a point are (x, y)
- The abscissa of every point on y-axis is zero (0,y)
- The ordinate of every point on x-axis is zero (x, 0)
- x-axis & y-axis intersect at origin, represented by O and its co-ordinate are (0,0)
Read and Learn More KSEEB Solutions for Class 9 Maths
| Class 9 Social Science | Class 9 Science | Class 9 Maths |
Plotting a point in the plane if its co-ordinates are given.

Let P→ (x, y), we start from o & count x- units along OX or OX’ according as x is positive or negative & reach a point M. From M, we count y – units along OY or OY’ accordind to y is positive or negative & reach P.
KSEEB Class 9 Maths Chapter 3 Solutions PDF
Note: If x ≠ y, then the position of (x, y) in the cartesian plane is different from the position of (y x). This shows that the order of x&y is important in (x, y). thus (x, y) is an ordered pair. Obviously, (x, y) ≠ (y, x), if x≠y&(x,y) = (y, x),if x=y.
Coordinate Geometry Exercise 3.1
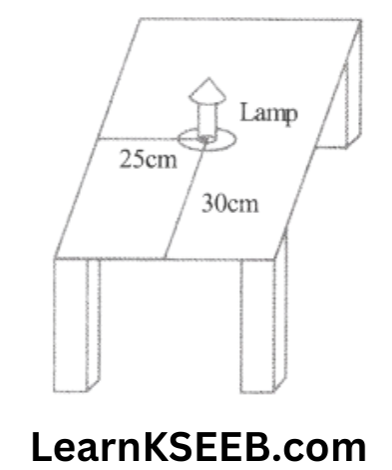
1. How will you describe the position of a table on your study table to another person?
Solution: Consider the lamp as a point & table as a plane. Choose any two perpendicular edges of the table. Measure the distance of the lamp from the longer edge, suppose it is 25cm. Again measure the distance of the lamp from the shorter edge & suppose it is 30cm, you can write the position of the lamp as (30,25) or (25, 30) depending on the order you fix.
2. (Street plan)
A city has two main roads which cross each other at the centre of the city. These two roads are along the North-south direction & East – west direction. All the other streets of the city run parallel to these roads & are 200m apart. There are about 5 streets in each di¬rection using 1 cm = 200m draw a model of the city on your note book. Represent the roads/streets by single lines.
There are many cross-streets in your model. A particular cross-street is made by two streets, one running in the north-south direction & another in street is referred to in the following manner. If the 2nd street running in the north-south direction & 5th in the east-west direction meet at some crossing, then we will call this cross-street (2,5). Using this convention, find (1) How many cross-streets can be referred to as (4, 3)? (2) How many cross-streets can be referred to as (4, 3)?
Solution:
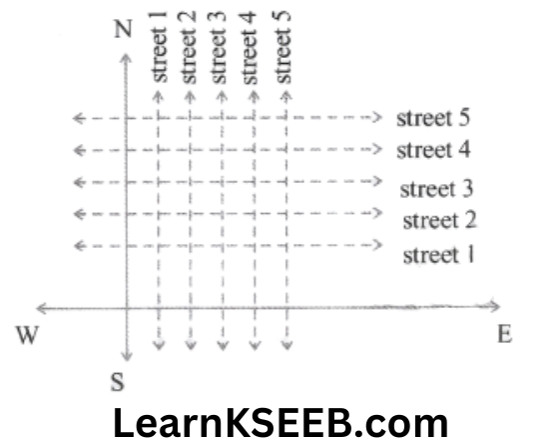
Both the cross-streets are marked in the above figure. It can be observed that there is only one cross-street which can be referred as (4,3) & again only one which can be referred as (3,4)
Karnataka 9th Standard Maths Chapter 3 Notes
Coordinate Geometry Exercise 3.2
1. Write the answer of each of the following questions.
1) What is the name of horizontal & the vertical lines drawn to determine the position of any point in the cartesian plane?
Solution: The x-axis & the y- axis.
2)What is the name of each part of the plane formed by these two lines?
Solution: Quadrants
3)Write the name of the point where these two lines intersect.
Solution: The origin.
2. See figure & write the following
1) The co-ordinates of B
2) The co-ordinates of C
3) The point identified by the coordinates
(-3,-5)
4) The point identified by the co-ordinate
(2, -4)
5) The abscissa of point D.
6) The ordinate of point H.
7) The co-ordinates of point L.
8) The co-ordinate of point M.
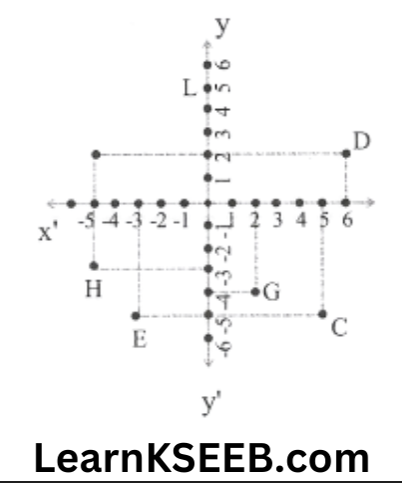
1) B → (-5, 2)
2)C→(5,-5)
3)E
4)G
5) 6
6) -3
7)L → (0,5)
8) M →(-3,0)
Coordinate Geometry Exercise 3.3
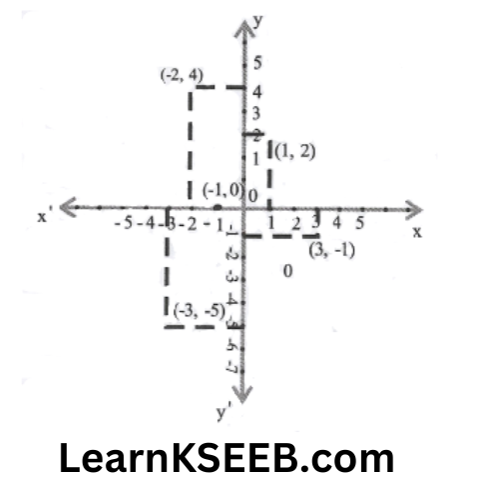
1. In which Quadrant or on which axis do each of the points (-2,4), (3,1), (-1,0) (1,2) & (-3, -5) lie? Verify your answer by locating them on the cartesian plane.
Solution: The point (-2,4) lies in the II Quadrant.
Point (3, -1) lies in the IV Quadrant.
The point (-1,0) lies on the negative x-axis.
Point (1,2) lies in the I Quadrant
The point (-3, -5) lies in the III Quadrant
2. Plot the points (x,y) given in the following table on the plane, choosing suitable units of distance on the axis.
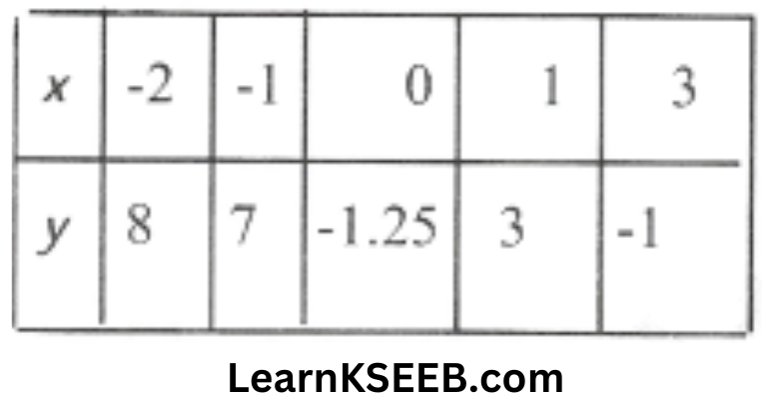
Solution:

KSEEB Class 9 Maths Coordinate Geometry Solutions
Additional Problems
1. A point lies on x-axis at a distance of 9 units from y-axis. What are its coordinates? What will be its coordinates if it lies on y-axis at a distance of 9 units from x-axis.
Solution: (0,9) , (0,-9)
2. In figure given below, Δ AOB with coordinates of A & O as (4, 0) & (0, 0) find the coordinates of B.

Solution:
In Right Δ AOB
\(\begin{aligned}& \mathrm{OA}^2+\mathrm{OB}^2=\mathrm{AB}^2 \\
& 4^2+\mathrm{OB}^2=5^2 \\
& \mathrm{OB}^2=5^2-4^2 \\
&=25-16=9 \\
& \mathrm{OB}=\sqrt{9}=3 \\
& \Rightarrow \quad \mathrm{B} \rightarrow(0,3)
\end{aligned}\)
3. In figure, Δ ABC & Δ ABD are equilateral Δles. Find the coordinates of points C & D.
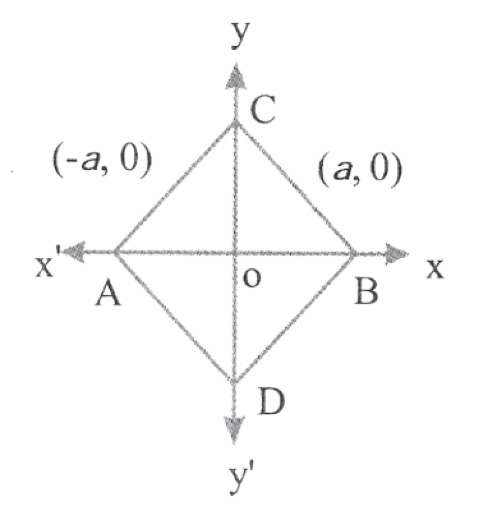
Solution:
Δ ABC is an equilateral Triangle
∴ AC = BC = AB
=> BC = AB
=> BC = 2a
In right triangle COB,
\(\begin{aligned}& \mathrm{OB}^2+\mathrm{OC}^2=\mathrm{BC}^2 \\
\Rightarrow & a^2+\mathrm{OC}^2=(2 a)^2 \\
\Rightarrow & \mathrm{OC}^2=4 a^2-a^2 \\
\Rightarrow & \mathrm{OC}^2=3 a^2 \\
\Rightarrow & \mathrm{OC}=\sqrt{3 a^2} \\
\Rightarrow & \mathrm{OC}=\sqrt{3} a
\end{aligned}\)
∴\(\mathrm{C} \rightarrow(0, \sqrt{3} a)\)
ΙΙ \(\mathrm{D} \rightarrow(0,-\sqrt{3} a)\)
4. Find the coordinates of a point
1) Whose ordinate is 6 & lies on y-axis.
2) Whose abscissa is -3 & lies on x-axis
Solution: 1)(0,6) 2)(-3,0)
5. Plot the points A (3,0), B(3, 3) & C(0, 3) in a cartesian plane. Join OA, AB, BC & CO. Name the figure so formed & write its one property.

KSEEB 9th Standard Maths Chapter 3 Important Questions
6. Which of the following points lie on x-axis which on y-axis?
A(0,2), B(5,6), c(-3,0), D(0, -3), E(0,4), F(6,0), G(3,0)
Solution: The points C, F & G lie on x-axis.
The points A, D & E lie on y-axis.
7. The following table gives the number of pairs of shoes & their corresponding price. Plot there as ordered pairs & join them. What type of graph do you get?
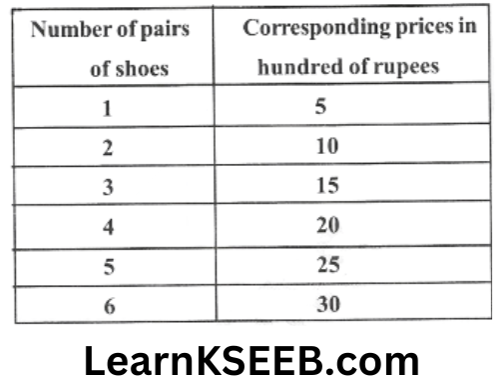
Solution:
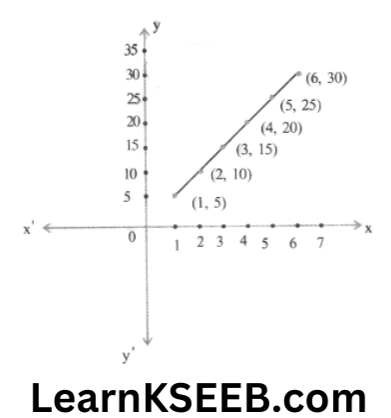
8. If (x+ 2,4) = (5, y-2), then what will be the co-ordinate of (x,y)?
Solution: Given: (x+2,4) = (5,y-2)
\(\begin{aligned}& \Rightarrow \quad x+2=5 \quad \& \quad 4=y-2 \\
& \Rightarrow \quad x=5-2 \quad \& \quad 4+2=y \\
& \Rightarrow \quad x=3 \quad \& \quad y=6
\end{aligned}\)
∴ co-ordinates of (x,y) = (3,6)
Karnataka Board Class 9 Maths Chapter 3 MCQs
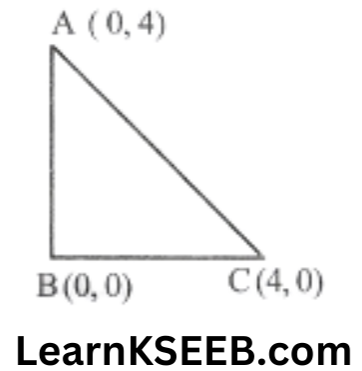
9. Calculate the area of Δle formed by joining the
points (4,0), (0,0) & (0,4)
Solution:
& \mathrm{AB}=\sqrt{(0-0)^2+(4-0)^2}=\sqrt{0+16}=\sqrt{16}=4 \\
& \mathrm{BC}=\sqrt{(0-4)^2+(0-0)^2}=\sqrt{16+0}=4
\end{aligned}\)
Class 9 Maths Coordinate Geometry KSEEB Guide
10. Express the equaion 2x+ y-4 = 0 in the form of y= mx+ c.
Solution: Given equation 2x+y-4 = 0
y=-2x+4
11. Find the point where line 3x + 6y – 4 = 0 intrersect the x- axis.
Solution: Given equation, 3x+6y-4=0
∴ Line intersect the x- axis
∴ y=o
3x+6x(0)-4 = 0
=> 3x-4 = 0
\(x=4 / 3\)So, the point where line intersect the x-axis
\(\left(\frac{4}{3}, 0\right)\)