KSEEB Solutions For Class 9 Maths Chapter 2 Polynomials Points to Remember
- The algebraic expression in which variables involved have only non-negative integral exponent is called polynomial. A polynomial p(a) in one variable x is an algebraic expression in a of the form
\(\mathrm{p}(x)=\) \(\begin{gathered}
a_n x^n+a_{n-1} x^{n-1}+a_{n-2} x^{n-2}+……… \\
+a_2 x^2+a_1 x+a_0
\end{gathered}\)
where \(a_0, a_1, a_2 \ldots \ldots \ldots \ldots a_n\)are constant &\(a_n \neq 0, a_0, a_1, a_2\) are respectively the coefficients of \(x^0, x^1, x^2\)……\(x^n\) & n is called the
degree of the polynomial. - A polynomial of degree zero is called a constant polynomial
Ex: 4, \(\frac{-7}{5}, \frac{3}{4}\)are constant polynomials. - A polynomial having all coefficients zero is called a zero polynomial. Also, the constant polynomial is called the zero polynomial & the degree of the zero polynomial is not defined.
- Highest power of variable in a polynomial is called the degree of polynomial.
- In polynomial of one variable, the highest power of the variable is called the degree of the polynomialEx: 1) \(4 x^7-5 x^3-4 x^2+3 x-6\) is a polynomial in x of degree 7.
2) \(\sqrt{5} x^2+5 \sqrt{5} x+7\) is a polynomial in x of degree x. - In polynomial of more than one variable, the sum of the powers of the variable in each term is taken up & the highest sum so obtained is called the degree of the polynomial.
Ex: \(6 y^3-5 x^2 y^2+4 x^2 y-3 y+9\) is a polynomial in x & y of degree 4. - A polynomial of one non-zero term is called a monomial.
Ex:\(3 x,-6 x^2, 7 x^3\) etc - A polynomial of two non-zero terms is called a binomial.
Ex:\(6 x^2+12, \quad 6 x^2+6 \sqrt{5} x\) - A polynomial of three, non-zero terms is called a trinomial.
Ex:\(\left(y^2+2 y+6\right),\left(4 x^2+5 \sqrt{3} x+\sqrt{5}\right)\) - A polynomial of degree 1 is called a linear polynomial, It is expressed in the form of ax+b, where a & b are real constants & \(a \neq 0\).
Ex:\(3 x+6\) is a linear polynomial in A. - A polynomial of degree 2 is called a quadratic polynomial. It is expressed in the form of \(a x^2+b x+c\) where a, b & c are real constant &\(a \neq 0\).
Ex:\(\frac{7}{5} y^2+3 y-2\) - A Polynomial of degree 3 is called a cubic polyno-mial. It is expressed in the form \(a x^3+b x^2+c x+d\), where a, b, c & d are real constant & \(a \neq 0\)
- Zeroes of a polynomial p(a) is a number c, such that p(c) = 0
– ‘O’ may be a zero of a polynomial
– Every linear po lynomial in one variable has a unique zero.
– A non-zero constant po lynomial has no zero.
– Every real number is a zero of the zero polynomial
– Maximum number of zeroes of a polynomial is equal to its degree.
| Class 9 Social Science | Class 9 Science | Class 9 Maths |
Read and Learn More KSEEB Solutions for Class 9 Maths
Remainder theorem:
Let p(x) & g(x) be two polynomials such that the degree of p(x) is equal to or greater than the degree of g(x) & g(x) * 0, then, we can find out two polynomials q(x) & r (x) such that
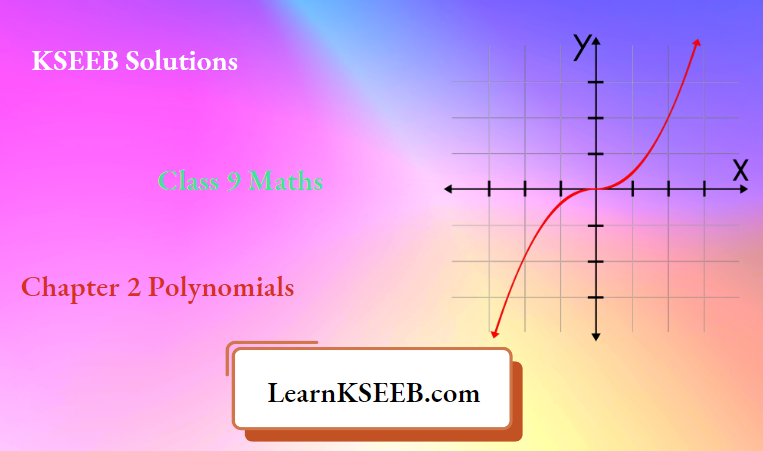
p(x) = g(x) q(x) + r(x) where
r(x) = 0 or degree of r(x) is less than degree of g(4)
The other way round, we can say that on dividing p(x) by g(x), we get q(x) as the quotient & r(x) as the remainder.
KSEEB Class 9 Maths Chapter 2 Solutions PDF
Formulatically:
Dividend = (Divisor x Quotient) + Remainder
Remainder theorem:
On dividing the polynomial p(x) of degree one or more than one by a linear polynomial x – a, the remainder obtained is p(a), where a is a real number.
Proof:
Suppose that when we divide p(x) by x – a, the quotient is q(x) & the remainder is r(x)
Then p(x) = (x- a) q(x) + r(x)
∴ degree of x – a is one & degree of r(x) is less than the degree (x – a) ,
∴ degree of r(x) = 0
=> r(x) is a constant, say r
\(\mathrm{p}(x)=(x-a) \mathrm{q}(x)+\mathrm{r}\)
put x=a,we get
p(a)=r
This proves the theorem.
KSEEB Class 9 Maths Chapter 2 Polynomials Exercises
Factor theorem:
Let p(*) be a polynomial of degree one or more than one & ‘a’ is a real number then
- x – a will be a factor of p(*) if p(a) = 0, conversely
- If x – a is a factor of p(jr) then p(a) = 0
- Factorisation of a quadratic polynomial by splitting the middle term.
\(\begin{aligned}
& x^2+I x+m \\
= & x^2+(a+b) x+a b
\end{aligned}\)
Where\(\begin{aligned}
I & =a+b \quad \& \quad m=a b \\
& =x^2+a x+b x+a b \\
& =x(x+a)+b(x+a) \\
& =(x+a)(x+b)
\end{aligned}\)
Algebraic Identities.
- \((a+b)^2=a^2+2 a b+b^2\)
- \((a-b)^2=a^2-2 a b+b^2\)
- \(a^2-b^2=(a+b)(a-b)\)
- \((x+a)(x+b)=x^2+(a+b) x+a b\)
- \((a+b+c)^2=a^2+b^2+c^2+2 a b+2 b c+2 c a\)
- \((a+b)^3=a^3+b^3+3 a b(a+b)\)
- \((a-b)^3=a^3-b^3-3 a b(a-b)\)
- \(\begin{aligned}
& a^3+b^3+c^3-3 a b c=(a+b+c) \\
& \left(a^2+b^2+c^2-a b-b c-c a\right)
\end{aligned}\) - \(\text { if } a+b+c=0 \text {, then } a^3+b^3+c^3=3 a b c\)
- \(a^3+b^3=(a+b)\left(a^2-a b+b^2\right)\)
- \(a^3-b^3=(a-b)\left(a^2+a b+b^2\right)\)
Polynomials Exercise 2.1
1. Which of the following expressions are polynomials in one variable & which are not? State reasons for your answers.
1. \(4 x^2-3 x+7\)
Solution: This expression is a polynomial in one variable x because in the expression. There is only one variable x & all the indices of x are whole numbers.
2. \(y^2+\sqrt{2}\)
Solution: This expression is a polynomial in one variable y because in the expression there is only one variable y & all the indices of y are whole numbers.
3. \(3 \sqrt{t}+t \sqrt{2}\)
Solution: This expression is not a polynomial because in the term\(3 \sqrt{t}\). The exponent of t is \(1 / 2\)which is not a whole number.
4. \(y+2 / y\)
Solution: This expression is not a polynomial because in the term \(\frac{2}{y}\), the exponent of y is(-1) which is not a whole number.
5. \(x^{10}+y^3+t^{50}\)
Solution: This expression is not a polynomial in one variable because in the expression, three variables x, y & t occur.
2. Write the co-efficients of \(x^2\) in each of the following.
1. \(2+x^2+x\)
Solution: co-efficient of \(x^2\) is 1
2. \(2-x^2+x^3\)
Solution: co-efficient of \(x^2\) is -1
3. \(\frac{\pi}{2} x^2+x\)
Solution: co-efficient of \( x^2+x\) is \(\frac{\pi}{2}\)
4. \(\sqrt{2} x-1\)
Solution: co-efficient of \(\frac{\pi}{2}\) is 0
3. Give one example each of a binomial of degree 35, & of a monomial of degree 100.
Solution: One example of a binomial of degree 35 is\(3 x^{35}-4\)
One example of a monomial of degree 100 is\(\sqrt{5} y^{100}\)
4. Write the degrees of each of the following polynomials
1. \(5 x^3+4 x^2+7 x\)
Solution: Term with the highest power of\(x=5 x^3\)
Exponent of x in this term = 3
∴ Degree of this polynomial = 3
2. \(4-y^2\)
Solution: \(4-y^2\)
Degree of this polynomial = 2
3. \(5 t-\sqrt{7}\)
Solution: Degree of this polynomial = 1
4.3
Solution: It is a non-zero constant. So the degree of the polynomial is zero.
5.Classify the following as linear, quadratic & cubic polynomials.
1. \(x^2+x\)
Solution: Quadratic polynomial.
2. \(x-x^3\)
Solution: Cubic polynomial.
3. \(y+y^2+4\)
Solution: Quadratic polynomial
4. 1+x
Solution: Linear polynomial
5. 3t
Solution: Linear polynomial.
6. \(r^2\)
Solution: Quadratic polynomial
7. \(7 x^3\)
Solution: Cubic polynomial.
Polynomials Exercise 2.2
1.Find the value of the polynomial.\(5 x-4 x^2+3\) at
1)x=0 2)x=-1 3)x=2
1. x=0
Solution: Let f(x)= 5x-4×2+3
Value of f(x) at x= 0
f(0) = 5 (0) – 4 (0)2 + 3
=0-0+3
= 3
2. x=-1
value of f(x) at x= -1
f(-l) = 5(-l)-4(-l)2 + 3
= -5 – 4 + 3
= – 6
3. x=2
value of f(x) at x= 2
f(2) = 5(2) – 4(2)2 + 3
= 10-16 + 3
= – 3
2. Find p(0), p(1) & p(2) for each of the following polynomials
1. \(p(y)=y^2-y+1\)
Solution: \(p(y)=y^2-y+1\)
\(p(0)=0^2-0+1\)= 1
p(l) = \(1^2-1+1=1\)
p(2) = \(2^2-2+1=1\)
2. \(p(t)=2+t+2 t^2-t^3\)
Solution: \(p(t)=2+t+2 t^2-t^3\)
\(\begin{aligned}& \mathrm{p}(0)=2+0+2(0)^2-0^3=2 \\
& \mathrm{p}(1)=2+1+2(1)^2-1^3=4 \\
& \mathrm{p}(2)=2+2+2(2)^2-2^3=4
\end{aligned}\)
3. \(\mathbf{p}(\boldsymbol{x})=x^3\)
Solution: \(\mathbf{p}(\boldsymbol{x})=x^3\)
∴ \(p(0)=0^3=1\)
\(\begin{aligned}& \mathrm{p}(1)=1^3=1 \\
& \mathrm{p}(2)=2^3=8
\end{aligned}\)
4. \(p(x)=(x-1)(x+1)\)
Solution: \(p(x)=(x-1)(x+1)\)
∴\(p(0)=(0-1)(0+1)=-1 \times 1=-1\)
\(\begin{aligned}& \mathrm{p}(1)=(1-1)(1+1)=0 \times 2=0 \\
& \mathrm{p}(2)=(2-1)(2+1)=1 \times 3=3
\end{aligned}\)
3. Verify whether the following zeroes of the polynomial are indicated against them.
1. \(p(x)=3 x+1, x=-\frac{1}{3}\)
Solution:
\mathrm{p}\left(-\frac{1}{3}\right) & =3\left(-\frac{1}{3}\right)+1 \\
& =-1+1 \\
& =0
\end{aligned}\)
∴\(-\frac{1}{3} \text { is a zero of } \mathrm{p}(x)\)
2. \(p(x)=5 x-\pi, \quad x=\frac{4}{5}\)
Solution:
p=\left(\frac{4}{5}\right) & =5\left(\frac{4}{5}\right)-\pi \\
& =4-\pi \neq 0
\end{aligned}\)
∴\(\frac{4}{5} \text { is not a zero of } \mathrm{p}(x)\)
3. \(p(x)=x^2-1, \quad x=1,-1\)
Solution:
& \mathrm{p}(1)=1^2-1=1-1=0 \\
& \mathrm{p}(-1)=(-1)^2-1=1-1=0
\end{aligned}\)
∴\(1,-1 \text { are zeroes of } \mathrm{p}(x)\)
4. \(p(x)=(x+1)(x-2), x=-1,2\)
Solution:
\(\begin{aligned}\mathrm{p}(-1) & =(-1+1)(-1-2) \\
& =0(-3) \\
& =0 \\
\mathrm{p}(2) & =(2+1)(2-2) \\
& =(3)(0) \\
& =0
\end{aligned}\)
∴\(-1,2 \text { are zeroes of } \mathrm{p}(x)\)
5. \(p(x)=x^2, \quad x=0\)
Solution:
∴ 0 is a zero of p(x)
6. \(p(x)=I x+m, \quad x=\frac{-m}{l}\)
Solution:
p=\left(\frac{-m}{I}\right)=I\left(\frac{-m}{I}\right)+m \\
=-\mathrm{m}+\mathrm{m}=0
\end{gathered}\)
∴\(\frac{-m}{l}\) is a zero of p(x)
7. \(p(x)=3 x^2-1, \quad x=\frac{-1}{\sqrt{3}}, \frac{2}{\sqrt{3}}\)
Solution:
p\left(-\frac{1}{\sqrt{3}}\right) & =3\left(-\frac{1}{\sqrt{3}}\right)^2-1 \\
& =3\left(\frac{1}{3}\right)-1=1-1= \\
p\left(\frac{2}{\sqrt{3}}\right) & =3\left(\frac{2}{\sqrt{3}}\right)^2-1 \\
& =3 \times \frac{4}{3}-1 \\
& =4-1 \\
& =3 \neq 0
\end{aligned}\)
∴\(\frac{-1}{\sqrt{3}}\) is a zero of p(x) but \(\frac{2}{\sqrt{3}}\) is not a zero of p(x)
Karnataka 9th Standard Maths Chapter 2 Notes
8. \(p(x)=2 x+1, \quad x=\frac{1}{2}\)
Solution:
p=\left(\frac{1}{2}\right) & =2 \times \frac{1}{2}+1 \\
& =1+1=2 \neq 0
\end{aligned}\)
∴ \(\frac{1}{2}\) is not a zero of p(x).
4. Find the zero of the polynomial in each of the following cases
1. \(p(x)=x+5\)
Solution:
\(\begin{aligned}& p(x)=0 \\
& \Rightarrow \quad x+5=0 \\
& \Rightarrow \quad x=-5
\end{aligned}\)
∴-5 is a zero of the polynomial p(x)
2. \(p(x)=x-5\)
Solution:
& p(x)=0 \\
& \Rightarrow \quad x-5=0 \\
& \Rightarrow \quad x=5
\end{aligned}\)
∴-5 is a zero of the polynomial p(x)
3. \(p(x)=2 x+5\)
Solution:
\(\begin{aligned}& \mathrm{p}(x)=0 \\
& \Rightarrow \quad 2 x+5=0 \\
& \Rightarrow \quad 2 x=-5 \\
& \Rightarrow \quad x=\frac{-5}{2}
\end{aligned}\)
∴\(\frac{-5}{2}\) is a zero of the polynomial p(x)
4. \(p(x)=3 x-2\)
Solution:
\(\begin{aligned}& \mathrm{p}(x)=0 \\
& \Rightarrow \quad 3 x-2=0 \\
& \Rightarrow \quad 3 x=2 \\
& \Rightarrow \quad x=\frac{2}{3}
\end{aligned}\)
∴\(\frac{2}{3}\) is a zero of the polynomial p(x)
5. \(p(x)=3 x\)
Solution:
\(\begin{aligned}& \mathrm{p}(x)=0 \\
& \Rightarrow \quad 3 x=0 \\
& \Rightarrow \quad x=0
\end{aligned}\)
∴ 0 is a zero of the polynomial p(x)
6. \(p(x)=a x, \quad a \neq 0\)
Solution:
\(\begin{aligned}& p(x)=0 \\
& \Rightarrow \quad a x=0 \\
& \Rightarrow \quad x=0
\end{aligned}\)
∴ 0 is a zero of the polynomial p(x)
7. \(p(x)=c x+d, \quad c \neq 0\) ,c,d are rael numbers
Solution:
& p(x)=0 \\
& \Rightarrow \quad c x+d=0 \\
& \Rightarrow \quad c x=-d \\
& \Rightarrow \quad x=\frac{-d}{c}
\end{aligned}\)
∴ \(-\frac{d}{c}\) is a zero of the polynomial p(x)
Polynomials Exercise 2.3
1. Find the remainder when \(x^3+3 x^2+3 x+1\) is divided by
1) x+1
2)\(x-\frac{1}{2}\)
3)x
4)x+π
5)5+2x
1. Solution:
1) Let \(\mathrm{p}(x)=x^3+3 x^2+3 x+1\)
\(\begin{aligned}& x+1=0 \\
& \Rightarrow \quad x=-1
\end{aligned}\)
∴Remainder
\(\begin{aligned}\mathrm{p}(-1) & =(-1)^3+3(-1)^2+3(-1)+1 \\
& =-1+3-3+1 \\
& =0
\end{aligned}\)
2. Solution:
\(\begin{aligned}& \Rightarrow \quad x-\frac{1}{2}=0 \\
& \Rightarrow \quad x=\frac{1}{2}
\end{aligned}\)
∴ Remainder
\(\begin{aligned}& =\left(\frac{1}{2}\right)^3+3\left(\frac{1}{2}\right)^2+3\left(\frac{1}{2}\right)+1 \\
& =\frac{1}{8}+3 \times \frac{1}{4}+\frac{3}{2}+1 \\
& =\frac{27}{8}
\end{aligned}\)
3. Solution:
Remainder =\(0^3+3(0)^2+3(0)+1=1\)
4. Solution:
\(\begin{array}{ll}\Rightarrow & x+\pi=0 \\
\Rightarrow & x=-\pi
\end{array}\)
∴Remainder = \(\begin{array}{r}
(-\pi)^3+3(-\pi)^2+3(-\pi)+1 \\
=-\pi^3+3 \pi^2-3 \pi+1
\end{array}\)
5. Solution:
\(\begin{array}{ll}\Rightarrow & 5+2 x=0 \\
\Rightarrow & x=-5 / 2
\end{array}\)
∴Remainder
\(\begin{aligned}& =\left(\frac{-5}{2}\right)^3+3\left(\frac{-5}{2}\right)^2+3\left(\frac{-5}{2}\right)+1 \\
& =\frac{125}{8}+\frac{75}{4}-\frac{15}{2}+1 \\
& =\frac{-27}{8}
\end{aligned}\)
2. Find the remainder when \(x^3-a x^2+6 x-a\) is divided by x-a
Solution:
Let \(\begin{aligned}
& p(x)=x^3-a x^2+6 x-a \\
& \quad x-a=0 \\
& x=a
\end{aligned}\)
∴Remainder
\(\begin{aligned}& =a^3-a(a)^2+6(a)-a \\
& =a^3-a^3+6 a-a \\
& =5 a
\end{aligned}\)
3.Check whether 7 + 3x is a factor of \(3 x^3+7 x\).
Solution:
7 + 3x will be a factor of \(3 x^3+7 x\) only if 7 +3x divecides \(3 x^3+7 x\) leaving no. remainder
Let \(p(x)=3 x^3+7 x\)
\(\begin{aligned}& 7+3 x=0 \\
& \Rightarrow \quad 3 x=-7 \\
& \Rightarrow \quad x=-7 / 3
\end{aligned}\)
∴Remainder = \(3\left(\frac{-7}{3}\right)^3+7\left(\frac{-7}{3}\right)\)
\(\begin{gathered}=-3 \times \frac{343}{27}-\frac{49}{3}=\frac{-343}{9}-\frac{49}{3} \\
=\frac{-490}{9} \neq 0
\end{gathered}\)
7+3x is not a factor of \(3 x^3+7 x\)
Polynomials Exercise 2.4
1. Determine which of the following polynomials has (X+1) a factor.
1. \(x^3+x^2+x+1\)
Solution:
Let \(p(x)=x^3+x^2+x+1\)
The zero of x+1 is -1
\(\begin{aligned}\mathrm{p}(-1) & =(-1)^3+(-1)^2+(-1)+1 \\
& =-1+1-1+1 \\
& =0
\end{aligned}\)
By factor theorem, x+ 1 is a factor of \(x^3+x^2+x+1\)
2. \(x^4+x^3+x^2+x+1\)
Solution:
Let \(p(x)=x^4+x^3+x^2+x+1\)
The zero of x+1 is -1
\(\begin{aligned}p(-1) & =(-1)^4+(-1)^3+(-1)^2+(-1)+1 \\
& =1-1+1-1+1=1 \neq 0
\end{aligned}\)
∴By factor theorem, x +1 is not a factor of \(x^4+x^3+x^2+x+1\)
3. \(x^4+3 x^3+3 x^2+x+1\)
Solution:
Let \(p(x)=x^4+3 x^3+3 x^2+x+1\)
The zero of x+1 is -1
\(\begin{aligned}\mathrm{p}(-1) & =(-1)^4+3(-1)^3+3(-1)^2+(-1)+1 \\
& =1-1+1-1+1=1 \neq 0
\end{aligned}\)
By factor theorem, x +1 is not a factor of \(x^4+3 x^3+3 x^2+x+1\)
4. \(x^3-x^2-(2+\sqrt{2}) x+\sqrt{2}\)
Solution:
Let \(p(x)=x^3-x^2-(2+\sqrt{2}) x+\sqrt{2}\)
The zero of x+1 is -1
\(\begin{aligned}\mathrm{p}(-1)= & (-1)^3-(1)^2-(2+\sqrt{2})(-1)+\sqrt{2} \\
& =-1-1+2+\sqrt{2}+\sqrt{2} \\
& =2 \sqrt{2} \neq 0
\end{aligned}\)
By factor theorem, x +1 is not a factor of
\(x^3-x^2-(2+\sqrt{2}) x+\sqrt{2}\)2. Use the factor theorem to determine whether g(x) is a factor of p(x) in each of the following cases.
1.\(\mathbf{p}(\boldsymbol{x})=2 x^3+x^2-2 x-1, \quad \mathbf{g}(\boldsymbol{x})=\boldsymbol{x}+\mathbf{1}\)
Solution:
g(x)=0
\(\begin{array}{ll}\Rightarrow & x+1=0 \\
\Rightarrow & x=-1
\end{array}\)
∴ zero of g(x) is -1,
Now p(-1)
\(\begin{aligned}& =2(-1)^3+(-1)^2-2(-1)-1 \\
& =-2+1+2-1 \\
& =0
\end{aligned}\)
∴By factor theorem, g(x) is a factor of p(x).
2.\(p(x)=x^3+3 x^2+3 x+1, \quad g(x)=x+2\)
Solution:
\(\begin{aligned}& g(x)=x+2 \\
& g(x)=0 \\
& \Rightarrow \quad x+2=0 \\
& \Rightarrow \quad x=-2
\end{aligned}\)
∴zero of g(x) is -2
Now, \(\begin{aligned}
p(-2) & =(-2)^3+3(-2)^2+3(-2)+1 \\
& =-8+12-6+1 \\
& =-1 \neq 0
\end{aligned}\)
∴By factor theorem, g(x) is a factor of p(x).
3.\(p(x)=x^3-4 x^2+x+6, g(x)=x-3\)
Solution:
\(\begin{aligned}& g(x)=0 \\
& \Rightarrow \quad x-3=0 \\
& \Rightarrow \quad x=3
\end{aligned}\)
∴zero of g(x) is 3
Now,p(3) \(\begin{aligned}
& =3^3-4(3)^2+3+6 \\
& =27-36+3+6 \\
& =0
\end{aligned}\)
∴By factor theorem, g(x) is a factor of p(x).
KSEEB Class 9 Maths Polynomials Solutions
3. Find the value of k, if x-1 is a factor of p(x) in each of the following cases.
1.\(\mathbf{p}(\boldsymbol{x})=x^2+x+\mathbf{k}\)
Solution:
If x-1 is a factor of p(x), then p( 1) = 0.
(By factor theorem)
\(\begin{array}{cc}\Rightarrow & 1^2+1+k=0 \\
\Rightarrow & 2+k=0 \\
\Rightarrow & k=-2
\end{array}\)
2.\(\mathbf{p}(x)=2 x^2+\mathbf{k} x+\sqrt{2}\)
Solution:
If x-1 is a factor of p(x), then p( 1) = 0.
\(2(1)^2+k(1)+\sqrt{2}=0\) \(\begin{aligned}& \Rightarrow \quad 2+k+\sqrt{2}=0 \\
& \Rightarrow \quad k=-2-\sqrt{2}=-(2+\sqrt{2})
\end{aligned}\)
3.\(p(x)=k x^2-\sqrt{2} x+1\)
Solution:
If x-1 is a factor of p(x), then p( 1) = 0.
\(\begin{array}{ll}\Rightarrow & \mathrm{k}(1)^2-\sqrt{2}(1)+1=0 \\
\Rightarrow & \mathrm{k}-\sqrt{2}+1=0 \\
\Rightarrow & \mathrm{k}=\sqrt{2}-1
\end{array}\)
4.\(p(x)=k x^2-3 x+k\)
Solution:
If x-1 is a factor of p(x), then p( 1) = 0.
\(\begin{array}{ll}\Rightarrow & \mathrm{k}(1)^2-3(1)+\mathrm{k}=0 \\
\Rightarrow & \mathrm{k}-3+\mathrm{k}=0 \\
\Rightarrow & 2 \mathrm{k}=3 \\
\Rightarrow & \mathrm{k}=3 / 2
\end{array}\)
4.Factorise
1.\(12 x^2-7 x+1\)
Solution:
\(\begin{aligned}& 12 x^2-4 x-3 x+1 \\
& =4 x(3 x-1)-1(3 x-1) \\
& =(3 x-1)(4 x-1)
\end{aligned}\)
2.\(2 x^2+7 x+3\)
Solution:
\(\begin{aligned}& 2 x^2+6 x+x+3 \\
& 2 x(x+3)+1(x+3) \\
& (x+3)(2 x+1)
\end{aligned}\)
3.\(6 x^2+5 x-6\)
Solution:
\(\begin{aligned}& 6 x^2+9 x-4 x-6 \\
& 3 x(2 x+3)-2(2 x+3) \\
& (2 x+3)(3 x-2)
\end{aligned}\)
4.\(3 x^2-4 x+3 x-4\)
Solution:
\(\begin{aligned}& 3 x^2-4 x+3 x-4 \\
& \quad x(3 x-4)+1(3 x-4) \\
& (3 x-4)(x+1)
\end{aligned}\)
5. Factorise
1.\(x^3-2 x^2-x+2\)
Solution:
Let \(p(x)=x^3-2 x^2-x+2\)
By tril, we find that
\(\begin{aligned}\mathrm{p}(1) & =1^3-2(1)^2-1+2 \\
& =1-2-1+2 \\
& =0
\end{aligned}\)
By factor theorem, (x -1) is a factor of p(x)
Now , \(\begin{aligned}
& x^2(x-1)-x(x-1)-2(x-1) \\
& (x-1)\left(x^2-x-2\right) \\
& (x-1)\left(x^2-2 x+x-2\right) \\
& (x-1)(x(x-2)+1(x-2)) \\
& (x-1)(x-2)(x+1)
\end{aligned}\)
2.\(x^3-3 x^2-9 x-5\)
Solution:
\(x^3-3 x^2-9 x-5\)Let \(p(x)=x^3-3 x^2-9 x-5\)
By tril, we find that
\(\begin{aligned}p(-1) & =(-1)^3-3(-1)^2-9(-1)-5 \\
& =-1-3+9-5 \\
& =0
\end{aligned}\)
By factor theorem, x -(-1) i.e. x+1 is a factor of p(x)
Now \(x^3-3 x^2-9 x-5\)
\(\begin{aligned}& x^2(x+1)-4 x(x+1)-5(x+1) \\
& x^2(x+1)-4 x(x+1)-5(x+1) \\
&(x+1)\left(x^2-4 x-5\right) \\
&(x+1)\left(x^2-5 x+x-5\right) \\
&(x+1)\{x(x-5)+1(x-5)\} \\
&(x+1)(x-5)(x+1)
\end{aligned}\)
3.\(x^3+13 x^2+32 x+20\)
Solution:
Let \(p(x)=x^3+13 x^2+32 x+20\)
By tril, we find that
\(\begin{aligned}p(-1) & =(-1)^3+13(-1)^2+32(-1)+20 \\
& =-1+13-32+20 \\
& =0
\end{aligned}\)
By factor theorem, x -(-1) i.e. x+1 is a factor of p(x)
Now , \(x^3+13 x^2+32 x+20\)
\(\begin{aligned}& =x^2(x+1)+12 x(x+1)+20(x+1) \\
& =(x+1)\left(x^2+12 x-20\right)
\end{aligned}\) \(\begin{aligned}
& =(x+1)\left(x^2+10 x+2 x+20\right) \\
& =(x+1)\{x(x+10)+2(x+10) \\
& =(x+1)(x+10)(x+2)
\end{aligned}\)
4.\(2 y^3+y^2-2 y-1\)
Solution:
Let \(p(y)=2 y^3+y^2-2 y-1\)
By tril, we find that
\(\begin{aligned}p(1) & =2(1)^3+1^2-2(1)-1 \\
& =2+1-2-1 \\
& =0
\end{aligned}\)
By factor theorem, (y-1) is a factor of p(y).
Now ,\(2 y^3+y^2-2 y-1\)
\(\begin{aligned}& =2 y^2(y-1)+3 y(y-1)+1(y-1) \\
& =(y-1)\left(2 y^2+3 y+1\right) \\
& =(y-1)\left(2 y^2+2 y+y+1\right) \\
& =(y-1)\{(2 y(y+1)+1(y+1)\} \\
& =(y-1)(y+1)(2 y+1)
\end{aligned}\)
Polynomials Exercise 2.5
1. Use suitable identities to find the following products.
1.\((x+4)(x+10)\)
Solution:
\(\begin{aligned}& (x+a)(x+b)=x^2+(a+b) x+a b \\
& \quad(x+4)(x+10)=x^2+(4+10) x+4 \times 10 \\
& =x^2+14 x+40
\end{aligned}\)
2.\((x+8)(x-10)\)
Solution:
\(\begin{aligned}& (x+a)(x-b)=x^2+(a-b) x-a b \\
& (x+8)(x-10)=x^2+(8-10) x-8 \times 10 \\
& =x^2-2 x-80
\end{aligned}\)
3.\((3 x+4)(3 x-5)\)
Solution:
\(\begin{aligned}& (x+a)(x-b)=x^2+(a-b) x-a b \\
& (3 x+4)(3 x-5)=(3 x)^2+(4-5)(3 x)-4 \times 5 \\
& =9 x^2-3 x-20 \\
&
\end{aligned}\)
4.\(\left(y^2+3 / 2\right)\left(y^2-3 / 2\right)\)
Solution:
\(\begin{aligned}& (a+b)(a-b)=a^2-b^2 \\
& \begin{aligned}
&\left(y^2+3 / 2\right)\left(y^2-3 / 2\right)=\left(y^2\right)^2-(3 / 2)^2 \\
&=y^4-\frac{9}{4}
\end{aligned}
\end{aligned}\)
5.\((3-2 x)(3+2 x)\)
Solution:
\(\begin{aligned}& (a-b)(a+b)=a^2-b^2 \\
& (3-2 x)(3+2 x)=3^2-(2 x)^2=9-4 x^2
\end{aligned}\)
2.Evaluate the following products without multiplying directly:
1.103 x 107
Solution:
(100 + 3) x (100 + 7)
\((x+a)(x+b)=x^2+(a+b) x+a b\)(100+ 3) (100+ 7)
= 1002 + (3 + 7) (100) + 3 x7
= 10000+ 1000 + 21
= 11021
2. 95 x 96
Solution:
95 x 96 = (100 -5) (100-4)
= (100 x 100) + {(-5) + (-4)} 100 + (-5) (-4)
= 10000-900 + 20
= 9120.
(OR)
95 x 96 = (90 + 5) (90 + 6)
= 902 + (5 + 6) (90) + (5) (6)
= 8100 + 990 + 30
= 9120
KSEEB 9th Standard Maths Chapter 2 Important Questions
Solution:
104 x 96 = (100 + 4) (100 – 4)
\((a+b)(a-b)=a^2-b^2\)= (100)2 – 42
= 1000 – 16
= 9984
3.Factorise the following using appropriate identities.
1.\(9 x^2+6 x y+y^2\)
Solution:
\(9 x^2+6 x y+y^2\) \(\begin{aligned}(3 x)^2 & +2(3 x)(y)+y^2\left\{a^2+2 a b+b^2=(a+b)^2\right\} \\
& =(3 x+y)^2 \\
& =(3 x+y)(3 x+y)
\end{aligned}\)
2.\(4 y^2-4 y+1\)
Solution:
\(\begin{aligned}& 4 y^2-4 y+1=(2 y)^2-2(2 y)(1)+1^2 \\
& =(2 y-1)^2 \quad\left\{a^2-2 a b+b^2=(a-b)^2\right\} \\
& =(2 y-1)(2 y-1)
\end{aligned}\)
3.\(x^2-y^2 / 100\)
Solution:
\(\begin{aligned}& x^2-y^2 / 100 \\
& x^2-\frac{y^2}{100}=\left(x^2\right)-\left(\frac{y}{10}\right)^2 \\
& a^2-b^2=(a+b)(a-b) \\
& x^2-\left(\frac{y}{10}\right)^2=\left(x+\frac{y}{10}\right)\left(x-\frac{y}{10}\right)
\end{aligned}\)
4. Expand each of the following using suitable identities.
1.\((x+2 y+4 z)^2\)
Solution:
\((a+b+c)^2=a^2+b^2+c^2+2 a b+2 b c+2 c a\) \(\begin{gathered}(x+2 y+4 z)^2=x^2+(2 y)^2+(4 z)^2+2 \times x \times 2 y \\
+2 \times 2 y \times 4 z+2 \times 4 z \times x \\
=x^2+4 y^2+16 z^2+4 x y+16 x z+8 x z
\end{gathered}\)
2.\((2 x-y+z)^2\)
Solution:
\((a-b+c)^2=a^2+b^2+c^2-2 a b-2 b c+2 c a\) \(\begin{gathered}(2 x-y+z)^2=(2 x)^2+(y)^2+(z)^2-2 \times 2 x \times y \\
-2 \times y \times z+2 \times 2 x \times z
\end{gathered}\) \(=4 x^2+y^2+z^2-4 x y-2 y z+4 x z\)
3.\((-2 x+3 y+2 z)^2\)
Solution:
\(\begin{gathered}(-a+b+c)^2=a^2+b^2+c^2-2 a b+2 b c-2 c a \\
(-2 x+3 y+2 z)^2=(2 x)^2+(3 y)^2+(2 z)^2 \\
-2 \times 2 x \times 3 y+2 \times 3 y \times 2 z-2 \times 2 z \times 2 x \\
=4 x^2+9 y^2+4 z^2-12 x y-12 y z-8 z x
\end{gathered}\)
4.\((3 a-7 b-c)^2\)
Solution:
\((a-b-c)^2=a^2+b^2+c^2-2 a b+2 b c-2 c a\) \(\begin{gathered}(3 a-7 b-c)^2=(3 a)^2+(7 b)^2+(c)^2-2 \times 3 a \times 7 b \\
+2 \times 7 b \times c-2 \times c \times 3 a \\
=9 a^2+49 b^2+c^2-42 a b+14 b c-6 c a
\end{gathered}\)
5.\((-2 x+5 y-3 z)^2\)
Solution:
\(\begin{aligned}& (-a+b-c)^2=a^2+b^2+c^2-2 a b-2 b c+2 c a \\
& =(2 x)^2+(5 y)^2+(3 z)^2-2 \times 2 x \times 5 y \\
& -2 \times 5 y \times 3 z+2 \times 3 z \times 2 x \\
& =4 x^2+25 y^2+9 z^2-20 x y-30 y z+12 z x \\
&
\end{aligned}\)
6.\(\left[\frac{1}{4} a-\frac{1}{2} b+1\right]^2\)
Solution:
\((a-b+c)^2=a^2+b^2+c^2-2 a b+2 c a-2 b c\)
\(\begin{gathered}
\left(\frac{1}{4} a-\frac{1}{2} b+1\right)^2=\left(\frac{1}{4} a\right)^2+\left(\frac{1}{2} b\right)^2+(1)^2 \\
-2 \times \frac{1}{4} a \times \frac{1}{2} b+2 \times 1 \times \frac{1}{4} a-2 \times \frac{1}{2} b \times 1 \\
=\frac{1}{16} a^2+\frac{1}{4} b^2+1-\frac{1}{4} a b+\frac{1}{2} a-b
\end{gathered}\)
5. Factorise
1.\(4 x^2+9 y^2+16 z^2+12 x y-24 y z-16 x z\)
Solution:
\(\begin{aligned}& 4 x^2+9 y^2+16 z^2+12 x y-24 y z-16 x z \\
& \begin{aligned}
(2 x)^2+(3 y)^2+ & +(-4 z)^2+2(2 x)(3 y) \\
& +2(3 y)(-4 z)+2(-4 z)(2 x) \\
= & {[2 x+3 y+(-4 z)]^2 } \\
= & (2 x+3 y-4 z)^2 \\
= & (2 x+3 y-4 z)(2 x+3 y-4 z)
\end{aligned}
\end{aligned}\)
2.\(2 x^2+y^2+8 z^2-2 \sqrt{2} x y+4 \sqrt{2} y z-8 z x\)
Solution:
\(\begin{aligned}& (-\sqrt{2} x)^2+y^2+(2 \sqrt{2} z)^2+2(-\sqrt{2} x) y+2 y \\
& (2 \sqrt{2}) x+2(2 \sqrt{2} z)(-\sqrt{2} x) \\
& \quad=(-\sqrt{2} x+y+2 \sqrt{2} z)^2 \\
& =(-\sqrt{2} x+y+2 \sqrt{2} z)(-\sqrt{2} x+y+2 \sqrt{2} z)
\end{aligned}\)
6.Write the following cubes in expanded form.
1.\((2 x+1)^3\)
Solution:
\(\begin{aligned}(a+b)^3=a^3 & +b^3+3 a b(a+b) \\
(2 x+1)^3 & =(2 x)^3+1^3+3 \times 2 x \times 1(2 x+1) \\
& =8 x^3+1+6 x(2 x+1) \\
& =8 x^3+1+12 x^2+6 x
\end{aligned}\)
2.\((2 a-3 b)^3\)
Solution:
\(\begin{aligned}&(a-b)^3=a^3-b^3-3 a^2 b+3 a b^2 \\
&=(2 a-3 b)^3=(2 a)^3-(3 b)^3 \\
&-3(2 a)^2(3 b)+3(2 a)(3 b)^2 \\
&=8 a^3-27 b^3-36 a^2 b+54 a b^2
\end{aligned}\)
3.\(\left[\frac{3}{2} x+1\right]^3\)
Solution:
\((a+b)^3=a^3+b^3+3 a^2 b+3 a b^2\) \(\begin{aligned}& =\left(\frac{3}{2} x\right)^3+1^3+3 \times\left(\frac{3}{2} x\right)^2 \times 1+3 \times \frac{3}{2} x \times 1^2 \\
& =\frac{27}{8} x^3+1+\frac{27}{4} x^2+\frac{9 x}{2}
\end{aligned}\)
4.\(\left(x-\frac{2}{3} y\right)^3\)
Solution:
\(\begin{aligned}& (a-b)^3=a^3-b^3-3 a^2 b+3 a b^2 \\
& \left(x-\frac{2}{3} y\right)^3=x^3-\left(\frac{2}{3} y\right)^3-3(x)^2\left(\frac{2}{3} y\right) \\
& +3 \times x \times\left(\frac{2}{3} y\right)^2 \\
& =x^3-\frac{8}{27} y^3-2 x^2 y+\frac{4 x y^2}{3} \\
&
\end{aligned}\)
7. Evaluate the following using suitable identities.
1.\((99)^3\)
Solution:
\((100-1)^3\) \(\begin{aligned}& (a-b)^3=a^3-b^3-3 a^2 b+3 a b^2 \\
& (100-1)^3=(100)^3-1^{3-3}(100)^2 \times 1+ \\
& \quad 3 \times 100 \times 1^2 \\
& =100000-1-30000+300 \\
& =970299
\end{aligned}\)
2.\((102)^3\)
Solution:
\((100+2)^3\) \(\begin{aligned}(a+b)^3= & a^3+b^3+3 a^2 b+3 a b^2 \\
(100+2)^3= & (100)^3+2^3+3(100)^2(2) \\
& +3 \times 100 \times 2^2 \\
= & 1000000+8+60000+1200 \\
= & 1061208
\end{aligned}\)
3.\((998)^3\)
Solution:
\((1000-2)^3\) \(\begin{aligned}& (a-b)^3=a^3-b^3-3 a^2 b+3 a b^2 \\
& =(1000)^3-2^3-3 \times(1000)^2 \times \\
& \quad 2+3 \times 1000 \times 2^2 \\
& =1000000000-8-6000000+12000 \\
& =994011992
\end{aligned}\)
Karnataka Board Class 9 Maths Chapter 2 MCQs
3. 104 x 96
8.Factorise each of the following
1.\(8 a^3+b^3+12 a^2 b+6 a b^2\)
Solution:
\(\begin{aligned}8 a^3 & +b^3+12 a^2 b+6 a b^2 \\
& =(2 a)^3+b^3+3(2 a) b(2 a+b) \\
& =(2 a+b)^3 \\
& =(2 a+b)(2 a+b)(2 a+b)
\end{aligned}\)
2.\(8 a^3-b^3-12 a^2 b+6 a b^2\)
Solution:
\(\begin{aligned}8 a^3 & -b^3-12 a^2 b+6 a b^2 \\
& =(2 a)^3-b^3-3(2 a)(b)(2 a-b) \\
& =(2 a-b)^3 \\
& =(2 a-b)(2 a-b)(2 a-b)
\end{aligned}\)
3.\(27-125 a^3-135 a+225 a^2\)
Solution:
\(\begin{aligned}27 & -125 a^3-135 a+225 a^2 \\
& =(3)^3-(5 a)^3-3(3)(5 a)(3-5 a) \\
& =(3-5 a)^3 \\
& =(3-5 a)(3-5 a)(3-5 a)
\end{aligned}\)
4.\(64 a^3-27 b^3-144 a^2 b+108 a b^2\)
Solution:
\(\begin{aligned}& 64 a^3-27 b^3-144 a^2 b+108 a b^2 \\
& \quad=(4 a)^3-(3 b)^3-3 \times 4 a \times 3 b(4 a-3 b) \\
& \quad=(4 a-3 b)^3 \\
& \quad=(4 a-3 b)(4 a-3 b)(4 a-3 b)
\end{aligned}\)
5.\(27 p^3-\frac{1}{216}-\frac{9}{2} p^2+\frac{1}{4} p\)
Solution:
\(\begin{aligned}27 & p^3-\frac{1}{216}-\frac{9}{2} p^2+\frac{1}{4} p \\
& =(3 p)^3-\left(\frac{1}{6}\right)^3-3 \times 3 p \times \frac{1}{6}\left(3 p-\frac{1}{6}\right) \\
& =\left(3 p-\frac{1}{6}\right)^3 \\
& =\left(3 p-\frac{1}{6}\right)\left(3 p-\frac{1}{6}\right)\left(3 p-\frac{1}{6}\right)
\end{aligned}\)
9. Verify
1.\(x^3+y^3=(x+y)\left(x^2-x y+y^2\right)\)
Solution:
Consider RHS
\(\begin{aligned}& (x+y)\left(x^2-x y+y^2\right) \\
& =x\left(x^2-x y+y^2\right)+y\left(x^2-x y+y^2\right)
\end{aligned}\) \(\begin{aligned}
& =x^3-y^2 y+y y+y x-y y+y^3 \\
& =x^3+y^3
\end{aligned}\)
LHS
2.\(x^3-y^3=(x-y)\left(x^2+x y+y^2\right)\)
Solution:
RHS=
\(\begin{aligned}& (x-y)\left(x^2+x y+y^2\right) \\
& =x\left(x^2+x y+y^2\right)-y\left(x^2+x y+y^2\right) \\
& =x^3+y^2 y+y^2-y x^2-y^2-y^3 \\
& =x^3-y^3
\end{aligned}\)
Hence verified.
10. Factorise each of the following
1.\(27 y^3+125 z^3\)
Solution:
\(\begin{aligned}& 27 y^3+125 z^3 \\
& =(3 y)^3+(5 z)^3 \\
& a^3+b^3=(a+b)\left(a^2-a b+b^2\right) \\
& (3 y)^3+(5 z)^3=(3 y+5 z)\left[(3 y)^2-3 y \times 5 z+(5 z)^2\right] \\
& =(3 y+5 z)\left(9 y^2-15 y z+25 z^2\right) \\
&
\end{aligned}\)
2.\(64 m^3-343 n^3\)
Solution:
\(\begin{aligned}& 64 m^3-343 n^3 \\
& =(4 m)^3-(7 n)^3 \\
& a^3-b^3=(a-b)\left(a^2+a b+b^2\right) \\
& (4 m-7 n)\left[(4 m)^2+4 m \times 7 n+(7 n)^2\right] \\
& (4 m-7 n)\left(16 m^2+28 m n+49 n^2\right)
\end{aligned}\)
11. Factorise \(27 x^3+y^3+z^3-9 x y z\)
Solution:
\(27 x^3+y^3+z^3-9 x y z\) \(\begin{aligned}& a^3+b^3+c^3-3 a b c=(a+b+c)\left(a^2+b^2+c^2-a b-b c-c a\right) \\
&(3 x)^3+y^3+z^3-3(3 x) y z= \\
&=(3 x+y+z)\left[(3 x)^2+y^2+z^2-3 x \times y-y \times z-z \times 3 x\right] \\
&=(3 x+y+z)\left(9 x^2+y^2+z^2-3 x y-y z-3 x z\right)
\end{aligned}\)
12. Verify that \(x^3+y^3+z^3-3 x y z\)
\(=\frac{1}{2}(x+y+z)\left[(x-y)^2+(y-z)^2+(z-x)^2\right]\)
Solution:
LHS=
\(x^3+y^3+z^3-3 x y z\) \(\begin{aligned}& =(x+y+z)\left(x^2+y^2+z^2-x y-y z-z x\right) \\
& =\frac{1}{2}(x+y+z) 2\left(x^2+y^2+z^2-x y-y z-z x\right) \\
& =\frac{1}{2}(x+y+z)\left(2 x^2+2 y^2+2 z^2-2 x y-2 y z-2 z x\right) \\
& =\frac{1}{2}(x+y+z)\left\{\left(x^2-2 x y+y^2\right)+\left(y^2-2 y z+z^2\right)\right. \\
& \left.\quad+\left(z^2-2 z x+x^2\right)\right\}
\end{aligned}\)
13.If x+y+z=0, show that \(x^3+y^3+z^3\) = 3xyz
Solution:
We know that
\(\begin{aligned}& x^3+y^3+z^3-3 x y z \\
& =(x+y+z)\left(x^2+y^2+z^2-x y-y z-z x\right) \\
& =(0)\left(x^2+y^2+z^2-x y-y z-z x\right)
\end{aligned}\)
(x + y + z = 0)
\(\Rightarrow \quad x^3+y^3+z^3=3 x y z\)14. Without actually calculating the cubes, find the value of each of the following.
1. \((-12)^3+(7)^3+(5)^3\)
Solution:
(-12) + (7) + (5) = 0
= -1260
2.\((28)^3+(-15)^3+(-13)^3\)
Solution:
\((28)^3+(-15)^3+(-13)^3=3(28)(-15)(-13)\)(-12) +(7) + (5) = 0
= -1260
15. Give possible expressions for the length & breadth of each of the following rectangles in which their areas are given:
1. Area = \(25 a^2-35 a+12\)
2. Area = \(35 y^2+13 y-12\)
Solution:
1.
\(\begin{gathered}
25 a^2-35 a+12 \\
=25 a^2-20 a-15 a+12
\end{gathered}\)
\(\begin{aligned}
& =5 a(5 a-4)-3(5 a-4) \\
& =(5 a-4)(5 a-3)
\end{aligned}\)
∴ The possible expressions for the length & breadth of the rectangle are 5a-3 & 5a-4
2. \(\begin{aligned}
& 35 y^2+13 y-12 \\
& =35 y^2+28 y-15 y-12 \\
& =7 y(5 y+4)-3(5 y+4) \\
& =(5 y+4)(7 y-3)
\end{aligned}\)
∴ The possible expressions for the length & breadth of the rectangle are7y – 3 & 5y + 4
16.What are the possible expressions for the dimensions of the cuboids whose volumes are given below?
1. Volume : \(3 x^2-12 x\)
2. Volume : \(12 k y^2+8 k y-20 k\)
Solution:
\(\begin{aligned}& 3 x^2-12 x \\
& \quad=3 x(x-4)
\end{aligned}\)
∴ The possible expressions for the dimensions of the cuboid are 3, x& x- 4.
2.\(12 k y^2+8 k y-20 k\)
Solution:
\(12 k y^2+8 k y-20 k\) \(\begin{aligned}& =4 k\left(3 y^2+2 y-5\right) \\
& =4 k\left(3 y^2+5 y-3 y-5\right) \\
& =4 k\{y(3 y+5)-1(3 y+5)\} \\
& =4 k(3 y+5)(y-1)
\end{aligned}\)
∴ The possible expressions for the dimensions of the cuboid are 4k, 3y + 5 &y- 1
Additional Problems
Choose the correct answer from the following:
1. The zeroes of the polynomial \(x^2(x-1)\) are :
- 0.1
- 0,0,1
- 0,1,1
- 1,1,1
Solution: 2. 0,0,1
2.If p(x) = \(2 x^3+5 x^2-3 x-2\) is divided by (x-1), then, the remainder is
- 2
- p(-l)
- p(0)
- p(2)
Solution: 1. 2
3.Zero of the zero polynomial is:
- 0
- 1
- any real number
- not defined
Solution: 3. any real number
4.Which of the following is a polynomial in one variable?
- \(3-x^2+x\)
- \(\sqrt{3 x}+4\)
- \(x^3+y^3+7\)
- \(x+\frac{1}{x}\)
Solution: 1. \(3-x^2+x\)
5.The value of the polynomial \(x^2-x-1\) at x=-1 is
- -3
- 1
- -1
- 0
Solution: 2. 1
6.The co-efficient of \(x^2\) in \(\left(3 x+x^3\right)\left(x+\frac{1}{x}\right)\) is
- 3
- 1
- 4
- 2
Solution: 3. 4
Class 9 Maths Polynomials KSEEB Guide
7.If the area of a rectangle is \(4 x^2+4 x-3\), then its possible dimensions are:
- \(2 x-3,2 x+1\)
- \(2 x-1,2 x+3\)
- \(3 x+1,2 x-3\)
- \(3 x-1,2 x+3\)
Solution: 2. \(2 x-1,2 x+3\)
8. Product of \(\left(x-\frac{1}{x}\right)\left(x+\frac{1}{x}\right)\left(x^2+\frac{1}{x^2}\right)\) is
- \(x^4+\frac{1}{x^4}\)
- \(x^3+\frac{1}{x^3}-2\)
- \(x^4-\frac{1}{x^4}\)
- \(x^2+\frac{1}{x^2}+2\)
Solution: 3. \(x^4-\frac{1}{x^4}\)
9. If \(x^2+k x+6=(x+2)(x+3)\) for all x, the value of k is
- 1
- -1
- 5
- 3
Solution: 3. 5
10.Apolynomial having one term is called
- monomial
- binomial
- trinomial
- zero polynomial
Solution: 1. monomial
One Mark Questions
1. What is the degree of the polynomial \(\left(x^3+5\right)\left(4-x^5\right)\) ?
Solution:
Degree of \(x^3+5=3\)
Degree of \(4-x^5=5\)
Degree of \(\left(x^3+5\right)\left(4-x^5\right)=3+5=8\)
2. Find p(o), if \(p(y)=y^2-y+1\)
Solution:
\(p(y)=y^2-y+1\) \(\begin{aligned}\mathrm{p}(0) & =0^2-0+1 \\
& =1
\end{aligned}\)
3.If \(x^{11}+101\) is divided by x+ 1, then what remainder do we get
Solution:
consider x+1 = 0
x= -1
Then remainder
\(\begin{aligned}& =x^{11}+101 \\
& =(-1)^{11}+101 \\
& =-1+101 \\
& =100
\end{aligned}\)
4. Factorise : \(x^3-3 x^2\)
Solution: \(x^2(x-3)\)
5. Write the factors of the polynomial \(x^2+5 \sqrt{2} x+12\)
Solution:
\(x^2+5 \sqrt{2} x+12\) \(\begin{aligned}& =x^2+3 \sqrt{2} x+2 \sqrt{2} x+12 \\
& =x(x+3 \sqrt{2})+2 \sqrt{2}(x+3 \sqrt{2}) \\
& =(x+3 \sqrt{2})(x+2 \sqrt{2})
\end{aligned}\)
6. Write the co-efficient of y in the expansion of \((x+2)^3\)
Solution:
\(\begin{aligned}& (x+2)^3=x^3+2^3+3 \times x \times 2(x+2) \\
& =x^3+8+6 x(x+2) \\
& =x^3+8+6 x^2+12 x
\end{aligned}\)
∴ co-efficient of y in the expansion of \((x+2)^3\) is 6.
7. Simplify : \(\left(a+\frac{1}{2}\right)\left(a+\frac{3}{2}\right)\)
Solution:
\(\begin{aligned}\left(a+\frac{1}{2}\right)\left(a+\frac{3}{2}\right) & =a^2+\frac{3}{2} a+\frac{1}{2} a+\frac{3}{4} \\
= & a^2+2 a+\frac{3}{4}
\end{aligned}\)
8. Find the value of k, if x-2 is a factor of p(x)=\(2 x^2+3 x-k\).
Solution:
x-2 is a factor of p(x), then p(2) = \(2(2)^2+3(2)-k=0\)
=8+6-k=0
k= 14
Two Mark Questions
1. If f{x) = 3x+ 5 , evaluate f{l)- f(5)
Solution:
f(x) = 3x+5
then, f( 7) = 3×7 + 5
= 21+5 =26
f(5) = 15 + 5 = 20
∴ f(7)- f(5) = 26-20 = 6
2. Find the value of the polynomial \(p(x)=x^3-3 x^2-2 x+6 \text { at } x=\sqrt{2}\)
Solution:
\(p(x)=x^3-3 x^2-2 x+6\)Then
\(\begin{aligned}p(\sqrt{2}) & =(\sqrt{2})^3-3(\sqrt{2})^2-2(\sqrt{2})+6 \\
& =2 \sqrt{2}-6-2 \sqrt{2}+6 \\
& =0
\end{aligned}\)
3.Find the remainder when \(x^3+x^2+x+1\) is divided by \(x-\frac{1}{2}\) , using remainder theorem.
Solution:
\(p(x)=x^3+x^2+x+1\) \(\text { put } x-\frac{1}{2}=0 \quad \Rightarrow x=\frac{1}{2} \text { in } p(x)\)Remainder
\(\begin{aligned}& =p\left(\frac{1}{2}\right) \\
& =\left(\frac{1}{2}\right)^3+\left(\frac{1}{2}\right)^2+\frac{1}{2}+1 \\
& =\frac{1}{8}+\frac{1}{4}+\frac{1}{2}+1
\end{aligned}\) \(=\frac{1+2+4+8}{8}=\frac{15}{8}\)
4. Factorise : \(x^4-125 x y^3\)
Solution:
\(\begin{aligned}& x^4-125 x y^3 \\
& =x\left(x^3-125 y^3\right) \\
& =x\left[(x)^3-(5 y)^3\right] \\
& =x(x-5 y)\left(x^2+(5 y)^2+x \times 5 y\right) \\
& =x(x-5 y)\left(x^2+25 y^2+5 x y\right)
\end{aligned}\)
5. Factorise : \((x+2)^2+p^2+2 p(x+2)\)
Solution:
\(\begin{aligned}& (x+2)^2+p^2+2 p(x+2) \\
& =(x+2)^2+p^2+2 \times(x+2) \times p
\end{aligned}\) \(=(x+2+p)^2\)
6. Factorise : \(x^4-y^4\)
Solution:
\(\begin{aligned}& x^4-y^4 \\
& =\left(x^2\right)^2-\left(y^2\right)^2 \\
& {\left[a^2-b^2=(a+b)(a-b)\right]} \\
& =\left(x^2+y^2\right)\left(x^2-y^2\right) \\
& =\left(x^2+y^2\right)(x+y)(x-y)
\end{aligned}\)
7. If a, b, c are all non-zero & a + b + c = 0 prove \(\frac{a^2}{b c}+\frac{b^2}{a c}+\frac{c^2}{a b}=3\)
Solution:
\(\mathrm{LHS}=\frac{a^2}{b c}+\frac{b^2}{a c}+\frac{c^2}{a b}=\frac{a^3+b^3+c^3}{a b c}=\frac{3 a b c}{a b c}\)=3
=RHS
8. Factorise : \(9 x^2+6 x y+y^2\)
Solution:
\(\begin{aligned}9 x^2+6 x y+y^2 & =(3 x)^2+2 \times 3 x+y+y^2 \\
& =(3 x+y)^2
\end{aligned}\)
9. If x & y are two positive real numbers such that \(x^2+4 y^2=17\) & xy = 2, then find the value of (x+2y).
Solution:
\(\begin{aligned}& (x+2 y)^2=x^2+4 y^2+2 \times x \times 2 y \\
& \quad=17+4 \times 2 \\
& \quad=25
\end{aligned}\) \(x+2 y=\sqrt{25}=5\)
10. Without actually calculating the cubes, evaluate \(14^3+13^3-27^3\).
Solution:
a= 14, b = 13, c = -27
a+b+c = 14+ 13-27 = 0
∴\(a^3+b^3+c^3=3 a b c∴\)
\(\begin{aligned}14^3+13^3-27^3 & =3 \times 14 \times 13 \times-27 \\
& =-14742
\end{aligned}\)
Three Mark Questions
1. Polynomial \(3 x^3-5 x^2+k x-2\)& \(-x^3-x^2+7 x+k\) leave the same remainder when divided by x+ 2 . Find the value at k.
Solution:
Let \(p(x)=3 x^3-5 x^2+k x-2\)
\(q(x)=-x^3-x^2+7 x+k\)put x + 2 = 0
x = -2 in p(x) & q(x)
\(\begin{aligned}\mathrm{p}(-2) & =3(-2)^3-5(-2)^2+\mathrm{k}(-2)-2 \\
& =-24-20-2 \mathrm{k}-2 \\
& =-2 \mathrm{k}-46 \\
\mathrm{q}(-2) & =-(-2)^3-(-2)^2+7(-2)+\mathrm{k} \\
& =8-4-14+\mathrm{k} \\
& =-10+\mathrm{k}
\end{aligned}\)
∴p (x) & q(x) leave the same remainder when divided by x+ 2
\(\begin{aligned}& \Rightarrow \quad-2 \mathrm{k}-46=-10+\mathrm{k} \\
& \Rightarrow \quad-46+10=\mathrm{k}+2 \mathrm{k} \\
& \Rightarrow-36=3 \mathrm{k} \\
& \Rightarrow \quad 3 \mathrm{k}=-36
\end{aligned}\) \(\begin{aligned}
& k=\frac{-36}{3}=-12 \\
& ∴k=-12
\end{aligned}\)
2. Factorise : \(9 x^2+y^2+z^2-6 x y+2 y z-6 x z\), Hence find its value when x= 1, y= 2 & z= -1
Solution:
\(9 x^2+y^2+z^2-6 x y+2 y z-6 x z\) \(\begin{aligned}= & (-3 x)^2+y^2+z^2+2 \times(-3 x)(y) \\
& +2 \times y \times z+2(-3 x)(z) \\
= & (-3 x+y+z)^2
\end{aligned}\)
If x=l, y= 2, z= -1 then
\(\begin{aligned}(-3 x+y+z)^2 & =[-3 \times 1+2+(-1)]^2 \\
& =(-3+2-1)^2 \\
& =(-2)^2 \\
& =4
\end{aligned}\)
3. If x- a is the factor of \(3 x^2-m x-n x\) then prove that \(a=\frac{m+n}{3}\)
Solution:
\(p(x)=3 x^2-m x-n x\)If (x- a) is a factor of p(x), then p(a) = 0
ie \(\begin{aligned}
& 3(a)^2-m(a)-n(a)=0 \\
& 3 a^2-m a-n a=0 \\
& a[3 a-m-n]=0, \quad a \neq 0
\end{aligned}\)
Since 3a-m-n = 0
∴ 3a = m+ n
\(a=\frac{m+n}{3}\)4. If (3x-2)is a factor of \(3 x^2+x^2-20 x+12\) find other factors.
Solution:
Let \(p(x)=3 x^3+x^2-20 x+12\)
Given 3 x – 2 is a factor of p(x)
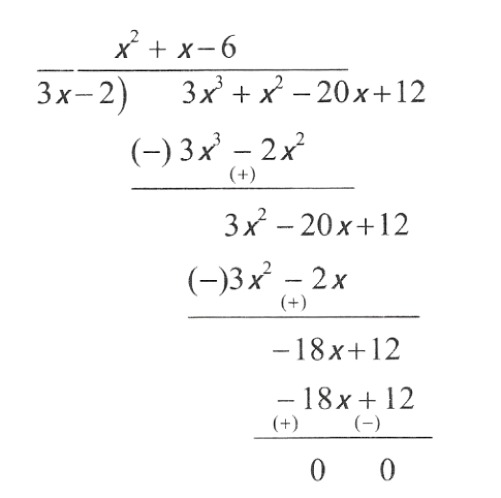
& x^2+x-6 \\
= & x^2+3 x-2 x-6 \\
= & x(x+3)-2(x+3)
\end{aligned}\)
∴The other factors are (x+3)&(x-2)
5. If \(a^2+b^2+c^2=280\) & \(a b+b c+c a=\frac{9}{2}\) then find the value of \((a+b+c)^3\)
Solution:
\(\begin{aligned}
& (a+b+c)^2=a^2+b^2+c^2+2(a b+b c+c a) \\
& =280+2 \times \frac{9}{2} \\
& =280+9 \\
& =289 \\
& a+b+c=\sqrt{289} \\
& =17 \\
& (a+b+c)^3=17^3 \\
& =4913 \\
&
\end{aligned}\)
6. 1) using suitable identity, evaluate \((98)^3\)
2) which mathematical concept is used in this problem.
3) What is its value.
Solution :
1) \(\begin{equation}
(98)^3=(100-2)^3
\end{equation}\)
w . k . t \((a-b)^3=a^3-b^3-3 a^2 b+3 a b^2\)
\(\begin{aligned}(100-2)^3 & =(100)^3-2^3-3(100)^2 x 2 + 3 x\times 2+ \\
100 \times 2^2 & =1000000-8-60000+1200 \\
& =941192
\end{aligned}\)
2)Algebraic identities
3)satisfaction solves the identity crisis among people.
7. If \(x+\frac{1}{x}=3\), then find \(x^3+\frac{1}{x^3}\)
Solution:
Consider \(x+\frac{1}{x}=3\)
Cubing both the sides we get
\(\begin{aligned}& \left(x+\frac{1}{x}\right)^3=3^3 \\
& x^3+\left(\frac{1}{x}\right)^3+3 \times x \times \frac{1}{x}\left(x+\frac{1}{x}\right)=27 \\
& x^3+\frac{1}{x^3}+3 \times 3=27 \\
& x^3+\frac{1}{x^3}+9=27 \\
& x^3+\frac{1}{x^3}=27-9 \\
& =18
\end{aligned}\)
8. Using remainder theorem factorise \(6 x^3-25 x^2+32 x-12\)
Solution:
Factors of 12 = (±1, ± 2, ± 3, ± 4, ± 6, ± 12)
\(\begin{aligned}p(x) & =6 x^3-25 x^2+32 x-12 \\
p(2) & =6(2)^3-25(2)^2+32 \times 2-12 \\
& =48-100+64-12 \\
& =112-112=0
\end{aligned}\)
∴ x – 2 is a zero of p(x), x – 2 is a factor of p(x)
\(\begin{array}{rl}6 x^3-2 & 5 x^2+32 x-12 \\
& =6 x^2(x-2)-13 x(x-2)+6(x-2) \\
& =(x-2)\left(6 x^2-13 x+6\right) \\
& =(x-2)\left(6 x^2-9 x-4 x+6\right) \\
& =(x-2)[3 x(2 x-3)-2(2 x-3)] \\
& =(x-2)(2 x-3)(3 x-2)
\end{array}\)
Four Mark Questions
1. If \(f(x)=x^2+5 x+7\), evaluate \(f(2)-f(-1)+f\left(\frac{1}{3}\right)\)
Solution:
\(f(x)=x^2+5 x+7\)Then
\(\begin{aligned}f(2) & =2^2+5 \times 2+7 \\
& =4+10+7 \\
& =21
\end{aligned}\) \(\begin{aligned}
f(-1) & =(-1)^2+5(-1)+7 \\
& =1-5+7 \\
& =3 \\
f\left(\frac{1}{3}\right)= & \left(\frac{1}{3}\right)^2+5\left(\frac{1}{3}\right)+7 \\
& =\frac{1}{9}+\frac{5}{3}+7 \\
= & \frac{9+15+63}{9} \\
& =\frac{87}{9}
\end{aligned}\)
∴ \(\begin{aligned}
& f(2)-f(1)+f\left(\frac{1}{3}\right) \\
& =21-3+\frac{87}{9} \\
& =\frac{189-27+87}{9}=\frac{249}{9}
\end{aligned}\)
2. Find the quotient & remainder when\(6 x^4+11 x^3+13 x^2-3 x+27\) is divided by 3 x+ 4 . Also check the remainder obtained by using remainder theorem
Solution:
Thus quotient = \(2 x^3+x^2+3 x-5\)
and remainder = 47
Let F(x) = \(6 x^4+11 x^3+13 x^2-3 x+27\)
Zero of \(3 x+4 \text { is } \frac{-4}{3}\)
Remainder \(=P\left(\frac{-4}{3}\right)\)
\(\begin{aligned}& =6\left(\frac{-4}{3}\right)^4+11\left(\frac{-4}{3}\right)^3+13\left(\frac{-4}{3}\right)^2-3\left(\frac{-4}{3}\right)+27 \\
& =\frac{512}{27}-\frac{704}{27}+\frac{208}{9}+4+27 \\
& =\frac{512-704+624}{27}+31 \\
& =\frac{432}{27}+31 \\
& =16+31=47
\end{aligned}\)
KSEEB Class 9 Maths Chapter 2 Exercise Solutions
3. If x=2& x=0 are zeroes of the polynomial \(2 x^3-5 x^2+p x+b\), then find the value of p & b.
Solution:
\(P(x)=2 x^3-5 x^2+P x+b\)x= 2 and x= 0 are the zeroes of polynomials
then
=16-20 + 2P + b = 0
= 2P + b = 4 _______(1)
and \(P(0)=2 \times 0^3-5(0)^2+P(0)+b=0\)
=0-0+0+b=0
b = 0 ________(2)
From (1) & (2), we get
2P + b = 4
2P + 0 = 4
2P = 4
\(\mathrm{P}=\frac{4}{2}=2\)∴P = 2 and b = 0
4. Find the values of a & b, if \(x^2-4\) is a factor of \(a x^4+2 x^3-3 x^2+b x-4\)
Solution:
Let \(P(x)=a x^4+2 x^3-3 x^2+b x-4\)
\(x^4-4 \text { (or) }(x-2)(x+2)\) is a factor of p (x) then put x -2 in p(x)
\(\begin{array}{rl}\mathrm{P}(2)= & a(2)^4+2(2)^3-3(2)^2+\mathrm{b}(2)-4=0 \\
= & 16 a+16-12+2 b-4=0 \\
& 16 a+2 b=0 \\
\div 2 & 8 a+b=0 ……………(1)
\end{array}\)
again put x=-2 in p(x)
\(\begin{array}{rl}\mathrm{P}(-2) & =a(-2)^4+2(-2)^3-3(-2)^2+\mathrm{b}(-2)-4=0 \\
& =16 a-16-12-2 b-4=0 \\
& =16 a-2 b=32 \\
\div 2 & 8 a-b=16 \ldots \ldots \ldots \ldots(2)
\end{array}\)
Adding eqn (1) & (2) we get
\(\begin{aligned}& 8 a+b=0 \\
& \underline{8 a-b}=16
\end{aligned}\) \(\begin{aligned}
16 a & =16 \\
a & =16 / 16=1
\end{aligned}\)
by eqn(l) we get
\(\begin{aligned}& 8 \times 1+b=0 \\
& 8+b=0 \\
& b=-8 \\
& ∴ a=1 \text { and } b=-8
\end{aligned}\)
5. Factorise completely : \(x^8-y^8\)
Solution:
\(x^8-y^8\) \(=\left(x^4\right)^2-\left(y^4\right)^2\)∴\(a^2-b^2=(a+b)(a-b)\)
\(\begin{aligned}& =\left(x^4+y^4\right)\left(\left(x^2\right)^2-\left(y^2\right)^2\right) \\
& =\left(x^4+y^4\right)\left(x^2+y^2\right)\left(x^2-y^2\right) \\
& =\left(x^4+y^4\right)\left(x^2+y^2\right)(x+y)(x-y)
\end{aligned}\)
6. If a-b = 7& \(a^2+b^2=85\) find \(a^3-b^3\).
Solution:
a-b = 7& \(a^2+b^2=85\)
consider a-b=7
square both side
\(\begin{aligned}& (a-b)^2=7^2 \\
& a^2-2 a b+b^2=49 \\
& 85-2 a b=49 \\
& 85-49=2 a b \\
& 2 a b=36 \\
& a b=\frac{36}{2}=18
\end{aligned}\)
then,
\(\begin{aligned}a^3-b^3 & =(a-b)\left(a^2+b^2+a b\right) \\
& =(7)(85+18) \\
& =7 \times 103 \\
a^3-b^3 & =721
\end{aligned}\)
