KSEEB Solutions For Class 9 Maths Chapter 11 Construction

KSEEB Solutions For Class 9 Maths Chapter 11 Construction

Steps to solve a construction problem

A solution to the construction problem may be divided into the following parts
1. We need to specify clearly

1. What is given?
2. What is required?

2. Steps of construction
This is the sequence of steps that we actually use in drawing the construction. These steps should be specified in the proper order.
3. Proof: For the construction, we need to reason out why the construction is valid.

Construction Exercise 11.1

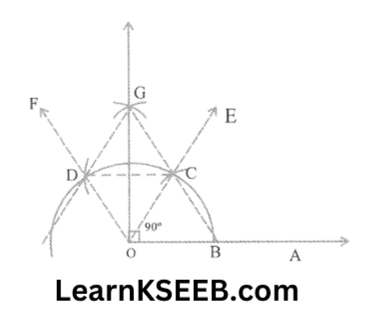
1. Construct an angle of 90° at the initial point of a given ray & justify the construction.

Solution:

Steps of Construction:

1. Taking O as centre & some radius, draw an arc of a circle, which intersects O A, say at a point B.

2. Taking B as centre & with the same radius as before, draw an arc, intersecting the previously draw an arc, say at point C.

KSEEB Class 9 Maths Chapter 11 Solutions PDF

3. Taking C as the centre & with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.

4. Draw the ray OE passing through C, then \(\lfloor\mathrm{EOA}\) = 60°

Class 9 Social Science

Class 9 Science

Class 9 Maths

 

5. Draw the ray OF passing through D, then \(\lfloor\mathrm{FOE}\) = 60°

6. Next, taking C & D as centres and with a radius more than 1/2CD, draw arcs to intersect each other. Say at G.

7. Draw the ray OG, this ray OG is the bisector of the angle \(\lfloor\mathrm{FOE}\), i.e.,

\(\lfloor\mathrm{FOG}\) = \(\lfloor\mathrm{EOG}\) = 1/2\(\lfloor\mathrm{FOE}\) =1/2×60 = 30°

thus \(\lfloor\mathrm{GOA}\) = \(\lfloor\mathrm{GOE}\) + \(\lfloor\mathrm{EOA}\) = 30 + 60 = 90°

Justification:

1) Join BC

Then OC = OB = BC (by construction)

∴ ΔCOB is an equilateral triangle

∴ ACOB =60°

\(\lfloor\mathrm{EOA}\) = 60°

2) Join CD

then OD = OC = OD

\(\lfloor\mathrm{DOC}\) is an equilateral triangle

∴ \(\lfloor\mathrm{DOC}\) = 60°

\(\lfloor\mathrm{FOE}\) = 60°

3) Join CG & DG

In ΔODG & ΔOCG

OD = OC (Radii)

DG = CG (arcs of equal radius)

OG OG (common)

∴ ΔODG ≅ ΔOCG (SSS rule)

\(\lfloor\mathrm{DOG}\) = \(\lfloor\mathrm{COG}\) (CPCT)

∴ \(\lfloor\mathrm{FOG}\) = \(\lfloor\mathrm{EOG}\)=

\(=\frac{1}{2}\left\lfloor\mathrm{FOE}=\frac{1}{2} \times 60=30^{\circ}\right.\)

Thus \(\lfloor\mathrm{GOA}\) = \(\lfloor\mathrm{GOE}\) + \(\lfloor\mathrm{EOA}\)

= 30 + 60-90°

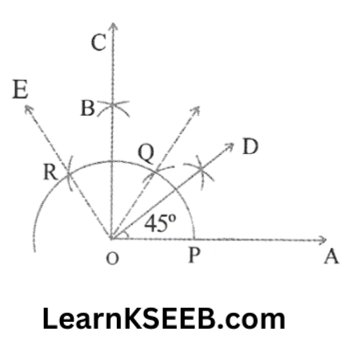
2. Construct an angle of 45° at the initial point of a given ray & justify the construction.

Solution: Steps of construction.

1. Draw a ray OA.

2. With O as the centre & any convenient radius draw an arc, cutting O A at P.

3. With P as the centre & the same radius draw an arc cutting the arc drawn in step 2 at Q.

4. With Q as the centre & the same radius as in steps 2 & 3, draw an arc, cutting the arc drawn in step 3 at R.

5. With Q as the centre & the same radius draw an arc.

Karnataka 9th Standard Maths Chapter 11 Notes

6. With R as the centre & the same radius, draw an arc, cutting the arc drawn in step 5 at B.

7. Draw OB & produce it to C, \(\lfloor\mathrm{AOC}\) is the angle measure 90°.

8. Draw OD, the bisector of \(\lfloor\mathrm{AOB}\)

9. The angle \(\lfloor\mathrm{AOD}\) so obtained is the required angle measure 45°

Justification : Join OQ & OR

We have \(\lfloor\mathrm{QOA}\) = \(\lfloor\mathrm{ROQ}\) = 60°

\(\lfloor\mathrm{BOQ}\) = 1/2\(\lfloor\mathrm{ROQ}\) = 60/2 = 30°

also \(\lfloor\mathrm{BOA}\) = \(\lfloor\mathrm{QOA}\) + \(\lfloor\mathrm{BOQ}\)

= 60 + 30 = 90°

OD is the bisector of \(\lfloor\mathrm{BOA}\)

∴ \(\lfloor\mathrm{DOA}\) = 1/2\(\lfloor\mathrm{BOA}\) = 1/2×90° = 45°

Karnataka 9th Standard Maths Chapter 11 Notes

3. 1) 30°

Solution:

Steps of construction :

1. Draw the given ray PQ, taking P as the centre & with some radius, and draw an arc of a circle which intersects PQ at R.

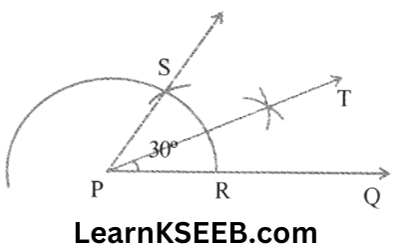
2. Taking R as the centre & with the same radius as before, draw an arc intersecting the previously drawn arc at point S.

3. Taking P & S as centre & with a radius more than 1/2 RS, draw arcs to intersect each other at T. Join PT which is the required ray making 30° with the given ray PQ.

2) 221/2°

Solution:

1. Take the given ray PQ, and draw an arc of some radius, taking point P as its centre which intersects PQ at R.

2. Taking R as the centre & with the same radius as before, draw an arc intersecting the previously drawn arc at S.

3. Taking S as the centre & with the same radius as before, draw an arc intersecting the arc at T.

4. Taking S & T as the centre, draw an arc of the same radius to intersect each other at U.

5. Join PU, and let it intersect the arc at point V.

6. From R & U, draw arcs with a radius of more than 1/2 RU to intersect each other at W and join PW.

7. Let it intersect the arc at X, Taking X & R as centre & radius more than 1/2 RX, draw arcs to intersect each other at Y. Join PY which is the required ray making 22 0 with the given ray PQ.

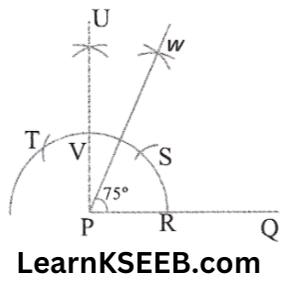
3)15°

Steps of construction:

1. Draw the given ray PQ. Taking P as the centre & with some radius, draw an arc of a circle which intersects PQ at R.

2. Taking R as the centre & with the same radius as before, draw an arc intersecting the previously drawn arc at point S.

3. Taking R & S as the centre & with a radius of more than 1/2 RS, draw arcs to intersect each other at T. Join PT.

4. Let it intersect the arc at U, Taking U & R as centre & with a radius more than 1/2RU, and draw an arc to intersect each other at V. Join PV which is the required ray making 15° with the given ray PQ.

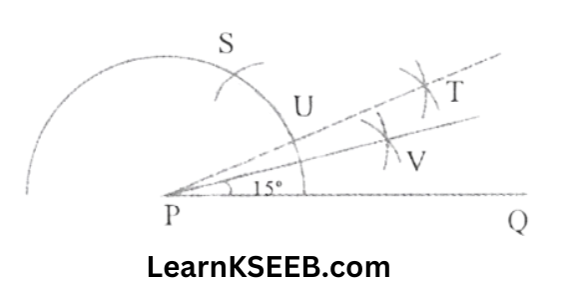
4. 1) 75°

Steps: 1) Take the given ray PQ. Draw an arc of some radius taking point P as its centre, which intersects PQ at R.

2. Taking R as the centre & with the same radius as before, Draw an arc intersecting the previously drawn arc at S.

3. Taking S as the centre & with the same radius as before draw an arc intersecting the arc at T.

4. Taking S & T as the centre, draw an arc of the same radius to intersect each other at U.

5. Join PU. Let it intersect the arc at V.Taking S & V as centres draw arcs with a radius of more than 1/2 SV. Let these intersect each other at W. Join PW which is the required ray making 75° with the given ray PQ.

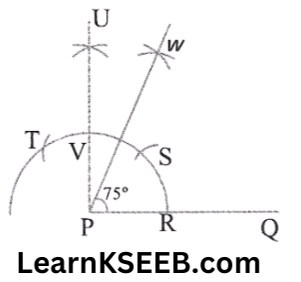
The angle so formed can be measured with the help of a protractor.

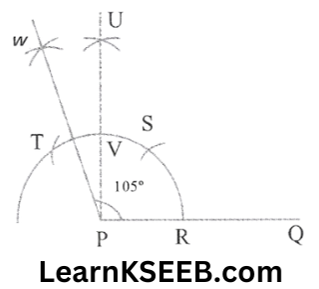
2) 105°

Steps:

1. Take the given ray PQ, Draw an arc of some radius taking point P as its centre, which in intersects PQ at R

2. Taking R as the centre & with the same radius as before, draw an arc intersecting the previously drawn arc at S.

3. Taking S as the centre & with the same radius as before, draw an arc intersecting the arc at T.

KSEEB Class 9 Maths Construction Solutions

4. Taking S & T as the centre, draw an arc of the same radius to intersect each other at U.
5. Join PU. let it intersect the arc at V. Taking T & V as the centre, draw arcs with a radius of more than 1/2 TV, and Let these arcs intersect each other at W.

Join PW which is the required ray making 105° with the given ray PQ

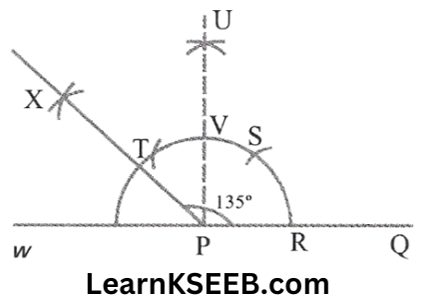
3) 135°

Steps: 1. Taking the given ray PQ. Extend PQ on the opposite side of Q. Draw a semicircle of some radius taking point P as its centre, which intersects PQ at R & W

2. Taking R as the centre & with the same radius as before, draw an arc intersecting the previously drawn arc at S.

3. Taking S as the centre & with the same radius as before draw an arc intersecting the arc at T.

4. Taking S & T as the centre, draw an arc of the same radius to intersect each other at U.

5. Join PU, and let it intersect the arc at V. Taking V & W as centre & with a radius of more than 1/2 VW draw arcs to intersect each other at X. Join PX, which is the required ray making

135° with the given line PQ

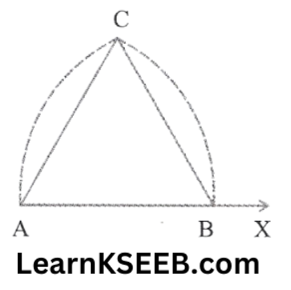
5. Steps: 1. Take a ray AX with initial point A.

From AX, cut off AB = 6cm.

2. Taking A as the centre & radius (6cm) draw an arc of a circle, which intersects AX, say at point B.

3. Taking B as the centre & with the same radius as before, draw an arc intersecting the previously drawn arc, say at point C.

4. Draw the ray AE, passing through C.

5. Draw the ray BF passing through C.

Then ΔABC is the required Δle with a given side of 6cm.

Justification:

AB=BC (by construction)

AB=AC (by construction)

AB = BC = CA

∴ ΔABC is an equilateral Δle.

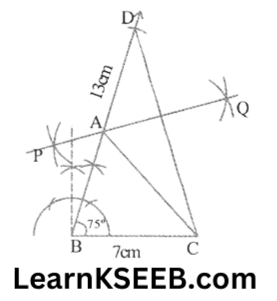
Construction Exercise11.3

1. Construct a ΔABC in which BC = 7cm, \(\lfloor B\) = 75° & AB + AC = 13cm

Solution: Steps of construction.

1. Draw the base BC = 7cm

2. At the point B make an angle XBC =75°

3. Cut a line segment BD equal to AB +AC (= 13 cm) from the ray BX

4. Join DC

5. Draw perpendicular bisector PQ of CD to intersect BD at a point A, Jo in AC then ABC is the required Δle.

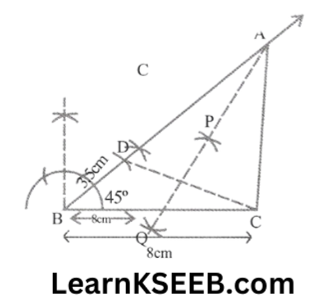
2. Construct a ΔABC in which BC = 8cm, \(\lfloor B\) = 45° & AB – AC = 3.5cm

Solution:

Steps: 1. Draw the base BC = 8cm.

2. At the point B make an angle XBC = 45°

3. Cut the line segment BD equal to AB – AC (= 3.5cm) from the ray BX.

4. Join DC

5. Draw the perpendicular bisector, say PQ of DC

6. Let it intersect BX at a point A

7. Join AC

Then ABC is the required Δle.

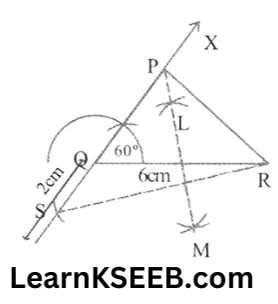
3. Construct a ΔPQR in which QR = 6cm, \(\lfloor Q\) = 60° & PR – PQ = 2cm

Solution:

Steps: 1. Draw the base QR = 6cm

2. At the point Q make an \(\lfloor\mathrm{XQR}\) = 60°

3. cut line segment QS = PR – PQ (2cm) from the line QX extended on the opposite side of line segment QR

4. Join SR

5. Draw the perpendicular bisector LM of SR

6. Let LM intersect QX at P

7. Join PR then PQR is the required Δle.

KSEEB Class 9 Maths Construction Solutions

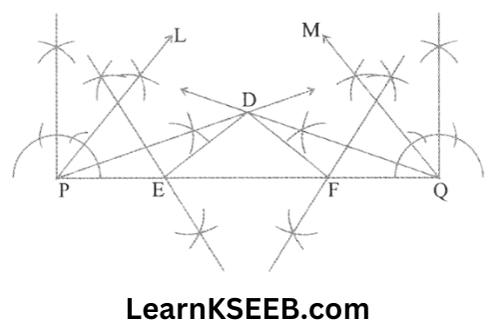
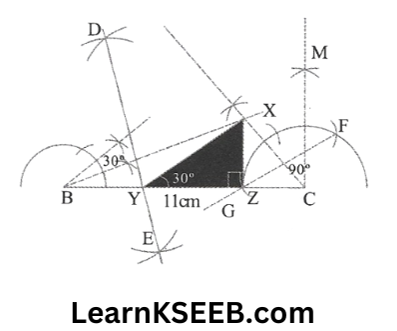
4. Construct a AXYZ which \(\lfloor Y\) = 30°, \(\lfloor Z\) = 90° & xy + yz + zx = 11cm

Soution:

Steps:

1. Draw a line segment BC = XY + YZ + ZX (11cm)

2. Make \(\lfloor\mathrm{LBC}\) = \(\lfloor Y\) = 30°&

\(\lfloor\mathrm{MCB}\) = \(\lfloor Z\) = 90°

3. Bisect \(\lfloor\mathrm{LBC}\) & \(\lfloor\mathrm{MCB}\) , let these bisectors meet at a point X

KSEEB 9th Standard Maths Chapter 11 Important Questions

4. Draw perpendicular bisectos DE of XB & FG of XC

5. Let DE intersect BC at y & FG intersect BC at z.

6. Join xy & xz, then xyz is the required Δle.

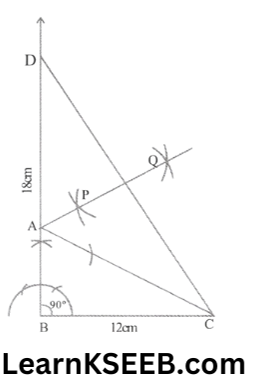
5. Construct a right Δle whose base is 12cm & sum of its hypotenuse & other side is 18cm.

Solution:

Steps: 1. Draw the base BC = 12cm

2. At point B, make an \(\lfloor\mathrm{XBC}\)= 90°

3. cut a line segment BD = AB + AC (= 18cm) from the ray BX

4. Join DC

5. Draw the perpendicular bisector PQ of CD to intersect BD at a point A

6. Join AC, then ABC is the required right Δle.

Construction EXTRA SUMS

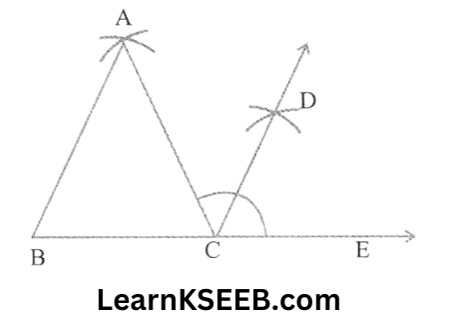
1. Draw any exterior angle of a Δle using a compass, and bisects it.

Solution: steps of construction:

1. construct a ΔABC

2. mark an exterior angle outside the ΔABC & name the point as E

3. Now, ACE is the exterior angle

4. Draw a bisector of \(\lfloor\mathrm{ACE}\)

 

2. Draw \(\lfloor\mathrm{DEF}\) = 72°, construct 3/4 \(\lfloor\mathrm{DEF}\) using a compass.

Solution: Steps: 1. Draw \(\lfloor\mathrm{DEF}\) = 72°, using a protractor

2. bisect it, let the bisected angle be \(\lfloor\mathrm{DEK}\)

3. Again bisect \(\lfloor\mathrm{DEK}\)

4 Now \(\lfloor\mathrm{GEF}\) = 3/4\(\lfloor\mathrm{DEF}\)

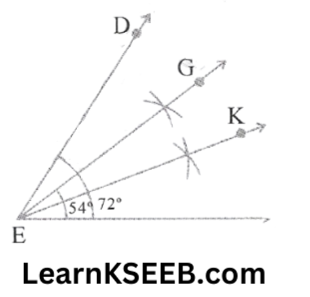
KSEEB Class 9 Maths Chapter 11 Exercise Solutions

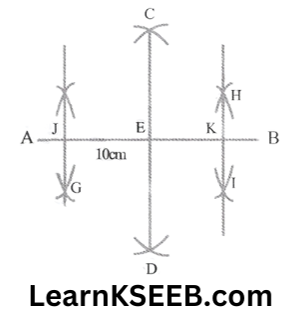
3. Draw a line segment SR of length 10cm. Divide it into 4 equal parts using a compass.

Solution: Steps :

1. We draw a line of length AB = 10cm

2. Then divide it into half as take an arc of more than half the length of the line & place the point at A & make two arcs on both sides of the line. Now repeat the same for point B.

3. This gives, AE = EB.

4. Now divide AE & EB to get four equal parts of our line, AB = 10cm.

5. By repeating step (2) for points AE & EB, we get FG & HI

∴ length of our sections AJ = JE = EK = KB = 2.5cm.

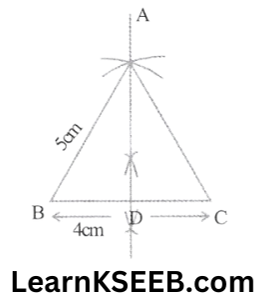
4. Construct a ΔABC ,such that AB = 5cm, BC = 4cm & median AD = 5cm.

Solution:

Steps: 1. Draw a line segment BC = 4cm

2. bisects BC at D

3. From B & D, draw arcs at a distance of 5cm each on the same side of BC, cutting each other at A.

4. Join AB &AC

Then ΔABC is the required Δle.

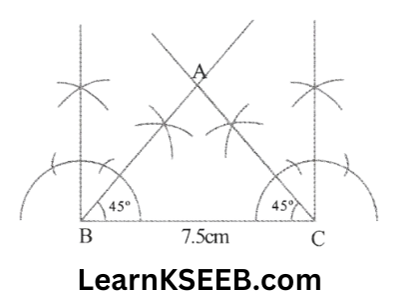
5. Construct an isosceles Δle whose base = 7.5cm & the vertical angle is twice each of its base angles.

Solution: Let each of the base angles =x°

∴ the vertical angle = 2x

∴ x°+ x°+2x° = 180°

=> 4x° = 180°

=> x°=45°

Each of the base angle is 45° & the vertical angle is 90°

Class 9 Maths Construction KSEEB Guide

Steps of construction

1. Draw BC = 7.5cm

2. AT B, construct \(\lfloor\mathrm{CBA}\) = 45° & at C, construct \(\lfloor\mathrm{BCA}\) = 45°, so that BA & CA intersect at A. ΔABC is required Δle.

6. Construct a ΔXYZin which \(\lfloor Y\) = 90°, XY = 8cm & XY – ZY = 4cm.

Solution:

Steps: 1. Draw the base XY = 8cm

2. at the point y, construct an angle of 90°

(i.e \(\lfloor\mathrm{PYX}\) = 90°)

3. cut a line segment YQ = 4cm from the line segment YP (as XY > ZY & XY – ZY=4cm) Join QX

4. Draw a perpendicular bisector of line segment QX, which intersects XY at Z. Join ZX

∴ ΔXYZ is the required Δle.

Karnataka Board Class 9 Maths Chapter 11 MCQs

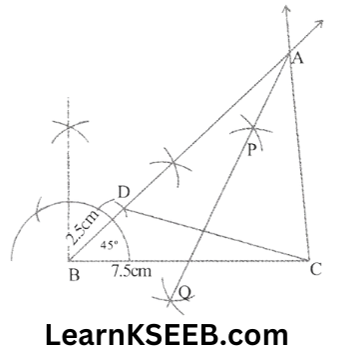
7. Construct a ΔABC in which BC = 7.5cm, \(\lfloor B\) = 45° & AB -AC = 2.5cm

Solution:

Steps: 1. Draw the line segment BC = 7.5cm & at point B construct an angle of 45°, i.e.

\(\lfloor\mathrm{XBC}\) = 45°

2. cut the line segment BD = 2.5cm (equal to AB – AC) on ray BX.

3. Join DC & draw the perpendicular bisector PQ of DC

4. The perpendicular intersects BX at point A. Join AC. ΔABC is the required Δle.

8. Construct an isosceles right Δle with a perimeter of 11cm.

Solution:

Steps: 1. Draw a line segment PQ = 11 cm.

2. at P, construct \(\lfloor\mathrm{LPQ}\) = 45° & at Q.

\(\lfloor\mathrm{PQM}\) = 45°

Karnataka Board Class 9 Maths Chapter 11 MCQs

3. Draw bisectors of these angles & mark their point of intersection as D

4. Draw perpendicular bisector of PD & QD which intersect PQ at points E & F respectively.

5. Join DE &DF, thus ADEF is the required Δle.