KSEEB Solutions For Class 9 Maths Chapter 10 Circles

KSEEB Solutions For Class 9 Maths Chapter 10 Circles Points to Remember

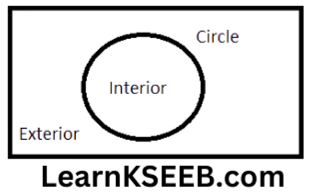
• A circle is a collection of all those points in a plane, each one of which is at a constant distance from a fixed point in the plane.
• The fixed point is called the centre & the constant distance is called the radius of the circle
• All the points lying inside a circle are called its interior points & all those points which lie outside the circle are called its exterior points.
• The collection of all interior points of a circle is
  called the interior of the circle while the collection of all exterior points of a circle is called the exterior of the circle.

• The line segment joining any two points on the circle is called a chord of the circle.
• A chord of the circles which passes through the centre of the circle is called the diameter.
• Diameter is the longest chord & all diameters are equal in length & each is equal to two times the radius.
• The part of the circle between any two points on it is called an arc of the circle.
• There are two arcs joining two points on a circle. One is longer while the other is smaller. The former is called the major arc while the latter is called the minor arc.
• If the two points are the two ends of a diameter, then the two arcs are equal.
• The length of the complete circle is called its circumference.
• The region between a chord & its corresponding arc is called a segment. There are two types of segments – minor & major.
• The region between an arc & the two radii joining the centre to the endpoints of the arc is called a sector.
• There are two types of sectors – major & minor.
• A minor arc corresponds to the minor sector & minor segment whereas a major arc corresponds to the major sector & major segment.
• If the two arcs are equal, then both segments & both sectors become the same & equal is called a semicircular region.

• Equal chords of a circle subtend equal angles at the centre. Conversely, if the angles subtended by the chords of a circle at the centre are equal then the chords are equal.
• The perpendicular from the centre of a circle to a chord bisects the chord. Conversely, the line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
• There is one & only one circle passing through three given non-collinear points.
• An Infinite number of circles can be drawn through a given point.

Class 9 Social Science

Class 9 Science

Class 9 Maths

• Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres)
• Conversely, chords equidistant from the centre of a circle are equal in length.
• The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.

KSEEB Class 9 Maths Chapter 10 Solutions PDF

• Angles in the same segment of a circle arc equal. Conversely, if a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment then the four points lie on a circle (i.e., they are con-cyclic)
• Angles in the semi-circle are right angles.
• The sum of either pair of opposite angles of a cyclic quadrilateral is 180, conversely, if the sum of a pair of opposite angles of a quadrilateral is 180°, then the quadrilateral is cyclic.
• If one side of a cyclic quadrilateral is produced, then the exterior angle is equal to its interior opposite angle.

KSEEB Class 9 Maths Chapter 10 Solutions PDF

Circles Exercise 10.1

Fill in the blanks :

1. The centre of a circle lies in interior of the circle, (exterior/interior)
2. A point, whose distance from the centre of a circle is greater than its radius lies in exterior of the circle, (exterior/ interior)
3. The longest chord of a circle is the diameter of the circle.
4. An arc is a semicircle, when its ends are the ends of a diameter.
5. Segment of a circle is the region between an arc & the chord of the circle.
6. A circle divides the plane, on which it lies, in three parts.

Karnataka 9th Standard Maths Chapter 10 Notes

1. Line segment joining the centre at any point on the circle is a radius of the circle.
Solution: True, Because all points on the circle are equidistant from its centre.

2. A circle has only finite number of equal chords.
Solution: False, because there are infinitely many points on the circle. So for each point on the circle, a point can be determined on the circle at a given distance from that point resulting into greatly many equal chords.

3. If a circle is divided into three equal arcs, each is a major arc.
Solution: False, because for each arc, the remaining arc will have a greater length.

4. A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
Solution: True, because of the definition of diameter.

5. Sector is the region between the chord & its corresponding arc.
Solution: False, because the sector is the region between an arc & two radii.

6. A circle is a plane figure
Solution: True, as it is a part of a plane.

Circles Exercise 10.2

1. Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Solution: Given: AB & CD are two equal chords of congruent circles with centres O & O’ respectively.

To prove: \(\lfloor\mathrm{AOB}\) = \(\lfloor\mathrm{COD}\)

Proof: In ΔOAB & ΔO’CD

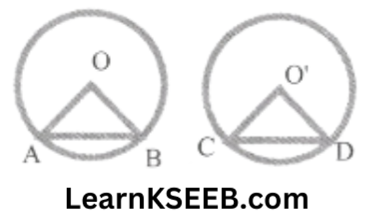
OA = O’ C (Radii of congruent circles)

OB = O’D (Radii of congruent circles)

AB = CD (given)

∴ ΔOAB ≅ ΔO’CD (SS8 rule)

∴ \(\lfloor\mathrm{AOB}\) = \(\lfloor\mathrm{CO’D}\) (C.P.C.T.)

2. Prove that if chords of congruent circles sub¬tend equal angles at their centres, then the chords are equal.

Solution: Given : \(\lfloor\mathrm{AOB}\) & \(\lfloor\mathrm{CO’D}\) are the two equal angles subtended by the chords AB & CD of two congruent circles with centres O & O’ respectively.

To prove: AB = CD

Proof: In ΔOAB ≅ ΔO’CD

OA = O’C (Radii of congruent circles)

OB = O’D (Radii of congruent circles)

∴ \(\lfloor\mathrm{AOB}\) = \(\lfloor\mathrm{CO’D}\) (given)

∴ ΔOAB ≅ ΔO’CD (SAS rule)

∴ AB = CD (C.RC.T.)

Circles Exercise 10.3

1. Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?

Solution: Each pair has at the most two common points.
1)

No point common
2)

One point common
3)

Two points common
∴ The maximum number of common points is two.

2. Suppose you are given a circle. Give a construction to find its centre.

Solution: Steps of construction.

1) Take any 3 points P, Q & R on the circle.

2) Join PQ&QR

3) Draw the perpendicular bisectors of PQ & QR. Let these intersect at O. Then, O is the centre of the circle.

3. If two circles intersect at two points. Prove that their centres lies on the perpendicular
bisector of the common chord.

Solution:

Given: Two circles with centres O & P intersecting at A &B.

To prove: OP is the perpendicular bisector of AB.

Construction: Join OA, OB,

PA&PB.

Let OP intersect AB at M.

Proof: In ΔOAP & ΔOBP

OA = OB (Radii of a circle)

PA=PB (Radii of a circle)

OP = OP (common)

∴ ΔOAP ≅ ΔOBP (SSS rule)

∴ \(\lfloor\mathrm{AOP}\) = \(\lfloor\mathrm{BOP}\) (CPCT)

=> \(\lfloor\mathrm{AOM}\) = \(\lfloor\mathrm{BOM}\) ………………(1)

In ΔAOM & ΔBOM

OA = OB (radii of a circle)

\(\lfloor\mathrm{AOM}\) = \(\lfloor\mathrm{BOM}\) (from(1))

OM = OM (common)

∴ ΔAOM ≅ ΔBOM (SAS rule)

∴ (AM = BM) (CPCT) ……………..(2)

& \(\lfloor\mathrm{AMO}\) = \(\lfloor\mathrm{BMP}\) (CPCT) (3)

But \(\lfloor\mathrm{AMO}\) + \(\lfloor\mathrm{BMP}\) = 180° (linear pair Axiom)

∴ \(\lfloor\mathrm{AMO}\) = \(\lfloor\mathrm{BMO}\) = 90° …………….(4)

∴ OM i.e OP is the perpendicular bisector of AB [(from (2) & (4)]

Circles Exercise 10.4

1. Two circles of radii 5cm & 3cm intersect at two points & the distance between their centres is 4cm. Find the length of the common chord.

Solution:

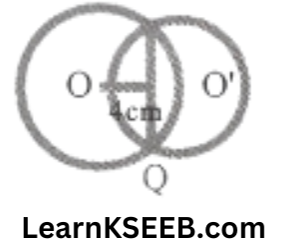
We know that if two circles intersect each other at two points, then the joining their centres is the perpendicular bisector of their common chord.

∴ Length of the common chord

= PQ = 2O’P

= 2 x 3 = 6cm

2. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.

Solution: Given: A circle with centre O. Its two equal chords AB & CD intersect at E.

To prove: AE = DE & CE = BE

Construction: Draw OM ⊥ AB & ON ⊥ CD. Join OE.

Proof: In ΔOME & ΔONE

OM = ON

(Equal chords of a circle are equidistant from the centre)

OE = OE (common)

∴ ΔOME ≅ ΔONE (RHS)

∴ ME = NE (C.P.C.T.)

=> AM + ME = DN + NE

(∵ AM = DN = 1/2 AB = 1/2CD )

=> AE = DE

=> AB – AE = CD – DE (∵ AB = CD)

=> BE = CE

Karnataka 9th Standard Maths Chapter 10 Notes

3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.

Solution:

Given: Two equal chords AB & CD of a circle with centre O intersect within the circle. Their point of intersection is E.

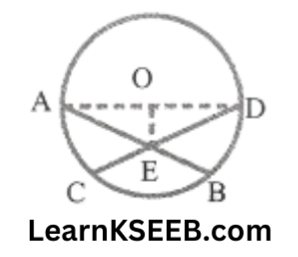
To prove: \(\lfloor\mathrm{OEA}\) = \(\lfloor\mathrm{OED}\)

Construction: Join OA & OD

Proof: In ΔOEA & ΔOED

OE = OE (common)

OA = OD (Radii of a circle)

AE = DE (proved above in Q – 2)

∴ ΔOEA ≅ ΔOED (SSS rule)

∴ \(\lfloor\mathrm{OEA}\) = \(\lfloor\mathrm{OED}\) (C.P.C.T)

4. If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C & D. Prove that AB = CD

Solution: Given: A line intersects two concentric circles with centre O at A, B, C & D

To prove: AB = CD

Construction: Draw OM ⊥ BC

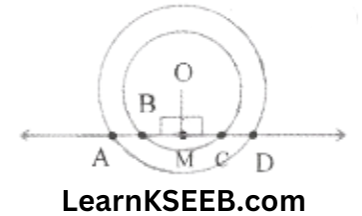
Proof: The perpendicular drawn from the centre of a circle to a chord bisects the chord.

∴ AM = DM ………………..(1)

& BM = CM …………………(2)

Subtracting (2) from (1), we get

AM – BM = DM – CM

=> AB = CD

5. Three girls Reshma, Salma & Mandip are playing a game by standing on a circle of radius 5m drawn in a park, Reshma throws a ball to Salma, Salma to Mandip, and Mandip to Reshma. If the distance between the Reshma & Salma & between Salma & Mandip is 6m each, what is the distance between Reshma & Mandip?

Solution: Let KR = xm

ar(ΔORS) = ar(ΔORK) + ar(ΔSRK)

\(=\frac{(\mathrm{OK})(\mathrm{KR})}{2}+\frac{(\mathrm{KS})(\mathrm{KR})}{2}\) \(=\frac{(\mathrm{KR})(\mathrm{OK}+\mathrm{KS})}{2}=\frac{(\mathrm{KR})(\mathrm{OS})}{2}\)

\(=\frac{(x)(5)}{2}\) …………………….(1)

Again, ar(ΔORS)\(=\frac{\mathrm{RS} \times \mathrm{OL}}{2}=\frac{6 \times \mathrm{OL}}{2}\)

\(=6 \times \frac{\sqrt{\mathrm{OR}^2-\mathrm{RL}^2}}{2}\)

(by pythagora’s Theorem)

\(=6 \times \frac{\sqrt{\left(5^2\right)-\left(\frac{6}{2}\right)^2}}{2}\) \(=6 \times \frac{\sqrt{25-9}}{2}=3 \times \sqrt{16}\)

= 3 x 4

= 12m ……………….(2)

from eq (1) & (2)

\(\frac{(x)(5)}{2}=12\)

=> \(x=\frac{12 \times 2}{5}=\frac{24}{5}=4.8 m\)

=> KR = 4.8m

∴ RM = 2KR = 2 x 4.8 = 9.6m

Hence the Distance between Reshma & Mandip is 9.6m.

6. A circular park of a radius of 20m is situated in a colony. Three boys Ankur, Syed & David are sitting at equal distances on its boundary each having a toy telephone in his hands to talk to each other. Find the length of the string of each phone.

Solution: Here A, B, and C are the three A points where three boys and sitting.

∴ ΔABC is an equilateral triangle

In an equilateral triangle, the circumcentre is the point of intersection of medians.

O divides AD in the ratio 2 :1

Hence, AO = 20m

then OD = 10m

Also median is same as the altitude for an equilateral triangle.

In ΔODC

\(\mathrm{OC}^2=\mathrm{OD}^2+\mathrm{DC}^2\)

=> \(20^2=10^2+\mathrm{DC}^2\)

=> \(\mathrm{DC}^2\) = 400- 100 = 300

=> DC = \(\sqrt{100 \times 3}\)

=> DC =\(10 \sqrt{3} m\)

=> BC = 2DC = 2 x \(10 \sqrt{3}\) = \(20 \sqrt{3} m\) Length of the string of each phone

= \(20 \sqrt{3} m\)

Circles Exercise 10.5

1. In figure, A, B & C are three points on a circle with centre O such that. If D is a point on the circle other than the arc ABC. Find \(\lfloor\mathrm{ADC}\).

Solution: \(\lfloor\mathrm{ADC}\)=1/2\(\lfloor\mathrm{AOC}\)

(The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle)

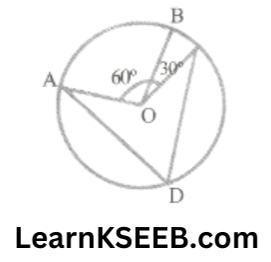
\(\lfloor\mathrm{ADC}\) = 1/2(\(\lfloor\mathrm{AOB}\) + \(\lfloor\mathrm{BOC}\))

=1/2(60 + 30°)

=1/2×90°

=45°

KSEEB Class 9 Maths Circles Solutions

2. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc & also at a point on the major arc.

Solution: OA= OB = AB (given)

∴ ΔOAB is equilateral

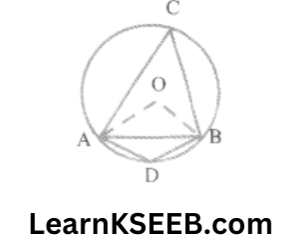
∴ \(\lfloor\mathrm{AOB}\) = 60°

\(\lfloor\mathrm{ACB}\) = 1/2\(\lfloor\mathrm{AOB}\)

=1/2x 60 = 30°

Now, ADBC is a cyclic quadrilateral

∴ \(\lfloor\mathrm{ADB}\) + \(\lfloor\mathrm{ACB}\) = 180°

(The sum of either pair of opposite angles of a cyclic quadrilateral is 180°)

=> \(\lfloor\mathrm{ADB}\) + 30°=180°=>\(\lfloor\mathrm{ADB}\) = 150°

3. In figure, |PQR = 100° where P, Q & R are points on a circle with centre O. Find \(\lfloor\mathrm{OPR}\).

Solution: Take a point S in the major arc.

Join PS & RS.

PQRS is a cyclic quadrilateral

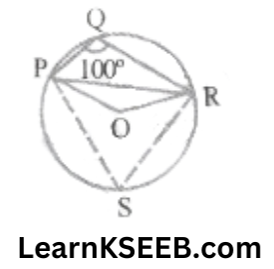
∴ \(\lfloor\mathrm{PQR}\) + \(\lfloor\mathrm{PSR}\) = 180°

(The sum of either pair of P opposite angles of a cyclic quadrilateral is 180°)

=> 100° + \(\lfloor\mathrm{PSR}\) = 180°

=> \(\lfloor\mathrm{PSR}\) = 180°-100°= 80° …………………(1)

Now, \(\lfloor\mathrm{PQR}\) = 2\(\lfloor\mathrm{PSR}\)

(The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle)

= 2 x 80°= 160° …………………..(2) (using (1))

In ΔOPR

OP = OR (Radii of a circle)

\(\lfloor\mathrm{OPR}\) = \(\lfloor\mathrm{ORP}\)

(angles opposite to equal sides of a Δle are equal)

In ΔOPR

\(\lfloor\mathrm{OPR}\) + \(\lfloor\mathrm{ORP}\) + \(\lfloor\mathrm{POR}\) = 180°

=> \(\lfloor\mathrm{OPR}\) + \(\lfloor\mathrm{OPR}\) + 160°=180°

(using (2) & (1))

=> 2\(\lfloor\mathrm{OPR}\) +160° = 180°

=> 2\(\lfloor\mathrm{OPR}\) = 180° -160° = 20

=> \(\lfloor\mathrm{OPR}\) = 20/2 = 10°

4. In figure, \(\lfloor\mathrm{ABC}\) = 69°, \(\lfloor\mathrm{ACB}\) = 31°, find \(\lfloor\mathrm{BDC}\).

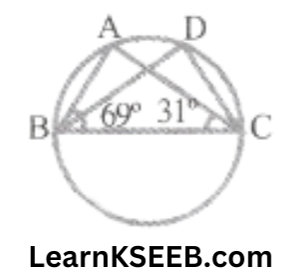
Solution: In ΔABC

\(\lfloor\mathrm{BAC}\)+ \(\lfloor\mathrm{ABC}\) + \(\lfloor\mathrm{ACB}\) = 180°

(Sum of all the angles of a triangle is 180°)

=> \(\lfloor\mathrm{BAC}\) +69°+ 31° = 180°

=> \(\lfloor\mathrm{BAC}\) + 100° = 180°

\(\lfloor\mathrm{BAC}\) =180° – 100° = 80° ………………….(1)

Now, \(\lfloor\mathrm{BDC}\) = \(\lfloor\mathrm{BAC}\) = 80° (using (1))

(Angles in the same segment of a circle are equal)

5. In figure, A, B, C & D are four points on a circle. AC & BD intersect at a point E. Such that \(\lfloor\mathrm{BEC}\) = 130°&\(\lfloor\mathrm{ECC}\) = 20°. Find \(\lfloor\mathrm{BAC}\).

Solution: \(\lfloor\mathrm{CED}\) +\(\lfloor\mathrm{BEC}\) = 180°

(linear pair)

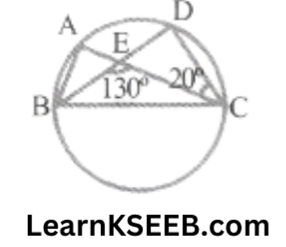
=> \(\lfloor\mathrm{CED}\)+ 130° = 180°

=> \(\lfloor\mathrm{CED}\) = 180°-130° = 50° ………………..(1)

\(\lfloor\mathrm{ECD}\) = 20° ………………….(2)

In ΔCED

\(\lfloor\mathrm{CED}\) + \(\lfloor\mathrm{ECD}\) + \(\lfloor\mathrm{CDE}\) =180°

(sum of all the angles of a Δle is 180°)

=> 50°+20°+\(\lfloor\mathrm{CDE}\) =180° (using (1) & (2))

=> 70° + \(\lfloor\mathrm{CDE}\) =180°

=> \(\lfloor\mathrm{CDE}\) =180°-70°

=> \(\lfloor\mathrm{CDE}\) =110° …………………(3)

Now, \(\lfloor\mathrm{BAC}\) = \(\lfloor\mathrm{CDE}\)

(angles in the same segment of a circle are equal)

∴ \(\lfloor\mathrm{BAC}\) = 110° (using (3))

6. ABCD is a cyclic quadrilateral whose diagonals intersect at point E. If \(\lfloor\mathrm{DBC}\) = 70°, \(\lfloor\mathrm{BAC}\) = 30°, find \(\lfloor\mathrm{BCD}\), further if AB = BC, find \(\lfloor\mathrm{ECD}\).

Solution: \(\lfloor\mathrm{CDB}\) = \(\lfloor\mathrm{BAC}\)

(angles in the same segment of a circle are equal)

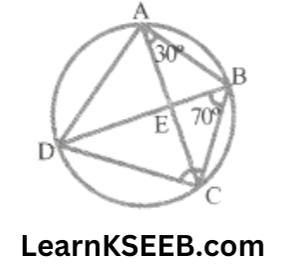
= 30° ……………….(1)

\(\lfloor\mathrm{DBC}\) = 70° (2)

In ΔBCD

\(\lfloor\mathrm{BCD}\) + \(\lfloor\mathrm{DBC}\) + \(\lfloor\mathrm{CDB}\) = 180°

(angle sum property)

=> \(\lfloor\mathrm{BCD}\) + 70° + 30° = 180°

=> \(\lfloor\mathrm{BCD}\) = 180°-100°

=> \(\lfloor\mathrm{BCD}\) = 80° (3)

In ΔABC

AB = BC

∴ \(\lfloor\mathrm{BCA}\) + \(\lfloor\mathrm{BAC}\) (angles opposite to equal sides of a Δle are equal)

= 30° …………………….(4) (∵ \(\lfloor\mathrm{BAC}\) = 30° given)

Now, \(\lfloor\mathrm{BCD}\) = 80° (from (3)) given

=> \(\lfloor\mathrm{BCA}\) +\(\lfloor\mathrm{ECD}\) = 80°

=> 30°+\(\lfloor\mathrm{ECD}\) = 80°

=> \(\lfloor\mathrm{ECD}\) = 80°-30°

=> \(\lfloor\mathrm{ECD}\) = 50°

7. If diagonals of a cyclic quadrilateral are the diameter of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

Solution:

In ΔOAB & ΔOCD

OA = OC (Radii of a circle)

OB = OD (Radii of a circle)

\(\lfloor\mathrm{AOB}\) = \(\lfloor\mathrm{COD}\) (V.O.A.)

∴ ΔOAB ≅ ΔOCD (SAS rule)

∴ AB = CD (C.RC.T.)

=> arc AB = arc CD …………………(1)

||ly, we can show that

arc AD =arc CB ………………..(2)

adding (1) & (2), we get

arc AB + arc AD = arc CD + arc CB

=> arc BAD = arc BCD

=> BD divides the circle into two equal parts (each a semicircle)

\(\lfloor A\) = 90°, \(\lfloor C\) = 90° (angle in a semicircle is 90°)

||ly, we can show that \(\lfloor B\) = 90°,\(\lfloor D\) = 90°

∴ \(\lfloor A\) = \(\lfloor B\) = \(\lfloor C\) = \(\lfloor D\) = 90°

∴ ABCD is a rectangle.

8. If the non-parallel sides of a trapezium are equal, prove that it is cyclic. Prove that an isosceles trapezium is cyclic.

Solution:

Given: ABCD is a trapezium whose two non-parallel sides AD & BC are equal.

To prove: Trapezium ABCD is cyclic.

Construction: Draw BE || AD

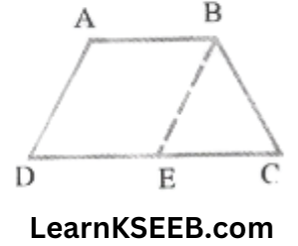
Proof: AB || DE (given)

AD || BE (by construction)

Quadrilateral ABCD is a ||gm.

∴ \(\lfloor\mathrm{BAD}\) = \(\lfloor\mathrm{BED}\) ………………(1) (opp. angle of a ||gm)

& AD = BE …………………(2) (opp. angle of a ||gm)

But AD-BC …………………(3) (given)

from (2) & (3)

BE = BC

\(\lfloor\mathrm{BEC}\) = \(\lfloor\mathrm{BCE}\) (angles opposite to equal sides) …………………..(4)

\(\lfloor\mathrm{BEC}\) +\(\lfloor\mathrm{BED}\) = 180° (linear pair)

=> \(\lfloor\mathrm{BCE}\) + \(\lfloor\mathrm{BAD}\) = 180° (from (4) & (1)

=> Trapezium ABCD is cyclic (If a pair of opposite angles of a quadrilateral is 180°, then the quadrilateral is cyclic)

9. Two circles intersect at two points B & C. Through B, two line segments ABD & PBQ are drawn to intersect the circles at A, D & P, and Q respectively. Prove that \(\lfloor\mathrm{ACP}\) = \(\lfloor\mathrm{QCD}\) .

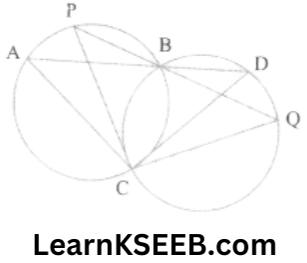
Solution:

Given: Two circles intersect at two points B & C, through B, two line segments ABD & PBQ are drawn to intersect the circles at A, D & P, Q respectively.

To prove: \(\lfloor\mathrm{ACP}\) = \(\lfloor\mathrm{QCD}\)

Proof: \(\lfloor\mathrm{ACP}\) = \(\lfloor\mathrm{ABP}\) ……………….(1)

(Angles in the same segment of a circle are equal)

\(\lfloor\mathrm{QCD}\) = \(\lfloor\mathrm{QBD}\) …………………(2)

(Angles in the same segment of a circle are equal)

\(\lfloor\mathrm{ABP}\) = \(\lfloor\mathrm{QBD}\) ……………………(3)

(Vertically opposite angles)

From(1), (2) & (3)

\(\lfloor\mathrm{ACP}\) – \(\lfloor\mathrm{QCD}\)

10. If circles are drawn taking two sides of triangles as diameters, Prove that the point of intersection of these circles lies on the third side.

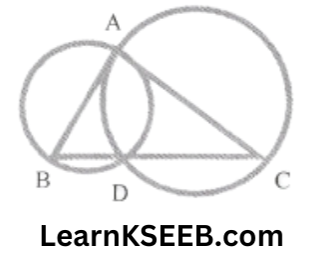
Solution:

Given: Circles are described with sides AB & AC of a ΔABC as diameters. They intersect at point D.

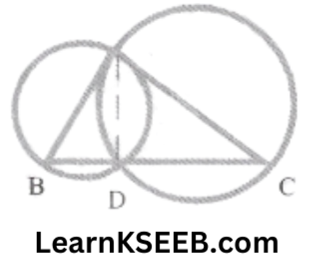
To prove: D lies on the third side BC of ΔABC

Construction: Join AD.

Proof: Circle described on AB as diameter intersects BC in D.

∴ \(\lfloor\mathrm{APB}\) = 90°

(angle in a semi-circle)

But \(\lfloor\mathrm{APB}\) + \(\lfloor\mathrm{ADC}\) = 180° (linearpair)

\(\lfloor\mathrm{ADC}\) = 90°

Hence, the circle described on AC as diameter must pass through D.

Thus, the two circles intersect in D.

Now, \(\lfloor\mathrm{APB}\)+ \(\lfloor\mathrm{ADC}\) = 180°

∴ Points B, D, and C are collinear

∴ D lies on BC.

11. ABC & ADC are two right triangles with common hypotenuse AC. Prove that
\(\lfloor\mathrm{CAD}\) = \(\lfloor\mathrm{CBD}\).

Solution:

Given: ABC & ADC are two right triangles with common hypotenuse AC.

To prove: \(\lfloor\mathrm{CAD}\) = \(\lfloor\mathrm{CBD}\)

Proof: AC is the common hypotenuse ABC & ADC are two right triangles

∴ \(\lfloor\mathrm{ABC}\) = 90°=\(\lfloor\mathrm{ADC}\)

=> Both the triangles are in the same semi-circle.

∴ Points A, B, D & C are concyclic.

∴ DC is a chord

∴ \(\lfloor\mathrm{CAD}\) = \(\lfloor\mathrm{CBD}\)

(∵ angles in the same segment are equal)

KSEEB 9th Standard Maths Chapter 10 Important Questions

12. Prove that a cyclic parallelogram is a rectangle.

Solution:

Given: ABCD is a cyclic ||gm

To prove: ABCD is a rectangle

Proof: ABCD is a cyclic quadrilateral

∴ \(\lfloor 1\) + \(\lfloor 2\)=180° …………………(1)

(opposite angles of a cyclic quadrilateral are supplementary)

ABCD is a ||gm

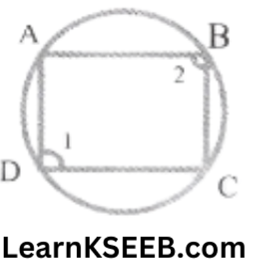
\(\lfloor 1\) = \(\lfloor 2\) …………………….(2)

(opp. angles of a ||gm) from(1)&(2)

∴ \(\lfloor 1\) = \(\lfloor 2\) = 90°

∴ ||gm ABCD is a rectangle.

Circles EXERCISES 10.6 (optional)

1. Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.

Solution:

Given: Two intersecting circles with centres A & B, their points of intersection are P & Q

To prove: \(\lfloor\mathrm{APB}\) = \(\lfloor\mathrm{AQB}\)

Proof: In ΔAPB & ΔAQB

AP = AQ (Radii of a circle)

BP = BQ (Radii of a circle)

AB = AB (common)

ΔAPB ≅ ΔAQB (SSS rule)

∴ \(\lfloor\mathrm{APB}\) = \(\lfloor\mathrm{AQB}\)

2. Two chords AB & CD of lengths 5cm & 11cm respectively of a circle are parallel to each other & are on opposite sides of its centre. If the distance between AB & CD is 6cm, find the radius of the circle.

Solution: Let the radius of the circle be r cm

Let OM = x cm

then ON = (6 – x) cm

∴ OM ⊥ CD

M is the midpoint of CD

∴ ON ⊥ AB N is the midpoint of AB

MD = MC = 1/2CD = 1/2(11)cm = 11/2

The perpendicular from the centre of a circle to a chord bisects the chord)

∴ NB = AN = 1/2AB = 1/2(5)=5/2cm

In right triangle ONB

\(\mathrm{OB}^2=\mathrm{ON}^2+\mathrm{NB}^2\) (By Pythagoras theorem)

\(\Rightarrow r^2=(6-x)^2+\left(\frac{5}{2}\right)^2\) …………………….(1)

In right Δle OMD

\(\mathrm{OD}^2=\mathrm{OM}^2+\mathrm{MD}^2\) (by Pythagoras theorem)

\(\Rightarrow r^2=x^2+\left(\frac{11}{2}\right)^2\)

from(1) &(2), we get

\(\begin{aligned}
& (6-x)^2+\left(\frac{5}{2}\right)^2=x^2+\left(\frac{11}{2}\right)^2 \\
& \Rightarrow 36-12 x+\frac{x^2}{2}+\frac{25}{4}=x^2+\frac{121}{4} \\
& \Rightarrow 12 x=36+\frac{25}{4}-\frac{121}{4} \\
& \Rightarrow 12 x=12 \\
& x=\frac{12}{12}=1
\end{aligned}\)

putting x= 1 in (2), we get

\(\begin{aligned}
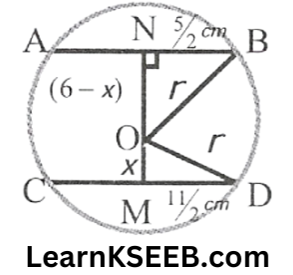
& r^2=1^2+\left(\frac{11}{2}\right)^2 \\
& =1+\frac{121}{4} \\
& =\frac{125}{4} \\
& r=\frac{\sqrt{125}}{4}=\frac{5 \sqrt{5}}{2}
\end{aligned}\)

Hence, the radius of the circle is \(\frac{5 \sqrt{5}}{2}\)cm.

3. The lengths of two parallel chords of a circle are 6cm & 8cm. If the smaller chord is at distance 4cm from the centre. What is the distance of the other chord from the centre?

Solution: OM⊥AB

M is the mid-point of AB (The perpendicular from the centre of a circle to a chord bisects the chord)

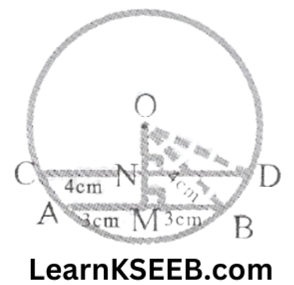
∴ \(\mathrm{BM}=\mathrm{AM}=\frac{1}{2} \mathrm{AB}=\frac{1}{2}(6)=3 \mathrm{~cm}\)

ON ⊥ CD

N is the midpoint of CD

(The perpendicular from the centre of a circle to a chord bisects the chord)

∴ \(\mathrm{DN}=\mathrm{CN}=\frac{1}{2} \mathrm{CD}=\frac{1}{2} \times 8=4 \mathrm{~cm}\)

In the right triangle OMB

\(\mathrm{OB}^2=\mathrm{OM}^2+\mathrm{MB}^2\) (By Pythagoras theorem)

\(\begin{gathered}
=4^2+3^2 \\
=16+9 \\
\mathrm{OB}^2=25 \\
\mathrm{OB}=\sqrt{25}=5 \mathrm{~cm}
\end{gathered}\)

∴ OD = OB = 5cm (Radii of a circle)

In right Δle OND

\(\mathrm{OD}^2=\mathrm{ON}^2+\mathrm{ND}^2\) (By Pythagoras theorem)

\(\begin{aligned}
& \Rightarrow 5^2=\mathrm{ON}^2+4^2 \\
& \Rightarrow \mathrm{ON}^2=25-16 \\
& \Rightarrow \mathrm{ON}^2=9 \\
& \Rightarrow \mathrm{ON}=\sqrt{9}=3 \mathrm{~cm}
\end{aligned}\)

Hence, the distance of the other chord from the centre is 3 cm.

4. Let the vertex of an angle ABC be located outside a circle & let the sides of the angle intersect equal chords AD & CE with the circle. Prove that \(\lfloor\mathrm{ABC}\) is equal to half the difference of the angles subtended by the chords AC & DE at the centre.

Solution:

Let \(\lfloor\mathrm{ABC}\) = x, \(\lfloor\mathrm{AOC}\) = y & \(\lfloor\mathrm{DOE}\)= z

\(\lfloor\mathrm{C’OD}\) + \(\lfloor\mathrm{A’OE}\) = z-y …………………..(1)

Let \(\lfloor\mathrm{C’OD}\) = θ

Then, \(\lfloor\mathrm{A’OE}\) = (z-y)-θ (from(1))

\(\lfloor\mathrm{AOD}\) = π – (\(\lfloor\mathrm{AOC}\) +\(\lfloor\mathrm{C’OD}\))

= π-(y + θ)

\(\lfloor\mathrm{COE}\) = π-(\(\lfloor\mathrm{C’OA’}\) +\(\lfloor\mathrm{A’OE}\))

= π-(y + z -y + θ)

= π -(z-θ)

∵ AD = CE

∴ \(\lfloor\mathrm{AOD}\) = \(\lfloor\mathrm{COE}\)

(equal chords subtend equal angles at the centre)

∴ π-(y + θ) = π-(z-θ)

=> y+θ = z-θ

2θ = z-y

\(\Rightarrow \theta=\frac{z-y}{2}\)

∴ \(\mathrm{C}^{\prime} \mathrm{OD}=\frac{\mathrm{z}-y}{2}\)

& \(\mathrm{A}^{\prime} \mathrm{OE}=\mathrm{z}-y-\frac{\mathrm{z}-y}{2}=\frac{\mathrm{z}-y}{2}\)

∴ \(\lfloor\mathrm{AOD}=\pi-(\mathrm{y}+\theta)\)

\(\begin{aligned}
& =\pi-\left(y+\frac{z-y}{2}\right) \\
& =\pi-\left(\frac{y+z}{2}\right)
\end{aligned}\)

In ΔOAD

OA = OD (Radii of the same circle)

∴ \(\lfloor\mathrm{OAD}\) = \(\lfloor\mathrm{ODA}\) (Angles opposite)

5. Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Solution:

Given: ABDC is a rhombus,

E is the point of intersection of its diagonals.

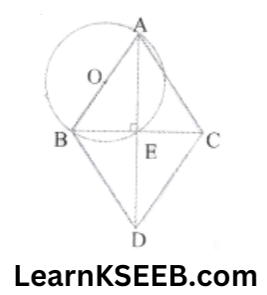
To prove: The circle drawn with any sides AB of rhombus ABDC as a diameter passes through point E.

Proof: In ΔAEB & ΔAEC

AB = AC (given)

\(\lfloor\mathrm{BEA}\) + \(\lfloor\mathrm{CEA}\)= 180° (linear pair)

=> 90° + \(\lfloor\mathrm{CEA}\) = 180° (angle in a semi-circle)

=> \(\lfloor\mathrm{CEA}\) = 90°

∴ \(\lfloor\mathrm{BEA}\) = \(\lfloor\mathrm{CEA}\) = 90°

AE =AE (common)

∴ ΔAEB ≅ ΔAEC (RHSrule)

∴ BE = CE (C.P.C.T.)

=> E is the mid-point of BC

=> E is the point of intersection of diagonals. Hence, the circle is drawn with AB as the diameter passes through point E.

6. ABCD is a ||gm. The circle through A, B & C intersect CD (produced if necessary) at E. Prove that AE = AD.

Solution:

Given: ABCD is a ||gm. The circle passes through A, B & C and intersects CD at E.

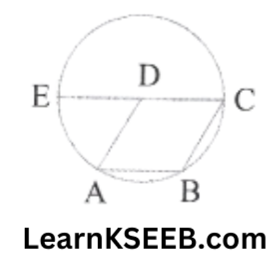
To prove: AE= AD

Proof: In cyclic quadrilateral E

ABCE

\(\lfloor\mathrm{AWD}\) + \(\lfloor\mathrm{ABC}\) = 180° …………………(1)

(∵ opp. angles of a cyclic quadrilateral are supplementary)

also, \(\lfloor\mathrm{ADE}\) + \(\lfloor\mathrm{ADC}\) = 180° (linear pair)

but \(\lfloor\mathrm{ADC}\) = \(\lfloor\mathrm{ABC}\) (opp. angles of a ||gm )

\(\lfloor\mathrm{ADE}\) +\(\lfloor\mathrm{ABC}\) = 180° ………………..(2)

from (1) & (2), we have

\(\lfloor\mathrm{AED}\)+ \(\lfloor\mathrm{ABC}\) = \(\lfloor\mathrm{ADE}\) +\(\lfloor\mathrm{ABC}\)

=> \(\lfloor\mathrm{AED}\) = \(\lfloor\mathrm{ADE}\)

In ΔADE

AE = AD ( ∵ sides opp. to equal angles of a Δle are equal)

7. AC & BD are chords of a circle which bisect each other. Prove that
(1) AC & BD are diameters.
(2) ABCD is a rectangle.

Solution:

Given: AC & BD are chords of a circle that bisect each other.

To prove : (1) AC & BD are diameters.

(2) ABCD is a rectangle

Construction: Join AB, BC, CD & DA.

Proof: (1) In ΔOAB & ΔOCD OA = OC (Radii of a circle)

OB = OD (Radii of a circle)

\(\lfloor\mathrm{AOB}\) = \(\lfloor\mathrm{COD}\) (vertically opposite angle)

∴ ΔOAB ≅ ΔOCD (SAS rule)

AB = CD (CPCT) ………………..(1)

||ly we can show that

AD = CB ……………….(2)

adding (1) & (2) we get

AB + AD = CD + CB

=> BAD = BCD

=> BD divides the circle into two equal parts & the angle of a semi-circle is 90°.

∴ \(\lfloor A\) = 90° & \(\lfloor C\) = 90°

||ly \(\lfloor B\) = 90°& \(\lfloor D\) = 90°

∴ \(\lfloor A\) = \(\lfloor B\) = \(\lfloor C\) =\(\lfloor D\)=90°

\(\lfloor A\) = 90°

∴ BD is a diameter (angle in a semi-circle is 90°) \(\lfloor D\) = 90°

∴ AC is the diameter (the angle in a semicircle is 90°)

Thus AC & BD are diameters &

ABCD is a rectangle.

Karnataka Board Class 9 Maths Chapter 10 MCQs

8. Bisectors of angles A, B & C of a Δe ABC intersect its circumcircle at D, E & F respectively. Prove that the angles of the ΔDEF are \(90^{\circ}-\frac{1}{2} A, 90^{\circ}-\frac{1}{2} B \& 90^{\circ}-\frac{1}{2} C\)

Solution: JoinDE, EF &FD

\(\lfloor\mathrm{FDE}\) = \(\lfloor\mathrm{FDA}\) + \(\lfloor\mathrm{EDA}\) = \(\lfloor\mathrm{FCA}\) + \(\lfloor\mathrm{EBA}\)

(angles in the same segment are equal)

\(\begin{aligned}
& =\frac{1}{2}\left\lfloor\mathrm{C}+\frac{1}{2}\lfloor\underline{B}\right. \\
& \Rightarrow\left\lfloor D=\frac{\lfloor C+\lfloor B}{2}=\frac{180^{\circ}-\lfloor A}{2}\right.
\end{aligned}\)

( ∵ In ΔABC, \(\left\lfloor\mathrm{A}+\left\lfloor\mathrm{B}+\left\lfloor\mathrm{C}=180^{\circ}\right.\right.\right.\))

\(=90^{\circ}-\frac{\lfloor\mathrm{A}}{2}\)

|||ly we can show that

\(\begin{aligned}
& \left\lfloor E=90^{\circ}-\frac{\lfloor B}{2}\right. \\
& \&\left\lfloor F=90^{\circ}-\frac{\lfloor C}{2}\right.
\end{aligned}\)

9. Two congruent circles intersect each other at points A & B. Through A any line segment PAQ is drawn so that P, and Q lie on the two circles. Prove that BP = BQ.

Solution:

Given: Two congruent circles intersect each other at points A & B.

A line through A meets the circles in P &Q.

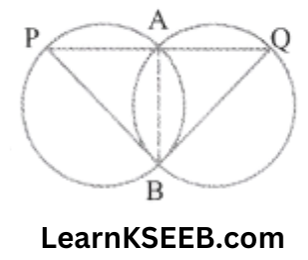
To prove: BP = BQ

Proof: AB is the common chord of the two congruent circles.

∴ \(\lfloor\mathrm{APB}\) = \(\lfloor\mathrm{AQB}\) (angles subtended by equal chords are equal)

∴ BP = BQ (sides opposite to equal angles are equal)

10. In any triangle ABC, if the angle bisector [A & perpendicular bisector of BC intersect prove that they intersect on the circumcircle of the Δle ABC.

Solution:

Given: Bisector AP of angle A of ΔABC & the perpendicular bisector PM of BC intersect at P

To prove: P lies on the circumcircle of ΔABC

Construction: Join OB & OC, where O is the circumcentre of the circumcircle of ΔABC

Proof: In right ΔOMB & right ΔOMC

Hyp OB = Hyp OC (Radius of the same circle are equal)

side OM = side OM (common)

∴ ΔOMB ≅ ΔOMC (RHS congruence criterion)

∴ \(\lfloor\mathrm{BOM}\) = \(\lfloor\mathrm{COM}\) (CPCT)

Again, \(\lfloor\mathrm{BAC}\) = 1/2\(\lfloor\mathrm{BOC}\)

(angle subtended by an arc of a circle at its centre is twice the angle subtended by it at any point of the remaining part of the circle)

\(\frac{1}{2} \lfloor\mathrm{BAC}\) \(=\frac{1}{2}\left(\frac{1}{2} \lfloor\mathrm{BOC}\right)\)

(Halves of equals are equal)

=> \(\lfloor\mathrm{BAP}\) = \(\lfloor\mathrm{BOP}\)

(AP is the bisector of \(\lfloor A\); \(\lfloor\mathrm{BOC}\) is bisector by OM)

which is possible only when BP is the chord of the circle with centre O.

∴ Quadrilateral ABPC is cyclic, i.e. The bisector of \(\lfloor A\) & the perpendicular bisector of BC intersect each other on the circumcircle of the ΔABC

Multiple Choice Questions

1. The centre of a circle lies

1. outside the circle
2. inside the circle
3. on the circle
4. none of these

Solution: 2. inside the circle

2. The angle of a minor segment is

1. acute
2. right angle
3. obtuse
   
4. straight

Solution: 3. obtuse

3. A chord of length 12cm of a circle is at a distance of 8cm from its centre. The radius of the circle is

1. 4cm
2. 6cm
3. 8cm
4. 10cm

Solution: 4. 10cm

4. In the following figure, PCQ is the diameter of the circle & C is the centre. Point O lies on the circle. If \(\lfloor\mathrm{OQP}\) = 60°, then \(\lfloor\mathrm{OCP}\) =

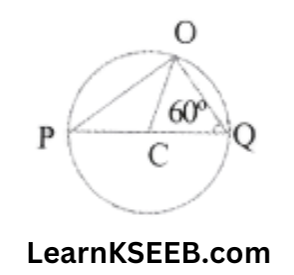
1. 80°
2. 100°
3. 120°
4. 130°

Solution: 3. 120°

5. The length of the diagonal of a rectangle is 10cm. The area of its circumscribed circle is

1. 10πcm²
2. 25πcm²
3. 100πcm²
4. 50πcm²

Solution: 2. 25πcm²

6. In the following figure, O is the centre of the circle. If measure of \(\lfloor\mathrm{BAC}\) = 50° then the measure of \(\lfloor\mathrm{BOC}\) is

1. 120°
2. 100°
3. 80°
4. 70°

Solution: 2. 100°

7. In the figure, O is the centre of the circle, \(\lfloor\mathrm{ABO}\) = 20° & \(\lfloor\mathrm{ACO}\) = 30° where A, B, C are points on the circle, The value of x is

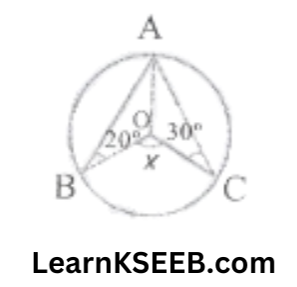
1. 120°
2. 130°
3. 100°
4. 150°
5. Solution: 3. 100°

8. In the adjoining figure, O is the centre of the circle. The value of x is

1. 100°
2. 200°
3. 250°
4. 260°
5. Solution: 4. 260°

One Mark Questions

1. In the figure, \(\lfloor\mathrm{CAO}\) = 30° & \(\lfloor\mathrm{ACB}\) = 70° then \(\lfloor\mathrm{BOC}\) is

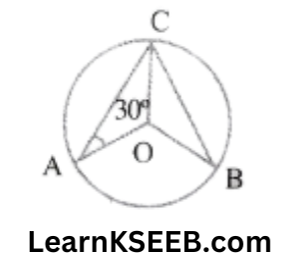
100°

2. In the given figure, O is the centre of the circle, \(\lfloor\mathrm{AOB}\) = \(\lfloor\mathrm{COD}\) = 50° & CD = 5 cm then AB is equal to

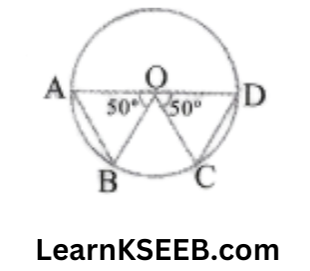
5cm

3. The opposite angles of a cyclic quadrilateral are
supplementary

4. The angle of a major segment is acute

5. In the following figure, O is the centre of the circle, OA = 10cm & perpendicular OC on chord AB = 8cm, then the length of the chord AB is

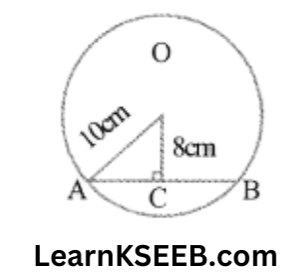
12cm

Two Mark Questions

1. In the given figure, A, B, C & D are the points on a circle. Such that \(\lfloor\mathrm{ACB}\) = 40° & \(\lfloor\mathrm{DAB}\) = 60° Find \(\lfloor\mathrm{DBA}\)

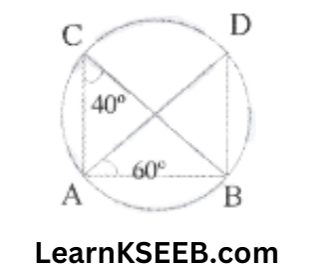
Solution: \(\lfloor\mathrm{ACB}\) =\(\lfloor\mathrm{ADB}\)

(angles in the same segment)

∴ \(\lfloor\mathrm{ADB}\) = 40°

Now in ΔAPB

\(\lfloor\mathrm{ADB}\) +\(\lfloor\mathrm{DBA}\)+\(\lfloor\mathrm{BAD}\) = 180°

=> 40° +\(\lfloor\mathrm{DBA}\) + 60° = 180°

=> \(\lfloor\mathrm{DBA}\) -180°-100

∴  \(\lfloor\mathrm{DBA}\) = 80°

2. In the given figure, AD || BC & \(\lfloor\mathrm{BCA}\) = 40°, find \(\lfloor\mathrm{DBC}\)

Solution: \(\lfloor\mathrm{BDA}\) = \(\lfloor\mathrm{BCA}\) = 40°

(angles in the same segment)

Now, since AP || BC

\(\lfloor\mathrm{DBC}\) = \(\lfloor\mathrm{BDA}\) (Alternate interior angle)

∴ \(\lfloor\mathrm{DBC}\) = 40°

Class 9 Maths Circles KSEEB Guide

3. If a line intersects two concentric circles with common centre O, at A, B, C & D. Prove that AB = CD.

Solution:

Draw OP perpendicular to xy from the centre to a chord bisecting it.

OP perpendicular to chord BC.

=> BP = PC ………………..(1)

=> ||ly AP = PD …………………(2)

subtracting Eqn (1) from Eqn (2) we get

AP – BP = PD – PC

=> AB = CD

4. In figure, O is the centre of the circle. If \(\lfloor\mathrm{AOB}\) = 80°, then find the measure of \(\lfloor\mathrm{ADB}\) & \(\lfloor\mathrm{ACB}\)

Solution: \(\lfloor\mathrm{AOB}\) = 80°

=> \(\lfloor\mathrm{ADB}\)=40°

(∵ \(\lfloor\mathrm{AOB}\) = 2\(\lfloor\mathrm{ADB}\))

\(\lfloor\mathrm{ACB}\)=\(\lfloor\mathrm{ADB}\) = 40°

(angles in the same segment are equal)

5. In the figure, find the value of x.

Solution: In a cyclic quadrilateral

\(\lfloor A\)+ \(\lfloor C\) = 180°

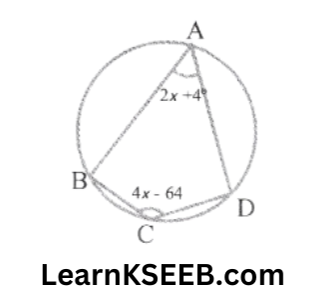
(opposite angles of a cyclic quadrilateral are supplementary)

=> 2x+ 4° +4x-64 = 180°

=> 6x-60° =180°
\(\begin{aligned}
& \Rightarrow \quad x=\frac{180+60}{6} \\
& \Rightarrow \quad x=\frac{240}{6}=40^{\circ}
\end{aligned}\)

6. In the adjoining figure if \(\lfloor\mathrm{DAB}\) = 60° &\(\lfloor\mathrm{ACB}\) = 70°, find the measure of \(\lfloor\mathrm{DBA}\)

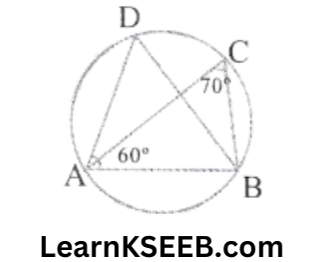
Solution: \(\lfloor\mathrm{ADB}\)=\(\lfloor\mathrm{ACB}\) = 70°

(angles in the same segments of a circle)

In ΔDAB

\(\lfloor\mathrm{DAB}\)+ \(\lfloor\mathrm{ADB}\) + \(\lfloor\mathrm{DBA}\) = 180°

(angle sum property)

=> 60°+ 70°+ \(\lfloor\mathrm{DBA}\) = 180°

=> \(\lfloor\mathrm{DBA}\) = 180°-130°

=> \(\lfloor\mathrm{DBA}\) = 50°

7. In the given figure, O is the centre of the circle & chord AC & BD intersect at P. Such that \(\lfloor\mathrm{APB}\) = 120° & \(\lfloor\mathrm{PBC}\) = 15° Find the value of \(\lfloor\mathrm{ADB}\)

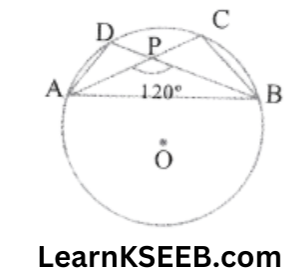
Solution: In ΔPCB

\(\lfloor\mathrm{PCB}\) + \(\lfloor\mathrm{PBC}\) = \(\lfloor\mathrm{APB}\)

\(\lfloor\mathrm{PCB}\) + 15° = 120°

∴ \(\lfloor\mathrm{PCB}\) = 120°-15°

= 105°

or \(\lfloor\mathrm{ACB}\) = 105°

=> \(\lfloor\mathrm{ADB}\) = \(\lfloor\mathrm{ACB}\) = 105°

8. In the figure \(\lfloor\mathrm{AOB}\) = 90° & \(\lfloor\mathrm{ABC}\) = 30°, then find the measure of \(\lfloor\mathrm{CAO}\)

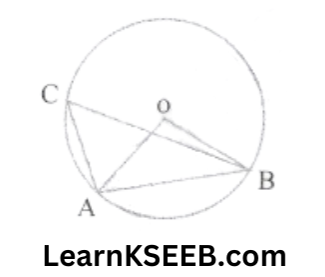
Solution:

\(\lfloor\mathrm{ACB}\) = 1/2 x \(\lfloor\mathrm{AOB}\)

= 1/2 x 90 = 45°

In ΔACB, \(\lfloor\mathrm{CAB}\) = 180° – (30 + 45)

=180 – 75

= 105°

\(\lfloor\mathrm{OAB}\) = \(\lfloor\mathrm{OBA}\) = 105°

(angles opposite to equal sides of Δles are equal as OA = OB radius of the same circle)

\(\lfloor\mathrm{CAO}\) = 105° –\(\lfloor\mathrm{OAB}\)

= 105-45°

= 60°

Three Mark Questions

1. OD is perpendicular to chord AB of a circle whose centre is O. If BC is a diameter, Prove that C A = 20D.

Solution:

Given: OD is perpendicular to chord AB of a circle where the centre is O. BC is the diameter of the circle.

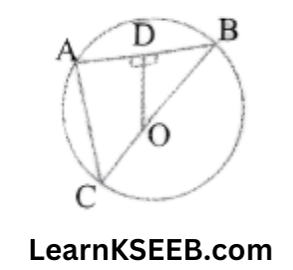
To prove :  CA= 20D.

Proof: OD ⊥ AB

∴ D is the midpoint of AB (The perpendicular drawn from the centre of a circle to a chord bisects the chord)

In ΔBAC

D is the midpoint of AB & O is the midpoint of BC.

∴ OD || AC (by midpoint theorem)

= 60°

& OD= 1/2 AC

=> CA = 20D.

2. In figure, AB & AC are two equal chords of a circle whos centre is O. If OD ⊥ AB & OE ⊥ AC Prove that ADE is an isosceles Δle

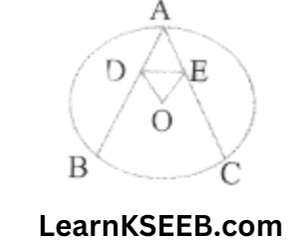
SoIution:

Given: AB & AC are two equal chords of a circle whose centre is O, OD ⊥ AB & OE ⊥ AC

To prove: ADE is an isosceles triangle

Proof: AB= AC

OD = OE (Equal chords are equidistant from the centre)

In ΔODE

\(\lfloor\mathrm{ODE}\) = \(\lfloor\mathrm{OED}\) (angle opp. to equal sides)

=> 90 –\(\lfloor\mathrm{ODE}\) = 90° – \(\lfloor\mathrm{OED}\)

=> \(\lfloor\mathrm{ODA}\) – \(\lfloor\mathrm{ODE}\) = \(\lfloor\mathrm{OEA}\) – \(\lfloor\mathrm{OED}\)

=> \(\lfloor\mathrm{ADE}\)–\(\lfloor\mathrm{AED}\)

∴ AD=AE (sides opposites to equal angles)

∴ ΔADE is an isosceles Δle.

3. In figure, AB = CD, prove that BE = DE & AE = CE, where E is the point of intersection of AD & BC.

Solution: Given: In figure, AB = CD. E is the point of intersection of AD & BC.

To prove: BE = DE & AE = CE

Proof: In ΔEAB & ΔECD

AB = CD (given)

\(\lfloor B\) = \(\lfloor D\) (angles in the same segment)

\(\lfloor A\) = \(\lfloor C\) (angles in the same segment)

∴ ΔEAB ≅ ΔECD (by ASA rule)

∴BE = DE (CPCT)

&AE = CE (CPCT)

4. Two chords PQ & RS of a circle are parallel to each other & AB is the perpendicular bisector of PQ without using any construction. Prove that AB bisects RS.

Solution: AB is the perpendicular bisector of PQ.

AB passes through the centre O.

(The perpendicular bisector of a chord of a circle passes through the centre)

PQ || RS

∴  AB⊥RS

∴ AB bisects RS

(The perpendicular is drawn from the centre of a circle bisects the chord)

5. In the figure, AB & CD are two chords of a circle with centre O. Such that MP = NP. If OM ⊥ AB & ON ⊥ DC Show that AB = CD.

Solution: Construction: Join OP.

In ΔOMP & ΔONP

\(\lfloor\mathrm{OMP}\) = \(\lfloor\mathrm{ONP}\) = 90°

OP = OP

MP = NP (given)

∴ ΔOMP ≅ ΔONP (RHS rule)

∴ OM = ON (CPCT)

∴ AB = CD

(chords equidistant from the centre are equal)

6. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc & also at a point on the major arc.

Solution: According to the question

OA = AB = OB.

ΔOAB is an equilateral Δle

\(\lfloor\mathrm{AOB}\) = 60°

\(\lfloor\mathrm{ACB}\) = 1/2 \(\lfloor\mathrm{AOB}\)

(Angle subtended by an arc at the centre is twice the angle at the remaining circle)

\(\lfloor\mathrm{ACB}\) = 1/2×60° = 30°

\(\lfloor\mathrm{ACB}\) = + \(\lfloor\mathrm{ADB}\) = 180°

(opp. angles of a cyclic quadrilateral are supplementary).

or \(\lfloor\mathrm{ADB}\) = 180-\(\lfloor\mathrm{ACB}\)

= 180°-30°

\(\lfloor\mathrm{ADB}\) =150°

7. In the given figure, AB is a chord equal to the radius of the given circle with centre O. Find the values of a & b.

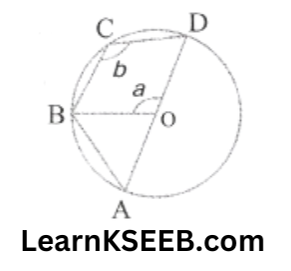
Solution: OB = OA (radius)

OA= OB = AB (given)

∴ AOAB is an equilateral Δle

∴ \(\lfloor\mathrm{AOB}\) = 60°

a + \(\lfloor\mathrm{AOB}\) = 180° (linear pair)

a+ 60° = 180°

=> a = 180-60 = 120°

Reflex angle \(\lfloor\mathrm{BOB}\) = 2\(\lfloor\mathrm{BCD}\)

(angle subtended by an arc at the centre is twice at the circumference)

360 – a = 2b

360-120 = 2b

=> 2b = 240

=> =240/2

=> b= 120°

8. In the given figure, PQ is the diameter of the circle. If \(\lfloor\mathrm{PQR}\) = 65° \(\lfloor\mathrm{QPT}\) = 60°, then find the measure of

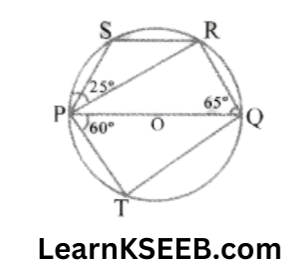
1) \(\lfloor\mathrm{QPR}\) 2) \(\lfloor\mathrm{PRS}\) 3) \(\lfloor\mathrm{PSR}\)

Solution: 1) \(\lfloor\mathrm{QPR}\) = 90°

(angle in the semi-circle)

\(\lfloor\mathrm{QPR}\) = 90° – 65°

= 25°

(angle sum property)

2) \(\lfloor\mathrm{QPS}\) = \(\lfloor\mathrm{QPR}\) + \(\lfloor\mathrm{RPS}\) = 50°

\(\lfloor\mathrm{QRS}\) = 180°-\(\lfloor\mathrm{QPS}\)

= 180° – 50° = 130° (PQRS is a cyclic quadrilateral)

\(\lfloor\mathrm{PRS}\) = 130 – \(\lfloor\mathrm{QRP}\)

= 130-90 = 40°

3) \(\lfloor\mathrm{PSR}\) + \(\lfloor\mathrm{PQR}\) =180°

\(\lfloor\mathrm{PSR}\) = 180°-\(\lfloor\mathrm{PQR}\)

= 180°-65°

\(\lfloor\mathrm{PSR}\) = 115°

KSEEB Class 9 Maths Chapter 10 Exercise Solutions

9. In the given figure AB is the diameter of the circle with centre O. If AC & BD are perpendicular on a line PQ & BD meets the circle at E, then prove that AC = ED

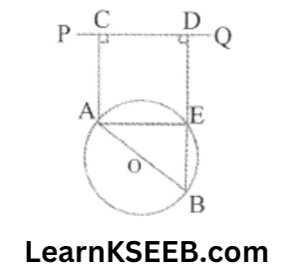
Solution:

\(\lfloor\mathrm{AEB}\) = 90°

(angle in a semicircle)

\(\lfloor\mathrm{AEB}\) = \(\lfloor\mathrm{AED}\) = 90°

\(\lfloor\mathrm{EAC}\)+\(\lfloor\mathrm{ACD}\)+

\(\lfloor\mathrm{CDE}\) + \(\lfloor\mathrm{AED}\) = 360°

(sum of angles in a quadrilateral)

=> \(\lfloor\mathrm{EAC}\) + 90° + 90° + 90° = 360°

=> \(\lfloor\mathrm{EAC}\) = 360°-270°

= 90°

Each angle = 90°

∴ EACD is a rectangle

=> AC = ED

10. Two circles whose centres are O & O’ intersect at P, and through P, a line parallel to O O’, intersecting the circles at C & D is drawn as shown. Prove that CD = 2OO’

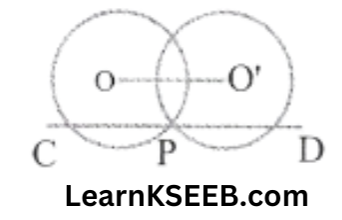
Solution:

Construction: Draw OA & O’ B perpendicular to CD from O & O’ respectively.

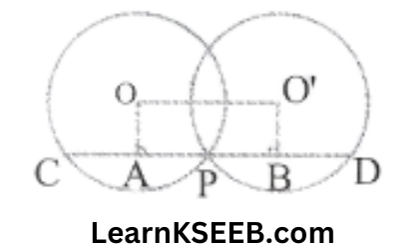
Proof: OA bisects the chord CP (perpendicular from the centre to the chord bisects the chord)

∴  AP = 1/2 CP

(or) CP = 2 AP ………………….(1)

||ly O’B⊥PD

PD = 2BP ………………….(2)

CD = CP + DP

= 2AP + 2BP [from (1) & (2)]

= 2 (AP + BP)

CD = 2AB …………………(3)

In quadrilateral AB O’O

O A = O’ B (two lines perpendicular to same line)

AB = OO’ (given)

∴ ABO’Ois ||gm

Opposite sides of ||gm are equal

AB = OO’

∴ CD = 2AB

=> CD = 2 OO’