KSEEB Solutions For Class 9 Maths Chapter 1 Number Systems

KSEEB Solutions for Class 9 Maths Chapter 1 Number Systems

Number of Systems Points To Remember

Any number that can be expressed in the form p/ q, where p & q are both integers & q * 0 is called a rational number usually, we take q>0, while p may be positive, negative or zero.
Rational numbers do not have a unique representation.

For example \( \frac{1}{3}=\frac{2}{6}=\frac{7}{21}=\frac{30}{90}\)  etc

•  Every rational number can be written in the form p/ q, where p, q are integers, q ≠ 0, p, q have no common factors (except 1). It is called in the lowest terms or simplest form.
• A number that cannot be expressed in the form p/q, where p, q are integers, q ≠ 0, p, q have no common factors (except l)is called an irrational number

For example  \( \sqrt{2}, \sqrt{3}, \sqrt{6},-\sqrt{7}, 2-\sqrt{5}, \pi\) all irrational number.

Read and Learn More KSEEB Solutions for Class 9 Maths 

The decimal expansion of a rational number is either terminating or non-terminating recurring (repeating), conversely, a number whose decimal expansion is terminating or non-terminating recurring is rational.

The decimal expansion of a rational number p/q, where p, q are integers, q>0, p & q have no common factors except 1 is:
1) Terminating if prime factors of q are 2 or 5 or both.
2) Non-terminating recurring if q has a prime factor other than 2 or 5.

The decimal expansion of an irrational number is non-terminating and non-recurring. Conversely, a number whose decimal expansion is non-terminating, and non-recurring is irrational.

• All rational numbers & all irrational numbers are real numbers. The collection of real numbers is denoted by R.
• Every real number (rational or irrational) can be represented by a unique point on the number line. Conversely, every point on the number line represents a unique real number.
• If m is rational & n is irrational, then m+n, m – n & n- mare irrational numbers.
• If m is a nonzero rational number & n is an irrational number, \(\frac{m}{n} \text { and } \frac{n}{m}\) — and — are irrational numbers.
• If a and b are positive real numbers, then the following results hold.

KSEEB Class 9 Maths Chapter 1 Solutions PDF

1) \(\sqrt{a b}=\sqrt{a} \sqrt{b} \\\)
2) \( \sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}} \\\)
3) \((\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=a-b \\\)
4) \((\sqrt{a}+\sqrt{b})^2=a+2 \sqrt{a b}+b \\\)
5) \((\sqrt{a}-\sqrt{b})^2=a-2 \sqrt{a b}+b \\\)
6) \((a+\sqrt{b})(a-\sqrt{b})=a^2-b\)

Class 9 Social Science

Class 9 Science

Class 9 Maths

 

• If the product of two irrational numbers is a rational number, then each number is called the rationalising factor of the other number.
• The process of multiplying an irrational number by its rationalising factor is called rationalisation.

KSEEB Class 9 Maths Number Systems Exercises 

Chapter 1 Number Systems Rule to Rationalise The Denominator Of a Fraction

• Multiply & divide the numerator & denominator of the given fraction by the rationalising factor of its denominator & simplify.
•  lf a>0 is areal number &n is a positive integer, then \(\sqrt[n]{a}=b\) if & only if \(\mathrm{b}^{\mathrm{n}}=a, \mathrm{~b}>0, \sqrt[n]{a}\) is also written as \(a^{1 / n}\)
• If a > 0 is a real number & m, n are integers n > o, m, n have no common factors except 1, then

\(\frac{a^m}{a^n}=\left(a^{\frac{1}{n}}\right)^m=(n \sqrt{a})^m=\sqrt[n]{a^m}\)

If a > 0 is a real number & m & n are rational num­bers then

1. \(a^m \cdot a^n=a^{m+n}\)

2. \(\left(a^m\right)^n=a^{m n}\)

3. \(\frac{a^m}{a^n}=a^{m-n}, m>n\)

4. \(\frac{a^m}{a^n}=\frac{1}{a^{n-m}}, \quad n>m\)

5. \(a^m b^m=(a b)^m\)

6. \(\frac{a^m}{b^m}=\left(\frac{a}{b}\right)^m\)

7. \(a^{-n}=\frac{1}{a^n}\)

8. \(a^0=1\)

9. \(a^1=a\)

Chapter 1 Number Systems Exercise 1.1

1. Is zero a rational number? Can you write it in the form\(\frac{p}{q}\), where p & q are integers & q≠0?

Solution: yes! zero is a rational number, we can write zero in the form\(\frac{p}{q}\) , where p & q are integers & \(q \neq 0\)as follows.

\(0=\frac{0}{1}=\frac{0}{2}=\frac{0}{3}\) etc.

2. Find six rational numbers between 3 & 4

Solution: There can be infinitely many rational numbers between 3 & 4.

Method 1:

\(\frac{3+4}{2}=\frac{7}{2}, \quad \frac{3+7 / 2}{2}=\frac{13}{4}\) \(\frac{3+\frac{13}{4}}{2}=\frac{25}{8}\) \(\frac{3+25 / 8}{2}=\frac{49}{16}, \quad \frac{3+\frac{49}{16}}{2}=\frac{97}{32}\) \(\frac{3+\frac{97}{32}}{2}=\frac{193}{64}\)

Thus, six rational numbers between 3 & 4 are

\(\frac{7}{2}, \frac{13}{4}, \frac{25}{8}, \frac{49}{16}, \frac{97}{32} \& \frac{193}{64}\)

Method 2 :

\(\begin{aligned}
& \frac{3}{1}=\frac{3 \times 7}{1 \times 7}=\frac{21}{7} \\
& \frac{4}{1}=\frac{4 \times 7}{1 \times 7}=\frac{28}{7}
\end{aligned} \mid 6+1=7\)

Thus, six rational numbers between 3 & 4 can be taken as \(\frac{22}{7}, \frac{23}{7}, \frac{24}{7}, \frac{25}{7}, \frac{26}{7} \& \frac{27}{7}\)

3. Find five rational numbers between \(\frac{3}{5} \& \frac{4}{5}\)

Solution:  \(\frac{3}{5}=\frac{3 \times 10}{5 \times 10}=\frac{30}{50}\)

\(\frac{4}{5}=\frac{4 \times 10}{5 \times 10}=\frac{40}{50}\)

Thus five rational numbers between \(\frac{3}{4} \& \frac{4}{5}\) can be taken as\(\frac{31}{50}, \frac{32}{50}, \frac{33}{50}, \frac{34}{50}, \frac{35}{50}\)

4. State whether the following statements are true or false. Give reasons for your answers

1. Every natural number is a whole number
   Solution: True, since the collection of whole numbers contains all natural numbers.
2. Every integer is a whole number.
   Solution: False, for example, -2 is an integer but not a whole number.
3. Every rational number is a whole number.
   Solution: False, for example, \(\frac{1}{2}\) is a rational number but not a whole number.

Karnataka 9th Standard Maths Chapter 1 Notes

Chapter 1 Number Systems Exercise 1.2

1. State whether the following statements are true or false. Justify your answers.

1.  Every irrational number is a real number.
   Solution: True, since the collection of real numbers is made up of rational & irrational numbers.
2. Every point on the number line is of the form \(\sqrt{m}\), where m is a natural number.
   Solution: False, because no negative number can be the square root of any natural number.
3. Every real number is an irrational number.
   Solution: False, for example, 2 is real but not irrational.

2. Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.

Solution: No, For example, \(\sqrt{9}\) = 3 is a rational number.

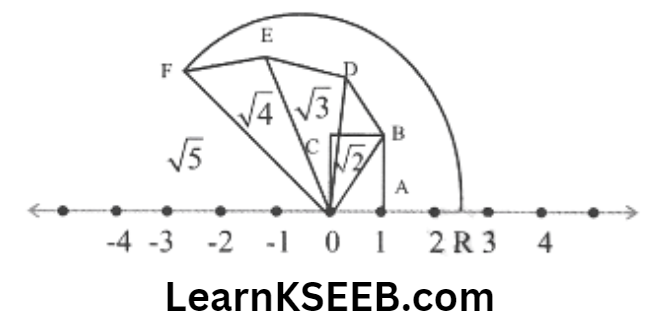
3. Show how \(\sqrt{5}\) can be represented on the number line.

Solution: Consider a unit square OABC & transfer it onto the number line making sure that the vertex O coincides with zero.

Then OB=\(\sqrt{1^2+1^2}=\sqrt{2}\)

Construct BD of unit length perpendicular to OB.

Then OD=\(\sqrt{(\sqrt{2})^2+1^2}=\sqrt{3}\)

construct DE of unit length perpendicular to OE.

Then OF=\(\sqrt{2^2+1^2}=\sqrt{5}\)

using a compass, with centre O & radius OF, draw an arc that intersects the number line in the point R, then R corresponds to \(\sqrt{5}\).

Chapter 1 Number Systems Exercise 1.3

1). Write the following in decimal form & say what kind of decimal expansion each has :

1.1\(\frac{36}{100}\)

1.2 \(\frac{1}{11}\)

1.3 \(4 \frac{1}{8}\)

1.4 \(\frac{3}{13}\)

1.5 \(\frac{2}{11}\)

1.6 \(\frac{329}{400}\)

Solution: 1.1) \(\frac{36}{100}=0.36\)

The decimal expansion is terminating

1.2)

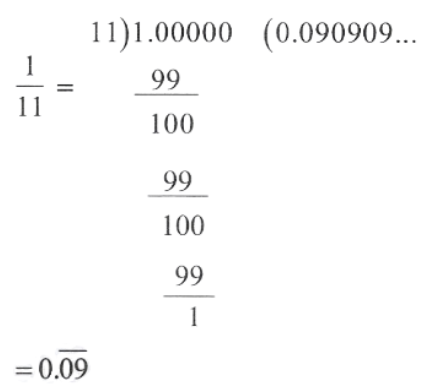
The decimal expansion is non terminating repeating

1.3) \(4 \frac{1}{8}\)

\(4 \frac{1}{8}\) =\(\frac{4 \times 8+1}{8}=\frac{33}{8}\)

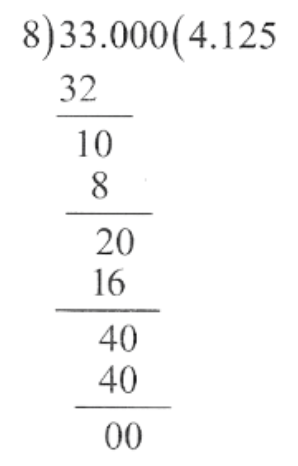
∴ \(4 \frac{1}{8}=4.125\)

The decimal expansion is terminating.

1.4) \(\frac{3}{13}\)

\(\frac{3}{13}=0.230769230769 \ldots \ldots=0 . \overline{230769}\)

The decimal expansion is non-terminating repeating.

1.5) \(\frac{2}{11}\)

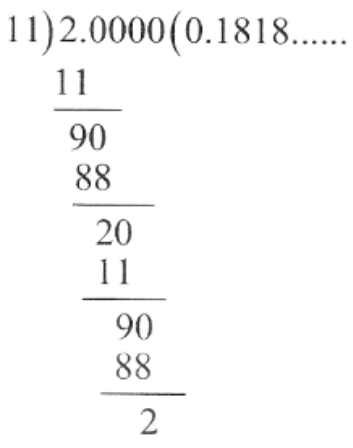
∴ \(\frac{2}{11}=0.1818\)

The decimal expansion is non terminating repeating.

1.6) \(\frac{329}{400}=0.8225\)

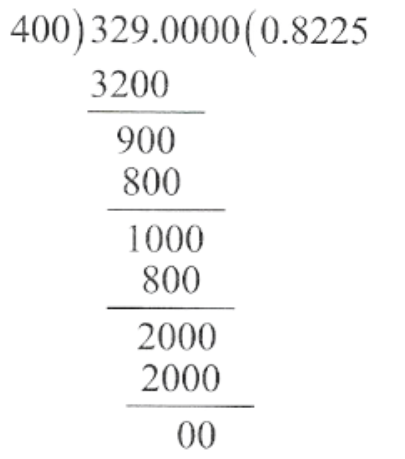
The decimal expansion is terminating g.

2. You know that \(\frac{1}{7}=0 . \overline{142857}\) can you predict
what the decimal expansions of \(\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}\) the long division? If so, how?
[Hint: Study the remainders while finding the value of \(\frac{1}{7}\) carefully] 

Solution: yes! we can predict the decimal expansions of \(\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}\) without actually doing the long division as follows:

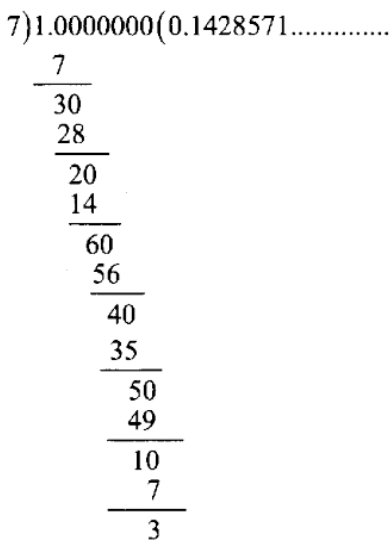
To predict the decimal expansion of \(\frac{2}{7}\), locate when the remainder becomes 2 & respective quotient (here it is 2). Then write the new quotient beginning from
there using the repeating digits 1,4,2,8,5,7.

∴ \(\frac{2}{7}=0 . \overline{285714}\)

\(\frac{3}{7}=0 . \overline{428571}\) \(\frac{4}{7}=0 . \overline{571428}\) \(\frac{5}{7}=0 . \overline{714285}\) \(\frac{6}{7}=0 . \overline{857142}\)

KSEEB Class 9 Maths Number Systems Solutions

3. Express the following in the form \(p / q\) , where p & q are integers & q≠0
1) \(0 . \overline{6}\)
2) \(0.4 \overline{7}\)
3) \(0 . \overline{001}\)

Solution: 1) \(0 . \overline{6}\)  = Let x =  \(0 . \overline{6}=0.6666 \ldots\)

Multiplying both sides by 10 (since one digit is repeating) we get

\(\begin{aligned}
& 10 x=6.666 \ldots \ldots . \\
& \Rightarrow 10 x=6+0.6666 \ldots \ldots \\
& \Rightarrow 10 x=6+x \\
& \Rightarrow 10 x-x=6 \\
& \Rightarrow 9 x=6 \\
& \Rightarrow x=\frac{6}{9} \\
& x=\frac{2}{3}
\end{aligned}\)

Thus, \(0 . \overline{6}=\frac{2}{3}\)

Here, P = 2,  q=3(≠0)

2) \(0.4 \overline{7}\) = Let \(x=0.4 \overline{7}=0.47777 \ldots \ldots\)

Multiplying both sides by 10 (since one digit is repeating), we get

\(\begin{aligned}
& 10 x=4.7777 \ldots \ldots \\
& \Rightarrow 10 x=4.3+0.4777 \ldots \ldots \\
& \Rightarrow 10 x=4.3+x \\
& \Rightarrow 10 x-x=4.3 \\
& \Rightarrow 9 x=4.3 \\
& \Rightarrow x=\frac{4.3}{9}=\frac{43}{90}
\end{aligned}\)

Thus, \(0.4 \overline{7}=\frac{43}{90}\)

Here P = 43 & q = 90 (≠ 0)

3) \(0 . \overline{001}\) =Let \(x=0 . \overline{001}=0.001001001 \ldots \ldots\)

Multiplying both sides by 1000 (since three digits are repeating), we get

\(\begin{aligned}
& 1000 x=1.001001 \ldots . \\
& \Rightarrow 1000 x=1+0.001001001 \ldots \\
& \Rightarrow 1000 x=1+x \\
& \Rightarrow 1000 x-x=1 \\
& \Rightarrow 999 x=1
\end{aligned}\) \(\Rightarrow x=\frac{1}{999}\)

Thus, \(0 . \overline{001}=\frac{1}{999}\)

Here P = 1, q = 999(≠0)

4. Express 0.99999 in the form p/q. Are you surprised by your answer? With your teacher & classmates discuss why the answer makes sense.

Solution: Let x= 0.99999………..

Multiplying both sides by 10 (since one digit is repeating) we get

10x = 9.9999……..

10x =9 + 0.9999……..

10x=9 + x

10x – x = 9

9x = 9

\(x=\frac{9}{9}=1\)

Thus \(0.99999=1=\frac{1}{1}\)

Here P = 1, q = 1

Since 0.99999 goes on forever, so there is no gap between 1 & 0.99999… & hence they are equal.

5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of \(\frac{1}{17}\)? Perform the division to check your answer.

Solution: The Maximum number of digits in the repeating block of digits in the decimal expansion of \(\frac{1}{17}\) can be 16.

Thus \(\frac{1}{17}=0 . \overline{058823529411747}\)

By long division, the number of digits in the repeating block of digits in the decimal expansion of \(\frac{1}{17}=16\)

∴ The answer is verified.

6. Look at several examples of rational numbers in the form \(\frac{p}{q}(q \neq 0)\) where p & q are integers with no common factors other than 1 & having terminating decimal representations (expansions) can you guess what property q must satisfy?

Solution: Examples:

1) \(\frac{1}{2}=\frac{1}{2} \times \frac{5}{5}=\frac{5}{10}=0.5 \quad q=2\)

2) \(\frac{1}{4}=\frac{1}{4} \times \frac{25}{25}=\frac{25}{100}=0.25 \quad q=2^2\)

3) \(\frac{3}{8}=\frac{3}{8} \times \frac{125}{125}=\frac{375}{1000}=0.375 \quad q=2^3\)

4) \(\frac{31}{25}=\frac{31 \times 4}{25 \times 4}=\frac{124}{100}=1.24 \quad q=5^2\)

5) \(\frac{7}{125}=\frac{7 \times 8}{125 \times 8}=\frac{56}{1000}=0.056 \quad q=5^3\)

6) \(\frac{13}{20}=\frac{13 \times 5}{20 \times 5}=\frac{65}{100}=0.65 \quad q=2^2 \times 5\)

7) \(\frac{29}{16}=\frac{29}{16} \times \frac{625}{625}=\frac{18125}{10000}=1.8125 \quad q=2^4\)

7. Write three numbers whose decimal expansions are non-terminating, and nonrecurring.

Solution: 0.01001000100001………………..

0. 20200220002200002……………………

0. 003000300003………….

8. Find three different irrational numbers between the rational numbers \(\frac{5}{7} \& \frac{9}{11}\)

Solution:

Thus, \(\frac{5}{7}=0.714285 \ldots\) \(=0 . \overline{714285}\)

Thus, = \(\frac{9}{11}=0.8181 \ldots\) \(=0 . \overline{81}\)

Three different irrational numbers between the \(\frac{9}{11}=0.8181 \ldots\) rational numbers \(\frac{5}{7} \& \frac{9}{11}\) can be taken as

0. 750750075000 …………………….

0.7670767000767 ……………………

0.808008000800008 …………………

9. Classify the following numbers as rational or irrational

1) \(\sqrt{23}\)
2) \(\sqrt{225}\)
3) 0.3796
4) 7.478478
5) 1.101001000100001… 

Solution:

1) \(\sqrt{23}\)

Thus, \(\sqrt{23}=4.795831\)
The decimal expansion is non – terminating nonrecurring
∴ \(\sqrt{23}\) is an irrational number

2) \(\sqrt{225}=15=\frac{15}{1}\)
\(=\left(\frac{p}{q} \text { form }\right)\)

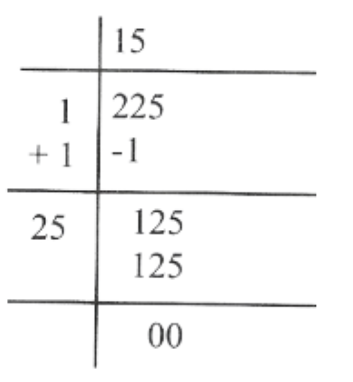
∴ \(\sqrt{225}\)
Here P = 15 & q = 1 (≠0)

3) 0.3796 = The decimal expansion is terminating
∴ 0.3796 is a rational number.

4) 7.478478 ………………..
7.478478 = \(7 . \overline{478}\)
∴ The decimal expansion is a non-terminating recurring
∴ 7.478478 is a rational number.

5) 1.101001000100001 …………………
The decimal expansion is non-terminating nonrecurring
∴ 1.101001000100001 is an irrational number.

Chapter 1 Number Systems Exercise 1.4

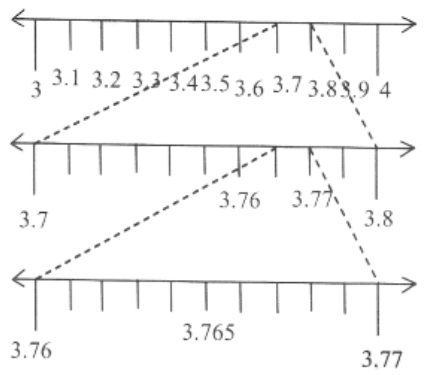
1. Visualise 3.765 on the number line using successive magnification.
Solution: 

2. Visualise \(4 . \overline{26}\) on the number line up to 4 decimal places.
Solution:

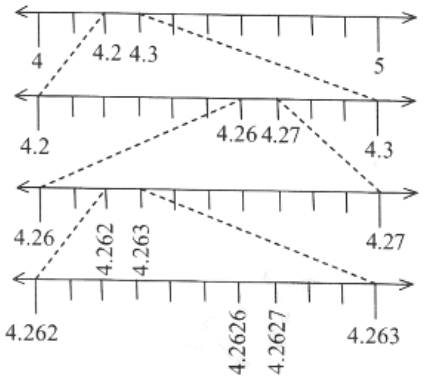
Chapter 1 Number Systems Exercise 1.5

1. Classify the following numbers as rational or irrational.

1) \(2-\sqrt{5}\)

Solution: 2 is a rational number & \(\sqrt{5}\) is an irrational number

∴ \(2-\sqrt{5}\) is an irrational number

(∵ The difference of a rational number & an irrational number is irrational)

2) \((3+\sqrt{23})-\sqrt{23}\)

Solution: \((3+\sqrt{23})-\sqrt{23}\) =3 which is a rational number.

3) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}=\frac{2}{7}\)

Solution: \(\frac{2 \sqrt{7}}{7 \sqrt{7}}=\frac{2}{7}\) Which is a rational number.

4) \(\frac{1}{\sqrt{2}}\)

Solution: 1 is a rational number & \(\sqrt{2}\) is an irrational number

∴ \(\frac{1}{\sqrt{2}}\) is an irrational number

(The quotient of a non zero rational number with an irrational number is irrational)

5) 2π

Solution: (2 ≠ 0) is a rational number & n is an irratio nal number.

∴2π is an irrational number.

∴ The product of a non-zero rational number with an irrational number is irrational.

2. Simplify each of the following expressions:

1) \((3+\sqrt{3})(2+\sqrt{2})\)

Solution: \((3+\sqrt{3})(2+\sqrt{2})\)

\(\begin{aligned}
& =3(2+\sqrt{2})+\sqrt{3}(2+\sqrt{2}) \\
& =3 \times 2 \times+3 \sqrt{2}+\sqrt{3} \times 2+\sqrt{3} \times \sqrt{2} \\
& =6+3 \sqrt{2}+2 \sqrt{3}+\sqrt{6}(\sqrt{a} \sqrt{b}=\sqrt{a b})
\end{aligned}\)

2) \((3+\sqrt{3})(3-\sqrt{3})\)

Solution: \((3+\sqrt{3})(3-\sqrt{3})=3^2-(\sqrt{3})^2\)

\(\left\{\begin{array}{l}
(a+\sqrt{b})(a-\sqrt{b}) \\
=a^2-b
\end{array}\right\}\)

3) \((\sqrt{5}+\sqrt{2})^2\)

Solution: \((\sqrt{5}+\sqrt{2})^2=(\sqrt{5})^2+2 \sqrt{5} \times \sqrt{2}+(\sqrt{2})^2\)

\(\begin{aligned}
& \left\{\begin{array}{c}
(\sqrt{a}+\sqrt{b})^2=(\sqrt{a})^2+2 \sqrt{a b}+(b)^2 \\
=a^2+2 \sqrt{a b}+b
\end{array}\right\} \\
& =5+2 \sqrt{10}+2 \\
& =7+2 \sqrt{10} \\
&
\end{aligned}\)

4) \((\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})\)

Solution: \((\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})\)

\(\begin{aligned}
& =(\sqrt{5})^2-(\sqrt{2})^2(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=a-b \\
& =5-2 \\
& =3
\end{aligned}\)

3. Recall π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is π=c/d This seems to contradict the fact that π is irrational. How will you resolve this contradiction?

Solution: There is no contradiction as either C or d is irrational & hence π is irrational.

KSEEB Chapter 1 Number Systems Solved Questions 

4. Represent \(\sqrt{9.3}\) on the number line.

Solution: Mark the distance 9.3 from a fixed point A on a given line to obtain a point B such that AB = 9.3 units. From B mark a distance of 1 unit & mark the new point as C. Find the midpoint of AC & mark that point as O. Draw a semi-circle with center O & radius OC.

Draw a line perpendicular to AC passing through B & intersecting the semi-circle at D. Then

BD = \(\sqrt{9.3}\)

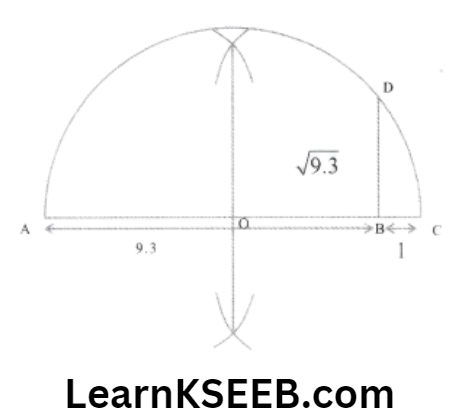
5. Rationalise the denominators of the following:

1) \(\frac{1}{\sqrt{7}}\)

\(\frac{1}{\sqrt{7}}=\frac{1}{\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}}\)(multiplying & dividing by)

\(\sqrt{7}=\frac{\sqrt{7}}{7}\)

2) \(\frac{1}{\sqrt{7}-\sqrt{6}}\)

Solution: \(\frac{1}{\sqrt{7}-\sqrt{6}}=\frac{1}{\sqrt{7}-\sqrt{6}} \times \frac{\sqrt{7}+\sqrt{6}}{\sqrt{7}+\sqrt{6}}\)

(multiplying & dividing by \(\sqrt{7}+\sqrt{6}\))

\(\frac{\sqrt{7}+\sqrt{6}}{7-6}=\sqrt{7}+\sqrt{6}\)

3) \(\frac{1}{\sqrt{5}+\sqrt{2}}\)

Solution: \(\frac{1}{\sqrt{5}+\sqrt{2}}=\frac{1}{\sqrt{5}+\sqrt{2}} \times \frac{\sqrt{5}-\sqrt{2}}{\sqrt{5}-\sqrt{2}}\)

(multiplying & dividing by \(\sqrt{5}-\sqrt{2}\))

\(=\frac{\sqrt{5}-\sqrt{2}}{5-2}=\frac{\sqrt{5}-\sqrt{2}}{3}\)

4) \(\frac{1}{\sqrt{7}-2}\)

Solution: \(\frac{1}{\sqrt{7}-2}=\frac{1}{\sqrt{7}-2} \times \frac{\sqrt{7}+2}{\sqrt{7}+2}\)

(multiplying & dividing by \(\sqrt{7}+2)\))

\(=\frac{\sqrt{7}+2}{7-4}=\frac{\sqrt{7}+2}{3}\)

Chapter 1 Number Systems Exercise 1.6

1. Find
1) \(64^{1 / 2}\)
Solution: \(64^{1 / 2}=\left(8^2\right)^{1 / 2}=8^{2 \times 1 / 2}=8^1=8\)

2) \(32^{1 / 5}\)
Solution: \(32^{1 / 5}=\left(2^5\right)^{1 / 5}=2^{5 \times 1 / 5}=2^1=2\)

3) \(125^{1 / 3}\)
Solution: \(125^{1 / 3}=\left(5^3\right)^{1 / 3}=5^{3 \times 1 / 3}=5^1=5\)

2. Find
1) \(9^{3 / 2}\)
Solution: \(9^{3 / 2}=\left(3^2\right)^{3 / 2}=3^{2 \times 3 / 2}=3^3=27\)

2) \(32^{2 / 5}\)
Solution: \(32^{2 / 5}=2^{5 \times 2 / 5}=2^2=4\)

3) \(16^{3 / 4}\)
Solution: \(16^{3 / 4}=2^{4 x^3 / 4}=2^3=8\)

4) \(125^{-1 / 3}\)
Solution: \(125^{-1 / 3}=\left(5^3\right)^{-1 / 3}=5^{3 \times-1 / 3}=5^{-1}=\frac{1}{5}\)

3. Simplify
1) \(2^{2 / 3} \times 2^{1 / 5}\)
solution: \(2^{2 / 3} \times 2^{1 / 5}=2^{\frac{2}{3}+\frac{1}{5}}=2^{\frac{10+3}{15}}=2^{\frac{13}{15}}\)

2) \(\left(\frac{1}{3^3}\right)^7\)
Solution: \(\left(\frac{1}{3^3}\right)^7=\frac{1^7}{\left(3^3\right)^7}=\frac{1}{3^{21}}=3^{-21}\)

3) \(\frac{11^{1 / 2}}{11^{1 / 4}}\)
Solution: \(\frac{11^{1 / 2}}{11^{1 / 4}}=11^{1 / 2-1 / 4}=11^{1 / 4}\)

4) \(7^{1 / 2} \times 8^{1 / 2}\)
Solution: \(7^{1 / 2} \times 8^{1 / 2}=(7 \times 8)^{1 / 2}=56^{1 / 2}\)

Chapter 1 Number Systems Choose the correct answer from the following

1. Which of the following is a rational number?

1. \(\sqrt{5}\)
2. π
3. 0.101001000100001
4. 0.853853853

Solution: 4) 0.853853853

2. π is :

1. a rational number
2. an integer
3. an irrational number
4. a whole number

Solution: 3) an irrational number

3. The value of \(\sqrt[4]{\sqrt[3]{2^2}}\) is equal to

1. \(2^{-1 / 6}\)
2. \(2^{-6}\)
3. \(2^{1 / 6}\)
4. \(2^6\)

Solution: 3) \(2^{1 / 6}\)

KSEEB 9th Standard Maths Chapter 1 Important Questions

4. Which of the following is irrational number?

1. 0.15
2. \(0.15 \overline{16}\)
3. \(0 . \overline{1516}\)
4. 0.501500150001

Solution: 3) \(0 . \overline{1516}\)

5. The value of \(\frac{2^{\circ} \times 7^{\circ}}{5^{\circ}}\) is

1. 1
2. 0
3. \(\frac{9}{5}\)
4. \(1 / 5\)

Solution: 1) 1

6. Two rational numbers between \(\frac{2}{3} \& \frac{5}{3}\) are

1. \(\frac{1}{6} \& \frac{2}{6}\)
2. \(\frac{1}{2} \& \frac{2}{7}\)
3. \(\frac{5}{6} \& \frac{7}{6}\)
4. \(\frac{2}{3} \& \frac{4}{3}\)

Solution: \(\frac{5}{6} \& \frac{7}{6}\)

7. Every rational number is

1. a natural number
2. an integer
3. a real number
4. a whole number

Solution: 3) a real number

8. If \(x^{1 / 2}=49^{1 / 24}\) then x is equal to :

1. 49
2. 2
3. 12
4. 7

Solution: 4) 7

9. If \(8^x=\frac{64}{2^x}\) then the value of x is

1. 3
2. 1
3. 1/2
4. 3/-2

Solution: 4) 3/-2

10. \((0.001)^{1 / 3}\) is equal to

1. 0.1
2. 0.001
3. 0.01
4. 0.0001

Solution: 1) 0.1

11. If a = 2 & b = 3, then the value of \(b^a\) is

1. 4
2. 9
3. 2
4. 3

Solution: 2) 9

12. The decimal form of \(\frac{1}{500}\) is

1. 0.002
2. 0.02
3. 0.2
4. 0.005

Solution: 1) 0.002

13. The product of any two irrational number is

1. always an irrational number
2. always a rational number
3. always an integer
4. sometimes rational, sometimes irrational.

Solution: 4) sometimes rational, sometimes irrational.

14. The value of \(0 . \overline{25}\) is equal to 

1. \(\frac{65}{99}\)
2. \(\frac{37}{99}\)
3. \(\frac{5}{9}\)
4. \(\frac{25}{99}\)

Solution: 4) \(\frac{25}{99}\)

15. After rationalising the denominator of \(\frac{7}{3 \sqrt{3}-2 \sqrt{3}}\) we get the denominator as.

1. 13
2. 19
3. 5
4. 35

Solution: 2) 19

Chapter 1 Number Systems One Mark Questions

1. Write the simplest form of a rational number \(\frac{177}{413}\)

Solution: \(\frac{177}{413}=\frac{59 \times 3}{59 \times 7}=\frac{3}{7}\)

2. Find two rational numbers between \(\frac{1}{3} \& \frac{4}{5}\)

Solution: \(\frac{1}{3}=\frac{1 \times 5}{3 \times 5}=\frac{5}{15}\)

\(\frac{4}{5}=\frac{4 \times 3}{5 \times 3}=\frac{12}{15}\)

Hence two rational numbers can be taken as \(\frac{6}{15}, \frac{8}{15}\)

3. Find two irrational numbers between 0.1 & 0.12

Solution: The two irrational numbers between 0.1 & 0.12 are

0.101001001 & 0.11010010001.

4. Write the sum of \(2 \sqrt{5} \& 3 \sqrt{7}\)

Solution: \(2 \sqrt{5}+3 \sqrt{7}\)

5. Write the sum of \(0 . \overline{3}+0 . \overline{4}\)

Solution: \(0 . \overline{3}+0 . \overline{4}=(0.333 \ldots \ldots \ldots)+(0.444 \ldots \ldots . .)\)

= 0.777……….

6. Simplify \((\sqrt{2}+\sqrt{5})^2\)

Solution:

\(\begin{aligned}
(\sqrt{2}+\sqrt{5})^2 & =(\sqrt{2})^2+2 \sqrt{2} \sqrt{5}+(\sqrt{5})^2 \\
= & 2+2 \sqrt{10}+5 \\
= & 7+2 \sqrt{10}
\end{aligned}\)

7. Write the equivalent of \(\sqrt{12} \times \sqrt{8}\)

Solution:

\(\begin{aligned}
\sqrt{12} \times \sqrt{8} & =\sqrt{4 \times 3} \times \sqrt{4 \times 2} \\
& =2 \sqrt{3} \times 2 \sqrt{2} \\
& =4 \sqrt{3 \times 2} \\
& =4 \sqrt{6}
\end{aligned}\)

8. If \(x=\frac{\sqrt{7}}{5} \& \frac{5}{x}=\mathrm{P} \sqrt{7}\) , then find the value of P

Solution:

\(\frac{5}{x}=P \sqrt{7}\) \(\begin{aligned}
& \frac{5}{\sqrt{7}} \times 5=P \sqrt{7} \\
& 25=P \sqrt{7} \times \sqrt{7} \\
& \Rightarrow \quad P=\frac{25}{7}
\end{aligned}\)

9. Calculate the quotient obtained when \(\sqrt{1500}\) is divided by \(2 \sqrt{15}\)

Solution:

\(\begin{aligned}
\frac{\sqrt{1500}}{2 \sqrt{15}} & =\frac{1}{2} \times \sqrt{\frac{1500}{15}} \\
& =\frac{1}{2} \sqrt{100}=\frac{10}{2}=5
\end{aligned}\)

10. Write the rationalising factor of \(\frac{1}{\sqrt{50}}\)

Solution: \(\frac{1}{\sqrt{50}}=\frac{1}{\sqrt{5 \times 5 \times 2}}=\frac{1}{5 \sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{10}\)

∴ \(\sqrt{2}\) is a rationalising factor.

Chapter 1 Number Systems Two Mark Questions

1. Calculate the value of \(2 . \overline{9}\) in the form of \(\frac{p}{q}\) where p & q are integers & q ≠ 0.

Soution: \(\text { Let } x=2 . \overline{9}=2.9999 \text {…………. }\)

\(\begin{aligned}
& \Rightarrow 10 x=29.999 \ldots \ldots \\
& \Rightarrow 10 x=27+2.999 \ldots . \\
& \Rightarrow 10 x=27+x \\
& \Rightarrow 10 x-x=27 \\
& \Rightarrow 9 x=27 \\
& \Rightarrow x=27 / 9 \\
& \Rightarrow x=3
\end{aligned}\)

2. If 7x= 1, then find the decimal expansion of x.

Solution: \(x=\frac{1}{7}\)

∴ \(x=0 . \overline{142857}\)

3. In the following equations, find which variables x, y, z etc., represent rational number & which represent irrational numbers.

1) \(x^2=5\)

Solution: \(x=\sqrt{5}\), which is an irrational number.

2) \(y^2=9\)

Solution: \(y=\sqrt{9}=3\), which is a rational number.

3) \(z^2=0.04\)

Solution: \(z^2=\sqrt{0.04}=0.2=\frac{2}{10}=\frac{1}{5}\) which is a rational number.

4) \(\mathbf{u}^2=\frac{17}{4}\)

Solution: \(u=\sqrt{\frac{17}{4}}=\frac{\sqrt{17}}{\sqrt{4}}=\frac{\sqrt{17}}{2}=\frac{1}{2} \times \sqrt{17}\)

\(\frac{1}{2}\) is a rational number & \(\sqrt{17}\) is an irrational number.

∴ \(\frac{1}{2} \times \sqrt{17}\) is an irrational number.

4. Express the decimal number \(2.2 \overline{18}\) in the form of \(\frac{p}{q}\) where p & q are integers & q ≠ 0

Solution: Let \(x=2.2 \overline{18}=2.2181818\)

\(\begin{aligned}
& 10 x=22.181818 \ldots \ldots \\
& 1000 x=2218.1818 \ldots . \\
& 1000 x=2196+22.181818 \ldots . \\
& 1000 x=2196+10 x \\
& 1000 x-10 x=2196 \\
& 990 x=2196
\end{aligned}\) \(x=\frac{2196}{990}=\frac{2 \times 3 \times 3 \times 122}{2 \times 3 \times 3 \times 55}\)

x = \(\frac{122}{55}\)

Karnataka Board Class 9 Maths Chapter 1 MCQs

5. Simplify: \(\sqrt[4]{16}-6 \sqrt[3]{343}+18 \sqrt[5]{243}-\sqrt{196}\)

Solution: \(\sqrt[4]{2^4}-6 \sqrt[3]{7^3}+18 \sqrt[5]{3^5}-\sqrt{14^2}\)

\(\begin{aligned}
& =2-(6 \times 7)+(18 \times 3)-14 \\
& =2-42+54-14 \\
& =56-56 \\
& =0
\end{aligned}\)

6. Simplify the product \((4 \sqrt{3}+3 \sqrt{2})(4 \sqrt{3}-3 \sqrt{2})\)

Solution: \((4 \sqrt{3}+3 \sqrt{2}) \times(4 \sqrt{3}-3 \sqrt{2})\)

\(\begin{aligned}
& =(4 \sqrt{3})^2-(3 \sqrt{2})^2\left\{(a+b)(a-b)=a^2-b^2\right\} \\
& =4^2(\sqrt{3})^2-3^2(\sqrt{2})^2 \\
& =16 \times 3-9 \times 2 \\
& =48-18=30
\end{aligned}\)

7. Calculate the value of \(\left[\left\{(81)^{-1 / 2}\right\}^{-\frac{1}{4}}\right]^2\)

Solution: \(\left[\left\{(81)^{-1 / 2}\right\}^{-\frac{1}{4}}\right]^2\)

\(\begin{aligned}
& =(81)^{-1 / 2 \times \frac{1}{4} \times 2} \\
& =(81)^{\frac{2}{8}} \\
& =(81)^{\frac{1}{4}}=\left(3^4\right)^{1 / 4} \\
& =3^1=3
\end{aligned}\)

8. Find the value of \(\frac{3^{30}+3^{29}+3^{28}}{3^{31}+3^{30}-3^{29}}\)

Solution: \(\frac{3^{30}+3^{29}+3^{28}}{3^{31}+3^{30}-3^{29}}=\frac{3^{28}\left(3^2+3^1+1\right)}{3^{29}\left(3^2+3^1-1\right)}\)

\(=\frac{1}{3} \frac{(9+3+1)}{(9+3-1)}\) \(=\frac{1}{3} \times \frac{13}{11}\) \(=\frac{13}{33}\)

9. If a = 3 & b= 2, then find the value of \(a^b+b^a\)

Solution: Given a = 3 & b = 2

\(\begin{aligned}
a^b+b^a & =3^2+2^3 \\
& =9+8 \\
& =17
\end{aligned}\)

10. Simplify: \(\frac{6-4 \sqrt{3}}{6+4 \sqrt{3}}\) by rationalising the denominator.

Solution: \(\frac{6-4 \sqrt{3}}{6+4 \sqrt{3}}=\frac{6-4 \sqrt{3}}{6+4 \sqrt{3}} \times \frac{6-4 \sqrt{3}}{6-4 \sqrt{3}}\)

\(=\frac{(6-4 \sqrt{3})^2}{6^2-4^2(\sqrt{3})^2}=\frac{36+48-48 \sqrt{3}}{36-48}\) \(\begin{aligned}
& =\frac{84-48 \sqrt{3}}{-12} \\
& =\frac{12(7-4 \sqrt{3})}{-12}
\end{aligned}\) \(\begin{aligned}
& =-(7-4 \sqrt{3}) \\
& =-7+4 \sqrt{3}
\end{aligned}\)

11. If \(\sqrt{2}\) =1.414, find the value of \(\frac{1}{\sqrt{2}+1}\)

Solution: \(\frac{1}{\sqrt{2}+1}=\frac{1}{\sqrt{2}+1} \times \frac{\sqrt{2}-1}{\sqrt{2}-1}\)

\(=\frac{\sqrt{2}-1}{(\sqrt{2})^2-1^2}\) \(=\frac{\sqrt{2}-1}{2-1}=\frac{1.1414-1}{1}=0.414\)

12. Find six rational numbers between 3 & 4

Solution: Let a = 3 & b = 4

Here, we find six rational numbers i.e., n = 6

So, d = \(\frac{b-a}{n+1}=\frac{4-3}{6+1}=\frac{1}{7}\)

1st rational number = \(a+d=3+\frac{1}{7}=\frac{22}{7}\)

2nd rational number = \(a+2 d=3+\frac{2}{7}=\frac{23}{7}\)

3rd rational number = \(a+3 d=3+\frac{3}{7}=\frac{24}{7}\)

4th rational number = \(a+4 d=3+\frac{4}{7}=\frac{25}{7}\)

5th rational number = \(a+5 d=3+\frac{5}{7}=\frac{26}{7}\)

6th rational number = \(a+6 d=3+\frac{6}{7}=\frac{27}{7}\)

So, six rational numbers are \(\frac{22}{7}, \frac{23}{7}, \frac{24}{7}, \frac{25}{7}, \frac{26}{7} \& \frac{27}{7}\)

Chapter 1 Number Systems Three Mark Questions

1. Find three rational numbers between \(\frac{5}{7} \& \frac{9}{11}\)

Solution: Since LCM of 7 & 11 is 77.

∴ \(\frac{9}{11}=\frac{9}{11} \times \frac{7}{7}=\frac{63}{77} \times \frac{3}{3}=\frac{441}{539}\)

\(\frac{5}{7}=\frac{5}{7} \times \frac{11}{11}=\frac{55}{77} \times \frac{3}{3}=\frac{385}{539}\)

Hence, three rational numbers between \(\frac{5}{7}\) & \(\frac{9}{11}\) are \(\frac{386}{539}, \frac{387}{539}, \frac{388}{539}\)

2. Represent \(\sqrt{5}\) on the number line.

Solution: w.k.t. \(\sqrt{5}=\sqrt{4+1}=\sqrt{2^2+1^2}\)

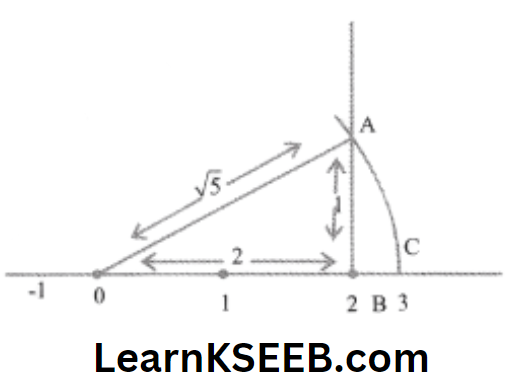
Draw a right angled ΔOBA such that OB = 2 units, AB = 1 unit & [\(\lfloor\mathrm{OBA}\) = 90°

By Pythagora’s theorem, we have

\(\mathrm{OA}^2=\mathrm{OB}^2+\mathrm{AB}^2=2^2+1^2\) \(\mathrm{OA}=\sqrt{4+1}=\sqrt{5}\)

Now, take O as, center, OA= \(=\sqrt{5}\) as radius draw an arc that intersects the line at point C. Hence, the point R represents \(\sqrt{5}\)

KSEEB Maths Chapter 1 Number Systems Free Solutions 

3. Evaluate: \(\sqrt{5+2 \sqrt{6}}+\sqrt{8-2 \sqrt{15}}\)

Solution: \(\sqrt{5+2 \sqrt{6}}=\sqrt{3+2+2 \sqrt{6}}=\sqrt{(\sqrt{3}+\sqrt{2})^2}\)

\(=\sqrt{3}+\sqrt{2}\) \(\begin{aligned}
\sqrt{8-2 \sqrt{15}} & =\sqrt{5+3-2 \sqrt{15}} \\
& =\sqrt{(\sqrt{5}-\sqrt{3})^2} \\
& =\sqrt{5}-\sqrt{3}
\end{aligned}\)

∴ \(\sqrt{5+2 \sqrt{6}}+\sqrt{8-2 \sqrt{5}}=\sqrt{3}+\sqrt{2}+\sqrt{5}-\sqrt{3}\)

\(=\sqrt{2}+\sqrt{5}\)

4. Show that: \(\frac{x^{a(b-c)}}{x^{b(a-c)}} \div\left[\frac{\left(x^b\right)}{\left(x^a\right)}\right]^c=1\)

Solution: LHS: \(\frac{x^{a(b-c)}}{x^{b(a-c)}} \times\left[\frac{\left(x^a\right)}{\left(x^b\right)}\right]^c\)

\(\begin{aligned}
& =\frac{x^{a b-a c}}{x^{b a-b c}} \times \frac{x^{a c}}{x^{b c}} \\
& =\frac{x^{a b-a c+a c}}{x^{a b-b c+b c}} \\
& =\frac{x^{a b}}{x^{a b}} \\
& =x^{a b-a b}
\end{aligned}\)

\(=x^0=1\) = RHS

Hence Proved.

5. Simplify: \(\left(\frac{5^{-1} \times 7^2}{5^2 \times 7^{-4}}\right)^{7 / 2} \times\left(\frac{5^{-2} \times 7^3}{5^3 \times 7^{-5}}\right)^{-5 / 2}\)

Solution: \(\left(\frac{5^{-1} \times 7^2}{5^2 \times 7^{-4}}\right)^{7 / 2} \times\left(\frac{5^{-2} \times 7^3}{5^4 \times 7^{-5}}\right)^{-5 / 2}\)

\(\begin{aligned}
& =\left(\frac{7^4 \times 7^2}{5^2 \times 5^1}\right)^{7 / 2} \times\left(\frac{7^5 \times 7^3}{5^3 \times 5^2}\right)^{-5 / 2} \\
& =\left(\frac{7^6}{5^3}\right)^{7 / 2} \times\left(\frac{7^8}{5^5}\right)^{-5 / 2}
\end{aligned}\) \(=\frac{7^{6 \times 7 / 2}}{5^{3 x^{7 / 2}}} \times\left(\frac{5^5}{7^8}\right)^{5 / 2}\) \(=\frac{7^{21}}{5^{21 / 2}} \times \frac{5^{25 / 2}}{7^{20}}\) \(=7^{21-20} \times 5^{\frac{25}{2}-\frac{21}{2}}\) \(=7^1 \times 5^{\frac{2}{4}}=7^1 \times 5^2=175\)

6. If x= 5 & y= 2, then find the value of
1) \(\left(x^y+y^x\right)^{-1}\)
2) \(\left(x^y+y^y\right)^{-1}\)

Solution: (1) = \(\left(5^2+2^5\right)^{-1}\)

\(\begin{aligned}
& =(25+32)^{-1} \\
& =(57)^{-1}=\frac{1}{57}
\end{aligned}\)

(2) \(=\left(5^2+2^2\right)^{-1}\)

\(\begin{aligned}
& =(25+4)^{-1} \\
& =(29)^{-1} \\
& =\frac{1}{29}
\end{aligned}\)

7. If x= \(x=3-2 \sqrt{2}\), find the value of \(\sqrt{x}+\frac{1}{\sqrt{x}}\)

Solution: \(x=3-2 \sqrt{2}\)

\(\frac{1}{x}=\frac{1}{3-2 \sqrt{2}} \times \frac{3+2 \sqrt{2}}{3+2 \sqrt{2}}\) \(\begin{aligned}
& =\frac{3+2 \sqrt{2}}{3^2-2^2(\sqrt{2})^2} \\
& =\frac{3+2 \sqrt{2}}{9-8}
\end{aligned}\) \(\begin{aligned}
& \frac{1}{x}=3+2 \sqrt{2} \\
& \left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)^2=x+\frac{1}{x}+2 \sqrt{x} \times \frac{1}{\sqrt{x}}
\end{aligned}\) \(=x+\frac{1}{x}+2\) \(=3-2 \sqrt{2}+3+2 \sqrt{2}+2\) \(\begin{aligned}
& \left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)^2=8 \\
& =\sqrt{8}
\end{aligned}\) \(=\pm 2 \sqrt{2}\)

8. Find the values of a & b when \(\frac{5+\sqrt{6}}{5-\sqrt{6}}\)

Solution: \(\frac{5+\sqrt{6}}{5-\sqrt{6}}=\frac{5+\sqrt{6}}{5-\sqrt{6}} \times \frac{5+\sqrt{6}}{5+\sqrt{6}}\)

\(=\frac{(5+\sqrt{6})^2}{5^2-(6)^2}=\frac{25+6+10 \sqrt{6}}{25-6}\) \(=\frac{31+10 \sqrt{6}}{19}\)

∴ \(a+b \sqrt{6}=\frac{31}{19}+\frac{10}{19} \sqrt{6}\)

comparing the powers of both sides, we

\(a=\frac{31}{19}\), \(b=\frac{10}{19}\)

9. Find the value of \(\left(x-\frac{1}{x}\right)^3\), if \(x=1+\sqrt{2}\)

Solution: \(x=1+\sqrt{2}\)

\(\frac{1}{x}=\frac{1}{1+\sqrt{2}} \times \frac{1-\sqrt{2}}{1-\sqrt{2}}\) \(\begin{gathered}
=\frac{1-\sqrt{2}}{1^2-\sqrt{2}} \\
=\frac{1-\sqrt{2}}{-1} \\
=-1+\sqrt{2}
\end{gathered}\) \(\left(x-\frac{1}{x}\right)^3=[(1+\sqrt{2})-(-1+\sqrt{2})]^3\) \(\begin{aligned}
& =(1+\sqrt{2}+1-\sqrt{2})^3 \\
& =(2)^3 \\
& =8
\end{aligned}\)

10. Write \(\sqrt[3]{4}, \sqrt{3}, \sqrt[4]{6}\) in ascending order.

Solution: \(4^{1 / 3}, 3^{1 / 2}, 6^{1 / 4}\), LCM of 3, 2, 4 is 12.

\(4^{1 / 3}=4^{1 / 3^{\times 2} 12}=4^{\frac{4}{12}}=\left(4^4\right)^{1 / 12}=(729)^{1 / 12}\) \(3^{1 / 2}=3^{1 / 2 \times \frac{12}{12}}=3^{\frac{6}{12}}=\left(3^6\right)^{1 / 12}=(256)^{1 / 12}\) \(6^{1 / 4}=6^{1 / 4^{\frac{12}{12}}}=6^{\frac{3}{12}}=\left(6^3\right)^{1 / 12}=(729)^{1 / 12}\)

ascending order =

\((216)^{1 / 12},(256)^{1 / 12},(729)^{1 / 12}\)

i.e; \(\sqrt[4]{6}, \quad \sqrt[3]{4}, \quad \sqrt{3}\)

11. Rationalise the denominator of \(\frac{30}{5 \sqrt{3}-3 \sqrt{5}}\)

Solution: \(\frac{30}{5 \sqrt{3}-3 \sqrt{5}}=\frac{30}{5 \sqrt{3}-3 \sqrt{5}} \times \frac{5 \sqrt{3}+3 \sqrt{5}}{5 \sqrt{3}+3 \sqrt{5}}\)

\(=\frac{30(5 \sqrt{3}+3 \sqrt{5})}{(5 \sqrt{3})^2-(3 \sqrt{5})^2}\)

⇒ \(\begin{aligned}
& =\frac{30(5 \sqrt{3}+3 \sqrt{5})}{75-45} \\
& =\frac{30(5 \sqrt{3}+3 \sqrt{5})}{30} \\
& =5 \sqrt{3}+3 \sqrt{5}
\end{aligned}\)

Class 9 Maths Number Systems KSEEB Guide

12. Prove that : \(\frac{a^{-1}}{a^{-1}+b^{-1}}+\frac{a^{-1}}{a^{-1}-b^{-1}}=\frac{-(2 b)^2}{a^2+b^2}\)

Solution: LHS = \(\frac{a^{-1}}{a^{-1}+b^{-1}}+\frac{a^{-1}}{a^{-1}-b^{-1}}\)

\(\begin{aligned}
& =\frac{\frac{1}{a}}{\frac{1}{a}+\frac{1}{b}}+\frac{\frac{1}{a}}{\frac{1}{a}-\frac{1}{b}} \\
& =\frac{\frac{1}{a}}{\frac{b+a}{a b}}+\frac{\frac{1}{a}}{\frac{b-a}{a b}} \\
& =\frac{1}{a} \times \frac{a b}{a+b}+\frac{1}{a} \times \frac{a b}{b-a} \\
& =\frac{b}{a+b}+\frac{b}{b-a} \\
& =\frac{(b-a) b+b(a+b)}{(a+b)(b-a)} \\
& =\frac{b^2-a b+a b+b^2}{b^2-a^2} \\
& =\frac{\left(2 b^2\right)}{b^2-a^2} \\
& =\frac{-\left(2 b^2\right)}{\left(a^2-b^2\right)} \\
&
\end{aligned}\)

13. Simplify: \(\frac{\sqrt{2}}{\sqrt{5}+2}-\frac{2}{\sqrt{10}-2 \sqrt{2}}+\frac{8}{\sqrt{2}}\)

 Solution: \(\left(\frac{\sqrt{2}}{\sqrt{5}+2} \times \frac{\sqrt{5}-2}{\sqrt{5}-2}\right)-\left(\frac{2}{\sqrt{10}-2 \sqrt{2}} \times \frac{\sqrt{10}+2 \sqrt{2}}{\sqrt{10}+2 \sqrt{2}}\right)\) + \(\frac{8}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}\)

\(=\left(\frac{\sqrt{10}-2 \sqrt{2}}{5-4}\right)-\left(\frac{2(\sqrt{10}+2 \sqrt{2})}{10-8}\right)+\frac{8 \sqrt{2}}{2}\) \(=(\sqrt{10}-2 \sqrt{2})-2\left(\frac{\sqrt{10}+2 \sqrt{2}}{2}\right)+4 \sqrt{2}\) \(=\sqrt{10}-2 \sqrt{2}-\sqrt{10}-2 \sqrt{2}+4 \sqrt{2}\)

= 0

Chapter 1 Number Systems Four Mark Questions

1. If a = \(\frac{3-\sqrt{5}}{3+\sqrt{5}}\) & b = \(\frac{3+\sqrt{5}}{3-\sqrt{5}}\) find \(a^2-b^2\)

Solution: \(\mathrm{a}^2-\mathrm{b}^2=(\mathrm{a}+\mathrm{b})(\mathrm{a}-\mathrm{b})\)

\(\begin{aligned}
a+b & =\frac{3-\sqrt{5}}{3+\sqrt{5}}+\frac{3+\sqrt{5}}{3-\sqrt{5}} \\
& =\frac{3-\sqrt{5}}{3+\sqrt{5}} \times \frac{3-\sqrt{5}}{3-\sqrt{5}}+\frac{3+\sqrt{5}}{3-\sqrt{5}} \times \frac{3+\sqrt{5}}{3+\sqrt{5}} \\
& =\frac{(3-\sqrt{5})^2}{9-5}+\frac{(3+\sqrt{5})^2}{9-5} \\
& =\frac{9+5-6 \sqrt{5}}{4}+\frac{9+5+6 \sqrt{5}}{4} \\
& =\frac{14-6 \sqrt{5}+14+6 \sqrt{5}}{4}
\end{aligned}\)

\(a+b=\frac{28}{4}=7\) ……………………..(1)

\(\begin{aligned}
& a-b=\left(\frac{3-\sqrt{5}}{3+\sqrt{5}}\right)-\left(\frac{3+\sqrt{5}}{3-\sqrt{5}}\right) \\
& =\left(\frac{3-\sqrt{5}}{3+\sqrt{5}} \times \frac{3-\sqrt{5}}{3-\sqrt{5}}\right)-\left(\frac{3+\sqrt{5}}{3-\sqrt{5}} \times \frac{3+\sqrt{5}}{3+\sqrt{5}}\right) \\
& =\frac{(3-\sqrt{5})^2}{9-5}-\frac{(3+\sqrt{5})^2}{9-5} \\
& =\frac{9+5-6 \sqrt{5}}{4}-\frac{9+5+6 \sqrt{5}}{4} \\
& =\frac{14-6 \sqrt{5}}{4}-\frac{14+6 \sqrt{5}}{4} \\
& =\frac{14-6 \sqrt{5}-14-6 \sqrt{5}}{4} \\
& =\frac{-12 \sqrt{5}}{4}
\end{aligned}\)

\(a-b=-3 \sqrt{5}\) ……………………(2)

from (1) & (2) we get

\(\begin{aligned}
& a^2-b^2=(a+b)(a-b) \\
& =7 \times(-3 \sqrt{5}) \\
& =-21 \sqrt{5} \\
&
\end{aligned}\)

2. Express \(1.3 \overline{2}+0 . \overline{35}\) in the form \(\frac{p}{q}\), where p & q are integers & q ≠ 0

Solution: Let \(x=1.3 \overline{2}=1.32222 \ldots \ldots\)

\(100 x=132.2222 \ldots \ldots\) \(\begin{aligned}
& 10 x=13.2222 \ldots \ldots . \\
& 100 x-10 x=(132.222 \ldots)-(13.222 \ldots .) \\
& 90 x=119 \\
& x=\frac{119}{90}
\end{aligned}\)

Again let y = \(0.3 \overline{5}=0.353535 \ldots\)

\(\begin{aligned}
& 100 y=35.3535 \ldots . \\
& 100 y-y=(35.3535)-(0.3535 \ldots \ldots)
\end{aligned}\) \(\begin{array}{r}
99 y=35 \\
y=\frac{35}{99}
\end{array}\)

∴ \(1.3 \overline{2}+0.3 \overline{5}=x+y=\frac{119}{90}+\frac{35}{99}\)

\(=\frac{119 \times 11+35 \times 10}{990}=\frac{1309+350}{990}=\frac{1659}{990}\)

3. Show that : \(\frac{1}{1+x^{a-b}}+\frac{1}{1+x^{b-a}}=1\)

Solution: LHS = \(\frac{1}{1+x^{a-b}}+\frac{1}{1+x^{b-a}}\)

\(=\frac{1}{1+\frac{x^a}{x^b}}+\frac{1}{1+\frac{x^b}{x^a}}\) \(=\frac{\frac{1}{x^b+x^a}}{x^b}+\frac{1}{\frac{x^a+x^b}{x^a}}\) \(=\frac{x^b}{x^a+x^b}+\frac{x^a}{x^a+x^b}\) \(=\frac{x^b+x^a}{x^a+x^b}\)

= 1

= RHS

Hence Proved

4. If \(x=\frac{1}{2-\sqrt{3}}\) , find the value of \(2 x^3-2 x^2+7 x+5\)

Solution: Given: \(x=\frac{1}{2-\sqrt{3}}\)

\(x=\frac{1}{2-\sqrt{3}} \times \frac{2+\sqrt{3}}{2+\sqrt{3}}\) \(\begin{array}{r}
=\frac{2+\sqrt{3}}{4-3} \\
x=2+\sqrt{3}
\end{array}\)

Consider \(2 x^3-2 x^2+7 x+5\)

\(=2(2+\sqrt{3})^3-2(2+\sqrt{3})^2+7(2+\sqrt{3})+5\)

\(=2[8+3 \sqrt{3}+12 \sqrt{3}+18]-2(4+3+4 \sqrt{3})\)\(+14+7 \sqrt{3}+5\)

= \(16+6 \sqrt{3}+24 \sqrt{3}+36-8-6-8 \sqrt{3}\)\(+14+7 \sqrt{3}+5=29 \sqrt{3}+57\)

KSEEB Class 9 Maths Chapter 1 Exercise Solutions 

5. Two classmates Salma & Anand simplified two different expressions during the revision hour & explained to each other their simplifications. Salma explains the simplification of \(\frac{\sqrt{2}}{\sqrt{5}+\sqrt{3}}\) &Anand explains the simplification of \(\sqrt{28}+\sqrt{98}+\sqrt{147}\) write both the simplification. What value does it depict?

Solution: Justify:

\(\frac{\sqrt{2}}{\sqrt{5}+\sqrt{3}}=\frac{\sqrt{2}}{\sqrt{5}+\sqrt{3}} \times \frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}-\sqrt{3}}\) \(=\frac{\sqrt{2}(\sqrt{5}-\sqrt{3})}{5-3}\) \(=\frac{\sqrt{10}-\sqrt{6}}{2}\)

Again, \(\sqrt{28}+\sqrt{98}+\sqrt{147}\)

\(\begin{aligned}
& =\sqrt{2 \times 2 \times 7}+\sqrt{2 \times 7 \times 7}+\sqrt{3 \times 7 \times 7} \\
& =2 \sqrt{7}+7 \sqrt{2}+7 \sqrt{3}
\end{aligned}\)

value: cooperative learning among classmates without any gender & religious bias.

6. Simplify: 

1) \(\left\{5\left(8^{1 / 3}+27^{1 / 3}\right)^3\right\}^{1 / 4}\)

Solution: \(\left\{5\left(8^{\frac{1}{3}}+27^{\frac{1}{3}}\right)^3\right\}^{\frac{1}{4}}\)

\(=\left[5\left(2^{3 \times \frac{1}{3}}+3^{3 \times \frac{1}{3}}\right)^3\right]^{\frac{1}{4}}\) \(\begin{aligned}
& =\left\{5(2+3)^3\right\}^{\frac{1}{4}} \\
& =\left(5 \times 5^3\right)^{\frac{1}{4}} \\
& =\left(5^4\right)^{\frac{1}{4}} \\
& =5^1
\end{aligned}\)

=5

2) \(\frac{9^{1 / 3} \times 27^{1 / 2}}{3^{-1 / 6} \times 3^{1 / 3}}\)

Solution: \(\frac{9^{\frac{1}{3}}+27^{\frac{1}{2}}}{3^{\frac{-1}{6}} \times 3^{\frac{1}{3}}}\)

\(=\frac{\left(3^2\right)^{\frac{1}{3}} \times\left(3^3\right)^{\frac{1}{2}}}{3^{-\frac{1}{6}} \times 3^{\frac{1}{3}}}\) \(=3^{\frac{2}{3}} \times 3^{\frac{3}{2}} \times 3^{\frac{1}{6}} \times 3^{-\frac{1}{3}}\) \(=3^{\frac{2}{3}+\frac{3}{2}+\frac{1}{6}-\frac{1}{3}}\) \(=3^{\frac{4+9+1-2}{6}}\) \(\begin{aligned}
& =3^{\frac{12}{6}} \\
& =3^2
\end{aligned}\)

=9