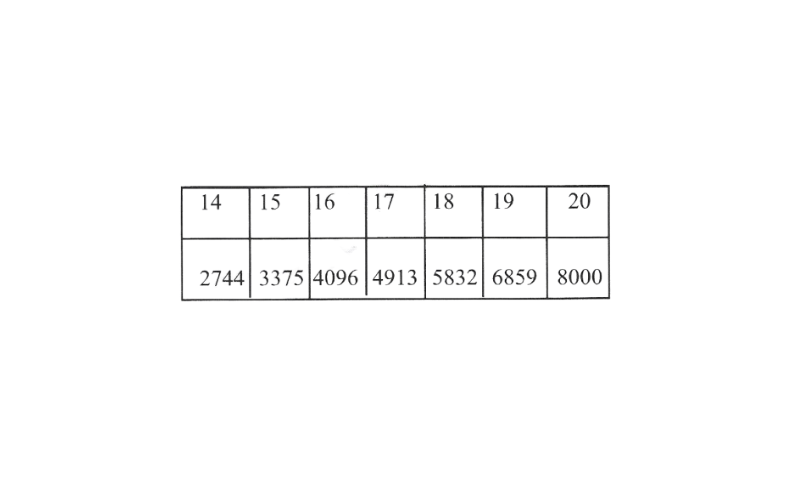
KSEEB Solutions for Class 8 Maths Chapter 8 Cube and Cube Roots

KSEEB Solutions For Class 8 Maths Chapter 8 Cubes And Cube Roots Points To Remember

Cube Number: Number obtained when a number is multiplied by itself three times
\(2^3 = 2x2x2 = 8\)
\(3^3 = 3x3x3 = 27\) etc.

Numbers like 1729,4104,13832 are known as Hardy Ramanujan Numbers. They can be expressed as sum of two cubes in two different ways.

Numbers obtained when a number is multiplied
by itself three times are known as cube numbers for example 1, 8, 27,……..etc.

If in the prime factorisation of any number each factor appears three times, then the number is a perfect cube.

The symbol denotes \( \sqrt[3]{ }\) denotes cube root, for example \( \sqrt[3]{27}=3\)

Perfect cube: A natural number is said to be a perfect cube if it is the cube of some natural number. Example: 8 is a perfect cube, because there is a natural number 2 such that \( 8 = 2^3\) , but 18 is not a perfect cube, because there is no natural number whose cube is 18.

Read and Learn More KSEEB Solutions for Class 8 Maths

The cube of a negative number is always negative

Properties of cube of Number.

1)Cube of even number are even.
2)Cubes of odd numbers are odd
3)The sum of the cubes of first n natural numbers is equal to the square of their sum.
4)Cubes ofthe numbers ending with the digits 0, 1,4, 5, 6 and 9 end with digits 0, 1,4, 5, 6 and 9 respectively.
5)Cube of the number ending in 2 ends in 8 and cube of the number ending in 8 ends in 2.
6)Cube of the number ending in 3 ends in 7 and cube of the number ending in 7 ends in 3.

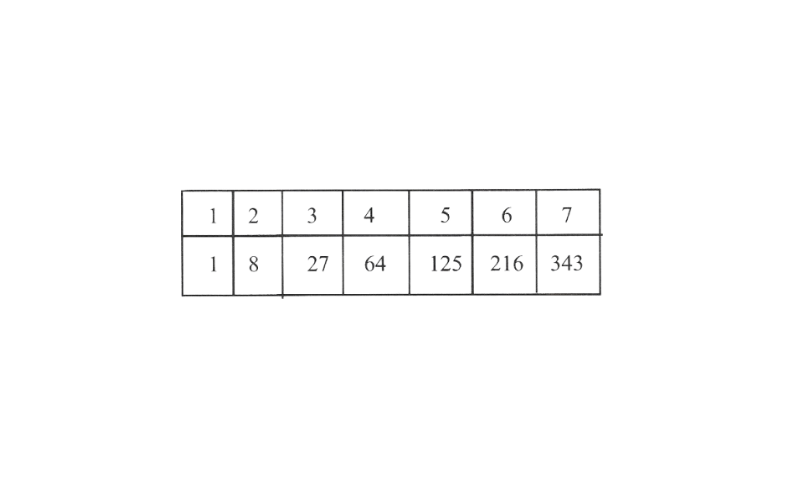
KSEEB Solutions For Class 8 Maths Chapter 8 Cube And Cube Roots PDF

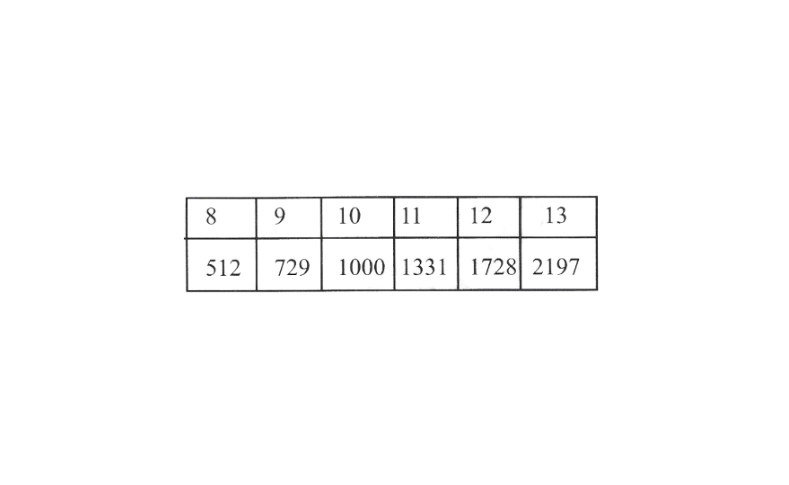
Karnataka Board Class 8 Maths Chapter 8 Cube And Cube Roots Solutions

Class 8 Maths KSEEB Cubes And Cube Roots Exercise 8.1

1. Which of the following numbers are not perfect cube?

1) 216

Prime factorisation of 216 is as follows

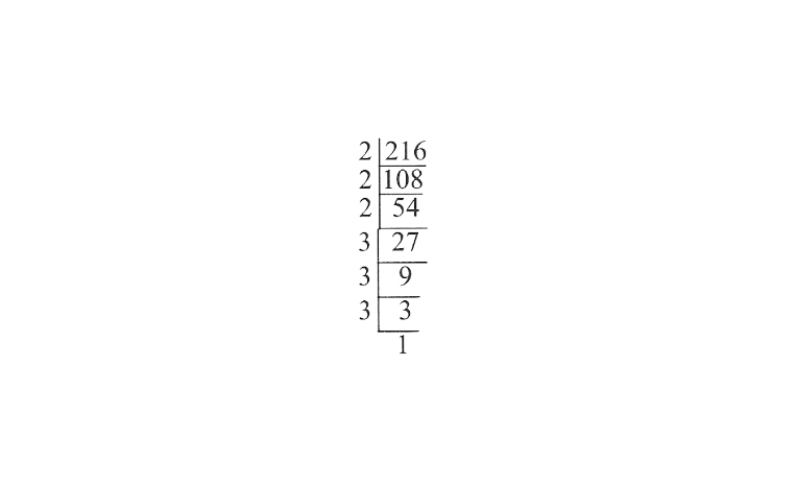
216 = 2 x 2 x 2 x 3 x 3 x 3
= \( 2^3 \times 3^3\)
Here, as each prime factor is appearing as many times as a perfect multiple of 3.
∴ 216 is a perfect cube.

2) 128

128 = 2 x 2 x 2 x 2 x 2 x 2 x 2

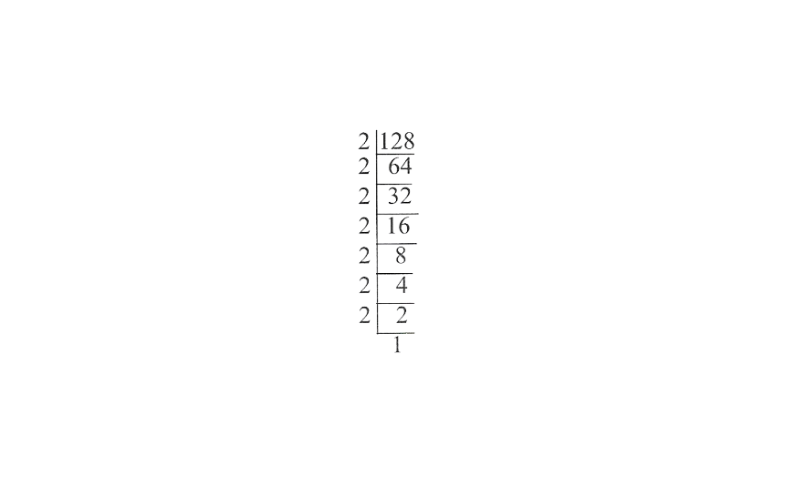
Here, each prime factor is not appearing as many times as a perfect multiple of 3. One 2 is remaining after grouping the triplets of 2.
∴ 128 is not a perfect cube.

Class 10 Science	Class 11 Chemistry
Class 11 Chemistry	Transformation of Sentences
Class 8 Maths	Class 8 Science

Cube And Cube Roots Class 8 KSEEB Solutions With Answers

3) 1000

1000 = 2 x 2 x 2 x 5 x 5 x 5

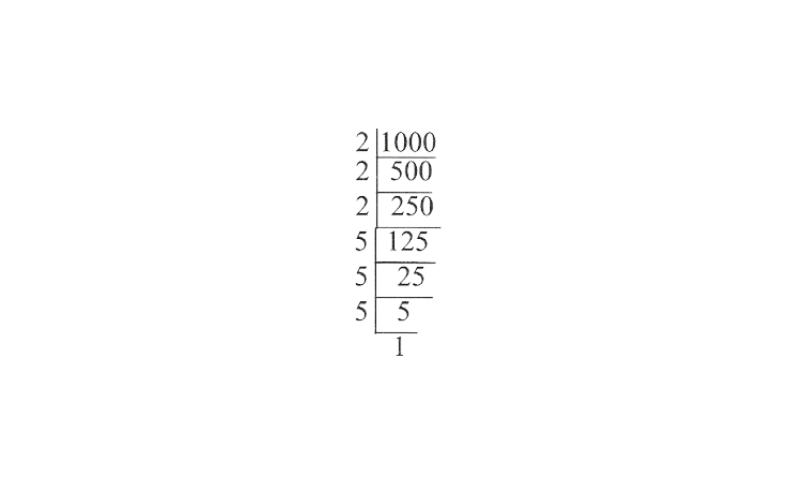
Here, as each prime factor is appearing as many times as a perfect multiple of 3.

∴ 1000 is a perfect cube

Download KSEEB Solutions For Cube And Cube Roots Chapter 8

4) 100

100 = 2 x 2 x 5 x 5

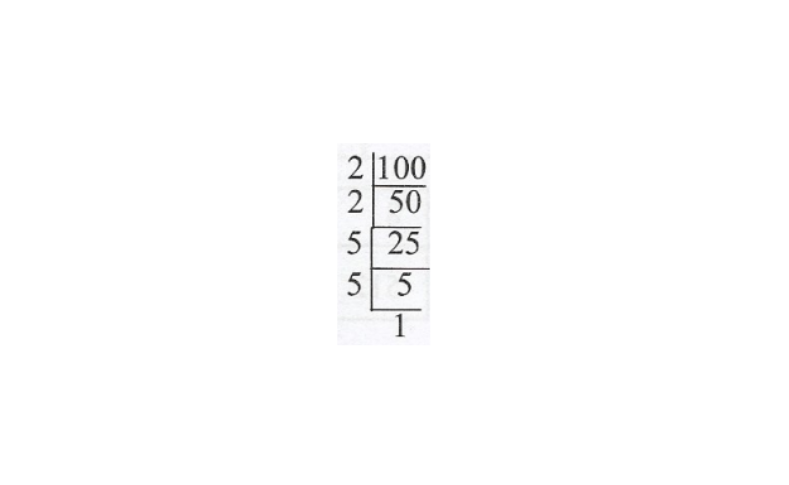
Here, each prime factor is not appearing as many times as a perfect multiplel of 3, two 2S and two 5S are remaining after grouping the triplets.

∴ 100 is not a perfect cube.

v)46656

466556 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3 x 3 x 3

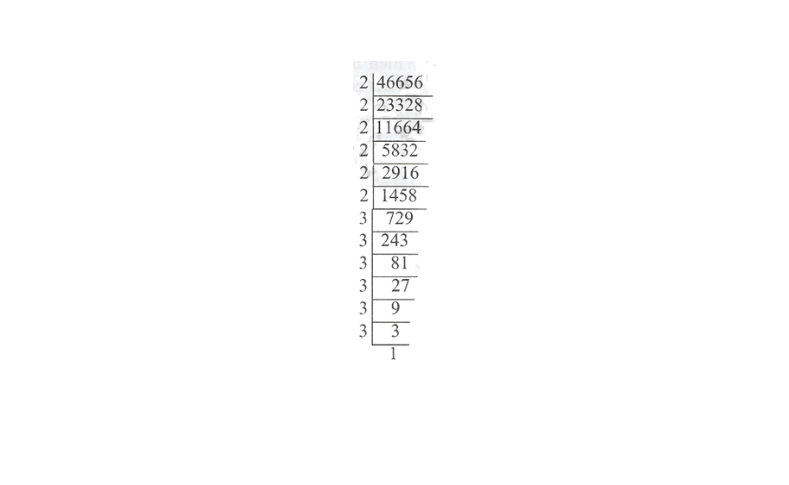
Here, as each prime factor is appearing as many times as a perfect multiple of 3.

∴ 46656 is a perfect cube.

2. Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.

1)243

Solution: 243 = 3 x 3 x 3 x 3 x 3

Here, two 3s are left which are not in a triplet. To make 243 a cube, one more 3 is required.

In that case, 243 x 3 = 3 x 3 x 3 x 3 x 3 x 3 = 729 is a perfect cube.

Hence, 3 is the smallest natural number by 243 should be multiplied to make it a perfect cube.

2) 256

Solution: 256 = 2x2x2x2x2x2x2x2

Here, two 2s are left which are not in a triplet.

To make 256 a cube, one more 2 is required. Then we obtain.

256×2 = 2x2x2x2x2x2x2x2x2 =512 is a perfect cube.

Hence, 2 is the smallest natural number by which 256 should be multiplied to make it a perfect cube.

3)72

Solution: 72 = 2x2x2x3x3

Here, two 3 s are left which are not in a triplet to make 72 a cube, one more 3 is required.

Then, we obtain

72×3 = 2x2x2x3x3x3 = 216 is a perfect cube.

Hence, the smallest natural number by which 675 should be multiplied to make it a perfect cube is 3.

KSEEB Class 8 Maths Cube And Cube Roots Exercise 8.1 Solutions

4)675

Solution: 675 = 3x3x3x5x5

Here, two 5s are left which are not in a triplet, to make 675 a cube, one more 5 is required.

Then, we obtain

675×5 = 3x3x3x5x5x5 = 3375 is a perfect cube.

Hence the smallest natural number by which 100 should be multiplied to make it a perfect cube is 5.

5)100

Solution: 100 = 2x2x5x5

Here, two 2s and two 5s are left which are not in a triplet, to make 100 a cube, we require one more 2 and one more 5.

Then, we obtain

100x2x5 = 2x2x2x5x5x5 = 1000 is a perfect cube.

Hence the smallest natural number by which 72 should be multiplied to make it a perfect cube is 2 x 5 = 10.

KSEEB Maths Class 8 Chapter 8 Detailed Answers

3. Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.

1)81

Solution: 81 = 3x3x3x3

Here, one 3 is left which is not a triplet.

If we divide 81 by 3, then it will become a perfect cube.

Thus, 81÷3 = 27 = 3x3x3 is a perfect cube.

Hence, the smallest number by which 81 should be divided to make it a perfect cube is 3.

2)128

Solution: 128 = 2x2x2x2x2x2x2

Here, one 2 is left which is not in a triplet

If we divide 128 by 2, then it will become a perfect cube. Thus, 128 ÷ 2 = 64 = 2x2x2 x2x2x2 is a perfect cube. Hence, 2 is the smallest number by which 128 should be divided to make

it a perfect cube.

3)135

Solution: 135=3x3x3x5

Here, one 5 is left which is not in a triplet.

If we divide 135 by 5, then it will become a perfect cube.

Thus, 135÷5 = 27 = 3x3x3 is aperfect cube.

Hence, 5 is the smallest number by which 135 should be divided to make it a perfect cube.

4)192

Solution: 192=2x2x2x2x2x2x3

Here, one 3 is left which is not in a triplet.

If we divide 192 by 3, then it will become a perfect cube.

Thus, 192÷3 = 64 = 2x2x2x2x2x2 is a perfect cube.

Hence, the smallest number by which 192 should be divided to make it a perfect cube is 3.

5)704

Solution: 704 = 2x2x2x2x2x2x11

Here, one 11 is left which is not in a triplet.

If we divide 704 by 11, then it will become a perfect cube.

Thus, 2x2x2x2x2x2 is a perfect cube. Hence, the smallest number by which 704 should be divided to make it a perfect cube is 11.

4. Parikshit makes a cuboid of plasticine of sides 5cm, 2cm, and 5cm. How many such cuboids will be need to form a cube?

Solution: Volume of the cube of sides 5cm, 2cm, 5cm = 5cm x 2cm x 5cm = \((5x5x2) cm^3\)

Here, two 5 s and one 2 are left which are not in a triplet.

If we multiply this expression by 2 x 2 x 5 = 20,

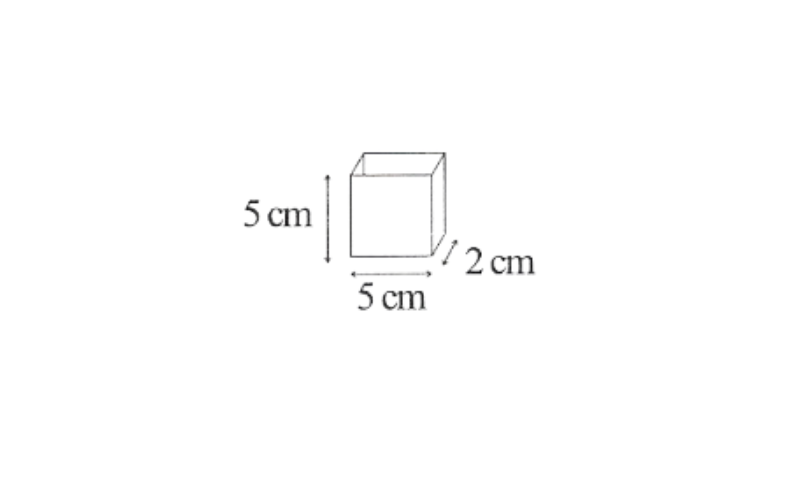
then it will become a perfect cube.

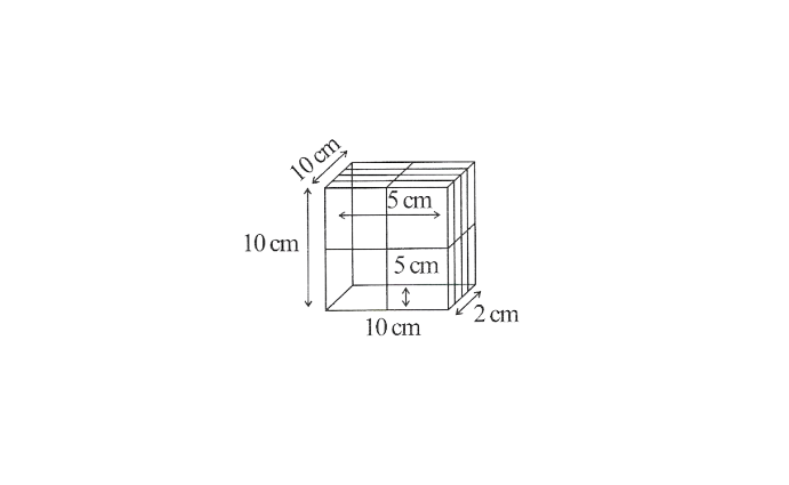
Thus (5x5x2x2x2x5) = (5x5x5x2x2x2) = 1000 is a perfect cube,

Hence 20 cuboids of 5cm, 2cm, 5cm are required to form a cube

KSEEB Class 8 Maths Solutions Cubes And Cube Roots Exercise 8.2

1. Find the cube root of each of the following numbers by prime factorisation method.

1) 64
2) 512
3) 10648
4) 27000
5) 15625
6) 13824
7) 110592
8) 46656
9) 175616
10) 91125

Solution:

1) 64

Solution:

\(64=\underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2}\)

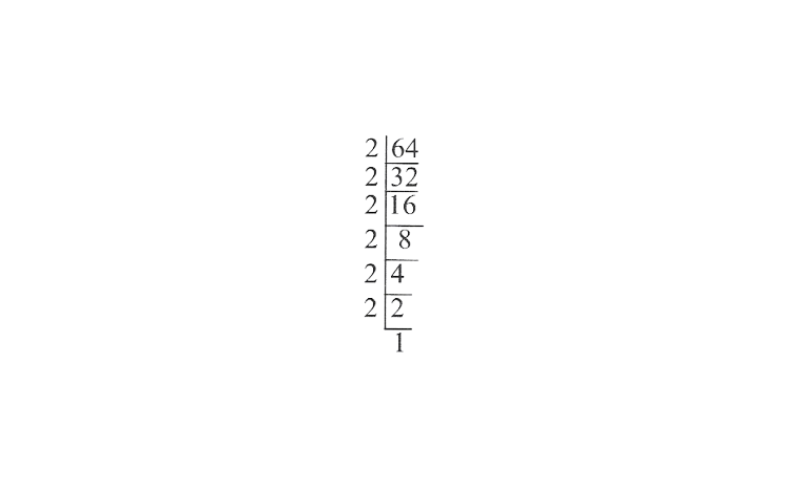
∴ \(\sqrt[3]{64}=2 \times 2\)

=4

2) 512

Solution:

\(512=2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2\)

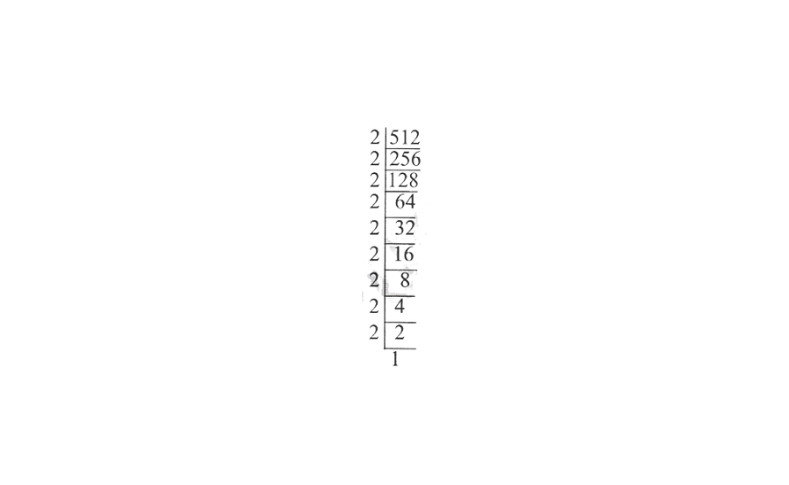
∴ \(\sqrt[3]{512}=2 \times 2 \times 2\)

= 8

Karnataka Board 8th Maths Chapter 8 Important Questions And Answers

3) 10648

Solution:

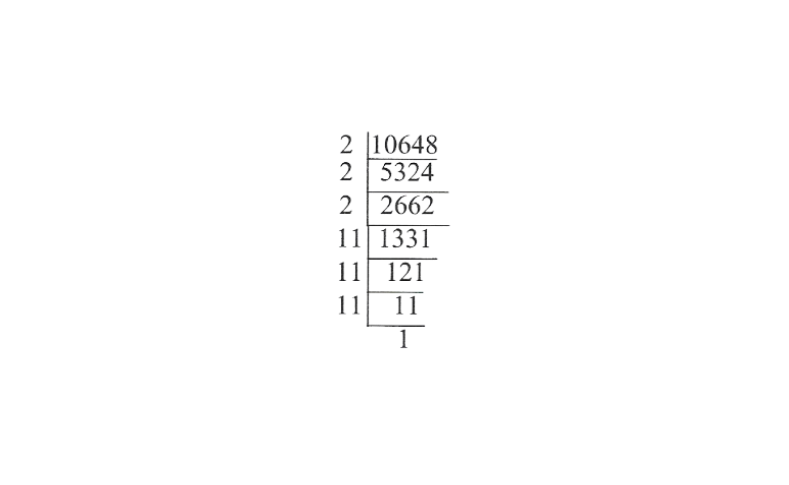
10648=\(2 \times 2 \times 2 \times 11 \times 11 \times 11\)

∴ \(\sqrt[3]{10648}=2 \times 11=22\)

=30

4) 27000

Solution:

27000 = \(\underline{2 \times 2 \times 2} \times \underline{3 \times 3 \times 3} \times \underline{5 \times 5 \times 5}\)

∴ \(\sqrt[3]{27000}=2 \times 3 \times 5\)

= 30

5) 15625

Solution:

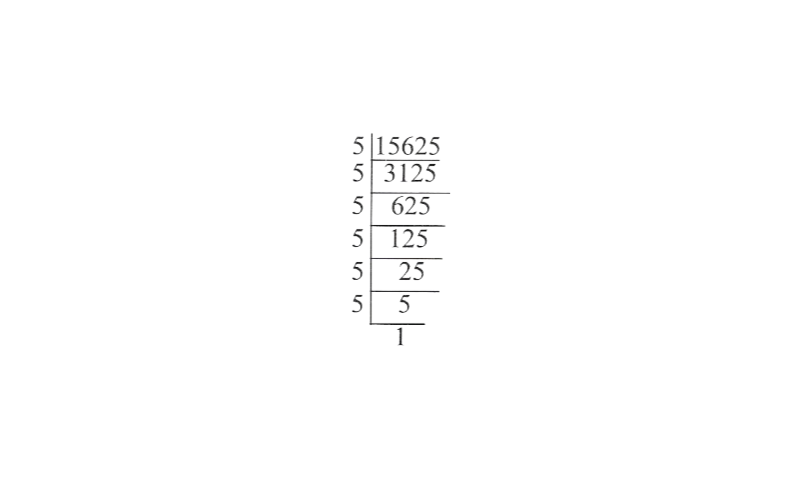
15625 = \(5 \times 5 \times 5 \times 5 \times 5 \times 5\)

∴ \(\sqrt[3]{15625}=5 \times 5\)

= 25

6) 13824

Solution:

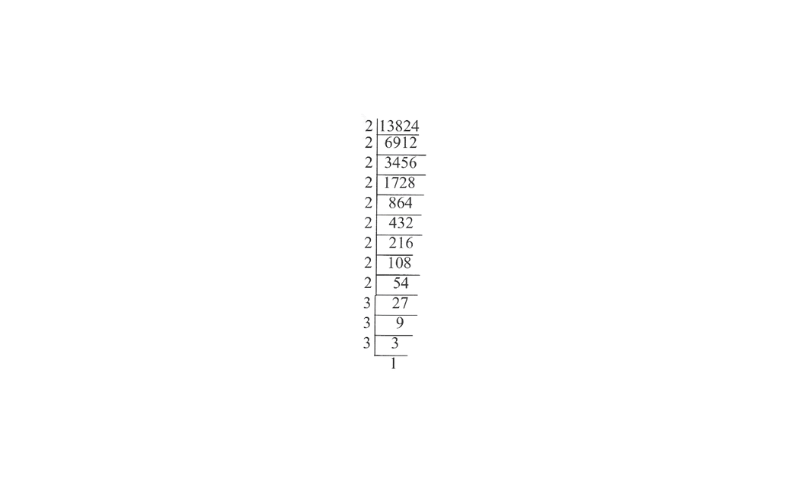
13824: =\(\underline{2 \times 2 \times 2 \times} \underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2 \times 3 \times 3 \times 3}\)

∴ \(\sqrt[3]{13824}=2 \times 2 \times 2 \times 3\)

= 24

7)110592

Solution:

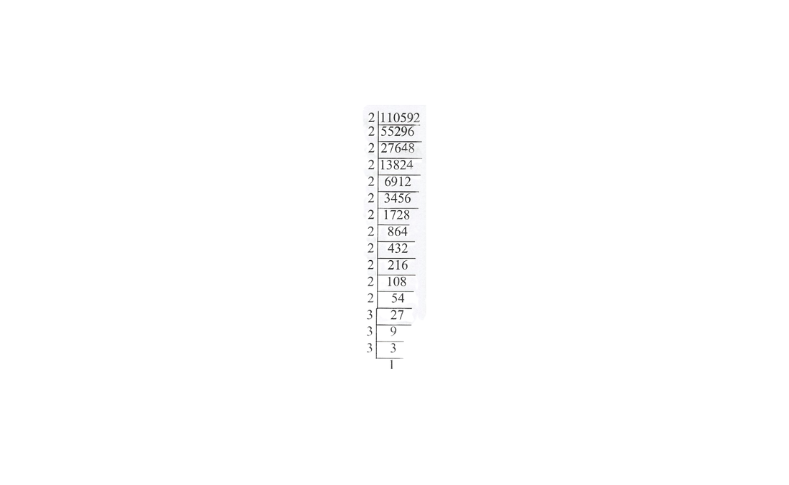
110592 = 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x3x3x3

∴ \(\sqrt[3]{110592}=2 \times 2 \times 2 \times 2 \times 3\)

= 48

KSEEB Class 8 Maths Chapter 8 Textbook Solutions PDF 

8) 46656

Solution:

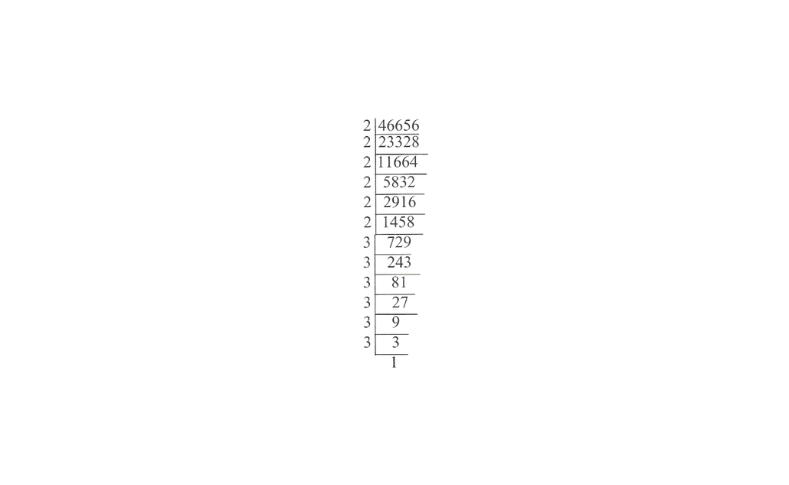
46656 = 2x2x2x2x2x2x3x3x3x3x3x3

∴ \(\sqrt[3]{46656}=2 \times 2 \times 3 \times 3\)

= 36

9) 175616

Solution:

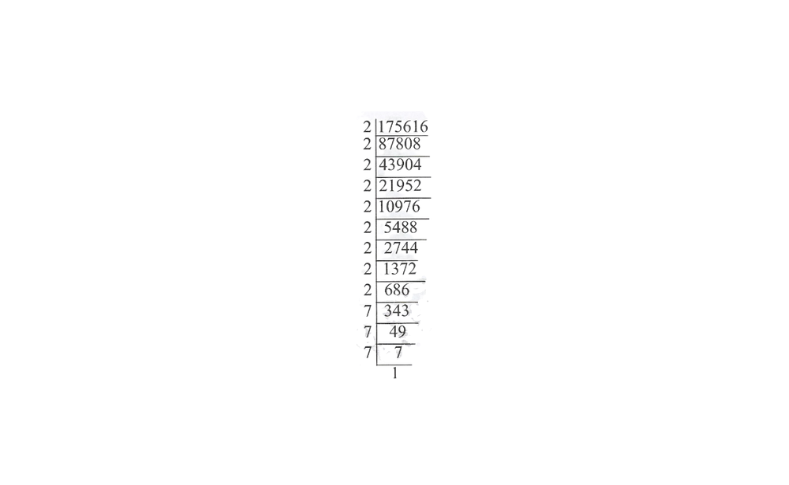
175616 = 2x2x2x2x2x2x2x2x2x7x7x7

∴ \(\sqrt[3]{175616}=2 \times 2 \times 2 \times 7\)

= 56

10) 91125

 

Solution:

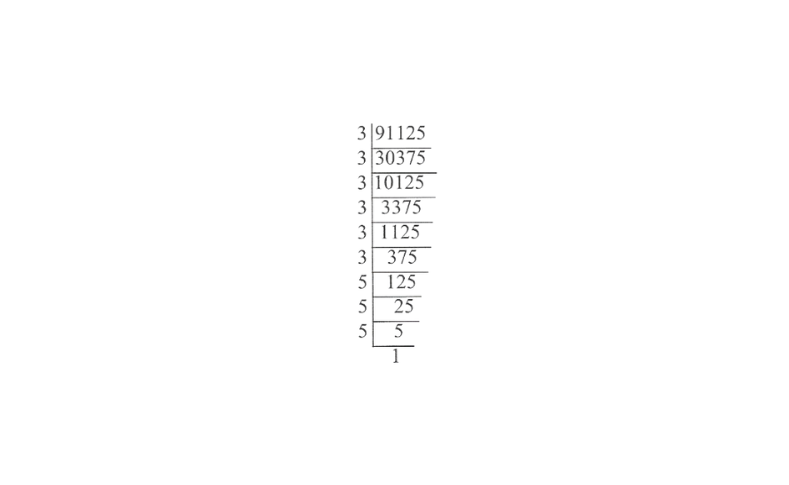
91125 = 3x3x3x3x3x3x5x5x5

∴ \(\sqrt[3]{91125}=3 \times 3 \times 5\)

= 45

Free KSEEB Solutions For 8th Class Cube And Cube Roots

2. State true or false.

1) Cube of any odd number is even.

Solution: False.

When we find out the cube of an odd number, we will find an odd number as the result because the unit place digit of an odd number is odd and we are multiplying three odd numbers.

∴ The product will be again an odd number.

For example, the cube of 3 is 27, which is again an odd number.

2) A perfect cube does not end with two zeroes.

Solution: True.

Perfect cube will end with a certain number of zeroes that are always a perfect multiple of 3. For example, the cube of 10 is 1000 and there are 3 zeroes at the end of it.

The cube of 100 is 1000000 and there are 6 zeroes at the end of it.

3) If square of a number ends with 5, then its cube ends with 25.

Solution: False.

It is not always necessary that if the square of a number ends with 5, then its cube will end with 25. For example, the square of 25 is 625 and 625 has its unit digit as 5. The cube of 25 is 15625.

However, the square of 35 is 1225 and also has its unit place digit as 5 but the cube of 35 is 42875 which does not end with 25.

4)There is no perfect cube which ends with 8.

Solution: False

There are many cubes which will end with 8. The cube of all the numbers having their unit place digit as 2 will end with 8.

The cube of 12 is 1728 and the cube of 22 is 10648

5)The cube of a two digit number may be a three-digit number.

Solution: False

The smallest two digit natural number is 10 and the cube of 10 is 1000 which has 4 digits in it.

6)The cube of a two digit number may have seven or more digits.

Solution: False, the largest two digit natural number is 99. and the cube of 99 is 970299 which has 6 digits in it. ∴ The cube of any two digit number cannot have 7 or more digits in it.

7)The cube of a single-digit number may be a single-digit number.

Solution: True, as the cube of 1 and 2 are 1 and 8 respectively.

KSEEB 8th Standard Maths Chapter 8 Notes And Solutions

3. You are told that 1331 is a perfect cube, can you guess without factorization what is its cube root? Similarly guess the cube roots of 4913,12167, 32768.

Solution: Firstly, we will make groups of three digits starting from the rightmost digit of the number as 1331. There are 2 groups 1 and 331 in it.

Considering 331

The digit at its unit place is 1, wkt if the digit 1 is at the end of a perfect cube number, then its cube root will have its unit place digit as 1 only.

∴ The unit place digit of the required cube root can be taken as 1.

Taking the other group ie 1

The cube of 1 exactly matches with the number of the second group. ∴the tens digit of our cube root will be taken as the unit place of the smallest number whose cube is near to the

number of the second group ie, 1, itself, 1 will be taken as tens place of the cube root of 1331

Hence, \(\sqrt[3]{1331}=11\).

The cube root of 4913 has to be calculated, we will make groups of three digits starting from the right most digit of 4913, as 4 913, the groups are 4 and 913.

Considering group 913

The number 913 ends with 3, wkt if the digit 3 is at the end of a perfect cube number, then its cube root will have its unit place digit as 7 only.

∴ The unit place digit of the required cube root is taken as 7.

Taking the other group ie, 4

wkt, \(l^3 = 1\) and \(2^3 = 8\)

Also, 1 < 4 < 8

∴ 1 will be taken at the tens place of the required cube root.

Thus \(\sqrt[3]{4913}=17\).

The cube root of 12167 has to be calculated. We will make groups of three digits starting from the rightmost digit of the number 12167, as 12 167, The groups are 12 and 167.

Considering the group 167.

167 ends with 7, wkt if the digit 7 is at the end of a perfect cube number, then its cube root will have its unit place digit as 3 only.

∴ The unit place digit of the required cube root can be taken as 3.

Taking the other group ie, 12

wkt \(2^3 = 8\) and \(3^3 = 27\)

Also 8 < 12 < 27

2 is smaller between 2 and 3.

∴ 2 will be taken at the tens place of the required cube root.

Thus \(\sqrt[3]{12167}=23\)

The cube root of 2768 has to be calculated. We will make groups of three digits starting from the rightmost digit of the number 32768, as 32 768

Considering the group 768

768 ends with 8, wkt if the digit 8 is at the end of a perfect cube number, then its cube root will have its unit place digit as 2 only. ∴ The unit place digit of the required cube root will be taken as 2.

Taking the other group i.e., 32., w.k.T 3

3= 27 and \(4^3 = 64\)

Also 27 < 32 < 64

3 is smaller between 3 and 4. ∴ 3 will be taken at the tens place of the required cube root. Thus \(\sqrt[3]{32768}=32\).

Cube And Cube Roots KSEEB 8th Class Additional Problems

1. Write cubes of first three multiples of 3.

Solution: 1st three multiples of 3 = 3, 6,9

Cubes of these numbers are as follows

\(3^3 =3x3x3 = 27\) \(6^3 = 6x6x6 = 216\) \(9^3 = 9 x 9 x 9 = 729\)

2. Is 9720 a perfect cube? If not, find the smallest number by which it should be divided to get a perfect cube.

Solution: 9720 = 2x2x2x3x3x3x3x3x5

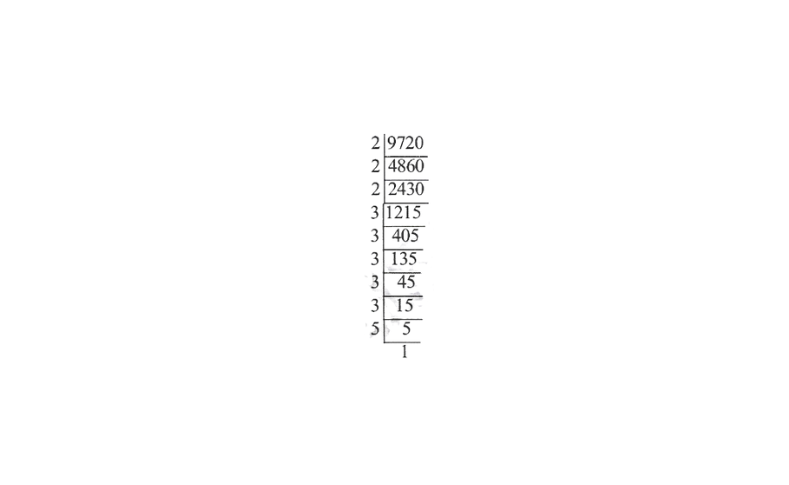
The primes 3 and 5 do not appear in groups of three. So, 9720 is not a perfect cube. We divide 9720 by 3 x 3 x 5 = 45, to make it a perfect cube.

3. Difference of two perfect cubes is 189. If the cube root of the smaller of the two numbers is 3, find the cube root of the large number.

Solution: Since, the cube root of smaller number = 3

So, smaller number = \(3^3 = 27\)

Since difference =189 Large number =189+ 27 = 216

∴ \( \sqrt[3]{216}=\sqrt[3]{2 \times 2 \times 2 \times 3 \times 3 \times 3}\)

= 2 x 3

= 6

Hence, the cube root of a large number is 6.

4. Which number is known as the Ramanujan number? What is the beauty of this number?

Solution: 1729 is known as the Ramanujan number. The beauty of this number is that it can be expressed as the sum of two cubes in two different ways

\( 1729 = 10^3 + 9^3 and 12^3 + l^3\)

5. If \( m^2\) ends in an even number of zeroes, then \( m^3\) ends in an odd number of zeroes. State true or false and justify your answer.

Solution: False.

Let m=200, then \(m^2 = 40000 and m^3 = 8000000\)

Here, both \(m^2 and m^3\) have even number of zeroes.

6. Find the value of \( \sqrt[3]{\sqrt[3]{\ell^3}}\)

Solution: \(\sqrt[3]{\sqrt[3]{\ell^3}}=\left[\left(\ell^3\right)^{\frac{1}{3}}\right]^{1 / 3}\)

=\(\left(\ell^3\right)^{\frac{1}{9}}=\ell^{\frac{1}{3}}\)

7. Evaluate \(\sqrt[3]{0.3 \times 0.3 \times 0.3 \times 11 \times 11 \times 11}\)

Solution: \(\sqrt[3]{0.3 \times 0.3 \times 0.3 \times 11 \times 11 \times 11}\)

=\(\sqrt[3]{\frac{3}{10} \times \frac{3}{10} \times \frac{3}{10} \times 11 \times 11 \times 11}\)

=\(\sqrt[3]{\left(\frac{3}{10}\right)^3 \times 11^3}\)

=\(\frac{3}{10} \times 11\)

=\(\frac{33}{10}=3.3\)

8. Show that \(\sqrt[3]{64 \times 729}=\sqrt[3]{64} \times \sqrt[3]{729}\)

Solution: \(\sqrt[3]{64 \times 729}=\sqrt[3]{64} \times \sqrt[3]{729}\)

LHS = \(\sqrt[3]{64 \times 729}\)

=\(\sqrt[3]{4 \times 4 \times 4 \times 9 \times 9 \times 9}\)

=\(\sqrt[3]{4^3 \times 9^3}=4 \times 9=36\)

RHS = \(\sqrt[3]{64} \times \sqrt[3]{729}\)

=\(\sqrt[3]{4 \times 4 \times 4} \times \sqrt[3]{9 \times 9 \times 9}\)

=\(\sqrt[3]{4^3} \times \sqrt[3]{9^3}\)

= 4 x 9

= 36

∴ LHS=RHS

Practice Problems For KSEEB Class 8 Cube And Cube Roots

9. Find the value of smallest positive integers m for which 864 x m is a perfect cube.

Solution: We have

864 = 2x2x2x2x2x3x3x3

since 2×2 is the only incomplete triplet.

so 864 has to be multiplied by 2 to make it a perfect cube

∴ m=2

10. Evaluate \(\left\{5^2+\left(12^2\right)^{1 / 2}\right\}^3\)

Solution: \(\left\{5^2+\left(12^2\right)^{1 / 2}\right\}^3\)

=\((25+12)^3\)

\((37)^3=50653\)

11. Three numbers are in the ratio 2:3:4. The sum of their cubes is 0.334125. Find the numbers.

Solution: Let the numbers be 2x,3x and 4x respectively.

Sum of their cubes = 0.334125(given)

According to the question

\((2 x)^3+(3 x)^3+(4 x)^3=0.334125\)

⇒ \(8 x^3+27 x^3+64 x^3=0.334125\)

⇒ \(99 x^3=0.334125\)

\(x^3=\frac{0.334125}{99}\) \(x^3=0.003375\) \(x^3=\frac{3375}{1000000}\)

\(x=\sqrt[3]{\frac{3375}{1000000}}\)

\(x=\sqrt[3]{\frac{3^3 \times 5^3}{10^3}}\) \(x=\frac{3 \times 5}{100}\)

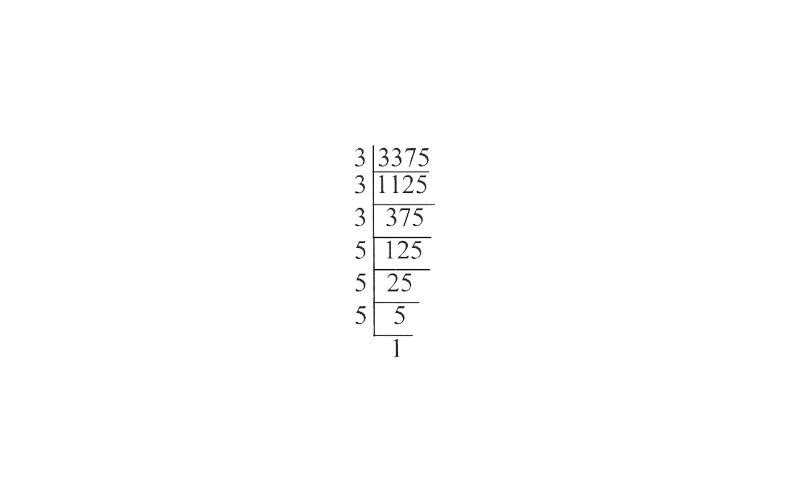
=\(\frac{15}{100}\)

= 0.15

∴ The required numbers are 0.3, 0.45, 0.6

Step-By-Step Solutions For Cube And Cube Roots Class 8 Karnataka Board

12.Write cubes of 5 natural numbers which are of the form 3n + 2 (eg. 5,8,11,…. ) and verify the following. The cube of a natural number of the form 3n + 2 is a natural number of the same form.

Solution: The 5 natural numbers which are of the form 3n + 2 (eg. 5,8,11,….) are as follows.

3 x 1 + 2 = 3 + 2 = 5

3 x 2 + 2 = 6 + 2 = 8

3 x 3 + 2 = 9 + 2 = 11

3 x 4 + 2 = 12 + 2 = 14

3 x 5 + 2 = 15 + 2 = 17

The cube of 5 natural numbers which are of the form 3n + 2 (eg. 5, 8,11….) are as follows.

\(5^3 = 125, 8^3 = 512, ll^3 = 1331, 14^3 = 2744, 17^3= 4913\)

Verification.

125 = 3 x 41 + 2

512 = 3 x 170 + 2

1331 = 3 x 443 + 2

2744 = 3 x 914 + 2

4913 = 3 x 1637 + 2

The cube of a natural number of the form 3n+2 is a natural number of the same form.

13. Divide the number 26244 by the smallest number. So that the quotient is a perfect cube. Also, find the cube root of the quotient.

Solution:

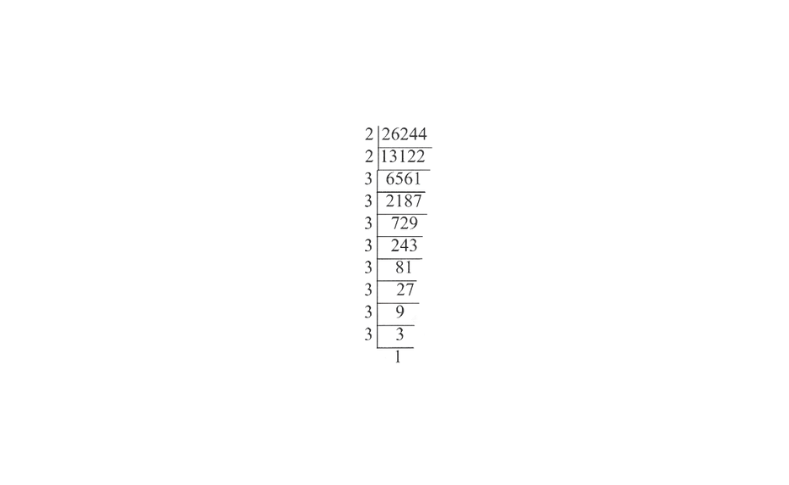
26244 = 2x2x3x3x3x3x3x3x3x3

2x2x3x3x = 36 is the smallest number by which 26244 must be divided so that the quotient is a perfect cube.

The required quotient is 729.

The cube root of the quotient

=\(\sqrt[3]{729}=\sqrt[3]{9 \times 9 \times 9}=9\)

14. Three numbers are in the ratio 1:2:3 and the sum of their cubes is 4500. Find the number.

Solution: Let the numbers be x, 2x and 3x

According to the question

\(x^3+(2 x)^3+(3 x)^3=4500\) \(x^3+8 x^3+27 x^3=4500\) \(36 x^3=4500\) \(x^3=\frac{4500}{36}\) \(x^3=125\)

x=5

∴ Three numbers are 5, 2×5, 3×5

ie, 5, 10 and 15

15. If \(\sqrt[3]{\frac{x}{y}}=\frac{2}{3}\),find\(\frac{x}{y}\)

Solution: Given \(\sqrt[3]{\frac{x}{y}}=\frac{2}{3}\)

cube both side

\(\left(\sqrt[3]{\frac{x}{y}}\right)^3=\left(\frac{2}{3}\right)^3\) \(\frac{x}{y}=\frac{2^3}{3^3}=\frac{8}{27}\)

16. Express the following numbers as the sum of odd numbers using the given pattern.

\(5^3-4^3=1+\frac{5 \times 4}{2} \times 6=61\) \(7^3-6^3=1+\frac{7 \times 6}{2} \times 6=127\)

1) \(9^3-8^3\)=—–=—–
2) \(12^3-11^3\)=—–=—–
3) \(51^3-50^3\)=—–=—–

Solution:

1) \(9^3-8^3=1+\frac{9 \times 8}{2} \times 6=217\)

2) \(12^3-11^3=1+\frac{12 \times 11}{2} \times 6=397\)

3) \(51^3-50^3=1+\frac{51 \times 50}{2} \times 6=7651\)

17. The volume of a cube is 512 cubic meters. Find the length of the side of the cube.

Solution: wkt, the volume of a cube = \((side)^3\)

The length of the side of a cube = \(\sqrt[3]{512}\)

= \(\sqrt[3]{2^3 \times 2^3 \times 2^3}=2 \times 2 \times 2=8 m\)

18. Difference of two perfect cubes is 189, If the cube root of the smaller of the two numbers is 3, then find the cube root of the large number.

Solution: Given difference of two perfect cubes = 189

and cube root of the smaller number = 3

∴ cube of smaller number = \(3^3 = 27\)

Let cube root of the larger number =\(x^3\)

According to the question, \(x^3 = 27 = 189\)

⇒ \(x^3 = 189 + 27 = 216\)

\(x=\sqrt[3]{216}=\sqrt[3]{6^3}=6\)

19. Three numbers are in the ratio 2:3:4. The sum of their cubes is 0.334125. Find the numbers.

Solution: Let the numbers be 2x, 3x and 4x respectively.

∴ Sum of their cubes = 0.334125

ie, \((2 x)^3+(3 x)^3+(4 x)^3=0.334125\)

\(8 x^3+27 x^3+64 x^3=0.334125\) \(99 x^3=0.334125\) \(x^3=0.334125 / 99=0.003375\) \(x^3=\frac{3375}{1000000}\) \(x=\sqrt[3]{\frac{3375}{1000000}}=\sqrt[3]{\frac{15 \times 15 \times 15}{100 \times 100 \times 100}}=\frac{15}{100}\)

= 0.15

Hence, the required numbers are 2×0.15, 3×0.15 & 4×0.15 ie, 0.3,0.45 & 0.5