KSEEB Class 8 Maths Solutions For Chapter 11 Direct And Inverse Proportions Points To Remember
Variations: If the values of two quantities depend on each other in such a way that a change in one cause corresponding change in the other, then the two quantities are said to be in variation.
Direct variation or Direct proportion
Two quantities x & y are said to be in direct proportion. If they increase (decrease) together in such a manner that the ratio of their corresponding
values remains constant that is if \(\frac{x}{y}=k\)
Read and Learn More KSEEB Solutions for Class 8 Maths
[k is a +ve number] then x & y are said to vary directly. In such a case ify,, y2 are the values of y corresponding to the values x{, x2 of x respectively then = \(\frac{x_1}{y_1}=\frac{x_2}{y_2}\)
If the number of articles purchased increases, the total cost also increases.
More than money deposited in a bank is the interest earned.
Quantities increasing or decreasing together need not always be in direct proportion, same in the case of inverse proportion.
When two quantities x & y are in direct proportion (or vary directly) they are written as x x y, symbol ‘∝’ stands for ‘is proportion to’.
| Class 10 Science | Class 11 Chemistry |
| Class 11 Chemistry | Transformation of Sentences |
| Class 8 Maths | Class 8 Science |
Inverse proportion :
Two quantities x & y are said to be in inverse proportion if an increase in X causes a proportional decrease in y (and vice versa) in such a manner that the product of their corresponding values remains constant, that is, ifxy=k then x & y are said to vary inversely.
In this case if y1,y2 are the values of y corresponding to the values X1,x2 of x respectively then \(x_1 y_1=x_2 y_2\) or \(\frac{x_1}{x_2}=\frac{y_2}{y_1}\)
When two quantities x & y are in inverse proportion (or vary inversely) they are written as \(x \alpha \frac{1}{y}\)
Example: If the number of workers increases, time taken to finish the job decreases, or if the speed will increase the time required to cover a given distance will decrease.

Kseeb Solutions For Class 8 Maths Chapter 11
Direct And Inverse Proportions Solutions KSEEB Class 8 Maths Exercise 11.1
1. Following are the car parking charges near a railway station up to

Check if the parking charges are in direct proportion to the parking time.
Solution:
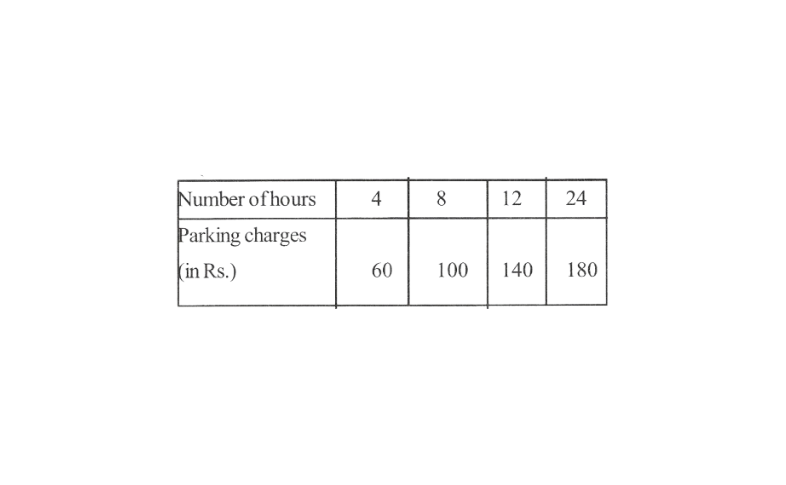
The ratio of parking charges to the respective number of hours(Rs/hour) can be calculated as.
\(\frac{60}{4}=15, \frac{100}{8}=\frac{25}{2}, \frac{140}{12}=\frac{35}{3}, \frac{180}{24}=\frac{15}{2}\)As each ratio is not same,
∴ The parking charges are not in a direct proportion to the parking time.
2. A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of base in the following table, find the parts of base that need to be added.

Karnataka Board 8th Maths Chapter 11 Direct And Inverse Proportions Solutions
Solution: The given mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of base. For more parts of red pigments. the parts of the base will also be more, therefore the parts of red pigments and the parts of base are in direct proportion. The given information in the form of a table is as follows.
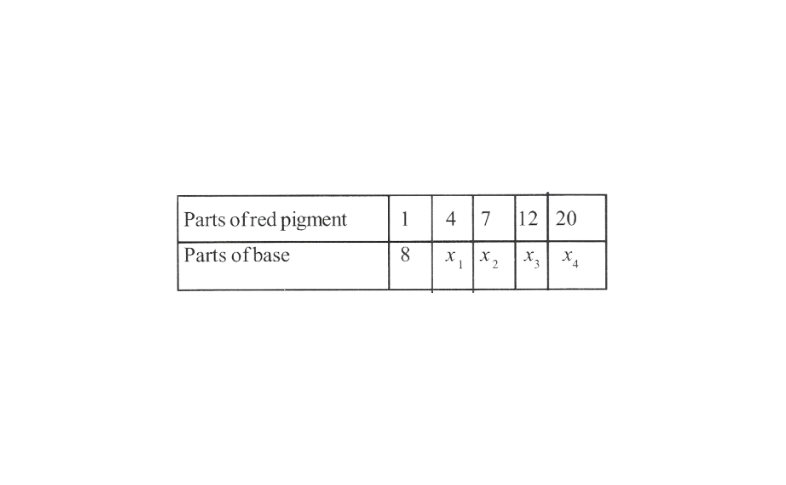
According to direct proportion
\(\frac{x_1}{4}=\frac{8}{1} \Rightarrow x_1=4 \times 8=32\) \(\frac{x_2}{7}=\frac{8}{1} \Rightarrow x_2=8 \times 7=56\) \(\frac{x_3}{12}=\frac{8}{1} \Rightarrow x_3=12 \times 8=96\) \(\frac{x_4}{20}=\frac{8}{1} \Rightarrow x_4=8 \times 20=160\)The table can be drawn as follows

Kseeb 8th Standard Maths Chapter 11 Textbook Solutions
3. In question 2 above, if 1 part of a red pigment requires 75ml of base, how much red pigment should we mix with 1800ml of base?
Solution: Let the parts of red pigment required to mix with 1800ml of base be z.
The given information in the form of a table is as follows.

The parts of red pigment and the parts of base are in direct proportion.
∴ we obtain
\(\frac{1}{75}=\frac{x}{1800}\)⇒ \(x=\frac{1 \times 1800}{75}\)
\(\frac{840}{6}=\frac{x}{5} x = 24\)Thus, 24 parts of red pigments should be mixed with 1800ml of base.
4. A machine in a soft drink factory fills 840 bottles in six hours, how many bottles will it fill in five hours?
Solution: Let the number of bottles filled by the machine in five hours be x.

Class 8 Maths Chapter 11 Kseeb Important Questions And Answers
The number of bottles and the time taken to fill these bottles are in direct proportion.
∴ we obtain
\(\frac{840}{6}=\frac{x}{5}\)⇒ \(x=\frac{{ }^{140} 840 \times 5}{6_1}\)
⇒ x = 700
Thus, 700 bottles will be filled in 5 hours.
5. A photograph of a bacteria enlarged 50,000 times attains a length of 5cm as shown in the diagram. What is the actual length of the bacteria? If the photograph is enlarged 20,000 times only, what would be its enlarged length?
Solution: Let the actual length of bacteria be ‘x’ cm and the enlarged length of bacteria be ‘y’ cm. If the photograph is enlarged for 20,000 times.
The given information in the form of a table is as follows.


The number of times the photograph of bacteria was enlarged and the length of bacteria are in direct proportion.
∴ we obtain \(\frac{5}{50,000}=\frac{x}{1}\)
⇒ \(x=\frac{1}{10000}=10^{-4}\)
Hence, the actual length of bacteria is \(10^{-4} \mathrm{~cm}\)
Let the length of bacteria when the photograph of bacteria is enlarged 20,000 times be y.
\(\frac{5}{50,000}=\frac{y}{20,000}\) \(y=\frac{20000 \times 5}{50,000}=2\)Hence, the enlarged length of bacteria is 2cm.
6. In a model of a ship, the mast is 9cm high, while the mast of the actual ship is 12m high, If the length of the ship is 28m, how long is the model ship?
Solution: Let the length of the mast of the model ship be ‘x’ cm.
The given information in the form of a table is as follows.
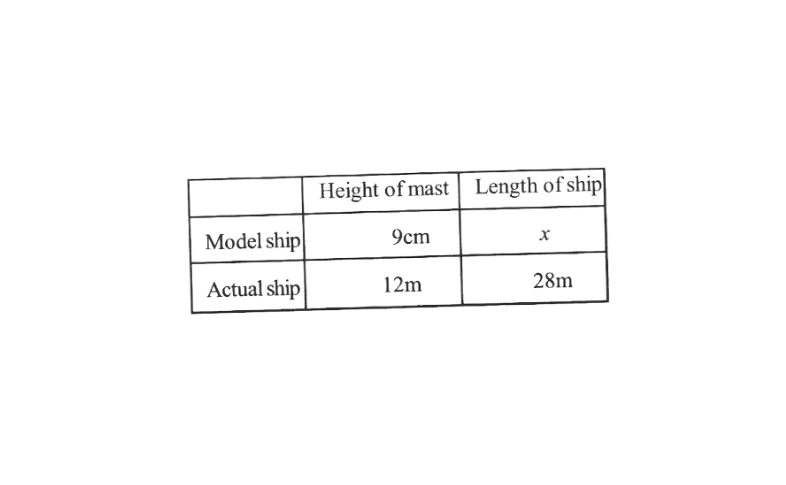
We know that the dimensions of the actual ship and the model ship are directly proportional to each other.
∴ we obtain \(\frac{12}{9}=\frac{28}{x}\)
\(x=\frac{28 \times 9}{12}=21\)Thus, the length of the model ship is 21cm
Direct And Inverse Proportions Class 8 Kseeb Notes
7. Suppose 2kg of sugar contains \(9 \times 10^6\) crystals. How many sugar crystals are there in
1) 5kg of sugar?
2) 1.2kg of sugar?
Solution: 1) Let the number of sugar crystals in 5kg of sugar be x.
The given information in the form of a table is as follows.

The amount of sugar and the number of crystals it contains are direct proportional to each other.
∴ we obtain \(\frac{2}{9 \times 10^6}=\frac{5}{x}\)
\(x=\frac{5 \times 9 \times 10^6}{2}=2.25 \times 10^7\)Hence, the number of sugar crystals is \(2.25 \times 10^7\)
2) Let the number of sugar crystals in 1.2kg of sugar be y. The given information in the form of a table is as follows.
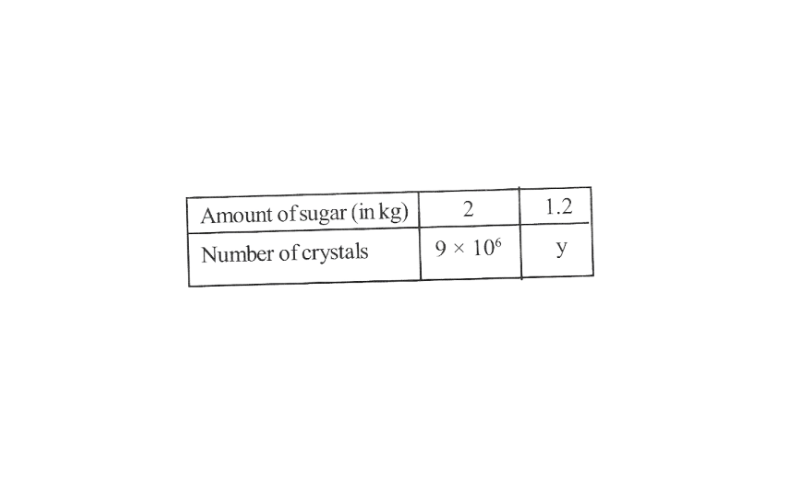
Hence, the number of sugar crystals is \(5.4 \times 10^6\)
Practice Questions For Direct And Inverse Proportions KSEEB Maths
8. Rashmi has a road map with a scale of 1cm representing 18km. She drives on a road for 72km. What would be her distance covered in the map?
Solution: Let the distance represented on the map be x cm
The given information in the form of a table is as follows.

The distance covered on road and represented on map are directly proportional to each other.
∴ we obtain \(\frac{18}{1}=\frac{72}{x}\)
⇒ \(x=\frac{72}{18}=4\)
Hence, the distance represented on the map is 4cm.
Kseeb 8th Maths Chapter 11 Exercise Solutions Step By Step
9. A 5m 60cm high vertical pole casts a shadow 3m 20cm long. Find at the same time
1)The length of the shadow cast by another pole lOm 50cm high
2)The height of a pole which casts a shadow 5m long.
Solution: 1) Let the length of the shadow of the other pole be x m.
1m= 100cm.
The given information in the form of a table is as follows.

more the height of an object, more will be the length of its shadow.
Thus, the height of an object and length of its shadow are directly proportional to each other.
∴ we obtain \(\frac{5.60}{3.20}=\frac{10.50}{x}\)
⇒ \(x=\frac{10.50 \times 3.20}{5.60}=\frac{33.6}{5.60}=6\)
Hence, the length of the shadow will be 6m.
2) Let the height of the pole be ym
The given information in the form of a table is as follows.

The height of the pole and the length of the shadow are directly proportional to each other
∴ \(\frac{5.60}{3.20}=\frac{y}{5}\)
⇒ \(y=\frac{5 \times 5.60}{3.20}=\frac{28}{3.20}=8.75\)
Thus, the height of the pole is 8.75m or 8m 75 cm.
10. A loaded truck travels 14km in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?
Solution: Let the distance travelled by the truck in 5 hours be x km
We know, 1 hour = 60 minutes
∴ 5 hours = (5 x 60) minutes = 300 minutes
The given information in the form of a table is as follows.
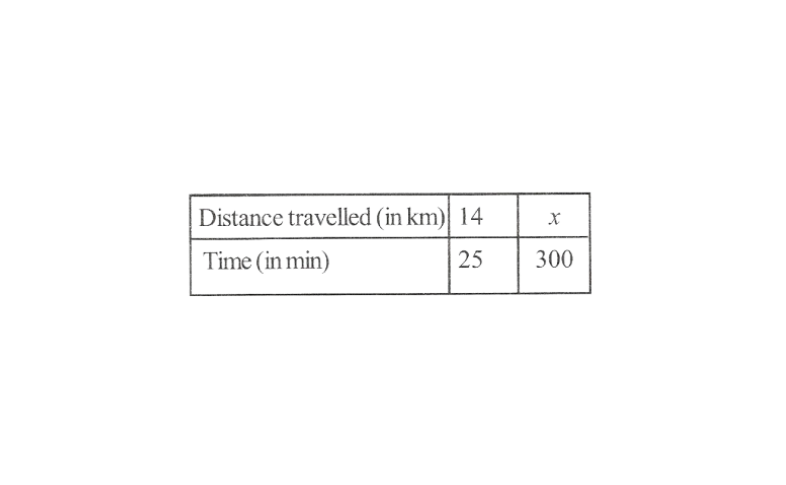
The distance travelled by the truck and the time taken by the truck are directly proportional to each other.
∴ \(\frac{14}{25}=\frac{x}{300}\)
⇒ \(x=\frac{300 \times 14}{25}=168\)
Hence, the distance travelled by the truck is 168/km
KSEEB Class 8 Maths Chapter 11 Solved Problems Direct And Inverse Proportions Exercise 11.2
1. Which of the following are in inverse proportion?
1)The number of workers on a job and the time to complete the job.
Solution: These are in inverse proportion because if there are more workers, then it will take lesser time to complete that job.
2)The time taken for a journey and the distance travelled in a uniform speed.
Solution: No, these are not in inverse proportion because, in more time, we may cover more distance with a uniform speed.
3)Area of cultivated land and the crop harvested.
Solution: No, these are not in inverse proportion because, in more area, more quantity of crop may be harvested.
4)The time taken for a fixed journey and the speed of the vehicle.
Solution: These are in inverse proportion because with more speed, we may complete a certain distance in a lesser time.
5)The population of a country and the area of land per person.
Solution: These are in inverse proportion because if the population is increasing, then the area of the land per person will be decreasing accordingly.
2. In a television game show, the prize money of 1,00,000 is to be divided equally amongst the winners. Complete the following table and find whether the prize money given to an individual winner is directly or inversely proportional to the number of winners.
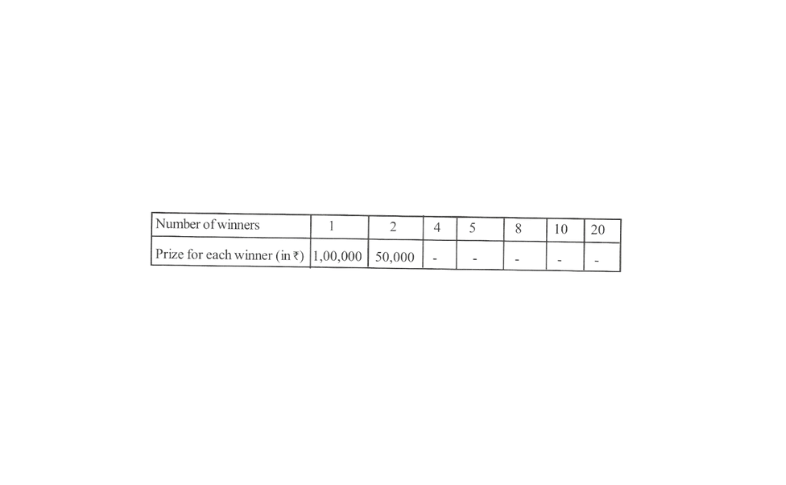
Solution: A table of the given information is as follows
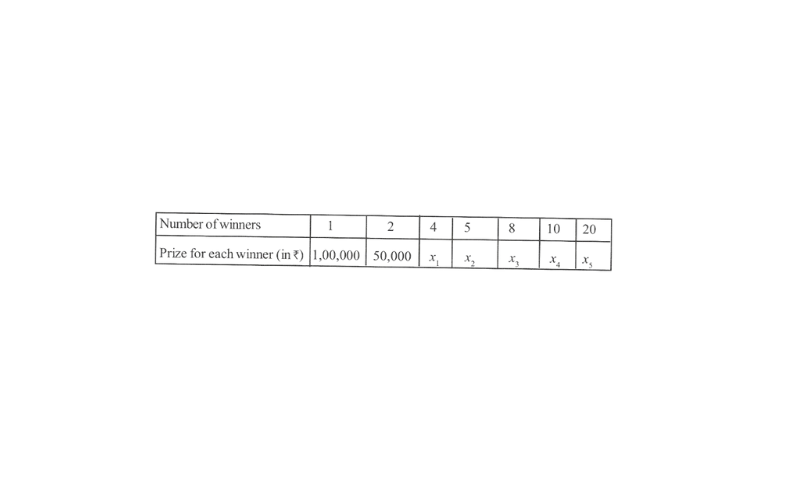
From the table, we obtain
1 x 100000 = 2 x 50000 = 100000
Thus, the number of winners and the amount given to each winner are inversly proportional to each other.
∴ \(1 \times 100000=4 \times x_1\)
⇒ \(x_1=\frac{100000}{4}=25000\)
\(1 \times 100000=5 \times x_2\)⇒ \(x_2=\frac{100000}{5}=20000\)
\(1 \times 100000=8 \times x_3\)⇒ \(x_3=\frac{100000}{8}=12500\)
\(1 \times 100000=10 \times x_4\)⇒ \(x_4=\frac{100000}{10}=10000\)
\(1 \times 100000=20 \times x_5\)⇒ \(x_5=\frac{100000}{20}=₹ 5000\)
Direct And Inverse Proportions Questions And Answers KSEEB Maths
3. Rehman is making a wheel using spokes. He wants to fix equal spokes in such a way that the angles between any pair of consecutive spokes are equal. Help him by completing the following table.
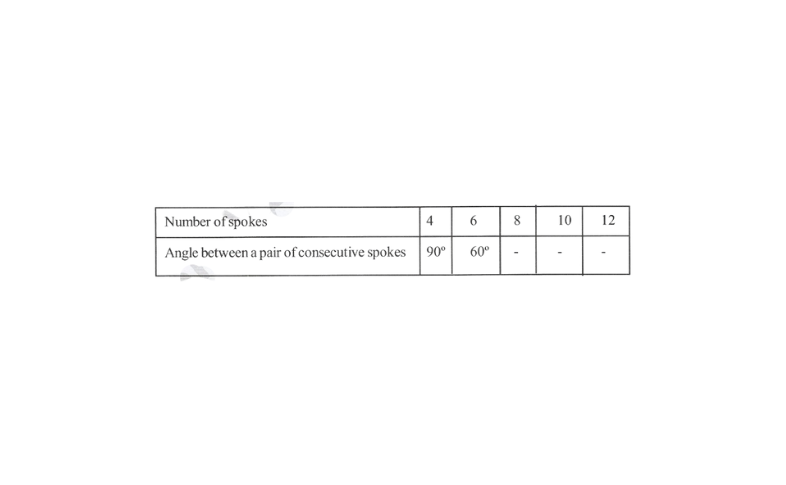
1)Are the number of spokes and the angles formed between the pairs of consecutive spokes in inverse proportion?
2)Calculate the angle between a pair of consecutive spokes on a wheel with 15 spokes
3)How many spokes would be needed, if the angle between a pair of consecutive spokes is 40°?
Solution: A table of the given information is as follows.
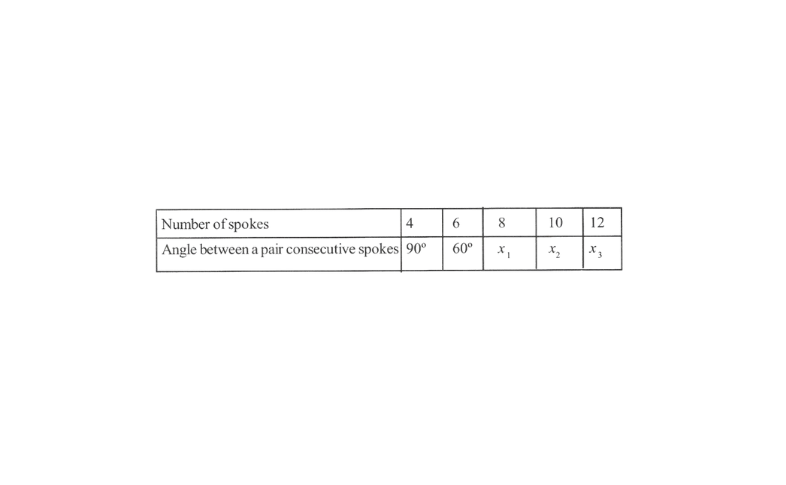
From the given table, we obtain
4 x 90° = 360° = 6 x 60°
Thus, the number of spokes and the angel between a pair of consecutive spokes are inversly proportional to each other,
∴ \(4 \times 90^{\circ}=x_1 \times 8\)
⇒ \(x_1=\frac{4 \times 90^{\circ}}{8}=45^{\circ}\)
\(\text { Illyy } x_2=\frac{4 \times 90^{\circ}}{10}=36^{\circ} \text { or }\) \(x_3=\frac{4 \times 90^{\circ}}{12}=30^{\circ}\)Thus the following table is obtained
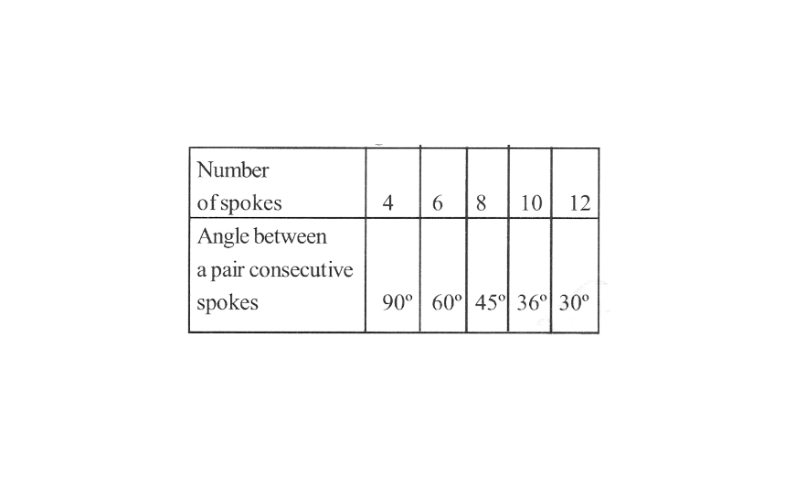
1) yes, the number of spokes and the angles formed between the pairs of consecutive spokes are in inverse proportion.
2) Let the angle between a pair of consecutive spokes on a wheel with 15 spokes be x.
∴ 4 x 90° = 15 x x
⇒ \(x=\frac{4 \times 90^{\circ}}{15}=24^{\circ}\)
Hence, the angle between a pair of consecutive spokes of a wheel, which has 15 spokes in it is 24°.
3) Let the number of spokes in a wheel, which has 40° angles between a pair of consecutive spokes be y.
∴ 4 x 90° = y x 40°
⇒ \(y=\frac{4 \times 90^{\circ}}{40}=9\)
Hence, the number of spokes in such a wheel is 9.
4. If a box of sweets is divided among 24 children, they will get 5 sweets each. How many would each get? If the number of children is reduced by 4?
Solution: Number of remaining children = 24 – 4 = 20
Let the number of sweets that each of the 20 students will get, be x.
The following table is obtained.

If the number of students is lesser then each student will get more number of sweets. Since this is a case of inverse proportion then 24 x 5 = 20 x x
⇒ \(x=\frac{24^6 \times \phi^1}{20}=6\)
Hence, each student will get 6 sweets.
5. A farmer has enough food to feed 20 animals in his cattled for 6 days, How long would the food last if there were 10 more animals in his cattle?
Solution: Let the number of days that the food will last if there were 10 more animals in the cattle be ‘x’.
The following table is obtained.

More the number of animals lesser will be the number of days for which the food will last. Hence, the number of days the food will last and the number of animals are inversly proportional to each other.
∴ 20 x 6 = 30 x x
⇒ \(x=\frac{20^4 \times 6^1}{30 z_1}=4\)
x = 4
Thus, the food will last for 4 days.
6. A contractor estimates that 3 persons could rewire Jasminder’s house in 4 days. If he uses 4 persons instead of three, how long should they take to complete the job?
Solution: Let the number of days required by 4 persons to complete the job be x.
The following table is obtained.
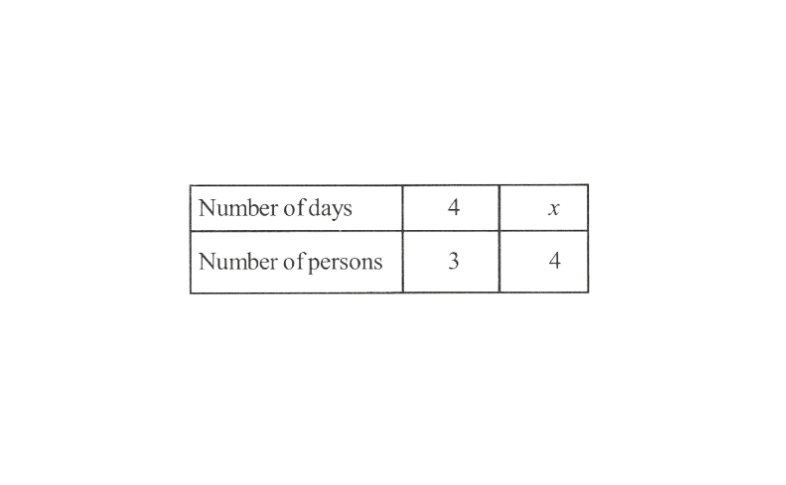
If the number of persons is more, then it will take lesser time to complete the job.
Hence, the number of days and the number of persons required to complete the job are inversely proportional to each other.
∴ 4 x 3 = x x 4
⇒ \(x=\frac{4 \times 3}{4}=3\)
Thus, the number of days required to complete the job is 3.
KSEEB Class 8 Maths Chapter 11 Direct And Inverse Proportions
7. A batch of bottles was packed in 25 boxes with 12 bottles in each box. If the same batch is packed using 20 bottles in each box, how many boxes would be filled?
Solution: Let the number of boxes filled, by using 20 bottles in each box be x.
The following table is obtained.

More the number of bottles, lesser will be the number of boxes.
Hence, the number of bottles and the number of boxes required to pack these are inversely proportional to each other.
∴ 12 x 25 = 20 x x
⇒ \(x=\frac{12^3 \times 25^5}{20 A_1}=15\)
Hence, the number of boxes required to pack these bottles is 15.
8. A factory required 42 machines to produce a given number of articles in 63 days. How many machines would be required to produce the same number of articles in 54 days?
Solution: Let the number of machines required to produce article in 54 days be x. The following table is obtained.
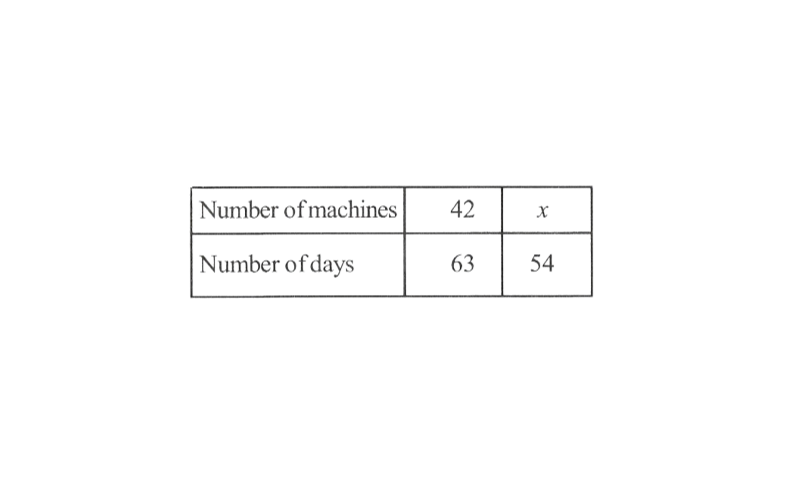
More the number of machines, lesser will be the number of days that it will take to produce the given number of articles, thus, this is a case of inverse proportion.
∴ 42 x 63 = 54 x x
⇒ \(=\frac{42^7 \times 63^7}{54 / 67_1}=49\)
Hence, the required number of machines to produce the given number of articles in 54 days is 49.
9. A car takes 2 hours to reach a destination by traveling at the speed of 60km/h. How long will it take when the car travels at the speed of 80km/h?
Solution: Let the time taken by the car to reach the destination, while traveling with a speed of 80km/hr be x hours.
The following table is obtained
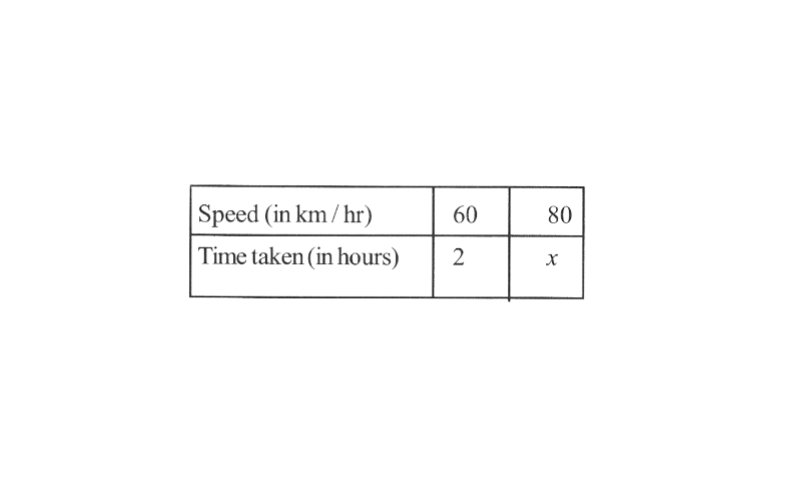
More the speed of the car, lesser will be the time taken by it to reach the destination.
Hence, the speed of the car and the time taken by the car are inversly proportional to each other.
∴ 60 x 2 = 80 x x
⇒ \(x=\frac{6 \sigma^{6^3} \times \not^1}{8 \sigma / 8 4_2}=\frac{3}{2}=1 \frac{1}{2}\)
The time required by the car to reach the given destination is \(1 \frac{1}{2}\)hours.
Karnataka Board Class 8 Maths Direct And Inverse Proportion Problems And Answers
10. Two persons could fit new windows in houses in 3 days.
1)One of the persons fell ill before the work started. How long would the job take now?
2)How many persons would be needed to fitthe windows in one day?
Solution: 1) Let the number of days required by 1 man to fit all the windows be x.
The following table is obtained
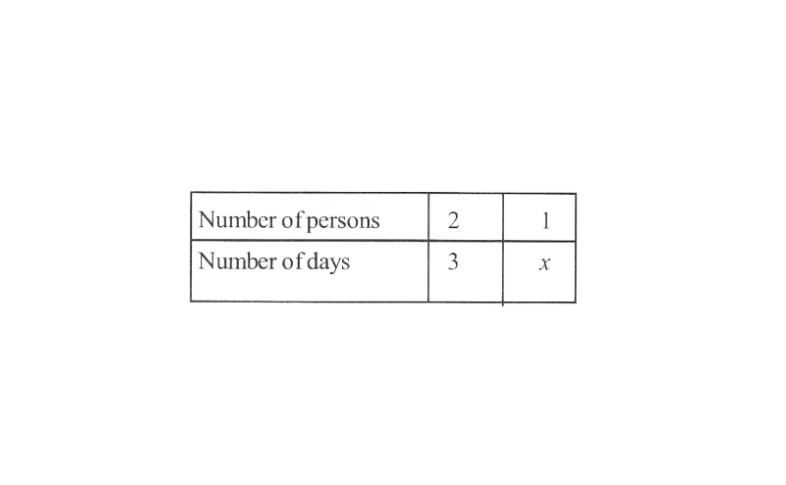
lesser the number of persons, more will be the number of days required to fit all the windows.
Hence, this is a case of inverse proportion
∴ 2 x 3 = 1 x x
x = 6
Hence, the number of days taken by 1 man to fit all the windows is 6.
2) Let the number of persons required to fit all the window in one day be y. The following table is formed.

Lesser the number of days, more will be the number of persons required to fit all the windows.
Hence, this is a case of inverse proportion.
∴ 2 x 3 = y x 1
y = 6
Hence, 6 persons are required to fit all the windows in one day.
11. A school has 8 periods a day each of 45 minutes duration. How long would each period be, if the school has 9 periods a day, assuming the number of school hours to be the same.
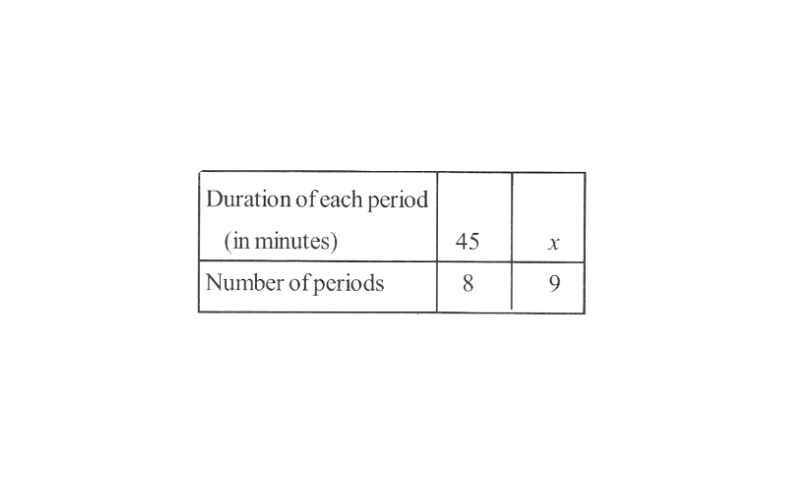
Solution: Let the duration of each period, when there are 9 periods a day in the school be x minutes.
The following table is obtained.
If there is more number of periods a day in the school, then the duration of each period will be lesser. Hence, this is a case of inverse proportion.
∴ 45 x 8 = x x 9
x = 40
Hence, the duration on of each period will be 40 minutes.
KSEEB Class 8 Maths solutions for Chapter 11 Direct and Inverse Proportions
KSEEB Maths Class 8 Chapter 11 Direct And Inverse Proportions Additional Problems
1. It is given that ‘ l ’ varies directly as m
1)Write an equation which relates l and m.
2)Find l, when m is 33 and k (constant of proportion) is \(\frac{1}{3}\).
Solution:1) \(\frac{\ell}{m}=k\)
2) Given, m= 33, \(k=\frac{1}{3}\)
\(\Rightarrow \frac{\ell}{m}=k \Rightarrow \frac{\ell}{33}=\frac{1}{3} \Rightarrow 3 \ell=33\) \(\Rightarrow \ell=\frac{33}{3}=11\)2. 44 cows can graze a field in 9 days. How many less/more cows will graze the same field in 12 days?
Solution: Let the number of cows graze the field be x. We form a table as shown below.
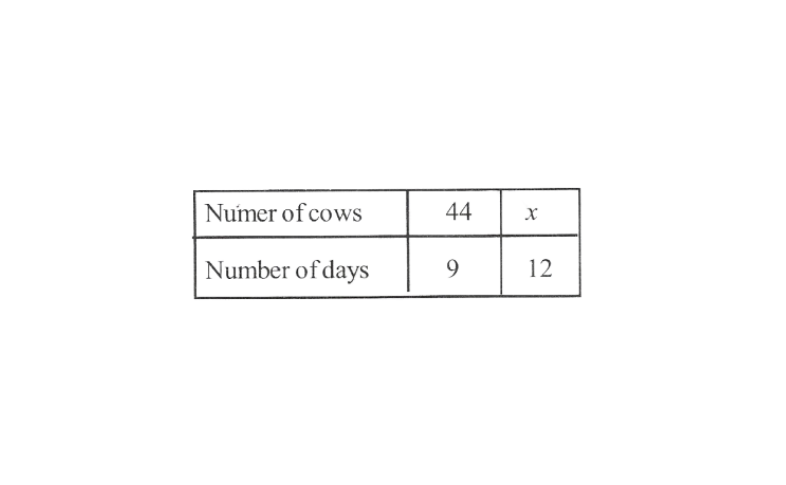
It is inverse proportion as less the number of cows more the number of days for which the field can be grazed.
i.e. \(x_1 y_1=x_2 y_2\)
we have 44 x 9 = x x l2
\(x=\frac{44^{22^{11}} \times 9^3}{12}=33\)Less number of cow can graze the field in 12 days and the difference is by 11 cows (44 – 33 cows)
3. 6 pipes are required to fill a tank in 1 hour 20 minutes. How long will it take if only 5 pipes of the same type are used?
Solution: Let the desired time to fill the tank be x minutes. Thus, we have the following table.

Lesser the number of pipes, more will be the time required by it to fill the tank. So, this is a case of inverse proportion.
Hence 80 x 6 = x x 5
\(\Rightarrow \quad x=\frac{80^{16} \times 6}{5_1}\)x = 96
Thus, time taken to fill the tank by 5 pipes is 96 minutes or 1 hour 36 minutes.
How To Solve Direct And Inverse Proportion Problems In Class 8 Kseeb Maths
4. The students of Somu’s class sold posters to raise money. Somu wanted to create a ratio for finding the amount of money her class would make for different numbers of posters sold. She knew they could raise ₹250 for every 60 posters sold.
1)How much money would Somu’s class make for selling 102 posters?
2)Could somu’s class raise exactly ₹2000? If so how many posters would they need to sell?
Solution: We are given,
Somu’s class raised ₹250 for every 60 posters.
1) Let x be the money Somu’s class will make by 102 posters. Table shown under
As, number of posters will increase, money raised will also increase.
so, it is direct proportion
∴ \(\frac{250}{60}=\frac{x}{102}\)
\(\Rightarrow \quad x=\frac{250 \times 102}{60}=425\)Money raised by 102 posters is ₹425.
2) Let the number of posters they need to sell be n.

∴ \(\frac{250}{60}=\frac{2000}{n}\)
\(\Rightarrow \quad n=\frac{2000 \times 60}{250}=480\)Required number of posters are 480.
5. The area of a square increases if we increase the length of its sides. Are the two quantities in direct proportion? Give reason.
Solution: No, the two quantities are not in direct proportion because, if we increase the length of its sides, the ratio of the two quantities (area, length) is not constant. So, it is not in direct proportion.
6. If 25 meters of cloth costs ₹337.50, then what will be the length of the cloth bought for ₹8102?
Solution: Let the length of cloth be x meters.
The following table is obtained

As the length will increase by increasing the amount.
Hence, it is directly proportional.
so \(\frac{25}{337.5}=\frac{x}{810}\)
\(\Rightarrow \quad x=\frac{25 \times 810}{337.5}\)⇒ x = 60meters.
7. If the cost of 4 copies of together with maths is ₹200, find the number of copies that can be bought for ₹1200.
Solution: The number of copies (x) and cost (y) are in direct variation or we can also say that y x or
y = k x, where K is the constant of variation
\(\frac{x}{y}=\frac{4}{200}=\frac{1}{50}\)∴ \(x=\frac{1}{50} y \text { or } y=50 x\)
The number of copies(x) that can be bought for \(1200=\frac{1}{50} \times 1200=24\)
8. A labourer earns ₹141.75 in 26 weeks. How much money will he earn in a year?
Solution: Since earning increases (or decreases) in proportional to the number of weeks.
∴ The two quantities vary directly
we know that
Income1 : Income2 = No. of weeks 1 : No. of weeks 2
so 141.75 : x = 26 : 52(As 1 year = 52 weeks)
141.75 x 52 = x x 26
\(\Rightarrow \quad x=\frac{141.75 \times 52^2}{26_1}\)⇒ x = ₹283.50
Thus, he earns ₹283.50 in a year.
9. A machine produces 180 tools in 6 hours. How many tools will it produce in 9 hours?
Solution: Let x be the number of tools and y be the number of hours. From the question
y x or y = k x
when number of tools is 180 and number of hours is 6. Then 6=k180 or \(k=\frac{6}{180}=\frac{1}{30}\)
Thus \(y=\frac{1}{30} x\)
we find the value of x when y = 9 hours.
\(\Rightarrow \quad 9=\frac{1}{30} \times x\) \(\Rightarrow \quad x=9 \times 30=270\)Thus, number of tools is 270
Direct and Inverse Proportions solutions KSEEB Class 8 Maths
10. Given that x varies inversely as y and when x=5, y=50 find
1) y when x=2 and
2) x when y=10
Solution: Since x and y vary inversely
\(\Rightarrow \quad x \alpha \frac{1}{y} \text { (or) } x=\frac{k}{y} \text { or } x y=k\)(k is a constant of variation)
⇒ when x=5, y=50
5 x 50 = k or k = 250
when x=2 then 2y=250
⇒ y = 125
and when y=10
then x x 10 = 250
⇒ \(x=\frac{250}{10}=25\)
Thus for x=2, y=125 and for y=10,x=25
11. A bicycle dealer has ₹20,000 to invest, when a bicycle is available for ₹800. If the price of a bicycle increases by 25%, find the number of cycles he can purchase with the same sum.
Solution: the more the cost, less is the number of biycles, he can buy with the given amount of money, thus it is an inverse variation.
No. of cycles = \(\frac{20000}{800}=25\)
car purchase \(x_2=25\)
New price of a bicycle
\(y_1=800+25 \% \times 800\)=\(800+\frac{25}{100} \times 800\)
=\(800+200=₹ 1000\)
\(\frac{x_1}{x_2}=\frac{y_2}{y_1}\)Thus, the number of cycles that can be purchased =20
12. If a car over 80km in 5 liters of petrol, how much distance will it cover in 13 litres of petrol?
Solution: In 5 litres of petrol, distance covered = 80km
In 1 litre of petrol, distance covered = \(\frac{80}{5}=16 \mathrm{~km}\)
In, 13 litres of petrol, distance covered = 16 x 13 = 208km
13. If 32 men cap reap a field in 15 days. In how many days can 40 men reap the same field? The given situation in a inverse variation(less men, more days)
Solution: Let x=men and y=No.of days.
\(x_1=32, \quad y_1=15\) \(x_2=40, \quad y_2=?\) \(x_1 y_1=x_2 y_2\) \(32 \times 15=40 \times y_2\) \(y_2=\frac{432 \times 15^3}{405_1}\) \(y_2=12\)Number of days 40 men to reap the same field = 12 days
14. Find the value of x and y if x:y=2:3 and 2:x=1:2
Solution: 2:x=1:2
\(\Rightarrow \quad \frac{2}{x}=\frac{1}{2}\) \(\Rightarrow \quad x=2 \times 2\)⇒ x=4
x:y=2:3
4:y=2:3
\(\frac{4}{y}=\frac{2}{3}\) \(y=\frac{4^2 \times 3}{2_1}=6\)y=6
15. Ranjith has enough money to buy 75 machines worth Rs. 200 each. How many machines can he buy if he get a discount of Rs. 50 on each machine?
Solution: Let x be the number of machines he can buy if a discount of Rs. 50 is offered on each machine.
Number of machines (x) : 75
Price of each machine (y): 200
Since each machine is having ₹50 discount then cost of each machine will be (200 – 50) = 150.
Given situation is inverse variation as price of machine is less more machines, he can buy.
75 x 200 = x x l50
\(\Rightarrow \quad x=\frac{75^5 \times 20 \emptyset}{15, \emptyset}=100\)⇒ x = 100
16. If 5 men or 7 women can earn ₹875 per day. How much would 10 men & 5 women earn per day?
Solution: 5 men= 7 women
1 man = \(\frac{7}{5} \text { women }\)
\(\Rightarrow 10 \text { men }=\left(\frac{7}{5} \times 10\right) \text { women }=14 \text { women }\)⇒ (10 men + 5 women)
=(14 women + 5 women) = 19 women
Let 10 men & 5 women would earn ₹x per day then, we have

Clearly, more women will earn more per day. So it is a case of direct proportion.
∴ \(\frac{7}{875}=\frac{19}{x} \Rightarrow \frac{1}{125}=\frac{19}{x}\)
⇒ (1 x x)=(125 x 19)
⇒ x = 2375
∴ 10 men & 5 women would earn ₹2375 per day.
17. In a fort, 300 men had provisions for 90 days. After 20 days, 50 men left the fort. How long would the food last at the same rate?
Solution: Clearly, the remaining food is sufficient for 300 men for (90-20)days = 70 days.
