KSEEB Solutions For Class 11 Physics Chapter 10 Mechanical Properties Of Solids

KSEEB Class 11 Physics Solutions For Chapter 10 Mechanical Properties Of Solids Important Points

Elasticity: The property of a body by virtue of which it tends to regain its original size (or) shape when the applied force is removed.

Plasticity: It is the inability of a body not to regain its original size (or) shape when external force is removed.

Substances that exhibit plasticity are called plastic substances.

Stress (σ): The restoring force per unit area is called stress (σ).

Stress (σ) = Force/area Unit Nm^-2 (or) pascal; D.F: ML^-1T^-2

Tensile Stress: When the applied force is normal to the area of cross-section of the body then restoring force per unit area is called tensile stress.

Tangential (Or) Shearing Stress: The restoring force developed per unit area of cross-section when a tangential force is applied is known as shear stress or tangential stress.

Hydraulic Stress (Volumetric Stress): For a body in a fluid force is applied on it in all directions perpendicular to its surface.

“The restoring force developed in the body per unit surface area under hydraulic compression is called hydraulic stress.”

Strain: The change produced per unit dimension is called strain. It is a ratio.

Mechanical Properties Of Solids Notes In KSEEB Physics

Strain Types:

1. Longitudinal Strain: The ratio of increase in length to original length is called as longitudinal strain. Longitudinal strain = \(\frac{\Delta \mathrm{L}}{\mathrm{L}}\)
2. Tangential (Or) Shear Strain: The ratio of relative displacement of faces Δx to the perpendicular distance between the faces is called shear strain. Shear strain = \(\frac{\Delta \mathrm{L}}{\mathrm{L}}\) = tanθ
3. Volume Strain: The ratio of change in volume ΔV to the original volume (V) is called volume strain. Volume strain = \(\frac{\Delta \mathrm{V}}{\mathrm{V}}\)

Hooke’s Law: For small deformations, the stress is proportional to strain.

Stress ∝ strain ⇒ stress/strain = constant.

This proportional constant is called the modulus of elasticity.

Elastic Constant: The ratio of stress to strain is called the “elastic constant”. Unit: Newton/m² • D.F: ML^-1T^-2

Elastic constants are three types.

Young’s Modulus (Y): The ratio of tensile stress (or) compressive stress to longitudinal strain or compressive strain is called Young’s modulus.

Y = \(\frac{\sigma}{\varepsilon}=\frac{\text { Tensile or compressive stress }(\sigma)}{\text { Tensile or compressive strain }(\varepsilon)}\)

Shear Modulus (G): The ratio of shearing stress to the corresponding shearing strain is called shear modulus.

Shear modulus (G) = \(\frac{\text { Shear stress }\left(\sigma_{\mathrm{s}}^{\prime}\right)}{\text { Shear strain }(\theta)}\)

Bulk Modulus(B): The ratio of hydraulic stress to the corresponding hydraulic strain is called Bulk modulus.

= –\(\frac{\text { Hydraulic pressure }(F / A)}{\text { Hydraulic strain }(\Delta V / V)}\)

Compressibility (K): The reciprocal of bulk modulus is called compressibility. Compressibility K = 1/B

Poisson’s Ratio: In a stretched wire the ratio of lateral contraction strain to longitudinal elongation strain is called Poisson’s ratio.

Poisson’s ration = \(\sigma=\frac{\Delta d / d}{\Delta L \cdot / L}\)

Poisson’s ratio Is a ratio of two strains so it has only numbers.

For steel Poisson’s ratio is 0.28 to 0.30, for aluminum alloys it is up to 0.33.

Elastic Potential Energy (u): When a wire is under tensile stress, work is done against the inter-atomic forces. This work is stored in the wire in the form of elastic potential energy.

(or)

Work done to stretch a wire against inter-atomic forces is termed as “elastic potential energy”.

Elastic potential energy \((\mathrm{u})=\frac{1}{2} \frac{\mathrm{YAl} l^2}{\mathrm{~L}}=\frac{1}{2} \sigma \varepsilon\)

or \(\mathrm{u}=\frac{1}{2}\) stress x strain x volume of wire.

Ductile Materials: If the stress difference between ultimate tensile strength and fracture point is high then it is called ductile material. Example: Silver, Gold.

Brittle Material: If the stress difference between ultimate tensile strength and fracture point is very less then that substance is called brittle material. Example: Cast iron.

Elastomers: Substances that can be stretched to cause large, strains are called elastomers. Example: Rubber, Tissues of aorta.

Mechanical Properties Of Solids Solutions KSEEB Class 11 Physics Important Formulae

Stress = \(\frac{\text { Force }}{\text { Area }}=\frac{\mathrm{F}}{\mathrm{A}}\); Unit: \(\mathrm{N} / \mathrm{m}^2\) (or) Pascal.

Strain \(=\frac{\text { elongation }}{\text { original length }}=\frac{\Delta \mathrm{L}}{\mathrm{L}}\); No units.

Hooke’s Law: Within elastic limit, stress \(\propto\) strain (or) \(\frac{\text { stress }}{\text { strain }}=\) constant (Elastic constant).

Young’s Modulus \((\mathrm{Y})=\frac{\text { longitudinal stress }}{\text { longitudinal strain }}\)

= \(\frac{\mathrm{F} / \mathrm{A}}{\Delta \mathrm{e} / \mathrm{L}}=\frac{\mathrm{FL}}{\mathrm{A} \Delta \mathrm{e}}\).

In Searle’s apparatus \(\mathrm{Y}:=\frac{\mathrm{gL}}{\pi \mathrm{r}^2} \cdot \frac{\mathrm{M}}{\mathrm{e}}\)

1. If two wires are Hindu with same materials have lengths l₁, l₂ and radii r₁, r₂ then ratio of elongations \(\frac{e_1}{e_2}=\frac{l_1}{l_2} \cdot \frac{r_2^2}{r_1^2}\) (because \(e \propto l / r\))
2. If two wires are made with the same material and the same volume and have areas A₁ and A₂ are, subject to the same force then the ratio of elongations \(\frac{\mathrm{e}_1}{\mathrm{e}_2}=\mathrm{r}_2^4 / \mathrm{r}_1^4\) (because \(\mathrm{e} \propto \frac{1}{\mathrm{r}^4}\))
3. If two wires of the same length and area of the cross-section are subjected to the same force then the ratio of elongations \(e_1 / e_2=\frac{y_2}{y_1}\) (because \(e \propto \frac{1}{y}\))
4. If two wires are made with same material have lengths l₁ and l₂ and masses m₁ and m₂ are subjected to same force then ratio \(\frac{\mathrm{e}_1}{\mathrm{e}_2}=\frac{l_1^2}{l_2^2} \times \frac{\mathrm{m}_2}{\mathrm{~m}_1}\) (because \(\mathrm{e} \propto \frac{l^2}{\mathrm{~m}}\))

Rigidity Modulus, \(\mathrm{G}=\frac{\text { shear stress }}{\text { shear strain }}\)

= \(\frac{\mathrm{F}}{\mathrm{A} \theta}=\frac{\mathrm{FL}}{\mathrm{Al}}\)

Shear Strain \(\theta=\frac{\text { relative displacement of upper layer }}{\text { perpendicular distance between layers}}=\frac{\Delta \mathrm{x}}{\mathrm{z}}=\frac{l}{\mathrm{~L}}\)

Bulk Modulus \((B)=\frac{\text { volumetric stress }}{\text { volumetric strain }}\)

= \(\frac{F / A}{\Delta V / V}=\frac{P V}{\Delta V}\)

∴ \(\frac{1}{B}\) is called the “coefficient of compressibility” (K).

Poisson’s Ratio, \(\sigma=\frac{\text { lateral contraction strain }}{\text { longitudinal elongation }}\)

= \(-\frac{\Delta \mathrm{D} / \mathrm{D}}{\mathrm{e} / \mathrm{L}}=-\frac{\mathrm{L} \Delta \mathrm{D}}{\mathrm{D} \cdot \mathrm{e}}\)

Theoretical limits of Poisson’s ratio \(\sigma\) is -1 to 0.5; Practical limits of Poisson’s ratio \(\sigma\) is 0 to 0.5

Relations between Y, G, B, and σ are

1. \(B=\frac{Y}{3(1-2 \sigma)}\)
2. \(ŋ=\frac{Y}{2(1+\sigma)}\)
3. \(\sigma=\frac{3B-2G}{2(3B+G}\)
4. Y = \(\frac{9G B}{3 B+G}\)

The relation between volume stress and linear stress is \(\frac{\Delta V}{V}=\frac{\Delta L}{L}(1-2 \sigma)\)

Strain energy \(=\frac{1}{2} \times\) load x extension

= \(\frac{1}{2} \times F \times e\)

Strain energy per unit volume \(=\frac{1}{2} \times\) stress x strain or \(\frac{\text { stress }^2}{2 Y}\) or \(\frac{\left(\text { strain }^2\right) Y}{2}\)

When a body is heated and expansion is prevented then thermal stress will develop in the body.

Thermal stress = Y ∝ Δt

Thermal force = YA ∝ Δt

When a wire of natural length L is elongated by tensions say T₁ and T₂ have final lengths l₁ and l₂ then the Natural length of wire = L

= \(\frac{l_2 \mathrm{~T}_1-l_1 \mathrm{~T}_2}{\left(\mathrm{~T}_1-\mathrm{T}_2\right)}\)

When a wire is stretched by a load has an elongation ‘e’. If the load is completely immersed in water then decrease in elongation e¹ = Vρ gl/(AY)

where V is the volume of load, ρ = density of water.

KSEEB Class 11 Physics Chapter 10 Mechanical Properties Of Solids Very Short Answer Questions

Question 1. State Hooke’s law of elasticity.
Answer:

Hooke’s law states that within an elastic limit stress is proportional to strain.

Stress \(\propto \text { strain } \Rightarrow \frac{\text { Stress }}{\text { Strain }}=\text { Constant. }\)

This constant is known as the elastic modulus of the body.

KSEEB Class 11 Physics Mechanical Properties Of Solids Key Concepts

Question 2. State the units and dimensions of stress.
Answer:

Stress = \(\frac{\text { Porce }}{\text { Area }}=\frac{\mathrm{N}}{\mathrm{m}^2}\);

S.I Unit = \(\mathrm{Nm}^{-2}\) or pascal.

Dimensional formula \(\mathrm{ML}^{-1} \mathrm{~T}^{-2}\)

Question 3. State the units and dimensions of the modulus of elasticity
Answer:

Modulus of elasticity = \(\frac{\text { Stress }}{\text { Strain }}\)

S.I Unit is \(\mathrm{Nm}^{-2}\) (or) pascal

Dimensional formula \(\mathrm{ML}^{-1} \mathrm{~T}^{-2}\)

Question 4. State the units and dimensions of Young’s modulus.
Answer:

Young’s modulus, \(\mathrm{Y}=\frac{\text { Longitudinal Stress }}{\text { Longitudinal Strain }}\)

= \(\frac{\mathrm{F}}{\mathrm{A}} \cdot \frac{l}{\Delta l}\); SI unit = \(\mathrm{Nm}^{-2}\) (or) pascal

Dimensional formula \(\mathrm{ML}^{-1} \mathrm{~T}^2\)

Question 5. State the units and dimensions of the modulus of rigidity.
Answer:

Modulus of rigidity,

G = \(\frac{\text { shear stress }}{\text { shear strain }}=\frac{F}{A} \frac{x}{\Delta x}, \text { Sl unit }=\mathrm{Nm}^{-2}\) (or) pascal

Dimensional formula ML^-1T^-2.

Question 6. State the units and dimensions of Bulk modulus.
Answer:

Bulk modulus, \(\mathrm{B}=\frac{\text { Bulk stress }}{\text { Bulk strain }}=\frac{\Delta \mathrm{P} \cdot \mathrm{V}}{\Delta \mathrm{V}}\); SI: unit is Nm^-2 (or) pascal

Dimensional formula ML^-1T^-2.

Question 7. State the examples of nearly perfect elastic and plastic bodies.
Answer:

There is no perfectly elastic body. However, the behavior of Quartz fiber is very near to a perfectly elastic body.

Real bodies are not perfectly plastic, but the behavior of wet clay, butter, etc., can be taken as examples of perfectly plastic bodies.

Solutions For Mechanical Properties Of Solids KSEEB Physics Short Answer Questions

Question 1. Define Hooke’s law of elasticity, proportionality, permanent set, and breaking stress.
Answer:

Hooke’s Law: It states that within the elastic limit, stress is proportional to strain.

i.e., \(\text { stress } \propto \text { strain } \Rightarrow \frac{\text { stress }}{\text { strain }}=\text { constant (E). }\)

This constant is called the elastic constant (E).

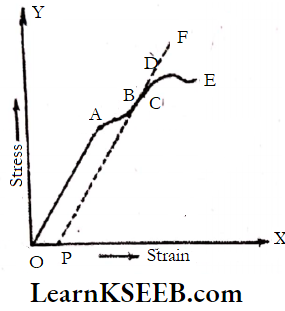
Proportionality Limit: When the load is increased the elongation of the wire will also increase. The maximum load up to which the elongation is directly proportional to the load is called the proportionality limit (A). The graph is drawn between load and extension. It is a straight line ‘OA’.

Permanent Set: If the load on the wire is increased beyond the elastic limit, the elongation is not proportional to the load. On removal of the load, the wire cannot regain its original length. The length of the wire increases permanently. In the figure permanent set is given by OP. This is called a permanent set.

Breaking Stress: If the load is increased beyond the yield point the elongation is very rapid, even for small changes in load and the wire becomes thinner and breaks. This is shown as E. The breaking force per unit area is called breaking stress.

Mechanical Properties Of Solids Chapter 10 KSEEB Physics

Question 2. Define the modulus of elasticity, stress, strain, and Poisson’s ratio.
Answer:

Stress: Restoring force acting on a unit area is called stress.

∴ Stress = \(\frac{\text { Force }}{\text { Area }}=\frac{\mathrm{F}}{\mathrm{A}} \text {; }\)

Unit: N/m² (or) pascal;

Dimensional formula: ML^-1T^-2.

Strain: The change in dimension per unit original dimension of a body is called strain.

∴ Strain = \(\frac{\text { elongation }}{\text { original length }}=\frac{\mathrm{e}}{l}\)

It is a ratio, so no units and dimensional formulas.

Modulus Of Elasticity: From Hooke’s Law Stress ∝Strain or \(\frac{\text { Stress }}{\text { Strain }}\) = Constant (E)

The ratio of stress to strain is called the modulus of elasticity

Unit: N/m².

Dimensional formula: ML^-1T^-2.

Poisson’s Ratio: It is defined as the ratio of lateral contraction strain to longitudinal, elongation strain.

Poisson’s ratio \((\sigma)=\frac{\text { Lateral contraction strain }}{\text { Longitudinal elongation strain }}\)

It is a ratio, so no units and dimensional.

Question 3. Define Young’s modulus, Bulk modulus, and Shear modulus.
Answer:

Young’s Modulus Y: Within the elastic limit, the ratio of longitudinal stress to longitudinal strain is called Young’s modulus

i.e., \(\mathrm{Y} =\frac{\text { Longitudinal stress }}{\text { Longitudinal strain }}\)

= \(\frac{\mathrm{F} / \mathrm{A}}{\Delta \mathrm{L} / \mathrm{L}}=\frac{\mathrm{FL}}{\mathrm{A} \Delta \mathrm{L}}\)

Bulk Modulus (B): Within the elastic limit, the ratio of volumetric stress to volumetric strain is called Bulk modulus

i.e., \(B=\frac{\text { Volumetric stress }}{\text { Volumetric strain }}\)

= \(\frac{\dot{F} / \mathrm{A}}{\Delta \mathrm{V} / \mathrm{V}}=\frac{\mathrm{FV}}{\mathrm{A} \cdot \Delta \mathrm{V}}\)

Shear Modulus Or Rigidity Modulus (G): With in elastic limit, the ratio of tangential or shearing stress to shearing strain is called Shear modulus or Rigidity modulus.

i.e., \(\mathrm{G}=\frac{\text { Shearing stress }}{\text { Shearing strain }}=\frac{F / A}{\theta}=\frac{F}{A \theta}\)

Question 4. Define stress and explain the types of stress.
Answer:

Stress: When a body is subjected to a deforming force, then restoring forces will develop inside the body. These restoring forces will oppose any sort of change in its original shape. The restoring force per unit area of the surface is called stress.

Stress: Stress is defined as force applied per unit area.

Stress = \(\frac{\text { Force }}{\text { Area }}=\frac{F}{A}\)

D.F. = ML^-1T^-2; Unit: N/m² (or) Pascal.

Types Of Stress: It is of three types. They are:

1. Longitudinal stress
2. Tangential stress (or) Shear stress
3. Volumetric stress.

Longitudinal Stress: If the force applied on a body is along its lengthwise direction then it is called longitudinal stress. It produces deformation in length.

Longitudinal stress = \(\frac{\text { Force }}{\text { Area }}\)

Tangential Stress (Or) Shear Stress: Force applied per unit area parallel to the surface of a body trying to displace the upper layers of the body is called shearing stress.

Shear (or) tangential stress = \(\frac{\text { Force }}{\text { Area }}\) (Parallel to the surface layers)

Volumetric Stress: If force is applied on all the sides of a body or on the volume of a body then it is called volumetric stress.

Volumetric stress = \(\frac{\text { Force }}{\text { Area }}\) = (applied on volume)

Question 5. Define strain and explain the types of strain.
Answer:

Strain: Strain is defined as deformation produced per unit dimension. It is a ratio. So no units.

Strain (e) = \(\frac{\text { Elongation }}{\text { Original length }}=\frac{\Delta \mathrm{L}}{\mathrm{L}} \text {. }\)

Types Of Strain: Strain is of three types. They are:

1. Longitudinal strain
2. Tangential strain or Shear strain
3. Volumetric strain

Longitudinal Strain: The ratio of elongation to original length along a lengthwise direction is defined as longitudinal strain.

Longitudinal strain \(\mathrm{e}=\frac{\text { elongation in length }}{\text { original length }}\) = \(\frac{\Delta l}{l}\)

Bulk strain = Change in volume per unit

volume = \(\frac{\text { Change in volume }}{\text { Original volume }}=\frac{\Delta \mathrm{V}}{\mathrm{V}}\)

Shearing Strain: If the force applied on a body produces a change in shape only it is called shearing force. The angle through which a plane originally perpendicular to the fixed surface shifts due to the application of shearing stress is called shearing strain or simplified shear θ.

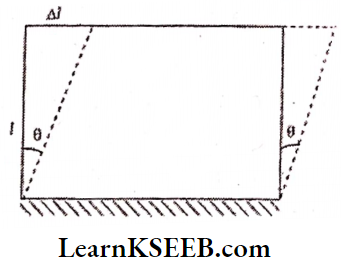
Shear strain = \(\theta=\left(\frac{\Delta l}{l}\right)=\tan \theta\) (since is a very small tan θ = θ)

Question 6. Define strain energy and derive the equation for the same.
Answer:

Strain Energy: The energy developed in (string), a body when it is strained is called strain energy.

Let a force F be applied on the lower end of the wire, fixed at the upper end. Let the extension be dl.

∴ Work done \(=\mathrm{dW}=\mathrm{Fd}\)

Total work done in stretching it from 0 to l = \(W=\int_0^1 \mathrm{dW}=\int_0^1 \mathrm{Fd} l\)

∴ W = \(\int_0^1 \frac{Y a l}{L} d l=\frac{Y a l^2}{2 L}=\frac{1}{2} \frac{\mathrm{Yal}}{L} \cdot l\)

(because \(\mathrm{F}=\frac{\mathrm{Yal}}{\mathrm{L}}\))

W = \(\frac{1}{2} \times \text { stretching force } \times \text { elongation }\)

= \(\frac{1}{2} \times \frac{\text { stretching force } \times \text { elongation }}{\mathrm{aL}}\)

= \(\frac{1}{2} \times \text { stress } \times \text { strain }\)

Mechanical Properties Of Solids Questions And Answers KSEEB Physics

Question 7. Explain why steel is preferred to copper, brass, and aluminum in heavy-duty machines and in structural designs.
Answer:

For metals Young’s moduli are large. Therefore, these materials require a large force to produce a small change in length. To increase the length of a thin steel wire of 0.1 cm² cross-sectional area by 0.1 %, a force of 2000 N is required.

The force required to produce the same strain in aluminum, brass, and copper wire having the same cross-sectional area are 690 N, 900N, and 1100 N respectively.

It means that steel is more elastic than copper, brass, and aluminum. It is for this reason that steel is preferred, in heavy-duty machines and in structural designs.

Question 8. Describe the behavior of a wire under a gradually increasing load.
Answer:

Behavior Of A Wire Under Increasing Load: Let a wire be suspended at one end and loads are attached to the other end. When loads are attached to the other end. When loads are gradually increased the following changes are noticed.

1. Proportionality Limit (A): When the load has increased the elongation of the wire gradually increases. The maximum load up to which the elongation is directly proportional to the load is called the proportionality limit (A). In this region, Hooke’s I Law is obeyed.
2. Elastic Limit (B): If the load is Increased above the proportionality limit the elongation is not proportional to the load. Hooke’s law is not obeyed. The maximum load on the wire up to which it exhibits elasticity is called the elastic limit (B in the graph).
3. Permanent Set (C): If the load on the wire is increased beyond the elastic limit say up to ‘C’, the elongation is not proportional to the load. On removal of the load, the wire does not regain its original length. The length of the wire increases permanently. In the figure permanent set is given by OP. So OP is called a permanent set.
4. Point Of Ultimate Tensile Strength (D): If the load is further increased, up to ‘D’ then strain increases rapidly even though there is no increase in stress. Elongation without an increase in load is called creeping. This behavior of metal is called yielding.
5. Fracture Point (E): If the load is increased beyond the Yield point the elongation is very rapid, even for small changes in load the wire becomes thinner and breaks. This is shown as E. The breaking force per unit area is called breaking stress.

Question 9. Two identical solid balls, one of ivory and the other of wet-clay Eire dropped from the same height onto the floor. Which one will rise to a greater height after striking the floor and why?
Answer:

We know that ivory bail is more elastic than wet-clay ball. Therefore, the ivory ball will tend to regain its original shape in a very short time after the collision. Due to this, there will be a large energy and momentum transfer to the ivory ball in comparison to the wet-clay ball. As a result of it, the ivory ball will rise higher after the collision.

Question 10. While constructing buildings and bridges a pillar with distributed ends is preferred to a pillar with rounded ends. Why?
Answer:

The use of pillars or columns is very common in buildings and bridges. A pillar with rounded ends supports less load than that with a distributed shape at the ends. Hence, for this reason, while constructing buildings and bridges a pillar with distributed ends is preferred to a pillar with rounded ends.

Question 11. Explain why the maximum height of a mountain on Earth is approximately 10 km.
Answer:

A mountain base is not under uniform compression and this provides some shearing stress to the rocks under which they can flow. The stress due to all the material on the top should be less than the critical shearing stress at which the rocks flow.

At the bottom of a mountain of height h’, the force per unit area due to the weight of the mountain is hρg where p is the density of the material of the mountain and g is the acceleration due to gravity.

The material at the bottom experiences this force in the vertical direction and the sides of the mountain are free. There is a shear component, approximately hρg itself. Now the elastic limit for a typical rock is 3 x 10⁷ Nm^-2. Equating this to hρg with ρ = 3 x 10³ kg m^-3 gives

h = \(\frac{30 \times 10^7}{3 \times 10^3 \times 10}=10 \mathrm{~km}\)

Hence, the maximum height of a mountain on Earth is approximately 10 km.

Question 12. Explain the concept of Elastic Potential Energy in a stretched wire and hence obtain the expression for it.
Answer:

When a wire is put under tensile stress, work is done against the inter-atomic forces. This work is stored in the form of Elastic potential energy.”

Expression To Elastic Potential Energy: To stretch a wire, force is applied. As a result, it elongates. So the force applied is useful to do some work. This work is stored in it as potential energy. When the deforming force is removed, this energy is liberated as heat. The energy developed in a body (string) when it is strained is called strain energy.

Let a force F be applied on a wire fixed at the upper end. Let the extension be dl.

∴  Work done = dW = Fdl

Total work done in stretching from 0 to l = \(W=\int_0^l \mathrm{~d} W=\int_0^l \mathrm{Fd} l\)

∴ W = \(\int_0^l \frac{\mathrm{Ya} l}{\mathrm{~L}} \mathrm{~d} l=\frac{\mathrm{Ya} l^2}{2 \mathrm{~L}}=\frac{1}{2} \frac{\mathrm{Ya} l}{\mathrm{~L}} \cdot l\)

(because \(\mathrm{F}=\frac{\mathrm{Ya} l}{\mathrm{~L}}\))

W = \(\frac{1}{2} \times\) stretching force x elongation

∴ Work done per unit volume

= \(\frac{1}{2} \times \frac{\text { stretching force } \times \text { elongation }}{A \times L}\)

= \(\frac{1}{2} \times \text { stress } \times \text { strain }\)

KSEEB Class 11 Physics Chapter 10 Mechanical Properties Of Solids

KSEEB Physics Class 11 Mechanical Properties of Solids Long Answer Questions

Question 1. Define Hooke’s law of elasticity and describe an experiment to determine Young’s modulus of the material of a wire.
Answer:

Hooke’s Law: Within elastic limit, stress is directly proportional to strain.

∴ strain \(\propto\) stress

∴ \(\frac{\text { stress }}{\text { strain }}=\text { constant }(E)\)

where E constant is called modulus or elasticity of the material of n body.

Determination Of Young’s Modulus Of A Wire: The apparatus used to find Young’s modulus of a wire consists of two long wires A and B of the same length made with the same material. These two wires are suspended from a rigid support and a vernier scale Y is attached to them. Wire A is connected to the main scale (M).

A fixed load is connected to this cord to keep tension in the wire. This is called reference wire. The second wire ‘B’ is connected to the vernier scale ‘V’. An adjustable load hanger is connected to this wire. This is called experimental wire.

Procedure: Let a load M₁ be attached to the weight hanger at the vernier. Main Scale Reading (M.S.R) and Vernier Scale Reading (V.S.R) are noted. Weights are gradually increased in the steps of \(\frac{1}{2}\) kg up to a maximum load of say 3 kg. Every time M.S.R and V.S.R are noted. They are placed in tabular form.

Now loads are gradually decreased in steps of \(\frac{1}{2}\) kg. While decreasing M.S.R and V.S.R are noted for every load, values are posted in tabular form.

Let 1st reading with mass M₁ is e₁ and 2nd reading with mass M₂ is e₂.

Change in load M = M₂ – M₁

elongation e = e₂-e₁

‘M’ and ‘e’ values are calculated and a graph is plotted.

Average m/e

Force on the wire = mg

Area of cross unction of the wire = πr² (r = radius of the wire)

Elongation = e

Original length = l

Stress = \(\left(\frac{\mathrm{F}}{\mathrm{a}}\right)=\frac{\mathrm{mg}}{\pi \mathrm{r}^2}\)

Strain \(=\left(\frac{\mathrm{e}}{l}\right)\)

Young’s modulus, \(\mathrm{Y}=\left(\frac{\text { stress }}{\text { strain }}\right)\)

Y = \(\left(\frac{\mathrm{mg} l}{\mathrm{e} \pi \mathrm{r}^2}\right)=\left(\frac{\mathrm{g} l}{\pi \mathrm{r}^2}\right)\left(\frac{\mathrm{m}}{\mathrm{e}}\right)\)

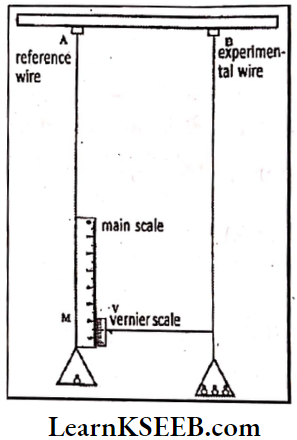
A graph between load (m) and elongation ‘e’, is a straight line passing through the origin.

The slope of the graph (tan θ) gives \(\frac{m}{e}\). This value is substituted in the above equation to find Young’s modulus of the material of the wire.

Precautions:

1. The load applied should be much smaller than the elastic limit.
2. Reading is noted only after the air bubble is brought to the center of spirit level.

Chapter 10 Mechanical Properties Of Solids KSEEB Problems

Question 1. A copper wire of 1mm diameter is stret¬ched by applying a force of 10 N. Find the stress in the wire.
Solution:

Diameter, d = 1mm

∴ radius, r = 0.5 mm = 0.5 x 10^-3 m

Force, F = 10N

Stress = \(\frac{\text { Force }}{\text { Area }}=\frac{F}{\pi r^2}\)

∴ Stress = \(\frac{10}{3.141 \times 0.5 \times 0.5 \times 10^{-6}}\)

= \(\frac{40 \times 10^6}{3.141}=1.273 \times 10^7 \mathrm{~Pa}\)

Question 2. A tungsten wire of length 20cm is stretched by 0.1cm. Find the strain on the wire.
Solution:

Length of wire, l =20cm =0.2m elongation, e = 0.1cm = 1 x 10^-3 m

Strain = \(\frac{\text { elongation }}{\text { original length }}=\frac{1 \times 10^{-3}}{0.2}\)

= \(5 \times 10^{-3}=0.005\)

Question 3. If an iron wire is stretched by 1 %, what is the strain on the wire?
Solution:

Increase in length = e = 1% = \(\frac{1}{100}\) l

∴ Strain = \(\frac{\text { elongation }}{\text { original length }}=\frac{\mathrm{e}}{l}\)

= \(\frac{1 \times l}{100 \times l}=\frac{1}{100}=0.01\)

Question 4. A brass wire of a cross-sectional area of 2mm is suspended from a rigid support and a body of volume 100cm³ is attached to its other end. If the decrease in the length of the wire is 0.11mm, when the body is completely immersed in water, find the natural length of the wire.
Solution:

Length of wire, l = 2m

Diameter, d = 1 mm = 10 m^-3

Force, F = 20N

Increase in length, e = 0.51 mm = 0.51 x 10^-3 m

Stress = \(\frac{\text { Force }}{\text { Area }}=\frac{F}{\pi \mathrm{d}^2 / 4}=\frac{20 \times 4}{3.141 \times 10^{-6}}\)

= \(2.546 \times 10^7 \mathrm{~N} / \mathrm{m}^2\)

Strain = \(\frac{\text { Elongation }}{\text { Length }}=\frac{\mathrm{e}}{\mathrm{L}}=\frac{0.51 \times 10^{-3}}{2}\)

= \(0.255 \times 10^{-3} \mathrm{~m}\)

Young’s modulus, Y = \(\frac{\text { stress }}{\text { strain }}\)

= \(\frac{2.546 \times 10^7}{0.255 \times 10^{-3}}=9.984 \times 10^{10} \mathrm{~N} / \mathrm{m}^2\)

Question 5. A copper wire and an aluminum wire have lengths in the ratio 3: 2, diameters in the ratio 2 : 3, and forces applied in the ratio 4: 5. Find the ratio of increase in length) of the two wires. (Y_Cu = 1.1 x 10¹¹ Nm^-2, Y_Al = 0.7 x 10¹¹ Nm^-2)
Solution:

Ratio of lengths, l₁: l₂ = 3: 2 ;

The ratio of diameters, d₁: d₂ = 2 : 3

Ratio of forces, F₁: F₂ = 4 : 5

Y₁ = Y of copper = 1.1 x 10¹¹

Y₂ = Y of Aluminium = 0.7 x 10¹¹;

The ratio of elongation, e₁: e₂?

e = \(\frac{\mathrm{Fl}}{\mathrm{AY}}=\frac{4 \mathrm{~F} l}{\pi \mathrm{d}^2 \mathrm{Y}}\)

∴ \(\frac{\mathrm{e}_1}{\mathrm{e}_2}=\frac{4 \mathrm{~F}_1 l_1}{\pi \mathrm{d}_1^2 \mathrm{Y}_1} \times \frac{\pi \mathrm{d}_2^2 \mathrm{Y}_2}{4 \mathrm{~F}_2 l_2}\)

⇒ \(\frac{\mathrm{e}_1}{\mathrm{e}_2}=\frac{\mathrm{F}_1 l_1 \mathrm{~d}_2^2 \mathrm{Y}_2}{\mathrm{~F}_2 l_2 \mathrm{~d}_1^2 \mathrm{Y}_1}=\frac{4 \times 3 \times 3^2 \times 0.7 \times 10^{11}}{5 \times 2 \times 2^2 \times 1.1 \times 10^{11}}\)

= \(\frac{189}{110}\)

∴ \(\mathrm{e}_1: \mathrm{e}_2=189: 110\)

Question 6. A brass wire of cross-sectional area 2mm² is suspended from a rigid support and a body of volume 100cm³ is attached to its other end. If the decrease in the length of the wire is 0.11mm, when the body is completely immersed in water, find the natural length of the wire. (Y_brass =0.91 x 10¹¹ Nm^-2 ρ_water = 10³ kg m^-3)
Solution:

Area of cross-section, A = 2mm² = 2 x 10^-6 m²

Volume of body, V = 100 cc = 100 x 10^-6 m³

Decrease in length, e’ = 0.11mm = 0.11 x 10^-3 m

Young’s modulus of brass, Y = 0.91 x 10¹¹ N/m²

Density of water, \(\rho=1000 \mathrm{~kg} / \mathrm{m}^3\)

Use \(\mathrm{e}^{\prime}=\frac{\mathrm{V} \rho g l}{\mathrm{AY}}\)

Natural length of wire, l = \(\frac{e^{\prime} \mathrm{AY}}{V_{\rho g}}\)

= \(\frac{0.11 \times 10^{-3} \times 2 \times 10^{-6} \times 0.91 \times 10^{11}}{100 \times 10^{-6} \times 1000 \times 9.8}\)

∴ I = \(\frac{0.2002 \times 10^2}{9.8}=\frac{20.02}{9.8}=2.043 \mathrm{~m}\)

Question 7. There are two wires of the same material. Their radii and lengths are both in the ratio 1: 2. If the extensions produced are equal, what is the ratio of the loads?
Solution:

Ratio of lengths, l₁ : l₂ = 1: 2

The ratio of radii, r₁: r₂ = 1: 2

Extensions produced are equal ⇒ e₁= e₂;

Made of same material ⇒ Y₁ = Y₂

Ratio of loads m₁: m₂ =? mg

Use \(\mathrm{Y}=\frac{\mathrm{mg}}{\pi \mathrm{r}^2} \frac{l}{\mathrm{e}}\) then \(\frac{\mathrm{m}_1}{\mathrm{~m}_2}=\frac{\mathrm{Y}_1 \mathrm{r}_1^2 l_2}{\mathrm{l}_1 \mathrm{Y}_2 \mathrm{r}_2^2}=\frac{1^2 \times 2}{1 \times 2^2}=\frac{1}{2}\)

∴ \(\mathrm{m}_1: \mathrm{m}_2=1: 2\)

Question 8. Two wires of different materials have the same lengths and areas of cross-section. What is the ratio of their increase in length when the forces applied are the same? (Y₁ = 0.90 x 10¹¹ Nm^-2, Y₂ = 3.60 x 10¹¹ Nm^-2)
Solution:

Lengths are same ⇒ l₁= l₂;

The area of cross sections are same, ⇒ A₁ = A₂

Y₁ = 0.9 x 10¹¹ N/m²

Y₂ = 3.60 x 10¹¹ N/m²

Elongation, e = \(\frac{F l}{A Y}\)

∴ \(\frac{e_1}{e_2}=\frac{F_1 l_1}{A_1 Y_1} \cdot \frac{A_2 Y_2}{F_2 l_2}\)

(because F, l, and A are the same)

∴ \(\frac{e_1}{e_2}=\frac{Y_2}{Y_1}\)

∴ \(\frac{e_1}{e_2}=\frac{3.60 \times 10^{11}}{0.9 \times 10^{11}}=\frac{4}{1} \text { or } \mathrm{e}_1: \mathrm{e}_2=4: 1\)

Question 9. A metal wire of length 2.5in and area of cross-section 1.5 x 10^-6 m² is stretched through 2mm. If Young’s modulus is 1.25 x 10¹¹ Nm^-2, find the tension In the wire.
Solution:

Length of wire, l = 2.5m

Y = 1.25 x 10¹¹ N/m²

Area of cross-section, A = 1.5 x 10^-6 m²

Elongation, e = 2 m.m = 2 x 10^-3 m

Tension, T = mg = F =?

Y= \(\frac{\mathrm{Fl}}{\mathrm{Ae}} \Rightarrow \mathrm{F}=\frac{\mathrm{YAe}}{l}\)

∴ Tension, \(\mathrm{T}=\frac{1.25 \times 10^{11} \times 1.5 \times 10^{-6} \times 2 \times 10^{-3}}{2.5}\)

= \(\frac{3.75 \times 10^2}{2.5}=150 \mathrm{~N}\)

Question 10. An aluminum wire and a steel wire of the same length and cross-section are joined end-to-end. The composite wire is hung from a rigid support and a load is suspended from the free end. If the increase in length of the composite wire is 1.35 mm, find the ratio of the

1. Stress in the two wires and
2. Strain in the two wires.

(Y_Al=0.7 x10¹¹ Nm^-2, Y_steel = 2 x 10¹¹ Nm^-2)

Solution:

1. Length is same ⇒ l₁ = I₂

Area is same ⇒ A₁ = A₂

In composite wire, the same load will act on both wires.

∴ Ratio of stress = 1:1

2. Total elongation, e = 1.35mm = e_Al+ e_s

Young’s modulus of aluminium = 7 x 10¹⁰ N/m²,

Y of steel = 2 x 10¹¹ N/m²

Elongation, e = \(\frac{F l}{A Y}\)

But F, l, and A are the same

∴ \(\mathrm{e} \propto \frac{1}{\mathrm{Y}} \text { or } \frac{\mathrm{e}_{\mathrm{Al}}}{\mathrm{e}_{\mathrm{s}}}=\frac{\mathrm{Y}_{\mathrm{s}}}{\mathrm{Y}_N}=\frac{20 \times 10^{10}}{7 \times 10^{10}}=\frac{20}{7}\)

∴ The ratio of strains in the wires is 20: 7

Question 11. A 2 cm cube of some substance has its upper face displaced by 0.15cm due to a tangential force of 0.3 N while keeping the lower face fixed. Calculate the rigidity modulus of the substance.
Solution:

Side of cube, a = 2.0 cm = 2 x10^-2 m

∴ Area, A = 4 x 10^-4 m²

Displacement of upper layer = 0.15cm = 0.15 x 10^-2 m

Tangential force, F = 0.30N

Rigidity modulus, \(\eta=\frac{\mathrm{F}}{\mathrm{A}} \cdot \frac{\mathrm{x}}{\Delta \mathrm{x}}\)

= \(\frac{0.30}{4 \times 10^{-4}} \frac{2 \times 10^{-2}}{0.15 \times 10^{-2}}\)

∴ \(\eta=\frac{0.60 \times 10^4}{0.60}=1 \times 10^4 \mathrm{~N} / \mathrm{m}^2\)

Question 12. A spherical ball of volume 1000 cm³ is subjected to a pressure of 10 atmospheres. The change in volume is 10^-8 cm³. If the ball is made of iron, find its bulk modulus. (1 atmosphere = 1 x 10⁵ Nm^-2)
Solution:

Volume of ball, V = 1000 cm³ = 10^-3 m³ (1M³ = 10⁶ cm³)

Pressure, P = 10 atmospheres = 10 x 10⁵ pa (1 atm = 10⁵ pascal)

Change in volume, ΔV = 10^-8 cm³

K = \(\frac{\mathrm{PV}}{\Delta \mathrm{V}}=\frac{10^6 \times 10^{-3}}{10^{-8}}=1 \times 10^{11} \mathrm{~N} / \mathrm{m}^2\)

Question 13. A copper cube of the side of length 1 cm is subjected to a pressure of 100 atmospheres. Find the change in its volume if the bulk modulus of copper is 1.4 x 10¹¹ Nm^-2 (1 atm = 1 x 10⁵ Nm^-2).
Solution:

Side of cube,‘a’ = 1 cm = 10^-2 m

∴ Volume of cube = 10^-6 m

Pressure, P = 100 atm = 100 x 10⁵ = 10⁷ pa

Bulk modulus, K = 1.4 x 10¹¹ N/m²;

Change in volume, \(\Delta V=\frac{P. V}{K}\)

= \(\frac{10^7 \times 10^{-6}}{1.4 \times 10^{11}}=\frac{10^{-10}}{1.4}=0.7143 \times 10^{-10} \mathrm{~m}^3\)

KSEEB Class 11 Physics solutions for Chapter 10 Mechanical Properties of Solids

Question 14. Determine the pressure required to reduce the given volume of water by 2%. The bulk modulus of water is 2.2 x 10⁹ Nm^-2
Solution:

Bulk strain = \(\frac{\Delta \mathrm{V}}{\mathrm{V}}=2 \% \Rightarrow \Delta \mathrm{V}=\frac{2}{100} \mathrm{~V}\)

Bulk modulus, \(\mathrm{K}=2.2 \times 10^9 \mathrm{~N} / \mathrm{m}^2\)

∴ Pressure required, \(\mathrm{P}=\frac{\mathrm{K} \Delta \mathrm{V}}{\mathrm{V}}\)

= \(\frac{2.2 \times 10^9 \times 2 \mathrm{~V}}{\mathrm{~V} \times 100}=4.4 \times 10^7 \text { pascal }\)

Question 15. A steel wire of length 20 cm is stretched to increase its length by 0.2 cm. Find the lateral strain in the wire if the Poisson’s ratio for steel is 0.19.
Solution:

Length of wire, l = 20, cm = 0.20m,

Poisson’s ratio, σ =0.19

Increase in length, Δl = 0.2 cm = 2 x 10^-3 m

lateral strain = ?

Lateral strain = σ x longitudinal strain ‘e’

But e = \(\frac{\Delta l}{l}\)

∴ Lateral strain = \(\sigma \frac{\Delta l}{l}=\frac{0.19 \times 2 \times 10^{-3}}{0.20}\)

= \(1.9 \times 10^{-3}=0.0019 \mathrm{~m}\).