Karnataka Class 9 Maths Model Question Papers 2023 Set 2

 

Karnataka Class 9 Maths Model Question Papers Set 2

Choose the correct alternative and Write the complete Solution along with its alphabet in the sheet provided:

Question 1. Which of the following is a set of rational nos.

1. w = {0,1,2,3, }
2. 2 = {….,-3,-2,-1,0,1,2,3,…….}
3. \(q=\left\{\frac{p}{q} ; p, q \in \mathrm{I}, q \neq 0\right\}\)
4. N= {1,2,3……..}

Solution : 3. \(q=\left\{\frac{p}{q} ; p, q \in \mathrm{I}, q \neq 0\right\}\)

Question 2.The degree of the polynomial x3 + x2+ 2x + 3 is

1. 2
2. 1
3. 3
4. 0

Solution : 3. 3

Karnataka 9th Standard Maths Model Question Paper 2023 Set 2 Free PDF

Question 3.When the polynomial p(y) =y³+  y² – 2y +1 is divided by (y + 3) then remainder is

1. 11
2. -11
3. 10
4. -10

Solution: 2. -11

Question 4. The expanded form of (a -b) is

1. a³ +b³ +3ab
2. a³ – b³ – 3ab
3. a³+b³ + 3a2b + 3ab²
4. a³ -b³ +3a2b + 3ab²

Solution: 4. a³ -b³ +3a2b + 3ab²

Question 5. In fig, PQ and RS are two lines intersecting at O.
If \(\text { POR }=50^{\circ}\). find \(\text { QOS, }\)  \(\text { |POS }\)

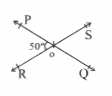
1. 50°, 80°
2. 50°, 130°
3. 50°, 90°
4. 50°, 100°

Solution: 2. 50°, 130°

Question 6. Area of a triangle =

1. 1/2 x base * height
2. 1/2 x height
3. 1/2 x base
4. base x height

Solution: 1. 1/2 x base x height

Class 9 Karnataka Maths Model Question Paper 2023 Set 2 with Solutions

Question 7.In fig. D is the midpoint of the side AB. DE || BC and EFIIAB. then DE =

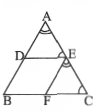
1. BC
2. 1/2 AE
3. 1/2 BC
4.  1/2 FC

Solution: 3.1/2 BC

Question 8. In the given figure, ABCD is a parallelogram. If \(\mid \mathrm{ABC}\)= 125° and |DCA – 25°, then |DAC is

1. 125°
2. 40°
3. 25°
4. 30°

Solution: 4. 30°

Question 9. If three or more points lie on the same line, then they are called _________ points.

1. Collinear
2. Non-collinear
3. Intersecting
4. Opposite

Solution: 1. Collinear

9th Standard Karnataka Maths Model Paper 2023 Set 2 Latest Exam Pattern

Question 10. 10a² + 2a+ 5 is an example of

1. Trinomial
2. Binomial
3. Monomial
4. Variable

Solution: 2. Binomial

Solution the following:

Question 1. Give one example each of a binomial of degree 5 and a monomial of degree 10.
Solution:
Binomial of degree \(5-x^5+x^4\)
Monomial of degree 10 – a¹⁰

Question 2. Simplify:  \((x+\sqrt{y})(x-\sqrt{y})\)

Solution: \( (x+\sqrt{y})(x-\sqrt{y})=x^2-(\sqrt{y})^2=x^2-y\)

Question 3. Find the value of : \( \frac{11^{\frac{1}{2}}}{11^{\frac{1}{4}}}\)

Solution :  \( \frac{11^{1 / 2}}{11^{1 / 4}}=11^{1 / 2-1 / 4}=11^{\frac{2-1}{4}}=11^{1 / 4} \)

Question 4. Find the value of K, if x-1 is a factor of p(x)
=\(\mathbf{k} x^2-\sqrt{2} x+1\)

Solution :

\(\begin{aligned}
& \mathbf{p}(\boldsymbol{x})=k x^2-\sqrt{2} x+1 \\
& \mathrm{p}(1)=\mathrm{k}(1)^2-\sqrt{2}(1)+1 \\
& \mathrm{p}(1)=k-\sqrt{2}+1 \\
& 0=k-\sqrt{2}+1 \\
& \sqrt{2}-1=k
\end{aligned}\)

Question 5. Find any two solutions forx= 5y

Solution: x= 5y

x = 0, 0 = 5y

x = 1, 1= 5y

∴ y = 0        1/5 = y

(0,0)          0.2 = y

(1,0.2)

∴The two solutions are (0, 0) and (1, 0.2)

Question 6. Write any two postulates.

Solution:

1. A straight line may be drawn from any one point to any other point.
2. A circle can be drawn with any center and radius.

Question 7. In fig. find the value of x.

Solution: x= 90°

Question 8. In the adjoining figure, identify and write the name of the parallel sides and the alternate angles.

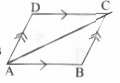
Solution: \(\mathrm{AB}\|\mathrm{CD}, \mathrm{AD}\| \mathrm{BC} \text { and }\lfloor\mathrm{BAC}=\lfloor\mathrm{DCA}\)

Question 9. In the fig, find the value of x.

Solution: x = 80°

Question 10.In the fig |CAD = 55° and |BAC = 45°, then find the |DAB

Solution: |DAB = 100°

Answer the following:

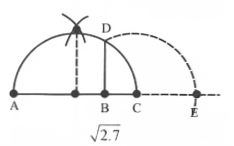
Question 1. Construct  \( \sqrt{2.7}\) on the number line
Solution:

 

Question 2. Simplify : \((\sqrt{a}+7)(\sqrt{a}+\sqrt{8})\)

Solution:

\(\begin{aligned}
& (\sqrt{a}+7)(\sqrt{a}+\sqrt{8}) \\
& =\sqrt{a}(\sqrt{a}+\sqrt{8})+7(\sqrt{a}+\sqrt{8}) \\
& =(\sqrt{a})^2+\sqrt{8} a+7 \sqrt{a}+7 \sqrt{8} \\
& =a+2 \sqrt{2 a}+7 \sqrt{a}+14 \sqrt{2}
\end{aligned}\)

Question 3. Find the remainder when t⁴+2 t² + 5 is divided by x – 2

Solution:

\(\begin{aligned}
\text { Let } \mathrm{p}(t) & =t^4+2 t^2+5 \\
\mathrm{p}(2) & =(2)^4+2(2)^2+5 \\
\mathrm{p}(2) & =16+8+5 \\
\mathrm{p}(2) & =29
\end{aligned}\)

Question 4. Expand(2x + 3y-5z)² using a suitable identity.

Solution : 

\(\begin{aligned}
& (2 x+3 y-5 z)^2 \\
& (a+b+c)^2=a^2+b^2+c^2+ \\
& 2 a b+a b c+2 c a \\
& (2 x+3 y-5 z)^2=4 x^2+9 y^2+25 z^2 \\
& +12 x y-30 y z-20 x z \\
&
\end{aligned}\)

Karnataka Class 9 Maths Previous Year Model Paper 2023 Set 2 with Key Answers

Question 5. Express x + 6y = 7 in the form of ax + by + c – 0 and indicate the values of a, b and c.

Solution:

x + 6y = 7

x + 6y – 7 = 0

ax + by + c = 0

a = 1, b = 6, c = -7

Question 6.In fig. \(\mathrm{PQR}=\mathrm{PRQ}\), P then proves that \( \angle \mathrm{PQS}=\lfloor\mathrm{PRT} \)

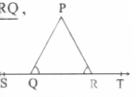
Solution:

\(In fig. \mid \mathrm{PQR}=\mathrm{PRQ}\)

∴\(\quad \mathrm{PQR}+\mathrm{PQS}=180^{\circ} \ldots .(1) \text { (linear pair) }\)

Similarly \(\left\lfloor P R Q+\left\lfloor P R T=180^{\circ}\right.\right.\)

(2) (linear pair)

From (1) and (2)

\(\angle \mathrm{PQR}+\angle \mathrm{PQS}=\angle \mathrm{PQR}+\angle P R T\)

∴\(\angle \mathrm{PQS}=\angle \mathrm{PRT}(\angle \mathrm{PQR}=\angle \mathrm{PRQ})
\)

Question 7. In fig. find the values of x andy and then S.T. AB || CD 

Solution:

In the fig, 50°+ x = 180°

x = 180° — 50°

x = 130° also y = 130°

∴x = y = 130°(Alternative angle)

Since alternate angles are equal AB || CD

Question 8. The line is the bisector of an angle ∠ A and ∠ B is any point on l. BP and BQ are perpendiculars from B to the arms of |A. S.T.

1. AAPB = AAQB
2. BP = BQ

Solution:

In the fig line,’ l ‘ bisects ∠A,

BQ and BP are perpendicular to the arms of ∠A.

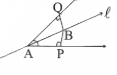
In △APB and △AQB

∠APB = ∠ABQ = 90° (given)

∠PAB = ∠QAB (l bisect ∠A)

AB = AB (common)

∴△APB ≅ △AQB (ASS congruence rule) BP = BQ (CPCT)

Question 9. Diagonal AC of a parallelogram ABCD bisects ∠A. S.T.

1. It bisects ∠C also
2. ABCD is a rhombus.

Solution:

In fig. AC bisects ∠A

∴∠DAC — ∠BAC ………. (1)

But ∠DAC — ∠BCA (Alternate angles)………….(2)

and ∠BAC — ∠DCA (Alternate angles)…………….(3)

From(1), (2), and (3)

∠BCA = ∠DCA

∴AC bisect ∠C

Also ∠DAC =  ∠DCA (From(1), (2) and (3))

∴AD = DC

But AD = BC

and DC = AB

∴AD = BC = AD = BC

∴ABCD is a rhombus

Question 10. ABC is a right-angled triangle at C. A line through the midpoint M of hypotenuse AB and parallel to BC intersects AC at D. S.T.
CM = MA = 1/2 AB

Solution:

In the fig join CM.

M is the midpoint of AB

∴ MA = 1/2 AB……………………….. (1)

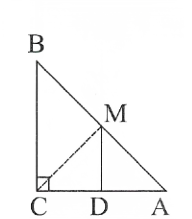
Now, In △AMD and △CMD

AD = DC

∠MDC = ∠MDA = 90°

MD = MD (common)

∴△AMD = △CMD (SAS congruence rule)

CM = MA (CPCT)……………….. (2)

comparing (1) and (2)

CM = MA = 1/2 AB

Karnataka 9th Maths Sample Paper 2023 Set 2 for Board Exam Preparation

Question 11.In fig. ABCD is a parallelogram, AE⊥DC and CF ⊥ AD • If AB = 16cm, AE = 8cm and CF = 10cm d E find AD.

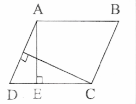
Solution:

In fig. ABCD is a parallelogram

Area of the ▱ABCD = base x height

= DC x AE

= 16 x 8

=128cm²

Area of  ▱ABCD = b x h

128 – AD x 10

AD = 128/10

AD = 12.8cm

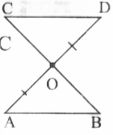
Question 12. S.T. the diagonals of a parallelogram divide it into four triangles of equal area

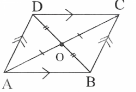
Solution:

ABCD is a parallelogram.

The diagonals AC and BD bisect each other at ’O’.

∴‘O’ is the midpoint of AC and BD

In △ADC, DO is the median on AC.

∴ar(△AOD) =ar{△COD)………. (1)

In ABDC j CO is the median on BD.

∴ar(△COD) = (△BOC)……………….(2)

In A ABC, BO if the median on AC

∴ar(△BOC) =ar(△AOB)……………….. (3)

In A ABD 5, AO is the median on BD

∴ar(△AOB) =ar(AOD)…………………….. (4)

comparing (1), (2), (3), and (4)

ar(△AOD) =ar(△COD)

=ar(△BOC)=ar(△AOB)

Question 13.In fig. ∠ABC-69°, ∠ACB = 31°, find ∠BDC

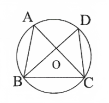
Solution:

In △ABC

∠BAC + ∠ABC + ∠ACB = 180°

69° + 31° + ∠BAC = 180°

100° + ∠BAC = 180°

∠BAC = 180° —100°

∠BAC = 80°

∠BAC = ∠ BDC

∴ ∠BDC = 80°

Question 14. Construct the angle of 15° and verify by measuring it with a protractor.

Solution : 

Question 15. Give four examples of data that you can collect from your day-to-day life.

Solution:

1. Number of T.V. viewers in a city
2. The number of colleges in a city.
3. Height of students in a class.
4. The number of children in the country under 15 years.

Question 16. Eleven bags of wheat flour, each marked 5kg, actually contained the following weights of flour(in kg):
4.97; 5.05; 5.08; 5.03; 5.00; 5.06; 5.08; 4.98; 5.04; 5.07; 5.00 Find the probability that any. of these bags chosen at random contains more than5kg of flour.

Solution:

Total Number of bags =11

Number of bags containing more than 5 kg of flour = 7

∴ P(bags containing more than 5kg flour) = 7/11

Question 17. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the center makes equal angles with the chords.

Solution:

In the circle ‘O’ is the

center of a circle Chord AB = Chord CD

Draw OP ⊥ CD and OQ ⊥ AB

In △OPE and △OQE ∠OPE = ∠OQE = 90°

OE = OE (common hypotenuse)

OPE = QOE

(RHS congruence rule)

∴ ∠OEP = ∠OEQ (CPCT)

Question 18. Identify and write the name of the quadrilateral and triangle from fig.

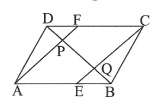
Solution:

Quadrilaterals ABCD and AECF

Triangles: △ADF, △EBC, △BDC, △BAD

Solution the following:

Question 1. Factorise : 27 x³ +  y³+ z³ – 9xyz

Solution:

27  x³+ y³ + z³ — 9xyz

(3x)³ + y³ + z³ — 3(3x)y

x³ +  y³+ z³ – 9xyz

(x² + y²+z²— xy — yz — zx)

(3x)³ +y³ + z³— 3 xyz =

(3x + y + z) (9x² + y²+z² — 3 xy — yz — 3 zx)

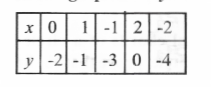
Question 2. Draw the graph of x-y = 2
Solution :

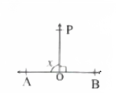
Question 3. In the figure, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ, respectively. If ∠POS – x, find ∠ROT.

Solution:

Ray OS stands on the line POQ

∠POS + ∠SOQ = 180°

x + ∠SOQ = 180°

∠SOQ = 180°—x

∠ROS = 1/2 x∠POS

= 1/2 x x

∠ROS = x/2

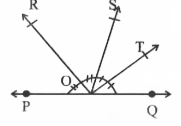
Similarly ∠SOT = 1/2  x∠SOQ

= 1/2x (l80° —x)

∠SOT = 90° – x/2

Now, ∠ROT = ∠ROS + ∠SOT

\(=\frac{x}{2}+90^{\circ}-\frac{x}{2}\)

∠ROT = 90°

9th Class Karnataka Maths Model Paper 2023 Set 2 Important Questions

Question 4. Line segment AB is parallel to another line segment CD. D is the mid-point of AD. S.T.

1. △AOB ≅ △DOC
2. O is also the midpoint of BD.

Solution :

1. consider △AOB and △DOC
   ∠ABO =∠DCO (AB || CD)
   ∠AOB – ∠DOC(V.O.A)
   OA = OD (given)
   ∴△AOB ≅ ∠DOC (AAS rule)
2. OB = OC (CPCT)
   ∴O is the midpoint of BC.

Question 5. In a parallelogram ABCD, E and F are the midpoints of sides AB and CD respectively. S.T. the line segments AF and EC trisect the diagonal BD.

Solution:

ABCD is a parallelogram

AB || DC and AB = DC

∴ 1/2 AB = 1/2 Dc

AE = CF and AE || CF (AB || CD)

∴ In the quadrilateral AECF

AE || CF and AE = CF

∴ AECF is a parallelogram

∴ AF || EC

In △DQC , PF || QC (•.• AF || EC) and F is the midpoint of DC

∴ P is the midpoint of DQ

△DQC DP = PQ…………………………… (1)

In △DAP, EQ [| AP (AF || CE)

‘E’ is the midpoint of AB

∴ Q is the midpoint of BP

PQ = BQ ……………………………(2)

From (1) and (2)

DP = PQ = BQ

∴Line segments AF and EC trisect the diagonal BD.

Question 6. The inner diameter of a circular well is 3.5m. It is 10m deep. Find

1. Its inner curved surface area,
2. The cost of plastering this curved surface at the rate of ₹40 per nr.

Solution:

The inner diameter of the well = 3.5m

r = 3.5/2 m

1. Inner CSA of the well = 2πrh
   = \(22 \times \frac{22}{7} \times \frac{3.5^{0.5}}{2} \times 10\)
   = 110m²
2. cost ofplastering the inner CSA at ₹40m² = 110×40 =₹4400

Solution the following :

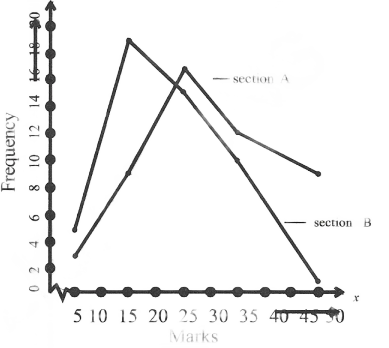
Question 1. The following table gives the distribution of students in two sections according to the marks obtained by them.
Section A                                      Section B
Marks Frequency                      Marks Frequency
0-10            3                            0-10            5
10-20          9                            10-20         19
20-30          17                           20-30        15
30 – 40        12                           30-40         10
40-50            9                           40-50           1

Represent the marks of the students of both sections on the same graph by two frequency polygons. The two polygons compare the performance of the two sections.

Solution:

Scale x – axis 1cm= 5units

y-axis 1cm= 3 units

Latest Karnataka Class 9 Maths Model Papers 2023 

Question 2.Prove that the line of centers of two intersecting circles subtends equal angles at the two points of intersection

Solution: Let two circles with respective centers A and B intersect each other at points C and D.

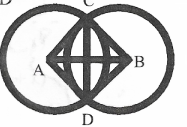
In A ABC and AABD AC =AD (radii)

BC = BD (radii)

AB = AB (common)

∴△ABC ≅ △ABD (By SSS congruence mle)

⇒∠ACB = ∠ADB (CPCT)

Question 3.Factorise :  x³ – 3x² – 9x – 5

Solution:

Let p(x) = x³ – 3x² – 9x – 5

By trial, we find that p(-l) = (-1)³-3(-1)²-9(-l)-5

= -1-3+9-5

= 0

∴(x + 1) is a factor of this polynomial.

Let us find the quotient for dividing

x³ + 3x² – 9x – 5 by (x+1) by long division method.

\(\begin{aligned}
& x+1) \frac{x^2-4 x-5}{x^6-3 x^2-9 x-5} \\
& \frac{\left.\frac{(-) x^8+x^2}{(-1}\right)}{4 x^2-9 x-5} \\
& \frac{(+) 4 x^2 \frac{-4 x}{(+)}}{-5 x-5} \\
&
\end{aligned}\)

∴ quotient= x² -4x – 5

Now factorise the,  x³ _ 3X² _ 9X_ 5

x²(x+l)- 4x(x+1)- 5(x+1)

= x²(x+1)- 4x(x+1)- 5(x+ 1)

= (x+l)(x²-4x-5) + (x+l)(x²– 5x+ x- 5)

= (x+ 1) {x (x- 5)+l(x- 5)}

= (x+l) (x-5) (x+l)

Karnataka Board 9th Class Maths Model Question Paper 2023 Set 2 Solved PDF 

Question 4. Prove that “parallelograms on the same base and between the same parallels are equal in area.”
Solution:

Data: Parallelogram ABCD and ABEF standing on the same base AB and between the parallels PQ and MN.

To prove : ar(ABCD) = ar(ABEF)

Proof: In ΔADF and ΔBCE

∠ADF = ∠BCE (corresponding angles)

∠AFP = ∠BEC (corresponding angles)

DF = CE

∴ ΔADF ≅ ΔBCE

ar (ΔADF ) = ar ΔBCE

consider fig. ABED

area (ABED) – area (BCE)

= area (ABED) – area (ADF)

area (ABCD) = area (ABEF)

∴area of ▱ ABCD = area of ▱ ABEF