Uncategorized

KSEEB Solutions for Class 8 Maths Chapter 16 Mensuration Points To Remember

Perimeter: Length of boundary of a simple closed figure.

Area: The measure of region enclosed in a simple closed figure.

Area of a trapezium=half of the sum of the lengths of parallel sides x perpendicular distance between them.

Area of a rhombus = half the product of its diagonals.

Perimeter of Rectangle = 2 (/ + b)

Square = 4a

Read and Learn More KSEEB Solutions for Class 8 Maths

Triangle = \(\frac{1}{2} \times \text { base } \times \text { height }\)

Parallelogram= 2 (sum of two adjacent sides)

Diagonal of: Rectangle = \(\sqrt{l^2+b^2}\)

Square = \(\sqrt{2 a}\)

Surface area of a solid is the sum of the areas of its faces, surface area of:

a cuboid = 2 (lb + bh + hi)

a cube = \(6 \ell^2\)

a cylinder = \(2 \pi r(r+h)\)

Amount of region occupied by a solid is called its volume.

Volume of a cuboid = \(\ell \times b \times h\)

a cube = \(\ell^3\)

a cylinder = \(\pi r^2 h\)

1)\(1 cm^3 = 1 mL\)

2)\(lL= 1000cm^3\)

3)\(1 m^3 = 1000000cm^3 = 1000L\)

Class 8 Maths KSEEB Mensuration Exercise 16.1

1. A square and a rectangular field with measurements as given in the figure have the same perimeter which field has a larger area?

Solution: Perimeter of square = 4(side) = 4(60) = 240m

Perimeter of Rectangle = 2(length + breadth)

= 2(80 + b)

= 160 +2b

It is given that the perimeter of the square and the rectangle are the same, ie 160 +2b = 240m

\(\mathrm{b}=\frac{240-160}{2}=\frac{80}{2}=40 \mathrm{~m}\)

Area of a square \((side)^2 = (60)^2 = 3600m^2\)

Area of rectangle =l x b = 80 x 40 = \(3200 m^2\)

Thus, the area of the square field is larger than the area of the rectangular field.

2. Mrs. Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of ₹55 per \(m^2\).

 

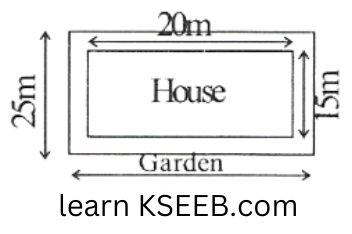
Solution: Area of the square plot = \((25m)^2 = 625 m^2\)

Area of the house = 15 x20 = \(300m^2\)

Area of the remaining portion=Area of square plot – Area of the house

= \(625m^2 – 300m^2 = 325m^2\)

The cost of developing the garden around the house is ₹55 per \(m^2\)

Total cost of developing the garden of area \(325m^2\)

= 55 x 325 = ₹17875

3. The shape of a garden is rectangular in the middle and semi-circular at the ends as shown in the diagram. Find the area and the perimeter of this garden (Length of rectangle is 20 – (3.5 + 3.5) meters)

 

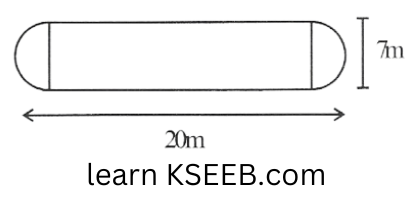
Solution: Length of the rectangle = 20-(3.5+3.5)m

= 20-7 = 13m

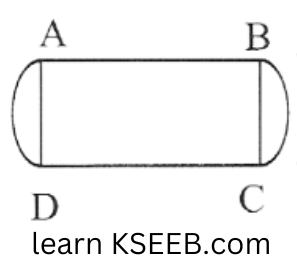
Circumference of 1 semi-circular part

\(\pi r=\left(\frac{22}{7} \times 3.5\right) \mathrm{m}=11 \mathrm{~m}\)

Circumference ofboth semi-circular parts

= (2 x 1l)m= 22m

Perimeter of the garden = AB + Length ofboth semi – circular regions BC and DA + CD

= 13m + 22m + 13 = 48m

Area of the garden = Area of rectangle + 2 x Area of two semi-circular region.

=\(\left[(13 \times 7)+2 \times \frac{1}{2} \times \frac{22}{7}(3.5)^2\right]\)

= \((91 +38.5)m^2 = 129.5 m^2\)

4. A flooring tile has the shape of a parallelogram whose base is 24cm and the corresponding height is 10cm. How many such tiles are required to cover a floor of the area \(1080m^2\)? (If required you can split the tiles in whatever way you want to fill up the corners)

Solution: Area of parallelogram=Base x Height

Hence, area of one tile = \(24 x 10= 240 cm^2\)

Required number of tiles = \(\frac{\text {Area of the floor } }{\text { Area of the each tile }}\)

=\(\frac{1080 \mathrm{~m}^2}{240 \mathrm{~m}^2}=\frac{1080 \times 10000 \mathrm{~cm}^2}{240 \mathrm{~cm}^2}\)

= 45000 tiles

Thus, 45000 tiles are required to cover a floor of area \(1080m^2\).

5. An ant is moving around a few food pieces of different shapes scattered on the floor. For which food – piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression \(C = 2 \pi r \), where r is the radius of the circle.

 

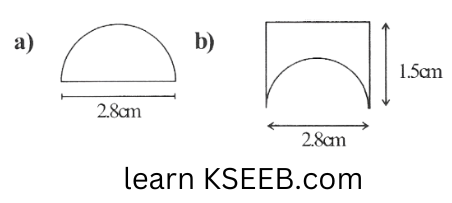
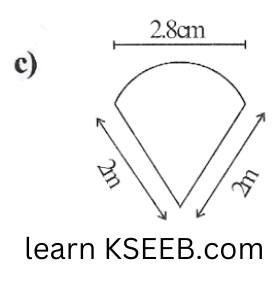
Solution: a) Radius (r) of semicircular part = \(\left(\frac{2.8}{2}\right) \mathrm{cm}\)

= 1.4cm.

Perimeter of the given figure = \(2.8 \mathrm{~cm}+\pi r\)

= \(2.8+\frac{22}{7} \times 1.4=2.8 \mathrm{~cm}+4.4 . \mathrm{cm}=7.2 \mathrm{~cm}\)

b) Radius of semicircular part = \(\frac{2.8}{2} = 1.4cm.\)

Perimeter of the given figure (b)

= \(1.5 \mathrm{~cm}+2.8 \mathrm{~cm}+1.5 \mathrm{~cm}+\pi(1.4 \mathrm{~cm})\)

= \(5.8 \mathrm{~m}+\frac{22}{7} \times 1.4 \mathrm{~cm}\)

= 5.8+4.4=10.2cm

c) Radius of semi-circular part = \(\frac{2.8}{2}=1.4 \mathrm{~cm}\)

perimeter of the figure (c) = \(2 \mathrm{~cm}+\pi r+2\)

= \(4+\frac{22}{7} \times 1.4=4+4.4 \mathrm{~cm}\)

= 8.4cm

Thus, the ant will have to take a longer round for the food piece (b) because the perimeter of the given figure (b) is the greatest among all.

KSEEB Class 8 Maths Mensuration Problems And Solutions

Mensuration Exercise 16.2

1. The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are lm and 1.2m and perpendicular distance between them is 0.8m.

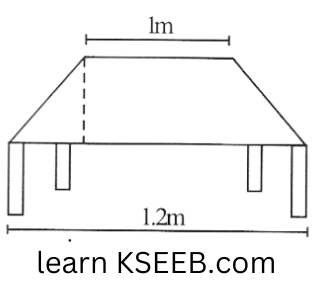
Solution: Area of trapezium

= 1/2(sum of parallel sides) x (Distance between parallel sides)

= \(\left[\frac{1}{2}(1+1.2) 0.8\right] \mathrm{m}^2=0.88 \mathrm{~m}^2\)

2. The area of a trapezium is \(34cm^3\) and the length of one of the parallel sides is 10cm and its height is 40m. Find the length of the other parallel side.

Solution: Given: area of trapezium = \(34cm^2\) and h = 4cm Let the length of one parallel side be a.

w.k.T, Area of trapezium = 1/2 (sum of parallel sides) x Distance between parallel sides.

\(34 \mathrm{~cm}^2=\frac{1}{2}(10 \mathrm{~cm}+a) \times 4 \mathrm{~cm}\)

34cm = 2(10+a) x 4cm

\(\frac{34}{2}=10+a\)

Thus, the length of the other parallel sides is 7 cm.

3. Length of the fence of a trapezium-shaped field. ABCD is 120m. If BC = 48m CD = 17m and AD = 40m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.

Solution: Length of the fence of trapezium ABCD

= AB + BC + CD + DA

120m = AB + 48m + 17m + 40m

AB= 120- 105 = 15m

Area of the field ABCD = \(\frac{1}{2}(\mathrm{AD}+\mathrm{BC}) \times \mathrm{AB}\)

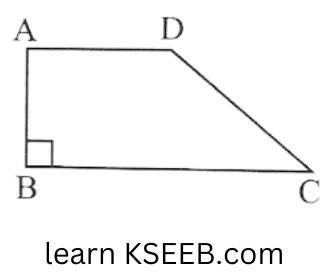
= \(\frac{1}{2}(40+48) \times 15\)

= \(\frac{1}{2} \times 88 \times 15\)

Area of the field ABCD = \(660 m^2\).

4. The diagonal of a quadrilateral-shaped field is 24m and the perpendiculars dropped on it from the remaining opposite vertices are 8m and 13m. Find the area of the field.

Solution: It is given that

Length of the diagonal, d = 24m

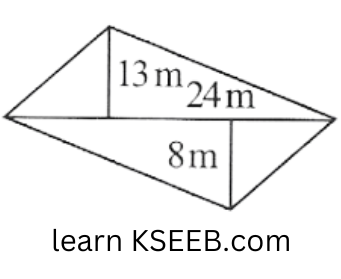
Length of the perpendicular, \(\mathrm{h}_1 \& \mathrm{~h}_2\) from the opposite vertices to the diagonal are \(h_1=8 \mathrm{~m} \& h_2=13 \mathrm{~m}\)

= \(\frac{1}{2} \times(24 m)(13 m+8 c m)\)

= \(\frac{1}{2} \times 24 \mathrm{~m} \times 21 \mathrm{~m}=252 \mathrm{~m}^2\)

Thus, the area of the field is \(252m^2\).

5. The diagonals of a rhombus are 7.5 cm and 12cm. Find its area.

Solution: Area of rhombus = \(\frac{1}{2} \text { (product of its diagonals) }\)

∴ area of the given rhombus =\(\frac{1}{2} \times 7.5 \mathrm{~cm} \times 12 \mathrm{~cm}\)

= \(45 \mathrm{~cm}^2\)

6. Find the area of a rhombus whose side is 5cm and whose altitude is 4.8cm. If one of its diagonals is 8cm long, find the length of the other diagonal.

Solution: Let the length of the other diagonal of the rhombus be x.

A rhombus is a special case of a parallelogram.

The area of a parallelogram is given by the product of its base and height.

Thus, area of the given rhombus = Base x height = \(5cm x 4.8cm = 24cm^2\)

Also, area of rhombus

=\(\frac{1}{2} \text { (product of its diagonals) }\)

=\(24 \mathrm{~cm}^2=\frac{1}{2} \times 8 \times x\)

\(x=\frac{24 \times 2}{8}=6 \mathrm{~cm}\)

Thus, the length of the other diagonal of the rhombus is 6cm.

Mensuration Class 8 KSEEB Questions And Answers 

7. The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45cm and 30cm in length. Find the total cost of polishing the floor, if the cost per \(m^2\) is ₹4.

Solution: Area of rhombus = \(\frac{1}{2} \text { (product of its diagonals) }\)

Area of each tile = \(\frac{1}{2} \times 45 \times 30 \mathrm{~cm}^2=675 \mathrm{~cm}^2\)

Area of3000 tiles = \(675 \times 3000=2025000 \mathrm{~cm}^2\)

The cost of polishing is 4 per\(m^2\).

Cost of polishing 202.5m2 area = 4 x 202.5 = ₹810.

Thus, the cost of polishing the floor is ₹810.

8. Mohan wants to buy a trapezium-shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is \(10500m^2\) and the perpendicular distance between the two parallel sides is 100m, find the length of the side along the river.

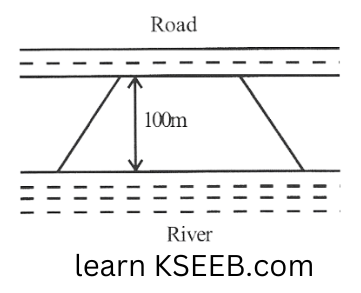
Solution: Let the length of the field along the road be £m Hence, the length of the field along the rive will be 2 lm

Area of trapezium = \(\frac{1}{2} \text { (sum of parallel sides) }\)

(Distance between the parallel sides)

\(10500 \mathrm{~m}^2=\frac{1}{2}(\ell+2 \ell)(100 \mathrm{~m})\) \(3 \ell=\frac{2 \times 10500}{100}=210 \mathrm{~m}\) \(\ell=\frac{210}{3}=70 \mathrm{~m}\)

Thus, length of the field along the river = 2 x 70= 140m.

9. Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.

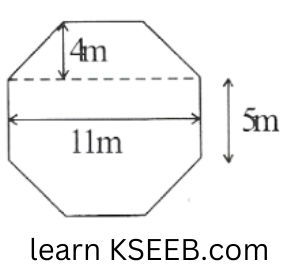
Solution:

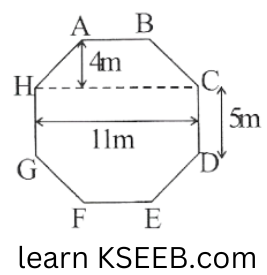
Side of regular Octagon = 5m

Area of trapezium ABCH = Area of trapezium DEFG

Area of trapezium ABCH

= \(\frac{1}{2} \times 4(11+5)=\frac{1}{2} \times 4 \times 16=32 \mathrm{~m}^2\)

Area of rectangle HGDC =\(11 x 5 = 55m^2\)

Area of Octagon = Area of trapezium ABCH + Area of trapezium DEFG + Area of rectangle HGDC

= \(32m^2 + 32m^2 + 55m^2 = 119m^2\)

10. There is a pentagonal-shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways.

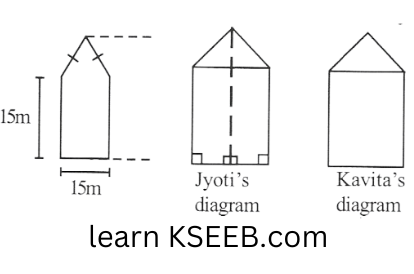
Find the area of this park using both ways, can you suggest some other way of finding its area.

Solution: Jyoti’s way of finding area is as follows.

Area of pentagon = 2(Area of trapezium ABCF)

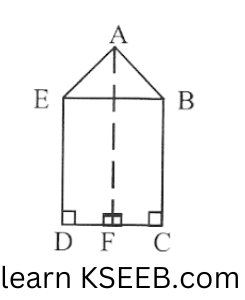
=\(2 \times \frac{1}{2}(15+30)\left(\frac{15}{2}\right)=337.5 \mathrm{~m}^3\)

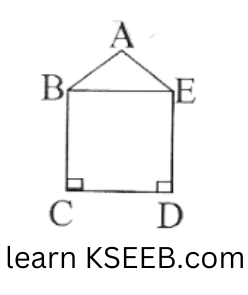
Kavita’s way of finding area is as follows.

Area of pentagon = Area of △ABE+Area of square BCDE

=\(\left[\frac{1}{2} \times 15(30-15)+(15)^2\right] \mathrm{m}^2\)

=\(\frac{1}{2}(15 \times 15 \times 225) \mathrm{m}^2\)

=\((112.5+225) \mathrm{m}^2\)

=\(337.5 \mathrm{~m}^2\)

Explanation Of Mensuration In KSEEB Class 8 Maths 

11.Diagram of the adjacent picture frame has outer dimensions = 24cm x 28cm & inner dimensions 16cm x 20cm. Find the area of each section of the frame if the width of each section is same.

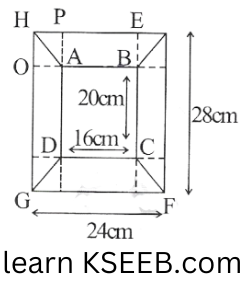
Solution: Given that, the width of each section is same, therefore

IB = BJ = CK = CL = DM = DN = AO = AP

IL = IB + BC + CL

28 = IB + 20 + CL

IB + CL = 28 – 20 = 8cm

IB = CL = 4cm

Hence 1B = BJ = CK = CL = DM = DN =AO = AP = 4cm

Area of section BEFC = Area of section DGHA

=\(\frac{1}{2}(20+28) 4=96 \mathrm{~cm}^2\)

Area of section ABEH=Area of section CDGF

⇒ Area of section ABEH = Area of section CDGF

= \(1216+ 244 = 80cm^2\)

Mensuration Exercise 16.3

1. There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?

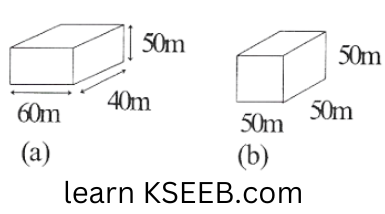
Solution: w.k.t

Total surface area of the cuboid = 2 (lb + bh + hl)

Total surface area of cuboid (a) = 2(60 + 40 + 40 x 50 + 50 x 60)

= \(2(2400 + 2000 + 3000)cm^2\)

= \(2 x 7400 cm^2\)

= \(14800 cm^2\)

Total surface area of cube (b) = \(6 (side)^2 = 6(5 0)^2\)

= \(6 x 2500 =15000cm^2\)

Thus, the cuboidal box (a) will require lesser amount of material.

2. A suitcase with measure 80cm x 48cm x 24cm is to be covered with a tarpaulin cloth. How many meters of tarpaulin of width 96cm is required to cover 100 such suitcases?

Solution: Total surface area of suitcase

= 2(80 x 48 + 48 x 24 + 24 x 80)

= 2(3840+ 1152+ 1920)

= \(13824cm^2\)

Total surface area of 100 suitcases =13824 x 100 = 1382400cm2

Required tarpaulin = length x breadth

\(1382400 cm^2 = length x 96cm\) \(\mathrm{L}=\frac{1382400}{96}=14400 \mathrm{~cm}=1^{\prime} 44 \mathrm{~m}\)

Thus, 144m of tarpaulin is required to cover 100 suitcases.

3. Find the side of a cube whose surface area is \(600cm^2\)

Solution: Given that, surface area of cube = \(600cm^2\)

Let the length of each side of cube be l

Surface area of cube = \(6(side)^2\)

\(600 \mathrm{~cm}^2=6 \ell^2\) \(\ell^2=\frac{600}{6}=100 \mathrm{~cm}^2\)

l = 10cm

Thus, the side of the cube is 10cm.

4. Rukhsar painted the outside of the cabine to measure lm x 2m x 1.5m. How much surface area did she cover if she painted all except the bottom of the cabinet?

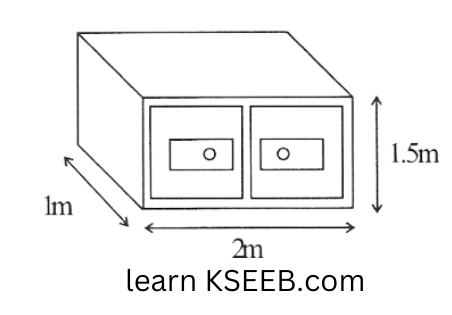
Solution: l= 2m

b = lm

h= 1.5m

Area of the cabinet that was painted

= 2h(£ + b) + £b

= 2 x 1.5(2+1) +2(1)

= \(3(3)+ 2 = 9+ 2= 11m^2\)

5. Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth and height of 15m, 10m and 7m respectively. From each can of paint \(100m^2\) of area is painted. How many cans of paint will she need to paint the room?

Solution: Given that:

l = 15m, b = 10m, h = 7m

Area of the hall to be painted=Area of the wall + Area of othe ceiling

= 2 h(£ + b) + £b

= \([2(7)(15+10)+15 \times 10] \mathrm{m}^2\)

= 14 x 25 + 150 = 350 + 150

= \(500m^2\)

It is given that \(100m^2\) area can be painted from each can. Number of cans required to paint an area of \(500m^2 = \frac{500}{100}=5\)

Hence, 5 cans are required to paint the walls and the ceiling of the cuboidal hall.

6. Describe how the two figures at the right are alike and how they are different. Which box has larger lateral surface area?

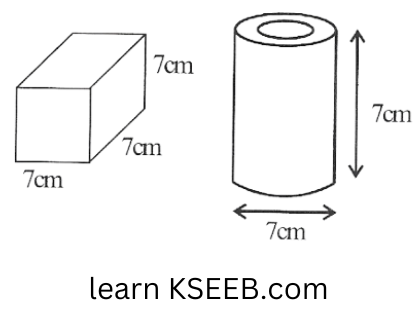
Solution: Similarity between both the figures is that both have the same heights.

The difference between the two figures is that one is a cylinder and the other is a cube.

Lateral surface area of the cube

= \(4 \ell^2=4(7)^2=4 \times 49=196 \mathrm{~cm}^2\)

LSA of the cylinder

= \(2 \pi r h=\not 2 \times \frac{22}{7} \times \frac{7}{\not 2} \times 7=154 \mathrm{~cm}^2\)

Hence, the cube has larger lateral surface area.

KSEEB Class 8 Maths Chapter 16 Mensuration Notes 

7. A closed cylindrical tank of radius 7m and height 3m is made from a sheet of metal. How much sheet of metal is required?

Solution: TSA of cylinder = \(2 \pi r(r+h)\)

=\(2 \times \frac{22}{7} \times 7(7+3) \mathrm{m}^2\)

=\(44 \times 10=440 \mathrm{~m}^2\)

Thus, \(440m^2\) sheet of metal is required

8. The LSA of a hollow cylinder is \(4224 cm^2\). It is cut along its height and formed a rectangular sheet of width 33cm. Find the perimeter of rectangular sheet?

Solution: A hollow cylinder is cut along its height to form a rectangular sheet.

Area of cylinder=Area of rectangular sheet.

\(4224cm^2 = 33 cm x l\)

=\(\ell=\frac{4224}{33}=128 \mathrm{~cm}\)

Thus, the length of the rectangular sheet is 128 cm.

Perimeter of the rectangular sheet

= 2(length + width)

= 2 (128 + 33)cm

= 2 x 161 = 322cm

9. A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84cm and length is lm.

Solution: In one revolution, the roller will cover an area equal to its lateral surface area.

Thus, in 1 revolution, area of the road covered

= \(2 \pi r h\)

= \(2 \times \frac{22}{7} \times 42 \mathrm{~cm} \times 1 \mathrm{~m}\)

= \(2 \times \frac{22}{7} \times \frac{42}{100} \mathrm{~m} \times \mathrm{lm}=\frac{264}{100} \mathrm{~m}^2\)

In 750 revolutions, area of the road covered

=\(\left(750 \times \frac{264}{100}\right) \mathrm{m}^2=1980 \mathrm{~m}^2\)

10. A company packages its milk powder in cylindrical container whose base has a diameter of 14cm and height 20cm. Company places a label around the surface of the container (as shown in the figure). If the label is placed 2cm from top and bottom, what is the area of the label.

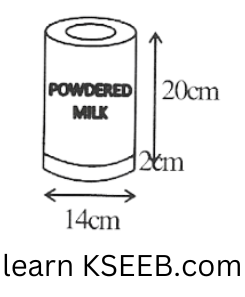
Solution: Height of the label = 20cm – 2cm – 2cm = 16cm

Radius of the label = \(\frac{14}{2}cm\) = 7cm

Label is in the form of a cylinder having its radius and height as 7cm and 16cm.

Area of the label = \(2 \pi(R)(h)\)

=\(2 \times \frac{22}{7} \times 7 \times 16=704 \mathrm{~cm}^2\)

Mensuration Exercise 16.4

1. Given a cylindrical tank, in which situation will you find surface area and in which situation volume.

a)To find how much it can hold.

b)Number of cement bags required to plaster it.

c)To find the number of smaller tanks that can be filled with water from it.

Solution: a) In this situation, we can find the volume.

b)In this siuation, we can find the surface area.

c)In this situation, we can find the volume.

2. Diameter of cylinder A is 7cm and height is 14cm. Diameter of cylinder B is 14cm and height is 7cm without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both cylinders. Check whether the cylinder with greater volume also has greater surface area?

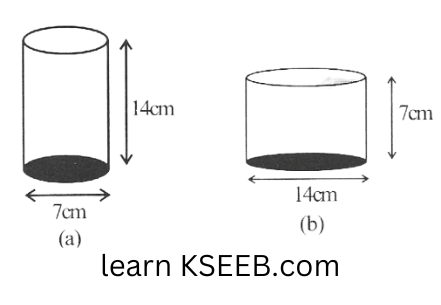
Solution: The heights and diameters of these cylinders A and B are interchanged, w.k.t

Volume of Cylinder = \(\pi r^2 h\)

If measures of r and h are same, then the cylinder with greater radius will have greater area.

Radius of cylinder A = 7/2cm.

Radius of cylinder B = 14/2 = 7cm.

As the radius of cylinder B is greater,

∴ The volume of cylinder B will be greater.

Let us verify it by calculating the volume of both cylinders.

Volume of cylinder

\(\mathrm{A}=\pi r^2 h=\frac{22^{11}}{7} \times \frac{7}{2} \times \frac{7}{2} \times 14 \mathrm{~cm}^3\)

=\(539 \mathrm{~cm}^3\)

Volume of cylinder

\(\mathrm{B}=\pi r^2 h=\frac{22}{7} \times 7 \times 7 \times 7 \mathrm{~cm}^3=1078 \mathrm{~cm}^3\)

Volume of cylinder B is greater

Surface area of cylinder \(\mathrm{A}=2 \pi r(r+h)\)

=\(2 \times \times \frac{22}{\not 7} \times \frac{\not 7}{\not 2}\left(\frac{7}{2}+14\right) \mathrm{cm} 2\)

=\(22\left(\frac{7+28}{2}\right) \mathrm{cm}^2=\frac{22 \times 35}{2}=385 \mathrm{~cm}^2\)

Surface area of cylinder B = \(\mathrm{B}=2 \pi r(r+h)\)

=\(2 \times \frac{22}{7} \times 7 \times(7+7)=44(14)=616 \mathrm{~cm}^2\)

Thus, the surface area of cylinder B is also greater than the surface area of cylinder A.

3. Find the height of a cuboid whose base area is \(180cm^2\) and volume is \(900 cm^3\)?

Solution: Base area of the cuboid = \(lxb = 180cm^2\)

Volume of cuboid = lxbxh = \(900cm^3\)

\(900cm^3 = lxbxh\) \(900cm^3 = 180cm^2 x h\) \(h=\frac{900 \mathrm{~cm}^3}{180 \mathrm{~cm}^2}=5 \mathrm{~cm}\)

Thus, the height of the cuboid is 5cm.

KSEEB Class 8 Maths Chapter 16 Important Questions 

4. A cuboid is of dimensions 60cm x 54cm x 30cm. How many small cubes with sides 6cm can be placed in the given cuboid?

Solution: Volume of cuboid = 60cm x 54cm x 30cm

= \(97200cm^3\)

Side of the cube = 6cm

Volume of the cube = \(63cm^3 = 216cm^3\)

Required number of cubes

=\(\frac{\text { Volume of the cuboid }}{\text { Volume of the cube }}\)

=\(\frac{97200}{216}=450\)

Thus, 450 cubes can be placed in the given cuboid.

5. Find the height of the cylinder whose volume is \(1.54m^3\) and diameter of the base is 140cm?

Solution: Diameter of the base = 140cm

Radius (r) of the base = \( \left(\frac{140}{2}\right) \mathrm{cm}=70 \mathrm{~cm}\)

=\( \frac{70}{100} \mathrm{~m}\)

Volume of cylinder = \( \pi r^2 h\)

\( \mathrm{h}=\frac{1.54 \times 100}{22 \times 7}=1 \mathrm{~m}\)

Thus, the height of the cylinder is lm.

6. A milk tank is in the form of cylinder whose radius is 1.5m and length is 7m. Find the quantity of milk in litres that can be stored in the tank?

Solution: Radius of cylinder = 1.5m

volume of cylinder = \(\pi r^2 h\)

=\(\frac{22}{7} \times 1.5 \times 1.5 \times 7\)

=\(49.5 \mathrm{~m}^3\)

\(1 \mathrm{~m}^3=10000 \mathrm{~L}\)

Required quantity = 49.5 x 1000 = 49500L
∴ 49500L of milk can be stored in the tank.

7. If each edge of a cube is doubled.

1)how many times will its surface area increase?

2)how many times will its volume increase?

Solution: Let initially the edge of the cube be l

if initial surface area = \(6 \ell^2\)

If each edge of the cube is doubled, then it becomes 2l

New surface area = \(6(2 \ell)^2=24 \ell^2=4 \times 6 \ell^2\)

Clearly, the surface area will be increased by 4 times.

2) initial volume of the cube = \(\ell^3\)

when each edge of the cube is doubled, it becomes 2l.

New volume = \((2 \ell)^3=8 \ell^3=8 \times \ell^3\)

Clearly, the volume of the cube will be increased by 8 times.

8. Water is pouring into a cuboidal reservoir at the rate of 60 litres per minute, if the volume of reservoir is \(108m^3\), find the number of hours it will take to fill the reservoir.

Solution: Volume of cuboidal reservoir

= \(108m^3 = (108 x 1000)L= 108000L\)

It is given that water is being poured at the rate of 60L per minute.

i.e., (60 x 60)L = 3600L per hour

Required number of hours = \(\frac{108000}{3600}\) = 30hours.

Thus, it will take 30 hours to fill the reservoir.

Mensuration Additional Problems

1. Find the altitude of a trapezium, the sum ofo the lengths of whose bases is 6cm and area is \(5.25cm^2\)

Solution: Let the altitude of the trapezium be h cm

w.k.T area of the trapezium =\(5.25cm^2\)

\(5.25=\frac{1}{2} \times(\text { sum of the base }) \times \text { altitude }\)

⇒ \(\frac{1}{2} \times 6 \times h=5.25\)

\(h=\frac{5.25 \times 2}{6}=1.75 \mathrm{~cm}\)

2. Find the sum of the length of the base of a trapezium whose altitude is 4cm and area is \(28cm^2\).

Solution: Given: altitude of the trapezium = 4cm

Area of trapezium = \(28cm^2\)

\(\frac{1}{2} \times(\text { sum of the base }) \times \text { altitude }=28 \mathrm{~cm}^2\) \(\frac{1}{2} \times(\text { sum of the base }) \times 4=28\)

sum of the base = \(\frac{28 \times 2}{4}=14 \mathrm{~cm}\)

3. The edges of a cuboid are in the ratio 1:2:3 and its volume is \(1296cm^3\). Find its length, breadth, and height.

Solution: Let length = xcm

breadth = 2xcm

and height = 3xcm

then volume = \((1 x \times 2 x \times 3 x)=\mathrm{cm}^3\)

= \(6 x^3 \mathrm{~cm}^3\)

\(1296=6 x^3\left(V=1296 \mathrm{~cm}^3\right)\)

or \(x^3=\frac{1296}{6}=216\)

\(x^3=216\) \(x=\sqrt[3]{216}=6\)

Hence, height = 3x = 3 x 6 = 18cm
breadth = 2x = 2 x 6 = 12cm
and length = 1x = 1 x 6 = 6cm.

4. Find the length of the longest pole that can be put in a room of dimensions 10m by 10m by 5m.

Solution: Here l=10m, b=10m, and h=5m.

length of the longest pole = length of the diagonal

=\(\sqrt{\ell^2+b^2+h^2} \text { units }\)

=\(\sqrt{(10)^2+(10)^2+5^2}\)

=\(\sqrt{225}=15 \mathrm{~m}\)

5. Find the volume of the wood used to make a closed box of outer dimensions 60cm x 45cm x 32cm thickness of wood being 2.5cm all around.

Solution: External dimensions are length = 60cm

breadth = 45cm

and height = 32cm

∴ External volume = \((60 x 45 x 32) cm^3\)

= \(86400cm^3\)

Internal dimensions are

length = {60-(2.5 x 2)}cm = 60-5= 55cm

breadth = {45-(2.5 x 2)}= 45-5 = 40cm

height = 32-(2.5 x 2) = 27cm

Internal volume = \((55 x 40 x 27)cm^3 = 59400cm^3\)

Volume of wood used to make the box

= (External Volume)-(Internal Volume)

= \((86400-59400)cm^3 = 27000cm^3 \)

6. A right circular cylinder has a height of 1m and a radius of 35cm. Find its volume.

Solution: h=1m, r=35cm ⇒ \(\frac{35}{100} \mathrm{~m}=0.35 \mathrm{~m}\)

∴ Volume = \(\pi r^2 h=\frac{22}{7} \times 0.35 \times 0.35 \times 1\)

= \(0.385m^3\)

Detailed Solutions For Mensuration KSEEB Class 8 

7. Find the volume of cylinder, circumference of whose base is 110cm and height = 20cm.

Solution: Let radius of the base of the right circular cylinder be r cm,

then circumference = 110cm

\(2 \pi r=110 \mathrm{~cm}\) \(r=\frac{110}{2 \pi}=\frac{110 \times 7}{2 \times 22}=\frac{35}{2} \mathrm{~cm}\)

so, the radius of the cylinder is 35/2cm

Thus, the volume of the cylinder

=\(\frac{22}{7} \times \frac{35}{2} \times \frac{35}{2} \times 20 \mathrm{~cm}^3\)

=\(19250 \mathrm{~cm}^3\)

8. The volume of a circular pipe of length 1metre is \(3850cm^3\). Find its diameter.

Solution: Let the radius of the cylinder be r cm,

Then, volume of the cylinder = \(\pi r^2 h \mathrm{~cm}^3\)

⇒ \(3850=\frac{22}{7} \times r^2 \times 100(\text { as } \mathrm{h}=1 \mathrm{~m}=100 \mathrm{~cm})\)

⇒ \(r^2=\frac{3850 \times 7}{22 \times 100}=\frac{49}{4}\)

or \(r=\frac{7}{2}=3.5 \mathrm{~cm}\)

Diameter = 2r = 2 x 3.5cm = 7cm

Thus, the diameter of the cylinder = 7cm.

9. A metallic pipe whose internal and external diameters are 6cm and 8cm has a length of 2.1cm. Find the volume of the metal.

Solution: Outer diameter = 8cm

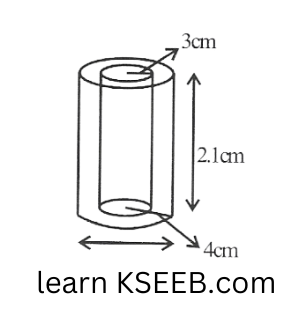
Outer volume = \(\pi R^2 h=\frac{22}{7} \times 4 \times 4 \times 2.1\)

=\(\frac{22}{7} \times 16 \times 2.1 \mathrm{~cm}^3\)

=\(105.6 \mathrm{~cm} 3\)

Inner diameter = 6cm

Inner radius = 3cm

Inner volume

=\(\frac{22}{7} \times(3)^2 \times 2.1=\frac{22}{7} \times 3 \times 3 \times 2.1\)

=\(59.4 \mathrm{~cm}^3\)

∴ volume of metal = outer volume – Inner volume

= 105.63-59.4

= \(46.2cm^3\)

10. The dimensions of a cube are doubled. By how many times will its surface area increase?

Solution: Let the side of the original cube a units then side of the new cube be 2a units.

\(\mathrm{S}_1=\text { surface area of original cube }=6 a^2\) \(\mathrm{S}_2=\text { surface area of new cube }=6(2 a)^2\)

=\(6 \times 4 a^2=24 a^2\)

∴ \(S_1: S_2=6 a^2: 24 a^2 \Rightarrow S_1: S_2=1: 4\)

∴ Surface area increases 4 times.

11. Find the total surface area of a chalk box whose length, breadth and height are 16cm, 8cm and 6cm respectively.

Solution: Here l = 16cm, b=8cm and h=6cm

Total surface area of the chalk box

=\(2(l b+b h+l h) \mathrm{cm}^2\)

=\(2(16 \times 8+8 \times 6+16 \times 6) \mathrm{cm}^2\)

=\(2(128+48+96) \mathrm{cm}^2\)

=\(2 \times 272=\mathrm{cm}^2\)

TSA of chalk box = \(544cm^2\)

12. Find the radius of the base of a right circular cylinder whose curved surface area is \(352cm^2\) and height is 16cm.

Solution: Let r be the radius of the base of the cylinder

we are given that h = 16cm and curved surface area = \(2 \pi r h=352 \mathrm{~cm}^2\)

=\(2 \times \frac{22}{7} \times r \times 16=352\)

\(r=\frac{352 \times 7}{2 \times 22 \times 16}=3.5\)

Thus, the radius of the base is 3.5cm.

13. What is the ratio of their heights if two cylinder of same voume have their radii in the ratio 1:6?

Solution: Equating the volume of 2 cylinders.

\(\pi r^2 h=\pi(6 r)^2 \times h_1\) \(h_1=\frac{\pi r^2 h}{\pi \times 36 r^2}=\frac{h}{h_1}=\frac{36}{1}\)

Hence, the ratio of their height = 36:1

14. What is the height of cylinder if the radius of a cylinder is tripled but its curved surface area is unchanged?

Solution: Let the height of new cylinder be \(\mathrm{h}_1\).

According to question

CSA of old cylinder = CSA of new cylinder

\(2 \pi r h=2 \times \pi \times 3 r \times h_1 \Rightarrow h_1=\frac{h}{3}\)

Means height will become 1/3rd of the old cylinder.

Practice Problems For KSEEB Class 8 Mensuration 

15. The area of a trapezium is \(150cm^2\) and its height is 12cm. If one of the parallel side is two third the other side, find the two parallel sides.

Solution: Area of trapezium = \(150cm^2\)

Height = 12cm

Let two parallel sides be x and \(\frac{2 x}{3}\)

Area of trapezium

= \(\frac{1}{2} \times \text { sum of parallel sides } \times \text { height }\)

\(150=\frac{1}{2}\left(x+\frac{2}{3} x\right) \times 12\) \(150 \times 2=\frac{3 x+2 x}{3} \times 12\) \(300=\frac{5 x}{3} \times 12\)

⇒ 300 = 20x

⇒ \(x=\frac{300}{20} \Rightarrow x=15 \mathrm{~cm}\)

∴ The parallel sides are 15cm and \(\frac{2}{3} \times 15=10 \mathrm{~cm}\)

16. Three cubes each of side 10cm are joined end to end. Find the surface area of the resultant figure.

Solution: Side of cube = 10cm

When 3 cubes are joined then the cuboid will form

Now l = 10 + 10 + 10 =30cm, b= 10cm, h= 10cm.

Total surface area of cuboid = 2 (lb + bh + lh)

= 2(30×10 + 10×10 + 10×30)

= 2(300 + 100 + 300)

=\(1400cm^2\)

17.Metallic discs of radius 0.75cm and thickness 0.2cm are melted to obtain \(508.68cm^3\) of metal. Find the number of discs melted (use π = 3.14).

Solution: Let the number of discs melted be n

Given n (volume of a disc) = volume of metal

\(n\left(\pi r^2 h\right)=508.68\) \(n\left(3.14 \times(0.75)^2 \times 0.2\right)=508.68\) \(n=\frac{508.68}{3.14 \times 0.2 \times 0.5625}=1440 \text { discs. }\)

18. A cube of side 5cm is cut into as many 1cm cubes as possible. What is the ratio of the surface area of the original cube to that of the sum of the surface areas of the smaller cubes?

Solution: Edge of original cube = 5 cm

Edge of small cubes = 1 cm

Surface area of othe original cube

=\(6 a^2=6 \times 5^2=6 \times 25=150 \mathrm{~cm}^2\)

Now number of small cubes

=\(\frac{\text { Volume of original cube }}{\text { Volume of small cube }}\)

=\(\frac{5 \times 5 \times 5}{1 \times 1 \times 1}=125\)

Surface area of a cube = \(6 a^2=6(1)^2=6 \mathrm{~cm}^2\)

∴ Surface area of 125 small cubes = \(6 x 125 = 750cm^2\)

Now,

\(\frac{\text { Surface area of original cube }}{\text { Sum of the surface area }}=\frac{150}{750}=1: 5 of smaller cubes\)

19. Four times the area of the curved surface of a cylinder is equal to 6 times the sum of the areas of its bases. If its height is 12cm, find its curved surface area.

Solution: According to equation

4 x C.S.A. of cylinder = 6 x sum of area of its bases

\(4 \times 2 \pi r h=6\left(2 \pi r^2\right)\)

4 x h = 6r

4 x 12 = 6r

\(r=\frac{12}{6} \times 4=8 \mathrm{~cm}\)

Now the CSA of cylinder

=\(2 \pi r h=2 \times \frac{22}{7} \times 8 \times 12\)

=\(603.428 \mathrm{~cm}^2\)

20. The circumference of the front wheel of a cart is 3m long and that of the back wheel is 4m long. What is the distance travelled by the cart, when the front wheel makes five more revolutions than the rear wheel?

Solution: Front wheels circumference = 3m

back wheel circumference = 4m

Let the revolution made by back wheel be x

The revolution made by front-wheel =x +5

Now the distance covered by front wheel

= distance covered by back wheel

⇒ 3(x + 5) = 4(x)

⇒ 3x +15 = 4x

⇒ 15 = 4x — 3x

⇒ 15 = x

Distance travelled by the cart = Number of revolution x circumference of back wheel

= 75 x 4 = 60m.

21. From a pipe of inner radius 0.75cm, water flows at the rate of 7m per second. Find the volume in litres of water delivered by the pipe in 1 hr.

Solution: Radius of pipe = 0.75cm = 0.0075m

The rate of water flow – 1m/s.

∴ length of water in 1 sec = 7m

∴ volume of water flow in 1 hour

=\(60 \times 60 \times \frac{22}{7} \times 0.0075 \times 0.0075 \times 7\)

=\(3600 \times 3.14 \times 0.0005625 \times 7\)

=\(79128 \times 0.00005625\)

=\(4.45095 \mathrm{~m}^3\)

=(∵\(1000cm^3=1L\))

\(4450000 \mathrm{~cm}^3=4450 \ell\)

22. Find the length of the longest pole that can be put in a room of dimensions 10m by 10m by 5m.

Solution: Here l=10m, b=10m & h=5m

length of the longest pole = length of the diagonal

=\(\sqrt{\ell^2+b^2+h^2} \text { units }\)

=\(\sqrt{10^2+(10)^2+5^2} \mathrm{~m}\)

=\(\sqrt{225 m}=15 m\)

23. The ratio between the curved surface area and the total surface area of ‘a right circular cylinder is 1 : 2. Find the ratio between the height and radius of the cylinder.

Solution: Curved surface area of a cylinder = \(2 \pi r h\)

Total surface area of a cylinder = \(2 \pi r(r+h)\)

The ratio between the curved surface area and the total surface area of a cylinder is 1 :2.

∴ \(\frac{1}{2}=\frac{2 \pi r h}{2 \pi r(r+h)}\)

\(\frac{1}{2}=\frac{h}{(r+h)}\)

⇒ 2h = r + h

⇒ 2h – h= r

⇒ h = r

∴ Ratio of height and radius = 1:1.

24. A swimming pool is 200m x 50m and has an average depth of 2m. By the end of a summer day, the water level drops by 2cm. How many cubic meters of water is lost on the day?

Solution: Dimensions of swimming pool are 200m x 50m

Average depth of the swimming pool = 2m

At the end of summer day the water level drops by 2 cm.

∴ Volume of water in swimming pool

= l x b x depth

= \(200 x 50 x 2 = 20000m^3\)

If water level drops by 2cm, it means new level of water = \(\left(2-\frac{2}{100}\right) m=1.98 m\)

volume of water after summer day = \(200 \times 50 \times 1.98=19800 \mathrm{~m}^3\)

so, water in cubic metres was lost on that day.

Initial volume-volume after summer day

=\(20000-19800=200 \mathrm{~m}^3\)

25. An iron pipe is 21cm long and its external diameter is 8cm, If the thickness of the pipe is 1cm and iron weighs \(8g/cm^3\), find the weight of the pipe.

Solution: External radius of the pipe = 4cm

Thickness of the pipe = 1cm

Internal radius of the pipe = (4 – l)cm = 3 cm

External volume = \(\left(\frac{22}{7} \times 4 \times 4 \times 21\right) \mathrm{cm}^3\)

= \(1056cm^3\)

Internal volume = \(\left(\frac{22}{7} \times 3 \times 3 \times 21\right) \mathrm{cm}^3\)

= \(594cm^3\)

Volume of the metal = (external volume)-(Internal volume)

= \((1056-594) \mathrm{cm}^3=462 \mathrm{~cm}^3\)

weight of the pipe = \((462 \times 8) \mathrm{g}=\left(\frac{462 \times 8}{1000}\right) \mathrm{kg}\)

= 3.696kg.