Class 8 Maths

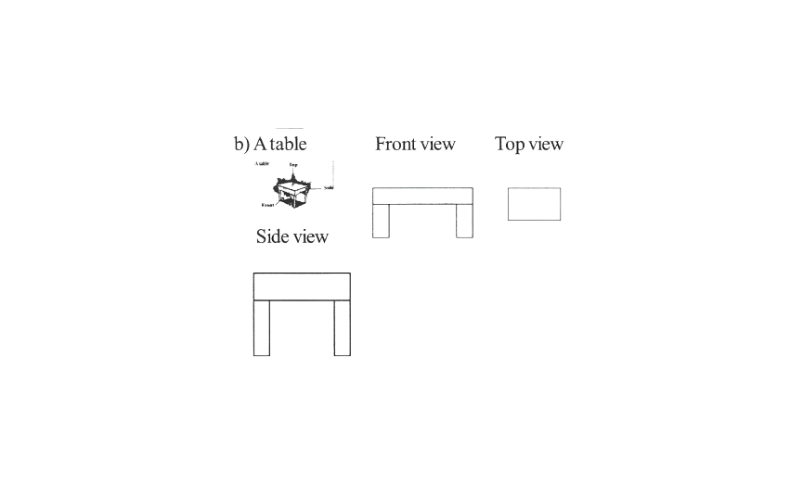
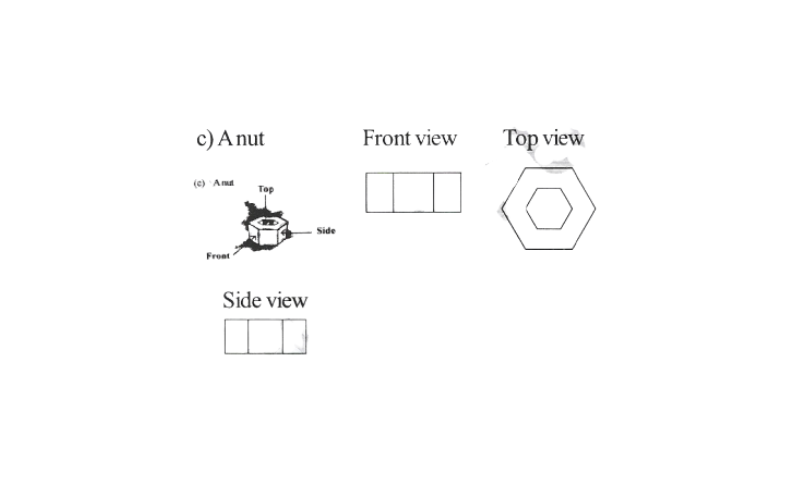
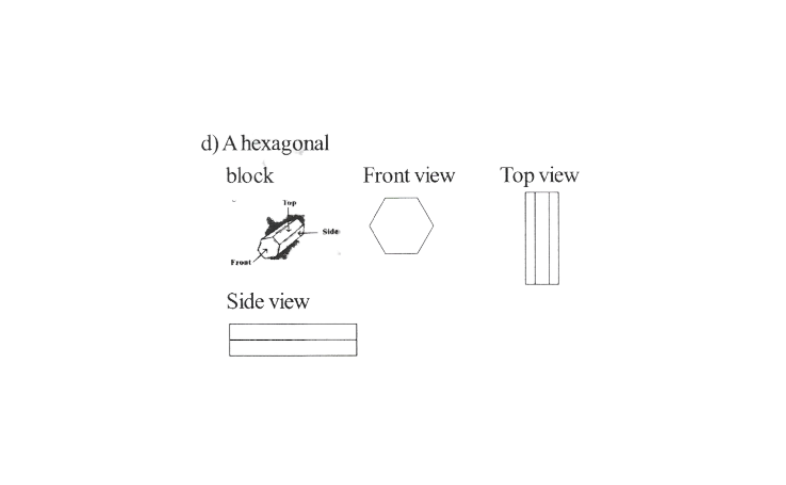
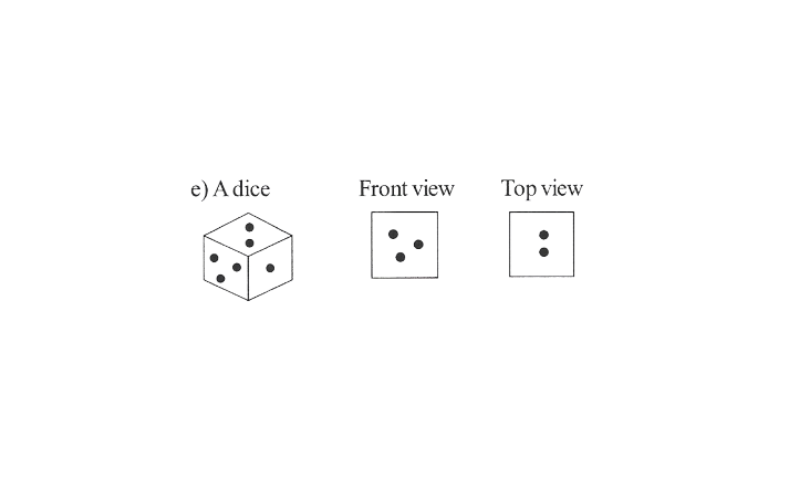
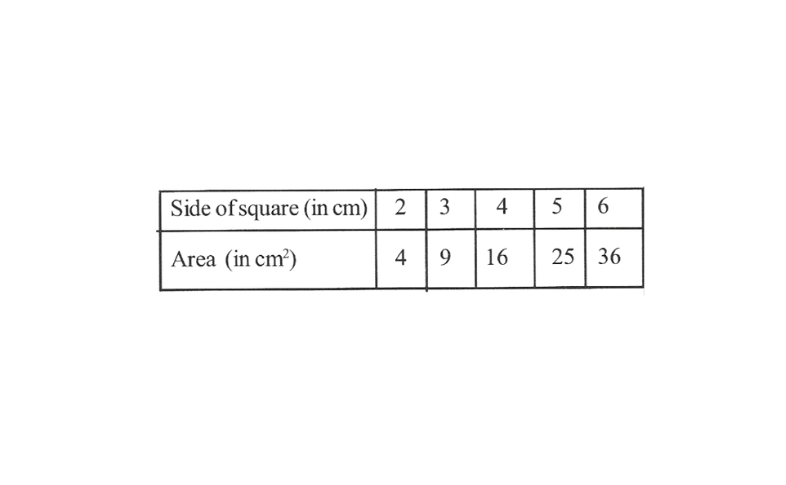
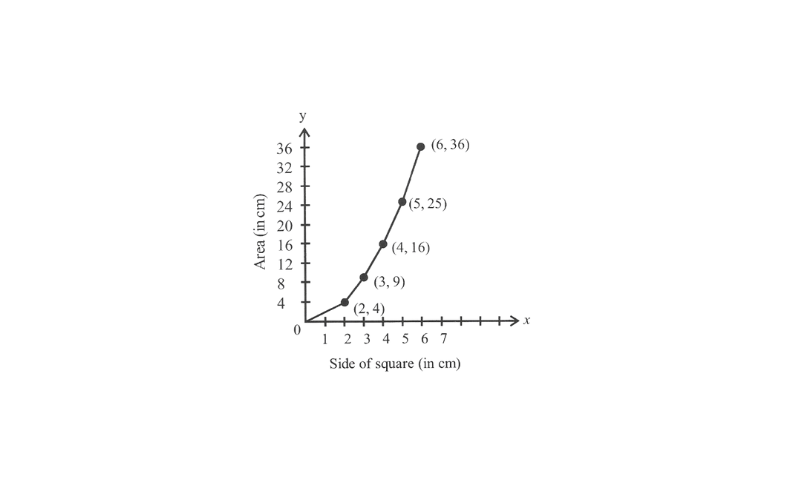
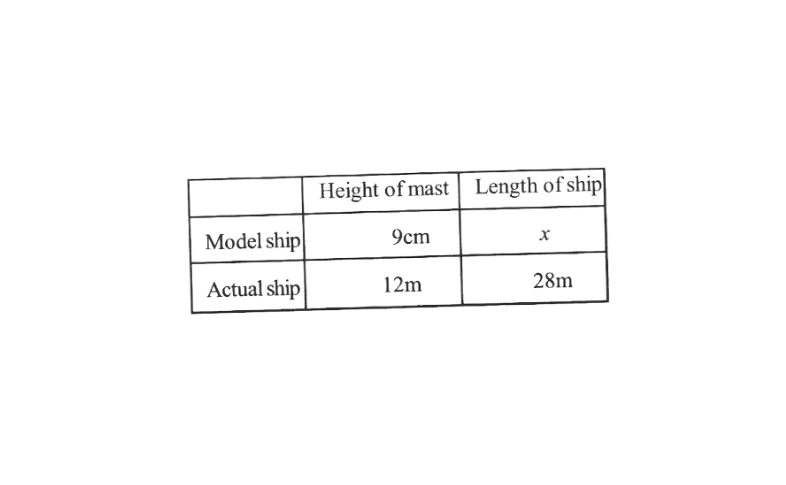
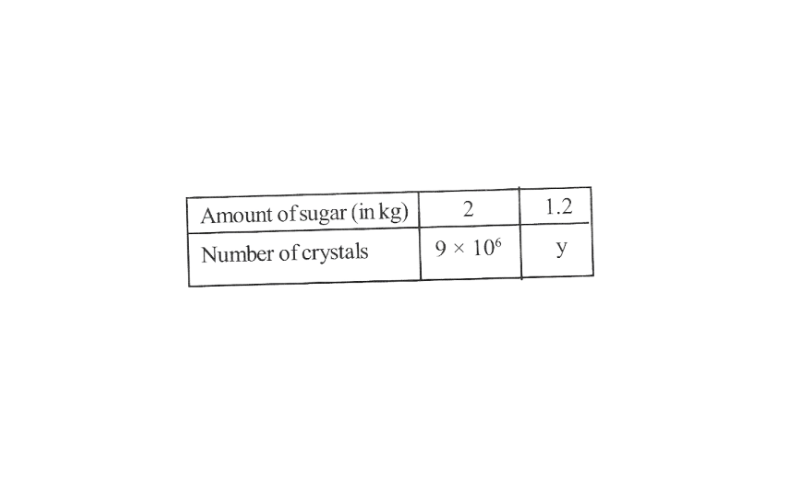
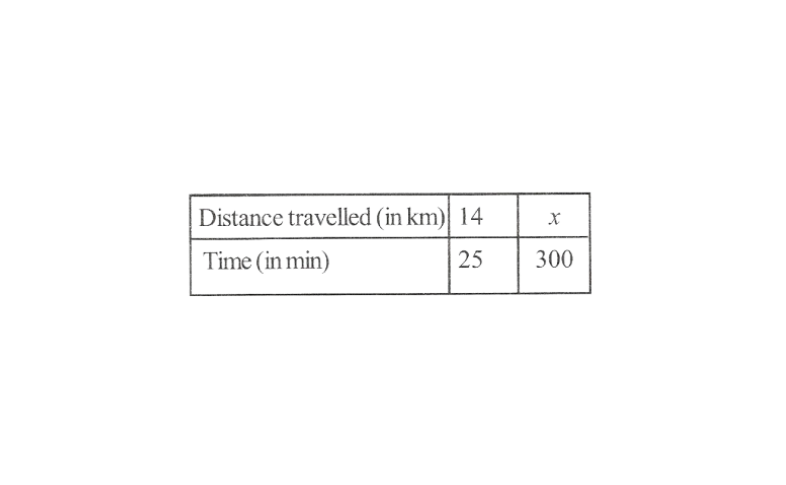
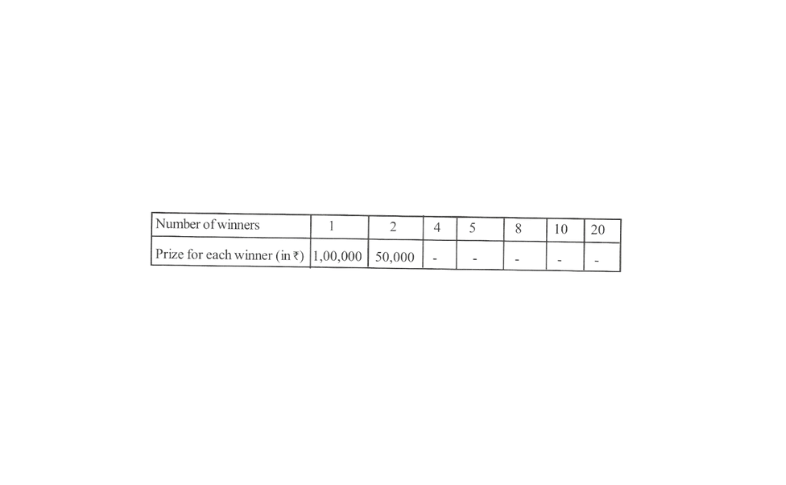
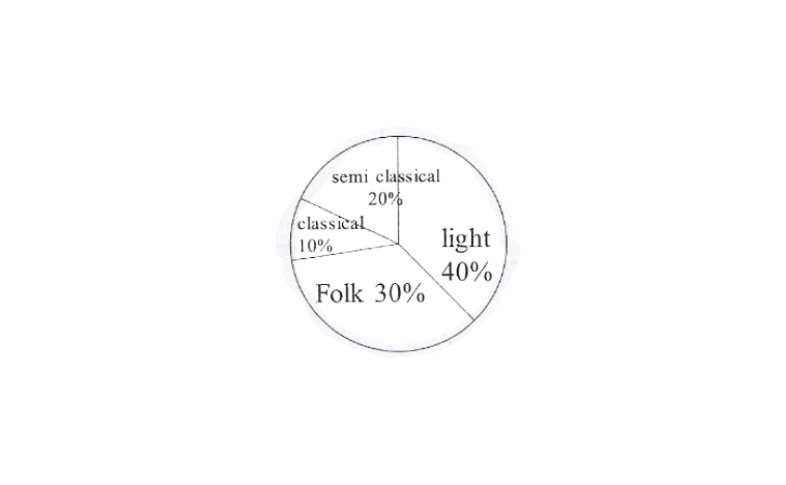
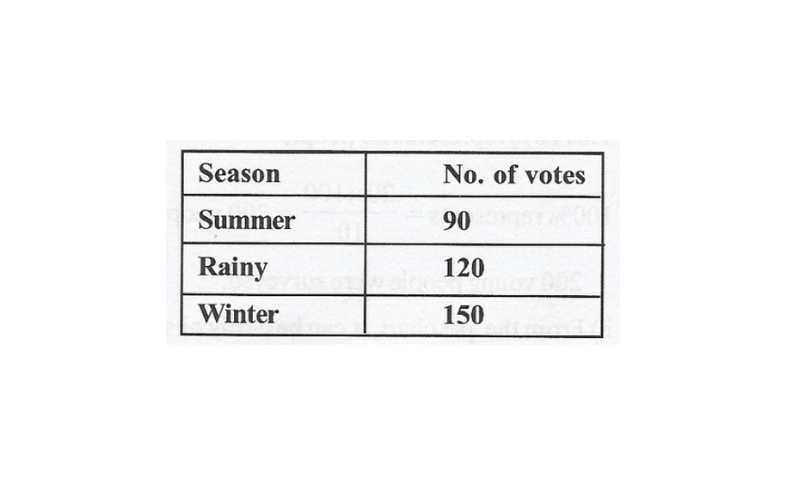
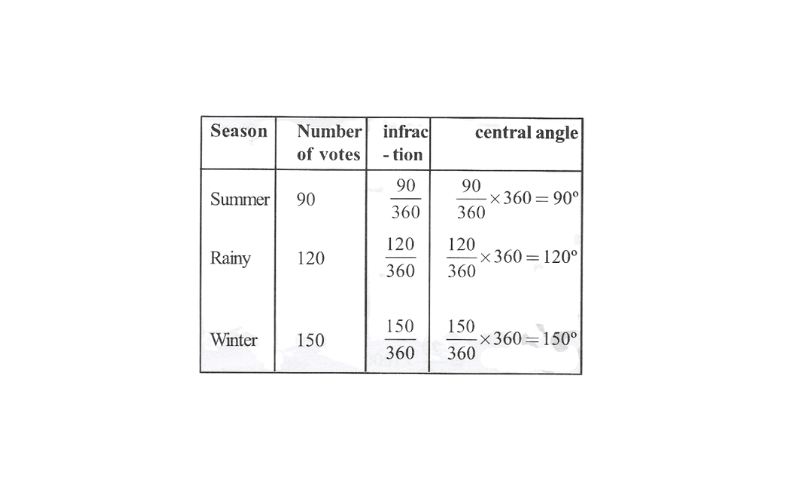
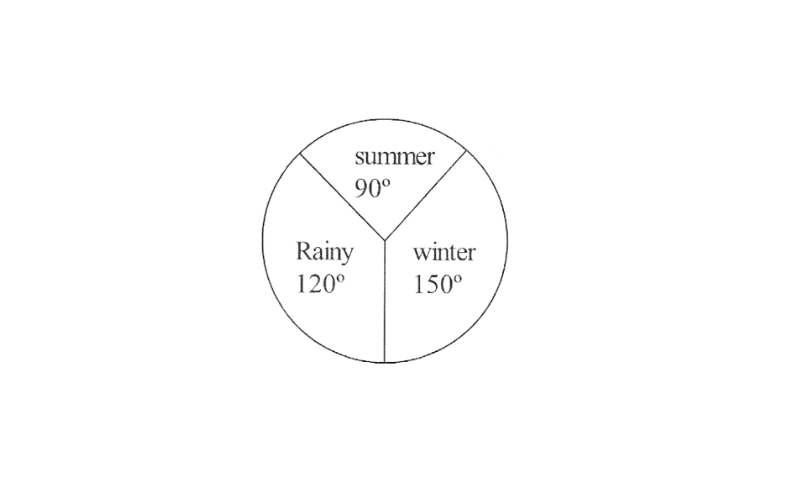
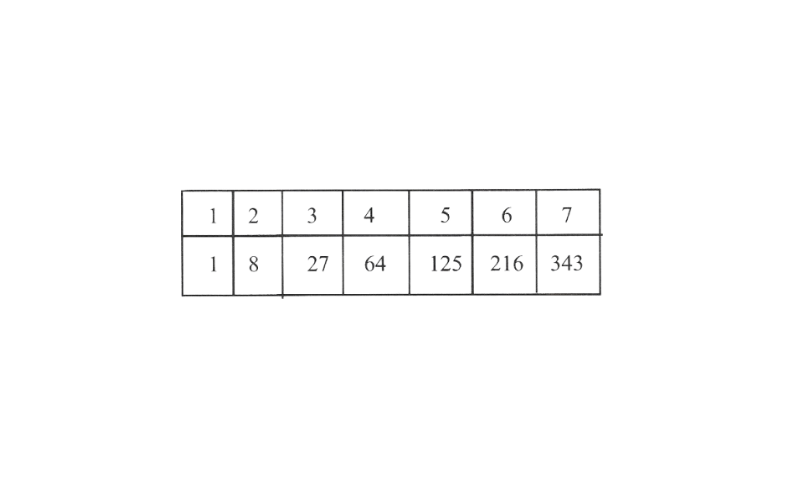
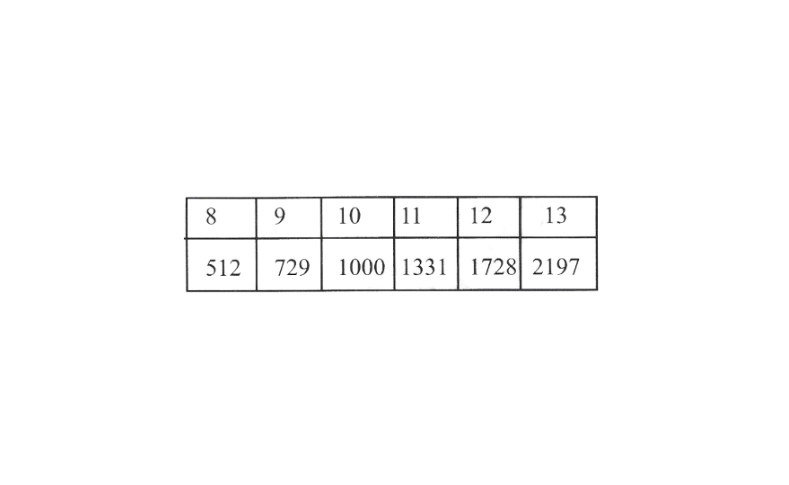
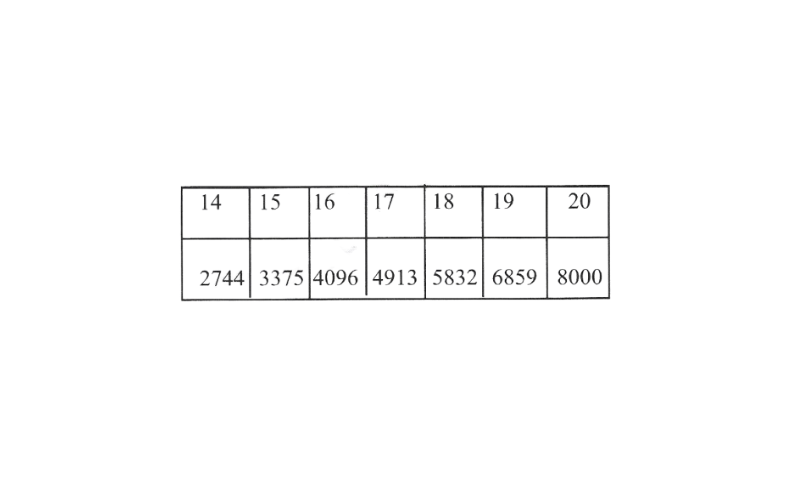
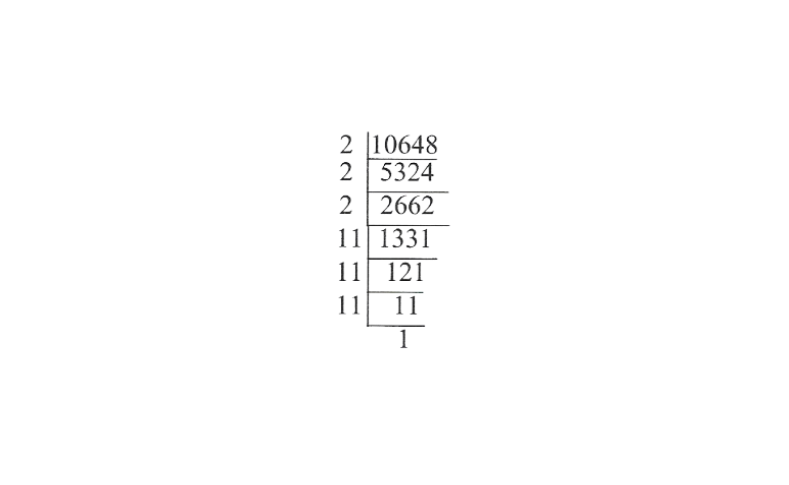
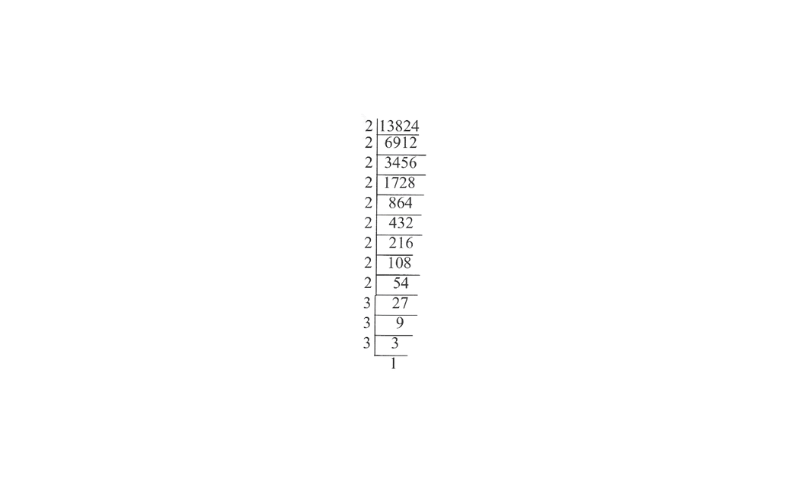
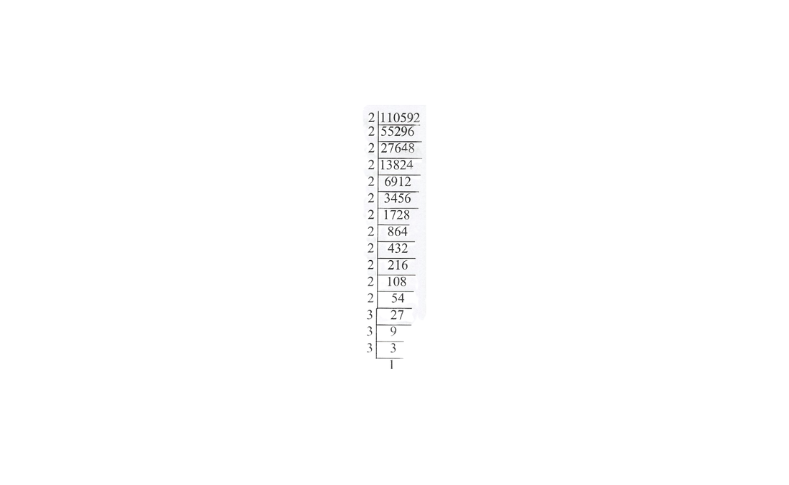
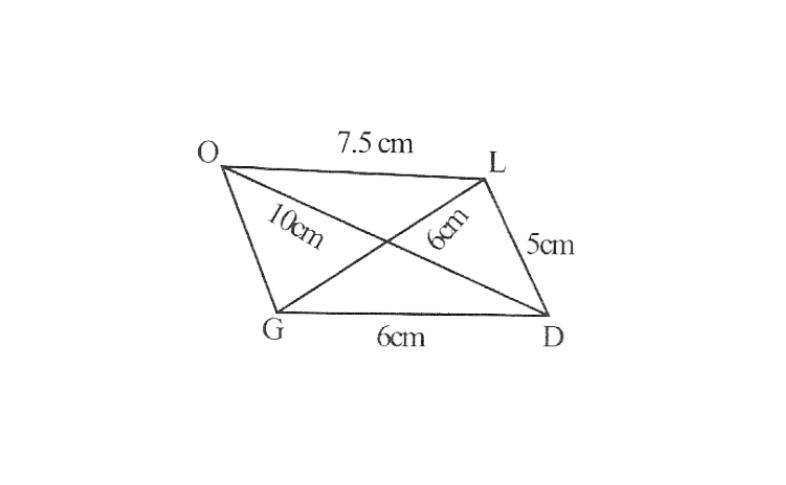
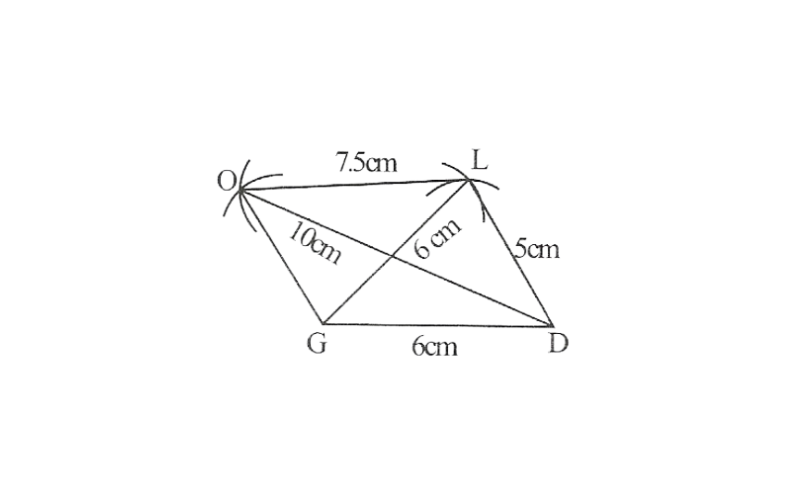
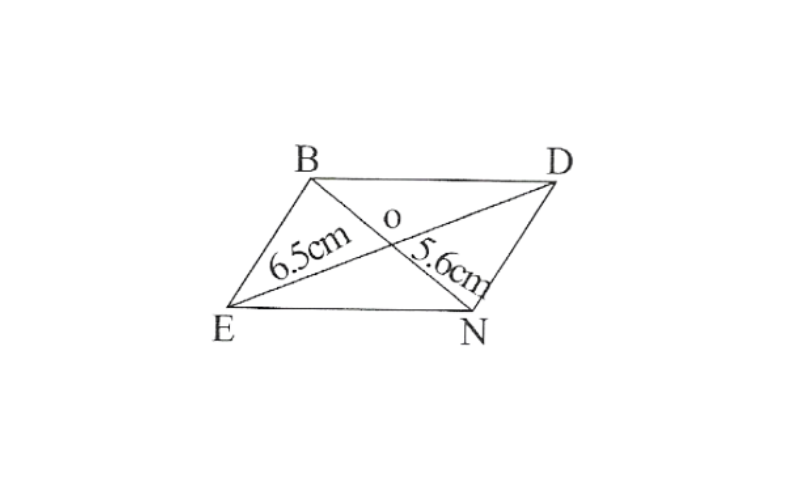
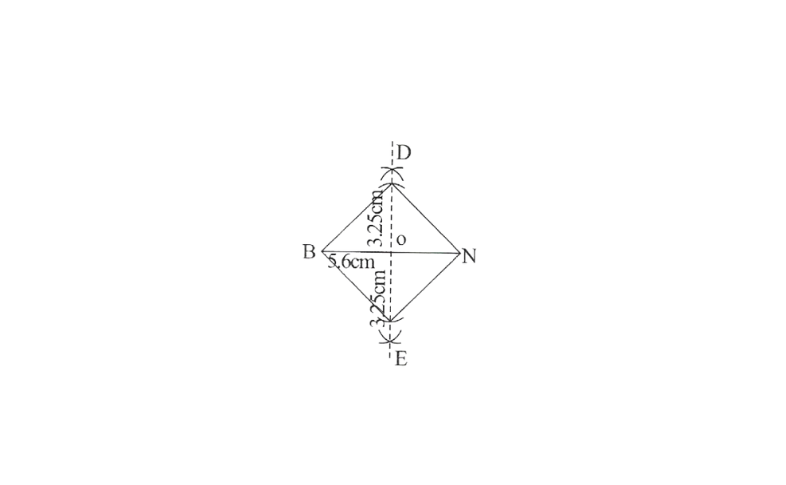
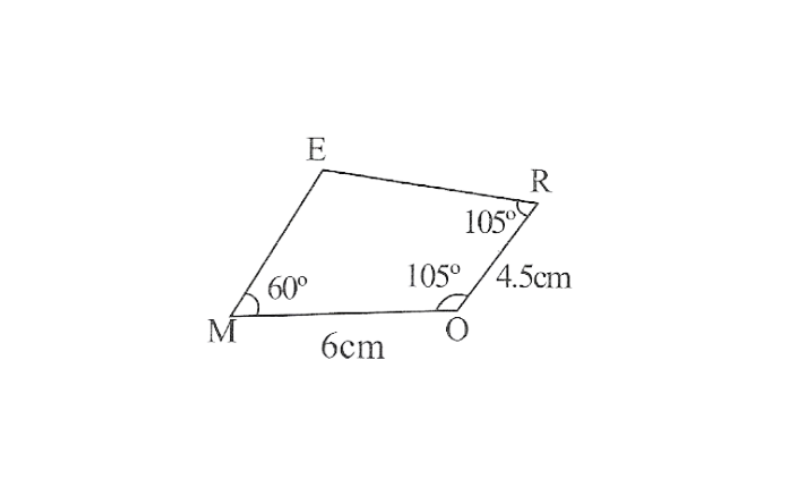
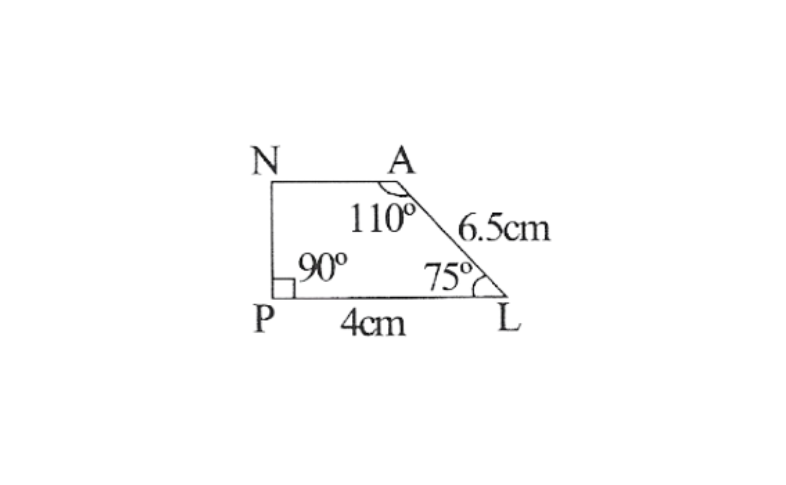
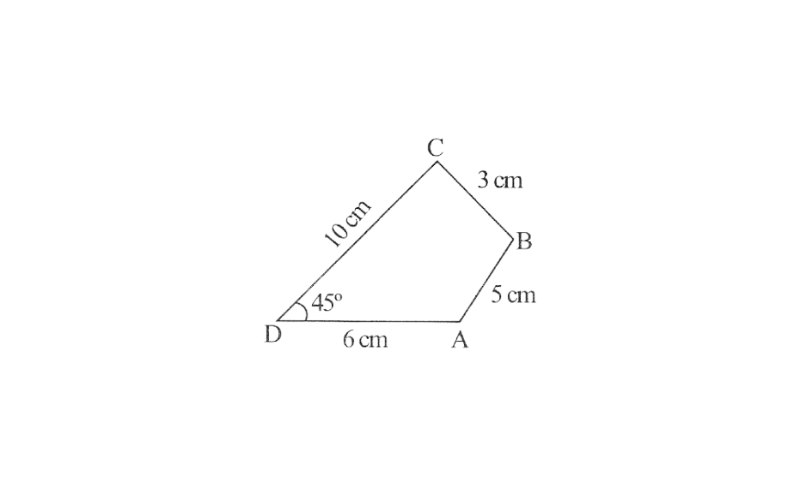
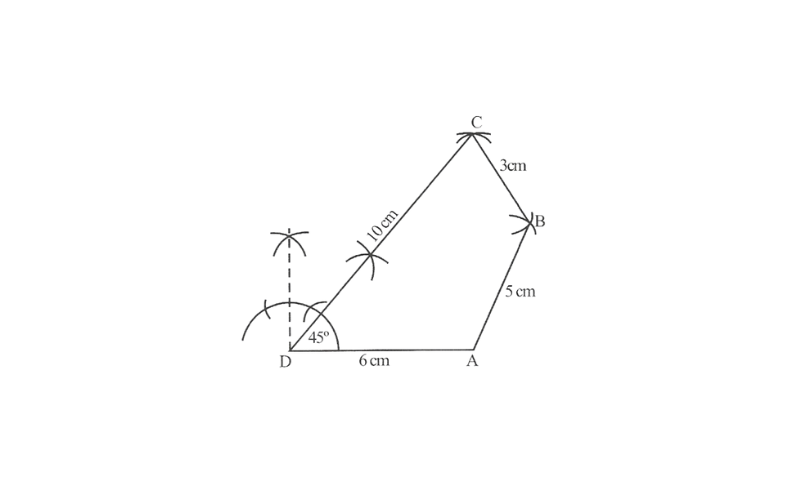
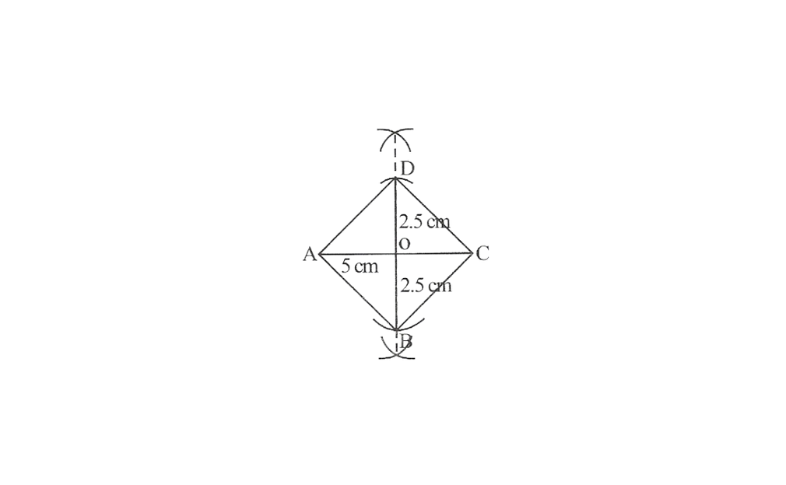
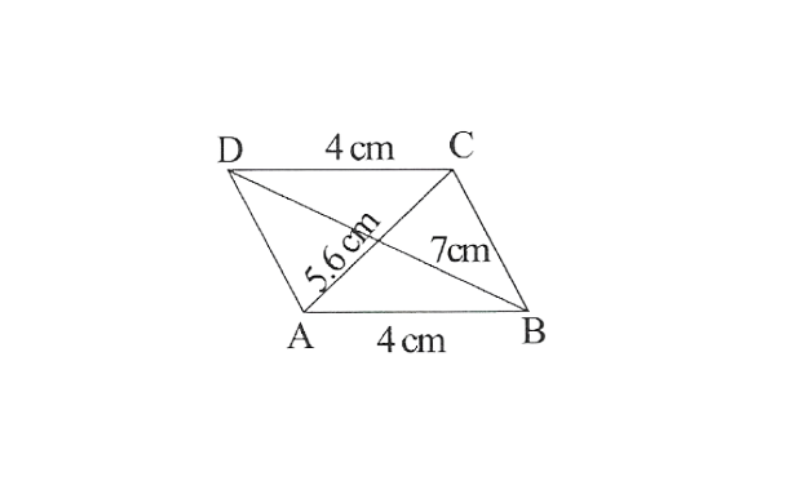
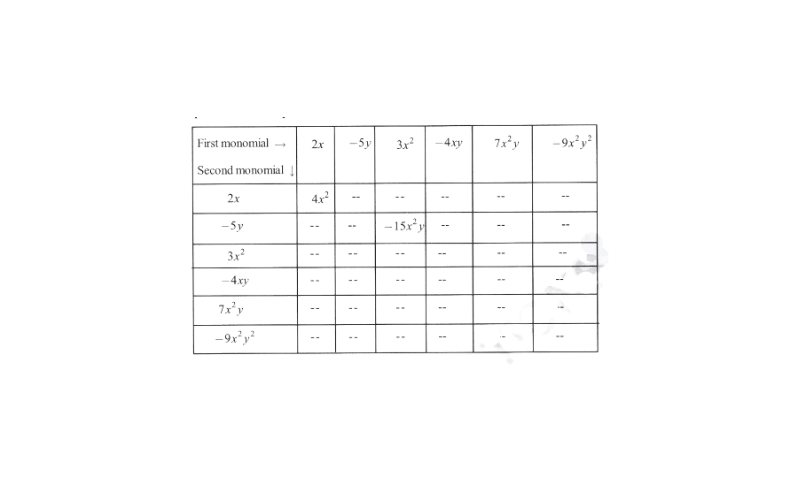
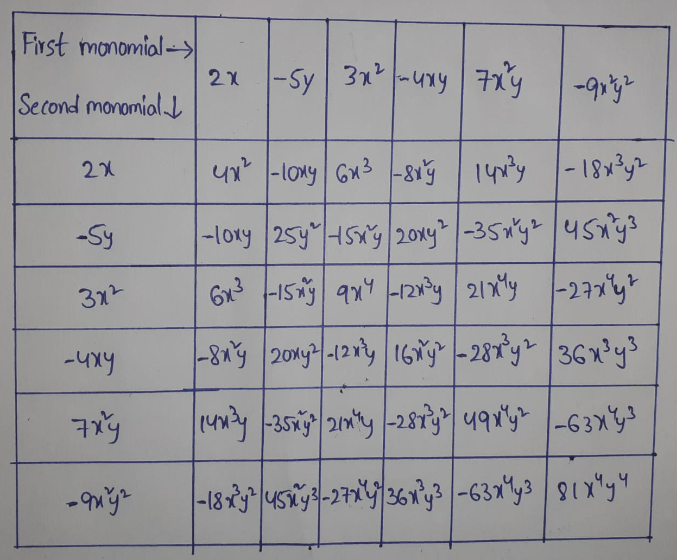
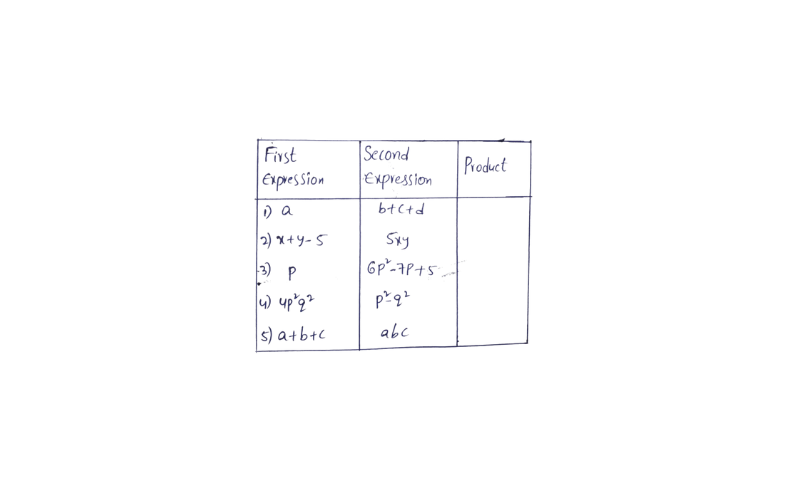
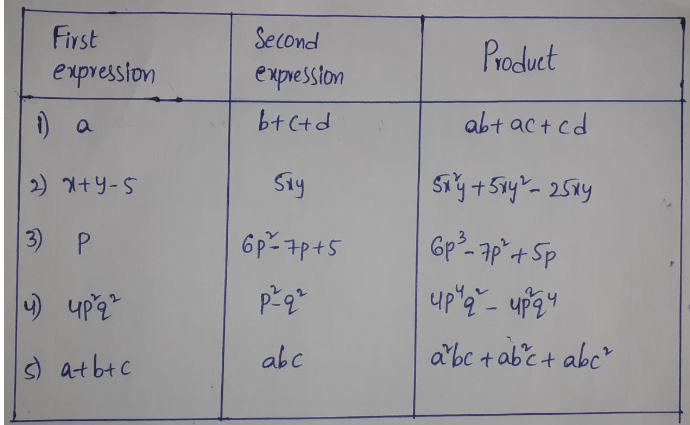
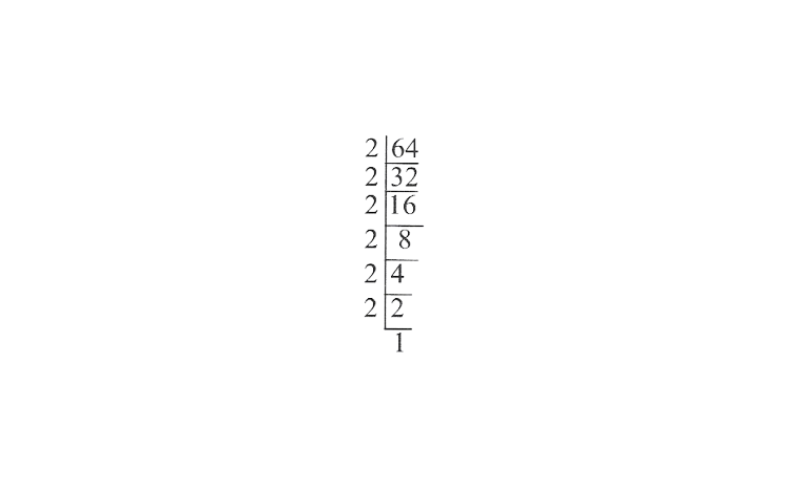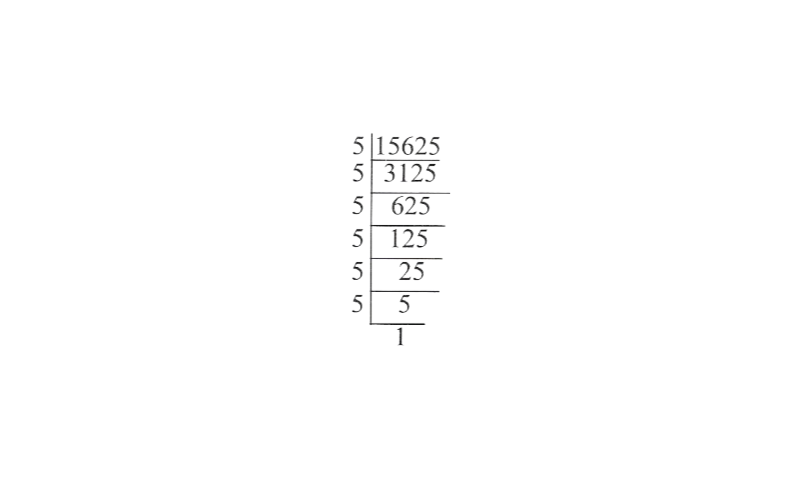KSEEB Class 8 Maths Solutions For Chapter 13 Factorisation Points To Remember

When we factorize an expression, we write it as a product of factors. These factors may be numbers, algebraic variables, or algebraic expressions.

An irreducible factor is a factor that cannot be expressed further as a product of factors.

A systematic way of factorizing an expression is the common factor method. It consists of three steps:

1) Write each term of the expression as a product of irreducible factors.
2) Look for and separate the common factors and
3) Combine the remaining factors in each term in accordance with the distributive law.

Sometimes, all terms in a given expression do not have a common factor, but the terms can be grouped in such a way that all the terms in each group have a common factor across all the groups leading to the required factorization of the expression.

This is the method of regrouping

In factorisation by regrouping, we should remember that any regrouping (i.e., rearrangement) of the terms in the given expression may not lead to factorisation. We must observe the expression and come out with the desired regrouping by trail and error.

KSEEB Class 8 Maths Chapter 13 Factorisation Solutions

A number of expressions to be factorised are of the form or can be put into the form: \(a^2+2 a b+b^2, a^2-2 a b+b^2, a^2-b^2 \text { and }\)\(x^2+(a+b)+a b\).

These expressions can be easily factorised using identities 1,2,3&4

⇒ \(a^2+2 a b+b^2=(a+b)^2\)

⇒ \(a^2-2 a b+b^2=(a-b)^2\)

⇒ \(a^2-b^2=(a+b)(a-b)\)

⇒ \(x^2+(a+b) x+a b=(x+a)(x+b)\)

In expressions which have factors of the type (x+a)(x+b) remember the numerical term gives ab. Its factors a and b should be so chosen that their sum, with signs taken care of, is the coefficient of x.

We know that in the case of numbers, division is the inverse of multiplication. This idea is applicable also to the division of algebraic expressions.

In the case of division of a polynomial by a monomial we may carry out the division either by dividing each term of the polynomial by the monomial or by the common factor method.

In the case of division of a polynomial by a polynomial. We cannot proceed by dividing each term in the dividend polynomial by the divisor polynomial. Instead, we factorise both the polynomials and cancel their common factors.

In the case of divisions of algebraic expressions that we studied in this chapter, we have

Dividend = Divisor x Quotient

In general, however, the relation is

Dividend = Divisor x Quotient + Remainder

Thus, we have considered in the present chapter only those divisions in which the remainder is zero.

There are many errors students commonly make when solving algebra exercises. One should avoid making such errors.

Factorisation Solutions KSEEB Class 8 Maths Exercise 13.1

1. Find the common factors of the given terms.

1) 12x, 36

Solution: 12x = 2 x 2 x 3 x x

36 = 2 x 2 x 3 x 3

The common factors are 2,2,3

i.e., 2 x 2 x 3 = 12

2) 2y, 22xy

Solution: 2y = 2 x y

22xy = 2 x 11 x x x y

The C.F. are 2y

KSEEB Solutions Class 8 Maths Factorisation Exercises

3) \(14 p q, 28 p^2 q^2\)

Solution: 14pq = 2 x 7 x p q

The C.F. are = 2 x 7 x p x q

= 14pq

KSEEB Class 8 Maths Solutions For Chapter 13 Factorisation 

4) \(2 x, 3 x^2, 4\)

Solution: 2x = 2 x x

⇒ \(3 x^2=3 \times x \times x\)

4 = 2 x 2

∴ C.F. are = 1

5) \( 6 a b c, 24 a b^2, 12 a^2 b\)

Solution: 6abc = 2 x 3 x a x b x c

⇒ \( 24 a b^2=2 \times 2 \times 2 \times 3 \times a \times b \times b\)

⇒ \( 12 a^2 b=2 \times 2 \times 3 \times a \times a \times b\)

The C.F. = 2 x 3 x a x b

= 6ab

6) \(16 x^3,-4 x^2, 32 x \)

Solution: \(16 x^3=2 \times 2 \times 2 \times 2 \times x \times x \times x\)

⇒ \(-4 x^2=-2 \times 2 \times x \times x\)

2x = 2 x 2 x 2 x 2 x 2 x x

The C.F. are = 2 x 2 x x

= 4x

7) 10pq, 20qr, 30rp

Solution: 10pq = 2 x 5 x p x q

20qr = 2 x 2 x 5 x q x r

30rp = 2 x 3 x 5 x r x p

The C.F. = 2 x 5 = 10

8) \(3 x^2 y^3, 10 x^3 y^2, 6 x^2 y^2 z\)

Solution: \(3 x^2 y^3=3 \times x \times x \times y \times y \times y\)

⇒ \(10 x^3 y^2=2 \times 5 \times x \times x \times x \times y \times y\)

⇒ \(6 x^2 y^2 z=2 \times 3 \times x \times x \times y \times y \times z\)

The C.F. are = x x x x y x y

= \(x^2 y^2\)

2. Factorize the following expressions.

1) 7x-42

Solution: 7x-42

= (7 x x)-(2x3x7)

= 7(x-6)

2) 6p-12q

Solution: 6p-12q

= 2 x 3 x p – 2 x 2 x 3 x q

= 2 x 3(p-2 x q)

= 6(p-2q)

3) \(7 a^2+14 a\)

Solution: 7 x a x a + 7 x 2 x a

= 7a(a+2)

4) \(-16 z+20 z^3\)

Solution: \(-16 z+20 z^3\)

= -4 x 4 x z + 4 x 5+z x z x z

= \(4 z\left(-4+5 z^2\right)\)

5) \(20 \ell^2 m+30 a \ell m\)

Solution: \(20 \ell^2 m+30 a \ell m\)

=\(10 \times 2 \times \ell \times \ell \times m+10 \times 3 \times a \times \ell \times m\)

=\(10 \ell m(2 \ell+3 a)\)

KSEEB Solutions Class 8 Maths Factorisation Exercises

6) \(5 x^2 y-15 x y^2\)

Solution: \(5 x^2 y-15 x y^2\)

=\(5 \times x \times x \times y-5 \times 3 \times x \times y \times y\)

=\(5 x y(x-3 y)\)

7) \(10 a^2-15 b^2+20 c^2\)

Solution: \(10 a^2-15 b^2+20 c^2\)

=\(5 \times 2 \times a \times a-5 \times 3 \times b \times b+4 \times 5 \times c \times c\)

=\(5\left(2 a^2-3 b^2+4 c^2\right)\)

8) \(-4 a^2+4 a b-4 c a\)

Solution: \(-4 a^2+4 a b-4 c a\)

=\(-4 a(a-b+c)\)

9) \(x^2 y z+x y^2 z+x y z^2\)

Solution: \(x^2 y z+x y^2 z+x y z^2\)

x y z(x+y+z)

10) \(a x^2 y+b x y^2+c x y z\)

Solution: \(x y(a x+b y+c z)\)

3. Factorize

1) \(x^2+x y+8 x+8 y\)

Solution: \(x \times x+x \times y+8 \times x+8 \times y\)

=x(x+y)+8(x+y)

=(x+y)(x+8)

2) 15 x y-6 x+5 y-2

Solution: \(5 \times 3 \times x y-2 \times 3 \times x \times+5 \times y-2\)

3 x(5 y-2)+1(5 y-2)

(5 y-2)(3 x+1)

3) a x+b x-a y-b y

Solution: x(a+b)-y(a+b)

(a+b)(x-y)

4) 15 p q+15+9 q+25 p

Solution: 15 p q+15+9 q+25 p

3 q(5 p+3)+5(3+5 p)

(5 p+3)(3 q+5)

5) z-7+7 x y-x y z

Solution: z-7+7 x y-x y z

z-x y z-7+7 x y

z(1-x y)-7(1-x y)

(1-x y)(z-7)

KSEEB Class 8 Maths Chapter 13 Solved Problems Factorization Exercise 13.2

1. Factorize the following expressions.

1) \(a^2+8 a+16\)

Solution: \(a^2+8 a+16\)

=\((a)^2+2 \times a \times 4+(4)^2\)

=\((a+4)^2 \quad\left[(a+b)^2=a^2+2 a b+b^2\right]\)

2) \(p^2-10 p+25\)

Solution: \(p^2-10 p+25\)

=\(p^2-2 \times p \times 5+5^2\)

=\((p-5)^2\)

∴ \([(a-b)^2=a^2-2ab+b^2]\)

3) \(25 m^2+30 m+9\)

Solution: \(25 m^2+30 m+9\)

=\((5 m)^2+2 \times 5 m \times 3+3^2\)

=\((5 m+3)^2 \quad\left[(a+b)^2=a^2+2 a b+b^2\right]\)

4) \(49 y^2+84 y z+36 z^2\)

Solution: \((7 y)^2+2(7 y) \times(6 z)+(6 z)^2\)

=\((7 y+6 z)^2\left[(a+b)^2=a^2+2 a b+b^2\right]\)

5) \(4 x^2-8 x+4\)

Solution: \((2 x)^2-2 \times(2 x) \times(2)+2^2\)

=\((2 x-2)^2 \quad\left[(a-b)^2=a^2-2 a b+b^2\right]\)

Class 8 Maths Chapter 13 KSEEB Detailed Answers

6) \(121 b^2-88 b c+16 c^2\)

Solution: \((11 b)^2-2 \times(11 b)(4 c)+(4 c)^2\)

=\((11-4 c)^2 \quad\left[(a-b)^2=a^2-2 a b+b^2\right]\)

7) \((\ell+m)^2-4 \ell m\)

Solution: \((\ell+m)^2-4 \ell m\)

⇒ \(\ell^2+2 \ell m+m^2-4 \ell m\)

⇒ \(\ell^2-2 \ell m+m^2\)

⇒ \((\ell-m)^2 \quad(a-b)^2=a^2-2 a b+b^2\)

8) \(a^4+2 a^2 b^2+b^4\)

Solution: \(\left(a^2\right)^2+2 \times a^2+b^2+\left(b^2\right)^2\)

= \(\left(a^2+b^2\right)^2 \quad\left[(a+b)^2=a^2+2 a b+b^2\right]\)

2. Factorize

1) \(4 p^2-9 q^2\)

Solution: \((2 p)^2-(3 q)^2\)

⇒ \(\quad\left(a^2-b^2=(a+b)(a-b)\right)\)

=\((2 p+3 q)(2 p-3 q)\)

2) \(63 a^2-112 b^2\)

Solution: \(63 a^2-112 b^2\)

=\(7\left(9 a^2-16 b^2\right)\)

=\(7\left[(3 a)^2-(4 b)^2\right]\)

=\(7(3 a+4 b)(3 a-4 b)\)

3) \(49 x^2-36\left(a^2-b^2=(a+b)(a-b)\right)\)

Solution: \((7 x)^2-6^2\)

=\((7 x+6)(7 x-6)\)

4) \(16 x^5-144 x^3\)

Solution: \(16 x^3\left(x^2-9\right)\)

=\(16 x^3 \quad\left(x^2-3^2\right)\)

=\(16 x^3(x+3)(x-3)\)

⇒ \(\left(a^2-b^2=(a+b)(a-b)\right)\)

5) \((\ell+m)^2-(\ell-m)^2\)

Solution: \([(\ell+m)+(\ell-m)][(\ell+m)-(\ell-m)]\)

=\((\ell+\not{m}+\ell-\not{m})(\ell+m-\ell+m)\)

=\(2 \ell \times 2 \mathrm{~m}\)

= 4lm

KSEEB 8th Maths Factorisation Solutions

6) \(9 x^2 y^2-16\)

Solution: \((3 x y)^2-(4)^2\)

=\((3 x y+4)(3 x y-4)\)

7) \(\left(x^2-2 x y+y^2\right)-z^2\)

Solution: \(\left(x^2-2 x y+y^2\right)-z^2\)

= \((x-y)^2-z^2\)

= \((x-y+z)(x-y-z)\)

8) \(25 a^2-4 b^2+28 b c-49 c^2\)

Solution: \(25 a^2-\left(4 b^2-28 b c+49 c^2\right)\)

=\((5 a)^2-\left[(2 b)^2-2 \times 2 b \times 7 c+(7 c)^2\right]\)

=\((5 a)^2-(2 b-7 c)^2\)

=\([5 a+(2 b-7 c)][5 a-(2 b-7 c)]\)

= \([5 a+2 b-7 c][5 a-2 b+7 c]\)

⇒ \(\left[a^2-b^2=(a+b)(a-b)\right]\)

3. Factorize the expressions.

1) \(a x^2+b x\)

Solution: x(ax+b)

2) \(7 p^2+21 q^2\)

Solution: \(7\left(p^2+3 q^2\right)\)

3) \(2 x^3+2 x y^2+2 x z^2\)

Solution: \(2 x\left(x^2+y^2+z^2\right)\)

4) \(a m^2+b m^2+b n^2+a n^2\)

Solution: \(\left(a m^2+b m^2\right)+\left(b n^2+a n^2\right)\)

=\(m^2(a+b)+n^2(b+a)\)

=\((a+b)\left(m^2+n^2\right)\)

5) (lm+l)+m+1

Solution: lm+l+m+1

= lm+m+l+1

= m(l+1)+1(l+1)

=(l+1)(m+1)

6) y(y+z)+9(y+z)

Solution: (y+z)(y+9)

7) \(5 y^2-20 y-8 z+2 y z\)

Solution: \(5 y^2-20 y-8 z+2 y z\)

=\(5 y(y-4)+2 z(y-4)\)

=\((y-4)(5 y+2 z)\)

8) 10ab+4a+5b+2

Solution: 10ab+5b+4a+2

= 5b(2a+1)+2(2a+1)

= (2a+1)(5b+2)

9) 6xy-4y+6-9x

Solution: 6xy-9x-4y+6

3x(2y-3)-2(2y-3)

(2y-3)(3x-2)

4. Factorize

1) \(a^4-b^4\)

Solution: \(\left(a^2\right)^2-\left(b^2\right)^2\)

=\(\left(a^2-b^2\right)\left(a^2+b^2\right)\)

=\((a-b)(a+b)\left(a^2+b^2\right)\)

2) \(p^4-81\)

Solution: \(\left(p^2\right)^2-9^2\)

=\(\left(p^2+9\right)\left(p^2-9\right)\)

=\(\left(p^2+9\right)\left(p^2-3^2\right)\)

=\(\left(p^2+9\right)(p+3)(p-3)\)

3) \(x^4-(y+z)^4\)

Solution: \(\left(x^2\right)^2-\left[(y+z)^2\right]^2\)

=\(\left[x^2+(y+z)^2\right][x+(y+z)][x-(y+z)]\)

=\(\left[x^2+(y+z)^2\right][x+y+z][x-y-z]\)

4) \(x^4-(x-z)^4\)

Solution: =\(\left(x^2\right)^2-\left[(x-z)^2\right]^2\)

=\(\left[x^2+(x-z)^2\right]\left[x^2-(x-z)^2\right]\)

=\(\left[x^2+(x-z)^2\right][x+(x-z)][x-(x-z)]\)

=\(\left[x^2+(x-z)^2\right](x+x-z)(x-x+z)\)

=\(\left[x^2+(x-z)^2\right](2 x-z) \times z\)

=\(z(2 x-z)\left(x^2+(x-z)^2\right)\)

=\(z^2(2 x-z)\left(x^2+x^2-2 x z+z^2\right)\)

=\(z(2 x-z)\left(2 x^2-2 x z+z^2\right)\)

5) \(a^4-2 a^2 b^2+b^4\)

Solution: \(\left(a^2\right)^2-2 a^2b^2+\left(b^2\right)^2\)

=\(\left(a^2-b^2\right)^2\)

=\([(a+b)(a-b)]^2\)

=\((a+b)^2(a-b)^2\)

5. Factorize the following expressions.

1) \(p^2+6 p+8\)

Solution: It can be observed that

8 = 4 x 2 and 4 + 2 = 6

∴ \(p^2+6 p+8\)

=\(p^2+2 p+4 p+8\)

=\(p(p+2)+4(p+2)\)

=\((p+2)(p+4)\)

KSEEB Solutions Class 8 Maths Chapter 13 Factorisation

2) \(q^2-10 q+21\)

Solution: It can be observed that

⇒ \(21=(-7) \times(-3) \text { and }(-7)+(-3)=-10\)

∴ \(q^2-10 q+21\)

=\(q^2-7 q-3 q+21\)

=\(q(q-7)-3(q-7)\)

∴ \((q-7)(q-3)\)

3) \(p^2+6 p-16\)

Solution: It can be observed that

-16 = \((-2) \times 8 \& 8+(-2)=6\)

∴ \(p^2+6 p-16\)

=\(p^2+8 p-2 p-16\)

=\(p(p+8)-2(p+8)\)

=\((p+8)(p-2)\)

KSEEB Maths Class 8 Factorization Exercise 13.3

1. Carry out the following divisions.

1) \(28 x^4 \div 56 x\)

Solution:

=\(\frac{x^3}{2}=\frac{1}{2} x^3\)

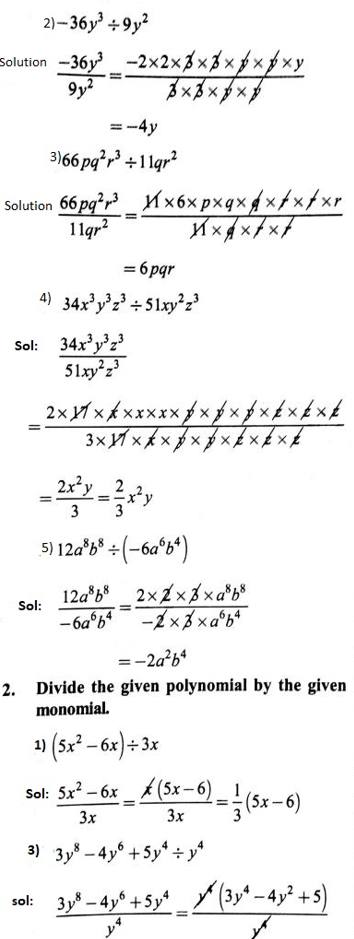
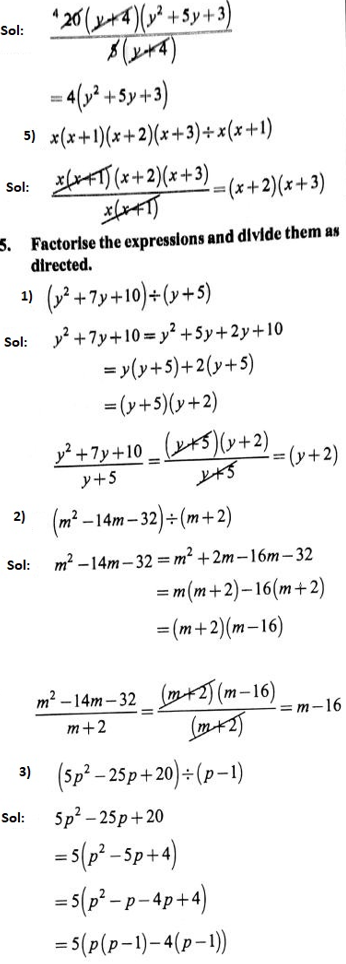
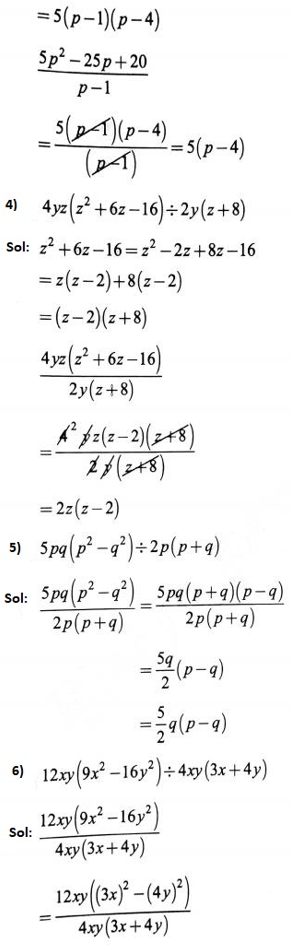
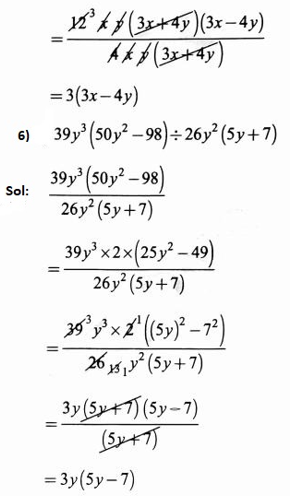
KSEEB Class 8 Maths Key Concepts Of Factorization Exercise 13.4

1. Find and correct the errors in the following mathematical statements.

1. 4(x-5)=4x-5

Solution: LHS = 4(x-5)=4×20 ≠ RHS

∴ The correct statement is

4(x-5)=4×20

2. \(x(3 x+2)=3 x^2+2\)

Solution: LHS = x(3x+2)

= \(x \times 3 x+x \times 2\)

=\(3 x^2+2 x\) ≠ RHS

The correct statement is

∴ \(x(3 x+2)=3 x^2+2 x\)

3. 2x+3y=5xy

Solution: LHS = 2x+3y ≠ RHS

The correct statement is

2x + 3y = 2x + 3y

4. x + 2x + 3x = 5x

Solution: LHS = x + 2x + 3x

= x(1+2+3)

= 6x ≠ RHS

The correct statement is x + 2x + 3x = 6x

5. 5y + 2y + y – 7y = 0

Solution: LHS = 5y + 2y + y – 7y

= 8y – 7y

= y ≠ RHS

The correct statement is

5y + 2y + y – 7y = y

6. \(3 x+2 x=5 x^2\)

Solution: LHS = 3x + 2x

= 5x

≠ RHS

∴ The CS is 3x + 2x = 5x

KSEEB Maths Class 8 Factorisation Examples Explained

7. \((2 x)^2+4(2 x)+7=2 x^2+8 x+7\)

Solution: LHS = \((2 x)^2+4(2 x)+7\)

=\(4 x^2+8 x+7\)

≠ RHS

∴ The CS is \((2 x)^2+4(2 x)+7\)

=\(4 x^2+8 x+7\)

8. \((2 x)^2+5 x=4 x+5 x=9 x\)

Solution: LHS = \((2 x)^2+5 x\)

=\(4 x^2+5 x\)

≠ RHS

The CS is \((2 x)^2+5 x\)

=\(4 x^2+5 x\)

9. \((3 x+2)^2=3 x^2+6 x+4\)

Solution: LHS = \((3 x+2)^2\)

=\((3 x)^2+2(3 x)(2)+2^2\)

=\(9 x^2+12 x+4\)

≠ RHS

∴ \((a+b)^2=a^2+2 a b+b^2\)

The CS is \((3 x+2)^2=9 x^2+12 x+4\).

10. Substituting x = -3 in.

a) \(x^2+5 x+4 \)gives

Solution: For x = -3

∴ \(x^2+5 x+4=(-3)^2+5(-3)+4=9-15+4\)

= 13 – 15 = -2

b) \(x^2-5 x+4\) gives \((-3)^2-5(-3)+4 = 9 – 15 + 4 = -2\)

Solution: \(x^2-5 x+4=(-3)^2-5(-3)+4\)

= 9 + 15 + 4 = 28

c) \(x^2+5 x gives (-3)^2+5(-3)=-9-15=-24\)

Solution: \(x^2+5 x=(-3)^2+5(-3)=+9-15=-6\)

11. \((y-3)^2=y^2-9\)

Solution: LHS = \((y-3)^2=y^2-2(y)(3)+3^2\)

=\(y^2-6 y+9\)

≠ RHS

The correct statement is \((y-3)^2=y^2-6 y+9\)

12. \((z+5)^2=z^2+25\)

Solution: LHS = \((z+5)^2=z^2+25=z^2+2 \times z \times 5+5^2\)

=\(z^2+10 z+25\)

≠ RHS

The correct statement is \((z+5)^2=z^2+10 z+25\)

13. \((2 a+3 b)(a-b)=2 a^2-3 b^2\)

Solution: LHS = (2a+3b)(a-b)

= \(2 a \times a+3 b \times a-2 a \times b-3 b \times b\)

=\(2 a^2+3 a b-2 a b-3 b^2\)

=\(2 a^2+a b-3 b^2 \neq \text { RHS }\)

The correct statement is (2a+3b)(a-b)

=\(2 a^2+a b-3 b^2\)

14. \((a+4)(a+2)=a^2+8\)

Solution: LHS = (a+4)(a+2)

∴ \((x+a)(x+b)=x^2+x(a+b)+a b\)

=\(a^2+(4+2)(a)+4 \times \)

=\(a^2+6 a+8\)

≠ RHS

The correct statement is

∴ \((a+4)(a+2)=a^2+6 a+8\)

15. \((a-4)(a-2)=a^2-8\)

Solution: LHS = (a-4)(a+2)

=\(a^2+[(-4)+(-2)] a+(-4)(-2)\)

=\(a^2-6 a+8 \neq \text { RHS }\)

The correct statement is

∴ \((a-4)(a-2)=a^2-6 a+8\)

16. \(\frac{3 x^2}{3 x^2}=0\)

Solution: LHS = \(\frac{3 x^2}{3 x^2}=\frac{3 \times x \times x}{3 \times x \times x}=1\) ≠ RHS

The correct statement is \(\frac{3 x^2}{3 x^2}=1\)

17. \(\frac{3 x^2+1}{3 x^2}=1+1=2\)

Solution: LHS = \(\frac{3 x^2+1}{3 x^2}=\frac{3 x^2}{3 x^2}+\frac{1}{3 x^2}\)

=\(1+\frac{1}{3 x^2}\) ≠ RHS

The correct statement is \(\frac{3 x^2+1}{3 x^2}=1+\frac{1}{3 x^2}\)

KSEEB 8th Class Maths Factorisation Solutions

18. \(\frac{3 x}{3 x+2}=\frac{1}{2}\)

Solution: LHS = \(\frac{3 x}{3 x+2}\) ≠ RHS

The correct statement is \(\frac{3 x}{3 x+2}=\frac{3 x}{3 x+2}\)

19. \(\frac{3}{4 x+3}=\frac{1}{4 x}\)

Solution: LHS = \(\frac{3}{4 x+3}\) ≠ RHS

The correct statement is \(\frac{3}{4 x+3}=\frac{3}{4 x+3}\)

20. \(\frac{7 x+5}{5}=7 x\)

Solution: LHS = \(\frac{7 x+5}{5}=\frac{7 x}{5}+\frac{5}{5}=\frac{7 x}{5}+1\) ≠ RHS

∴ The correct statement is \(\frac{7 x+5}{5}=\frac{7 x}{5}+1\)

21. \(\frac{4 x+5}{4 x}=5\)

Solution: LHS = \(\frac{4 x+5}{4 x}=\frac{4 x}{4 x}+\frac{5}{4 x}=1+\frac{5}{4 x}\) ≠ RHS

The correct statement is \(\frac{4 x+5}{4 x}=1+\frac{5}{4 x}\)

Factorization Chapter 13 KSEEB Maths Additional Problems

1. Find the common factor of \(7 p^3 q\) and 5pq

Solution: \(7 p^3 q=7 \times p \times p \times p \times q\)

5pq = 5 x p x q

common factor of \(7 p^3 q\) and 5pq is pq.

2. Factorize: \(3 x-15 x^2\)

Solution: \(3 x-15 x^2=3 \times x-3 \times 5 \times x \times x\)

= 3x(1-5x)

3. Factorize: \(5 p(2 q-3 r)^2+2 p(2 q-3 r)\)

Solution: \(5 p(2 q-3 r)^2+2 p(2 q-3 r)\)

=\(p\left[5(2 q-3 r)^2+2(2 q-3 r)\right]\)

=\(p(2 q-3 r)[5(2 q-3 r)+2]\)

=\(p(2 q-3 r)(10 q-15 r+2)\)

4. Factorize: \(36 x^2-\frac{1}{169}\)

Solution: \(36 x^2-\frac{1}{169}\)

=\((6x)^2-\left(\frac{1}{13}\right)^2\left[\left(a^2-b^2\right)=(a+b)(a-b)\right]\)

=\(\left(6 x+\frac{1}{13}\right)\left(6 x-\frac{1}{13}\right)\)

5. Factorize: \(9 p^2+24 p+16\)

Solution: \(9 p^2+24 p+16\)

=\((3 p)^2+2 \times 3 p \times 4+4^2\)

∴ \(\left[a^2+2 a b+b^2=(a+b)^2\right]\)

=\((3 p+4)^2\)

6. If x=16 and y=5 find the value of \(\frac{x^2+y^2+x y}{x^2-y^2}\)

Solution: \(\frac{x^2+y^2+x y}{x^2-y^2}=\frac{16^2+5^2+16 \times 5}{16^2-5^2}\)

=\(\frac{256+25+80}{(16+5)(16-5)}=\frac{361}{21 \times 1}=\frac{361}{21}\)

7. Factorise: \(x^3 y^2+x^2 y^3-x y^4+x y\)

Solution: \(x^3 y^2+x^2 y^3-x y^4+x y\)

⇒ \(x y\left(x^2 y+x y^2-y^3+1\right)\)

8. Factorize: \(a^2 x^2+2 a x+1\)

Solution: \(a^2 x^2+2 a x+1\)

=\((a x)^2+2(a x)(1)+1^2\)

using identities \(\left[(a+b)^2=a^2+2 a b+b^2\right]\)

Here a=ax, b=1

=\((a x+1)^2\)

=(ax+1)(ax+1)

9. Factorize: \(9 y^2-4 x y+\frac{4 x^2}{9}\)

Solution: \(9 y^2-4 x y+\frac{4 x^2}{9}\)

=\(4\left(\frac{9}{4} y^2-x y+\frac{x^2}{9}\right)\)

=\(4\left(\left(\frac{3}{2} y\right)^2-x y+\left(\frac{x}{3}\right)^2\right)\)

=\(4\left(\left(\frac{3}{2} y\right)^2-2\left(\frac{3}{2} y\right)\left(\frac{x}{3}\right)+\left(\frac{x}{3}\right)^2\right)\)

=\(4\left(\frac{3}{2} y-\frac{x}{3}\right)^2\)

10. Factorize: \(y^2+7 y+12\)

Solution: Here 12 = 4 x 3 and 4 + 3 = 7

∴ \(y^2+7 y+12=y^2+4 y+3 y+12\)

=y(y+4)+3(y+4)

∴ \(y^2+7 y+12=(y+4)(y+3)\)

KSEEB Class 8 Maths Chapter 13 Practice Questions

11. Divide \(24\left(x^2 y z+x y^2 z+x y z^2\right) \text { by } 8 x y z\)

Solution: \(\frac{24\left(x^2 y z+x y^2 z+x y z^2\right)}{8 x y z}\)

=\(\frac{3 x^2 y z+3 x y^2 z+3 y z^2}{x y z}\)

=\(\frac{3 x^2 y z}{x y z}+\frac{3 x y^2 z}{x y z}+\frac{+3 x y z^2}{x y z}\)

=\(3 x+3 y+3 z=3(x+y+z)\)

12. Divide \((-q r x y+p r y z-r x y z) \div(-x y z)\)

Solution: \(\frac{-q r x y+p r y z-r x y z}{-x y z}\)

∴ \(\frac{-q r x y}{-x y z}+\frac{p r y z}{-x y z}-\frac{r x y z}{-x y z}\)

=\(\frac{q r}{z}-\frac{p r}{x}+r\)

13. Factorize: \(x^2+\frac{1}{x^2}+2-3 x-\frac{3}{x}\)

Solution: \(x^2+\frac{1}{x^2}+2-3 x-\frac{3}{x}\)

=\(\left[x^2+\frac{1}{x^2}+2\right]-3\left[x+\frac{1}{x}\right]\)

=\(\left(x+\frac{1}{x}\right)^2-3\left(x+\frac{1}{x}\right)\)

=\(\left(x+\frac{1}{x}\right)\left(x+\frac{1}{x}-3\right)\)

14. The sum of the square of n natural number is \(\frac{2 n^3+3 n^2+n}{6}\). Factorize this expression.

Solution: \(\frac{2 n^3+3 n^2+n}{6}=\frac{n\left(2 n^2+3 n+1\right)}{6}\)

=\(\frac{n\left(2 n^2+2 n+n+1\right)}{6}\)

[we know 3 = 2 + 1 & 2 x 1 = 2]

⇒ \(\frac{n[2 n(n+1)+(n+1)]}{6} \Rightarrow \frac{n(2 n+1)(n+1)}{6}\)

15. Using factorization, find the positive square root of  \(\frac{(a+b)^2-(c+d)^2}{(a+b)^2-(c-d)^2} \times \frac{(a+b+c)^2-d^2}{(a+b-c)^2-d^2}\)

Solution: \(\frac{(a+b)^2-(c+d)^2}{(a+b)^2-(c-d)^2} \times \frac{(a+b+c)^2-d^2}{(a+b-c)^2-d^2}\)

using identity \(a^2-b^2=(a+b)(a-b)\)

⇒ \((a+b)^2-(c+d)^2 =[(a+b+c+d)(a+b-c-d)]\)

⇒ \((a+b+c)^2-d^2 =(a+b+c+d)(a+b+c-d)\)

⇒ \((a+b)^2-(c-d)^2 =(a+b+c-d)(a+b-c+d)\)

⇒ \((a+b-c)^2-d^2 =(a+b-c+d)(a+b-c-d)\)

putting the identities together, we get

=\(\frac{(a+b+c+d)(a+b-c-d)}{(a+b+c-d)(a+b+d-c)}\times \frac{(a+b+c+d)(a+b+c-d)}{(a+b+c-d)(a+b-c+d)}\)

=\(\frac{(a+b+c+d)(a+b+c+d)}{(a+b-c+d)(a+b-c+d)}\)

=\(\frac{(a+b+c+d)^2}{(a+b-c+d)^2}\)

16. Evaluate \((205)^2-(195)^2\)

Solution: \((205)^2-(195)^2\)

= (205+195)(205-195)

⇒ \(\left\{a^2-b^2=(a+b)(a-b)\right\}\)

= 400 x 10

= 4000

17. Factorize: \(x^2+x y+9 x+9 y\)

Solution: \(x^2+x y+9 x+9 y\)

= x(x+y)+9(x+y)

= (x+y)(x+9)

18. Factorize:  \(2 a^2\left(b^2-c^2\right)+b^2\left(2 c^2-2 a^2\right)+2 c^2\left(a^2-b^2\right)\)

Solution: \(2 a^2\left(b^2-c^2\right)+b^2\left(2 c^2-2 a^2\right)+2 c^2\left(a^2-b^2\right)\)

=\(2\left(a^2 b^2-a^2 c^2\right)+2\left(b^2 c^2-b^2 a^2\right)+2\left(c^2 a^2-c^2 b^2\right)\)

= 2 x 0

= 0

19. Divide: \(\left(4 x^2-100\right) \div 6(x+5)\)

Solution: \(\frac{4 x^2-100}{6(x+5)}=\frac{4\left(x^2-25\right)}{6(x+5)}\)

= \(\frac{4_2(x+5)(x-5)}{6_3(x+5)}=\frac{2}{3}(x-5)\)

20. Find two numbers A and B so that A+B=12 and AB=27.

Solution: Given A+B=12 and AB=27

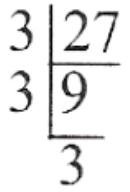
A x B = 27 = 9 x 3
A + B = 12 = 9 + 3
Such that A=9 and B=3

21. If \(a^2+b^2=74 \& a b=35 \text {, }\) then find a+b?

Solution: Given \(a^2+b^2=74 \& a b=35\)

since, \((a+b)^2=a^2+b^2+2 a b\)

⇒ \((a+b)^2=74+2 \times 35=74+70=144\)

⇒ \(a+b=\sqrt{144}\)

⇒ a+b=12

22. If m-n=16 & \(m^2+n^2=400\), then find mn.

Solution: \(m-n=16 \& m^2+n^2=400\)

⇒ \((m-n)^2=m^2+n^2-2 m n\)

⇒ \((16)^2=400-2 m n\)

⇒ \(2 m n=400-(16)^2=400-256\)

⇒ \(m n=\frac{144}{2}=72\)

23. The height of a Δle is \(x^4+y^4\) and its base is 14xy. Find the area of the Δle.

Solution: Given, the height of a Δle and its base are \(x^4+y^4\) and 14xy respectively

wkt, the area of a Δle =\(\frac{1}{2} \times b \times h\)

=\(\frac{1}{2} \times 14 x y \times\left(x^4+y^4\right)\)

=\(7 x y\left(x^4+y^4\right)\)

24. The area of a square is given by \(4 x^2+12 x y+9 y^2\). find the side of the square.

Solution: We have

Area of square = \(4 x^2+12 x y+9 y^2\)

so, we factorize the given expression

∴ \(4 x^2+12 x y+9 y^2\)

=\((2 x)^2+2 \times 2 x \times 3 y+(3 y)^2\)

=\((2 x+3 y)^2\)

Since the area of a square having side length a is \(a^2\), hence, side of the given square is 2x+3y.

KSEEB Solutions For Class 8 Maths Chapter 15 Comparing Quantities Points To Remember

Ratio comparing by division is called ratio. Quantities written in ratio have the same unit. Ratio has no unit. Equality of two ratios is called proportion.

Product of extremes = Product of means.

Percentage: Percentage means for every hundred. The result of any division in which the divisor is 100 is a percentage. The divisor is denoted by a special symbol % read as percent.

Profit and Loss.

1)Cost price (P): The amount for which an article is bought.

2)Selling price (SP): The amount for which an article is sold.

Read and Learn More KSEEB Solutions for Class 8 Maths

Additional expenses made after buying an article are included in the cost price and are known as overhead expenses. These may include expenses like amount spent on repairs, labor charges, transportation, etc.

Discount is a reduction given on marked price. Discount = marked price – sale price.

Discount can be calculated when discount % is given. Discount = Discount % of marked price.

Additional expenses made after buying an article are included in the cost price and are known as overhead expenses.

CP = Buying price + Overhead expenses.

Sales tax is charged on the sale of an item by the government and is added to the Bill amount. Sales tax = Tax % of Bill amount.

Simple interest: If the principle remains the same for the entire loan period, then the interest paid is called simple interest.

Compound interest is the interest calculated on the previous year’s amount(A=P+I)

1) Amount when interest is compounded annually

=\(P\left(1+\frac{R}{100}\right)^n\)

P=principle, R=Rate of interest, n=time period.

2) Amount when interest is compounded half yearly =\(P\left(1+\frac{R}{100}\right)^{2 n}\)

R/2 is half-yearly rate and 2n is = Number of ‘half-years’.

Class 8 Maths KSEEB Chapter 15 Solutions Comparing Quantities Exercise 15.1

1 .Find the ratio of the following.

a)Speed of a cycle 15km per hour to the speed of scooter 30 km per hour.

b)5km to 10km

c) 50 paise to ₹5.

Solution: a) Ratio of the speed of cycle to the speed of scooter =\(\frac{15}{30}=1: 2\)

b) Since 1 km = 1000m

Required ratio

c)Since ₹1 = 100 paise.

=\(\frac{5 \text { paise }}{500 \text { paise }}=1: 10\)

2. Convert the following ratios to percentages

a) 3:4

b) 2:3

Solution: a) \(3: 4=\frac{3}{4}=\frac{3}{4} \times \frac{100}{100}=\frac{3}{4} \times 100 \%=75 \%\)

b) \(2: 3=\frac{2}{3}=\frac{2}{3} \times \frac{100}{100}=\frac{2}{3} \times 100 \%=\frac{200}{3} \%\)

=\(\left(\frac{66 \times 3+2}{3}\right) \%=66 \frac{2}{3} \%\)

3. 72% of 25 students are good in mathematics. How many are not good in mathematics?

Solution: It is given that 72% of 25 students are good in mathematics.

∴ Percentage of students who are not good in mathematics = (100-72)% =28%

∴ Number of students who are not good in mathematics = \(\frac{28}{100} \times 25=7\)

4. A football team won 10 matches out of the total number of matches they played. If their win percentage was 40, then how many matches did they play in all?

Solution: Let the total number of matches played by the team be x.

It is given that the team won 10 matches and the winning percentage of the team was 40%

∴ \(\frac{40}{100} \times x=10\)

Thus, the team played 25 matches.

5. If chameli had ₹600 left after spending 75% of her money, how much did she have in the beginning?

Solution: Let the amount of money which chameli had, in the beginning, be x.

It is given that after spending 75% of ₹x, she was left with ₹600.

∴ (100-75)% of x = ₹600

or, 25% of x = ₹600

thus, she had ₹2400 in the beginning.

6. If 60% people in city like cricket, 30% like football, and the remaining like other games, then what % of the people like other games? If the total number of people are 50 lahks,

Solution: % of people who like other games

= (100-60-30)%

= 10%

Total number of people = 50 lakh

∴ number of people who like cricket

=\(\left(\frac{600}{100} \times 50\right) \text { lakh }\)

Number of people who like football

=\(\left(\frac{30}{100} \times 50\right) \text { lakh }=15 \text { lakh }\)

Number of people who like other games

= \(\left(\frac{10}{100} \times 50\right) l a k h=5 l a k h\)

Comparing Quantities KSEEB Class Exercise 15.2

1. A man got a 10% increase in his salary. If his new salary is ₹1,54,000, find his original salary.

Solution: Let the original salary be x

it is given that the new salary is ₹1,54,000,

Original salary + Increment = New salary.

However, it is given that the increment is 10% of the original salary.

∴ \(x+\frac{10}{100} \times x=154000\)

x=140000

Thus, the original salary was ₹1,40,000

2. on Sunday 845 people went to the zoo. On Monday only 169 people went. What is the percent decrease in the people visiting the zoo on Monday?
Solution: It is given that on Sunday, 845 people went to the zoo and on Monday, 169 people went.

Decrease in the number of people

= 845-169 = 676

% decrease = \(\left(\frac{\text { Decrease in the number of people } \times 100}{\text { Number of people who went to zoo on }}\right) \%\)

= \(\frac{676}{845} \times 10\)

=80%

3. A shopkeeper buys 80 articles for ₹2400 and sells them for a profit of 16%. Find the selling price of one article.

Solution: It is given that the shopkeeper buys 80 articles for ₹2400.

Cost of one article = \(₹ \frac{2400}{80}=₹ 30\)

profit% = 16

Selling price of one article = CP + Profit

= 30 + 4.80 = ₹34.80

4. The cost of an article was ₹15,500, and ₹450 were spent on its repairs. If it is sold for a profit of 15%. Find the selling price of the article.

Solution: Total cost of an article = cost + overhead expenses

= ₹1500+₹450

= ₹15950

selling price of the article
= c.p. + profit = ₹(15950+2392.50)
=₹18342.50

5. A VCR and TV were bought for ₹8000 each. The shopkeeper made a loss of 4% on the VCR and a profit of 8% on the TV. Find the gain or loss percent on the whole transaction.

Solution: C.P. of VCR = ₹8000

The shopkeeper made a loss of 4% on VCR.

This means if C.P. is ₹100, then S.P. is ₹96.

When C.P. is ₹8000, S.P. = \( ₹\left(\frac{96}{100} \times 8000\right)\) = ₹7680

C.P. of a TV = ₹8000

The shopkeeper made a profit of 8% on TV

This means that if C.P. is ₹100, then S.P. is ₹108.

When C.P. is ₹8000, S.P. = \(\left(\frac{108}{100} \times 8000\right)\) = ₹8640

Total S.P. = ₹7680+₹8640=₹16320

Total C.P. = ₹8000+₹8000=₹16000

Since total S.P.>total C.P. There was a profit.

Profit = ₹16320-₹16000 = ₹320

∴ The shopkeeper had a gain of 2% on the whole transaction.

6. During a sale, a shop offered a discount of 10% on the marked prices of all the items. What would a customer have to pay for a pair of jeans marked at ₹1450 and two shirts marked at ₹850 each?

Solution: Total marked price =₹(1450+2×850)

= ₹3150
Given that, discount% = 10%

Discount = \(₹\left(\frac{10}{100} \times 3150\right)=₹ 315\)

also, Discount=marked price-sale price

₹315=₹3150-sale price

∴ sale price = ₹(3150-315) =₹2835

Thus, the customer will have to pay ₹2835

7. A milkman sold two of his buffaloes for ₹20,000 each on one he made a gain of 5% and on the other a loss of 10%. Find his over all gain or loss.

Solution: S.P. of each buffalo =₹20000

The milkman made a gain of 5% while selling one buffalo.

This mean if C.P. is ₹100, then S.P. is ₹105.

C.P. of one buffalo = \(₹\left(20000 \times \frac{100}{105}\right)\)

= ₹19,0467.62

Also, the second buffalo was sold at a loss of 10%.

This means if C.P. is ₹100, then S.P. is ₹90.

∴ C.P. of other buffalo = \(₹\left(20000 \times \frac{100}{90}\right)\)

= ₹22222.22

Total C.P. =₹19047.62+₹22222.22

= ₹41269.84

Total S.P. = ₹20000+₹20000=₹400000

loss=₹41269.84-₹400000=₹1269.84

Thus, the overall loss of milkman was ₹1269.84.

8. The price of a TV is ₹13,000. The sales tax charged on it is at the rate of 12%. Find the amount that Vinod will have to pay if he buys it.

Solution: On ₹100, the tax to be paid = ₹12

On ₹13000, the tax to be paid

= \(₹\left(\frac{12}{100} \times 13000\right)\)

Required amount = cost+salestax

= ₹13000+₹1560=₹14560

Thus, Vinod will have to pay ₹14560 for the TV.

9. Arun bought a pair of skates at a sale where the discount given was 20%. If the amount he pays is ₹1600, find the marked price.

Solution: Let the marked price be x.

Also, Discount = marked price – sale price

Thus, the marked price was ₹2000.

10. I purchased a hair dryer for ₹5400 including 8% VAT. Find the price before VAT was added.

Solution: The price includes VAT

Thus, 8% VAT means that if the price without VAT is ₹ 100. The price including VAT will be 108. When price including VAT is ₹108,

Original price = ₹100

When price including VAT is ₹5400,

Original price = \(₹ \frac{100}{108} \times 5400=₹ 5000\)

Thus, the price of the hair dryer before the addition of VAT was ₹5000

11. An article was purchased for ₹1239 including a GST of 18%. Find the price of the article before GST was added.

Solution: Given, GST = 18%

Cost with GST included =₹1239

Cost without GST = ₹x

Cost before GST + GST = cost with GST

x = 1050

Price before GST = 1050 rupees.

KSEEB Class 8 Maths Comparing Quantities Exercise 15.3

1. Calculate the amount and compound interest on

a) ₹10,800 for 3 years at 12 1/3% per annum compounded annually.

Solution: Principle (P) = ₹10800, Number of years (n)= 3

Rate (R) = \(12 \frac{1}{2} \%=\frac{25}{2} \%=\text { (annual) }\)

=\(10800\left(\frac{225}{200}\right)^3=10800 \times \frac{225}{200} \times \frac{225}{200} \times \frac{225}{200}\)

= 15377.34375

= ₹15377.34(approximately)

CI=A-P = 15377.34-10800 = ₹4577.34

b) ₹18,000 for \(2 \frac{1}{2}\) years at 10% per annum compounded annually.

Solution: P = ₹18000, R= 10%, n= 2 \(\frac{1}{2}\)years.

The amount for 2 years and 6 months can be calculated by 1 st calculating the amount for 2 years using the compound interest formula, and then calculating the simple interest for 6 months on the amount obtained at the end of 2 years.

Firstly, the amount for 2 years has to be calculated

=\(18000 \times \frac{11}{10} \times \frac{11}{10}=₹ 21780\)

By taking ₹21780 as principal, the S.I. for the next \(\frac{1}{2}\) year will be calculated.

∴ interest for the 1st 2years = ₹(21789-18000) = ₹3780

and interest for the next \(\frac{1}{2}\) year = ₹1089.

Total C.I. = ₹3780 + ₹1089 = ₹4869

A = P + C.I. = ₹18000 + ₹4869 = ₹22869

c) ₹62,500 for \(1 \frac{1}{2}\) years at 8% per annum compounded half yearly

Solution: P = ₹62500, R = 8% per annum or 4% per half-year

Number of years = \(1 \frac{1}{2}\)

There will be 3 half years in \(1 \frac{1}{2}\)

=\(62500 \times \frac{26}{25} \times \frac{26}{25} \times \frac{26}{25}\) = ₹70304

C.I. = A-P = ₹70304-₹62500 = ₹7,804

d) ₹8,000 for 1 year at 9% per annum compounded half yearly.

Solution: P = ₹8000, R = 9% per annum or \(\frac{9}{2}\) % per half year, n=1 year

There will be 2 half years in 1 year.

=\(8000\left(1+\frac{9}{200}\right)^2=8000 \times\left(\frac{209}{200}\right)^2\)

C.I. = A-P = ₹8736.20-₹8000

= ₹736.20

e) ₹10000 for 1 year at 8% per annum compounded half yearly.

Solution: P = ₹10,000, R = 8% per annum or 4% per half year, n = 1 year. There are 2 half years in 1 year.

=\(10000\left(1+\frac{1}{25}\right)^2\)

=\(10000 \times \frac{26}{25} \times \frac{26}{25}=₹ 10,816\)

CI = A-P = ₹10816-₹10000 = ₹816

2. Kamala borrowed ₹26400 from a bank to buy a scooter at a rate of 15% p.a. compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan?

(Hint: Find A for 2 years with interest compounded yearly and then find SI on the 2nd year amount for \(\frac{4}{12}\) years)

Solution: P = ₹26400, R = 15% per annum, n = \(2 \frac{4}{12}\) years. The amount for 2 years and 4 months can be calculated by first calculating the amount for 2 years using the compounded interest formula, and then calculating the simple interest for 4 months on the amount obtained at the end of the years. Firstly, the amount for 2 years has to be calculated.

=\(26400 \times \frac{23}{20} \times \frac{23}{20}=₹ 34914\)

By taking ₹34916 as principal, the S.I. for the next \(\frac{1}{3}\) years will be calculated.

Interest for the 1 st two years = 34914 – 26400 =₹8514

and interest for the next \(\frac{1}{3}\) years =₹1,745.70

Total C.I. = 8514+ 1745.70 = ₹10,259.70

Amount = P + C.I. = ₹26400 + ₹10259.70 = ₹36659.70

3. Fabina borrows ₹12500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually, who pays more interest, and by how much?

Solution: Interest paid by Fabina = \(\frac{\text { PTR }}{100}\)

=\(\frac{12500 \times 3 \times 12}{100}=₹ 4500\)

Amount paid by Radha at the end of 3 years

=\(12500 \times \frac{110}{100} \times \frac{110}{100} \times \frac{110}{100}=₹ 16,637.50\)

C.I. — A – P= 16637.50 – 12500 = 4137.50.

The interest paid by Fabina is ₹4500 and by Radha is ₹4137.50.

Thus, Fabina pays more interest.

₹4500 -4137.50 = ₹362.50

Hence, Fabina will have to pay ₹362.50 more.

Download KSEEB Solutions For 8th Maths Chapter 15

4. I borrowed ₹12000 from Jamshed at 6% per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest. What extra amount would I have to pay?

Solution: P = ₹12000, R = 6% per annum, T = 2 years

To find the C.I., the amount (A) has to be calculated.

=\(12000\left(1+\frac{3}{50}\right)^2=12000 \times\left(\frac{53}{50}\right) \times\left(\frac{53}{50}\right)\)

= ₹13483.20

∴ CI = A-P = 13483.20-12000 = ₹1483.20

CI – SI = ₹1483.20 – ₹1400 = ₹43.20

Thus the extra amount to be paid is ₹43.20.

5. Vasudevan invested ₹60000 at an interest rate of 12% per annum compounded half yearly. What amount would he get?

1) after 6 months?

2) after 1 year?

Solution:1) P = ₹60,000, R = 12% p.a. = 6% per half year. n = 6 months = 1 half year.

=\(60000\left(1+\frac{6}{100}\right)^1=60000 \times \frac{106}{100}\)

= ₹63,600.

2) There are 2 half years in 1 year.
n=2

= ₹67,416

6. Arif took a loan of ₹80,000 from a bank. If the rate of interest is 10% p.a. Find the difference in amounts he would be paying after 1 \(\frac{1}{2}\) years, if the interest is

1)compounded annually

2)compounded half-yearly.

Solution: 1) P = ₹80000, R= 10% p.a., n = 1 1/2years.

The amount for 1 year and 6 months can be calculated by first calculating the amount for 1 year using the compound interest formula and then calculating the simple interest for 6 months on the amount obtained at the end of 1 year.

Firstly, the amount for 1 year has to be calculated.

By taking ₹88000 as principal. The SI for the next 1/2 year will be calculated

Total C.I. = ₹8000 + ₹4,400 = ₹12,400

A = P + C.I. = 80000 + 12400 = ₹92400

2) The interest is compounded half-yearly. R = 10% p.a. = 5% per half year.

There will be three half year in 1 \frac{1}{2} years

=\(80000 \times \frac{21}{20} \times \frac{21}{20} \times \frac{21}{20}=₹ 92,610\)

Difference between the amounts = ₹92,610-₹92400 = ₹210

KSEEB Maths 8th Standard Chapter 15 Comparing Quantities guide

7. Maria invested ₹8000 in a business, and she would be paid interest at 5% per annum compounded annually. Find

1)The amount credited against her name at the end of the second year.

2)The interest for the 3rd year.

Solution: a) 1) P = ₹8000, R = 5% p.a. n = 2 years.

=\(80000\left(\frac{21}{20}\right)^2=8000 \times \frac{21}{20} \times \frac{21}{20}=₹ 8820\)

2) The interest for the next one year.

i.e., The third year has to be calculated. By taking ₹8820 as principal. The S.I. for the next year will be calculated.

8. Find the amount and the compound interest on ₹10,000 for 1 1/2 years at 10% per annum compounded half yearly. Would this interest be more than the interest he would get if it was compounded annually?

Solution: p = ₹10000, R=10%p.a. = 5% per half year \(n=1 1 / 2 \text { years. }\)

There will be 3 half years in 1 1/2 years.

=\(10000 \times \frac{21}{20} \times \frac{21}{20} \times \frac{21}{20}=₹ 11576.25\)

C.I. = A-P= 11576.25 – 10000= 1576.25

The amount for 1 year and 6 months can be calculated by first calculating the amount for 1 year using the compound interest formula, and then calculating. The simple interest for 6 months on the amount obtained at the end of 1 year.

The amount for the first year has to be calculated first.

=\(10000 \times \frac{11}{10}=₹ 11000\)

By taking ₹11000 as the principal, the S.I. for the next 1/2 year will be calculated.

∴ Interest for the first year = ₹11000=₹10000

= ₹1000+₹550 = ₹1550

∴ The interest would be when compounded half yearly than the interest when compounded annually.

9. Find the amount which Ram will get on ₹4096, he gave it for 18 months at 12 1/2%p.a., interest being compounded half-yearly.

Solution: P = ₹4096, R= 12 1/2% p.a. = 25/4% per half year. n=18 months.

There will be 3 half years in 18 months.

∴ \(A=P\left(R+\frac{1}{100}\right)^n=4096\left(1+\frac{25}{400}\right)^3\)

=\(4096\left(1+\frac{1}{16}\right)^3\)

=\(4096\left(\frac{17}{16}\right)^3=4096 \times \frac{17}{16} \times \frac{17}{16} \times \frac{17}{16}=4913\)

Thus, the required amount is ₹4913.

10. The population of a place increased to 54,000 in 2003 at a rate of 5% per annum.

1)Find the population in 2001

2)What would be its population in 2005?

Solution: 1) it is given that, the population in the year 2003 = 54,000

∴ \(54000=(\text { Population in 2001 })\left(1+\frac{5}{100}\right)^2\) population in 2001

=\(\frac{54000}{\left(1+\frac{5}{100}\right)^2}=\frac{54000}{\left(1+\frac{1}{20}\right)^2}=\frac{54000}{\left(\frac{21}{20}\right)^2}\)|

=\(54000 \times\left(\frac{20}{21}\right)^2=54000 \times \frac{20}{21} \times \frac{20}{21}\)

= 48979.59

Thus, the population in the year 2001 was approximately 48980.

2)\(\text { Population in } 2005=54000 \times\left(1+\frac{5}{100}\right)^2\)

=\(5400 \times\left(1+\frac{1}{20}\right)^2=54000 \times \frac{20}{21} \times \frac{20}{21}=59535\)

Thus the population in the year 2005 would be 59535.

11. In a laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5%. per hour. Find the bacteria at the end of 2 hours if the count was initially 506000.

Solution: The initial count of bacteria is given as 506000.

Bacteria at the end of 2 hours

=\(506000\left(1+\frac{1}{40}\right)^2=506000 \times \frac{41}{40} \times \frac{41}{40}\)

= 531616.25 = 531616(approx.)

Thus, the count of bacteria at the end of 2 hours will be 531616 approx.

12. A scooter was bought of ₹42000. Its value depreciated at the rate of 8% p.a. Find its value after one year.

Solution: Principal = cost price of the scooter = ₹42000

Depriciation=8% of ₹42000 per year

=\(\left(\frac{42000 \times 8 \times 1}{100}\right)=₹ 3360\).

Value after 1 year = ₹(42000-3360) = ₹38640.

 Class 8 Maths Chapter 15 KSEEB Comparing Quantities Additional Problems

1. A jacket was sold for ₹4120 after allowing a discount of 20%. Find marked price of the Jacket.

Solution: Let the marked price of the jacket be ₹x.

Discount % on marked price = 20%

Selling price of Jacket = ₹1120.

Then \(1120=x-x \times \frac{20}{100}\)

So, marked price of the jacket is ₹1400.

2. Anubha’s income is 20% less than that of Shubra. How much percent is Shubra’s income more than Anubha’s?

Solution: I Method: Suppose Shubra’s income = ₹100.

\(20 \% \text { of } 100=\frac{20}{100} \times 100=₹ 20\) .

∴ Anubha’s income = ₹(100 – 20) = ₹80

If Anubha’s income is ₹80.

Then Shubhra’s income = ₹100

If Anubha’s income is ₹1

Then Shubhra’s income = \( ₹ \frac{100}{80}\)

If Anubha’s income is ₹100

Then Shubhra’s income = \( ₹ \frac{100}{80} \times 100=₹ 125\)

∴ Shubhra’s income is ₹(125 – 100) or ₹25 i.e. 25% more than Anubha’s

(or)

II Method

Let Shubhra’s income = ₹100 then Anubha’s income = ₹(100 – 20) = ?80

Then Shubhra’s income is ₹20 more than Anubha’s.

Shubhra’s income = \(\frac{20}{80} \times 100\) = 25% more than 80 Anubha’s.

3. The price of sugar increased by 20%. By how much percent should Divesh reduce her consumption of sugar? So that her expenditure of sugar does not increase?

Solution: Suppose original consumption of sugar = 100kg

Suppose price of 100kg of sugar = ₹100

Increase in the price of sugar = 20% = ₹20.

Price of sugar after increase=₹100 + 20 = ₹120.

But expenditure has to remain ₹100 only.

So for ₹120, Divesh gets 100kg sugar

For ₹1 Divesh gets = \(\frac{100}{120}\)kg sugar

For ₹100 Divesh gets =\(\frac{100}{120} \times 100=\frac{10000}{120} \mathrm{~kg}\)

=\(83 \frac{1}{3} \mathrm{~kg} \text { sugar }\)

∴ Reduction in consumption =\(\left(100-83 \frac{1}{3}\right) \%\)

=\(\left(100-\frac{250}{3}\right) \mathrm{kg}=\frac{50}{3} \%=16 \frac{2}{3} \%\)

4. Tarun purchased a calculator for ₹500 and sold it to his friend at ₹560. Find his gain percent.

Solution: Here C.P. ₹500 and S.P. ₹560

Since S.P > C.P So, there is a profit.

Profit = S.P. – C.P. = ₹560 – ₹500 = ₹60

Profit percent

=\(\frac{\text { Profit }}{\text { C.P. }} \times 100=\frac{60}{500} \times 100=12 \%\)

5. If the selling price of 16 water bottles is equal to the cost price of 17 water bottles, find the gain percent earned by the dealer.

Solution: Let the cost price of each water bottle be ₹1

So the cost price of 17 water bottles will be ₹17.

C.P. of 16 water bottles = ₹16

S.P. of 16 water bottles = ₹17

∴ S.P. > C.P.

∴ There is gain and

Gain = S.P. – C.P. = ₹17- ₹l6 = ₹1

Gain% =

6. A dealer marks his goods at 35% above the cost price and allows a discount of 20% on the marked price. Find his gain or loss percentage.

Solution: Suppose C.P. =₹100

Marked price = ₹100 + 35% of 100

= ₹100 + ₹35 = ₹135

Discount = \(₹ \frac{20}{100} \times 135=₹ 27\)

S.P.= ₹135-₹27 = ₹108

∴ Gain = ₹108 – ₹100 = ₹8

∴ Gain % = \(\frac{8}{100} \times 100=8 \%\)

7. Meena bought a pen for ₹23.75, after getting 5% discount on it. What is its list price? Ans:

Solution: Let the list price be = ₹x.

Discount % = 5%

Discount = 5% of x

Net price = ₹23.75

Net price = \(x-\frac{x}{20}=\frac{19 x}{20}\)

8. Calculate the time in which ₹8000 would become ₹9500 at an interest rate of 7 1/2% p.a.

Solution: P = ₹8000, A= ?9500, R = \(7 \frac{1}{2} \%=\frac{15}{2} \%\)

I =A-P = 9500 – 8000 = 1500

=\(\frac{150^{1 \phi^5} \emptyset \times 100 \times 2^1}{4 28 \emptyset \emptyset 0 \times 15}=\frac{5}{2}=2 \frac{1}{2} \text { years. }\)

9. What principal will earn an interest of ₹576 at 6% per annum in 3 years?

Solution: I = ₹576, R = 6% p.a, T = 3 y ears.

=\(\frac{576 \times 100}{18}=₹ 3200\)

∴ p = ₹3200

10. Reema borrowed ₹5000. At the end of 5 years. Reema had to pay back ₹6225. What was the rate of interest?

Solution: P = ₹5000, A = ₹6225, T = 5 years.

Since A = P + I

∴ I = A – P = 6225 – 5000 = ₹1225

= 4.9% p.a.

R = 4.9% p.a.

11. If P = ₹3000, R = 8%, T = 13 weeks, find the total amount to be paid.

Solution: P = ₹3000, R = 8%, and T= 13 weeks

∴ \(\text { S.I. }=\frac{\text { PTR }}{100}=\frac{₹ 3000 \times 8 \times 13}{100 \times 52}=₹ 60\)

12. Heema deposited a sum of ₹500 at the rate of 5% in the bank on August 5. On October 17, she withdraw the sum deposited along with the interest. Find the amount she got.

Solution: P=₹500, T=Aug 5 to Oct = 17, R = 5% p.a.

Aug 5 to Aug 31            26 days

Sept                              30 days

Oct                               17 days

Total \(\frac{73}{365} \text { years }\)

Manavi got amount = P + I = ₹500+₹5

= ₹505

13. In what time will ₹1600 amount to ₹2025 and 12 1/2% per annum compounded annually.

Solution: Let time be n conversion periods.

Amount = ₹2025, principal = 1600 and Rate = \(12 \frac{1}{2} \% \text { p.a. }=\frac{25}{2} \% \text { p.a. }\)

∴ n=2

Hence, time = 2 years.

14. Find the amount on compound interest a sum of ₹5000 for 2 years at the rate of 2% per annum.

Solution: P1 = 5000, R = 2% p.a. T = 1 year.

Thus, amount at the end of the second year = ₹5202, and compound interest

= A – P =₹(5202-5000) = ₹202.

15. On selling a chair of ₹736, a shopkeeper suffers a loss of 8%. At what price should he sell it, so as to gain 8%?

Solution: Let the cost price of a chair = ₹x

Selling price of a chair = ₹736.

At selling a shopkeeper suffers 8% loss.

According to the question,

To gain 8% profit the price should be

=\(800+\frac{8}{100} \times 800=800+64\)

= ₹864

16. Find the S.P. if M.P. = ₹5450 and discount = 5%

Solution: Discount = 5% of ₹5450= \(\frac{5}{100} \times 5450\)

= ₹272.50

S.P. = M.P. – Discount = ₹5450-₹272.50

= ₹5177.50

17. Find the compound interest by calculating simple interest when principal is ₹3000, rate is 5% per annum and time is 2 years.

Solution: Principal for the 1 st year = ₹3000, R = 5, T = 2 years.

Interest for the 1st year= \(\frac{3000 \times 5 \times 1}{100}=₹ 150\)

Amount at the end of first year = ₹3000+150 = ₹3150.

Principle for the second year = ₹3150.

Interest for the second year = \(\frac{₹ 3150 \times 5 \times 1}{100}\)

= ₹157.50

Amount at the end of second year = ₹3150 + 157.50 = ₹3307.50

Compound interest = ₹3307.50 + ₹3000 = ₹307.50.

18. The difference between SI and CI of a certain sum of money is ₹48 at 20% p.a. for 2 years. Find the principal.

Solution: Let the certain sum be ₹P

=\(P\left(\frac{36}{25}-1\right)=\frac{11 P}{25}\)

As CI-SI = 48

p = 48 x 25 = ₹1200.

19. In a factory, women are 35% of all the workers the rest of the workers being men. The number of men exceeds that of women by 252. Find the total number of workers in the factory.

Solution: Let total number of workers be x.

Women = 35% of \(x = \frac{35}{100} x\)

Men = (100-35)% of x = 65% of \(x = \frac{65}{100} x\)

According to question,

x = 840

20. Karthik purchased a hair dryer for ₹5450 including 8% VAT. Find the price before VAT was added.

Solution: Let the original price of dryer be ₹100

Price including VAT = ₹108

When price including VAT is ₹108, original price = ₹100

When price including VAT is ₹5400, original price

=\(\frac{100}{108} \times 5400=₹ 5000\)

Thus, the price including VAT was added = ₹5000

21. A student used the proportion w100 = 532 to find 5% of 32. What did the student do wrong?

Solution: 5% of 32 will be calculated as

but student finding percent is 5 of 32

22. The human body is made up mostly of water. In fact about 67% of a person total body weight is water. If Jyoti weights 56kg. How much of her weight is water?

Solution: Jyoti’s weight = 56kg

where 67% of a person is total body weight is water.

Water in Jyoti body =

23. At a toy shop price of all the toys is reduced to 66% of the original price.

a)What is the sale price of a toy that originally costs ₹90?

b)How much money would you save on a toy costing ₹90?

Solution: a) Original cost of the toy = ₹90

If the price, reduced to 66% of the original price, then

price became = \(90-\frac{66}{100} \times 90=90-59.4\) = ₹30.6

b) We have discounted amount = 66% of 90

=\(\frac{66}{100} \times 90=₹ 59.4\)

24. In a certain experiment, the count of bacteria was increasing at the rate of 2.5% per hour. Initially, the count was 512000. Find the bacteria at the end of 2 hours.

Solution: Bacteria at the end of 2 hours

=\(\left\{512000 \times\left(1+\frac{5}{2 \times 100}\right)^2\right\}\)

=\(\left(512000 \times \frac{41}{40} \times \frac{41}{40}\right)=537920\)

Hence, the bacteria at the end of 2 hours = 537920.

25. A motorcycle is bought at ₹160000. Its value depreciates at the rate of 10% per annum. Find its value after

1) 1 year

2) 2 years.

Solution: 1) Value of the motorcycle after 1 year

=\(₹\left\{160000 \times\left(1-\frac{10}{100}\right)\right\}\)

=\(₹\left(160000 \times \frac{9}{10}\right)=₹ 144000\)

∴ value after 1 year = ₹144000

2) Value of the motorcycle after 2 years

=\(₹\left\{160000 \times\left(1-\frac{10}{100}\right)^2\right\}\)

=\(₹\left(160000 \times \frac{9}{10} \times \frac{9}{10}\right)=₹ 129600\)

∴ Value after 2 years = ₹129600

KSEEB Solutions For Class 8 Maths Chapter 14 Visualising Solid Shapes Points To Remember

There are three types of shapes

1) One-dimensional shapes: Shapes having length only, Example: aline

2) Two-dimensional shapes: Plane shapes having two measurements like length and breadth. Example: a polygon, a triangle, a rectangle etc., generally, two-dimensional figures are known as 2- D figures.

3) Three-dimensional shapes: Solid objects and shapes having length, breadth and height or depth. Example. cubes, cylinders, cone, cuboid, spheres etc.,

Read and Learn More KSEEB Solutions for Class 8 Maths

4)Face: A flat surface of a three-dimensional figure.

5) Edge: line segment where two faces of solid meet.

Polyhedron: A 3 – D figure whose faces are all polygons.

Prism: Apolyhedron whose bottom and top faces (known as base) are congruent polygons and faces known as lateral faces are parallelograms. When the sides faces are rectangles. The shape is known as right prism.

Pyramid: Apolyhedron whose base is a polygon and lateral faces are triangles.

Vertex: Apoint where three or more edges meet.

Base: The face that is used to name a polyhedron

Euler’s Formula for any polyhedron is F + V – E= 2 where F stands for number of faces, V for number of vertices and E for number of edges.

3D objects have different views from different positions.

Practice Questions For KSEEB Class 8 Visualising Solid Shapes

Mapping: A map depicts the location of a particular object/place in relation to other objects/places.

A map is different from a picture.

Symbols are used to depict the different object places

There is no reference or perspective in a map.

Maps involve a scale which is fixed for a particular map.

Convex: The line segment joining any two points on the surface of a polyhedron entirely lies inside or on the polyhedron. Ex: Cube, cuboid tetrahedron, pyramid, prism etc.,

Class 8 Maths KSEEB Chapter 14 Solved Examples Visualizing Solid Shapes Exercise 14.1

1. For each of the given solid, the two views are given. Match for each solid the corresponding top and front views. The first one is done for you.

Solution:

Object                 side view            Top view

a) A bottle                 3                        4

b) A weight               1                        5

c) A flask                   4                       2

d) cup & saucer        5                       3

e) container               2                      1

2. For each of the given solid, the three views are given. Identify for each solid the corresponding top, front and side views.

Solution:

Object                              1                                      2                                      3

a) An almirah           Front view                        Side view                            Top view

b) A matchbox        Side view                         Front view                            Top view

c) A Television        Front view                         Side view                             Top view

d) A car                  Front view                         Side view                             Top view

3. For each given solid, identify the top view, front view, and side view.

Solution:

Object                            1                            2                           3

a)                           Top view                Front view              Side view

b)                          Side view               Front view               Top view

c)                          Top view                Side view                Front view

d)                         Side view               Front view                Top view

e)                         Front view             Top view                   Side view

Simplified Guide For KSEEB 8th Maths Visualising Solid Shapes

4. Draw the front view, side view, and top view of the given objects

Solution:

KSEEB Solutions for Class 8 Maths Chapter 14 Visualising Solid Shapes

Visualizing Solid Shapes Class 8 KSEEB Guide Exercise 14.2

1. Look at the given map of a city.

a)Colour the map as follows: Blue-water, red-fire station, orange – library, yellow – schools, Green – park, pink-college, purple – hospital, Brown – cemetery.

b)mark a green ‘X’ at the intersection of Road ‘C’ and Nehru road, Green ‘Y’ at the intersection of Gandhi Road and Road A.

c)In red, draw a short street route from library to the bus depot.

d)Which is further east, the city park or the market?

e)Which is further south, the primary school or the Sr. secondary school?

Solution:
a)

b)

c)

d) Between the market and the city park, the city park is further east.

e) Between the primary school and the Sr. secondary school. The Sr. secondary is further south.

KSEEB Class 8 Visualising Solid Shapes Solutions Exercise 14.3

1. Can a polyhedron have for a face?

1) 3 triangles?

2) 4 triangles?

3) a square and four triangles?

Solution: 1) No, such a polyhedron is not possible. A polyhedron has minimum 4 faces.

2)yes, a triangular pyramid has 4 triangular faces.

3) yes, a square pyramid has a square face and 4 triangular faces.

2. Is it possible to have a polyhedron with any given number of faces?

Solution: A polyhedron has a minimum of 4 faces.

3. Which are prisms among the following?

1) 

Solution: It is not a polyhedron as it has a curved surface.

∴ it will not be a prism also.

2) 

un-sharpened pencil.

Solution: It is a prism

3)   

a table weight.
Solution: It is not a prism, it is a pyramid

4)           

A box

Solution: it is a prism

4. 1) How are prisms and cylinder alike?

Solution: A cylinder can be thought of as a circular prism. i.e., a prism that has a circle as its base.
2) How are pyramids and cones alike?

Solution: A cone be thought of as a circular pyramid, i.e., a pyramid that has a circle as its base.

5. Is a square prism same as a cube? Explain.

Solution: A square prism has a square as its base. However, its height is not necessarily same as the side of the square. Thus, a square prism can also be a cuboid.

Class 8 Maths KSEEB Chapter 14 Solved Examples

6. Verify Euler’s formula for these solids.
1)
Faces = 7
Vertices = 10
Edges = 15
2)
F = 9, V = 9, E = 16
F + V – E = 9 + 9 -16
= 18 – 16 = 2
F + V – E = 7 + 10 – 15 = 2
Hence, Euler’s formula is verified

7. Using Euler’s formula find the unknown

Faces           7          5         20

Vertices      6          ?         12

Edges        12         9          ?

Solution: By Euler’s formula, we have F + V – E = 2

1) F + 6 – 12 = 2

F – 6 = 2

F = 2 + 6 = 8

2) 5 + V – 9 = 2

V – 4 = 2

V = 2 + 4 = 6

3) 20 + 12 – E = 2

32 – E = 2

32 – 2 = E

E = 30

Thus, the table can be written as

8. Can a polyhedron have 10 faces, 20 edges, and 15 vertices?

Solution:  F=10, E=20, V=15

Any polyhedron satisfies Euler’s formula

According to which F+V-E=2

For the given polygon F+V-E

⇒ 10+15-20=25-20=5≠2

Since Euler’s formula is not satisfied, such a polyhedron is not possible.

KSEEB Maths Class 8 Chapter 14 Visualising Solid Shapes Additional Problems

1. Height of a building is 9m and this building is represented by 9cm on a map. What is the scale used for the map?

Solution: Scale of map = Size drawn/Actual size = 9cm/900cm = 1/100

[∵ 9m = 900cm]

Thus, scale is 1:100

2. The distance between city A and city B on a map is given as 6cm. If the scale represents 1cm=200km, then find the actual distance between city A and city B

Solution: Actual distance represented by 1cm = 200km

Actual distance represented by 6cm

So, actual distance between city A and city B is 1200km.

3. What do you mean by regular polyhedron? Write all polyhedron shapes.

Solution: A polyhedron is said to be regular if its faces are made up of regular polygons and the same number of faces meet at each vertex. There are five such solids: tetrahedron cube octahedron, dodecahedron, and icosahedron.

4. Identify the shape whose net is given below

Solution: This shape is entirely made of equilateral triangles. When folded, it results in a regular octahedron. Note that since these are all equilateral and congruent faces, it is a regular polyhedron.

5. Using Euler’s formula find the unknown

1) F=?      v=5     E=18

Solution: F+V-E=2

F+5-18=2

F-13=2

F=2+13=15

2) F=6    V=?     E=12

Solution: F+V-E=2

6+V-12=2

V-6=2

V=2+6=8

6. The side of a square board is 50cm. A student has to draw its image in her notebook. If the drawing of the square board in the notebook has perimeter of 40cm, then by which scale the figure has been drawn?

Solution: Given, the side of a square board is 50cm. So, perimeter of thr square board = 4 x side = 4 x 50 = 200cm

On drawing in the notebook, the perimeter of a square board = 40cm.

∴ Scale

Size of actual square board/Size in notebook = 200/40 = 5 : 1

Hence, the used scale is 5 : 1.

7. A polyhedron has 60 edges and 40 vertices. Find the number of its faces.

Solution: By using Euler’s formula for polyhedron.

F+V-E=2

F+40-60=2

F-20=2

F=2+20=22

Hence, the number of faces are 22

8. The distance school and house of a girl is given by 5cm in a picture, using the scale 1cm : 5km. Find the actual distance between the two places?

Solution: Given scale = 1cm: 5km.

i.e., 1cm in picture =5km of actual distance

∴ 5cm in picture = 5 x 5km of actual distance.

Hence, the actual distance between the two places is 25km.

So 5cm represent = 5 x 5 = 25km distance.

9. What do you mean by regular polyhedra? Write all polyhedron shapes.

Solution: A polyhedron is said to be regular if its faces are made up of regular polygons and the same number of faces meet at each vertex.

There are five such solids: tetrahedron, cube, octahedron, dodecahedron and icosahedron.

10. Name the polyhedron that can be made by folding each net.

Solution: 1) Square pyramid

2) Triangular prism.

11. Name the following polyhedrons and verify Euler’s formula for each of them.

Solution: 1) Tetrahedron, F=4, V=4, E=6

Euler’s formula

F+V-E=2

LHS = 4+4-6

= 8-6=2 = RHS

Hence verified.

2) Cuboid, F=6, V=8, E=12

F+V-E=2

LHS = F+V-E = 6+8-12 = 14-12=2 = RHS

Hence Verified.

12. What figure is formed if only the height of a cube is increased or decreased?

Solution: If we only increase on decrease the height of a cube, the obtained figure is cuboid.

13. In a town, an icecream parlour has displalyed an ice-cream sculpture of height 360cm, the parlour claims that the ice-creams and the sculpture are in the scale 1:30. What is the height of the icecream served? hence, the height of the ice-cream served is 12cm.

Solution: Given, height of icecream sculpture = 360cm

Scale used for ice-cream sculpture & sculpture = 1:30

the height of the ice-creams served = scale x Actual size

=\(\frac{1 \times 360}{30}=12 \mathrm{~cm}\)

Hence, the height of the ice-cream served is 12cm.

KSEEB Class 8 Maths Solutions For Chapter 12 Introduction Of Graphs Points To Remember

Graphical representation of data is easier to understand.

1) A bar graph is used to show comparison among categories.

2) A pie graph is used to compare parts of a whole.

3) A Histogram is a bar graph that shows data in intervals.

A line graph displays data that changes continuously over periods of time.

A line graph which is a whole unbroken line is called a linear graph.

Read and Learn More KSEEB Solutions for Class 8 Maths

For fixing a point on the graph sheet we need, x – co-ordinate and y – co-ordinate

The relation between dependent variable and independent variable is shown through a graph.

A bar graph: A pictorial representation of numerical data in the form of bars (rectangles) of uniform width with equal spacing. The length (or height) of each bar represents the given number.

A pie graph: A pie graph is used to compare parts of a whole. The various observations or components are represented by the sectors of the circle.

A Histogram: Histogram is a type of a bar diagram, where the class intervals are shown on the horizontal axis and the heights of the bars (rectangles) show the frequency of the class interval, but there is no gap between the bars as there is no gap between the class intervals.

Linear graph: A line graph in which all the line segments form a part of a single line.

Coordinates: A point in cartesian plane is represented by an ordered pair of numbers.

Ordered pair: A pair of numbers written in specified order.

Introduction To Graphs Solutions KSEEB Class 8 Maths Introduction To Graphs Exercise 12.1

1. The following graph shows the temperature of a patient in a hospital, recorded every hour.

a)What was the patient’s temperature at 1 p.m.?

b)When was the patient’s temperature 38.5°c?

c)The patient’s temperature was the same two times during the period given. What were these two times?

d)What was the temperature at 1.30 p.m.? How did you arrive at your answer?

e)During which periods did the patient’s temperature showed an upward trend?

Solution: a)At 1 p.m., the patient’s temperature was 36.5°c.

b)The patient’s temperature was 38.5°c at 12 noon.

c)The patient’s temperature was the same at 1 pm and 2 pm.

d)The graph between the times 1 pm and 2 p.m. is parallel to the x-axis. The temperature at 1 pm and 2pm is 36.5°c. So the temperature at 1.30pm is 36.5°c.

e)During the following periods, the patient’s temperature showed an upward trend.

9 am to 10 am, 10 am to 11am,

2 pm to 3 pm

2. The following line graph shows the yearly sales figures for a manufacturing company.

a)What were the sales in

1) 2002

2) 2006?

b)What were the sales in

1) 2003

2) 2005?

c)Compute the difference between the sales in 2002 and 2006.

d)In which year was there the greatest difference between the sales as compared to its previous year?

Solution: a) 1) In 2002, the sales were ₹4 crores.

2)In 2006, the sales were ₹8 crores.

b)1) In 2003, the sales were ₹7 crores.

2)In 2005, the sales were ₹10 crores.

c)In 2002, the sales were ₹4 crores and in 2006, the sales were ?8 crores.

Difference between the sales in 2002 and 2006 = ₹(8 – 4) crores = ₹4 crores.

d)Difference between the sales of the year 2006 and 2005 = ₹(10 – 8) = ₹2 crores.

Difference between the sales of the year 2005 and 2004 = ₹(10 – 6) = ₹4 crores.

Difference between the sales of the year 2004 and 2003 = ₹(7 – 6) = ₹1 crores.

Difference between the sales of the year 2003 and 2002 = ₹(7 – 4) = ₹3 crores

Hence, the difference was the maximum in the year 2005 as compared to its previous year 2004.

Practice Questions For Introduction To Graphs KSEEB Maths 

3. For an experiment in Botany, two different plants, plant A and plant B were grown under
similar laboratory conditions. Their heights were measured at the end of each week for 3 weeks, the results are shown by the following graph.

a)How high was plant A after

1)2 week

2) 3 weeks?

b)How high was plant B after

1) 2 weeks

2) 3 weeks?

c)How much did plant A grow during the 3rd week?

d)How much did plant B grow from the end of the 2nd week to the end of the 3rd week?

e)During which week did plant A grow most?

f)During which week did plant B grow least?

g)were the two plants of the same height during any week shown here? specify.

Solution: a) 1) After 2 weeks, the height of plant A was 7cm.

2)After 3 weeks, the height of plant A was 9 cm

b)1) After 2 weeks, the height of plant B was 7 cm.

2) After 3 weeks, the height of plant B was 10cm.

c)Growth of plant A during 3rd week = 9 cm – 7cm = 2 cm

d)Growth of plant B from the end of the 2nd week to the end of the 3rd week

= 10cm – 7cm = 3cm

e)Growth of plant A during 1 st week = 2cm – 0 cm = 2cm

Growth of plant A during 2nd week = 7cm – 2cm = 5 cm Growth of plant A during 3rd week = 9cm – 7cm = 2 cm

∴ Plant A grew the most i.e., 5 cm during the 2nd week.

f)Growth of plant B during 1st week = 1cm – 0 cm = 1cm

Growth of plant B during 2nd week

= 7cm- lcm = 6cm

Growth of plant B during 3rd week

= 10cm- 7cm = 3 cm

Plant B grew the most i.e., 6 cm during the 2nd week.

g)At the end of the 2nd week, the heights of both plants were same.

4. The following graph shows the temperature forecast and the actual temperature for each day of a week.

a) On which days was the forecast temperature the same as the actual temperature?

b) What was the maximum forecast temperature during the week?

c) What was the minimum actual temperature during the week?

d) On which day did the actual temperature differ the most from the forecast temperature?

Solution: a) The forecast temperature was same as the actual temperature on Tuesday, Friday and Sunday.

b) The maximum forecast temperature during the week was 35°c.

c) The minimum actual temperature during the week was 15°c.

d) The actual temperature differs the most from the forecast temperature on thursday.

5. Use the tables below the draw linear graphs.

a) The number of days a hill side city received snow in different years.

b) Population (in thousands) of men and women in a village in different years.

Solution: a) By taking the years on x- axis and the number of days on the y-axis and taking scale as 1 unit = 2 days only – the axis and 2 unit = 1 year on x-axis, the linear graph of the given information can be drawn as follows.

b)By taking the years on x – axis and population on y- the axis and scale as 1 unit = 0.5 thousand on the y-axis and 2 unit = 1 year on x-axis, the linear graph of the given information can be drawn as follows.

KSEEB Class 8 Maths Chapter 12 Solved Problems 

6. A courier – a person cycles from a town to a neighboring suburban area to deliver a parcel to a merchant. This distance from the town at different times is shown by the following graph.

a)What is the scale taken for the time axis?

b)How much time did the person take for the travel?

c)How far is the place of the merchant from the town?

d)Did the person stop on his way? Explain.

e)During which period did he ride fastest?

Solution: a) Scale taken for the time axis is 4 units = 1 hour.

b) The person traveled during the time 8 am. – 11.30 am.

∴ The person took 3 1/2 hours to travel

c)The merchant is 22 km far from the town.

d)Yes, the person stopped on his way from 10 am to 10.30 am. This is indicated by the horizontal part of the graph.

e)from the graph, it can be observed that during 8 am to 9 am, The person travelled the maximum distance. Thus, the person’s ride was the fastest between 8 am and 9 am.

7. Can there be a time-temperature graph as follows? Justify your answer.

Solution: 1) This can be a time-temperature graph, as the temperature can increase with the increase in time.

2)This can be a time-temperature graph, as the temperature can decrease with the decrease in time.

3)This cannot be a time-temperature graph since different temperatures at the same time are not possible.

4)This can be a time-temperature graph, as same temperature at different times is possible.

KSEEB Maths Class 8 Introduction To Graphs Exercise 12.2

1. Plot the following points on a graph sheet verify if they lie on a line.

a)A(4, 0), B(4, 2), C(4, 6), D(4, 2.5)

b)P(l, 1),Q(2,2),R(3,3),S(4,4)

c)K(2, 3), L(5,3), M(5,5), N(2,5)

Solution:

a)From the graph, it can be observed that the points A, B, C and D lie on the same line.

b)Hence, points P, Q, R & S lie on the same line.

c)Hence, points K, L, M & N are not lying on the same line.

2. Draw the line passing through (2,3) and (3, 2). Find the co-ordinates of the points at which this line meets the x – axis and y -axis.

Solution:

From the graph, it can be observed that the line joining the points (2, 3) and (3, 2) meet the x – axis at the point x(5, 0) and the y – axis at the point (0, 5).

3. Write the co-ordinates of the vertices of each of these adjoining figures.

Solution: The co-ordinates of the vertices in the given figure are as follows.

0(0,0)

A(2, 0)

B(2, 3)

C(0, 3)

P(4,3)

Q(6, 1)

R(6, 5)

S(4, 7)

K(10, 5)

L(7, 7)

M(10, 8)

4. State whether True or False. Correct that are false.

1)A point whose x – co-ordinate is zero and y – co-ordinate is non-zero will lie on the y -axis.

Solution: True

2) A point whose y – co-ordinate is zero and x – co-ordinate is 5 will lie on y -axis.

Solution: False

The point whose y – co-ordinate is zero and x – co-ordinate is 5 will lie on x – axis.

3)The co-ordinates of the origin are (0,0)

Solution: True

Introduction To Graphs Exercise 12.3

1. Draw the graphs for the following tables of values, with suitable scales on the axes
a) cost of apples

b) Distance traveled by a car

1)How much distance did the car cover during the period 7.30 a.m to 8 a.m.?

2)What was the time when the car had covered a distance of 100 km since it’s start?

c) Interest on deposit for a year.

1)Does the graph pass through the origin?

2)Use the graph to find the interest on ₹2500 for a year.

3)To get an interest of ₹280 per year, how much money should be deposited?

Solution: a) Taking a suitable scale for x-axis 1 unit = 1 apple and for the y-axis, 1 unit = ₹5), we can mark the number of apples on the x-axis and the cost of apples on the y-axis, A graph of the given data is as follows.

b) Taking a suitable scale (for the x-axis, 2 units = 1 hour and for the y-axis, 2 units = 40km) we can represent the time on the x-axis and the distance covered by the car on the y-axis. A graph of the given data is as follows.

1)During the period 7.30a.m to 8 a.m. The car covered a distance of 20 km.

2)The car covered a distance of 100km at 7.30 am. Since its start.

c) Taking a suitable scale

For x -axis, 1 unit = X1000 and for y – axis 1 unit = ₹80. We can represent the deposit on x – axis and the interest earned on that deposit on y – axis. A graph of the given data is obtained as follows.

From the graph, the following points can be observed.

1)Yes, the graph passes through the origin.

2)The interest earned in a year on a deposit of ₹2500 is ₹200.

3)To get an interest of ₹280 per year, ₹3500 should be deposited.

2. Draw a graph for the following.

1) is it a linear graph?

2) is it a linear graph?

Solution: 1) choosing a suitable scale,

For x – axis, 1 unit = 1cm, and for y – axis, 1 unit = 4cm. We can represent the side of a square on x – axis and the perimeter of that square on y – axis. A graph of the given data is drawn as follows.

It is a linear graph.

2)Choosing a suitable scale

For x – axis, 1 unit = 1 cm and for y – axis 1 unit = \(4cm^2\). We can represent the side of a square on the x-axis and the area of that square on y – axis. A graph of the given data is as follows.

It is not a linear graph.

KSEEB Class 8 Maths Introduction To Graphs Additional Problems

1. The point (4, -3) lies in which quadrant?

Solution: The point (4, -3) lies in 4 quadrant.

2. Write the x-co-ordinate (abscissa) of each of the given points :

1) (3,7)

2) (7,5)

Solution: We know the point on graph is denoted by (x,y), and x – co – ordinate is abscissa.

point (1) (3,7), 3 is the x-co-ordinate

(2)(7,5), 7 is the x-co-ordinate

3. Write the y – co – ordinate (ordinate) of each of the given points,

1) (3,5)

2) (5,0)

Solution: (1) point (3, 5), 5 is the y – co – ordinate

(2) (5, 0), 0 is the y – co – ordinate

4. Plot the following points on graph paper.

a) A(4,5) b) (0,7) c) C(6, 0) d) D(6,3)

Solution:

5. Write the co-ordinates of all the points in the given graph.

Solution:

A(4, 1) E(5,3)
B(7,4)F(3,5)
C(4, 7) G(3, 5)
D(l, 4) H(5, 5)

6. Plot the points (4, 4), (1, 3), (4, 2), and (7,3) on a paper and connect them with line segments. Name the shape formed by these points.

Solution:

The shape formed is a rhombus.

7. Study the given map of a zoo and answer the following questions.

1)Give the location of lions in the zoo

2)(D, f) and (C, d) represent location of which animals in the zoo?

3)where are the toilets located?

4)Give the location of canteen

Solution:

1) (A, f)

2)By seeing through graph, point (D, f) represents monkeys point (C, d) represent elephants

3)(0, e)

4)(C,c)

8. The following graph shows the journey made by two cyclists, one from A to B and the other from town B to A.

1)At what time did cyclist II rest? How long did the cyclist rest?

2)Was cyclist n cyclind faster or slower after the rest?

3)At what time did the two cyclists meet?

4)How far had cyclist II travelled when he met cyclist I?

Solution:

Solution: 1) Cyclist II rest for 15 minute from 8 :45 am to 9:00am

2)Cyclist II was cycling faster after the rest.

3)Two cyclist meet at 9 : 00 am.

4)cyclist II travelled 10 km when he met cyclist I.

9. Draw a graph for the radius and circumference of circle using a suitable scale.

(Hint: Take radius 7,14,21 units and so on)

From the graph,

1) Find the circumference of the circle when radius is 42 units.

2) At what radius will the circumference of the circle be 220 units?

Solution:

1)When radius is 42 units, circumference is 264 units

2)When circumference of the circle is 220 units, radius is 35 units.

10. The following graph shows the number of people present at a certain shop at different times. Observe the graph and answer the following questions.

1)What type of graph of this?

2)What information does the graph give?

3)What is busiest time of day at the shop?

4)How many people enter the shop when it open

5)About how many people are there in the shop at 1: 30 pm?

Solution:

1)It is a line graph

2)It represents the number of people visited the shop at different time.

3)It is 1 pm as 25 people visited the shop which is maximum.

4)Less than 5 people entered the shop when it opened.

5)20 people were there at 1: 30 p.m.

KSEEB Class 8 Maths Solutions For Chapter 11 Direct And Inverse Proportions Points To Remember

Variations: If the values of two quantities depend on each other in such a way that a change in one cause corresponding change in the other, then the two quantities are said to be in variation.

Direct variation or Direct proportion

Two quantities x & y are said to be in direct proportion. If they increase (decrease) together in such a manner that the ratio of their corresponding

values remains constant that is if \(\frac{x}{y}=k\)

Read and Learn More KSEEB Solutions for Class 8 Maths

[k is a +ve number] then x & y are said to vary directly. In such a case ify,, y2 are the values of y corresponding to the values x{, x2 of x respectively then = \(\frac{x_1}{y_1}=\frac{x_2}{y_2}\)

If the number of articles purchased increases, the total cost also increases.

More than money deposited in a bank is the interest earned.

Quantities increasing or decreasing together need not always be in direct proportion, same in the case of inverse proportion.

When two quantities x & y are in direct proportion (or vary directly) they are written as x x y, symbol ‘∝’ stands for ‘is proportion to’.

Inverse proportion :

Two quantities x & y are said to be in inverse proportion if an increase in X causes a proportional decrease in y (and vice versa) in such a manner that the product of their corresponding values remains constant, that is, ifxy=k then x & y are said to vary inversely.

In this case if y1,y2 are the values of y corresponding to the values X1,x2 of x respectively then \(x_1 y_1=x_2 y_2\) or \(\frac{x_1}{x_2}=\frac{y_2}{y_1}\)

When two quantities x & y are in inverse proportion (or vary inversely) they are written as \(x \alpha \frac{1}{y}\)

Example: If the number of workers increases, time taken to finish the job decreases, or if the speed will increase the time required to cover a given distance will decrease.

Direct And Inverse Proportions Solutions KSEEB Class 8 Maths Exercise 11.1

1. Following are the car parking charges near a railway station up to

Check if the parking charges are in direct proportion to the parking time.

Solution:

The ratio of parking charges to the respective number of hours(Rs/hour) can be calculated as.

As each ratio is not same,

∴ The parking charges are not in a direct proportion to the parking time.

2. A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of base in the following table, find the parts of base that need to be added.

Solution: The given mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of base. For more parts of red pigments. the parts of the base will also be more, therefore the parts of red pigments and the parts of base are in direct proportion. The given information in the form of a table is as follows.

According to direct proportion

The table can be drawn as follows

KSEEB Class 8 Maths Key Concepts Of Direct And Inverse Proportions

3. In question 2 above, if 1 part of a red pigment requires 75ml of base, how much red pigment should we mix with 1800ml of base?

Solution: Let the parts of red pigment required to mix with 1800ml of base be z.

The given information in the form of a table is as follows.

The parts of red pigment and the parts of base are in direct proportion.

∴ we obtain

⇒ \(x=\frac{1 \times 1800}{75}\)

Thus, 24 parts of red pigments should be mixed with 1800ml of base.

4. A machine in a soft drink factory fills 840 bottles in six hours, how many bottles will it fill in five hours?

Solution: Let the number of bottles filled by the machine in five hours be x.

The number of bottles and the time taken to fill these bottles are in direct proportion.

∴ we obtain

⇒ \(x=\frac{{ }^{140} 840 \times 5}{6_1}\)

⇒ x = 700

Thus, 700 bottles will be filled in 5 hours.

5. A photograph of a bacteria enlarged 50,000 times attains a length of 5cm as shown in the diagram. What is the actual length of the bacteria? If the photograph is enlarged 20,000 times only, what would be its enlarged length?

Solution: Let the actual length of bacteria be ‘x’ cm and the enlarged length of bacteria be ‘y’ cm. If the photograph is enlarged for 20,000 times.

The given information in the form of a table is as follows.

The number of times the photograph of bacteria was enlarged and the length of bacteria are in direct proportion.

∴ we obtain \(\frac{5}{50,000}=\frac{x}{1}\)

⇒ \(x=\frac{1}{10000}=10^{-4}\)

Hence, the actual length of bacteria is \(10^{-4} \mathrm{~cm}\)

Let the length of bacteria when the photograph of bacteria is enlarged 20,000 times be y.

Hence, the enlarged length of bacteria is 2cm.

6. In a model of a ship, the mast is 9cm high, while the mast of the actual ship is 12m high, If the length of the ship is 28m, how long is the model ship?

Solution: Let the length of the mast of the model ship be ‘x’ cm.

The given information in the form of a table is as follows.

We know that the dimensions of the actual ship and the model ship are directly proportional to each other.

∴ we obtain \(\frac{12}{9}=\frac{28}{x}\)

Thus, the length of the model ship is 21cm

7. Suppose 2kg of sugar contains \(9 \times 10^6\) crystals. How many sugar crystals are there in

1) 5kg of sugar?

2) 1.2kg of sugar?

Solution: 1) Let the number of sugar crystals in 5kg of sugar be x.

The given information in the form of a table is as follows.

The amount of sugar and the number of crystals it contains are direct proportional to each other.

∴ we obtain \(\frac{2}{9 \times 10^6}=\frac{5}{x}\)

Hence, the number of sugar crystals is \(2.25 \times 10^7\)

2) Let the number of sugar crystals in 1.2kg of sugar be y. The given information in the form of a table is as follows.

Hence, the number of sugar crystals is \(5.4 \times 10^6\)

Practice Questions For Direct And Inverse Proportions KSEEB Maths

8. Rashmi has a road map with a scale of 1cm representing 18km. She drives on a road for 72km. What would be her distance covered in the map?

Solution: Let the distance represented on the map be x cm

The given information in the form of a table is as follows.

The distance covered on road and represented on map are directly proportional to each other.

∴ we obtain \(\frac{18}{1}=\frac{72}{x}\)

⇒ \(x=\frac{72}{18}=4\)

Hence, the distance represented on the map is 4cm.

9. A 5m 60cm high vertical pole casts a shadow 3m 20cm long. Find at the same time

1)The length of the shadow cast by another pole lOm 50cm high

2)The height of a pole which casts a shadow 5m long.

Solution: 1) Let the length of the shadow of the other pole be x m.

1m= 100cm.

The given information in the form of a table is as follows.

more the height of an object, more will be the length of its shadow.

Thus, the height of an object and length of its shadow are directly proportional to each other.

∴ we obtain \(\frac{5.60}{3.20}=\frac{10.50}{x}\)

⇒ \(x=\frac{10.50 \times 3.20}{5.60}=\frac{33.6}{5.60}=6\)

Hence, the length of the shadow will be 6m.

2) Let the height of the pole be ym

The given information in the form of a table is as follows.

The height of the pole and the length of the shadow are directly proportional to each other

∴ \(\frac{5.60}{3.20}=\frac{y}{5}\)

⇒ \(y=\frac{5 \times 5.60}{3.20}=\frac{28}{3.20}=8.75\)

Thus, the height of the pole is 8.75m or 8m 75 cm.

10. A loaded truck travels 14km in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?

Solution: Let the distance travelled by the truck in 5 hours be x km

We know, 1 hour = 60 minutes

∴ 5 hours = (5 x 60) minutes = 300 minutes

The given information in the form of a table is as follows.

The distance travelled by the truck and the time taken by the truck are directly proportional to each other.

∴ \(\frac{14}{25}=\frac{x}{300}\)

⇒ \(x=\frac{300 \times 14}{25}=168\)

Hence, the distance travelled by the truck is 168/km

KSEEB Class 8 Maths Chapter 11 Solved Problems Direct And Inverse Proportions Exercise 11.2

1. Which of the following are in inverse proportion?

1)The number of workers on a job and the time to complete the job.

Solution: These are in inverse proportion because if there are more workers, then it will take lesser time to complete that job.

2)The time taken for a journey and the distance travelled in a uniform speed.

Solution: No, these are not in inverse proportion because, in more time, we may cover more distance with a uniform speed.

3)Area of cultivated land and the crop harvested.

Solution: No, these are not in inverse proportion because, in more area, more quantity of crop may be harvested.

4)The time taken for a fixed journey and the speed of the vehicle.

Solution: These are in inverse proportion because with more speed, we may complete a certain distance in a lesser time.

5)The population of a country and the area of land per person.

Solution: These are in inverse proportion because if the population is increasing, then the area of the land per person will be decreasing accordingly.

2. In a television game show, the prize money of 1,00,000 is to be divided equally amongst the winners. Complete the following table and find whether the prize money given to an individual winner is directly or inversely proportional to the number of winners.

Solution: A table of the given information is as follows

From the table, we obtain

1 x 100000 = 2 x 50000 = 100000

Thus, the number of winners and the amount given to each winner are inversly proportional to each other.

∴ \(1 \times 100000=4 \times x_1\)

⇒ \(x_1=\frac{100000}{4}=25000\)

⇒ \(x_2=\frac{100000}{5}=20000\)

⇒ \(x_3=\frac{100000}{8}=12500\)

⇒ \(x_4=\frac{100000}{10}=10000\)

⇒ \(x_5=\frac{100000}{20}=₹ 5000\)

Direct And Inverse Proportions Questions And Answers KSEEB Maths

3. Rehman is making a wheel using spokes. He wants to fix equal spokes in such a way that the angles between any pair of consecutive spokes are equal. Help him by completing the following table.

1)Are the number of spokes and the angles formed between the pairs of consecutive spokes in inverse proportion?

2)Calculate the angle between a pair of consecutive spokes on a wheel with 15 spokes

3)How many spokes would be needed, if the angle between a pair of consecutive spokes is 40°?

Solution: A table of the given information is as follows.

From the given table, we obtain

4 x 90° = 360° = 6 x 60°

Thus, the number of spokes and the angel between a pair of consecutive spokes are inversly proportional to each other,

∴ \(4 \times 90^{\circ}=x_1 \times 8\)

⇒ \(x_1=\frac{4 \times 90^{\circ}}{8}=45^{\circ}\)

Thus the following table is obtained

1) yes, the number of spokes and the angles formed between the pairs of consecutive spokes are in inverse proportion.

2) Let the angle between a pair of consecutive spokes on a wheel with 15 spokes be x.

∴ 4 x 90° = 15 x x

⇒ \(x=\frac{4 \times 90^{\circ}}{15}=24^{\circ}\)

Hence, the angle between a pair of consecutive spokes of a wheel, which has 15 spokes in it is 24°.

3) Let the number of spokes in a wheel, which has 40° angles between a pair of consecutive spokes be y.

∴ 4 x 90° = y x 40°

⇒ \(y=\frac{4 \times 90^{\circ}}{40}=9\)

Hence, the number of spokes in such a wheel is 9.

4. If a box of sweets is divided among 24 children, they will get 5 sweets each. How many would each get? If the number of children is reduced by 4?

Solution: Number of remaining children = 24 – 4 = 20

Let the number of sweets that each of the 20 students will get, be x.

The following table is obtained.

If the number of students is lesser then each student will get more number of sweets. Since this is a case of inverse proportion then 24 x 5 = 20 x x

⇒ \(x=\frac{24^6 \times \phi^1}{20}=6\)

Hence, each student will get 6 sweets.

5. A farmer has enough food to feed 20 animals in his cattled for 6 days, How long would the food last if there were 10 more animals in his cattle?

Solution: Let the number of days that the food will last if there were 10 more animals in the cattle be ‘x’.

The following table is obtained.

More the number of animals lesser will be the number of days for which the food will last. Hence, the number of days the food will last and the number of animals are inversly proportional to each other.

∴ 20 x 6 = 30 x x

⇒ \(x=\frac{20^4 \times 6^1}{30 z_1}=4\)

x = 4

Thus, the food will last for 4 days.

6. A contractor estimates that 3 persons could rewire Jasminder’s house in 4 days. If he uses 4 persons instead of three, how long should they take to complete the job?

Solution: Let the number of days required by 4 persons to complete the job be x.

The following table is obtained.

If the number of persons is more, then it will take lesser time to complete the job.

Hence, the number of days and the number of persons required to complete the job are inversely proportional to each other.

∴ 4 x 3 = x x 4

⇒ \(x=\frac{4 \times 3}{4}=3\)

Thus, the number of days required to complete the job is 3.

KSEEB Class 8 Maths Chapter 11 Direct And Inverse Proportions

7. A batch of bottles was packed in 25 boxes with 12 bottles in each box. If the same batch is packed using 20 bottles in each box, how many boxes would be filled?

Solution: Let the number of boxes filled, by using 20 bottles in each box be x.

The following table is obtained.

More the number of bottles, lesser will be the number of boxes.

Hence, the number of bottles and the number of boxes required to pack these are inversely proportional to each other.

∴ 12 x 25 = 20 x x

⇒ \(x=\frac{12^3 \times 25^5}{20 A_1}=15\)

Hence, the number of boxes required to pack these bottles is 15.

8. A factory required 42 machines to produce a given number of articles in 63 days. How many machines would be required to produce the same number of articles in 54 days?

Solution: Let the number of machines required to produce article in 54 days be x. The following table is obtained.

More the number of machines, lesser will be the number of days that it will take to produce the given number of articles, thus, this is a case of inverse proportion.

∴ 42 x 63 = 54 x x

⇒ \(=\frac{42^7 \times 63^7}{54 / 67_1}=49\)

Hence, the required number of machines to produce the given number of articles in 54 days is 49.

9. A car takes 2 hours to reach a destination by traveling at the speed of 60km/h. How long will it take when the car travels at the speed of 80km/h?

Solution: Let the time taken by the car to reach the destination, while traveling with a speed of 80km/hr be x hours.

The following table is obtained

More the speed of the car, lesser will be the time taken by it to reach the destination.

Hence, the speed of the car and the time taken by the car are inversly proportional to each other.

∴ 60 x 2 = 80 x x

⇒ \(x=\frac{6 \sigma^{6^3} \times \not^1}{8 \sigma / 8 4_2}=\frac{3}{2}=1 \frac{1}{2}\)

The time required by the car to reach the given destination is \(1 \frac{1}{2}\)hours.

10. Two persons could fit new windows in houses in 3 days.

1)One of the persons fell ill before the work started. How long would the job take now?

2)How many persons would be needed to fitthe windows in one day?

Solution: 1) Let the number of days required by 1 man to fit all the windows be x.

The following table is obtained

lesser the number of persons, more will be the number of days required to fit all the windows.

Hence, this is a case of inverse proportion

∴ 2 x 3 = 1 x x

x = 6

Hence, the number of days taken by 1 man to fit all the windows is 6.

2) Let the number of persons required to fit all the window in one day be y. The following table is formed.

Lesser the number of days, more will be the number of persons required to fit all the windows.

Hence, this is a case of inverse proportion.

∴ 2 x 3 = y x 1

y = 6

Hence, 6 persons are required to fit all the windows in one day.

11. A school has 8 periods a day each of 45 minutes duration. How long would each period be, if the school has 9 periods a day, assuming the number of school hours to be the same.

Solution: Let the duration of each period, when there are 9 periods a day in the school be x minutes.

The following table is obtained.

If there is more number of periods a day in the school, then the duration of each period will be lesser. Hence, this is a case of inverse proportion.

∴ 45 x 8 = x x 9

x = 40

Hence, the duration on of each period will be 40 minutes.

KSEEB Class 8 Maths solutions for Chapter 11 Direct and Inverse Proportions

KSEEB Maths Class 8 Chapter 11 Direct And Inverse Proportions Additional Problems

1. It is given that ‘ l ’ varies directly as m

1)Write an equation which relates l and m.

2)Find l, when m is 33 and k (constant of proportion) is \(\frac{1}{3}\).

Solution:1) \(\frac{\ell}{m}=k\)

2) Given, m= 33, \(k=\frac{1}{3}\)

2. 44 cows can graze a field in 9 days. How many less/more cows will graze the same field in 12 days?

Solution: Let the number of cows graze the field be x. We form a table as shown below.

It is inverse proportion as less the number of cows more the number of days for which the field can be grazed.

i.e. \(x_1 y_1=x_2 y_2\)

we have 44 x 9 = x x l2

Less number of cow can graze the field in 12 days and the difference is by 11 cows (44 – 33 cows)

3. 6 pipes are required to fill a tank in 1 hour 20 minutes. How long will it take if only 5 pipes of the same type are used?

Solution: Let the desired time to fill the tank be x minutes. Thus, we have the following table.

Lesser the number of pipes, more will be the time required by it to fill the tank. So, this is a case of inverse proportion.

Hence 80 x 6 = x x 5

x = 96

Thus, time taken to fill the tank by 5 pipes is 96 minutes or 1 hour 36 minutes.

4. The students of Somu’s class sold posters to raise money. Somu wanted to create a ratio for finding the amount of money her class would make for different numbers of posters sold. She knew they could raise ₹250 for every 60 posters sold.

1)How much money would Somu’s class make for selling 102 posters?

2)Could somu’s class raise exactly ₹2000? If so how many posters would they need to sell?

Solution: We are given,

Somu’s class raised ₹250 for every 60 posters.

1) Let x be the money Somu’s class will make by 102 posters. Table shown under

As, number of posters will increase, money raised will also increase.

so, it is direct proportion

∴ \(\frac{250}{60}=\frac{x}{102}\)

Money raised by 102 posters is ₹425.

2) Let the number of posters they need to sell be n.

∴ \(\frac{250}{60}=\frac{2000}{n}\)

Required number of posters are 480.

5. The area of a square increases if we increase the length of its sides. Are the two quantities in direct proportion? Give reason.

Solution: No, the two quantities are not in direct proportion because, if we increase the length of its sides, the ratio of the two quantities (area, length) is not constant. So, it is not in direct proportion.

6. If 25 meters of cloth costs ₹337.50, then what will be the length of the cloth bought for ₹8102?

Solution: Let the length of cloth be x meters.

The following table is obtained

As the length will increase by increasing the amount.

Hence, it is directly proportional.

so \(\frac{25}{337.5}=\frac{x}{810}\)

⇒ x = 60meters.

7. If the cost of 4 copies of together with maths is ₹200, find the number of copies that can be bought for ₹1200.

Solution: The number of copies (x) and cost (y) are in direct variation or we can also say that y x or

y = k x, where K is the constant of variation

∴ \(x=\frac{1}{50} y \text { or } y=50 x\)

The number of copies(x) that can be bought for \(1200=\frac{1}{50} \times 1200=24\)

8. A labourer earns ₹141.75 in 26 weeks. How much money will he earn in a year?

Solution: Since earning increases (or decreases) in proportional to the number of weeks.

∴ The two quantities vary directly

we know that

Income1 : Income2 = No. of weeks 1 : No. of weeks 2

so 141.75 : x = 26 : 52(As 1 year = 52 weeks)

141.75 x 52 = x x 26

⇒ x = ₹283.50

Thus, he earns ₹283.50 in a year.

9. A machine produces 180 tools in 6 hours. How many tools will it produce in 9 hours?

Solution: Let x be the number of tools and y be the number of hours. From the question

y x or y = k x

when number of tools is 180 and number of hours is 6. Then 6=k180 or \(k=\frac{6}{180}=\frac{1}{30}\)

Thus \(y=\frac{1}{30} x\)

we find the value of x when y = 9 hours.

Thus, number of tools is 270

Direct and Inverse Proportions solutions KSEEB Class 8 Maths

10. Given that x varies inversely as y and when x=5, y=50 find

1) y when x=2 and

2) x when y=10

Solution: Since x and y vary inversely

(k is a constant of variation)

⇒ when x=5, y=50

5 x 50 = k or k = 250

when x=2 then 2y=250

⇒ y = 125

and when y=10

then x x 10 = 250

⇒ \(x=\frac{250}{10}=25\)

Thus for x=2, y=125 and for y=10,x=25

11. A bicycle dealer has ₹20,000 to invest, when a bicycle is available for ₹800. If the price of a bicycle increases by 25%, find the number of cycles he can purchase with the same sum.

Solution: the more the cost, less is the number of biycles, he can buy with the given amount of money, thus it is an inverse variation.

No. of cycles = \(\frac{20000}{800}=25\)

car purchase \(x_2=25\)

New price of a bicycle

=\(800+\frac{25}{100} \times 800\)

=\(800+200=₹ 1000\)

Thus, the number of cycles that can be purchased =20

12. If a car over 80km in 5 liters of petrol, how much distance will it cover in 13 litres of petrol?

Solution: In 5 litres of petrol, distance covered = 80km

In 1 litre of petrol, distance covered = \(\frac{80}{5}=16 \mathrm{~km}\)

In, 13 litres of petrol, distance covered = 16 x 13 = 208km

13. If 32 men cap reap a field in 15 days. In how many days can 40 men reap the same field? The given situation in a inverse variation(less men, more days)

Solution: Let x=men and y=No.of days.

Number of days 40 men to reap the same field = 12 days

14. Find the value of x and y if x:y=2:3 and 2:x=1:2

Solution: 2:x=1:2

⇒ x=4

x:y=2:3

4:y=2:3

y=6

15. Ranjith has enough money to buy 75 machines worth Rs. 200 each. How many machines can he buy if he get a discount of Rs. 50 on each machine?

Solution: Let x be the number of machines he can buy if a discount of Rs. 50 is offered on each machine.

Number of machines (x) : 75

Price of each machine (y): 200

Since each machine is having ₹50 discount then cost of each machine will be (200 – 50) = 150.

Given situation is inverse variation as price of machine is less more machines, he can buy.

75 x 200 = x x l50

⇒ x = 100

16. If 5 men or 7 women can earn ₹875 per day. How much would 10 men & 5 women earn per day?

Solution: 5 men= 7 women

1 man = \(\frac{7}{5} \text { women }\)

⇒ (10 men + 5 women)

=(14 women + 5 women) = 19 women

Let 10 men & 5 women would earn ₹x per day then, we have

Clearly, more women will earn more per day. So it is a case of direct proportion.

∴ \(\frac{7}{875}=\frac{19}{x} \Rightarrow \frac{1}{125}=\frac{19}{x}\)

⇒ (1 x x)=(125 x 19)

⇒ x = 2375

∴ 10 men & 5 women would earn ₹2375 per day.

17. In a fort, 300 men had provisions for 90 days. After 20 days, 50 men left the fort. How long would the food last at the same rate?

Solution: Clearly, the remaining food is sufficient for 300 men for (90-20)days = 70 days.

KSEEB Solutions For Class 8 Maths Chapter 10 Data Handling Points To Remember

Data handling: Deals with the process of collecting data, presenting it and getting results.

Data mostly available to us in an unorganized form is called raw data.

Grouped data can be presented using a histogram Histogram is a type of bar diagram, where the class intervals are shown on the horizontal axis and the heights of the bars show the frequency of the class interval. Also, there is no gap between the bars as there is no gap between the class intervals.

Read and Learn More KSEEB Solutions for Class 8 Maths

In order to draw meaningful inferences from any data we need to organize the data systematically

Frequency gives the number of times that a particular entry occurs.

Raw data can be ‘grouped’ and presented systematically through ‘grouped frequency distribution’.

Statistics: The science which deals with the collection, presentation, analysis and interpretation of numerical data.

Observation: Each entry (number)in raw data.

Range: The difference between the lowest and the highest observation in a given data.

Array: Arranging raw data in ascending or descending order of magnitude.

Data can also presented using circle graph or pie chart. A circle graph shows the relationship between a whole and its part.

There are certain experiments whose outcomes have an equal chance of occuring.

A random experiment is one whose outcome cannot be predicted exactly in advance

Outcomes of an experiment are equally likely if each has the same chance of occuring.

Frequency: The number of times a particular observation occurs in the given data.

Class interval: A group in which the raw data is condensed.

1)Continuous: The upper limit of a class interval coincides with the lower limit of the next class.

2)Discontinuous: The upper limit of a class interval does not coincide with the lower limit of the next class.

Class limits: Each class in a bounded by two figures which are called class limits

1) Upper-class limit: The upper value of a class interval

2)Lower class limit: The lower value of a class interval

Class size or width: The difference between the upper-class limit and lower-class limit of a class.

Classmark: The mid-value of a class interval.

Class mark = Upper limit + lower limit/2

Graphic representation of data:

1)Pictograph: Pictorial representation of data using symbols.

2)Bar graph: A display of information using bars of uniform width, their heights proportional to the respective values.

3) Double bar graph: A bar graph showing two sets of data simultaneously. It is useful for the comparison of the data.

4)Histogram: A graphical representation of frequency distribution in the form of rectangles with class intervals as bases and heights proportional to corresponding frequencies such that there is no gap between any successive rectangles.

Circle graph or pie chart: A pictorial representation of the numerical data in the form of sectors of a circle such that area of each sector is proportional to the magnitude of the data represented by the sector. Probability: The chance of occurring of a certain event when measured quantitatively.

Probability of an event =Number of outcomes that make an event/Total number of outcomes of the experiment
when the outcomes are equally likely.
1)Experiment: An operation which can produce some well defined outcomes.

2)Trial: The performance of an experiment.

3)Random experiment: An experiment in which all possible outcomes are known and the exact outcome cannot be predicted in advance

4)Equally likely outcomes: Certain experiments whose outcomes have an equal chance of occurring

Event: Each outcome of an experiment or a collection of outcomes is called an event. Chances and probability are related to real life.

KSEEB Class 8 Maths Solutions For Chapter 10 Data Handling Exercise 10.1

1. For which of these would you use a histogram to show the data?
a)The number of letters for different areas in the postman’s bag.
b)The height of competitors in an athletics meet.
c)The number of cassettes produced by 5 companies.
d)The number of passengers boarding trains from 7 : 00 am to 7 : 00 p.m. station
Give reasons for each.

Solution: In case of the data given in alternative (b) and (d) we will use histogram as we can divide the given data in class intervals.
In case of alternatives (a) & (c) we do not know about the number of letters of different areas and the number of cassettes produced by the given companies. We do not have any approximate idea about it.
∴ We cannot define class intervals for this data and thus, we will not use a histogram.

Practice Questions For Data Handling KSEEB Maths

2. The Shoppers who come to a departmental store are marked as man(M), women (W), boy (B) or Girl (G). The following list gives the shoppers who came during the first hour in the morning. W W W G B W W M G G M M W W W W G B M W B G G M W W M M W W W M W B W G M W W W W G W M M W W M W G W M G W M M B G G W make a frequency distribution table using tally marks. Draw a bar graph to illustrate it.

Solution: By observing the data given above we can make a frequency distribution table as follows:

The bar graph of this data can be drawn as follows.

3. The weekly wages (in of 30 workers in a factory are: 830, 835, 890, 810, 835, 836, 869, 845, 898, 890, 820, 860, 832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 835, 836, 878, 840, 868, 890, 806, 840. Using tally marks make a frequency table with intervals as 800 – 810,810 – 820 and so on.

Solution: A frequency distribution table by using tally marks for the above data is as follows.

4.Draw a histogram for the frequency table made for the data in Q 3. and answer the following questions.
1)which group has the maximum number of workers?
2)How many workers earn ₹850 and more?
3)How many workers earn less than ₹850?

Solution: A histogram for the above frequency distribution table is as follows.
1)830 – 840 is the group which has the maximum number of workers
2)The workers who earn more than ₹850 are the number of workers who fall in the group of 850 – 860 or 860 – 870 or 870 – 880 or 880 – 890.
Hence, the total number of workers earning more than 850 will be the sum of the number of all these workers i.e. 1 + 3 + 1 + 1 + 4 = 10.
3)The workers who earn less than ₹850 are the number of workers who fall in the group of 800 – 810 or 810 – 820 or 820 – 830 or 830 – 840 or 840 – 850. Hence the total number of workers earning less than 850 will be the sum of the numbers of all these workers i.e., 3 + 2 + 1 + 9 + 5 = 20.

5.The number of hours for which students of a particular class watched television during holidays is shown through the given graph.
Answer the following.
1)For how many hours did the maximum number of students watch TV?
2)How many students watched TV for less than 4 hours?
3)How many students spent more than 5 hours in watching TV?

Solution: 1) From the graph, it can be observed that the maximum number of students (i.e., 32) watched TV for 4-5 hours.
2)The students who watched TV for less than 4 hours are the students who watched TV for 1 – 2 hours or 2 – 3 hours or 3 – 4 hours. Hence, total number of students = 4 + 8 + 22 = 34.
3)The students who watched TV for more than
5 hours are the students who watched TV for 5 –
6 hours (or) 6 – 7 hours.
Hence, the total number of students =8 + 6=14

Data Handling Questions And Answers KSEEB Maths

KSEEB Class 8 Maths Chapter 10 Data Handling Exercise 10.2

1. A survey was made to find the type of music that a certain group of young people liked in a city. Adjoining pie chart shows the findings of this survey. From this pie chart answer the following:

1) If 20 people liked classical music, how many young people were surveyed?
2) Which type of music is liked by the maximum number of people?
3) If a cassette company were to make 1000 CD’s how many of each type would they make?

Solution: 1) Number of people who like classical music = 10%
This 10% represents 20 people 20×100
100% represents = \(\frac{20 \times 100}{10}\) = 200 people
∴ 200 young people were surveyed.
2)From the pie chart, it can be easily observed that the light music is represented by the maximum part of the pie chart (Le., 40%). Hence, most of the people like light music.
3)Number of CD’s of classical music
= 10% of 1000
= \(\frac{10}{100} \times 1000\)
=100
Number of CD’s of semi-classical music
= 20% of 1000
= \(\frac{20}{100} \times 1000\)
= 200
Number of CD’s of folk music
= 30% of 1000
= \(\frac{30}{100} \times 1000\)
= 300
Number of cassettes of light music
= 40% of 1000
= \(\frac{40}{100} \times 1000\)
= 400

2. A group of 360 people were asked to vote for their favourite season from the three seasons rainy, winter and summer.
1) Which season got the most votes?
2)Find the central angle of each sector.
3)Draw a pie chart to show this information.

Solution: 1) Winter
2) Total number of votes = 90 + 120 + 150= 360

3) A pie chart can be drawn for the above data as follows:

3. Draw a pie chart showing the following information. The table shows the colours preferred by a group of people.

Solution: The central angle for each colour can be calculated as follows:

The pie chart of the above data is as follows.

KSEEB Class 8 Maths Chapter 10 Data Handling

4.The adjoining pie chart gives the marks scored in an examination by a student in Hindi, English, Mathematics, social science and science. If the total marks obtained by the students were 540, answer the following questions.
1)In which subject did the student score 105 marks?
2)How many more marks were obtained byy the student in mathematics than in Hindi?
3)Examine whether the sum of the marks obtained in social science and mathematics is more than that in science and Hindi.

Solution: 1) Total marks obtained by the student are 540. Hence 540 marks represent 360°. The central angle for 105 marks has to be calculated.
Central angle for 105 marks = \(\frac{105}{540} \times 360^{\circ}=70^{\circ}\)
Hindi is the subject having its central angle as 70°
∴ The student scored 105 marks in Hindi
2) Difference between the central angles of mathematics and Hindi = 90°-70°=20°
Marks for 20° central angle =\(\frac{20^{\circ}}{360^{\circ}} \times 540=30\)
There is a difference of 30 marks between the score obtained in mathematics and Hindi.
∴ 30 more marks were obtained by the student in mathematics than in Hindi.
3) Sum of central angles of social science and mathematics = 90° + 65° = 155°
Sum of central angle of science and Hindi = 80 + 70 = 150°.
The sum of the central angles for social science and mathematics is mote than that of science and Hindi.
∴ The student scored more in social science and mathematics than in science and Hindi.

5. The number of students in a hostel, speaking different languages is given below, display the data in a pie chart.

Solution: The central angle for each subject can be calculated as follows:

A pie chart of the above data is as follows.

Chapter 10 Solutions For KSEEB Maths Data Handling Exercise 10.3

1. List the outcomes you can see in these experiments.
a) Spinning a wheel
b) Tossing two coins together

Solution: a) On spinning the given wheel, the possible outcomes are A, B, C, D.
b) By tossing two coins together, the possible outcomes are HT, TH, HH, TT, where H and T represents Head, and Tail of the coins respectively.

2. When a die is thrown, list the outcomes of an event of getting
1)a) a prime number
b) not a prime number
2) a) a number greater than 5
b) a number not greater than 5.

Solution: When a dice is thrown, the possible outcomes are 1, 2, 3, 4, 5 and 6.
1) a) out of these outcomes 2, 3, and 5 are prime numbers. Hence, these are the outcomes of an event of getting a prime number on the face of a dice.
b) out of these outcomes 1,4,6 are not prime number. Hence, these are the outcomes of an event of not getting a prime number on the face of a dice.
2)a) out of these outcomes, a number greater than 5 is possible when 6 comes on the face of the dice.
b) out of these outcomes, a number not greater than 5 is possible when the number on the face of the dice is any one of the outcomes 1,2,3,4,5.

KSEEB Class 8 Maths Solutions For Chapter 10 Data Handling

3. Find the
a)Probability of the pointer stopping on D in (Q-l-(a))?
b)Probability of the getting an ace from a well-shuffled deck of 52 playing cards?
c)Probability of getting a red apple.

Solution: a) The pointer can stop at one of the following regions. A, A, B, C, D
out of these 5 cases, it is possible only in 1 case that the pointer will stop at region D.
∴ the probability that the pointer will stop at region \(D=1 / 5\)
b) There are 52 cards in a deck of cards and there are 4 ace cards in 1 deck of cards.
probability of getting an ace card = =\(\frac{4}{52}=\frac{1}{13}\)
c) There are a total of 7 apples, out of which 4 are red and 3 are green.
probability of getting a red apple = \(\frac{4}{7}\)

4. Numbers 1 to 10 are written on ten separate slips. (One number on one slip) kept in a box and mixed well. One slip is chosen from the box without looking into it. What is the probability of
1) getting a number 6?
2) getting a number less than 6?
3) getting a number greater than 6?
4) getting a 1-digit number?

Solution: 1) There are 10 slips in the box. However 6 is written only on 1 slip
1 Probability of gettiing a number \(6=\frac{1}{10}\).
2)The numbers less than 6 are 1,2, 3,4, 5
Probability of getting a number less than \(6=\frac{5}{10}\)
=\(\frac{1}{2}\)
3)The numbers greater than 6 are 7, 8, 9, 10 probability of getting a number greater than
\(6=\frac{4}{10}=\frac{2}{5}\)
4) There are 9 numbers which are single digit numbers, 1,2,3,4,5,6,7,8,9
probability of getting a single digit number = \(\frac{9}{10}\).

5.If you have a spinning wheel with 3 green sectors, 1 blue sector and 1 red sector. What is the probability of getting a green sector? What is the probability of getting a non blue sector?

Solution: Total sector = 3 + 1 + 1 = 5
There are 5 sectors and we can get a green sector in three cases.
Probability of getting a green sector = \(3 / 5\)
We will get a non blue sector when we will get either a green sector or a red sector.
Hence, 4 cases of such type are possible in which we will get a non blue sector.
Probability of getting a non blue sector = \(4 / 5\)

6.Find the probabilities of the events given in Question 2.

Solution: (1) (a) Out of 6 possible outcomes, a prime number can be obtained in three cases.
∴ Probability of getting a prime number = \(\frac{3}{6}=\frac{1}{2}\).
b) Out of 6 possible outcomes, a prime number may not be obtained in three cases.
∴ Probability of getting not a prime number
=\(\frac{3}{6}=\frac{1}{2}\)
2) (a) out of 6 possible outcomes, a number greater than 5 can be obtained in only 1 case.
∴ Probability of getting a number greater than
\(5=\frac{1}{6}\)
(b) Out of 6 possible outcomes, a number not greater than 5 can be obtained in 5 cases.
∴ Probability of getting a number not greater than
\(5=\frac{5}{6}\).

KSEEB Class 8 Maths Data Handling Additional Problems

1. The following pie charts give you a different piece of information about your class. Find the fraction of the circle representing the information.

Solution: Fraction of the circle representing the girl’s 50%
=\(\frac{50}{100}=\frac{1}{2}\)

2. When a die is thrown, what are the possible outcomes?

Solution: The possible outcomes are 1,2,3,4,5 or 6.

3. Classify the following statement under appropriate headings.
1) Getting the sum of angles of a △le as 180°.

Solution: certain to happen.

2) India winning a cricket match against Pakistan

Solution: may or may not happen.

3) Sun setting in the evening.

Solution: Certain to happen.

4) Getting 7 when a die is thrown

Solution: Impossible to happen.

5) Sun rising from the west

Solution: Impossible to happen.

6) Winning a racing competition by you

Solution: May or may not happen.

KSEEB Class 8 Maths Chapter 10 Solved Problems

4.Following are the number of members in 25 families of a village : 6,8,7,7,6,5,3,2,5,6, 8,7,7,4,3,6,6,7,5,4,3,3,3,2,5 prepare a frequency distribution table for the data using class intervals. 0 – 2, 2 – 4 etc.

Solution:

5. Draw a histogram for the following data.

Solution:

6. Given below is a frequency distribution table. Read it and answer the questions that follows:

1) What is the lower limit of the second class interval?
2) What is the upper limit of the last class interval?
3) What is the frequency of the third class?
4) Which interval has a frequency of 10?
5) Which interval has the lowest frequency?
6) What is the class size?

Solution: 1)The second class interval is 20-30
∴ The lower limit = 20
2)The last class interval = 50 – 60
∴ The upper limit = 60
3)The frequency of the third class (30 – 40) = 4
4)The class interval having frequency 10
= 20-30
5)The interval having lowerst frequency
= 30-40
6)The class size = upper class limit – lower class limit = 20 – 10= 10

7.A dice is rolled once. What is the probability that the number on top will be
1) odd
2) Greater than 5
3) A multiple of 3
4) less than 1
5)A factor of 36
6) A factor of 6.

Solution: On rolling a die, all possible outcomes are 1, 2, 3,4,5,6. Total number of possible outcomes = 6
1) Odd number on the top of a die = 1, 3, 5
∴ Number of favourable outcomes = 3
The probability of getting odd number on the top.
P(E)=Number of favourable outcomes/Total number of outcomes
=\(\frac{3}{6}=\frac{1}{2}\)

8.The following data represents the approximate percentage of water in various oceans. Prepare a pie chart for the given data.

Solution: Total angle at the centre of the circle is 360°. We make a table to find the central angle of the sectors.

The pie chart is drawn as follows:

KSEEB Maths Class 8 Data Handling Notes

9. Identify which symbol should appear in each row.

Solution: Total value = 800 + 700 + 550 + 450 = 2500
32% represents \(
\frac{32}{100} \times 2500=800\)
∴ 32% represents the symbol

28% represents \(\frac{28}{100} \times 2500=700\)
∴ 28% represents the symbol

22% represents \(\frac{22}{100} \times 2500=550\)
∴ 22% represents the symbol

18% represents \(\frac{18}{100} \times 2500=450\)
∴ 18% represents the symbol

10. Draw an appropriate graph to represent the given information.

KSEEB Class 8 Maths Chapter 10 Data Handling

11. A survey was conducted to find out the type of TV programmes a group of 60 children watched through a week. The data collected consisted of the type of program most watched by each child. It is as follows.

Solution:

12. There are 20 students in class 8. As per the school record there ages in years are as follows :
11 13 12 11 13 12 11 14 12 13 13 13 13
12 12 13 13 13 12 11
What is the probability that a student of this class selected at random is
(a) of age 11 years?
(b) of 14 years.

Solution: a) There are 4 students of age 11 years in the class of 20 students. So, the probability of the selected student will be 11 years of age is
\(4 / 20=1 / 5\)
b) There is only one student of age 14 years in the class of 20 students. So, the probability of the
selected student to be of age 14 years is \(\frac{1}{20}\).

13. A coin is tossed 40 times and tail turns up 16 times. What is the probability of occurrence of tail?

Solution: Since, the tail turns up 16 times out of 40, the probability of occurrence of tail is
= Number of times tail turns up/Total number of trails
=\(\frac{16}{40}=\frac{2}{5}\)

14. A die is thrown 50 times and number 4 turns up 16 times, what is the probability of occurrence of 4?

Solution: Since 4 turns up 16 times out of 50, the probability of occurrence of 4 is
= Number of times 4 turns up 16/Total number of trails
= \(\frac{16}{50}=\frac{8}{25}\)

15. A coin is tossed 100 times and tail is obtained 52 times. Now, if a coin is tossed at random, what is the probability of getting a head?

Solution: Total number of tosses =100
Number of times tail appeared = 52
Number of times head appeared = 100 – 52 = 48 Probability of a getting a head
= Number of times head appeared/Total number of tails
=\(\frac{48}{100}=\frac{12}{25}\)

16. A die is thrown, what is the probability of getting
1) a prime number?
2) a number greater
3) a number not greater than 5?

Solution: In throwing a die, all possible outcomes are 1,2, 3, 4, 5,6
number of all possible outcomes = 6
1)prime numbers are 2, 3, 5
Number of prime numbers = 3
∴ P(getting a prime number = \(\frac{3}{6}=\frac{1}{2}\)
2)Numbers greater than 4 are 5 & 6 their number is 2
∴ P(getting a number greater than 4 ) = \(\frac{2}{6}=\frac{1}{3}\)
3)Numbers not greater than 5 are 1, 2, 3,4, 5 their number is 5
∴ P(getting a number not greater than 5 = \(5 / 6\)

17.From a well shuffled deck of 52 cards, one card is drawn at random, what is the probability that the card drawn is
1) a diamond
2) an ace
3) 5 of club?

Solution: Total number of all cards = 52
Total number of all possible outcomes = 52
1)No. of diamonds =13
P(getting a diamond) = \(\frac{13}{52}=\frac{1}{4}\)
2)Number of all aces = 4
∴ p(getting an ace) = \(4 / 52=1 / 13\)
3) No. of 5 of club = 1
∴ p(getting an club)= \(1 / 52\)

18.On throwing a die once. Find the probability of occurrence of a composite number.

Solution: On throwing a die, the occurrence of composite numbers can be as 4,6.
Hence, probability of occurrence of a composite number = No. of composite numbers on a die/Total numbers on a die
=\(\frac{2}{6}=\frac{1}{3}\)

KSEEB Class 8 Maths Solutions For Chapter 9 Exponents And Powers Points To Remember

Numbers with negative exponents obey the following laws of exponents.
a)\(a^m \times a^n=a^{m+n}\)
b)\(a^m \div a^n=a^{m-n}\)
c)\(\left(a^m\right)^n=a^{m n}\)
d)\(a^m \times b^m=(a b)^m\)
e)\(a^0=1\)
f)\(\frac{a^m}{b^m}=\left(\frac{a}{b}\right)^m\)

Very small numbers can be expressed in standard form.

Use of exponents small numbers in standard form.

1) Very large and very small numbers in standard form.

2) Standard form is also called scientific notation form.

3) A number written as \(m \times 10^n\) is said to be in standard form if m is a decimal number such that \(1 \leq m<10\) and n is either a positive or a negative integer.

Read and Learn More KSEEB Solutions for Class 8 Maths

Examples: 150,000,000,000 = \(1.5 \times 10^{11}\)

Exponential notation is a powerful way to express repeated multiplication of the same number. For any non-zero rational number ‘a’ and a natural number n, the product \(a x a x a x ….. x a(n times)=a^n\).

It is known as the nth power of ‘a’ and is read as ‘a’ raised to the power ‘n’, The rational number a is called the base, and n is called exponent.

Exponents And Powers Solutions KSEEB Class 8 Maths Chapter 9 Exercise 9.1

1. Evaluate
1) \(3^{-2}\)

Solution: \(3^{-2}=\frac{1}{3^2}=\frac{1}{9}\)
\(\left(a^{-m}=\frac{1}{a^m}\right)\)

2) \((-4)^{-2}\)

Solution: \((-4)^{-2}=\frac{1}{(-4)^2}=\frac{1}{16}\)
\(\left(a^{-m}=\frac{1}{a^m}\right)\)

3) \(\left(\frac{1}{2}\right)^{-5}=\frac{1} {(2)^{-5}}=2^5=32\)

2. simplify and express the result in power notation with a positive exponent.

1) \((-4)^5 \div(-4)^8\)

Solution: \((-4)^5 \div(-4)^8\)

= \((-4)^{5-8} \quad\left(a^m \div a^n=a^{m-n}\right)\)

= \((-4)^{-3}\)

= \(\frac{1}{(-4)^3} \quad\left(a^{-m}=\frac{1}{a^m}\right)\)

2) \(\left(\frac{1}{2^3}\right)^2\)

Solution: \(\left(\frac{1}{2^3}\right)^2 \quad\left(\left(a^m\right)^n=a^{m m}\right)\)

=\(\left(\frac{1}{2^3}\right)^2=\frac{1}{2^6}\)

3) \((-3)^4 \times\left(\frac{5}{3}\right)^4\)

Solution: \((-3)^4 \times\left(\frac{5}{3}\right)^4\)

=\((-3)^4 \times \frac{5^4}{3^4}\)

=\((-1)^4 \times 3^4 \times \frac{5^4}{3^4} \quad\left[(a b)^m=a^m \times b^m\right]\)

=\((-1)^4 \times 5^4=5^4\)

4) \(\left(3^{-7} \div 3^{-10}\right) \times 3^{-5}\)

Solution: \(\left(3^{-7} \div 3^{-10}\right) \times 3^{-5}\)

= \(\left(3^{-7-(-10)}\right) \times 3^{-5} \quad\left(a^m \div a^n=a^{m-n}\right)\)

= \(3^3 \times 3^{-5}\)

= \(3^{3+(-5)} \quad\left(a^m \times a^n=a^{m+n}\right)\)

= \(3^{-2}\)

= \(\frac{1}{3^2} \quad\left(a^{-m}=\frac{1}{a^m}\right)\)

5) \(2^{-3} \times(-7)^{-3}\)

Solution: \(2^{-3} \times(-7)^{-3}\)

= \(\frac{1}{2^3} \times\left(\frac{1}{(-7)^3}\right) \quad\left(a^{-m}=\frac{1}{a^m}\right)\)

= \(\frac{1}{\left[2 \times(-7)^3\right]}=\frac{1}{(-14)^3}\left(a^m \times b^m=(a b)^m\right)\)

KSEEB Class 8 Maths Key Concepts Of Exponents And Powers

3. Find the value of

1) \(\left(3^0+4^{-1}\right) \times 2^2\)

Solution: \(\left(3^0+4^{-1}\right) \times 2^2 \quad\left[a^0=1 \& a^{-m}=\frac{1}{a^m}\right]\)

=\(\left(1+\frac{1}{4}\right) \times 2^2\)

=\(\frac{5}{4} \times 4=5\)

2) \(\left(2^{-1} \times 4^{-1}\right) \div 2^{-2}\)

Solution: \(\left(2^{-1} \times 4^{-1}\right) \div 2^{-2}\)

=\(\left[2^{-1} \times\left\{(2)^2\right\}^{-1}\right] \div 2^{-2}\)

=\(\left(2^{-1} \times 2^{-2}\right) \div 2^{-2}\left[\left(a^m\right)^n=a^{m n}\right]\)

=\(2^{-1+(-2)} \div 2^{-2} \quad\left(a^m \times a^n=a^{m+n}\right)\)

=\(2^{-3} \div 2^{-2}\)

=\(2^{-3-(-2)} \quad\left(a^m \div a^n=a^{m-n}\right)\)

=\(2^{-3+2}=2^{-1} \quad\left(a^{-m}=\frac{1}{a^m}\right)\)

=\(\frac{1}{2}\)

3) \(\left(\frac{1}{2}\right)^{-2}+\left(\frac{1}{3}\right)^{-2}+\left(\frac{1}{4}\right)^{-2}\)

Solution: \(\left(\frac{1}{2}\right)^{-2}+\left(\frac{1}{3}\right)^{-2}+\left(\frac{1}{4}\right)^{-2}\)

=\(\left(\frac{2}{1}\right)^2+\left(\frac{3}{1}\right)^2+\left(\frac{4}{1}\right)^2 \quad\left(a^{-m}=\frac{1}{a^m}\right)\)

=\(2^2+3^2+4^2=4+9+16=29\)

4) \(\left(3^{-1}+4^{-1}+5^{-1}\right)^0\)

Solution: \(\left(3^{-1}+4^{-1}+5^{-1}\right)^0 \quad\left(a^{-m}=\frac{1}{a^m}\right)\)

=\(\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{5}\right)^0\)

=\(1\left(a^0=1\right)\)

5) \(\left\{\left(\frac{-2}{3}\right)^{-2}\right\}^2\)

Solution: \(\left\{\left(\frac{-2}{3}\right)^{-2}\right\}^2\)

=\(\left\{\left(\frac{3}{2}\right)^2\right\}^2 \quad\left(a^{-m}=\frac{1}{a^m}\right)\)

=\(\left\{\frac{3^2}{(-2)^2}\right\}^2\)

=\(\left(\frac{9}{4}\right)^2 \quad\left[\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}\right]\)

=\(\frac{81}{16}\)

4. Evaluate

1. \(\frac{8^{-1} \times 5^3}{2^{-4}}\)

Solution: \(\frac{8^{-1} \times 5^3}{2^{-4}}\)

=\(\frac{2^4 \times 5^3}{8^1} \quad\left(a^{-m}=\frac{1}{a^m}\right)\)

=\(\frac{2^4 \times 5^3}{2^3}=2^{4-3} \times 5^3 \quad\left(a^m \div a^n=a^{m-n}\right)\)

=\(2 \times 125=250\)

2) \(\left(5^{-1} \times 2^{-1}\right) \times 6^{-1}\)

Solution: \(\left(5^{-1} \times 2^{-1}\right) \times 6^{-1}\)

=\(\left(\frac{1}{5} \times \frac{1}{2}\right) \times \frac{1}{6} \quad\left(a^{-m}=\frac{1}{a^m}\right)\)

=\(\frac{1}{10} \times \frac{1}{6}=\frac{1}{60}\)

5. Find the value of m for which \(5^m \div 5^{-3}=5^5\)

Solution: \(5^m \div 5^{-3}=5^5\)

\(5^{m+3}=5^5\)
Since the powers have the same bases on both sides their respective exponents must be equal.
m + 3 = 5
m = 5 – 3
m = 2

KSEEB Class 8 Maths key concepts of Exponents and Powers

6. Evaluate

1) \(\left\{\left(\frac{1}{3}\right)^{-1}-\left(\frac{1}{4}\right)^{-1}\right\}^{-1}\)

Solution: \(\left\{\left(\frac{1}{3}\right)^{-1}-\left(\frac{1}{4}\right)^{-1}\right\}^{-1}\)

=\(\left\{\left(\frac{3}{1}\right)^1-\left(\frac{4}{1}\right)^1\right\}^{-1} \quad\left(a^{-m}=\frac{1}{a^m}\right)\)

=\((3-4)^{-1}=(-1)^{-1}=\frac{1}{-1}=-1\)

2) \(\left(\frac{5}{8}\right)^{-7} \times\left(\frac{8}{5}\right)^{-4}\)

Solution: \(\left(\frac{5}{8}\right)^{-7} \times\left(\frac{8}{5}\right)^{-4}\)

=\(\frac{5^{-7}}{8^{-7}} \times \frac{8^{-4}}{5^{-4}}\)

=\(\frac{8^7}{5^7} \times \frac{5^4}{8^4} \quad\left(a^{-m}=\frac{1}{a^m}\right)\)

=\(\frac{8^{7-4}}{5^{7-4}}=\frac{8^3}{5^3}=\frac{512}{125} \quad\left(a^m \div a^n=a^{m-n}\right)\)

Practice Questions For Exponents And Powers KSEEB Maths

7. Simplify

1) \(\frac{25 \times t^{-4}}{5^{-3} \times 10 \times t^{-8}} \quad(t \neq 0)\)

Solution: \(\frac{25 \times t^{-4}}{5^{-3} \times 10 \times t^{-8}}\)

=\(\frac{5^2 \times t^{-4}}{5^{-3} \times 5 \times 2 \times t^{-8}}\)

=\(\frac{5^2 \times t^{-4}}{5^{-3+1} \times 2 \times t^{-8}} \quad\left(a^m \times a^n=a^{m+n}\right)\)

=\(\frac{5^2 \times t^{-4}}{5^{-2} \times 2 \times t^{-8}}\)

=\(\frac{5^{2-(-2)} t^{-4-(-8)}}{2} \quad\left(a^m \div a^n=a^{m-n}\right)\)

=\(\frac{5^4 t^4}{2}=\frac{625 t^4}{2}\)

2) \(\frac{3^{-5} \times 10^{-5} \times 125}{5^{-7} \times 6^{-5}}\)

Solution: \(\frac{3^{-5} \times 10^{-5} \times 125}{5^{-7} \times 6^{-5}}\)

=\(\frac{3^{-5} \times(2 \times 5)^{-5} \times 5^3}{5^{-7} \times 6^{-5}}\)

=\(\frac{3^{-5} \times(2 \times 5)^{-5} \times 5^3}{5^{-7} \times(2 \times 3)^{-5}}\)

=\(\frac{3^{-5} \times 2^{-5} \times 5^{-5} \times 5^3}{5^{-7} \times 2^{-5} \times 3^{-5}}\)

=\(3^{-5-(-5)} \times 2^{-5-(-5)} \times 5^{-5+3-(-7)}\)

=\(3^0 \times 2^0 \times 5^5 \quad\left(a^m \div a^n=a^{m-n}\right)\)

=\(5^5 \quad\left(a^0=1\right)\)

KSEEB Class 8 Maths Chapter 9 Exponents And Powers Exercise 9.2

1. Express the following numbers in standard form.

1) 0.0000000000085
Solution: \(8.5 \times 10^{-12}\)

2) 0.00000000000942
Solution: \(9.42 \times 10^{-12}\)

3) 6020000000000000
Solution: \(6.02 \times 10^{15}\)

4) 0.00000000837
Solution: [/latex]3.186 \times \times 10^{10}[/latex]

2. Express the following numbers in decimal form.
1) \(3.02 \times 10^{-6}\)
Solution: 0.00000302

2) \(4.5 \times 10^4\)
Solution: 45000

3) \(3 \times 10^{-8}\)
Solution: 0.00000003

4) \(1.0001 \times 10^9\)
Solution: 1000100000

5) \(5.8 \times 10^{12}\)
Solution: 5800000000000

6) \(3.61492 \times 10^6\)
Solution: 3614920

KSEEB Class 8 Maths Chapter 9 Exponents And Powers

3. Express the number appearing in the following statements in standard form.

1) 1 micron is equal to \(\frac{1}{1000000} m\)

Solution: \(\frac{1}{1000000} m=1 \times 10^{-6} m\)

2) The charge of an electron is 0.000,000,000,000,000,000,16 coulomb

Solution: 0.000,000,000,000,000,000,16
=\(1.6 \times 10^{-19} \text { coulomb }\)

3) Size of a bacteria is 0.0000005m

Solution: \(0.0000005=5 \times 10^{-7} \mathrm{~m}\)

4) The size of a plant cell is 0.00001275m

Solution: \(0.00001275 \mathrm{~m}=1.275 \times 10^{-5} \mathrm{~m}\)

5) The thickness of a thick paper is 0.07mm

Solution: \(0.07 \mathrm{~mm}=7 \times 10^{-2} \mathrm{~mm}\)

4. In a stack there are 5 books each of thickness 20mm and 5 paper sheets each of thickness 0.016mm. What is the total thickness of the stack?

Solution: Thickness of each book = 20mm
Hence, thickness of 5 books = (5 x 20)mm
= 100mm
The thickness of each paper sheet = 0.016mm
Hence, thickness of 5 paper sheets = (5 x 0.016)mm = 0.080mm
Total Thickness of the stack = Thickness of 5 books + Thickness of 5 paper sheets
= (100 + 0.080)mm
= 100.08mm
= \(1.0008 x 10^2mm\)

KSEEB Maths Class 8 Chapter 9 Exponents And Powers Additional Problems

1. Find the value of \(\frac{1}{4^{-2}}\)

Solution: \(\frac{1}{4^{-2}}=4^2=4 \times 4=16 \quad\left(\frac{1}{a^{-m}}=a^m\right)\)

2. If \(x=\left(\frac{3}{7}\right)^{-3} find x^{-2}\)

Solution: Given \(x=\left(\frac{3}{7}\right)^{-3}\)

=\(\left(\frac{3}{7}\right)^6\)

3. simplify
\(\left[\left\{\left(\frac{-1}{2}\right)^2\right\}^{-2}\right]^{-1}\)

Solution: \(\left[\left\{\left(\frac{-1}{2}\right)^2\right\}^{-2}\right]^{-1}=\left(\frac{-1}{2}\right)^{2 x-2 x-1}\)

=\(\left(\frac{-1}{2}\right)^4 \quad\left(\left(a^m\right)^n=a^{m n}\right)\)

=\(\frac{(-1)^4}{(2)^4}=\frac{1}{16}\)

4. Find the value of x for the expression \(3^{5 x-1} \div 27=3^{-5}\)

Solution: \(3^{5 x-1} \div 27=3^{-5}\)
=\(3^{5 x-1} \div 3^3=3^{-5}\)
\(\Rightarrow \frac{3^{5 x-1}}{3^3}=3^{-5}\)
\(\Rightarrow 3^{5 x-1-3}=3^{-5}\)
\(\Rightarrow 3^{5 x-4}=3^{-5}\) (Base are equal)
5x – 4 = -5
∴ 5x = -5+4
⇒ 5x = -1
⇒ \(x=-1 / 5\)

5. What is the value of S if 379500000 is written in the form \(\mathrm{S} \times 10^m\) with m=7?

Solution: x = 379500000
⇒ \(x=37.95 \times 10^7\)

6. What is the value of \(\left(12^{-1}+8^{-2}+7^{-1}+6^{-1}\right)^0\) ?

Solution: As we know that 0 exponent of any base equals
1. Hence \(\left(12^{-1}+8^{-2}+7^{-1}+6^{-1}\right)^0=1\)

7. What is the multiplicative inverse of \(\left(\frac{-6}{13}\right)^{-99}\)?

Solution: Let the multiplicative inverse be x
then \(\left(\frac{-6}{13}\right)^{-99} \times x=1\)
(∵1 is identity element)
\(x=\left(\frac{-6}{13}\right)^{99}\)

8. What is the expression for \(8^{-3}\) as a power with the base 2 ?

Solution: \((8)^{-3}=\left(2^3\right)^{-3}\)
=\(2^{-9}\) which is the required expression

9. Find the value of K so that \(\left(\frac{5}{3}\right)^{-2} \times\left(\frac{5}{3}\right)^{-14}=\left(\frac{5}{3}\right)^{8 k}\)

Solution: \(\left(\frac{5}{3}\right)^{-2} \times\left(\frac{5}{3}\right)^{-14}=\left(\frac{5}{3}\right)^{8 k}\)
\(\left(\frac{5}{3}\right)^{-2-14}=\left(\frac{5}{3}\right)^{8 k}\)
\(\left(\frac{5}{3}\right)^{-16}=\left(\frac{5}{3}\right)^{8 k}\)
8K = -16 (comparing the exponents)
⇒ \(k=\frac{-16}{8}=-2\)
⇒ k = -2

10. Express \(\frac{1.5 \times 10^6}{2.5 \times 10^{-4}}\) in the standard form.

Solution: \(\frac{1.5 \times 10^6}{2.5 \times 10^{-4}}=\frac{1.5^{0.50 .6}}{2.50 .5_1} \times 10^6 \times 10^4\)

=\(0.6 \times 10^{10}\left(a^m \times a^n=a^{m+n}\right)\)

=\(6.0 \times 10^9\)

11. If m=2, n= -1, then find the value of the following.

1) \(m^n-n^m\)

Solution: =\((2)^{-1}-(-1)^2\)
=\(\frac{1}{2}-1\)
=\(-\frac{1}{2}\)

2) \(m^n \div n^m\)

Solution: =\((2)^{-1} \div(-1)^2\)
=\(\frac{2^{-1}}{(-1)^2}\)
=\(\frac{2^{-1}}{1}\)
=\(\frac{1}{2} \times 1=\frac{1}{2}\)

KSEEB Maths Class 8 Exponents and Powers 

12. Simplify
\(\left[\left(\frac{-2}{3}\right)^{-2}\right]^3 \times\left(\frac{1}{3}\right)^{-4} \times 3^{-1} \times \frac{1}{6}\)

Solution: \(\left[\left(\frac{-2}{3}\right)^{-2}\right]^3 \times\left(\frac{1}{3}\right)^{-4} \times 3^{-1} \times \frac{1}{6}\)

=\(\left(\frac{-2}{3}\right)^{-6} \times\left(3^{-1}\right)^{-4} \times 3^{-1} \times \frac{1}{3 \times 2}\)

=\((-2)^{-6} \times 3^6 \times 3^4 \times 3^{-1} \times 3^{-1} \times 2^{-1}\)
\(\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}\)
=\((-2)^{-6-1} \times 3^{6+4-1-1}\)
(∵\((-2)^m=(2)^m\), if m is even)
=\(-2^{-7} \times 3^8\)
\(\Rightarrow \frac{3^8}{2^7}\)

13. By what number should \((-8)^{-3}\) be multiplied so that the product may be equal to \((-6)^{-3}\) ?

Solution: Let the number be x
\((-8)^{-3} \times x=(-6)^{-3}\)
\(\left(\frac{1}{-8}\right)^3 \times x=\left(-\frac{1}{6}\right)^{+3}\)

=\(\left(\frac{z^4}{6_3}\right)^3\)

=\(\left(\frac{4}{3}\right)^3=\frac{64}{27}\)

∴ \(x=\frac{64}{27}\)

14. Simplify \(\left(x^{\frac{b+c}{c-a}}\right)^{\frac{1}{a-b}}\left(x^{\frac{c+a}{a-b}}\right)^{\frac{1}{b-c}}\left(x^{\frac{a+b}{b-c}}\right)^{\frac{1}{c-a}}=1v prove that

Solution: LHS = [latex]\left(x^{\frac{b+c}{c-a}}\right)^{\frac{1}{a-b}}\left(x^{\frac{c+a}{a-b}}\right)^{\frac{1}{b-c}}\left(x^{\frac{a+b}{b-c}}\right)^{\frac{1}{c-a}\)

=\(\frac{b+c}{x^{(a-b)(c-a)}}+\frac{c+a}{(a-b)(b-c)}+\frac{a+b}{(b-c)(c-a)}\)

=\(x \quad \frac{(b+c)(b-c)+(c+a)(c-a)+(a+b)(a-b)}{(a-b)(b-c)(c-a)}\)

=\(x \frac{b^2-a^2+a^2-a^2+a^2-b^2}{(a-b)(b-c)(c-a)}\)
[∵\((a+b)(a-b)=a^2 – b^2\)]
=\(\frac{0}{x^{(a-b)(b-c)(c-a)}}\)

=\(x^0\)
= 1
= RHS
Hence proved.

15. By what number should \(\left(\frac{1}{2}\right)^{-1}\) be divided so that the quotient is \(\left(\frac{-5}{4}\right)^{-1}\) ?

Solution: Let the required number be x.
Then \(\left(\frac{1}{2}\right)^{-1} \div x=\left(\frac{-5}{4}\right)^{-1}\)

=\(2 \times \frac{-5}{4}\)
\(x=\frac{-5}{2}\)
Hence, the required number is \(\frac{-5}{2}\).

16. If \(6^{2 x+1} \div 36=216\), find the value of x.

Solution: Given \(6^{2 x+1} \div 36=216\)
\(\frac{6^{2 x+1}}{6^2}=6^3\)

\(6^{2 x+1}=6^5\)
⇒ 2x + 1 = 5
⇒ 2x = 4
\(x=\frac{4}{2}\)
∴ x = 2

17. Express \(\frac{216}{1000}\) in exponential notation. Express the answer in lowest terms.

Solution: \(\frac{216}{1000}=\frac{6^3}{10^3}=\left(\frac{6}{10}\right)^3=\left(\frac{3}{5}\right)^3\)

18. Find the value of \(\left(3^2\right)^3+\left(\frac{2}{3}\right)^0+3^5\)

Solution: \(\left(3^2\right)^3+\left(\frac{2}{3}\right)^0+3^5\)
=\(3^6+1+3^5 \quad\left(a^m\right)^n=a^{m n}\)
= 729 + 1 + 243
= 973

19. Evaluate \(\left\{\left(\frac{4}{3}\right)^{-1}-\left(\frac{1}{4}\right)^{-1}\right\}^{-1}\)

Solution: \(\left\{\left(\frac{4}{3}\right)^{-1}-\left(\frac{1}{4}\right)^{-1}\right\}^{-1}\)

=\(\left[\left(\frac{3}{4}\right)^1-\left(\frac{4}{1}\right)^1\right]^{-1}\)

=\(\left(\frac{3}{4}-\frac{4}{1}\right)^{-1}\)

=\(\left(\frac{3-16}{4}\right)^{-1}\)

=\(\left(\frac{-13}{4}\right)^{-1}\)

=\(\left(\frac{-4}{13}\right)^1\)

=\(\frac{-4}{13}\)

20. Find the value of \(m+m^m(m) \text { When } m=3 \text {. }\)

Solution: \(m+m^m(m)\)
=\(3+3^3(3)\)
= 3 + 27 x 3
= 3 + 81
= 84

21. A new born bear weighs 4kg, how many kilograms might a five-year-old bear weigh if its weight increases by the power of 2 in 5 yr?

Solution: Weight of newborn bear = 4kg
Weight increases by the power of 2 in 5yrs.
Weight of bearin 5 yrs =\(4^2\) = 16kg.

22. The cells of a bacteria double itself every hour. How many cells will be there after 8h. If initially, we start with cell. Express the answer in powers.

Solution: The cell of a bacteria double itself every hour = \(1 + 1 = 2 = 2^1\)
Since, the process started with 1 cell
∴ The total number of cell in 8h
= 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
=\(2^{1+1+1+1+1+1+1+1}=2^8\)

23. If a = -1, b = 2, then find the value of \(a^b+b^a\text { \& } a^b \div b^a\)

Solution: 1) Given \(a^b+b^a\)
If \(a=-1 \& b=2, \text { then }(-1)^2+(2)^{-1}\)
=\(1+\frac{1}{2}=\frac{2+1}{2}=\frac{3}{2}\)

2) \(a^b \div b^a, \text { If } a=-1 \& \mathrm{~b}=2\)
\(\text { then }(-1)^2 \div(2)^{-1}=1 \div \frac{1}{2}=\frac{1 \times 2}{1}=2\)

24. Find x, \(\left(\frac{2}{5}\right)^{2 x+6} \times\left(\frac{2}{5}\right)^3=\left(\frac{2}{5}\right)^{x+2}\)

Solution: wkt \(a^m \times a^n=a^{m+n}\)
then \(\left(\frac{2}{5}\right)^{2 x+6}\) \(\times\left(\frac{2}{5}\right)^3=\left(\frac{2}{5}\right)^{2 x+6+3}=\left(\frac{2}{5}\right)^{x+2}\)

2x + 9 = x + 2
2x – x = 2 – 9
x = -7

25. Find three machines that can be replaced with hook-up of \((x^5 machines)\).

Solution: Since \(5^2=25,5^3=125,5^4=625\)
Hence \(\left(x 5^2\right),\left(x 5^3\right) \&\left(x 5^4\right)\) machine can replace \((x^5)\) hook – up machine.

KSEEB Solutions For Class 8 Maths Chapter 8 Cubes And Cube Roots Points To Remember

Cube Number: Number obtained when a number is multiplied by itself three times
\(2^3 = 2x2x2 = 8\)
\(3^3 = 3x3x3 = 27\) etc.

Numbers like 1729,4104,13832 are known as Hardy Ramanujan Numbers. They can be expressed as sum of two cubes in two different ways.

Numbers obtained when a number is multiplied
by itself three times are known as cube numbers for example 1, 8, 27,……..etc.

If in the prime factorisation of any number each factor appears three times, then the number is a perfect cube.

The symbol denotes \( \sqrt[3]{ }\) denotes cube root, for example \( \sqrt[3]{27}=3\)

Perfect cube: A natural number is said to be a perfect cube if it is the cube of some natural number. Example: 8 is a perfect cube, because there is a natural number 2 such that \( 8 = 2^3\) , but 18 is not a perfect cube, because there is no natural number whose cube is 18.

Read and Learn More KSEEB Solutions for Class 8 Maths

The cube of a negative number is always negative

Properties of cube of Number.

1)Cube of even number are even.
2)Cubes of odd numbers are odd
3)The sum of the cubes of first n natural numbers is equal to the square of their sum.
4)Cubes ofthe numbers ending with the digits 0, 1,4, 5, 6 and 9 end with digits 0, 1,4, 5, 6 and 9 respectively.
5)Cube of the number ending in 2 ends in 8 and cube of the number ending in 8 ends in 2.
6)Cube of the number ending in 3 ends in 7 and cube of the number ending in 7 ends in 3.

Class 8 Maths KSEEB Cubes And Cube Roots Exercise 8.1

1. Which of the following numbers are not perfect cube?

1) 216

Prime factorisation of 216 is as follows

216 = 2 x 2 x 2 x 3 x 3 x 3
= \( 2^3 \times 3^3\)
Here, as each prime factor is appearing as many times as a perfect multiple of 3.
∴ 216 is a perfect cube.

2) 128

128 = 2 x 2 x 2 x 2 x 2 x 2 x 2

Here, each prime factor is not appearing as many times as a perfect multiple of 3. One 2 is remaining after grouping the triplets of 2.
∴ 128 is not a perfect cube.

3) 1000

1000 = 2 x 2 x 2 x 5 x 5 x 5

Here, as each prime factor is appearing as many times as a perfect multiple of 3.

∴ 1000 is a perfect cube

Download KSEEB Solutions For Cube And Cube Roots Chapter 8

4) 100

100 = 2 x 2 x 5 x 5

Here, each prime factor is not appearing as many times as a perfect multiplel of 3, two 2S and two 5S are remaining after grouping the triplets.

∴ 100 is not a perfect cube.

v)46656

466556 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3 x 3 x 3

Here, as each prime factor is appearing as many times as a perfect multiple of 3.

∴ 46656 is a perfect cube.

2. Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.

1)243

Solution: 243 = 3 x 3 x 3 x 3 x 3

Here, two 3s are left which are not in a triplet. To make 243 a cube, one more 3 is required.

In that case, 243 x 3 = 3 x 3 x 3 x 3 x 3 x 3 = 729 is a perfect cube.

Hence, 3 is the smallest natural number by 243 should be multiplied to make it a perfect cube.

2) 256

Solution: 256 = 2x2x2x2x2x2x2x2

Here, two 2s are left which are not in a triplet.

To make 256 a cube, one more 2 is required. Then we obtain.

256×2 = 2x2x2x2x2x2x2x2x2 =512 is a perfect cube.

Hence, 2 is the smallest natural number by which 256 should be multiplied to make it a perfect cube.

3)72

Solution: 72 = 2x2x2x3x3

Here, two 3 s are left which are not in a triplet to make 72 a cube, one more 3 is required.

Then, we obtain

72×3 = 2x2x2x3x3x3 = 216 is a perfect cube.

Hence, the smallest natural number by which 675 should be multiplied to make it a perfect cube is 3.

4)675

Solution: 675 = 3x3x3x5x5

Here, two 5s are left which are not in a triplet, to make 675 a cube, one more 5 is required.

Then, we obtain

675×5 = 3x3x3x5x5x5 = 3375 is a perfect cube.

Hence the smallest natural number by which 100 should be multiplied to make it a perfect cube is 5.

5)100

Solution: 100 = 2x2x5x5

Here, two 2s and two 5s are left which are not in a triplet, to make 100 a cube, we require one more 2 and one more 5.

Then, we obtain

100x2x5 = 2x2x2x5x5x5 = 1000 is a perfect cube.

Hence the smallest natural number by which 72 should be multiplied to make it a perfect cube is 2 x 5 = 10.

KSEEB Maths Class 8 Chapter 8 Detailed Answers

3. Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.

1)81

Solution: 81 = 3x3x3x3

Here, one 3 is left which is not a triplet.

If we divide 81 by 3, then it will become a perfect cube.

Thus, 81÷3 = 27 = 3x3x3 is a perfect cube.

Hence, the smallest number by which 81 should be divided to make it a perfect cube is 3.

2)128

Solution: 128 = 2x2x2x2x2x2x2

Here, one 2 is left which is not in a triplet

If we divide 128 by 2, then it will become a perfect cube. Thus, 128 ÷ 2 = 64 = 2x2x2 x2x2x2 is a perfect cube. Hence, 2 is the smallest number by which 128 should be divided to make

it a perfect cube.

3)135

Solution: 135=3x3x3x5

Here, one 5 is left which is not in a triplet.

If we divide 135 by 5, then it will become a perfect cube.

Thus, 135÷5 = 27 = 3x3x3 is aperfect cube.

Hence, 5 is the smallest number by which 135 should be divided to make it a perfect cube.

4)192

Solution: 192=2x2x2x2x2x2x3

Here, one 3 is left which is not in a triplet.

If we divide 192 by 3, then it will become a perfect cube.

Thus, 192÷3 = 64 = 2x2x2x2x2x2 is a perfect cube.

Hence, the smallest number by which 192 should be divided to make it a perfect cube is 3.

5)704

Solution: 704 = 2x2x2x2x2x2x11

Here, one 11 is left which is not in a triplet.

If we divide 704 by 11, then it will become a perfect cube.

Thus, 2x2x2x2x2x2 is a perfect cube. Hence, the smallest number by which 704 should be divided to make it a perfect cube is 11.

4. Parikshit makes a cuboid of plasticine of sides 5cm, 2cm, and 5cm. How many such cuboids will be need to form a cube?

Solution: Volume of the cube of sides 5cm, 2cm, 5cm = 5cm x 2cm x 5cm = \((5x5x2) cm^3\)

Here, two 5 s and one 2 are left which are not in a triplet.

If we multiply this expression by 2 x 2 x 5 = 20,

then it will become a perfect cube.

Thus (5x5x2x2x2x5) = (5x5x5x2x2x2) = 1000 is a perfect cube,

Hence 20 cuboids of 5cm, 2cm, 5cm are required to form a cube

KSEEB Class 8 Maths Solutions Cubes And Cube Roots Exercise 8.2

1. Find the cube root of each of the following numbers by prime factorisation method.

1) 64
2) 512
3) 10648
4) 27000
5) 15625
6) 13824
7) 110592
8) 46656
9) 175616
10) 91125

Solution:

1) 64

Solution:

∴ \(\sqrt[3]{64}=2 \times 2\)

=4

2) 512

Solution:

∴ \(\sqrt[3]{512}=2 \times 2 \times 2\)

= 8

3) 10648

Solution:

10648=\(2 \times 2 \times 2 \times 11 \times 11 \times 11\)

∴ \(\sqrt[3]{10648}=2 \times 11=22\)

=30

4) 27000

Solution:

27000 = \(\underline{2 \times 2 \times 2} \times \underline{3 \times 3 \times 3} \times \underline{5 \times 5 \times 5}\)

∴ \(\sqrt[3]{27000}=2 \times 3 \times 5\)

= 30

5) 15625

Solution:

15625 = \(5 \times 5 \times 5 \times 5 \times 5 \times 5\)

∴ \(\sqrt[3]{15625}=5 \times 5\)

= 25

6) 13824

Solution:

13824: =\(\underline{2 \times 2 \times 2 \times} \underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2 \times 3 \times 3 \times 3}\)

∴ \(\sqrt[3]{13824}=2 \times 2 \times 2 \times 3\)

= 24

7)110592

Solution:

110592 = 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x3x3x3

∴ \(\sqrt[3]{110592}=2 \times 2 \times 2 \times 2 \times 3\)

= 48

8) 46656

Solution:

46656 = 2x2x2x2x2x2x3x3x3x3x3x3

∴ \(\sqrt[3]{46656}=2 \times 2 \times 3 \times 3\)

= 36

9) 175616

Solution:

175616 = 2x2x2x2x2x2x2x2x2x7x7x7

∴ \(\sqrt[3]{175616}=2 \times 2 \times 2 \times 7\)

= 56

10) 91125

Solution:

91125 = 3x3x3x3x3x3x5x5x5

∴ \(\sqrt[3]{91125}=3 \times 3 \times 5\)

= 45

Free KSEEB Solutions For 8th Class Cube And Cube Roots

2. State true or false.

1) Cube of any odd number is even.

Solution: False.

When we find out the cube of an odd number, we will find an odd number as the result because the unit place digit of an odd number is odd and we are multiplying three odd numbers.

∴ The product will be again an odd number.

For example, the cube of 3 is 27, which is again an odd number.

2) A perfect cube does not end with two zeroes.

Solution: True.

Perfect cube will end with a certain number of zeroes that are always a perfect multiple of 3. For example, the cube of 10 is 1000 and there are 3 zeroes at the end of it.

The cube of 100 is 1000000 and there are 6 zeroes at the end of it.

3) If square of a number ends with 5, then its cube ends with 25.

Solution: False.

It is not always necessary that if the square of a number ends with 5, then its cube will end with 25. For example, the square of 25 is 625 and 625 has its unit digit as 5. The cube of 25 is 15625.

However, the square of 35 is 1225 and also has its unit place digit as 5 but the cube of 35 is 42875 which does not end with 25.

4)There is no perfect cube which ends with 8.

Solution: False

There are many cubes which will end with 8. The cube of all the numbers having their unit place digit as 2 will end with 8.

The cube of 12 is 1728 and the cube of 22 is 10648

5)The cube of a two digit number may be a three-digit number.

Solution: False

The smallest two digit natural number is 10 and the cube of 10 is 1000 which has 4 digits in it.

6)The cube of a two digit number may have seven or more digits.

Solution: False, the largest two digit natural number is 99. and the cube of 99 is 970299 which has 6 digits in it. ∴ The cube of any two digit number cannot have 7 or more digits in it.

7)The cube of a single-digit number may be a single-digit number.

Solution: True, as the cube of 1 and 2 are 1 and 8 respectively.

3. You are told that 1331 is a perfect cube, can you guess without factorization what is its cube root? Similarly guess the cube roots of 4913,12167, 32768.

Solution: Firstly, we will make groups of three digits starting from the rightmost digit of the number as 1331. There are 2 groups 1 and 331 in it.

Considering 331

The digit at its unit place is 1, wkt if the digit 1 is at the end of a perfect cube number, then its cube root will have its unit place digit as 1 only.

∴ The unit place digit of the required cube root can be taken as 1.

Taking the other group ie 1

The cube of 1 exactly matches with the number of the second group. ∴the tens digit of our cube root will be taken as the unit place of the smallest number whose cube is near to the

number of the second group ie, 1, itself, 1 will be taken as tens place of the cube root of 1331

Hence, \(\sqrt[3]{1331}=11\).

The cube root of 4913 has to be calculated, we will make groups of three digits starting from the right most digit of 4913, as 4 913, the groups are 4 and 913.

Considering group 913

The number 913 ends with 3, wkt if the digit 3 is at the end of a perfect cube number, then its cube root will have its unit place digit as 7 only.

∴ The unit place digit of the required cube root is taken as 7.

Taking the other group ie, 4

wkt, \(l^3 = 1\) and \(2^3 = 8\)

Also, 1 < 4 < 8

∴ 1 will be taken at the tens place of the required cube root.

Thus \(\sqrt[3]{4913}=17\).

The cube root of 12167 has to be calculated. We will make groups of three digits starting from the rightmost digit of the number 12167, as 12 167, The groups are 12 and 167.

Considering the group 167.

167 ends with 7, wkt if the digit 7 is at the end of a perfect cube number, then its cube root will have its unit place digit as 3 only.

∴ The unit place digit of the required cube root can be taken as 3.

Taking the other group ie, 12

wkt \(2^3 = 8\) and \(3^3 = 27\)

Also 8 < 12 < 27

2 is smaller between 2 and 3.

∴ 2 will be taken at the tens place of the required cube root.

Thus \(\sqrt[3]{12167}=23\)

The cube root of 2768 has to be calculated. We will make groups of three digits starting from the rightmost digit of the number 32768, as 32 768

Considering the group 768

768 ends with 8, wkt if the digit 8 is at the end of a perfect cube number, then its cube root will have its unit place digit as 2 only. ∴ The unit place digit of the required cube root will be taken as 2.

Taking the other group i.e., 32., w.k.T 3

3= 27 and \(4^3 = 64\)

Also 27 < 32 < 64

3 is smaller between 3 and 4. ∴ 3 will be taken at the tens place of the required cube root. Thus \(\sqrt[3]{32768}=32\).

Cube And Cube Roots KSEEB 8th Class Additional Problems

1. Write cubes of first three multiples of 3.

Solution: 1st three multiples of 3 = 3, 6,9

Cubes of these numbers are as follows

2. Is 9720 a perfect cube? If not, find the smallest number by which it should be divided to get a perfect cube.

Solution: 9720 = 2x2x2x3x3x3x3x3x5

The primes 3 and 5 do not appear in groups of three. So, 9720 is not a perfect cube. We divide 9720 by 3 x 3 x 5 = 45, to make it a perfect cube.

3. Difference of two perfect cubes is 189. If the cube root of the smaller of the two numbers is 3, find the cube root of the large number.

Solution: Since, the cube root of smaller number = 3

So, smaller number = \(3^3 = 27\)

Since difference =189 Large number =189+ 27 = 216

∴ \( \sqrt[3]{216}=\sqrt[3]{2 \times 2 \times 2 \times 3 \times 3 \times 3}\)

= 2 x 3

= 6

Hence, the cube root of a large number is 6.

4. Which number is known as the Ramanujan number? What is the beauty of this number?

Solution: 1729 is known as the Ramanujan number. The beauty of this number is that it can be expressed as the sum of two cubes in two different ways

5. If \( m^2\) ends in an even number of zeroes, then \( m^3\) ends in an odd number of zeroes. State true or false and justify your answer.

Solution: False.

Let m=200, then \(m^2 = 40000 and m^3 = 8000000\)

Here, both \(m^2 and m^3\) have even number of zeroes.

6. Find the value of \( \sqrt[3]{\sqrt[3]{\ell^3}}\)

Solution: \(\sqrt[3]{\sqrt[3]{\ell^3}}=\left[\left(\ell^3\right)^{\frac{1}{3}}\right]^{1 / 3}\)

=\(\left(\ell^3\right)^{\frac{1}{9}}=\ell^{\frac{1}{3}}\)

7. Evaluate \(\sqrt[3]{0.3 \times 0.3 \times 0.3 \times 11 \times 11 \times 11}\)

Solution: \(\sqrt[3]{0.3 \times 0.3 \times 0.3 \times 11 \times 11 \times 11}\)

=\(\sqrt[3]{\frac{3}{10} \times \frac{3}{10} \times \frac{3}{10} \times 11 \times 11 \times 11}\)

=\(\sqrt[3]{\left(\frac{3}{10}\right)^3 \times 11^3}\)

=\(\frac{3}{10} \times 11\)

=\(\frac{33}{10}=3.3\)

8. Show that \(\sqrt[3]{64 \times 729}=\sqrt[3]{64} \times \sqrt[3]{729}\)

Solution: \(\sqrt[3]{64 \times 729}=\sqrt[3]{64} \times \sqrt[3]{729}\)

LHS = \(\sqrt[3]{64 \times 729}\)

=\(\sqrt[3]{4 \times 4 \times 4 \times 9 \times 9 \times 9}\)

=\(\sqrt[3]{4^3 \times 9^3}=4 \times 9=36\)

RHS = \(\sqrt[3]{64} \times \sqrt[3]{729}\)

=\(\sqrt[3]{4 \times 4 \times 4} \times \sqrt[3]{9 \times 9 \times 9}\)

=\(\sqrt[3]{4^3} \times \sqrt[3]{9^3}\)

= 4 x 9

= 36

∴ LHS=RHS

Practice Problems For KSEEB Class 8 Cube And Cube Roots

9. Find the value of smallest positive integers m for which 864 x m is a perfect cube.

Solution: We have

864 = 2x2x2x2x2x3x3x3

since 2×2 is the only incomplete triplet.

so 864 has to be multiplied by 2 to make it a perfect cube

∴ m=2

10. Evaluate \(\left\{5^2+\left(12^2\right)^{1 / 2}\right\}^3\)

Solution: \(\left\{5^2+\left(12^2\right)^{1 / 2}\right\}^3\)

=\((25+12)^3\)

11. Three numbers are in the ratio 2:3:4. The sum of their cubes is 0.334125. Find the numbers.

Solution: Let the numbers be 2x,3x and 4x respectively.

Sum of their cubes = 0.334125(given)

According to the question

⇒ \(8 x^3+27 x^3+64 x^3=0.334125\)

⇒ \(99 x^3=0.334125\)

\(x=\sqrt[3]{\frac{3375}{1000000}}\)

=\(\frac{15}{100}\)

= 0.15

∴ The required numbers are 0.3, 0.45, 0.6

12.Write cubes of 5 natural numbers which are of the form 3n + 2 (eg. 5,8,11,…. ) and verify the following. The cube of a natural number of the form 3n + 2 is a natural number of the same form.

Solution: The 5 natural numbers which are of the form 3n + 2 (eg. 5,8,11,….) are as follows.

3 x 1 + 2 = 3 + 2 = 5

3 x 2 + 2 = 6 + 2 = 8

3 x 3 + 2 = 9 + 2 = 11

3 x 4 + 2 = 12 + 2 = 14

3 x 5 + 2 = 15 + 2 = 17

The cube of 5 natural numbers which are of the form 3n + 2 (eg. 5, 8,11….) are as follows.

Verification.

125 = 3 x 41 + 2

512 = 3 x 170 + 2

1331 = 3 x 443 + 2

2744 = 3 x 914 + 2

4913 = 3 x 1637 + 2

The cube of a natural number of the form 3n+2 is a natural number of the same form.

13. Divide the number 26244 by the smallest number. So that the quotient is a perfect cube. Also, find the cube root of the quotient.

Solution:

26244 = 2x2x3x3x3x3x3x3x3x3

2x2x3x3x = 36 is the smallest number by which 26244 must be divided so that the quotient is a perfect cube.

The required quotient is 729.

The cube root of the quotient

=\(\sqrt[3]{729}=\sqrt[3]{9 \times 9 \times 9}=9\)

14. Three numbers are in the ratio 1:2:3 and the sum of their cubes is 4500. Find the number.

Solution: Let the numbers be x, 2x and 3x

According to the question

x=5

∴ Three numbers are 5, 2×5, 3×5

ie, 5, 10 and 15

15. If \(\sqrt[3]{\frac{x}{y}}=\frac{2}{3}\),find\(\frac{x}{y}\)

Solution: Given \(\sqrt[3]{\frac{x}{y}}=\frac{2}{3}\)

cube both side

16. Express the following numbers as the sum of odd numbers using the given pattern.

1) \(9^3-8^3\)=—–=—–
2) \(12^3-11^3\)=—–=—–
3) \(51^3-50^3\)=—–=—–

Solution:

1) \(9^3-8^3=1+\frac{9 \times 8}{2} \times 6=217\)

2) \(12^3-11^3=1+\frac{12 \times 11}{2} \times 6=397\)

3) \(51^3-50^3=1+\frac{51 \times 50}{2} \times 6=7651\)

17. The volume of a cube is 512 cubic meters. Find the length of the side of the cube.

Solution: wkt, the volume of a cube = \((side)^3\)

The length of the side of a cube = \(\sqrt[3]{512}\)

= \(\sqrt[3]{2^3 \times 2^3 \times 2^3}=2 \times 2 \times 2=8 m\)

18. Difference of two perfect cubes is 189, If the cube root of the smaller of the two numbers is 3, then find the cube root of the large number.

Solution: Given difference of two perfect cubes = 189

and cube root of the smaller number = 3

∴ cube of smaller number = \(3^3 = 27\)

Let cube root of the larger number =\(x^3\)

According to the question, \(x^3 = 27 = 189\)

⇒ \(x^3 = 189 + 27 = 216\)

19. Three numbers are in the ratio 2:3:4. The sum of their cubes is 0.334125. Find the numbers.

Solution: Let the numbers be 2x, 3x and 4x respectively.

∴ Sum of their cubes = 0.334125

ie, \((2 x)^3+(3 x)^3+(4 x)^3=0.334125\)

= 0.15

Hence, the required numbers are 2×0.15, 3×0.15 & 4×0.15 ie, 0.3,0.45 & 0.5

KSEEB Solutions For 8 Class Maths Chapter 7 Practical Geometry Points To Remember

A quadrilateral has 10 parts – 4 sides, 4 angles and 2 diagonals. Five measurements can determine a quadrilateral uniquely.

Five measurements can determine a quadrilateral uniquely.

A quadrilateral can be constructed uniquely if the lengths of its four sides and a diagonal is given.

A quadrilateral can be constructed uniquely, if its two diagonals and three sides are known.

Read and Learn More KSEEB Solutions for Class 8 Maths

A quadrilateral can be constructed uniquely if its two adjacent sides and three angles are known.

A quadrilateral can be constructed uniquely if its three sides and two included angles are given.

KSEEB Class 8 Maths Solutions For Chapter 7 Practical Geometry Exercise 7.1

1. Construct the following quadrilaterals

1) Quadrilateral ABCD
AB=4.5cm
BC=5.5cm
CD=4cm
AD=6cm
AC=7cm

2)Quadrilateral JUMP,
JU=3.5cm
UM=4cm
MP=5cm
PJ=4.5cm
PU=6.5cm

3)Parallelogram MORE
OR=6cm
RE=4.5cm
EO=7.5cm

4)Rhombus BEST
BE=4.5cm
ET=6cm

Solution:1)Quadrilateral ABCD

AB=4.5cm,BC=5.5cm, CD=4cm, AD=6cm, AC=7cm

1. Draw △ABC using SSS construction.

2. Vertex D is 6cm away from vertex A taking A as centre, draw an arc of radius 6cm.

3. taking C as centre, drawn arc of radius 4cm, cutting the previous arc at point D

4. ABCD is the required quadrilateral

2) Rough sketch of the quadrilateral JUMP

1. Draw △JUP using SSS construction

2. Vertex M is 5cm away from vertex P and 4cm away from Vertex U. Taking P and U as centres, draw arcs of radii 5cm and 4cm respectively. Let the point of intersection be M

3. Join M to P and U

4. JUMP is the required quadrilateral.

3) Parallelogram MORE

OR=6cm, RE=4.5cm, EO=7.5cm

1. △EOR can be constructed by using SSS.

2. Vertex M is 4.5cm away from Vertex O and 6cm away from vertex E.

∴ While taking O and E as centres draw arcs of 4.5cm radius and 6cm radius respectively these will interest each other at point M.

3. Join M to O and E

MORE is the required parallelogram.

4) All sides of a rhombus are of the same measure. Hence, BE=ES=ST=TB

A rough sketch of this rhombus can be drawn as follows

Step 1. △BET can be drawn using SSS.

2. Vertex S is 4.5cm away from vertex E and also from vertex

∴ While taking E and T as centres, draw arcs of 4.5cm radius, which will be intersecting each other at point S.

3. Join S to E and T.

BEST is the required Rhombus.

Practical Geometry Solutions KSEEB Class 8 Maths Practical Geometry Exercise 7.2

1. Construct the following quadrilaterals.

1) Quadrilateral LIFT,
LI=4cm
IF=3cm
TL=2.5cm
LF=4.5cm
IT=4cm

2) Quadrilateral GOLD,
OL=7.5cm
GL=6cm
GD=6cm
LD=5cm
OD=10cm

3) Rhombus BEND,
BN=5.6cm
DE=6.5cm
Solution:

Step 1. △ITL can be constructed by using SSS construction.
2. Vertex F is 4.5cm away from vertex L and 3cm away from Vertex I.
∴ while taking L and I as centres draw arcs of 4.5cm radius and 3cm radius respectively, which will be intersecting each other at point F.

2) A rough sketch of this quadrilateral can be drawn as follows.

Step 1. △GDL can be constructed by using SSS construction.
2. Vertex O is 10cm away from vertex D and 7.5cm away from vertex L.
∴ while taking D and L as centres, draw arcs of 10cm radius and 7.5 cm radius respectively. These will intersect each other at point O.
3. Join O to G and L
GOLD is the required quadrilateral.

3) wkt The diagonals of a rhombus always bisect each other at 90°. Let us assume that these are intersecting each other at point O in this rhombus.
Hence, EO=OD=3.25cm

Step 1. Draw a line segment BN of 5.6cm and also draw its perpendicular bisector. Let it intersect the line segment BN at O.
2. Taking O as centre, draw arcs of 3.25cm radius to intersect the perpendicular bisector at point D and E.
3. Join points D and E to points B and N.
BEND is the required quadrilateral.

KSEEB Class 8 Maths Chapter 7 Solved Problems Practical Geometry Exercise 7.3

1. Construct the following quadrilaterals.

1) Quadrilateral MORE,
MO=6cm
OR=4.5cm
 ∠M=60°
 ∠O=105°
 ∠R=105°

2) Quadrilateral PLAN,
PL=4cm
LA=6.5cm
 ∠P=90°
 ∠A=110°
 ∠N=85°

3) Parallelogram HEAR,
HE=5cm
EA=6cm
 ∠R=85°

4) Rectangle OKAY,
OK=7cm
KA=5cm

Solution: 1) Rough sketch of this quadrilateral can be drawn as follows.

Step 1. Draw a line segment MO of 6cm and an angle of 105° at point O. As vertex R is 4.5cm away from the vertex O. Cut a line segment OR of 4.5cm from this ray.
2. Again draw an angle of 105° at point R.
3. Draw an angle of 60° at point M. Let this ray meet the previously drawn ray from R at point E.
MORE is the required quadrilateral.

2) The sum of the angles of a quadrilateral is 360°
1) In quadrilateral PLAN,
∠P+ ∠L+ ∠A+ ∠N=360°
90°+ ∠L+110°+85°=360°
∠L=360°-285°=75°
2)A rough sketch of this quadrilateral is as follows.

3) Draw a line segment PL of 4cm and draw an angle of 75° at point L. As vertex A is 6.5 away from vertex L, cut a line segment LA of 6.5cm from this ray.
4) Again draw an angle of 110° at point A.
5) Draw an angle of 90° at point P. This ray will meet the previously drawn ray from A at point N. PLAN is the required quadrilateral.

3. 1) A rough sketch of this quadrilateral

2) Draw a line segment HE of 5cm and an angle of 85° at point E. As vertex A is 6cm away from vertex E, cut a line segment EA of 6cm from this ray.
3) Vertex R is 6cm and 5cm away from vertex H and A respectively, these will be intersecting each other at point R.
4) Join R to H and A.
HEAR is the required quadrilateral.

4. 1) A rough sketch of this Rectangle as follows.

2) Draw a line segment OK of 7cm and an angle of 90° at point K. As vertex A is 5cm away from vertex K. Cut a line segment KA of 5cm from this ray.
3) Vertex Y is 5cm and 7cm away from vertex O and A respectively. By taking radius as 5cm and 7cm draw arcs from point O and A respectively, these will be intersecting each other at point Y.
4) Join Y to A and O
OKAY is the required Rectangle.

KSEEB Maths Class 8 Practical Chapter 7 Geometry Practical Geometry Exercise 7.4

1. Construct the following Quadrilaterals.

1) Quadrilateral DEAR
DE=4cm
EA=5cm
AR=4.5cm
 ∠E=60°
 ∠A=90°

2) Quadrilateral TRUE
TR=3.5cm
RU=3cm
UE=4cm
 ∠R=75°
 ∠U=120°

Solution: Steps
1. A rough sketch of this quadrilateral can be drawn as follows

2. Draw a line segment DE of 4cm and an angle of 60° at point E. As vertex A is 5cm away from vertex E, cut a line segment EA of 5cm from this ray.
3. Again draw an angle of 90° at point A. As vertex R is 4.5cm away from vertex A, cut a line segment RA of 4.5cm from this ray.
4. Join D to R
DEAR is the required quadrilateral.

2) Steps
1. A rough sketch of this quadrilateral can be drawn as follows

2. Draw a line segment RU of 3cm and an angle of 120° at point U. As vertex E is 4cm away from vertex U, cut a line segment UE of 4cm from this ray.
3. Draw an angle of 75° at point R as vertex T is 3.5cm away from vertex R, cut a line segment RT of 3.5cm from this ray.
4. Join T to E
TRUE is required quadrilateral

Practical Geometry KSEEB Maths Practical Geometry Exercise 7.5

1. Draw the following.
1. The square READ with RE=5.1cm
2. A rhombus whose diagonals are 5.2cm and 6.4cm long
3. A rectangle with adjacent sides of lengths 5cm and 4cm.
4. A parallelogram OKAY where OK=5.5cm and KA=4.5cm Is it unique?
Solution: Steps
1)

2) Draw a line segment RE of 5.1cm and an angle of 90° at point R and E.
3) As vertex A and D are 5.1cm away from vertex E and R respectively, cut line segment EA and RD, each of 5.1cm from these rays.
4. Join D to A
READ is the required square.

2. Steps
1. A rough sketch of Rhombus ABCD is as follows.

2. Draw a line segment AC of 5.2cm and draw its perpendicular bisector. Let it intersect the line segment AC at point O.
3. Draw arcs of 3.2cm \(\left(\frac{6.4}{2} \mathrm{~cm}\right)\) on both sides of this perpendicular bisector. Let the arcs intersect the perpendicular bisector at point B and D with points A and C.
4. Join points B and D with points A and C.
ABCD is the required rhombus.

3. Steps
1. A rough sketch of Rhombus ABCD can be drawn as follows.

2. Draw a line segment AB of 5cm and an angle of 90° at point A and BC
3. As vertex C and D are 4cm away from vertex B and A respectively, cut line segments AD and BC each of 4cm from these rays.
4. Join D to C
ABCD is the required rectangle.

4. Steps
1. A rough sketch of parellelogram OKAY is as follows.

2. Draw a line segment OK of 5.5cm and a ray at point K at a convenient angle.
3. Draw a ray at point O parallel to the ray at K. As the vertices, A and Y are 4.2cm away from the vertex K and O respectively, cut line segments KA and OY, each of 4.2cm from these rays.
4. Join Y to A
OKAY is the required parallelogram.

It is a unique parallelogram.

KSEEB Class 8 Maths Of Practical Geometry Additional Problems

1. Is it possible to construct a quadrilateral ABCD in which AB = 3cm, BC = 4cm, CD = 5.4cm, DA = 5.9cm and diagonal AC = 8cm? If not, why?
Solution: No.
In a △le, sum of two sides is always greater than the third side but here
AB+BC<AC.

2.Is it possible to construct a quadrilateral ROAM in which RO = 4cm, OA = 5cm,
∠0 = 120°,  ∠R = 105° and  ∠A = 135° ? If not, why?
Solution: No, We know that the sum of four angles of a quadrilateral is 360°

But, here,  ∠O+ ∠R+ ∠A
= 120°+105°+135°
= 360°
∴ Construct of quadrilateral ROAM is not possible.

3.Draw a circle of radius 3cm and draw its diameter and label it as AC. Construct its perpendicular bisector and let it intersect the circle at B and D. What type of quadrilateral is ABCD? Justify your answer.
Solution: Cyclic quadrilateral Justification,
∠B = ∠D = 90°
(Angle in a semicircle)

∠A =  ∠C = 90°
(Angle in a semicircle)
∠B +  ∠D = 180°
∠A +  ∠C = 180°
(opposite angles of a cyclic quadrilateral are supplementary)

4.Construct a trapezium ABCD where AB || CD, AD = BC = 3.2cm AB = 6.4cm and CD =9.6cm. Measure  ∠B and  ∠A.
(Hint: Difference of two parallel sides gives an equilateral △le ).
Solution:

△BEC is an equilateral △le
∴  ∠BEC = 60°
⇒  ∠BED = 120°
Now, ∠A = ∠BED = 120°
(Opposite angles of a parallelogram)
∠A +  ∠D = 180° (Adjacent angle of parallelogram)
∠D = 180° –  ∠A = 180° —120°= 60°=  ∠ABE Finally,  ∠B =  ∠ABE +  ∠CBE
⇒  ∠B = 60° +60° = 120°

5.Construct a quadrilateral ABCD such that AB = 5cm, BC = 3cm, CD = 10cm, DA = 6cm,∠D = 45°
Solution: Rough sketch of a quadrilateral can be drawn as follows:

Steps 1. Draw a line segment DA of 6cm and angle of 45° at point D.
2. With D as centre and 1 Ocm as radius, mark an arc intersecting DX at the point C.
3. With C as the centre and 3 cm as radius draw an arc intersecting DX at the point C.
4. With C as the centre and 3cm as radius draw an arc
5. With A as centre and 5cm as radius, draw another arc intersecting the previous one at the point B.
6. Join BC and AB.

6. Construct a square in which each diagonal is 5cm long
Solution: Steps of construction
1.Draw AC = 5cm
2.Draw a perpendicular bisector of AC.
3.with O as centre cut off OB = OD = 2.5cm along the bisector line.
4.Join AD, CD, AB and CB
This is the required square ABCD

7. Construct a parallelogram when one of its side is 4cm and its two diagonals are 5.6cm and 7cm. Measure the otherside.
Solution: Rough sketch of a given parallelogram can be drawn as follows.

Steps of construction.
1. Draw AB = 4cm
2.with A as centre and radius 2.8cm, draw an arc.
3.with B as centre and radius 3.5cm, draw another arc cutting the previous arc at O.
4.Join OA and OB
5.produce AO to C such that OC = AO and produce BO to D such that OD = BO
6.Join AD, BC and CD
Thus ABCD is the required parallelogram and other side measures 5 cm.

8.Construct a Rhombus CLUE in which CL = 7.5cm and LE = 6cm.
Solution: Rough sketch of a given
Rhombus can be drawn as follows.
Steps of construction
1. Draw a line segment LC = 7.5cm.
2. with C as centre draw an arc CE = 7.5cm
3. with L as centre draw another arc LE = 6cm which cut off previous arc CE.
4. with L as centre draw an arc LU = 7.5cm and E as centre draw an arc UE = 7.5cm which cut off previous arc LU.
5. Now Join UL, CE and EU
Thus CLUE is the required rhombus.

KSEEB Class 8 Maths Solutions For Chapter 6 Algebraic Expressions And Identities Points To Remember

Expressions are formed from variables and constants

Constant: A symbol having a fixed numerical 2 value. Example: 2, 2/3, 2,1, etc.

Variable: A symbol that takes various numerical values.

Example: x, y, z, etc.

Read and Learn More KSEEB Solutions for Class 8 Maths

Algebraic expression: A combination of constants and variables connected by the sign +, —, x, and ÷ is called Algebraic expression.

Terms are added to form expressions. Terms themselves are formed as product of factors.

Expressions that contain exactly one, two and three terms are called monomials, binomials, and trinomials respectively.

In general, any expression containing one or more terms with non-zero coefficients (and with variables having non-negative exponents) is called a polynomial.

Like terms are formed from the same variables and the powers of these variables are the same, too.
Co-efficient of like terms need not be the same.

While adding (or subtracting) polynomials, first look for like terms and add (or subtract) them, then handle the unlike terms.

There are number of situations in which we need to multiply algebraic expressions for example, in finding the area of a rectangle, the sides of which are given as expressions.

Monomial: An expression containing only one term Example: -3, 4x, 3xy, etc.

Binomial: An expression containing two terms
Example: 2x – 3, 4x + 3y, xy – 4 etc.

Trinomial: An expression containing three terms.
Example: \(2x^2\) + 3xy + 9, 3x + 2y + 5z etc.

Polynomial: In general, any expression containing one or more terms with non-zero coefficients (and with variables having non-negative exponents). A polynomial may contain any number of terms, one or more than one.

A monomial multiplied by a monomial always gives a monomial.

While multiplying a polynomial by a monomial, we multiply every term in the polynomial by the monomial.

In carrying out the multiplication of a polynomial by a binomial (or trinomial), we multiply term by term. i.e. every term of the polynomial is multiplied by every term in the binomial or (trinomial). Note that in such multiplication, we may get terms in the product which are like and have to be combined.

An identity is an equality, which is true for all values of the variables in the equality. On the other hand, an equation is true only for certain values of its variables. An equation is not an identity.

The following are the standard identities.

• \((a + b)^2 = a^2 + 2ab + b^2\)
• \((a – b)^2 = a^2 – 2ab + b^2\)
• \((a + b)(a – b) = a^2 – b^2\)
• \((x + a)(x + b) = x^2 +(a + b)x + ab\)

The above four identities are useful in carrying out squares and products of algebraic expressions, they also allow easy alternative methods to calculate products of numbers and so on.

Coefficients: In the term of an expression any of the factors with the sign of the term is called the coefficient of the product of the other factors.

Terms: Various parts of an algebraic expression that are separated by + and – signs.

Example : The expression 4x + 5 has two terms 4X and 5.

1) Constant term: A term of expression having no lateral factor.

2) Like term: The term having the same literal factors.

Example : 2xy and -4xy are like terms.

3) Unlike terms: The terms having different literal factors.

Example: \(4x^2\) and 3xy are unlike terms.

Factors: Each term in an algebraic expression is a product of one or more number (S) and / or literals. These numbers (S) and/or literal (S) are known as the factor of that term. A constant factor is called numerical factor, while a variable factor is known as a literal factor. The term 4x is the product of its factors 4 and x.

Algebraic Expressions And Identities Solutions KSEEB Class 8 Maths Exercise 6.1

1. Identify the terms, their co-efficients for each of the following expressions.

1) \(5xyz^2 —3zy\)

Solution:

Terms : \(5xyz^2\) ,—3zy

Co – efficients : 5, -3

2) \(1 + x + x^2\)

Solution:

Terms : 1, x, \( x^2\)

Co-efficients: 1,1,1

3) \( 4x^2y^2 – 4x^2 y^2 z^2 + z^2\)

Solution:

Terms : \(4x^2y^2\) , \(-4x^2 y^2 z^2\) , \(z^2\)

Co – efficients : 4, -4, 1

4) 3 – pq + qr – rp

Solution:

Terms : 3 — pq, qr, rp

Co – efficients : 3, -1, 1,-1

5)\( \frac{x}{2}+\frac{y}{2}-x y\)

Solution:

Terms: x/2, y/2, -xy

Coefficients: 1/2, 1/2, -1

6) 0.3a -0.6ab + 0.5/)

Solution:

Terms : 0.3a, — 0.6ab, 0.5b

Coefficient : 0.3, — 0.6, 0.5

2. Classify the following polynomials as monomials, binomials, or trinomials, which polynomials do not fit in any of these three categories?
x+y, 1000, \(x+x^2+x^3+x^4\) , 7+y+5x, \( 2y-3y^2+4y^3\) ,5x-4y+3xy, \( 4z-15z^2\) , ab+bc+cd+da, pqr, \( p^2q+pq^2\) , 2p+2q

Solution:

MonomiaLs: 1000, QPR

Binomials: x + y, \(2y-3y^2\), \(4z-15z^2\),\(p^2q+pq^2\), 2P + 2q

Trinomials : 7 + y + 5x, \(2y-3y^2+4y^3\), 5x – 4y + 3xy

Polynomials that do not fit in any of these categories are: \(x + x^2+x^3+x^4\), ab + bc + cd + da

3. Add the following

1) ab – bc, bc – ca, ca – ab

2) a – b + ab, b – c + bc, c – a + ac

Solution:
1)
2) a -b + ab, b -c + bc,c – a + ac

Solution:
\(a-\not b+a b+b-c+b c+\not c-a c+a c\)
= ab+bc+ac

3) \(2p^2q^2 -3pq + 4,5 + 7pq -3p^2q^2\)
Solution: \(2p^2q^2 — 3pq + 4 + 5+ 7pq— 3p^2q^2\)
= \(-p^2q^2 +4pq + 9\)

4)\(l^2+m^2\), \(m^2+n^2\), 2lm+2mn+2nl
Solution: \(\begin{aligned}
& \ell^2+m^2+m^2+n^2+n^2+\ell^2 \\
&+2 \ell m+2 m n+2 n \ell
\end{aligned}\)
= \(2 \ell^2+2 m^2+2 n^2+2 \ell m+2 m n+2 n \ell\)

4. 1) Subtract 4a-7ab+3b+12 from 12a-9ab+5b-3

Solution:
\(\begin{aligned}
& 12 a-9 a b+5 b-3 \\
& (-) 4 a-7 a b+3 b+12 \\
& 8 a-2 a b+2 b-15 \\
&
\end{aligned}\)

b) Subtract 3xy + 5yz — 7zx from 5 xy — 2 yz — 2 zx +10 xyz

Solution:

c) Subtract \(4 p^2 q-3 p q+5 p q^2-8 p+7 q-10\) from \(18-3 p-11 q+5 p q-2 p q^2+5 p^2 q\)

Solution:

KSEEB Class 8 Maths Chapter 6 Algebraic Expressions And Identities Exercise 6.2

1. Find the product of the following pairs of monomials.

1) 4,7p

2) -4p,7p

3) -4p,7pq

4) \(4 p^3\), -3p

5) 4p,0

Solution:

1) \(4 \times 7 \times p=28 p\)

2) \(-4 p \times 7 p=-28 p^2\)

3)\(-4 p \times 7 p q=-28 p^2 q\)

4) \(4 p^3 \times-3 p=-12 p^4\)

5)\(4 p \times 0=0\)

2. Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively.

1)(p,q)

2) (10m, 5n)

3) \(\left(20 x^2, 5 y^2\right)\)

4) \(\left(4 x, 3 x^2\right)\)

5) (3mn,4np)

Solution:

1) (p, q)

Area of rectangle = length x breadth

= pxq = pq

2) (10m, 5n)

Area of rectangle = l x b = 10m x 5n

= 50 mn

3) \(\left(20 x^2, 5 y^2\right)\)

Area of reactangle = l x b = \(20x^2 x 5y^2\)

= \(100x^2y^2\)

4) \(\left(4 x, 3 x^2\right)\)

Solution: Area of rectangle = l x b = \(4x x 3x^2\)

=\(12x^3\)

v) 3mn x 4np

Solution: Area ofrectangle = l x b = 3mn x 4np

=\(12mn^2p\)

3. Complete the table of products

Solution:

4. Obtain the volume of rectangular boxes with the following length, breadth and height respectively.

1) \(5 a, 3 a^2, 7 a^4\)

2) \(2 p, 4 q, 8 r\)

3) \(x y, 2 x^2 y, 2 x y^2\)

4) \(a, 2 b, 3 c\)

Solution: Volume = Length x Breadth x Height

1) \(\vartheta=5 a \times 3 a^2 \times 7 a^4=5 \times 3 \times 7 \times a \times a^2 \times a^4=105 a^7\)

2) \(\vartheta=2 p \times 4 q \times 8 r=2 \times 4 \times 8 \times p \times q \times r=64 p q r\)

3) \(\vartheta=x y \times 2 x^2 y \times 2 x y^2=2 \times 2 \times x \times x^2 \times x \times y \times y \times y^2=4 x^4 y^4\)

4)\(\vartheta=a \times 2 b \times 3 c=2 \times 3 \times a \times b \times c=6 a b c\)

5) Obtain the product of

1) xy, yz, zx

Solution: \(x \times y \times y \times z \times z \times x==x^2 y^2 z^2\)

2) \(a,-a^2, a^3\)

Solution: \(a \times\left(-a^2\right) \times a^3=-a^6\)

3) \( 2,4 y, 8 y^2, 16 y^3\)

Solution: \(2 \times 4 y \times 8 y^2 \times 16 y^3=1024 y^6\)

4) \(a \times 2 b \times 3 c \times 6 a b c=36 a^2 b^2 c^2\)

Solution: \(a \times 2 b \times 3 c \times 6 a b c=36 a^2 b^2 c^2\)

5) \(m,-m n, m n p\)

Solution: \(m \times(-m n) \times(m n p)=-m^3 n^2 p\)

KSEEB Maths Class 8 Algebraic Expressions And Identities Exercise 6.3

1. Carry out the multiplication of the expression in each of the following pairs.

1) \(4 p, q+r\)

2) \(a b, a-b\)

3) \(a+b, 7 a^2 b^2\)

4) \(a^2-9,4 a\)

5) \(p q+q r+r p, 0\)

Solution:

1) \((4 p) \times(q+r)\)

=\((4 p \times q)+(4 p \times r)\)

= \(4 p q+4 p r\)

2) \((a b) \times(a-b)\)

=\(a b \times a-a b(b)\)

=\(a^2 b-a b^2\)

3)\((a+b)\left(7 a^2 b^2\right)\)

=\(a \times 7 a^2 b^2+b \times 7 a^2 b^2\)

=\(7 a^3 b^2+7 a^2 b^3\)

4) \( \left(a^2-9\right)(4 a)\)

=\(a^2 \times 4 a-9 \times 4 a\)

=\(4 a^3-36 a\)

5) \((p q+q r+r p)(0)\)

=\((p q \times 0)+(q r \times 0)+(r p \times 0)\)

=\(0+0+0=0\)

2. Complete the table

Solution:

3. Find the product

1) \(\left(a^2\right) \times\left(2 a^{22}\right) \times\left(4 a^{26}\right)\)

Solution: \(2 \times 4 \times a^2 \times a^{22} \times a^{26}\)

=\(8 a^{50}\)

2) \(\left(\frac{2}{3} x y\right) \times\left(\frac{-9}{10} x^2 y^2\right)\)

Solution: \(\left(\frac{2}{3}\right) \times\left(\frac{-9}{10}\right) \times x \times y \times x^2 \times y^2\)

=\(\frac{-3}{5} x^3 y^3\)

3) \(\left(\frac{-10}{3} p q^3\right) \times\left(\frac{6}{5} p^3 q\right)\)

Solution: \(\frac{-10}{3} \times \frac{6}{5} \times p \times q^3 \times p^3 \times q\)

=\(-4 p^4 q^4\)

4) \(x \times x^2 \times x^3 \times x^4\)

Solution: \(x^{10}\)

4. a) Simplify 3x(4x-5)+3 and find its values for

1) x=3

2) \(x=\frac{1}{2}\)

Solution: \(3 x(4 x-5)+3\)

=\(

= [latex]12 x^2-15 x+3\)

1) For x=3,\(12 x^2-15 x+3\)

=\(12(3)^2-15(3)+3\)

=\(12 \times 9-15 \times 3+3\)

=\(108-45+3\)

= 66

2) For \(x=\frac{1}{2}\)

= \(12 \times\left(\frac{1}{2}\right)^2-15 \times \frac{1}{2}+3\)=\(12^3\times\frac{1}{4}-\frac{15}{2}+3\)

= \(3-\frac{15}{2}+3\)

= \(6-\frac{15}{2}=\frac{12-15}{2}\)

= \(\frac{-3}{2}\)

b) Simplify \(a\left(a^2+a+1\right)+5\) and find its value for

1) a=0

2) a=1

3) a= -1

Solution:

For a=1, \( a^3+a^2+a+5\)

⇒ \( 1^3+1^2+1+5=1+1+1+5=8\)

For a= -1, \( a^3+a^2+a+5\)

⇒ \( (-1)^3+(-1)^2+(-1)+5\)

= \( -1+1-1+5=4\)

5. a) Add: p(p-q), q(q-r) and r(r-p)

Solution: p(p-q)+q(q-r)+r(r-p)

= \(p^2-p q+q^2-q r+r^2-r p\)

= \(p^2+q^2+r^2-p q-q r-r p\)

b) Add: 2x(z-x-y) and 2y(z-y-x)

Solution: 2x(z-x-y)+2y(z-y-x)

= \(2 x z-2 x^2-2 x y+2 y z-2 y^2-2 x y\)

= \(-2 x^2-2 y^2-4 x y+2 y z+2 z x\)

c) 3l(l-4m+5n) from 4l(10n-3m+5n)

Solution: 4l(10n-3m+2l)-3l(l-4m+5n)

= \(40ln-12ml+8l^2-3l^2+12ml-15ln\)

= \(25ln+5l^2\)

d) Subtract: 3a(a+b+c)-2b(a-b+c) from 4c(-a+b+c)

Solution: \(4 c(a+b+c)-3 a(a+b+c)+2 b(a-b+c)\)

= \(-4 a c+4 b c+4 c^2-3 a^2-3 a b-3 a c+2 a b-2 b^2+2 b c\)

= \(-4 a c-3 a c+4 b c+2 b c-3 a b+2 a b+4 c^2-3 a^2-2 b^2\)

= \(-7 a c+6 b c-a b+4 c^2-3 a^2-2 b^2\)

Chapter 6 Algebraic Expressions And Identities In KSEEB Maths Exercise 6.4

1. Multiply the binomials.

1) (2x+5) and (4x-3)

Solution: (2x+5)x(4x-3)

=2 x(4 x-3)+5(4 x-3)

=\(2 x \times 4 x-2 x \times 3+5 \times 4 x-5 \times 3\)

=\(8 x^2-6 x+20 x-15\)

=\(8 x^2+14 x-15\)

2) (y-8) and (3y-4)

Solution: (y-8)x(3y-4)

=\(y \times(3 y-4)-8(3 y-4)\)

=\(y \times 3 y-y \times 4-8 \times 3 y-8 \times(-4)\)

=\(3 y^2-4 y-24 y+32\)

=\(3 y^2-28 y+32\)

3) (2.5l-0.5m) and (2.5l+0.5m)

Solution: (2.5l-0.5m)x(2.5l+0.5m)

=2.5l(2.5l+0.5m)-0.5m(2.5l+0.5m)

=2.5l x 2.5l + 2.5l x 0.5m -0.5m x 2.5

= \(6.25l^2+1.25lm-1.25lm-0.25m^2\)

=\(6.25l^2-0.25m^2\)

4) (a+3b) and (x+5)

Solution: \((a+3 b) \times(x+5)\)

=\(a(x+5)+3 b(x+5)\)

=\(a x+a 5+3 b x+15 b\)

=\(a x+5 a+3 b x+15 b\)

5) \(\left(2 p q+3 q^2\right) \text { and }\left(3 p q-2 q^2\right)\)

Solution: \(\left(2 p q+3 q^2\right) \text { and }\left(3 p q-2 q^2\right)\)

= \(2 p q \times 3 p q-2 p q \times 2 q^2+3 q^2\times 3 p q-3 q^2 \times 2 q^2\)

= \(6 p^2 q^2-4 p q^3+9 p q^3-6 q^4\)

6) \(\left(\frac{3}{4} a^2+3 b^2\right) \text { and } 4\left(a^2-\frac{2}{3} b^2\right)\)

Solution:  \(\left(2 p q+3 q^2\right) \times\left(3 p q-2 q^2\right)\)

= \(\left(\frac{3}{4} a^2+3 b^2\right) \times\left(4 a^2-\frac{8}{3} b^2\right)\)

= \(\frac{3}{4} a^2\left(4 a^2-\frac{8 b^2}{3}\right)+3 b^2\left(4 a^2-\frac{8 b^2}{3}\right)\)

= \(\frac{3}{4} a^2 \times 4 a^2-\frac{\not \beta}{4} a^2 \times \frac{8^2}{\not 8} b^2+3 b^2\times 4 a^2-\frac{8}{3} b^2 \times \not 3 b^2\)

= \(3 a^4-2 a^2 b^2+12 a^2 b^2-8 b^4\)

= \(3 a^4+10 a^2 b^2-8 b^4\)

2. Find the Product

1) (5-2x)(3+x)

Solution: (5-2x)(3+x)

= 5(3+x)-2x(3+x)

= \(15+5 x-6 x-2 x^2\)

= \(15-x-2 x^2\)

2) (x+7y)(7x-y)

Solution: (x+7y)x(7x-y)

= x(7 x-y)+7 y(7 x-y)

= \(7 x^2-x y+49 x y-7 y^2\)

= \(7 x^2+48 x y-7 y^2\)

3) \(\left(a^2+b\right)\left(a+b^2\right)\)

Solution: \(\left(a^2+b\right)\left(a+b^2\right)\)

= \(a^2\left(a+b^2\right)+b\left(a+b^2\right)\)

= \(a^3+a^2 b^2+a b+b^3\)

4) \(\left(p^2-q^2\right)(2 p+q)\)

Solution: \(\left(p^2-q^2\right) \times(2 p+q)\)

= \(p^2(2 p+q)-q^2(2 p+q)\)

= \(2 p^3+p^2 q-2 p q^2-q^3\)

3. Simplify

1) \(\left(x^2-5\right)(x+5)+25\)

Solution: \(\left(x^2-5\right)(x+5)+25\)

= \(x^2(x+5)-5(x+5)+25\)

= \(x^3+5 x^2-5 x-25+25\)

= \(x^3+5 x^2-5 x\)

2) \(\left(a^2+5\right)\left(b^3+3\right)+5\)

Solution: \(\left(a^2+5\right)\left(b^3+3\right)+5\)

=\(a^2\left(b^3+3\right)+5\left(b^3+3\right)+5\)

= \(a^2 b^3+3 a^2+5 b^3+15+5\)

= \(a^2 b^3+3 a^2+5 b^3+20\)

3) \(\left(t+s^2\right)\left(t^2-s\right)\)

Solution: \(\left(t+s^2\right) \times\left(t^2-s\right)\)

= \(t\left(t^2-s\right)+s^2\left(t^2-s\right)\)

= \(t^3-s t+s^2 t^2-s^3\)

4) \((a+b)(c-d)+(a-b)(c+d)+2(a c+b d)\)

Solution: \((a+b) \times(c-d)+(a-b) \times(c+d)+2(a c+b d)\)

= \(a(c-d)+b(c-d)+a(c+d)-b(c+d)+2(a c+b d)\)

= \(a c-a a+b c-b a+a c+a d-b c-b a+2 a c+2 b a\)

= 4ac

5) (x+y)(2 x+y)+(x+2 y)(x-y)

Solution: \((x+y) \times(2 x+y)+(x+2 y) \times(x-y)\)

= \(x(2 x+y)+y(2 x+y)+x(x-y)+2 y(x-y)\)

= \(2 x^2+y y+2 x y+y^2+x^2-y y+2 x y-2 y^2\)

= \(3 x^2-y^2+4 x y\)

6) \((x+y)\left(x^2-x y+y^2\right)\)

Solution: \((x+y)\left(x^2-x y+y^2\right)\)

= \(x\left(x^2-x y+y^2\right)+y\left(x^2-x y+y^2\right)\)

= \(x^3-y^2 y+y y^2+y^2 y-y y^2+y^3\)

= \(x^3+y^3\)

7) (1.5 x-4 y)(1.5 x+4 y+3)-4.5 x+12 y

Solution: (1.5 x-4 y)(1.5 x+4 y+3)-4.5 x+12 y

= 1.5 x(1.5 x+4 y+3)-4 y(1.5 x+4 y+3)-4.5 x+12 y

= \(2.25 x^2+6 x y+4.5 x-6 x y-16 y^2-12 y-4.5 x+12 y\)

= \(2.25 x^2-16 y^2\)

8) (a+b+c)(a+b-c)

Solution:(a+b+c)x(a+b-c)

= a(a+b-c)+b(a+b-c)+c(a+b-c)

= \(a^2+a b-\not c c+a b+b^2-b c+\not c c+b c-c^2\)

= \(a^2+b^2-c^2+2 a b\)

Practice For Algebraic Expressions and Identities KSEEB Maths Exercise 6.5

1. Use a suitable identity to get each of the following products.

1) (x+3)(x+3)

Solution: (x+3)(x+3)

a=x, b=3

2) (2y+5)(2y+5)

Solution: (2y+5)(2y+5)

= \((2y+5)^2\)

= \(4 y^2+20 y+25\)

3) (2a-7)(2a-7)

Solution: (2a-7)(2a-7)

=\(4 a^2-28 a+49\)

4) \(\left(3 a-\frac{1}{2}\right)\left(3 a-\frac{1}{2}\right)\)

Solution: \(\left(3 a-\frac{1}{2}\right)\left(3 a-\frac{1}{2}\right)\)

=\(9 a^2-3 a+\frac{1}{4}\)

5) (1.1 m-0.4)(1.1 m+0.4)

solution: (1.1 m-0.4)(1.1 m+0.4)

(1.1 m-0.4)(1.1 m+0.4)

= \((1.1 m)^2-(0.4)^2\)

= \(1.21 m^2-0.16\)

6) \(\left(a^2+b^2\right)\left(-a^2+b^2\right)\)
Solution: \(\left(a^2+b^2\right)\left(-a^2+b^2\right)\)
= \(\left(a^2+b^2\right)\left(b^2-a^2\right)\)
= \(\left(b^2+a^2\right)\left(b^2-a^2\right)\)
=\(\left(b^2\right)^2-\left(a^2\right)^2\left\{(a+b)(a-b)=a^2-b^2\right\}\)
= \(b^4-a^4\)

7) (6x-7)(6x+7)
Solution: (6x-7)(6x+7)
= \((6 x)^2-7^2 \quad\left\{(a+b)(a-b)=a^2-b^2\right\}\)
= \(36 x^2-49\)

8) (-a+c)(-a+c)
Solution: (-a+c)(-a+c)
= (c-a)(c-a)
= \((c-a)^2 \quad\left\{(a-b)^2=a^2-2 a b+b^2\right\}\)
= \(c^2-2 \times c \times a+a^2\)
= \(c^2-2 a c+a^2\)

9) \(\left(\frac{x}{2}+\frac{3 y}{4}\right)\left(\frac{x}{2}+\frac{3 y}{4}\right)\)
Solution: \(\left(\frac{x}{2}+\frac{3 y}{4}\right)\left(\frac{x}{2}+\frac{3 y}{4}\right)\)
= \(\left(\frac{x}{2}+\frac{3 y}{4}\right)^2 \quad\left\{(a+b)^2=a^2+2 a b+b^2\right\}\)
= \(\left(\frac{x}{2}\right)^2+\not 2\left(\frac{x}{\not 2}\right)\left(\frac{3 y}{4}\right)+\left(\frac{3 y}{4}\right)^2\)
= \(\frac{x^2}{4}+\frac{3 x y}{4}+\frac{9 y^2}{16}\)

10) (7a-9b)(7a-9b)
Solution: (7a-9b)(7a-9b)
\((7 a-9 b)^2 \quad\left\{(a-b)^2=a^2-2 a b+b^2\right\}\)
= \((7 a)^2-2 \times 7 a \times 9 b+(9 b)^2\)
= \(49 a^2-126 a b+81 b^2\)

2. Use the identity \((x+a)(x+b) = x^2+(a+b) x+a b\) to find the following products.
1) (x+3)(x+7)
Solution: (x+3)(x+7)
\((x+a)(x+b)=x^2+(a+b) x+a b\)
a=3 b=7
\((x+3)(x+7)=x^2+(3+7) x+3 \times 7\)
= \(x^2+10 x+21\)

2) (4x+5)(4x+1)
Solution: (4x+5)(4x+1)
x=4x, a=5, b=1
\((x+a)(x+b)=x^2+(a+b) x+a b\)
\((4 x+5)(4 x+1)=(4 x)^2+(5+1)(4 x)+5 \times 1\)
= \(16 x^2+24 x+5\)

3) (4x-5)(4x-1)
Solution: (4x-5)(4x-1)
= \((4 x)^2+(5-1)(4 x)+5(-1)\)
= \(16 x^2+16 x-5\)

4)(4x+5)(4x-1)
Solution: (4x+5)(4x-1)
= \((4 x)^2+(5-1)(4 x)+5(-1)\)
= \(16 x^2+16 x-5\)

5) (2x+5y)(2x+3y)
Solution: \((2x+5y)(2x+3y)\)
= \(2 x)^2+(5 y+3 y)(2 x)+(5 y)(3 y)\)
= \(4 x^2+(8 y)(2 x)+15 y^2\)
= \(4 x^2+16 x y+15 y^2\)

6) \(\left(2 a^2+9\right)\left(2 a^2+5\right)\)
Solution: \(\left(2 a^2+9\right)\left(2 a^2+5\right)\)
= \(\left(2 a^2\right)^2+(9+5)\left(2 a^2\right)+9 \times 5\)
= \(4 a^4+28 a^2+45\)

7) (xyz-4)(xyz-2)
Solution: (xyz-4)(xyz-2)
= \((x y z)^2+(-4-2)(x y z)+(-4)(-2)\)
= \(x^2 y^2 z^2-6 x y z+8\)

3. Find the following squares by using the identities.
1) \((b-7)^2\)
Solution: \((b-7)^2\)
= \(b^2-2 \times b \times 7+7^2\)
\((a-b)^2=a^2-2 a b+b^2\)
= \(b^2-14 b+49\)

2) \((x y+3 z)^2\)
Solution: \((x y+3 z)^2\)
\(\left\{(a+b)^2=a^2+2 a b+b^2\right\}\)
= \((x y)^2+2(x y)(3 z)+(3 z)^2\)
= \(x^2 y^2 z^2+6 x y z+9 z^2\)

3)\(\left(6 x^2-5 y\right)^2\)
Solution: \(\left(6 x^2-5 y\right)^2\)
\((a-b)^2=a^2-2 a b+b^2\)
= \(\left(6 x^2\right)^2-2\left(6 x^2\right)(5 y)+(5 y)^2\)
= \(36 x^4-60 x^2 y+25 y^2\)

4) \(\left(\frac{2}{3} m+\frac{3}{2} n\right)^2\)
Solution: \(\left(\frac{2}{3} m+\frac{3}{2} n\right)^2\)
\(\left\{(a+b)^2=a^2+2 a b+b^2\right\}\)
= \(\frac{4}{9} m^2+2 m n+\frac{9}{4} n^2\)

5) \((0.4 p-0.5 q)^2\)
Solution: \((0.4 p-0.5 q)^2\)
\((a-b)^2=a^2-2 a b+b^2\)
= \((0.4 p)^2-2 \times 0.4 p \times 0.5 q+(0.5 q)^2\)
= \(0.16 p^2-0.4 p q+0.25 q^2\)

6) \((2 x y+5 y)^2\)
Solution: \((2 x y+5 y)^2\)
\(\left\{(a+b)^2=a^2+2 a b+b^2\right\}\)
= \((2 x y)^2+2(2 x y)(5 y)+(5 y)^2\)
= \(4 x^2 y^2+20 x y^2+25 y^2\)

4. Simplify
1) \(\left(a^2-b^2\right)^2\)
Solution: \(\left(a^2-b^2\right)^2\)
\((a-b)^2=a^2-2b+b^2\)
= \(\left(a^2\right)^2-2 \times a^2 \times b^2+\left(b^2\right)^2\)
= \(a^4-2 a^2 b^2+b^4\)

2) \((2 x+5)^2-(2 x-5)^2\)
Solution: \((2 x+5)^2-(2 x-5)^2\)
\(\begin{aligned}
& (a+b)^2=a^2+2 a b+b^2 \\
& (a-b)^2=a^2-2 a b+b^2
\end{aligned}\)
\(\left\{(2 x)^2+2 \times 2 x \times 5+5^2\right\}-\left\{(2 x)^2-2 \times 2 x \times 5+5^2\right\}\)
= \(\left(4 x^2+20 x+25\right)-\left(4 x^2-20 x+25\right)\)
= \(4 x^2+20 x+25-4 x^2+20 x-25\)
= 40x

3) \((7 m-8 n)^2+(7 m+8 n)^2\)
Solution: \((7 m-8 n)^2+(7 m+8 n)^2\)
\(\left\{\begin{array}{l}
(a+b)^2=a^2+2 a b+b^2 \\
(a-b)^2=a^2-2 a b+b^2
\end{array}\right\}\)
\(\left\{(7 m)^2-2 \times 7 m \times 8 n+(8 n)^2\right\}+\left\{(7 m)^2+2(7 m)(8 n)+(8 n)^2\right\}\)
= \(49 m^2-112 m n+64 n^2+49 m^2+112 m n+64 n^2\)
= \(98 m^2+128 n^2\)

4) \((4 m+5 n)^2+(5 m+4 n)^2\)
Solution: \((4 m+5 n)^2+(5 m+4 n)^2\)
=\(\left\{(4 m)^2+2 \times 4 m \times 5 n+(5 n)^2\right\}+\left\{(5 m)^2+2(5 m)(4 n)+(4 n)^2\right\}\)
= \(16 m^2+40 m n+25 n^2+25 m^2+40 m n+16 n^2\)
= \(41 m^2+80 m n+41 n^2\)

5) \((2.5 p-1.5 q)^2-(1.5 p-2.5 q)^2\)
Solution: \((2.5 p-1.5 q)^2-(1.5 p-2.5 q)^2\)
\(\left\{(a-b)^2=a^2-2 a b+b^2\right\}\)
= \(\left\{(2.5) p^2-2(2.5 p)(1.5 q)+(1.5 q)^2\right\}-\left\{(1.5 p)^2-2(1.5 p)(2.5 q)+(2.5 q)^2\right\}\)
= \(\left(6.25 p^2-7.5 p q+2.25 q^2\right)-\left(2.25 p^2-7.5 p q+6.25 q^2\right)\)
= \(6.25 p^2-7.5 p q+2.25 q^2-2.25 p^2+75 p q-6.25 q^2\)
= \(4 p^2-4 q^2\)

6) \((a b+b c)^2-2 a b^2 c\)
Solution: \((a b+b c)^2-2 a b^2 c\)
\(\left\{\begin{array}{l}
(a+b)^2 \\
=a^2+2 a b+b^2
\end{array}\right\}\)
= \((a b)^2+2(a b)(b c)+(b c)^2-2 a b^2 c\)
= \(a^2 b^2+2 a b^2 c+b^2 c^2-2 a b^2 c\)
= \(a^2 b^2+b^2 c^2\)

7) \(\left(m^2-n^2 m\right)^2+2 m^3 n^2\)
Solution: \(\left(m^2-n^2 m\right)^2+2 m^3 n^2\)
\(\left\{(a-b)^2=a^2-2 a b+b^2\right\}\)
=\(\left(m^2\right)^2-2 \times m^2 \times n^2 m+\left(n^2 m\right)^2+2 m^3 n^2\)
= \(m^4-2 m^3 n^2+n^4 m^2+2 m^3 n^2\)
= \(m^4+n^4 m^2\)

5. Show that
1) \((3 x+7)^2-84 x=(3 x-7)^2\)
Solution: LHS = \((3 x+7)^2-84 x\)
= \((3 x)^2+2 \times 3 x \times 7+7^2-84 x\)
= \(9 x^2+42 x+49-84 x\)
= \(9 x^2-42 x+49\)
RHS = \((3 x-7)^2\)
= \((3 x)^2-2 \times(3 x)(7)+7^2\)
= \(9 x^2-42 x+49\)
∴ LHS=RHS

2) \((9 p-5 q)^2+180 p q=(9 p+5 q)^2\)
Solution: LHS = \((9 p-5 q)^2+180 p q\)
= \((9 p)^2-2 \times 9 p(5 q)+(5 q)^2+180 p q\)
= \(81 p^2-90 p q+25 q^2+180 p q\)
= \(81 p^2+90 p q+25 q^2\)
RHS = \((9 p+5 q)^2\)
= \((9 p)^2+2 \times 9 p \times 5 q+(5 q)^2\)
= \(81 p^2+90 p q+25 q^2\)
∴LHS=RHS

3) \(\left(\frac{4}{3} m-\frac{3}{4} n\right)^2+2 m n=\frac{16}{9} m^2+\frac{9}{16} n^2\)
Solution: LHS = \(\left(\frac{4}{3} m-\frac{3}{4} n\right)^2+2 m n\)
= \(\frac{16}{9} m^2-2 m n+\frac{9 n^2}{16}+2 m n\)
= \(\frac{16}{9} m^2+\frac{9 n^2}{16}\)
RHS = \(\frac{16}{9} m^2+\frac{9}{16} n^2\)
∴ LHS = RHS

4) \((4 p q+3 q)^2-(4 p q-3 q)^2=48 p q^2\)
Solution: LHS =\((4 p q+3 q)^2-(4 p q-3 q)^2\)
= \(\left\{(4 p q)^2+2(4 p q)(3 q)+(3 q)^2\right\}-\left\{(4 p q)^2-2(4 p q)(3 q)+(3 q)^2\right\}\)
= \(16 p^2 q^2+24 p q^2+9 q^2-16 p^2 q^2+24 p q^2-9 q^2\)
= \(48 p q^2\)
RHS = \(48 p q^2\)
∴ LHS = RHS

5) (a-b)(a+b)+(b-c)(b+c)+(c-a)(c+a)=0
Solution: LHS = (a-b)(a+b)+(b-c)(b+c)+(c-a)(c+a)=0
= \(\left(a^2-b^2\right)+\left(b^2-c^2\right)+\left(c^2-a^2\right)\)
= \(a^2-b^2+b^2-c^2+c^2-a^2\)
=0
=RHS =0
∴ LHS = RHS

6. Using identities, evaluate
1) \(71^2\)
Solution: \(71^2=(70+1)^2\)
=\(\left\{\begin{array}{l}
(a+b)^2 \\
=a^2+2 a b+b^2
\end{array}\right\}\)
= \((70)^2+2 \times 70 \times 1+1^2\)
= 4900+140+1
= 5041

2) \(99^2\)
Solution: \((99)^2=(100-1)^2\)
=\(\left\{\begin{array}{l}
(a+b)^2 \\
=a^2+2 a b+b^2
\end{array}\right\}\)
= \((100)^2-2 \times 100 \times 1+1^2\)
= 10000-200+1
= 9801

3)\(102^2\)
Solution: \((102)^2=(100+2)^2\)
=\(\left\{\begin{array}{l}
(a+b)^2 \\
=a^2+2 a b+b^2
\end{array}\right\}\)
= \((100)^2+2 \times 100 \times 2+2^2\)
= 10000+400+4
= 10404

4) \(998^2\)
Solution: \((998)^2=(1000-2)^2\)
=\(\left\{\begin{array}{l}
(a+b)^2 \\
=a^2+2 a b+b^2
\end{array}\right\}\)
= \((1000)^2-2 \times 1000 \times 2+2^2\)
= 1000000-4000+4
= 996004

5) \(5.2^2\)
Solution: \((5.2)^2=(5.0+0.2)^2\)
=\(\left\{\begin{array}{l}
(a+b)^2 \\
=a^2+2 a b+b^2
\end{array}\right\}\)
= \((5.0)^2+2 \times 5.0 \times 0.2+(0.2)^2\)
= 25+2+0.04
= 27.04

6) 297 x 303
Solution: 297 x 303
= (300-3)(300+3)
= \((300)^2-(3)^2\)
=\(\left\{\begin{array}{l}
(a+b)^2 \\
=a^2+2 a b+b^2
\end{array}\right\}\)
= 90000-9
= 89991

7) 78 x 82
Solution: 78 x 82
= (80-2)(80+2)
=\(\left\{\begin{array}{l}
(a+b)^2 \\
=a^2+2 a b+b^2
\end{array}\right\}\)
= \((80)^2-2^2\)
= 6400-4
= 6396

8) \(8.9^2\)
Solution: \((8.9)^2=(9.0-0.1)^2\)
= \((9.0)^2-2 \times(9.0)(0.1)+(0.1)^2\)
= 81-1.8+0.01
= 79.21

9) 10.5 x 9.5
Solution: (10.5)(9.5)
= (10+0.5)(10-0.5)
= \((10)^2-(0.5)^2\)
= 100-0.25
= 99.75

7. Using \(a^2-b^2=(a+b)(a-b)\) find
1) \(51^2-49^2\)
Solution: \((51)^2-(49)^2\)
= (51+49)(51-49)
= 100 x 2
= 200

2) \((1.02)^2-(0.98)^2\)
Solution: \((1.02)^2-(0.98)^2\)
= (1.02+0.98)(1.02-0.98)
= 2 x 0.04
= 0.08

3) \(153^2-147^2\)
Solution: (153+147)(153-147)
= 300 x 6
= 1800

4) \((12.1)^2-(7.9)^2\)
Solution: \((12.1)^2-(7.9)^2\)
= (12.1+7.9)(12.1-7.9)
= 20 x 4.2
= 84

8. Using \((x+a)(x+b)=x^2+(a+b) x+a b\), find
1) 103 x 104
Solution: 103 x 104
= (100+3)(100+4)
= \(100^2+(3+4)(100)+3 \times 4\)
= 10000+700+12
= 10712

2) 5.1 x 5.2
Solution: \((5.1) \times(5.2)=(5+0.1)(5+0.2)\)
= \(5^2+(0.1+0.2) 5+(0.1 \times 0.2)\)
= 25+1.5+0.02
= 26.52

3)103 x 98
Solution: \((103) \times(98)\)
= (100+3)(100-2)
= \(100^2+(3-2) \times 100+(3)(-2)\)
= 10000+100-6
= 10094

4) 9.7 x 9.8
Solution: 9.7 x 9.8
= (10-0.3)(10-0.2)
= \(10^2+(-0.3-0.2) 10+(-0.3)(-0.2)\)
= 100 – (0.5 x 10) + 0.06
= 100 – 5 + 0.06
= 95.06

Algebraic Expressions And Identities Questions And Answers KSEEB Maths Additional Problems

1. Subtract \(6 x^2-4 x y+5 y^2\) from \(8 y^2+6 x y-3 x^2\)
Solution:

2. Using suitable identity, evaluate
\((69.3)^2-(30.7)^2\)
Solution: \((69.3)^2-(30.7)^2\)
= (69.3+30.7)(69.3-30.7)
\(\left\{\begin{array}{l}
a^2-b^2 \\
=(a+b)(a-b)
\end{array}\right\}\)
= 100 x 38.6
= 3860

3. Add: 9ax, 3by-cz and -5by+ax+3cz
Solution: 9ax+3by-cz-5by7+ax+3cz
= 10ax-2by+2cz

4. Expand the following, using suitable identities
1) \(\left(\frac{4 x}{5}+\frac{y}{4}\right)\left(\frac{4 x}{5}+\frac{3 y}{4}\right)\)
Solution: \((x+a)(x+b)=x^2+(a+b) x+a b\)
\(\left(\frac{4 x}{5}+\frac{y}{4}\right)\left(\frac{4 x}{5}+\frac{3 y}{4}\right)\)
= \(\left(\frac{4 x}{5}\right)^2+\left(\frac{y}{4}+\frac{3 y}{4}\right)\left(\frac{4 x}{5}\right)+\frac{y}{4} \times \frac{3 y}{4}\)
= \(\frac{16 x^2}{25}+\frac{16^4 x y}{4 \times 5}+\frac{3 y^2}{16}\)
= \(\frac{16 x^2}{25}+\frac{4 x y}{5}+\frac{5}{16} y^2\)

2) \((0.9 p-0.5 q)^2\)
Solution: \((0.9 p)^2-2 \times 0.9 p \times 0.5 q+(0.5 q)^2\)
= \(0.81 p^2-0.90 p q+0.25 q^2\)

5. Evaluate \(\left(\frac{a}{b}+\frac{b}{a}\right)^2\) using identity
Solution: \(\left(\frac{a}{b}+\frac{b}{a}\right)^2=\left(\frac{a}{b}\right)^2+2 \times \frac{a}{b} \times \frac{b}{a}+\left(\frac{b}{a}\right)^2\)
\(\left\{\begin{array}{l}
(a+b)^2 \\
=a^2+2 a b+b^2
\end{array}\right\}\)
=\(\frac{a^2}{b^2}+2+\frac{b^2}{a^2}\)

6. Evaluate: \((\sqrt{5} a+\sqrt{3} b)^2\)
Solution: =\((\sqrt{5} a)^2+(\sqrt{3} b)^2+2 \times \sqrt{5} \times a \times \sqrt{3} \times b\)
= \(5 a^2+3 b^2+2 \sqrt{15} a b\)
= \(5 a^2+3 b^2+2 \sqrt{15} a b\)
\((\sqrt{5} a+\sqrt{3} b)^2=5 a^2+3 b^2+2 \sqrt{15} a b\)

7. Subtract the sum of \( 3l-4m-7n^2 and 2l+3m-4n^2 from the sum of 9l+2m-3n^2 and -3l+m+4n^2\)
Solution:

Subtracting \(5l-m-11n^2 from 6l+3m+n^2 we get\)

8. Subtract 7p(3q+7p) from 8p(2p-7q)
Solution: 8p(2p-7p)-7p(3q+7p)
= \(16 p^2-56 p q-21 p q-49 p^2\)
= \(-33 p^2-77 p q\)

9. Simplify \((ab-c)^2\)
Solution: \((ab-c)^2+2abc\)
= \((a b)^2-2 \times a b \times c+c^2+2 a b c\)
= \(a^2 b^2-2 a b c+c^2+2 a b c\)
= \(a^2 b^2+c^2\)

10. Expand (2x+9)(2x-7) using identity
Solution: (2x+9)(2x-7)
= \((2 x)^2+(9-7)(2 x)+(9)(-7)\)
= \(4 x^2+4 x-63\)

11. Expand: \((49)^2\)
Solution: \((49)^2=(50-1)^2\)
\(\left\{\begin{array}{l}
(a-b)^2 \\
=a^2-2 a b+b^2
\end{array}\right\}\)
= \((50)^2-2 \times 50 \times 1+1^2\)
= 2500-100+1
= 2400+1
= 2401

12. Write the greatest common factor in each of the following.

1) \(2 x y,-y^2, 2 x^2 y\)

Solution: \(2 x y,-y^2, 2 x^2 y\)

G.C.F = y-16

2) \(3 x^3 y^2 z,-6 x y^3 z^2, 12 x^2 y z^3\)

Solution: \(3 x^3 y^2 z,-6 x y^3 z^2, 12 x^2 y z^3\)

G.C.F = 3xyz

13. Multiply the binomials

a) (2x+5)(4x-3)

Solution: (2x+5)(4x-3)

= 2x(4x-3)+5(4x-3)

= 2x x 4x +2x(-3)+5 x 4x + 5(-3)

= \(8 x^2-6 x+20 x-15\)

= \(8 x^2+14 x-15\)

14. Find the areas of rectangles with the following pairs of monomials as their lenghts and breadths respectively.

Solution: W.K.T. Area of rectangle = Length x Breadth

Area of 1st rectangle = \(3mn x 4np = 12mn^2p\)

Area of 2nd reactangle =\(4 x \times 3 x^2=12 x^3\)

15. If \(a+\frac{1}{a}=7, find a^2+\frac{1}{a^2}\)

Solution: Consider \(a+\frac{1}{a}=7\) square bothside, we get

16. Multiply \(x^2+2 y \text { by } x^3-2 x y+y^3 and find the value of the product for x=1 and y= -1\)

Solution: \(\left(x^2+2 y\right)\left(x^3-2 x y+y^3\right)\)

= \(x^2\left(x^3-2 x y+y^3\right)+2 y\left(x^3-2 x y+y^3\right)\)

= \(x^5-2 x^3 y+x^2 y^3+2 x^3 y-4 x y^2+2 y^4\)

= \(x^5+x^2 y^3-4 x y^2+2 y^4\)

put x=1 & y= -1

= \((1)^5+(1)^2(-1)^3-4(1)(-1)^2+2(-1)^4\)

= 1+(1)(-1)-4(1)(1)+2(1)

= 1-1-4+2 = -2

17. If \(x^2+\frac{1}{x^2}=38\), find the values of

1) \(x-\frac{1}{x}\)

2) \(x^4+\frac{1}{x^4}\)

Solution:

1)\(\left(x-\frac{1}{x}\right)^2=x^2+\frac{1}{x^2}-2 \times x \times \frac{1}{x}\)

= \(x^2+\frac{1}{x^2}-2=38-2=36\)

∴ \(x-\frac{1}{x}=\sqrt{36}=6\)

2)\(\left(x^2+\frac{1}{x^2}\right)^2=x^4+\frac{1}{x^4}+2 \times x^2 \times \frac{1}{x^2}\)

= \(1444-2=x^4+\frac{1}{x^4}\)

∴ \(x^4+\frac{1}{x^4}=1442\)

18. Find the area of the reactangle whose length and breadths are \(3 x^2 y m and 5 x y^2 m\) respectively.

Solution: Length = \(3 x^2 y m\), breadth = \(5 x y^2m\)

Area of rectangle = length x breadth

= \(3 x^2 y \times 5 x y^2 \text { sq m }\)

= \(15 x^3 y^3 \text { sq } \mathrm{m}\)

19. Find the value of the expression \(\left(81 x^2+16 y^2-72 x y\right) \text {, when } x=\frac{2}{3} \& y=\frac{3}{4}\)

Solution: \(\left(81 x^2+16 y^2-72 x y\right)\)

= \((9 x)^2+(4 y)^2-2 \times 9 x+4 y\)

= \((9 x-4 y)^2\)

= \(\left(9 \times \frac{2}{3}-4 \times \frac{3}{4}\right)^2 \text {, when } x=\frac{2}{3} \& y=\frac{3}{4}\)

= \((6-3)^2=3^2=9\)