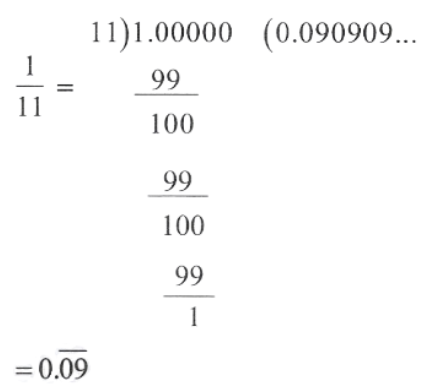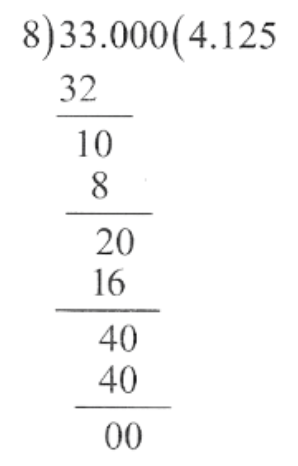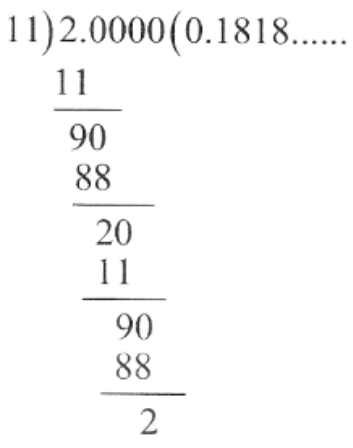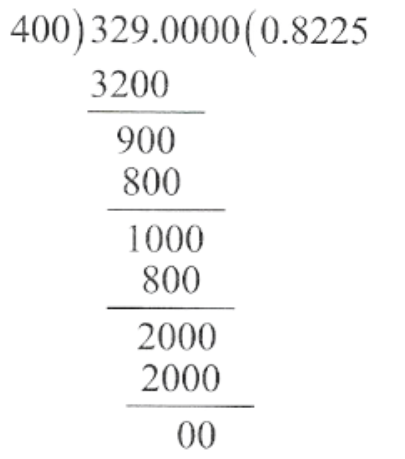Kumar

KSEEB Solutions For Class 9 Maths Chapter 7 Triangles

Triangles Points to Remember

• A triangle is formed by three line segments obtained by joining three pairs of points taken from a set of three non-collinear points in a plane. A triangle has three vertices, three sides & three angles.
  A triangle ABC is denoted by ΔABC

• Criteria for congruence of triangles.
  Congruence of triangle.
  The geometrical figures of same shape & size are congruent to each other i.e., two Δles ΔABC & ΔPQR are congruent if and only if their corresponding sides & the corresponding angles are equal.

Class 9 Social Science

Class 9 Science

Class 9 Maths

 

Read and Learn More KSEEB Solutions for Class 9 Maths 

• If two triangles ΔABC & ΔPQR are congruent under the correspondence A → P, B → Q & C → R, then symbolically it is expressed as ΔABC ≅ ΔPQR
• SAS congruence Rule:
  Two triangles are congruent if two sides & the included angle of one triangle are equal to the sides & the included angle of the other triangle.
• ASA congruence Rule: Two triangles are congruent if two angles & the included side of one triangle are equal to two angles & the included side of the other triangle.
• AAS congruence Rule :
  Two triangles are congruent if any two pairs of angles & one pair of corresponding sides are equal.
• SSS congruence Rule:
  If three sides of a triangle are equal to the three sides of another triangle, then the two triangles are congruent.
• RHS congruence Rule:
  If in two right triangles, the hypotenuse & one side of a triangle are equal to the hypotenuse & one side of the other triangle then the two triangles are congruent.
  Note: It shall be noted that in SAS criteria the equality of included angles is very essential. If two sides & one angle (not included between the two sides) of one triangle are equal to two sides & one angle of the other triangle, then the triangles need not be congruent. So, the equal angle should be the angle included between the sides

• Some properties of triangles.
  A triangle is isosceles if any two sides are equal. Here, we prove some properties related to isosceles triangle.
  (1) Angles opposite to equal sides of a triangle are equal.
  In figure, \(\lfloor B\) = \(\lfloor C\)
  2) The sides opposite to equal angles of a triangle are equal.
  In figure, AB = AC

• In an isosceles triangle, bisector of the vertical angle of a triangle bisect the base.
• The medians of an equilateral triangle are equal in length.
• A point equidistance from two intersecting lines lies on the bisector of the angles formed by two lines.
  Inequalities of a triangle
• Angle opposite to the longer side is larger (greater)
• Side opposite to the larger (greater) angle is longer.
• Sum of any two sides is greater than the third side
  i. e., in ΔABC, AB + BC > CA
• Difference of any two sides of a triangle is less than
  the third side i.e., in ΔABC, AB – BC <CA

KSEEB Class 9 Maths Chapter 7 Triangles Exercises 

Triangles Exercise 7.1

1. In quadrilateral ACBD, AC =AD( & AB bisects \(\lfloor A\). Show that ΔABC ≅ ΔABD. What can you say about BC & BD?

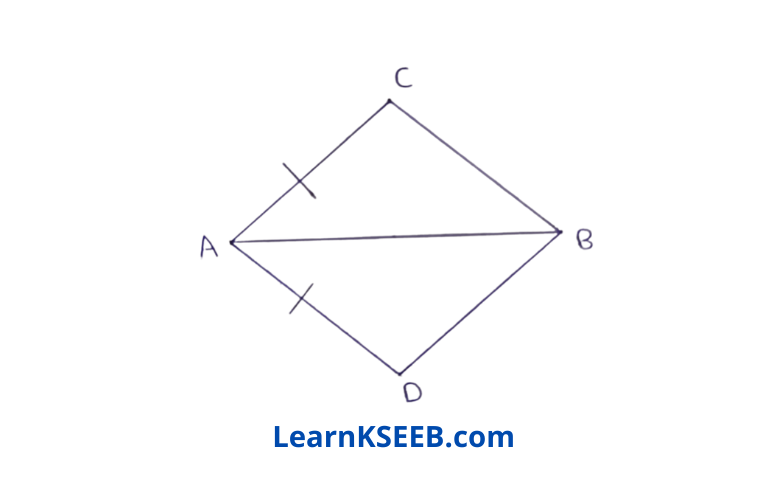
Solution:

Given: In quadrilaterial ACBD, AC = BD & AB bisects \(\lfloor A\).

To prove : ΔABC ≅ ΔABD

Proof: In ΔABC & ΔABD

AC = AD (given)

AB =AB (common)

\(\lfloor\mathrm{CAB}\) = \(\lfloor\mathrm{DAB}\) (∵ AB bisects \(\lfloor A\))

∴  ΔABC ≅ ΔABD (SAS rule)

∴ BC = BD (C.P.C.T.)

2. ABCD is a quadrilateral in which AD = BC and [DAB = [CBA prove that
i) ΔABD ≅ ΔBAC
ii) BD =AC
iii) \(\lfloor\mathrm{ABD}\) = \(\lfloor\mathrm{BAC}\)

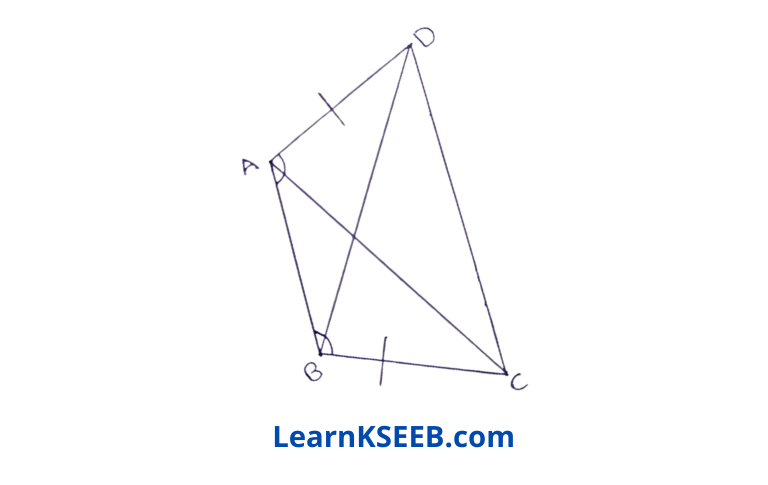
Solution:

Given : ABCD is a quadrilateral in which AD = BC & \(\lfloor\mathrm{DAB}\) = \(\lfloor\mathrm{CBA}\)

To prove:

1) ΔABD ≅ ΔBAC

2) BD = AC

3) \(\lfloor\mathrm{ABD}\) = \(\lfloor\mathrm{BAC}\)

Proof: 1) In ΔABD & ΔBAC

AD = BC (given)

AB = BA (common)

\(\lfloor\mathrm{DAB}\) = \(\lfloor\mathrm{CBA}\) (given)

∴ ΔABD ≅ ΔBAC (SAS rule)

2) ΔABD ≅ ΔBAC (proved in (1))

∴ BD = AC (CPCT)

3) ΔABD ≅ ΔBAC (proved in (1))

\(\lfloor\mathrm{ABD}\) = \(\lfloor\mathrm{BAC}\) (CPCT)

3. AD & BC are equal perpendicular to a line segment AB. Show that CD bisects AB.

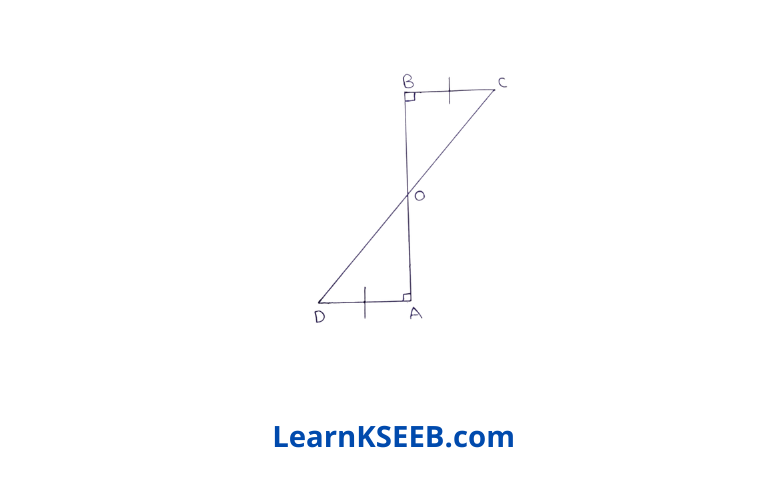
Solution:

Given : AD & BC are equal perpendicular to a line segment AB.

To prove : CD bisects AB.

Proof: In ΔOAD & ΔOBC

AD = BC (given)

\(\lfloor\mathrm{OAD}\) = \(\lfloor\mathrm{OBC}\) (each = 90°)

\(\lfloor\mathrm{AOD}\) = \(\lfloor\mathrm{BOC}\) (vertically opposite angles)

∴ ΔOAD ≅ ΔOBC (AAS rule)

∴ OA = OB (CPCT)

∴ CD bisects AB.

KSEEB Maths Chapter 7 Triangles Answers 

4. l and m are two parallel lines intersected by another pair of parallel lines p & q. Show that ΔABC ≅ ΔCDA.

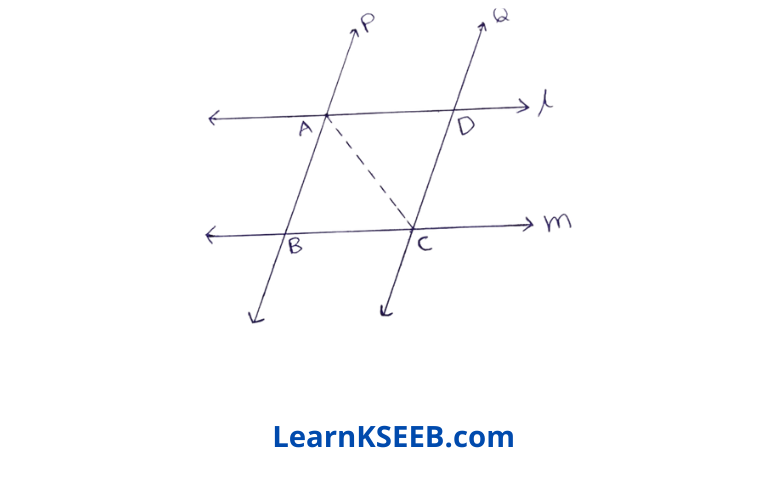
Solution:

Given : l and m are two parallel lines interested by another pair of parallel lines p & q.

To prove : ΔABC ≅ ΔCDA

Proof: AB || DC

& AD || BC

Quadrilateral ABCD is a parallelogram.

(a quadrilateral ABCD is a parallelogram, if both the pairs of opposite sides are parallel)

∴ BC = AD …………….(1)

(opposite sides of a ||gm are equal)

∴ AB = CD ……………(2)

(opposite sides of a ||gm are equal)

& \(\lfloor\mathrm{ABC}\) = \(\lfloor\mathrm{CDA}\) ……………..(3)

(opposite angles of a ||gm are equal).

In ΔABC & ΔCDA

AB = CD from (2)

BC = DA from(1)

\(\lfloor\mathrm{ABC}\) = \(\lfloor\mathrm{CDA}\)from (3)

∴ ΔABC = ΔCDA (SAS rule)

5. Line l is the bisector of an angle\(\lfloor A\) & B is any point on l. BP & BQ are perpendicular from B to the arms of \(\lfloor A\). Show that 1) ΔAPB ≅ ΔAQB, 2) BP = BQ or B is equidistant from the arms of \(\lfloor A\).

Solution:

Given : Line l is the bisector of an angle A & B is any point on A BP & BQ are perpendicular from B to the arms of \(\lfloor A\).

To prove :

1) ΔAPB ≅ ΔAQB

2) BP = BQ

or

B is equidistance from the arms of \(\lfloor A\).

Proof: 1) In ΔAPB & ΔAQB,

\(\lfloor\mathrm{BAP}\) = \(\lfloor\mathrm{BAQ}\)(∵ l is the bisector of \(\lfloor A\))

AB = AB (common)

\(\lfloor\mathrm{BPA}\) =\(\lfloor\mathrm{BQA}\) =90°

(y BP & BQ are perpendiculars from B to the arms of \(\lfloor A\).)

∴  ΔAPB ≅ ΔAQB (AASrule)

2) ΔAPB ≅ ΔAQB (proved in (1) above)

∴ BP = BQ (CPCT)

6. In figure, AC = AE, AB = AD & \(\lfloor\mathrm{BAD}\) = \(\lfloor\mathrm{EAC}\). Show that BC =DE.

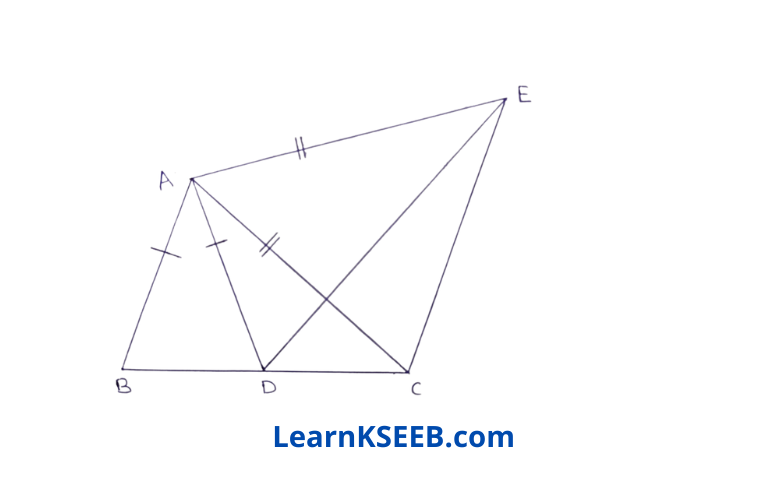
Solution:

Given : In figure, AC = AE, AB = AD & \(\lfloor\mathrm{BAD}\) = \(\lfloor\mathrm{EAC}\).

To prove: BC = DE

Proof: In ΔABC & ΔADE,

AB = AD (given)

AC = AE (given)

\(\lfloor\mathrm{BAD}\) = \(\lfloor\mathrm{EAC}\) (given)

=> \(\lfloor\mathrm{BAD}\) + \(\lfloor\mathrm{DAC}\) = \(\lfloor\mathrm{DAC}\)+ \(\lfloor\mathrm{EAC}\)

(adding \(\lfloor\mathrm{DAC}\) to both sides)

=>\(\lfloor\mathrm{BAC}\) = \(\lfloor\mathrm{DAE}\)

∴ ΔABC ≅ ΔADE (SAS rule)

∴ BC = DE (CPCT)

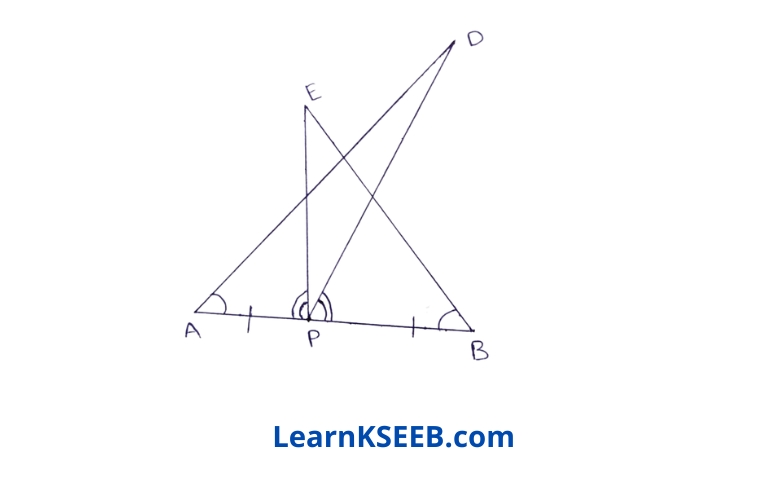
7. AB is a line segment & P is its mid-point D & E are points on the same side of AB such that
\(\lfloor\mathrm{BAD}\) = \(\lfloor\mathrm{ABE}\) & \(\lfloor\mathrm{EPA}\)=\(\lfloor\mathrm{DPB}\)
Show that i) ΔDAP ≅ ΔEBP 2) AD = BE

Solution:

Given: AB is a line segment & P is its mid-point D & E are points on the same side of AB such that

\(\lfloor\mathrm{BAD}\) = \(\lfloor\mathrm{ABE}\) & \(\lfloor\mathrm{EPA}\) = \(\lfloor\mathrm{DPB}\)

To prove : (1) ΔDAP = ΔEBP

(2) AD = BE

Proof: (1) In ΔDAP & ΔEBP

AP = BP (∵ P is the midpoint of the line segment AB)

\(\lfloor\mathrm{DAP}\) = \(\lfloor\mathrm{EBP}\) (given)

\(\lfloor\mathrm{EPA}\)=\(\lfloor\mathrm{DPB}\) (given)

=> \(\lfloor\mathrm{EPA}\) + \(\lfloor\mathrm{EPD}\)=\(\lfloor\mathrm{EPD}\) + \(\lfloor\mathrm{DPB}\)

(adding \(\lfloor\mathrm{EPD}\) to both sides)

=> \(\lfloor\mathrm{APD}\) –\(\lfloor\mathrm{BPE}\)

ΔDAP ≅ ΔEBP (ASA rule)

2) ΔDAP ≅ ΔEBP (from(1) above)

∴ AD = BE (CPCT)

KSEEB Solutions Class 9 Triangles Practice Problems 

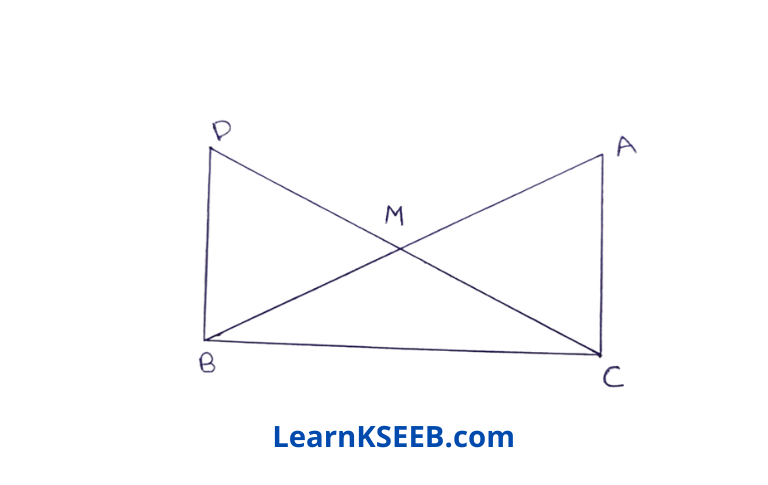
8. In right angle triangle ABC, right-angled at C, M is the midpoint of hypotenuse AB, C is joined to M & produced to a point D. Such that DM = CM. Point D is joined to point B show that
1) ΔAMC ≅ ΔBMD
2) \(\lfloor\mathrm{DBC}\) is a right-angled
3) ΔDBC ≅ ΔACB
4) CM = 1/2AB.

Solution:

Given: In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M & produced to a point D. Such that DM = CM, Point D is joined to Point B.

To prove : 1) ΔAMC ≅ ΔBMD

2) \(\lfloor\mathrm{DBC}\) is a right angle

3) ADBC ≅ AACB

4) CM = 1/2AB

Proof: 1) In ΔAMC & ΔBMD

AM = BM (M is the midpoint of the hypotenuse AB)

CM = DM (given)

\(\lfloor\mathrm{AMC}\) = \(\lfloor\mathrm{BMD}\) (vertically opposite angle) (SAS rule)

∴ ΔAMC ≅ ΔBMD

2) ΔAMC ≅ ΔBMD (from(1) above)

∴\(\lfloor\mathrm{ACM}\) = \(\lfloor\mathrm{BDM}\) (CPCT)

but these are alternate interior angles and they are equal.

AC || BD

Now, AC || BD & a transversal BC intersects them

∴ \(\lfloor\mathrm{DBC}\)+\(\lfloor\mathrm{ACB}\) = 180°

(The sum of the consecutive interior angles on the same side of a transversal is 180°)

=> \(\lfloor\mathrm{DBC}\) + 90° = 180°

(∵ \(\lfloor\mathrm{ACB}\) = 90° given)

=> \(\lfloor\mathrm{DBC}\)-180 – 90 – 90°

=> \(\lfloor\mathrm{DBC}\) is a right angle.

3) In ΔDBC & ΔACB

\(\lfloor\mathrm{DBC}\) = \(\lfloor\mathrm{ACB}\)(each = 90°)

(proved in (2) above)

BC = CB (common)

ΔAMC ≅ ΔBMD (proved in (1) above)

∴ AC = BD (CPCT)

ΔDBC ≅ ΔACB (SAS rule)

4) ΔDBC ≅ ΔACD (proved in (3) above)

∴ DC = AB  (CPCT)

=> 2CM = AB (∵ DM = CM = 1/2 DC)

=> CM = 1/2AB

Triangles Exercise 7.2

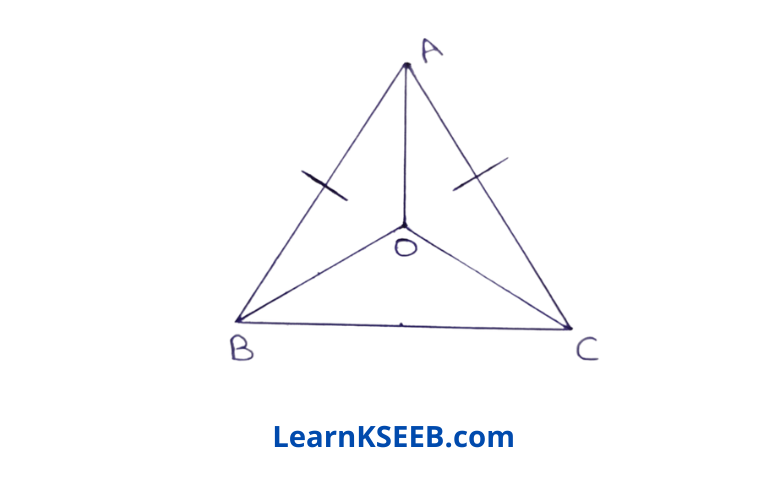
1. In an isosceles triangle ABC, with AB =AC, the bisectors of \(\lfloor b\) & \(\lfloor c\) intersect each other at O. Join A to O. Show that
1) OB = OC
2) AO bisects \(\lfloor A\)

Solution:

Given: In an isosceles triangle ABC, with AB =AC, the bisectors of \(\lfloor B\) & \(\lfloor C\) intersectAach other at O. Join A to O.

To prove : 1) OB = OC

2) AO bisects \(\lfloor A\)

Proof: 1) AB = AC (given)

\(\lfloor B\) = \(\lfloor C\) (Angles opposite to equal sides of a triangle are equal)

1/2\(\lfloor B\)=1/2\(\lfloor C\)

\(\lfloor\mathrm{OBC}\) = \(\lfloor\mathrm{OCB}\) (∵ BO & CO are the

bisectors of \(\lfloor B\) & \(\lfloor C\) respectively)

∴ OB = OC

(sides opposite to equal angles of triangles are equal)

2) In ΔOAB & ΔOAC

AB = AC (given)

OB = OC (proved in (1) above)

OA = OA (common)

\(\lfloor B\) = \(\lfloor C\)(Angles opposite to equal sides of a Δle are equal)

1/2\(\lfloor B\) = 1/2\(\lfloor C\)

∴ \(\lfloor\mathrm{ABO}\) = \(\lfloor\mathrm{ACO}\) (∵ BO & CO are the

bisectors of \(\lfloor B\) & \(\lfloor C\) respectively)

\(\lfloor\mathrm{OAB}\) = \(\lfloor\mathrm{OAC}\) (CPCT)

∴ AO bisects \(\lfloor C\)

Class 9 Maths KSEEB Chapter 7 Triangles Examples 

2. In ΔABC,AD is the perpendicular bisector of BC. Show that ΔABC is an isosceles triangle in which AB= AC

Solution:

Given: In AABC, AD is the perpendicular bisector of BC.

To prove: AABC is an isosceles triangle in which AB = AC

Proof: In ΔADB & ΔADC

\(\lfloor\mathrm{ADB}\) = \(\lfloor\mathrm{ADC}\) = 90°

DB = DC (AD is the perpendicular bisector of BC)

AD=AD (common)

ΔADB ≅ ΔADC (by SAS rule)

∴ AB = AC (CPCT)

ΔABC is an isosceles triangle in which AB = AC.

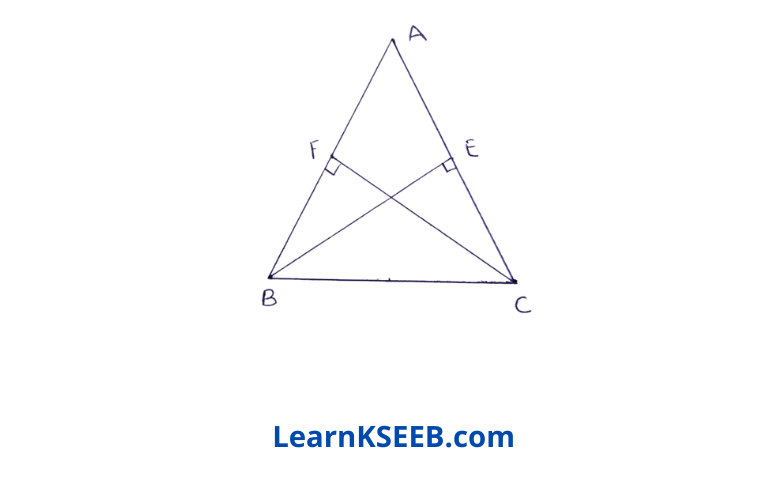
3. ABC is an isosceles triangle in which altitudes BE & CF are drawn to sides AC & AB respectively. Show that these altitudes are equal.

Solution:

Given: ABC is an isosceles triangle in which altitudes BE & CF are drawn to sides AC & AB respectively.

To prove : BE = CF

Proof: ABC is an isosceles triangle

∴ AB = AC

& \(\lfloor\mathrm{ABC}\) = \(\lfloor\mathrm{ACB}\) (angles opposite to …………(1) equal sides of a Δle are equal)

In ΔBEC&ΔCFB \(\lfloor\mathrm{BEC}\) = \(\lfloor\mathrm{CFB}\) = 90°

BC = CB (common)

\(\lfloor\mathrm{ECB}\) = \(\lfloor\mathrm{FBC}\) (from(1))

∴ ΔBEC & ΔCFB (by AAS rule)

∴ BE = CF (CPCT)

4. ABC is a Δle in which altitudes BE & CF to sides AC & AB are equal Show that

1) ΔABE ≅ ΔACF
2) AB=AC ie, ΔABC is an isosceles Δle

Solution:

Given : ABC is a Δe in which altitudes BE & CF to sides AC & AB are equal

To prove : 1) ΔABE ≅ ΔACF

2) AB = AC i.e. ABC is an isosceles Δle.

Proof: 1) In ΔABE & ΔACF

BE = CF (Given)

\(\lfloor\mathrm{ABE}\) = \(\lfloor\mathrm{CAF}\) (common)

\(\lfloor\mathrm{AEB}\)= \(\lfloor\mathrm{AFC}\) = 90°

ΔABE = ΔACF (byAAS rule)

2) ΔABE = ΔACF (proved in (1) above)

AB = AC (C.P.C.T.)

ΔABC is an isosceles Δle.

5. ABC & DBC are two isosceles Δle on the same base BC (see figure) show that \(\lfloor\mathrm{ABD}\) = \(\lfloor\mathrm{ACD}\)

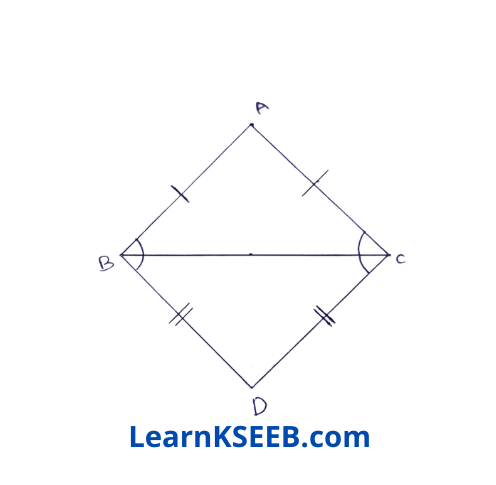
Solution:

Given : ABC & DBC are two isosceles Δle on the same base BC.

To prove : \(\lfloor\mathrm{ABD}\) = \(\lfloor\mathrm{ACD}\)

Proof: ABC is an isoscles Δle on the base BC.

∴ \(\lfloor\mathrm{ABC}\) = \(\lfloor\mathrm{ACB}\) …………..(1)

DBC is an isosceles Δle on the base BC.

\(\lfloor\mathrm{DBC}\) – \(\lfloor\mathrm{DCB}\) ……………..(2)

adding the corresponding sides of (1) & (2) we get

\(\lfloor\mathrm{ABC}\) + \(\lfloor\mathrm{DBC}\)= \(\lfloor\mathrm{ACB}\)+ \(\lfloor\mathrm{DCB}\)

=> \(\lfloor\mathrm{ABD}\) = \(\lfloor\mathrm{ACD}\)

Hence proved.

6. ΔABC is an isosceles Δle triangle in which AB = AC. side BA is produced to D such that AD = AB (see fig). Show that \(\lfloor\mathrm{BCD}\) is a right angle.

Solution:

Given : ΔABC is an isosceles Δle in which AB = AC. side BA is produced to D such that AD =AB.

To prove: \(\lfloor\mathrm{BCD}\)is a right angle.

Proof: ABC is an isosceles Δle

∴\(\lfloor\mathrm{ABC}\) = \(\lfloor\mathrm{ACB}\) ………………(1)

AB = AC &

AD =AB

=> AC = AD In ΔACD

\(\lfloor\mathrm{CDA}\) = \(\lfloor\mathrm{ACD}\) (angles opposite to equal sides of a Δle are equal).

\(\lfloor\mathrm{CDB}\) – \(\lfloor\mathrm{ACD}\) …………..(2)

adding the corresponding sides of (1) & (2) we get.

\(\lfloor\mathrm{ABC}\) + \(\lfloor\mathrm{CDB}\) = \(\lfloor\mathrm{ACB}\) + \(\lfloor\mathrm{ACD}\)

=> \(\lfloor\mathrm{ABC}\)+\(\lfloor\mathrm{CDB}\) = \(\lfloor\mathrm{BCD}\) ……………….(3)

In ΔBCD

\(\lfloor\mathrm{BCD}\) + \(\lfloor\mathrm{DBC}\)+ \(\lfloor\mathrm{CDB}\) = 180° (sum of all the angles of a is 180°)

=> \(\lfloor\mathrm{BCD}\) + \(\lfloor\mathrm{ABC}\) + \(\lfloor\mathrm{CDB}\) = 180°

=> \(\lfloor\mathrm{BCD}\)+ \(\lfloor\mathrm{BCD}\) =180° (using(3))

=> 2\(\lfloor\mathrm{BCD}\) =180°

=> \(\lfloor\mathrm{BCD}\) =180°/2= 90°

=> \(\lfloor\mathrm{BCD}\) is a right angle.

KSEEB Chapter 7 Triangles Solved Questions 

7.  ABC is a right angled Δle in which \(\lfloor A\) = 90° & AB =AC. Find \(\lfloor B\) & \(\lfloor C\).

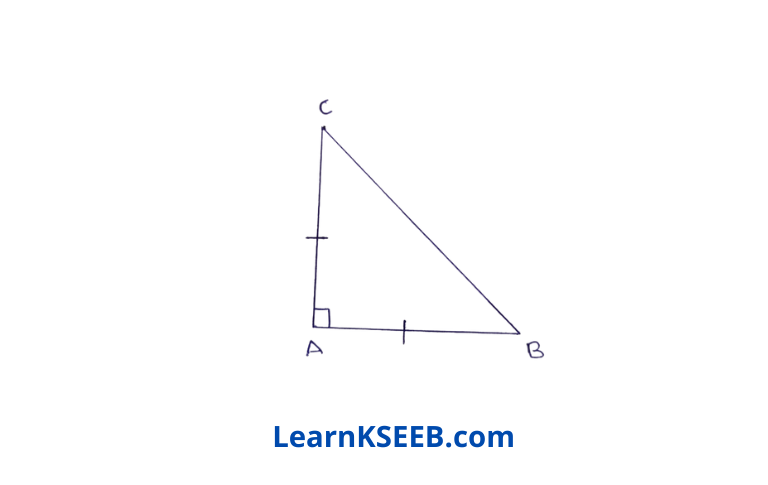
Solution: In ΔABC

AB = AC

∴ \(\lfloor B\) = \(\lfloor C\) (angles opposite to equal sides of a Δle are equal)……………..(1)

In ΔABC

\(\lfloor A\)+\(\lfloor B\)+ \(\lfloor C\) = 180° (angle sum property)

=> 90° +\(\lfloor B\) + \(\lfloor C\) = 180° (∵ \(\lfloor A\)= 90° given)

=> \(\lfloor B\)+ \(\lfloor C\) = 180°- 90° = 90° ……………..(2)

from (1) & (2) we get.

\(\lfloor B\) = \(\lfloor C\) = 45°

8. Show that the angles of an equilateral Δle are 60° each.

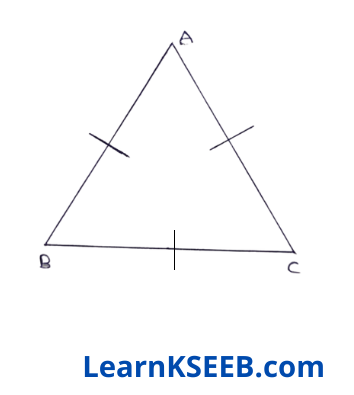
Solution:

Given : An equilateral Δle ABC.

To prove : \(\lfloor A\) = \(\lfloor B\)= \(\lfloor C\)= 60°

Proof: ABC is an equilateral Ale.

∴ AB = AC = CA ……………..(1)

AB = BC

=> \(\lfloor A\) = \(\lfloor C\) (Angles opposite to equal sides of a triangle are equal) …………….(2)

BC = CA

=> \(\lfloor A\) = \(\lfloor B\) (Angles opposite to equal sides ……………(3) of a triangle are equal)

from (2) & (3) we get

\(\lfloor A\) = \(\lfloor B\) = \(\lfloor C\) …………………(4)

In ΔABC

\(\lfloor A\)+\(\lfloor B\) + \(\lfloor C\) = 180° (angle sum property)

=> \(\lfloor A\)=\(\lfloor B\) = \(\lfloor C\) = 60°

Triangles Exercise 7.3

1. ΔABC & ΔDbC are two isosceles triangles on the same base BC & vertices A & D are on the same side of BC (see figure). If AD is extended to intersect BC at P. Show that

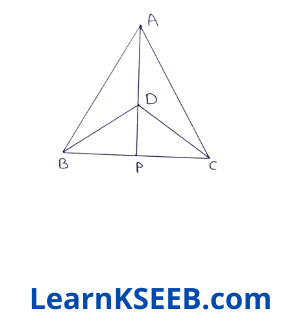
1) ΔABD ≅ ΔACD
2) ΔABP ≅ ΔACP
3) AP bisects \(\lfloor A\) as well as \(\lfloor D\)
4) AP is the perpendicular bisector of BC

Solution:

Given: ΔABC & ΔDBC are two isosceles Δle s on the same base BC & vertices A & D are on the same side of BC. AD is extended to intersect BC at P.

To prove : 1) ΔABD ≅ ΔACD

2) ΔABP ≅ ΔACP

3) AP bisects \(\lfloor A\) as well as \(\lfloor D\)

4) AP is the perpendicular bisector of BC.

Proof: (1) In ΔABD & ΔACD

AB =AC ……….(1) (AABC is an isosceles A/e)

BD = CD …………(2)( ADBC is an isosceles A/e)

AD = AD …………..(3) (common)

ΔABD ≅ ΔACD (SSSrule)

2) In ΔABP & ΔACP

AB=AC ………………(4) (from 1)

\(\lfloor\mathrm{ABP}\) = \(\lfloor\mathrm{ACP}\) ……………(5)

{(∵ AB = AC from (1)

∴\(\lfloor\mathrm{ABP}\) = \(\lfloor\mathrm{ACP}\) angles opposite to equal sides of a Δle are equal)}

∴ ΔABD ≅ ΔACD (proved in (1) above)

∴ \(\lfloor\mathrm{BAP}\) – \(\lfloor\mathrm{CAP}\) …………….(6) (CPCT)

In view (4), (5) & (6)

ΔABP ≅ ΔACP (ASA rule)

(3) ∵ ΔABP ≅ ΔACP (proved in (2) above)

=> AP bisects \(\lfloor A\)

In \(\lfloor\mathrm{BDP}\) & \(\lfloor\mathrm{CDP}\)

BD = CD ………….(7) (from (2))

DP = DP ………….(8) (common)

∴ ΔABP ≅ ΔACP (proved in (2) above)

BP = CP …………..(9) (CPCT)

In view of (7), (8) (9)

ΔBDP ≅ ΔCDP (SSS Rule)

\(\lfloor\mathrm{BDP}\) = \(\lfloor\mathrm{CDP}\) (CPCT)

=> DP bisects \(\lfloor D\)

=> AP bisects \(\lfloor D\)

(4) ∵ ΔBDP ≅ ΔCDP (proved in (3) above)

∴ BP = CP ……………(10) (CPCT)

\(\lfloor\mathrm{BPD}\) = \(\lfloor\mathrm{CPD}\) (CPCT)

but \(\lfloor\mathrm{BPD}\) + \(\lfloor\mathrm{CPD}\)= 180° ……………….(11)

linear pair

In view of (10 & (11)

AP is the perpendicular bisector of BC.

2. AD is an altitude of an isosceles A triangle ABC in which AB = AC.
Show that
1) AD bisects BC
2) AD bisects \(\lfloor A\)

Solution:

Given : AD is an altitude of an isosceles Δle ABC in which AB = AC

To prove : 1) AD bisects BC

2) AD bisects \(\lfloor A\)

Proof: 1) In right ΔADB & right ΔADC

Hyp AB = Hyp. AC (Given)

side AD = side AD (common)

\(\lfloor\mathrm{ADB}\) = \(\lfloor\mathrm{ADC}\)= 90°

ΔADB ≅ ΔADC (RHS rule)

BD = CD (C.P.C.T.)

=> AD bisects BC

ii) ΔADB ≅ ΔADC (proved in (1) above)

\(\lfloor\mathrm{BAD}\) = \(\lfloor\mathrm{CAD}\) (C.P.C.T.)

=> AD bisects \(\lfloor A\)

3. Two sides AB & BC & median AM of one triangle ABC are respectively equal to sides PQ & QR & median PN of triangle PQR (see figure). Show that
1) ΔABM ≅ ΔPQN
2) ΔABC ≅ ΔPQR

Solution:

Given : Two sides AB & BC & median AM of one triangle ABC are respectively equal to sides PQ & QR & median PN of ΔPQR

To prove : 1) ΔABM ≅ ΔPQN

2) ΔABC ≅ ΔPQR

Proof: 1) In ΔABM & ΔPQN

AB = PQ ……………(1) (given)

AM = PN …………….(2) (given)

BC = QR

=> 2BM = 2QN (M & N are the mid-points of BC & QR respectively)

=> BM = QN …………….(3)

In view of(l), (2) & (3)

2) ΔABM = ΔPQN (proved in (1) above)

\(\lfloor\mathrm{ABM}\) = \(\lfloor\mathrm{PQN}\) (C.P.C.T.)

=> \(\lfloor\mathrm{ABC}\) = \(\lfloor\mathrm{PQR}\) (4)

In ΔABC & ΔPQR

AB = PQ (given)

BC = QR (given)

\(\lfloor\mathrm{ABC}\) = \(\lfloor\mathrm{PQR}\) (from (4))

∴ ΔABC = ΔPQR (by SAS rule)

KSEEB Solutions for 9th Standard Maths Chapter 7 Triangles 

4. BE & CF are two equal altitudes of a ΔABC using RHS congruence rule, prove that the triangle ABC is isosceles.

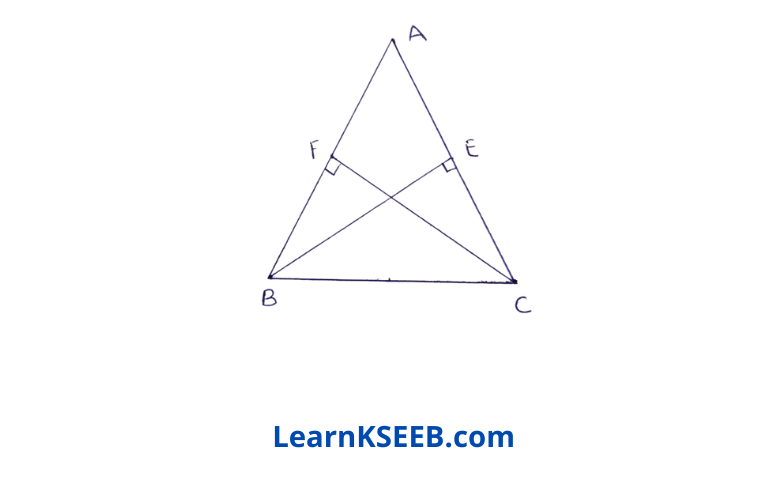
Solution:

Given : BE & CF are two equal A altitudes of a ΔABC

To prove : ABC is isosceles. F E

Proof: In right ΔBEC & right

ΔCFB

side BE = side CF (given)

Hyp. BC = Hyp. CB (common)

ΔBEC = ΔCFB (RHS rule)

\(\lfloor\mathrm{BCE}\) = \(\lfloor\mathrm{CBF}\) (C.P.C.T)

AB = AC (sides opposite to equal angles of a Δle are equal)

∴ ΔABC is isosceles.

5. ABC is an isosceles A/e with AB = AC. Draw AP⊥BC show that \(\lfloor B\) = \(\lfloor C\)

Solution:

Given: ABC is an isosceles A/e with AB=AC

To prove : \(\lfloor B\)= \(\lfloor C\)

Construction : Draw AP ⊥ BC

Proof: In right triangle APB & right triangle APC.

Hyp. AB = Hyp. AC (given)

side AP = side AP (common)

∴ ΔAPB ≅ ΔAPC (RHS rule)

\(\lfloor\mathrm{ABP}\) = \(\lfloor\mathrm{ACP}\) (C.P.C.T.)

=> \(\lfloor B\)= \(\lfloor C\)

Triangles Exercise 7.4

1. Show that in a right-angled triangle, the hypotenuse is the longest side.

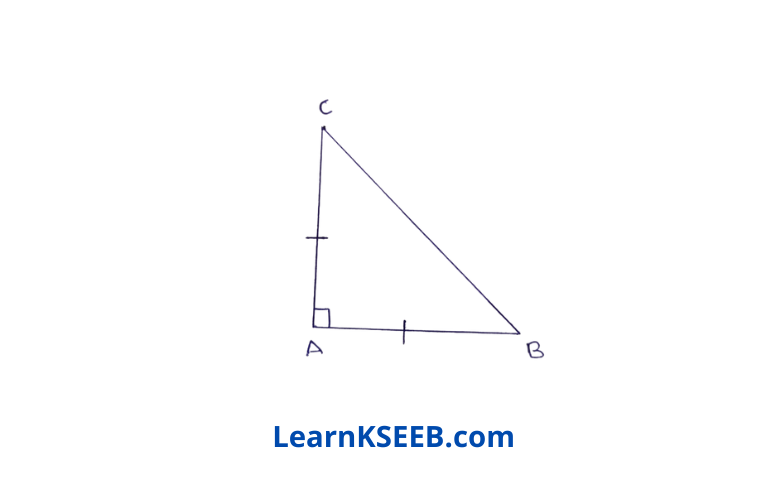
Solution: Let ABC be a right-angled triangle in which \(\lfloor B\) = 90°

then \(\lfloor A\) + \(\lfloor C\) = 90° (sum of all the angles of a Δle is 180°)

∴ \(\lfloor B\) = \(\lfloor A\) + \(\lfloor C\)

∴ \(\lfloor B\)>\(\lfloor A\) & \(\lfloor B\)>\(\lfloor C\)

∴ AC>BC (∴ side opposite to greater angle is longer)

& AC > AB

∴ AC is the longest side, i.e., the hypotenuse is the longest side.

2. In figure sides AB & AC of AABC are extended to points P & Q respectively. Also \(\lfloor\mathrm{PBC}\) < \(\lfloor\mathrm{QCB}\), Show that AC > AB.

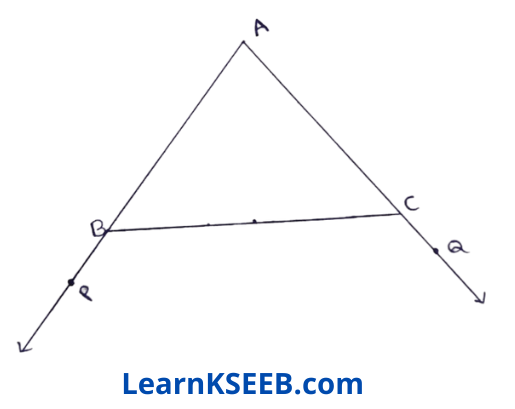
Solution:

Given: sides AB &AC are extended to points P & Q respectively. Also,\(\lfloor\mathrm{PBC}\)< \(\lfloor\mathrm{QCB}\)

To prove : AC > AB

Proof: \(\lfloor\mathrm{PBC}\) < \(\lfloor\mathrm{QCB}\) (given)

=> –\(\lfloor\mathrm{PBC}\) > –\(\lfloor\mathrm{QCB}\)

=> 180 – \(\lfloor\mathrm{PBC}\) > 180°-\(\lfloor\mathrm{QCB}\)

∴ \(\lfloor\mathrm{ABC}\)>\(\lfloor\mathrm{ACB}\)

∴ AC > AB

∴ sides opposite to greater angle is longer.

3. In figure, \(\lfloor B\) < \(\lfloor A\)& \(\lfloor C\) < \(\lfloor D\) show that AD < BC.

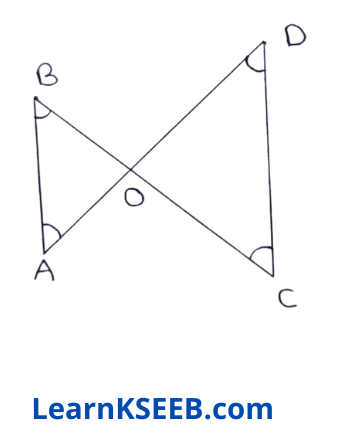
Solution:

Given : In figure, \(\lfloor B\) < \(\lfloor A\) & \(\lfloor C\) < \(\lfloor D\)

To prove :

AD < BC

Proof: \(\lfloor B\)< \(\lfloor A\)(given)

\(\lfloor A\)>\(\lfloor B\)

OB >OA …………….(1)

(side opposite to greater angle is longer)

\(\lfloor C\) < \(\lfloor D\) (given)

∴ \(\lfloor D\) > \(\lfloor C\)

∴ OC>OD ……………..(2)

(side opposite to greater angle is longer)

from (1) & (2), we get

OB + OOOA + OD

=>BC > AD

=> AD < BC

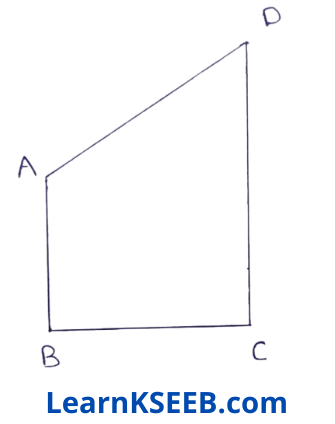
4. AB & CD are respectively the smallest & longest sides of a quadrilateral ABCD (see figure).
Show that \(\lfloor A\) > \(\lfloor C\) & \(\lfloor B\) > \(\lfloor D\)

Solution:

Given: AB & CD are respectively the smallest and longest sides of a quadrilateral ABCD.

To prove : \(\lfloor A\) > \(\lfloor C\) & \(\lfloor B\) > \(\lfloor D\)

Construction: Join AC

Proof: In ΔABC AB < BC (∵ AB is the smallest side of quadrilateral ABCD)

=> BC > AB

\(\lfloor\mathrm{BAC}\)> \(\lfloor\mathrm{BCA}\) (angle opposite to longer ……………(1)side is greater)

In ΔACD

CD > AD (∵ CD is the longest side of quadrilateral ABCD)

∴ \(\lfloor\mathrm{CAD}\) > \(\lfloor\mathrm{ACD}\) (angle opposite to longer side is greater) from(l) & (2), we obtain

\(\lfloor\mathrm{BAC}\) + \(\lfloor\mathrm{CAD}\) > \(\lfloor\mathrm{BCA}\)+ \(\lfloor\mathrm{ACD}\)

\(\lfloor A\)>\(\lfloor C\)

||ly joining B to D, we can prove that \(\lfloor B\) > \(\lfloor D\)

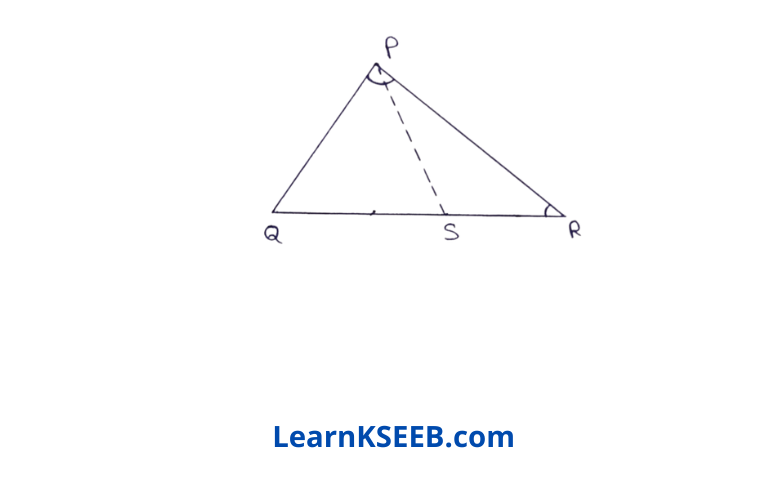
5. In figure, PR > PQ & PS bisects \(\lfloor\mathrm{QPR}\). Prove that \(\lfloor\mathrm{PSR}\) > \(\lfloor\mathrm{PSQ}\)

Solution:

Given: In figure, PR > PQ & PS bisects \(\lfloor\mathrm{QPR}\)

To prove : \(\lfloor\mathrm{PSR}\) > \(\lfloor\mathrm{PSQ}\)

Proof: In ΔPQR

PR>PQ (given)

∴ \(\lfloor\mathrm{PQR}\) > \(\lfloor\mathrm{PRQ}\) ………………..(1) (angle opposite to the longer side is greater)

PS bisects \(\lfloor\mathrm{QPR}\)

∴ \(\lfloor\mathrm{QPS}\) = \(\lfloor\mathrm{RPS}\) ……………….(2)

In ΔPQS

\(\lfloor\mathrm{PQR}\) + \(\lfloor\mathrm{QPS}\) + \(\lfloor\mathrm{PSQ}\) = 180° ………………..(3)

(angle sum property of a Δle)

In ΔPRS

\(\lfloor\mathrm{PRS}\)+\(\lfloor\mathrm{SPR}\) + \(\lfloor\mathrm{PSR}\) = 180° ……………….(4)

(Angle sum property of a Δle) from (3) & (4) we get

\(\lfloor\mathrm{PQR}\) + \(\lfloor\mathrm{QPS}\)+ \(\lfloor\mathrm{PSQ}\) = \(\lfloor\mathrm{PRS}\) + \(\lfloor\mathrm{SPR}\)+

\(\lfloor\mathrm{PSR}\)

=> \(\lfloor\mathrm{PQR}\) + \(\lfloor\mathrm{PSQ}\) = \(\lfloor\mathrm{PRS}\) + \(\lfloor\mathrm{PSR}\)

(∵ \(\lfloor\mathrm{QPS}\) = \(\lfloor\mathrm{SPR}\))

=> \(\lfloor\mathrm{PRS}\) + \(\lfloor\mathrm{PSR}\) = \(\lfloor\mathrm{PQR}\)+ \(\lfloor\mathrm{PSQ}\)

=> \(\lfloor\mathrm{PRS}\) + \(\lfloor\mathrm{PSR}\) > \(\lfloor\mathrm{PRQ}\)+ \(\lfloor\mathrm{PSQ}\)(from(1))

=> \(\lfloor\mathrm{PRQ}\) + \(\lfloor\mathrm{PSR}\) > \(\lfloor\mathrm{PSR}\)+ \(\lfloor\mathrm{PSQ}\)

(∵ \(\lfloor\mathrm{PSQ}\) = \(\lfloor\mathrm{PSR}\))

=> \(\lfloor\mathrm{PSR}\) > \(\lfloor\mathrm{PSQ}\)

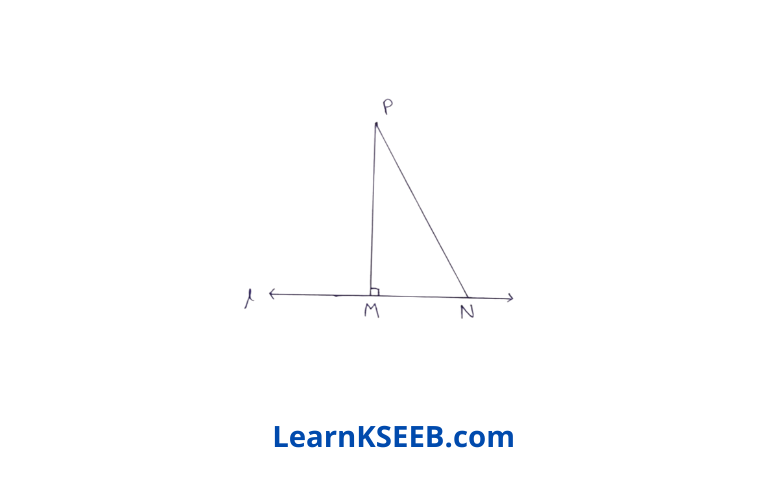
6. Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.

Solution: Let l is a line & P is a point not lying on l , PM ⊥ l N is any point on l other than M.

To prove : PM < PN

Proof: In ΔPMN

\(\lfloor M\) = 90°

∴ \(\lfloor N\) is an acute angle

(angle sum property of a Δle)

\(\lfloor M\) >\(\lfloor N\)

PN > PM (side opposite to greater angle is greater)

=> PM < PN

Additional Problems

Choose the correct answer from the following:

1. In ΔABC = ΔACB then ΔABC is isosceles with

1. AB = AC A
2. AB = BC
3. AC = BC
4. None of these

Solution: 1. AB = AC

2. Which of the following is not a criterion for congruence of triangles?

1. SAS
2. SSA
3. ASA
4. SSS

Solution: 2. SSA

KSEEB Maths Chapter 7 Triangles Free Solutions 

3. In triangle ABC & PQR, if \(\lfloor A\) = \(\lfloor R\) ,\(\lfloor B\)= \(\lfloor P\) & AB = RP, then which one of the following congruence conditions applies.

1. SAS
2. ASA
3. SSS
4. RHS

Solution: 2. ASA

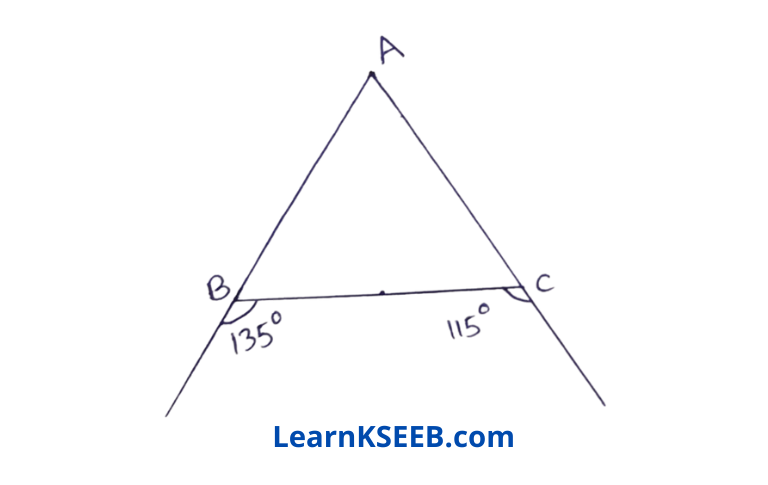
4. In the following figure, write the relation between AB & AC.

1. AB > AC
2. AB < AC
3. AB = AC
4. AB = 1/2 AC

Solution: 1. AB > AC

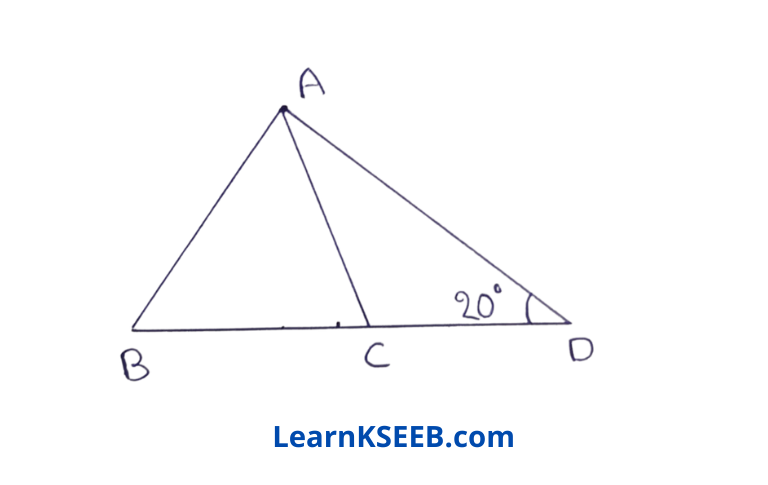
5. In the following figure, in ΔABC, AB = AC, CD = CA & \(\lfloor\mathrm{ADC}\) = 20°, then \(\lfloor\mathrm{ABC}\) =

1. 10°
2. 20°
3. 30°
4. 40°

Solution: 4. 40°

6. In ΔABC, \(\lfloor C\) = \(\lfloor A\) & BC = 6cm & AC = 5cm then the length of AB is

1. 6cm
2. 5cm
3. 3cm
4. 2.5cm

Solution: 1. 6cm

7. ΔABC ≅ ΔPQR, then which of the following is true

1. A↔R
2. AB = QR
3. AC = PQ
4. AB = PQ

Solution: 4. AB = PQ

8. Two sides of a triangle are of length 7cm & 3.5 cm. The length of the third side of the triangle cannot be

1. 3.6cm
2. 4.1cm
3. 3.4cm
4. 3.8cm

Solution: 3. 3.4cm

9. In given figure, if AE || DC & AB = AC, the value of \(\lfloor\mathrm{ABD}\) is

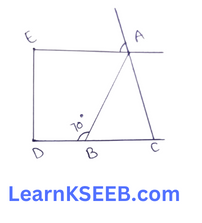
1. 70°
2. 110°
3. 120°
4. 130°

Solution: 2. 110°

10. In given figure, the measure of \(\lfloor\mathrm{PQR}\) is _

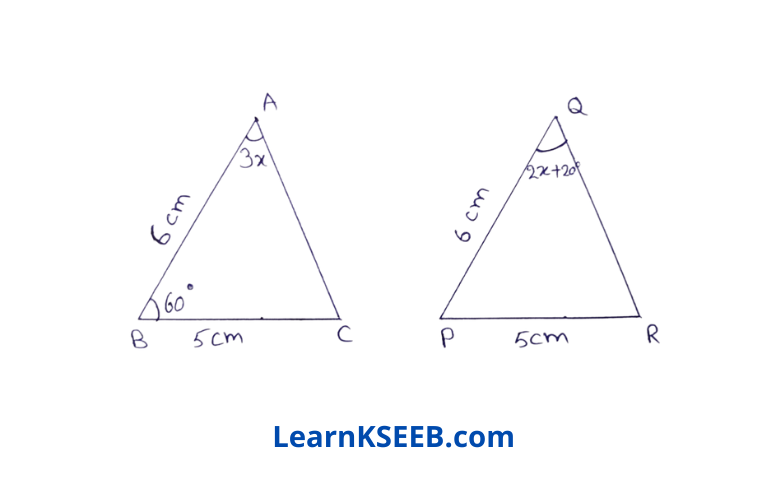
1. 50°
2. 60°
3. 70
4. 80°

Solution: 2. 60°

11. In ΔABC AB = AC, BD = EC, then ΔADE is

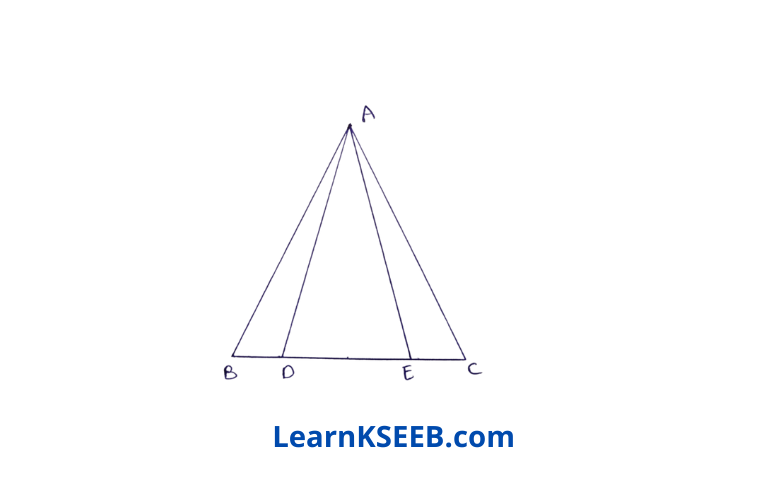
1. right-angled
2. Scalene
3. Isosceles
4. equilateral

Solution: 3. Isosceles

One Mark Questions

1. In ΔABC & ΔDEF, AB = DE, \(\lfloor A\) = \(\lfloor D\) What will be the condition in which the two triangles will be congruent by SAS axiom?

Solution: Since AB = DE

\(\lfloor A\) = \(\lfloor D\)

& ΔABC ≅ ΔDEF

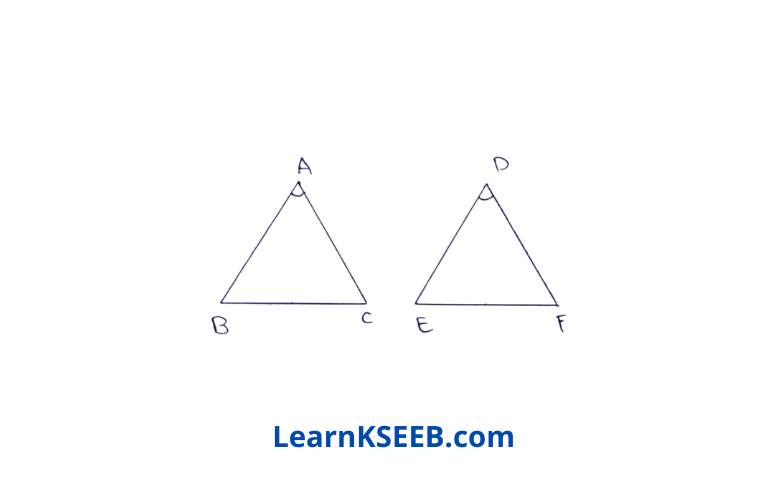
by SAS

∴ AC = DF

2. What do we call a triangle if the angles are in the ratio 5:3:7?

Solution: Let the angles of triangles are 5x, 3x& 7x, then

5x+3x + 7x=180°

15x= 180

x = 180/15=12°

∴ Angles are 60°, 36°, 84°

∴ Each angle is less than 90°

The Δle is an acute-angled triangle.

3. In the figure below, if AB = AC, then what is the value of x?

Solution: \(\lfloor\mathrm{ABC}\) = 180- 125 = 55°

AB = AC,

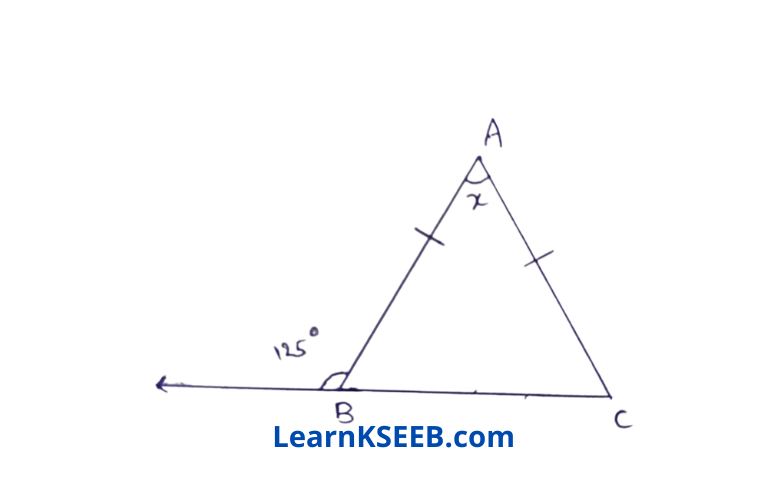
=> \(\lfloor\mathrm{ACB}\) = \(\lfloor\mathrm{ABC}\) = 55°

=> x = 180-55-55°

=> x=70°

4. Is it possible to construct a triangle, when its sides are 5.4cm, 2.3cm, 3.1cm?

Solution: No, Because 2.3 + 3.1 = 5.4cm

Not possible to construct a Δle.

5. From the given figure A show that AB > BD

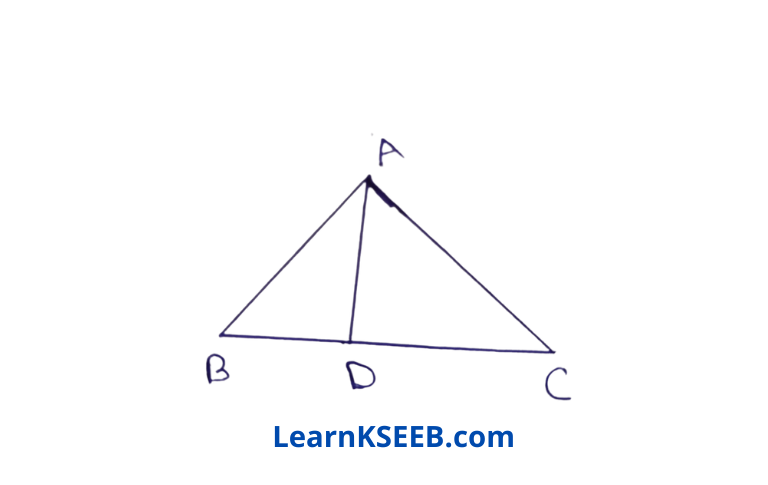
Solution: If D is a point on the side BC of a ΔABC such that

AD bisects \(\lfloor\mathrm{BAC}\) then AB > BD

6. In ΔABC \(\lfloor B\) = 30°, \(\lfloor C\) = 80°&\(\lfloor A\) = 70° then prove that AB > BC > AC

Solution:

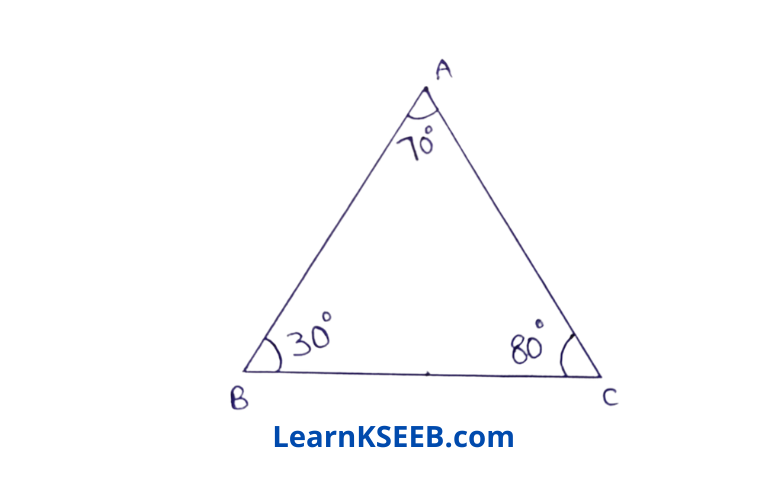
Since \(\lfloor C\) > \(\lfloor A\) > \(\lfloor B\)

∴ AB > BC > AC

7. ΔABC is an isosceles right-angled triangle in which \(\lfloor A\) =90°. Calculate \(\lfloor B\).

Solution: AB=AC \(\lfloor B\) = \(\lfloor C\)

By angle sum property.

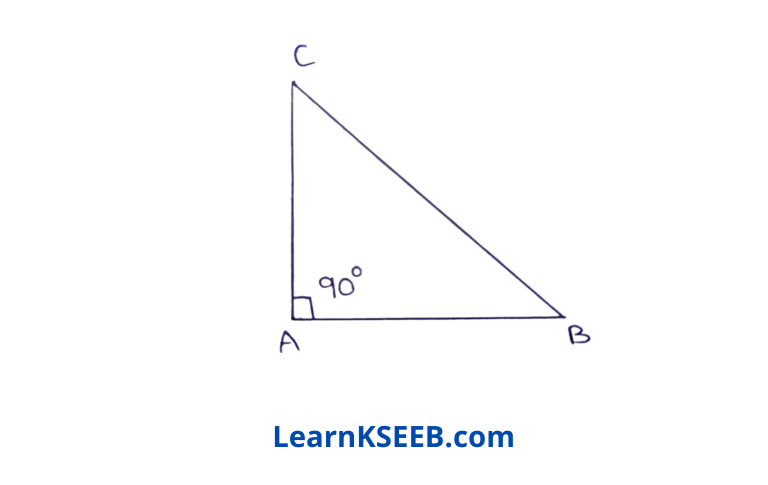
\(\lfloor A\) + \(\lfloor B\) + \(\lfloor C\) = 180°

=> 90° + \(\lfloor B\) + \(\lfloor B\) = 180°

2\(\lfloor B\) = 90°

\(\lfloor B\) = 9%/2 = 45°

8. In ΔPQR PE is the perpendicular bisector of \(\lfloor\mathrm{QPR}\) , then prove that PQ = PR

Solution: In ΔPEQ & ΔPER

\(\lfloor\mathrm{PEQ}\) = \(\lfloor\mathrm{PER}\) = 90°

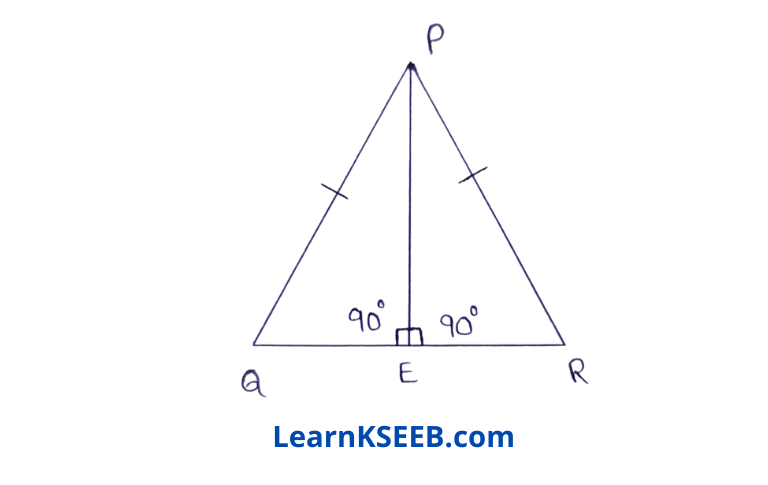
PE = PE (common)

ΔQPE = ΔRPE (given)

ΔPEQ ≅ ΔPER

PQ = PR (cpct)

9. ΔPQR ≅ ΔABC if PQ = 5cm, \(\lfloor Q\) = 40° & \(\lfloor P\) 80°. Calculate the value of \(\lfloor C\)

Solution: \(\lfloor R\) = 180-80°-40° = 60°

ΔPQR ≅ ΔABC

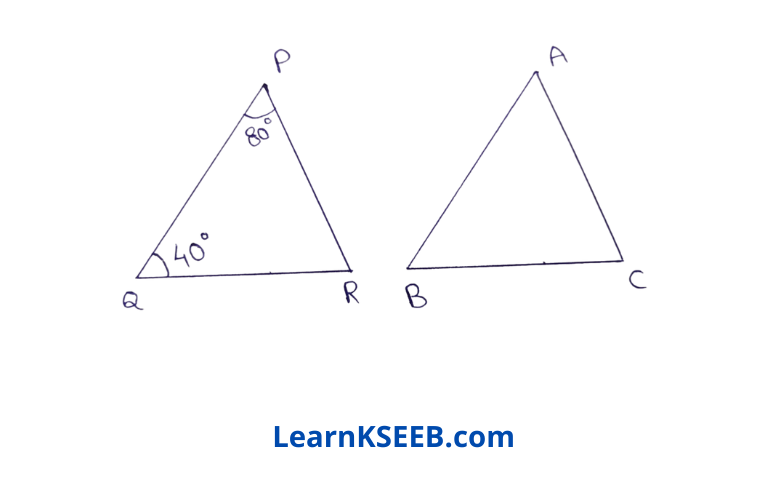
\(\lfloor R\) = \(\lfloor C\) = 60°

 

KSEEB Class 9 Chapter 7 Triangles Revision Notes 

10. Given ΔOAP =ΔOBP in the figure below. Prove the criteria by which the triangles are congruent.

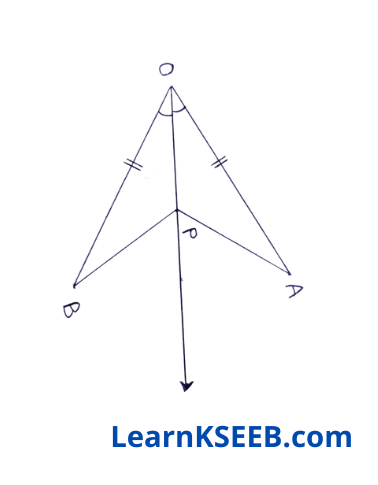
Solution: OA = OB (given)

OP = OP (common)

\(\lfloor\mathrm{AOP}\) = \(\lfloor\mathrm{BOP}\) (given)

∴ ΔOAP ≅ ΔOBP (bySAS)

Two Mark Questions

1. In the figure below, ABC is a Δle in which AB = AC, x & y are points on AB & AC. Such that AX = AY. Prove that ΔABY ≅ ΔACX

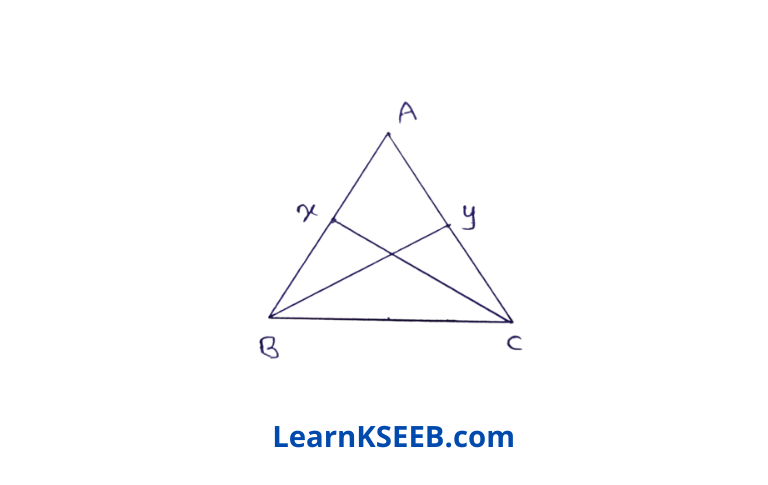
Solution: In ΔABY & ΔACX

AB=AC (given)

AY=AX (given)

\(\lfloor A\) = \(\lfloor A\) (common)

ΔABY = ΔACX (by SAS rule)

2. In the figure below ABCD A is a square & P is the midpoint of AD. BP & CP are joined. Prove that \(\lfloor\mathrm{PCB}\) = \(\lfloor\mathrm{PBC}\)

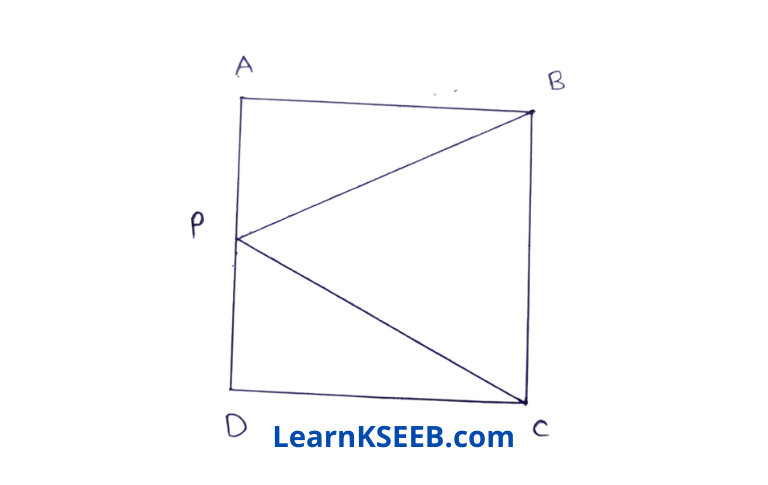
Solution: In ΔPAB &ΔPDC

PA= PD

(P is the mid-point of AD)

AB = CD

\(\lfloor\mathrm{PAB}\) = \(\lfloor\mathrm{PDC}\)= 90°

ΔPAB ≅ ΔPDC (by RHS rule)

PB = PC (C.P.C.T.)

=> \(\lfloor\mathrm{PCB}\) = \(\lfloor\mathrm{PBC}\)

3. In the figure below, the diagonal AC of quadrilateral ABCD, A bisects \(\lfloor\mathrm{BAD}\)& \(\lfloor\mathrm{BCD}\) .
Prove that BC = CD

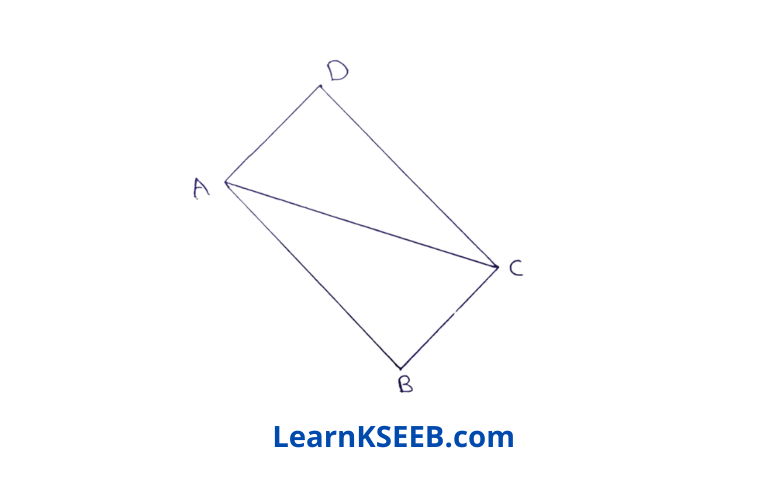
Solution: In ΔADC & ΔABC

AC = AC (common)

\(\lfloor\mathrm{DAC}\) = \(\lfloor\mathrm{BAC}\) (given)

\(\lfloor\mathrm{DCA}\) = \(\lfloor\mathrm{BCA}\) (given)

Hence ΔADC ≅ ΔABC (by AAS rule)

=> CD = BC (byCPCT)

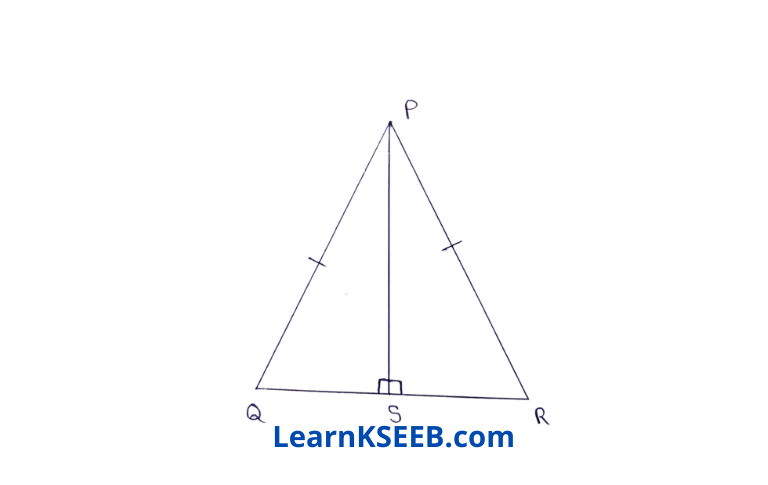
4. PS is an altitude of an isosceles Δle PQR in which PQ = PR. Show that PS bisects \(\lfloor P\)

Solution: In ΔPQS & ΔPRS

PQ = PR (given)

PS = PS (common)

\(\lfloor\mathrm{PSQ}\) = \(\lfloor\mathrm{PSR}\) = 90°

ΔPQS ≅ ΔPRS (byR.H.S. rule)

\(\lfloor\mathrm{QPS}\) = \(\lfloor\mathrm{RPS}\) (CPCT)

Hence, PS bisects \(\lfloor P\)

5. In the figure, given AC > AB & AD is the bisector of \(\lfloor A\). Show that \(\lfloor\mathrm{ADC}\) > \(\lfloor\mathrm{ADB}\)

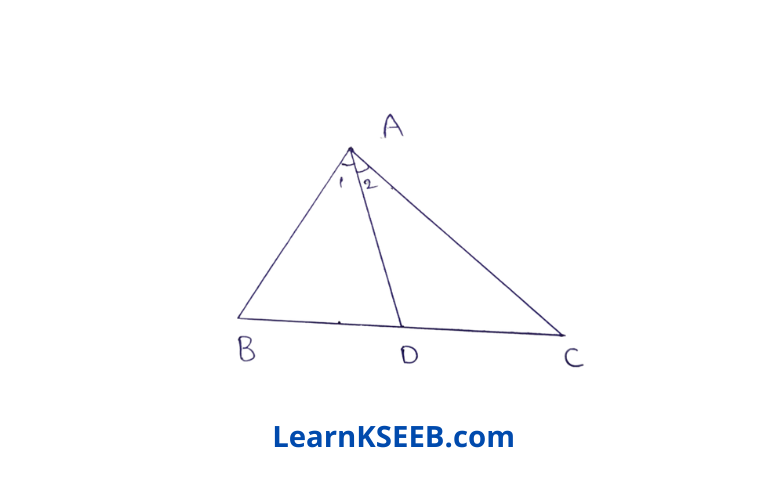
Solution:

In ΔABC

AC>AB (given)

∴ \(\lfloor\mathrm{ABC}\) >\(\lfloor\mathrm{ACB}\) (angles opposite to larger side is greater)

\(\lfloor\mathrm{ABC}\) + \(\lfloor 1\) > \(\lfloor\mathrm{ACB}\) + \(\lfloor 1\) (adding \(\lfloor 1\) on both sides)

\(\lfloor\mathrm{ABC}\)+ \(\lfloor 1\) > \(\lfloor\mathrm{ACB}\) +\(\lfloor 2\) (AD bisects \(\lfloor A\),\(\lfloor 1\) =

\(\lfloor 2\))

∴ \(\lfloor\mathrm{ADC}\)>\(\lfloor\mathrm{ADB}\)

(Exterior angle property of Δle)

6. In figure, AD ⊥ CD & BC ⊥ CD & If AQ = BP & DP = CQ. Prove that
\(\lfloor\mathrm{DAQ}\) = \(\lfloor\mathrm{CBP}\)

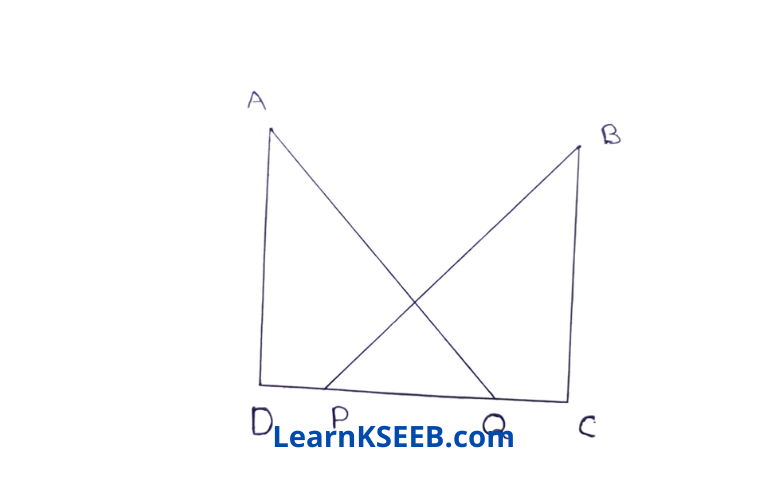
Solution: DP = CQ

=> DP + PQ = CQ + PQ (adding PQ to both side)

=> DQ = CP

In right Δles ADQ&BCP

\(\lfloor\mathrm{ADQ}\) = \(\lfloor\mathrm{BCP}\) = 90°

Hyp. AQ = Hyp. BP (given)

side DQ = side CP

ΔADQ ≅ ΔBCP (by RHS rule)

∴ \(\lfloor\mathrm{DAQ}\)– \(\lfloor\mathrm{CBP}\) (C.P.C.T.)

7. Angles A, B & C of a triangle ABC are equal to each other, prove that ΔABC is equilateral Solution: \(\lfloor A\)= \(\lfloor B\)

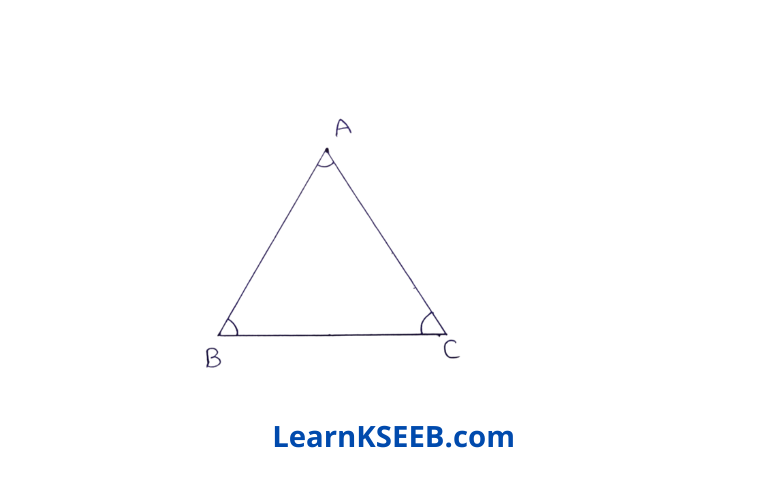
=> BC = CA (sides opp. to equal angles of AABC) ………………(1)

\(\lfloor B\)=\(\lfloor C\)

=> CA=AB ……………(2) (sides opp. to equal angles of ΔABC)

\(\lfloor C\)= \(\lfloor A\)

=> AB = BC ………………(3) (sides opp. to equal angles of ΔABC)

from(l), (2) & (3) we get

AB = BC = CA

=> ΔABC is equilateral.

Three Mark Questions

1. In figure PQRS is a square & SRT is an equilateral triangle. Prove that
1) PT = QT
2) \(\lfloor\mathrm{TQR}\) =15°

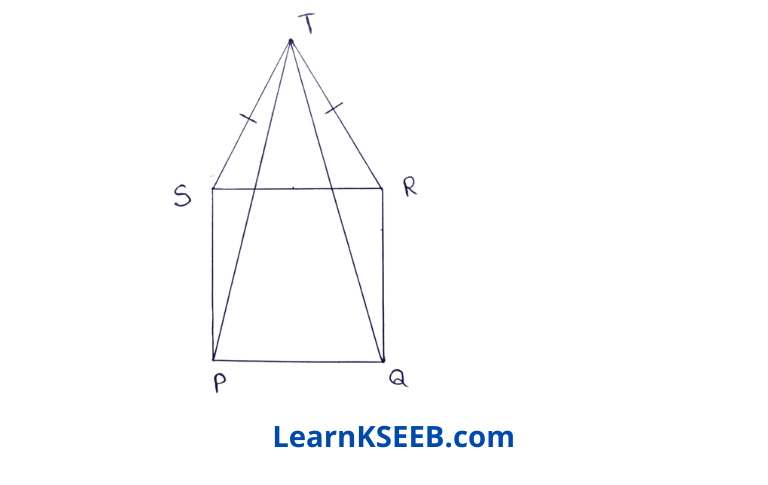
Solution: 1) SRT is an equilateral Δle.

\(\lfloor\mathrm{PSR}\) = 90°, \(\lfloor\mathrm{TSR}\) – 60°

=> \(\lfloor\mathrm{PSR}\) + \(\lfloor\mathrm{TSR}\)=150°

||ly \(\lfloor\mathrm{QRT}\) = 150°

In ΔPST & ΔQRT

PS = QR

\(\lfloor\mathrm{PST}\) = \(\lfloor\mathrm{QRT}\) = 150°

ST = RT (sides of equilateral Δle)

ΔPST ≅ ΔQRT (by SAS rule)

=> PT=QT (byCPCT)

2) In ΔTQR

Square & equilateral Δle on same base)

=> \(\lfloor\mathrm{TQR}\) = \(\lfloor\mathrm{QTR}\) = x

∴ x + x+\(\lfloor\mathrm{QRT}\)= 180°

∴ 2x+150 = 180°

=> x=(180-150)/2

=> \(\lfloor\mathrm{TQR}\) = x =30/2=15°

2. In the figure, prove that CD+DA+AB+BC > 2AC.

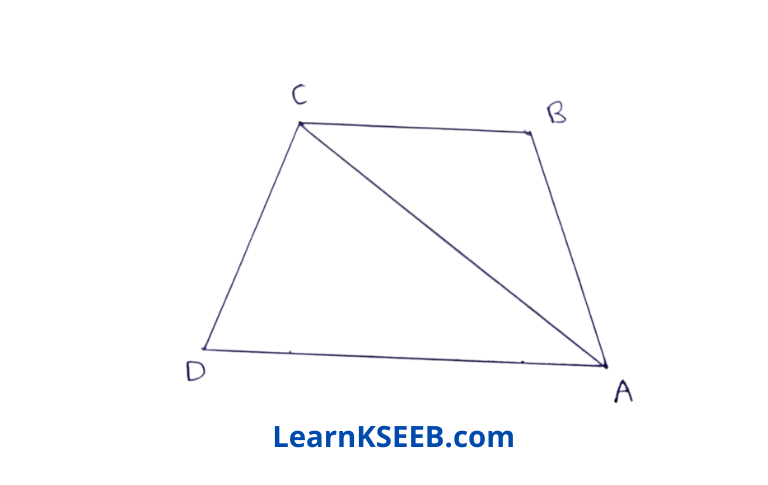
Solution: In ΔABC

AB + BC > AC …………….(1) (as sum of two sides is greater than the 3rd side)

In ΔACD

CD + DA > AC …………….(2) (as sum of two sides is greater than the 3rd side)

adding (1) & (2), we get

CD + DA +AB + BC > 2AC

3. PQR is a Δle in which PQ = PR. S is any point on the side PQ, through S, a line is drawn parallel to QR intersecting PR at T. Prove that PS = PT.

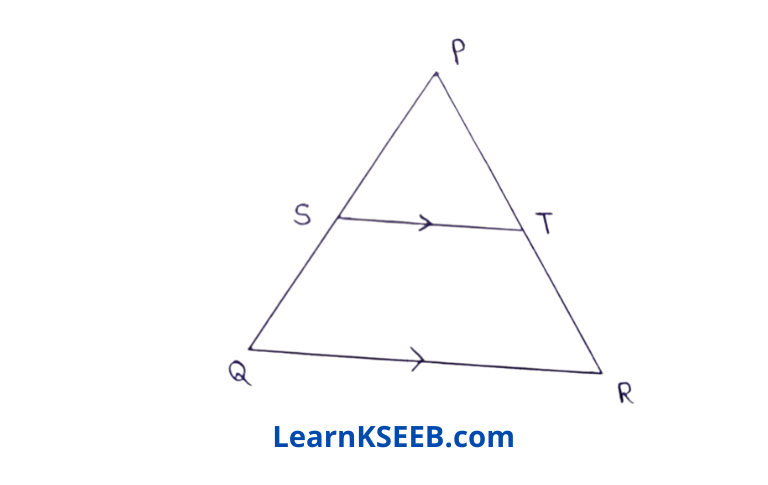
Solution: PQ = PR

\(\lfloor\mathrm{PQR}\) = \(\lfloor\mathrm{PRQ}\)(angles opp. to p equal sides are equal)

ST || QR

=> \(\lfloor\mathrm{PST}\) = \(\lfloor\mathrm{PQR}\)(corresponding angles)

∴ \(\lfloor\mathrm{PTS}\) = \(\lfloor\mathrm{PRQ}\)(corresponding angles)

\(\lfloor\mathrm{PST}\) = \(\lfloor\mathrm{PTS}\)

=> PS = PT (sides opp. to equal angles are equal)

4. In the given figure, AD = BD, prove that BD < AC

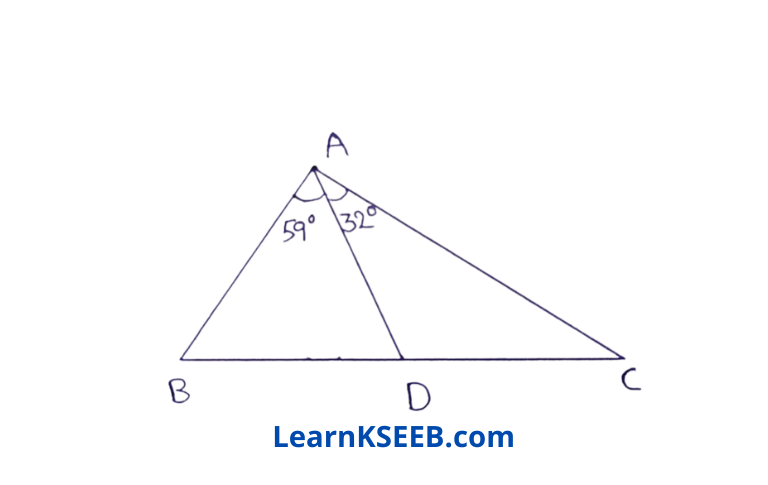
Solution:

AD = BD

\(\lfloor\mathrm{ABD}\) = \(\lfloor\mathrm{DAB}\) = 59° (anglesopp. to equal sides are equal)

In ΔABD

59° + 59° + \(\lfloor\mathrm{ADB}\) = 180°

\(\lfloor\mathrm{ADB}\) = 180 – 118 = 62°

\(\lfloor\mathrm{ACD}\) = 62 – 32 = 30° (exterior angle is equal to the sum of interior opp. angles)

In ΔABD, AB > BD

(sides opp. to greater angle is the longest)

Also in ΔABC AB < AC

BD < AC

KSEEB Class 9 Maths Chapter 7 Triangles Exercises 

5. In figure, OA = OD & \(\lfloor 1\) = \(\lfloor 2\) Prove that ΔOCBis an isosceles Δle.

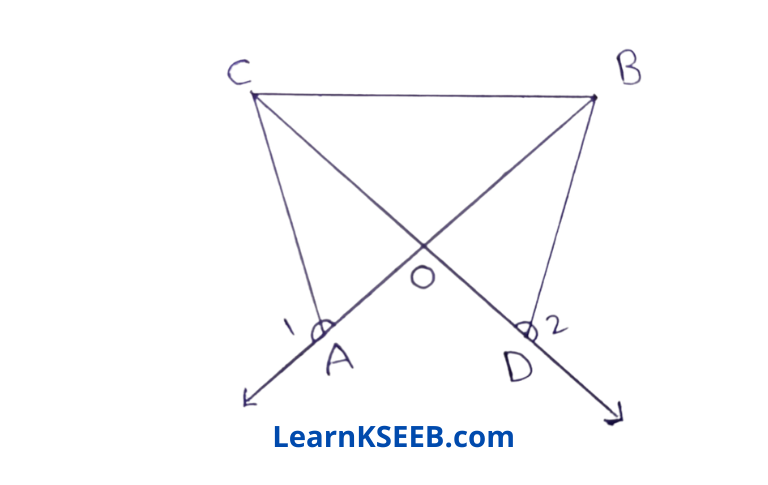
Solution: \(\lfloor 1\) + \(\lfloor 3\) = 180° (linear pair)

\(\lfloor 2\)+ \(\lfloor 4\) = 180° (linear pair)

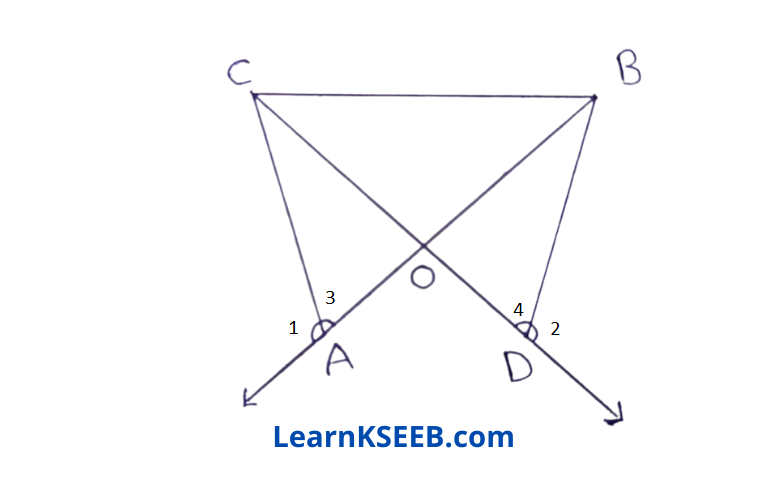
\(\lfloor 1\) + \(\lfloor 3\) = \(\lfloor 2\) + \(\lfloor 4\)

but \(\lfloor 1\) = \(\lfloor 2\) (given)

=> 12 = 14

In ΔDAC & ΔODB \(\lfloor 3\) = \(\lfloor 4\)

\(\lfloor\mathrm{AOC}\) = \(\lfloor\mathrm{DOB}\) (verticallyopp. angle)

OA = OD (given)

∴ ΔOAC ≅ ΔODB (by AS A rule)

OC = OB (C.P.C.T.)

=> ΔOCB is an isosceles triangle.

6. AD & BC are equal perpendiculars to a line segment AB
(1) show that CD bisects AB.
(2) What is its value?

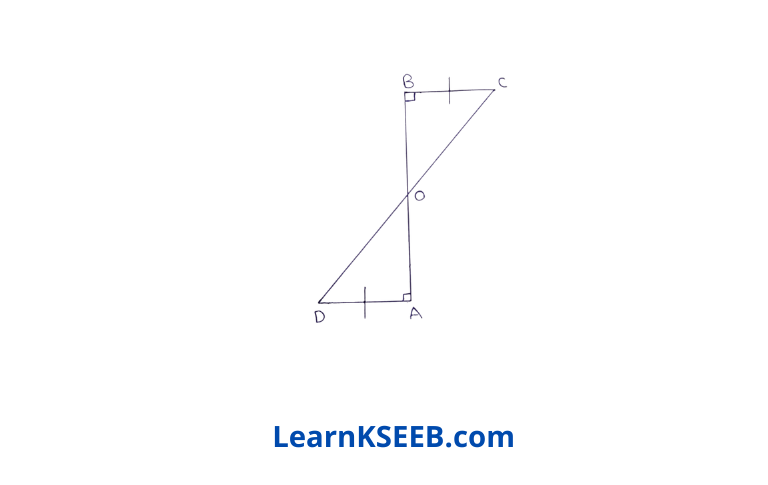
Solution: AB & CD intersect at O

\(\lfloor\mathrm{AOB}\) = \(\lfloor\mathrm{BOC}\)

(vertically opp. angles)……..(1)

In ΔAOD & ΔBOC

\(\lfloor\mathrm{AOD}\) = \(\lfloor\mathrm{BOC}\) (V.O.A)

\(\lfloor\mathrm{DAO}\) = \(\lfloor\mathrm{CBO}\) = 90° (given)

AD = BC (given)

∴ ΔAOD ≅ ΔBOC (by AAS rule)

=> OA = OB

ie, O is the mid point of AB Hence CD bisects AB.

2) Equality is the sign of democracy.

7. l & m are two parallel equal lines intersected by another pair of parallel lines p & q. Show that ΔABC ≅ ΔCD A

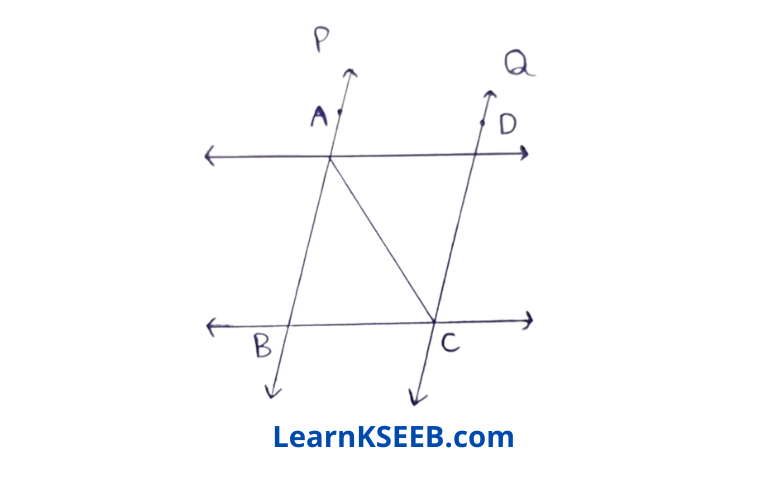
Solution: l and m are two parallel equal lines intersected by another pair of parallel lines p & q.

AD || BC

& AB || CD

=> ABCD is a parallelogram

i.e.,AB = CD

& BC = AD

Now in ΔABC & ΔCDA

AB = CD

BC =AD

& AC = AC

∴ ΔABC ≅ ΔCDA (by SSS rule)

Four Mark Questions

1. If two parallel lines are intersected by a transversal then prove that bisectors of the interior angles form a rectangle

Solution: \(\lfloor\mathrm{AGH}\) = \(\lfloor\mathrm{HGD}\) (Alternate angle)

 

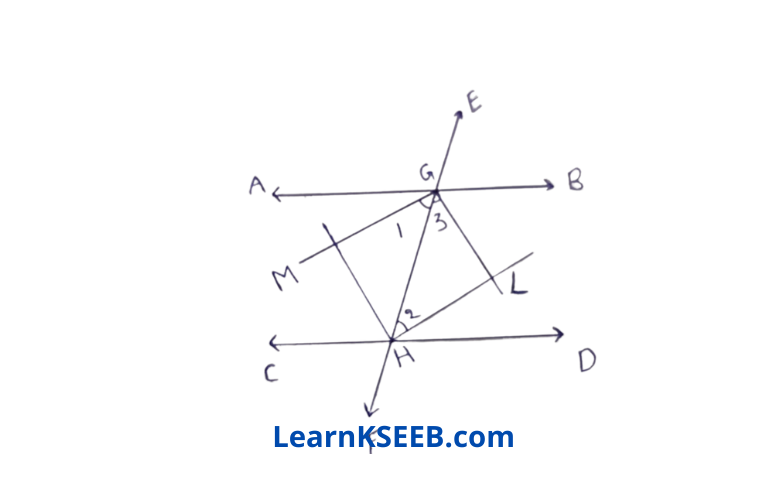
=> 1/2\(\lfloor\mathrm{AGH}\) = 1/2\(\lfloor\mathrm{GHD}\)

=> \(\lfloor 1\) =\(\lfloor 2\)

GM II LH

|| ly GL || MH

=> GMHL is a parallelogram

\(\lfloor\mathrm{BGH}\) + \(\lfloor\mathrm{GHD}\) = 180°

=> 1/2\(\lfloor\mathrm{BGH}\) + 1/2\(\lfloor\mathrm{GHD}\) = 90°

=> \(\lfloor 3\) + \(\lfloor 2\) = 90°

In ΔGLH

\(\lfloor\mathrm{GLH}\) = 180 — (\(\lfloor 2\)+ \(\lfloor 3\)) =180-90

\(\lfloor\mathrm{GLH}\) = 90°

=> \(\lfloor\mathrm{GMH}\) = 90°

So \(\lfloor\mathrm{MGL}\) + \(\lfloor\mathrm{GLH}\) = 180°

=>\(\lfloor\mathrm{MGL}\) +90°= 180°

=> \(\lfloor\mathrm{MGL}\) = 90°

∴ MGLH is a rectangle.

KSEEB Solutions Class 9 Triangles Practice Problems 

2. In figure, the sides AB & AC of AABC are produced to points E&D respectively. If bisectors BO & CO of \(\lfloor\mathrm{CBE}\) & \(\lfloor\mathrm{BCD}\) respectively meet at a point O, then prove that
\(\lfloor\mathrm{BOC}\) = 90°-1/2\(\lfloor\mathrm{BAC}\)

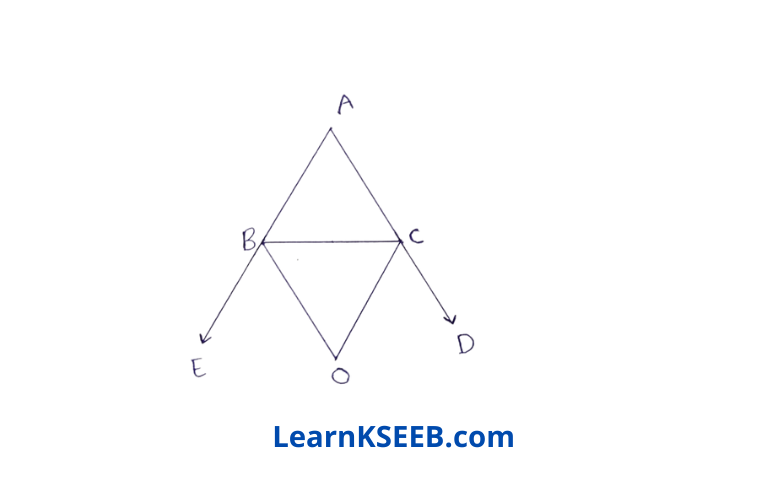
Solution: As \(\lfloor\mathrm{ABC}\) & \(\lfloor\mathrm{CBE}\) form a linear pair.

\(\lfloor\mathrm{ABC}\) + \(\lfloor\mathrm{CBE}\) = 180°

BO is the bisector of \(\lfloor\mathrm{CBE}\)

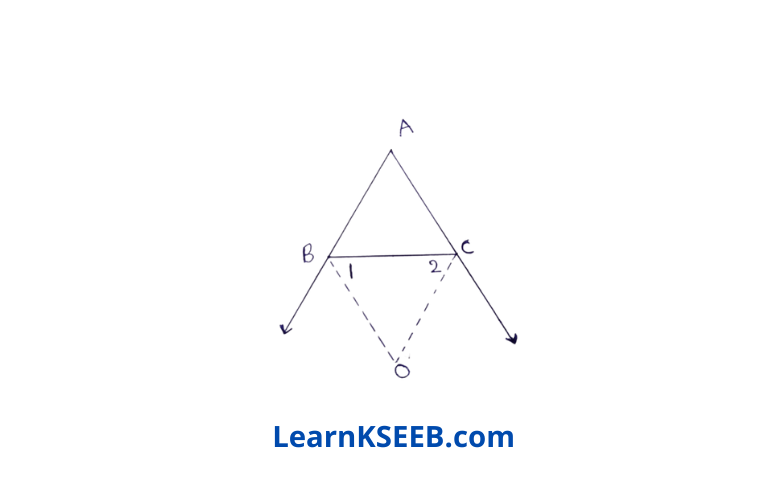\(\lfloor\mathrm{CBE}\)= 2\(\lfloor 1\)\(\lfloor\mathrm{ABC}\)+ 2\(\lfloor 1\) = 180°

=> 2\(\lfloor 1\) = 180°-\(\lfloor\mathrm{ABC}\)

=> \(\lfloor 1\) = 90°-1/2\(\lfloor\mathrm{ABC}\) ……………..(1)

Again, \(\lfloor\mathrm{ACB}\)& \(\lfloor\mathrm{BCD}\) form a linear pair.

\(\lfloor\mathrm{ACB}\) + \(\lfloor\mathrm{BCD}\) = 180°

As CO if the bisector of \(\lfloor\mathrm{BCD}\)

\(\lfloor\mathrm{BCD}\) = 2\(\lfloor 2\)

\(\lfloor\mathrm{ACB}\) + 2\(\lfloor 2\) = 180°

2\(\lfloor 2\) = 180°-\(\lfloor\mathrm{ACB}\)

\(\lfloor 2\) = 90°-1/2\(\lfloor\mathrm{ACB}\) ……………(2)

In ΔOBC, we have

\(\lfloor 1\) + \(\lfloor 2\) + \(\lfloor\mathrm{BOC}\) = 180° …………….(3)

from (1), (2) & (3) we have

90- 1/2\(\lfloor\mathrm{ABC}\) + 90-1/2\(\lfloor\mathrm{ACB}\) + \(\lfloor\mathrm{BOC}\) = 180° ……………….(4)

Now in AABC we have \(\lfloor A\)+\(\lfloor B\) + \(\lfloor C\)=180°

\(\lfloor B\)+ \(\lfloor C\)=180°-\(\lfloor A\) …………………(5)

from equations (4) & (5), we have

180 – 1/2(180°-\(\lfloor A\)) + \(\lfloor\mathrm{BOC}\) = 180°

=> \(\lfloor\mathrm{BOC}\) = 180-180 +1/2(180-\(\lfloor A\))

\(\lfloor\mathrm{BOC}\) = 1/2(180-\(\lfloor A\))

=> \(\lfloor\mathrm{BOC}\)=90-1/2\(\lfloor A\)

3. In figure, ABCD is a square & EF is parallel to diagonal BD & EM = FM. Prove that
1) DF = BE
2) AM bisects \(\lfloor\mathrm{BAD}\)

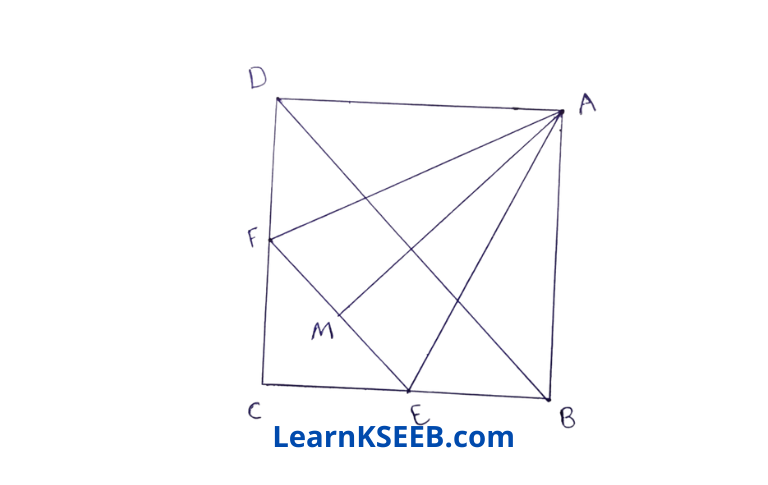
Solution:

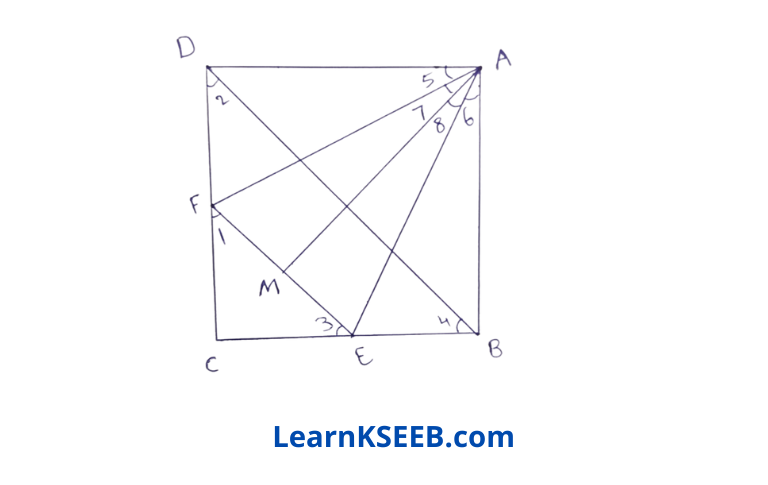
1) EF || BD

=> \(\lfloor 1\) = \(\lfloor 2\) [corresponding angles ]

\(\lfloor 3\) = \(\lfloor 4\)

but\(\lfloor 2\)= \(\lfloor 4\)

∴ \(\lfloor 3\) = \(\lfloor 1\)

=> FC = EC (sides opp. to equal angle)

CD – FC = CB – CE

=>  DF = BE

AD =AB

\(\lfloor D\) = \(\lfloor B\) = 90°

∴ ΔADF = ΔABE(by SAS rule)

=> AF=AE (C.P.C.T.)

\(\lfloor 5\) = \(\lfloor 6\)

2) In ΔAMF & ΔAME

AF = AE

AM = AM (common)

FM = EM (given)

ΔAMF = ΔAME (by SSS rule)

∴  \(\lfloor 7\)= \(\lfloor 8\) (by CPCT)

\(\lfloor 7\) + \(\lfloor 5\) = \(\lfloor 8\)+ \(\lfloor 6\)

=> \(\lfloor\mathrm{MAD}\) = \(\lfloor\mathrm{MAB}\)

=> AM bisects \(\lfloor\mathrm{BAD}\)

4. Show that the difference of any two sides of a triangle is less than the third side.

Solution:

Construction: Take BD = AB, join AD

Proof: In ΔABD

AB = BD

=> \(\lfloor 1\) = \(\lfloor 3\) & \(\lfloor 4\)>\(\lfloor 1\)

=> \(\lfloor 4\) > \(\lfloor 3\)

In ΔADC

\(\lfloor 3\)>\(\lfloor 2\)

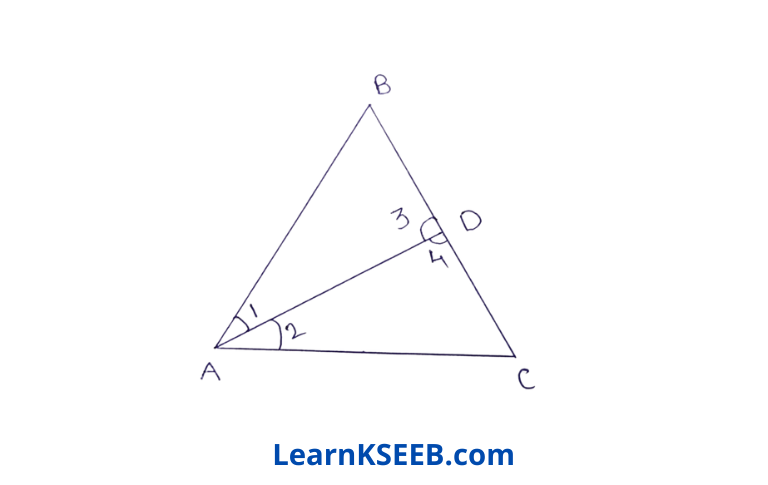
∴ \(\lfloor 4\)>\(\lfloor 3\)>\(\lfloor 2\)

=> \(\lfloor 4\)>\(\lfloor 2\)

=> AC > DC

=> AC > BC – BD (BC = BD + CD)

AC> BC – AB  (BD = AB)

BC – AB < AC || ly,  AC – AB < BC

& BC – AC < AB

5. In the figure, BL ⊥ AC, MC⊥LN, AL= CN & BL = CM, prove that ΔABC ≅ ΔNML

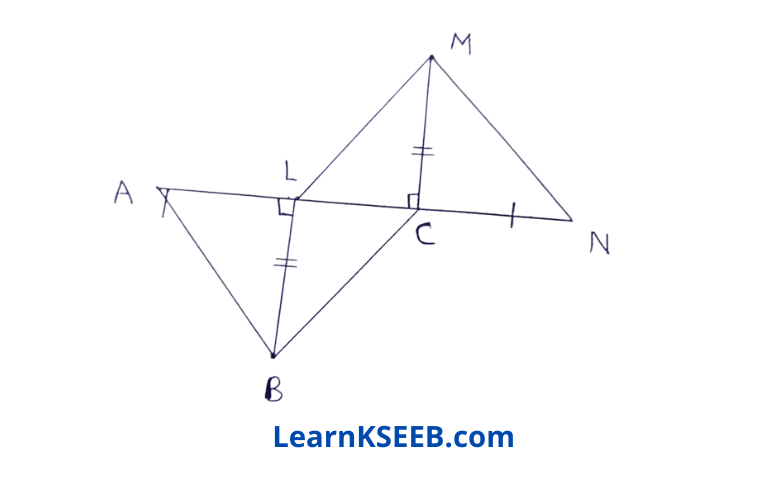
Solution: AL = CN (given)

AL + LC = CN + LC

ie AC = LN …………..(1)

In ΔALB & ΔNCM

AL = CN (given)

\(\lfloor\mathrm{ALB}\) = \(\lfloor\mathrm{NCM}\) = 90°

BL = CM (given)

∴ ΔALB & ΔNCM (by SAS rule)

=> AB=NM(CPCT) ……………(2)

In ΔBLC & ΔMCL

BL = MC (given)

\(\lfloor\mathrm{BLC}\)= \(\lfloor\mathrm{MCL}\) = 90°

LC = CL ……………(3)

∴ ΔBLC = ΔMCL (by SAS rule)

=> BC = ML(CPCT)

In ΔABC & ΔNML

AB=NM (proved in (1))

AC = NL (proved in (2))

BC = ML (proved in (3)

∴  ΔABC ≅ ΔNML (by SSS rule)

KSEEB Solutions For Class 9 Maths Chapter 4 Linear Equations in Two Variables

Linear Equations in Two Variables Points to Remember

• The standard form of a linear equation in two variables x & y is ax+ by+c = 0, where a, b & c are real numbers & a ≠ 0, b ≠ 0

Solution of a linear equation

• Infinitely many solutions of a linear equation in two variables can be obtained.
• To find a solution of a linear equation in two variables easily, we put X- 0 in the equation & find the corresponding value of y, we can also put y = 0, & find the corresponding value of x
• Every point on the graph of a linear equation in two variables represents a solution of the linear equation. Also, every solution of the linear equation represents a point on the graph of the linear equation.

Class 9 Social Science

Class 9 Science

Class 9 Maths

 

Graph of a linear equation in 2 variables

• We find two convenient solutions of a linear equa¬tion in two variables & plot them on a graph paper. Then we join these points by a ruler to get the line which represents the graph of the given linear equation in two variables.
  Equations of lines parallel to the x- axis & y- axis.
•  x= a represents a straight line parallel to y – axis at a distance of | a | units from 0 to be right or left of 0 according as a is +ve or -ve. Similarly y= a represents a straight line parallel to x – axis at a distance of | a | units from 0 above or below 0. According as a is +ve or -ve.
•  The equation of the form y= mx represents a line passing through the origin.

Read and Learn More KSEEB Solutions for Class 9 Maths 

Linear Equations in Two Variables Exercise 4.1

1.  The cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement.

Solution: Let the cost of a notebook be  x & the cost of a pen by  y

Then, according to the given condition of the question,

x=2y

=> x-2y=0

This is the required linear equation in two variables x&y.

2. Express the following linear equations in the form ax+ by+c= 0 & indicate the values of a, b & c in each case.
1) 2x+3y = 9.35
2)\(2 x+3 y=9.3 \overline{5}\)
3) -2x+3y=6
4) x=3y
5)2x = -5y
6) 3x+ 2 = 0
7) y- 2 = 0
8) 5 = 2x

Solution: 1) \(2 x+3 y=9.3 \overline{5}\)
\(\begin{gathered}
\Rightarrow \quad 2 x+3 y-9.3 \overline{5}=0 \\
a=2, \quad b=3, \quad c=9.3 \overline{5}
\end{gathered}\)

2) \(x-\frac{y}{5}-10=0\)
\(a=1 \quad b=\frac{-1}{5} \quad c=-10\)

3) \(-2 x+3 y=6\)
\(\begin{aligned}
& \Rightarrow \quad-2 x+3 y-6=0 \\
& a=-2 \quad b=3 \quad c=-6
\end{aligned}\)

4) \(x=3 \mathrm{y}\)
\(\begin{aligned}
& \Rightarrow \quad x-3 y=0 \\
& a=1 \quad b=-3 \quad \mathrm{c}=0
\end{aligned}\)

5) \(2 x=-5 y\)
\(\Rightarrow \quad 2 x+5 y=0\)
\(a=2 \quad b=5 \quad c=0\)

6) \(3 x+2=0\)
\(\begin{aligned}
& \Rightarrow \quad 3 x+o y+2=0 \\
& a=3 \quad b=0 \quad c=2 \\
&
\end{aligned}\)

7) \(y-2=0\)
\(\begin{aligned}
& \Rightarrow \quad 0 x+y-2=0 \\
& \begin{array}{lll}
a=0 & b=1 & c=-2
\end{array} \\
&
\end{aligned}\)

8) \(5=2 x\)
\(\begin{aligned}
& \Rightarrow \quad-2 x+o y+5=0 \\
& a=-2 \quad b=0 \quad c=5
\end{aligned}\)

KSEEB Class 9 Maths Chapter 4 Linear Equations in Two Variables Exercises 

Linear Equations in Two Variables Exercise 4.2

1. Which one of the following options is true & why? y = 3x+5 has
1) a unique solution
2) only two solutions,
3) infinitely many solutions

Solution: The true option is (3)

y = 3 x+ 5 has infinitely many solutions.

Reason: For every value of x, there is a corresponding value of y & vice versa

2. Write four solutions for each of the following equations.

1) 2x+y=7

Solution:

\(\begin{aligned}
& 2 x+y=7 \\
& \Rightarrow \quad y=7-2 x \\
& \text { when } \quad x=0, \quad y=7-2(0)=7-0=7
\end{aligned}\) \(\begin{array}{ll}
x=1, & y=7-2(1)=7-2=5 \\
x=-1, & y=7-2(-1)=7+2=9 \\
x=2, & y=7-2(2)=7-4=3
\end{array}\)

four solutions are (0,7) (1, 5) (-1, 9) & (2,3)

2) πx+y=9

y=9-πx

When

\(\begin{aligned}
& x=0, \quad y=9-\pi(0)=9-0=9 \\
& x=1, \quad y=9-\pi(1)=9-\pi \\
& x=-10, y=9-\pi(-1)=9+\pi \\
& x=2, \quad y=9-\pi(2)=9-2 \pi
\end{aligned}\)

four solutions are (0,9), (1,9-π ),

(-1,9+π), (2, 9-2π)

3) x=4y

Solution: x=4y

when

\(\begin{aligned}
& y=0, \quad x=4(0)=0 \\
& y=1, \quad x=4(1)=4 \\
& y=-1, \quad x=4(-1)=-4 \\
& y=2, \quad x=4(2)=8 \\
&
\end{aligned}\)

∴ four solutions are (0, 0), (4,1) (-4, -1) & (8,2)

3.  Check which of the following are solutions of the equation x-2y=4 & which are not

1) (0,2)

Solution: Consider the given equation: x-2y= 4……….(1)

i) (0,2)

Put x=0, y= 2 in (1) we get

x-2y=4

0 – 2(2) = 4

-4 ≠4

∴ (0,2) is not a solution of (1)

2) (2,0)

Solution: (2, 0)

put x=2, y=0 in(1) we get

x—2y=4

2-2(0) = 4

2-0 = 4

2≠4

∴ (2,0) is not a solution of (1)

3) (4,0)

Solution: (4,0)

put x = 4, y= 0 in(1) we get

x-2y=4

4 – 2 (0) = 4

4 = 4

∴ (4,0) is a solution of (1)

4) \((\sqrt{2}, 4 \sqrt{2})\)

Solution:

\((\sqrt{2}, 4 \sqrt{2})\) \(\begin{aligned}
& \text { put } x=\sqrt{2}, \quad y=4 \sqrt{2} \text { in (1) } \\
& x-2 y=4 \\
& \sqrt{2}-2(4 \sqrt{2}))=4 \\
& \sqrt{2}-8 \sqrt{2}=4 \\
& -7 \sqrt{2} \neq 4
\end{aligned}\)

∴ \((\sqrt{2}, 4 \sqrt{2})\) is not a solution of (1)

5) (1, 1)

Solution:

(1, 1)

\(\begin{aligned}
& \text { put } x=1, \quad y=1 \text { in }(1) \\
& x-2 y=4 \\
& 1-2(1)=4 \\
& 1-2=4 \\
& -1 \neq 4
\end{aligned}\)

∴ (1,1) is not a solution of (1)

KSEEB Maths Chapter 4 Linear Equations In Two Variables Answers 

4.  Find the value of k, if x= 2, y= 1 is a solution of the equation 2x+ 3y= k

Solution : If x=2, y= 1 is a solution of the equation 2x+ 3y=k. Then these values will satisfy the equation.

So putting x= 2 & y= 1 in the equation, we get

2(2) + 3(1) = k

=> 4 + 3-k

=> 7 = k

Linear Equations in Two Variables Exercise 4.3

1. Draw the graph of each of the following linear equations in two variables
1) x+y=4
Solution; x + y =4
y= 4-x

2) x-y = 2
Solution: x – y = 2
=> y = x – 2

3) y = 3x

4) 3 = 2x + y
Solution: 3 = 2x + y
=> y = 3 – 2x

 

2. Give the equations of two lines passing through (2,14). How many more such lines are there and why?

Solution: The equations of two lines passing through (2, 14) can be taken as x+y- 16 & 7x-y-0

There are infinitely many such lines because through a point an infinite number of lines can be drawn.

3. If the point (3,4) lies on the graph of the equation 3y= ax+7, find the value of a.

Solution: If the point (3,4) lies on the graph of the equation 3y= ax+ 7, then

=> 3(4) = a(3) + 7

=> 12 = 3a + 7

=> 12- 7 = 3a

=> 5 = 3a

=> 3a = 5

=> a =\(5 / 3\)

KSEEB Solutions Class 9 Linear Equations In Two Variables Problems 

4. The taxi fare in a city is as follows: For the 1st kilometer, the fare is ₹8 & for the subsequent distance. It is ₹5 per km. Taking the distance covered as x km & total fare as y, write a linear equation for this information & draw its graph.

Solution: Total distance covered = x km

Total fare = ₹y

Fare for the 1 st km = ₹8

Subsequent distance = (x-1) km

Fare for the subsequent distance = ₹ 5(x- 1)

According to the question

y= 8 + 5(x— 1)

=> y=8 + 5x-5

=> y= 5x+3

5. From the choices given below choose the equation whose graphs are given in fig (1) & fig(2)
For fig (1) For fig (2)
1) y = x 
2)x+y=0 
3) y=2x 
4) 2 + 2y =1 x

For fig (2)
1) y= x+2
2)y=x-2
3) y= x+2
4) x+2y=6

Solution: For fig (1)

The correct equation is (2) x+ y = 0

For fig (2)

The correct equation is (3) y=-x+2

6. If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables & draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance traveled by the body is (1) 2 units (2) 0 units.

Solution: Let the work done by the constant force be y units & the distance traveled by the body be x units.

constant force = 5 units.

W.K.T.

work done = Force x Displacement

=> y= 5x

1) Let A —>(2,0) through A, draw a line parallel to OY to intersect the graph of the equation

y = 5 x at B. Through B draw a line parallel to OX to intersect OY at C. Then, C —> (0,10)

work done when the distance travelled by the body is 2 units =10 units.

2) Clearly y = 0 when x = 0, so, the work done when the distance travelled by the body is 0 unit is 0 units.

7. Yamini & Fatima two students of class IX of a school together contributed ? 100 towards the Prime minister’s Relief Fund to help the earthquake victims. Write a linear equation which satisfied this data. (You may take their contributions as ₹x, ₹ y) Draw the graph of the same.

Solution:

Let the contributions of yamini & Fatima be ₹ x & ₹ y respectively.

Then according to the question

x+y=100

=> y =100-x

8. In countries like USA & Canada temperature is measured in Fahrenheit, where as in countries like India, it is measured in Celsius. Here is a linear equation Fahrenheit to Celsius:
\(\mathrm{F}=\left(\frac{9}{5}\right) \mathrm{C}+32\)
1) Draw the graph of the linear equation above using Celsius for x- axis & Fahrenheit for y- axis.
2) If the temperature is 30°C, what is the temperature in Fahrenheit?
3) If the temperature is 95°F, what is the tem¬perature in Celsius?
4) If the temperature is 0°C, what is the tem-perature in Fahrenheit & if the temperature is 0°F, what is the temperature in Celsius?
5) Is there a temperature which is numerically the same in both Fahrenheit & Celsius? If yes, find it.

Solution:

\(\mathrm{F}=\frac{9}{5} \mathrm{C}+32\)

2) When C=30

Then

\(\mathrm{F}=\frac{9}{5} \mathrm{C}+32\) \(\mathrm{}=\frac{9}{5} \mathrm{x30}+32\)

=9×6+32

= 54 + 32

F = 86

∴ Required temperature is 86°F

3) When F = 95° then \(\mathrm{F}=\frac{9}{5} \mathrm{C}+32\)

=> 95 = 9/5 C+32

95-32 = 9/5C

63 = 9/5C

(63 x 5)/9=C

C=35

∴ Required temperature =35°C

4.)  When C = 0

Then F = 9/5C + 32

=(9/5) x 0 +32

= 32°F

When F=0, then

\(\begin{aligned}
& \mathrm{F}=\frac{9}{5} \mathrm{C}+32 \\
\Rightarrow & 0=\frac{9}{5} C+32 \\
\Rightarrow & 0-32=\frac{9}{5} C \\
\Rightarrow & \frac{-32 \times 5}{9}=C \\
\Rightarrow & C=\frac{-160}{0}
\end{aligned}\)

5) Let the temperature be x numerically then

\(\begin{aligned}
& \mathrm{F}=\frac{9}{5} \mathrm{C}+32 \\
& \Rightarrow \quad x=\frac{9}{5} x+32 \\
& x-\frac{9}{5} x=32 \\
& x\left(1-\frac{9}{5}\right)=32 \\
& x\left(\frac{5-9}{5}\right)=32
\end{aligned}\) \(\begin{aligned}
& x\left(\frac{-4}{5}\right)=32 \\
& x=\frac{32 \times 5}{-4} \\
& \Rightarrow \quad x=-40
\end{aligned}\)

∴ Numerical value of required temperature is – 40°

Class 9 Maths KSEEB Chapter 4 Linear Equations In Two Variables Examples 

Linear Equations in Two Variables Exercise 4.4

1. Give geometric representations of y= 3 as an equation.

1) in one variable

Solution: In one variable

The representation of y = 3 on the number line is as shown below.

2) in two variable

Solution: In two variables

y=3

=>0 x X+1 x Y =3

2. Give the geometric representations of 2x+ 9 = 0 as an equation.

1) in one variable

Solution: In one variable

2x+9 = 0

=> 2x= -9

=>x=(-9/2)

=>x=-4.5

2) in one variables

Solution: In two variables

2x + 9=0

=> 2x + 0 x y =0

ie   x=-9/2,    y=0

& x=-9/2,     y=0

Additional Problems

1. The standard form of a linear equation in two variables x& y is

1. ax+ by + c= 0
2. ax = c
3. by=c
4. x+y+c=0

Solution: 1) ax+ by + c= 0

2. The equation 3x+4y = 12 has

1. a unique solution
2. no solution
3. two solutions
4. Infinitely many solutions

Solution: 4) Infinitely many solutions

3. How many lines pass through O?

1. 1
2. 2
3. 4
4. Infinitely many

Solution: 4) Infinitely many

4. The force applied on a body is directly proportional to the acceleration produced in the body. Express this in the form of a linear equation in two variables.

1. y= x
2. y+x=0
3. y=kx
4. none of these

Solution: 3) y= kx

5. Where does the line 2x+ 3 y=6 cut the x-axis?

1. at (3,0)
2. at (0,3)
3. at (0,0)
4. at (3,3)

Solution: 1) at (3,0)

6. Which of the following is a solution of the equation x-y= -1?

1. (0,1)
2. (1, 0)
3. (1,1)
4. (2,1)

Solution: 1) (0,1)

7. x= 4 is a line

1. parallel to y= -4
2. parallel to x- axis
3. passing through the origin
4. parallel to x= -4

Solution: 4) parallel to x= -4

8. The point of intersection of the lines intersecting the equation 3x = 2y+1 & 2x=3y-1 is

1. (2,3)
2. (3,2)
3. (1,1)
4. (0, 0)

Solution : 3) (1,1)

KSEEB Chapter 4 Linear Equations in Two Variables Solved Questions 

9. The equation of a line parallel to y-axis is

1. x=l
2. x+ y= 0
3. y=0
4. y= 1

Solution: 1) x= 1

10. If x= 3 & y= -2 is a solution of the equation 4px- 3y= 12, then the value of p is

1.  0
2. 1/2
3.  2
4. 3

Solution: 2) 1/2

Solve

1. Plot the following points in a rectangular co-ordinates system. In which quadrant do they lie?
i) (4,5)
ii) (4, -5)
iii) (-7, 5)
iv)(9,-3)

Solution:

i) I quadrant

ii) IV quadrant

iii) II quadrant

iv) IV quadrant

2. Plot the points (-1,0), (1,0), (1,1), (0,2) (-1, 1) & join them in order. What figure do you get?
Solution:

The figure we got is pentagon.

3. In which quadrant will the point lie, if
1) The ordinate is 3 & the abscissa is -4?
2) The abscissa is -5 & the ordinate is – 3?
3) The ordinate is 4 & the abscissa is 5
4) The ordinate is 4 & The abscissa is – 4?

Solution:

1) The point whose ordinate is 3 & The abscissa is -4 lies in II Quadrant.

2) The point whose abscissa is -5 & The ordi¬nate is -3 lies in III Quadrant.

3) The point whose ordinate is 4 & The abscissa is 5 lies in I Quadrant.

4) The point whose ordinate is 4 & The abscissa is -4 lies in II Quadrant.

4. Draw the quadrilateral whose vertices are
1) (1,1), (2,4), (8, 4) & (10,1)
Solution:

2)(-2,2), (-4,2), (-6, -2) & (-4, -6)
Name the type of quadrilateral so formed in each case.
Solution:

The quadrilateral so formed is a trapezium .

5. Express the linear equation 7 = 2jrin the form ax+ by+ c= 0 & also write the values of a, b & c.

Solution:

7 = 2x

=> 2x-7 = 0

=> 2x+ oy-1 = 0

comparing with ax+by+c= 0

we get a = 2, b = 0, c = -7

KSEEB Maths Solutions Chapter 4 Practical Problems 

6. Find at least 3 solutions for the following lin¬ear equation in two variables 2x+5y= 13

Solution:

2x+5y= 13

=> 5y=13-2x

\(y=\frac{13-2 x}{5}\)

put x=0,

\(y=\frac{13-2(0)}{5}=\frac{13}{5}\)

put x=1,

\(y=\frac{13-2(1)}{5}=\frac{13-2}{5}=\frac{11}{5}\)

put x=-1,

\(y=\frac{13-2(-1)}{5}=\frac{13+2}{5}=\frac{15}{5}=3\)

∴ The three solutions are (0,13/5), (1,11/5)

(-1,3)

7. If x = -2, y = 6 is a solution of equation 3ax+ 2by = 6, then find the value of b from 2(a-1) + 2 (3b- 4) = 4

Solution:

If x= -2, y= 6 is a solution of  equation

3ax+2by= 6, then

3a(-2) + 2b(6) = 6

-6 a +12b = 6

÷ 6     -3+2b=1…………….. (1)

also    2(a-1) + 2(3b-4) = 4

=> 2a-2 + 6b-8 = 4

=> 2a + 6b-10-4 = 0

=> 2a + 6b-14 = 0

=> 2a + 6b = 14

÷ 2        => a + 3b = 7……………..(2)

adding Eqn (1) & (2) we get

\(\begin{array}{r}
-a+2 b=1 \\
a+3 b=7 \\
\hline 5 b=8 \\
b=8 / 5
\end{array}\)

putting b = 8/5 in (1) we get

\(\begin{gathered}
-a+2 \times \frac{8}{5}=1 \\
-a+\frac{16}{5}=1 \\
-a=1-\frac{16}{5} \\
=\frac{5-16}{5} \\
-a=\frac{-11}{5}
\end{gathered}\)

∴ a=11/5

Hence a=11/5 & b=8/5

8. Find the coordinates of the points where the line representing the equation \(\frac{x}{4}=1-\frac{y}{6}\) cuts the x-axis & the y-axis

Solution:

\(\frac{x}{4}=1-\frac{y}{6}\)

For intersection with x-axis, put y= 0

∴ \(\frac{x}{4}=1-\frac{0}{6}\)

=> x/4=1

=> x=4

∴ The point of intersection with x – axis is (4,0) For intersection with y – axis, put x=0, then

\(\frac{0}{4}=1-\frac{y}{6}\)

=> 1-y/6=0

=> y/6=1

=> y=6

Hence the point of intersection with y – axis is (0,6).

9. Determine the point on the graph of equation 2x+5y= 20 where x- co-ordinate is 5/2 times its ordinate.

Solution:

2x+5y= 20

x – coordinate is 5/2 times its ordinate

ie  x=5/2y

∴ \(2\left(\frac{5}{2} y\right)+5 y=20\)

5y+5y=10

10y=20

y=20/10=2

∴ \(x=\frac{5}{2} \times 2=5\)

Hence the required point is (5,2)

KSEEB Solutions for 9th Standard Maths Chapter 4 Linear Equations In Two Variables 

10. Plot the graph of equations using the same pair of axes;
1) y=2x+3
Solution:

2) y=2x-3/2
Solution:

3) 2 x- y = 0 are these lines parallel?

Solution:

2x-y=0

=> y=2x

11. Shade the triangle formed by the graph of 2x-y=4, x+y= 2 & the axis. Write the coordinates of the vertices of the triangle.

Solution:

2x-y=4

=> y= 2x-4

x+y=2
=> y=2-x

From the graph, we see that the co-ordinates of the verti¬ces of the triangle are (2,0), (0,2) & (0, -4)
The triangle has been shaded.

12. Solve for: \(x: 3 x-12+\frac{3}{7} x=2(x-1)\) What type of graph is it in two dimensions?

Solution:

\(3 x-12+\frac{3}{7} x=2(x-1)\) \(\begin{aligned}
& 3 x+\frac{3}{7} x-2 x=-2+12 \\
& \frac{3 x}{7}+x=10 \\
& \frac{3 x+7 x}{7}=10 \\
& 10 x=70
\end{aligned}\)

x=70/10

x=7

The graph of this equation is a line parallel to y-axis at a distance of 7 units to the right of origin O.

13. Given the geometrical representation of 2y+ 7 as equation in
1) one variable

Solution:

one variable

2y+7 = 0

=> 2y= -7

y=-7/2

2)  two variables

Solution:

In two variables

2y+7=0

=> 0 . x+2y+ 7 = 0

If x=0, y=-7/2

14. 1f the point (3,4) lies on the graph of the equation 3 y = ax+ 7, find the value of a.

Solution:

Since every point on the graph of a linear equation is a solution of the equation.

x = 3 & y= 4 is a solution of the equation 3 y= ax+1

3×4 = ax3 + 7

12 = 3a+7

3a=5

=> a =5/3

KSEEB Maths Chapter 4 Linear Equations In Two Variables Free Solutions 

15. Give the equations of two lines passing through (2,14). How many more such lines are there & why?

Solution:

We observe that x= 2 & y= 14 is a solution of each of the equations.

1) 1x- y= 0

2) 3x-y+8 = 0

3) x-y+12 = 0 etc.

We know that passing through a given point infinitely many lines can be drawn. So, there are infinitely many lines passing through (2,14)

16. Draw the graphs of 2x+y=6 & 2x- y+ 2 = 0 shade the region bounded by these lines & x – axis. Find the area of the shaded region.

Solution:

We have

2 x+y=6  &  2x-y+2 = 0

2x+ y=6

=> y = 6-2x

2x- y+2 = 0

=> 2x+2-y

=> y= 2x+ 2

Area of the shaded region = Area of Δ ABC

= 1/2x Base x height

=1/2xBCxAD

=1/2x4x=8

Area of the shaded region = 8 sq. units

17. Find out which of the following equations have x = 2, y= 1 as a solution.
1) 2x+5y=9
2) 5x+3y=14
3) 2x+3y= 7

Solution:

1) 2x+ 5y = 9

put x= 2 & y = 1

LHS = 2 (2) +5(1)

= 4+5

= 9

= RHS,

∴  x=2 & y = 1 is a solution of the given equation

2) 5x+3y-14

LHS = 5x+3y

= 5 (2) + 3 (1)

= 10 + 3

= 13

≠14

≠ RHS

∴ x=2 S& y= 1 is not a solution of the given equation.

3) 2x+3y=7

LHS = 2x+3y=7

= 2 (2)+ 3(1)

= 4 + 3

= 7

= RHS

x=2 & y= 1 is a solution of the given equation.

KSEEB Solutions For Class 9 Maths Chapter 3 Coordinate Geometry Points to Remember

• The system by which we can describe the position of a point in a plane is called cartesian system.
•  In cartesian system, there are two perpendicular lines (one horizontal & other vertical) are required to locate the position of a point or an object.
•  The plane is called the cartesian or coordinate plane & the lines.
• The horizontal line xx’ is called the x-axis & vertical line yy’ is called the y-axis.

 

• The point where xx’ & yy’ cross is called the origin & is denoted by O.
• The co-ordinate axis divide the plane into four parts called quadrants (one-fourth part) numbered I, II, III
  & IV

• x – co-ordinate (or absicca)= perpendicular distance of a point from y-axis.
• y co-ordinate (or ordinates) = perpendicular distance of a point from x-axis.
• If abscissa of a point is x & ordinate is y,then the coordinates of a point are (x, y)
• The abscissa of every point on y-axis is zero (0,y)
• The ordinate of every point on x-axis is zero (x, 0)
• x-axis & y-axis intersect at origin, represented by O and its co-ordinate are (0,0)

Read and Learn More KSEEB Solutions for Class 9 Maths 

Class 9 Social Science

Class 9 Science

Class 9 Maths

 

Plotting a point in the plane if its co-ordinates are given.

Let P→ (x, y), we start from o & count x- units along OX or OX’ according as x is positive or negative & reach a point M. From M, we count y – units along OY or OY’ accordind to y is positive or negative & reach P.

KSEEB Class 9 Maths Chapter 3 Coordinate Geometry Exercises 

Note: If x ≠ y, then the position of (x, y) in the cartesian plane is different from the position of (y x). This shows that the order of x&y is important in (x, y). thus (x, y) is an ordered pair. Obviously, (x, y) ≠ (y, x), if x≠y&(x,y) = (y, x),if x=y.

Coordinate Geometry Exercise 3.1

1. How will you describe the position of a table on your study table to another person?
Solution: Consider the lamp as a point & table as a plane. Choose any two perpendicular edges of the table. Measure the distance of the lamp from the longer edge, suppose it is 25cm. Again measure the distance of the lamp from the shorter edge & suppose it is 30cm, you can write the position of the lamp as (30,25) or (25, 30) depending on the order you fix.

2. (Street plan)
A city has two main roads which cross each other at the centre of the city. These two roads are along the North-south direction & East – west direction. All the other streets of the city run parallel to these roads & are 200m apart. There are about 5 streets in each di¬rection using 1 cm = 200m draw a model of the city on your note book. Represent the roads/streets by single lines.
There are many cross-streets in your model. A particular cross-street is made by two streets, one running in the north-south direction & another in street is referred to in the following manner. If the 2nd street running in the north-south direction & 5th in the east-west direction meet at some crossing, then we will call this cross-street (2,5). Using this convention, find (1) How many cross-streets can be referred to as (4, 3)? (2) How many cross-streets can be referred to as (4, 3)?
Solution:

Both the cross-streets are marked in the above figure. It can be observed that there is only one cross-street which can be referred as (4,3) & again only one which can be referred as (3,4)

KSEEB Maths Chapter 3 Coordinate Geometry Answers 

Coordinate Geometry Exercise 3.2

1. Write the answer of each of the following questions.

1) What is the name of horizontal & the vertical lines drawn to determine the position of any point in the cartesian plane?
Solution: The x-axis & the y- axis.

2)What is the name of each part of the plane formed by these two lines?
Solution: Quadrants

3)Write the name of the point where these two lines intersect.
Solution: The origin.

2. See figure & write the following
1) The co-ordinates of B
2) The co-ordinates of C
3) The point identified by the coordinates
(-3,-5)
4) The point identified by the co-ordinate
(2, -4)
5) The abscissa of point D.
6) The ordinate of point H.
7) The co-ordinates of point L.
8) The co-ordinate of point M.

1) B → (-5, 2)
2)C→(5,-5)
3)E
4)G
5) 6
6) -3
7)L → (0,5)
8) M →(-3,0)

Coordinate Geometry Exercise 3.3

1. In which Quadrant or on which axis do each of the points (-2,4), (3,1), (-1,0) (1,2) & (-3, -5) lie? Verify your answer by locating them on the cartesian plane.

Solution: The point (-2,4) lies in the II Quadrant.

Point (3, -1) lies in the IV Quadrant.

The point (-1,0) lies on the negative x-axis.

Point (1,2) lies in the I Quadrant

The point (-3, -5) lies in the III Quadrant

 

2. Plot the points (x,y) given in the following table on the plane, choosing suitable units of distance on the axis.

Solution:

KSEEB Solutions Class 9 Coordinate Geometry Problems 

Additional Problems

1.  A point lies on x-axis at a distance of 9 units from y-axis. What are its coordinates? What will be its coordinates if it lies on y-axis at a distance of 9 units from x-axis.

Solution: (0,9) ,   (0,-9)

2. In figure given below, Δ AOB with coordinates of A & O as (4, 0) & (0, 0) find the coordinates of B.

Solution:

In Right Δ AOB

\(\begin{aligned}
& \mathrm{OA}^2+\mathrm{OB}^2=\mathrm{AB}^2 \\
& 4^2+\mathrm{OB}^2=5^2 \\
& \mathrm{OB}^2=5^2-4^2 \\
&=25-16=9 \\
& \mathrm{OB}=\sqrt{9}=3 \\
& \Rightarrow \quad \mathrm{B} \rightarrow(0,3)
\end{aligned}\)

3. In figure, Δ ABC & Δ ABD are equilateral Δles. Find the coordinates of points C & D.

 

 

Solution:

Δ ABC is an equilateral Triangle

∴ AC = BC = AB

=> BC = AB

=> BC = 2a

In right triangle COB,

\(\begin{aligned}
& \mathrm{OB}^2+\mathrm{OC}^2=\mathrm{BC}^2 \\
\Rightarrow & a^2+\mathrm{OC}^2=(2 a)^2 \\
\Rightarrow & \mathrm{OC}^2=4 a^2-a^2 \\
\Rightarrow & \mathrm{OC}^2=3 a^2 \\
\Rightarrow & \mathrm{OC}=\sqrt{3 a^2} \\
\Rightarrow & \mathrm{OC}=\sqrt{3} a
\end{aligned}\)

∴\(\mathrm{C} \rightarrow(0, \sqrt{3} a)\)

ΙΙ \(\mathrm{D} \rightarrow(0,-\sqrt{3} a)\)

4. Find the coordinates of a point
1) Whose ordinate is 6 & lies on y-axis.
2) Whose abscissa is -3 & lies on x-axis

Solution: 1)(0,6)  2)(-3,0)

5. Plot the points A (3,0), B(3, 3) & C(0, 3) in a cartesian plane. Join OA, AB, BC & CO. Name the figure so formed & write its one property.

Class 9 Maths KSEEB Chapter 3 Coordinate Geometry Examples 

6. Which of the following points lie on x-axis which on y-axis?
A(0,2), B(5,6), c(-3,0), D(0, -3), E(0,4), F(6,0), G(3,0)

Solution: The points C, F & G lie on x-axis.

The points A, D & E lie on y-axis.

7. The following table gives the number of pairs of shoes & their corresponding price. Plot there as ordered pairs & join them. What type of graph do you get?

Solution:

8. If (x+ 2,4) = (5, y-2), then what will be the co-ordinate of (x,y)?

Solution: Given: (x+2,4) = (5,y-2)

\(\begin{aligned}
& \Rightarrow \quad x+2=5 \quad \& \quad 4=y-2 \\
& \Rightarrow \quad x=5-2 \quad \& \quad 4+2=y \\
& \Rightarrow \quad x=3 \quad \& \quad y=6
\end{aligned}\)

∴ co-ordinates of (x,y) = (3,6)

KSEEB Chapter 3 Coordinate Geometry Solved Questions 

9. Calculate the area of Δle formed by joining the
points (4,0), (0,0) & (0,4)

Solution:

\(\begin{aligned}
& \mathrm{AB}=\sqrt{(0-0)^2+(4-0)^2}=\sqrt{0+16}=\sqrt{16}=4 \\
& \mathrm{BC}=\sqrt{(0-4)^2+(0-0)^2}=\sqrt{16+0}=4
\end{aligned}\)

\(\text { Area of } \Delta^{le}=\frac{1}{2} \times b \times h\) \(=\frac{1}{2} \times 4 \times 4=8 \text { sq. units }\)

10. Express the equaion 2x+ y-4 = 0 in the form of y= mx+ c.

Solution: Given equation 2x+y-4 = 0

y=-2x+4

11.  Find the point where line 3x + 6y – 4 = 0 intrersect the x- axis.

Solution: Given equation, 3x+6y-4=0

∴ Line intersect the x- axis

∴ y=o

3x+6x(0)-4 = 0

=> 3x-4 = 0

\(x=4 / 3\)

So, the point where line intersect the x-axis

\(\left(\frac{4}{3}, 0\right)\)

KSEEB Solutions For Class 9 Maths Chapter 2 Polynomials Points to Remember

• The algebraic expression in which variables involved have only non-negative integral exponent is called polynomial. A polynomial p(a) in one variable x is an algebraic expression in a of the form
  \(\mathrm{p}(x)=\)  \(\begin{gathered}
  a_n x^n+a_{n-1} x^{n-1}+a_{n-2} x^{n-2}+……… \\
  +a_2 x^2+a_1 x+a_0
  \end{gathered}\)
  where \(a_0, a_1, a_2 \ldots \ldots \ldots \ldots a_n\)are constant &\(a_n \neq 0, a_0, a_1, a_2\) are respectively the coefficients of \(x^0, x^1, x^2\)……\(x^n\) & n is called the
  degree of the polynomial.
• A polynomial of degree zero is called a constant polynomial
  Ex: 4, \(\frac{-7}{5}, \frac{3}{4}\)are constant polynomials.
• A polynomial having all coefficients zero is called a zero polynomial. Also, the constant polynomial is called the zero polynomial & the degree of the zero polynomial is not defined.
• Highest power of variable in a polynomial is called the degree of polynomial.
• In polynomial of one variable, the highest power of the variable is called the degree of the polynomialEx: 1) \(4 x^7-5 x^3-4 x^2+3 x-6\) is a polynomial in x of degree 7.
  2) \(\sqrt{5} x^2+5 \sqrt{5} x+7\) is a polynomial in x of degree x.
• In polynomial of more than one variable, the sum of the powers of the variable in each term is taken up & the highest sum so obtained is called the degree of the polynomial.
  Ex: \(6 y^3-5 x^2 y^2+4 x^2 y-3 y+9\) is a polynomial in x & y of degree 4.
• A polynomial of one non-zero term is called a monomial.
  Ex:\(3 x,-6 x^2, 7 x^3\) etc
• A polynomial of two non-zero terms is called a binomial.
  Ex:\(6 x^2+12, \quad 6 x^2+6 \sqrt{5} x\)
• A polynomial of three, non-zero terms is called a trinomial.
  Ex:\(\left(y^2+2 y+6\right),\left(4 x^2+5 \sqrt{3} x+\sqrt{5}\right)\)
• A polynomial of degree 1 is called a linear polynomial, It is expressed in the form of ax+b, where a & b are real constants & \(a \neq 0\).
  Ex:\(3 x+6\) is a linear polynomial in A.
• A polynomial of degree 2 is called a quadratic polynomial. It is expressed in the form of \(a x^2+b x+c\) where a, b & c are real constant &\(a \neq 0\).
  Ex:\(\frac{7}{5} y^2+3 y-2\)
• A Polynomial of degree 3 is called a cubic polyno-mial. It is expressed in the form \(a x^3+b x^2+c x+d\), where a, b, c & d are real constant & \(a \neq 0\)
• Zeroes of a polynomial p(a) is a number c, such that p(c) = 0
  – ‘O’ may be a zero of a polynomial
  – Every linear po lynomial in one variable has a unique zero.
  – A non-zero constant po lynomial has no zero.
  – Every real number is a zero of the zero poly­nomial
  – Maximum number of zeroes of a polynomial is equal to its degree.

Class 9 Social Science

Class 9 Science

Class 9 Maths

 

Read and Learn More KSEEB Solutions for Class 9 Maths 

Remainder theorem:

Let p(x) & g(x) be two polynomials such that the degree of p(x) is equal to or greater than the de­gree of g(x) & g(x) * 0, then, we can find out two polynomials q(x) & r (x) such that

p(x) = g(x) q(x) + r(x) where
r(x) = 0 or degree of r(x) is less than degree of g(4)

The other way round, we can say that on dividing p(x) by g(x), we get q(x) as the quotient & r(x) as the remainder.

Formulatically:
Dividend = (Divisor x Quotient) + Remainder

Remainder theorem:

On dividing the polynomial p(x) of degree one or more than one by a linear polynomial x – a, the re­mainder obtained is p(a), where a is a real number.

Proof:

Suppose that when we divide p(x) by x – a, the quotient is q(x) & the remainder is r(x)

Then p(x) = (x- a) q(x) + r(x)
∴ degree of x – a is one & degree of r(x) is less than the degree (x – a)  ,
∴ degree of r(x) = 0
=> r(x) is a constant, say r
\(\mathrm{p}(x)=(x-a) \mathrm{q}(x)+\mathrm{r}\)
put x=a,we get
p(a)=r

This proves the theorem.

KSEEB Class 9 Maths Chapter 2 Polynomials Exercises 

Factor theorem:

Let p(*) be a polynomial of degree one or more than one & ‘a’ is a real number then

• x – a will be a factor of p(*) if p(a) = 0, con­versely
• If x – a is a factor of p(jr) then p(a) = 0
• Factorisation of a quadratic polynomial by splitting the middle term.
  \(\begin{aligned}
  & x^2+I x+m \\
  = & x^2+(a+b) x+a b
  \end{aligned}\)
  Where\(\begin{aligned}
  I & =a+b \quad \& \quad m=a b \\
  & =x^2+a x+b x+a b \\
  & =x(x+a)+b(x+a) \\
  & =(x+a)(x+b)
  \end{aligned}\)

Algebraic Identities.

1. \((a+b)^2=a^2+2 a b+b^2\)
2. \((a-b)^2=a^2-2 a b+b^2\)
3. \(a^2-b^2=(a+b)(a-b)\)
4. \((x+a)(x+b)=x^2+(a+b) x+a b\)
5. \((a+b+c)^2=a^2+b^2+c^2+2 a b+2 b c+2 c a\)
6. \((a+b)^3=a^3+b^3+3 a b(a+b)\)
7. \((a-b)^3=a^3-b^3-3 a b(a-b)\)
8. \(\begin{aligned}
   & a^3+b^3+c^3-3 a b c=(a+b+c) \\
   & \left(a^2+b^2+c^2-a b-b c-c a\right)
   \end{aligned}\)
9. \(\text { if } a+b+c=0 \text {, then } a^3+b^3+c^3=3 a b c\)
10. \(a^3+b^3=(a+b)\left(a^2-a b+b^2\right)\)
11. \(a^3-b^3=(a-b)\left(a^2+a b+b^2\right)\)

Polynomials Exercise 2.1

1. Which of the following expressions are poly­nomials in one variable & which are not? State reasons for your answers.

1. \(4 x^2-3 x+7\)

Solution: This expression is a polynomial in one variable x because in the expression. There is only one variable x & all the indices of x are whole num­bers.

2. \(y^2+\sqrt{2}\)

Solution: This expression is a polynomial in one variable y because in the expression there is only one variable y & all the indices of y are whole numbers.

3. \(3 \sqrt{t}+t \sqrt{2}\)

Solution: This expression is not a polynomial because in the term\(3 \sqrt{t}\). The exponent of t is \(1 / 2\)which is not a whole number.

4. \(y+2 / y\)

Solution: This expression is not a polynomial because in the term \(\frac{2}{y}\), the exponent of y is(-1) which is not a whole number.

5. \(x^{10}+y^3+t^{50}\)

Solution: This expression is not a polynomial in one variable because in the expression, three variables x, y & t occur.

2. Write the co-efficients of \(x^2\) in each of the following.

1. \(2+x^2+x\)

Solution: co-efficient of \(x^2\) is 1

2. \(2-x^2+x^3\)

Solution: co-efficient of \(x^2\) is -1

3. \(\frac{\pi}{2} x^2+x\)

Solution: co-efficient of \( x^2+x\) is \(\frac{\pi}{2}\)

4. \(\sqrt{2} x-1\)

Solution: co-efficient of \(\frac{\pi}{2}\) is 0

3. Give one example each of a binomial of degree 35, & of a monomial of degree 100.
Solution: One example of a binomial of degree 35 is\(3 x^{35}-4\)
One example of a monomial of degree 100 is\(\sqrt{5} y^{100}\)

KSEEB Maths Chapter 2 Polynomials Answers 

4. Write the degrees of each of the following polynomials

1. \(5 x^3+4 x^2+7 x\)
Solution: Term with the highest power of\(x=5 x^3\)
Exponent of x in this term = 3
∴ Degree of this polynomial = 3

 2. \(4-y^2\)
Solution: \(4-y^2\)
Degree of this polynomial = 2

3. \(5 t-\sqrt{7}\)
Solution: Degree of this polynomial = 1

4.3
Solution: It is a non-zero constant. So the degree of the polynomial is zero.

5.Classify the following as linear, quadratic & cubic polynomials.

1. \(x^2+x\)
Solution: Quadratic polynomial.

2. \(x-x^3\)
Solution: Cubic polynomial.

3. \(y+y^2+4\)
Solution: Quadratic polynomial

4. 1+x
Solution: Linear polynomial

5. 3t
Solution: Linear polynomial.

6. \(r^2\)
Solution: Quadratic polynomial

7. \(7 x^3\)
Solution: Cubic polynomial.

Polynomials Exercise 2.2

1.Find the value of the polynomial.\(5 x-4 x^2+3\) at

1)x=0   2)x=-1    3)x=2

1. x=0

Solution: Let f(x)= 5x-4×2+3

Value of f(x) at x= 0

f(0) = 5 (0) – 4 (0)2 + 3

=0-0+3

= 3

2. x=-1

value of f(x) at x= -1

f(-l) = 5(-l)-4(-l)2 + 3

= -5 – 4 + 3

= – 6

3. x=2

value of f(x) at x= 2

f(2) = 5(2) – 4(2)2 + 3

= 10-16 + 3

= – 3

KSEEB Solutions Class 9 Polynomials Practice Problems 

2. Find p(0), p(1) & p(2) for each of the following polynomials

 1. \(p(y)=y^2-y+1\)

Solution: \(p(y)=y^2-y+1\)

\(p(0)=0^2-0+1\)

= 1

p(l) = \(1^2-1+1=1\)

p(2) = \(2^2-2+1=1\)

2. \(p(t)=2+t+2 t^2-t^3\)

Solution: \(p(t)=2+t+2 t^2-t^3\)

\(\begin{aligned}
& \mathrm{p}(0)=2+0+2(0)^2-0^3=2 \\
& \mathrm{p}(1)=2+1+2(1)^2-1^3=4 \\
& \mathrm{p}(2)=2+2+2(2)^2-2^3=4
\end{aligned}\)

3. \(\mathbf{p}(\boldsymbol{x})=x^3\)

Solution: \(\mathbf{p}(\boldsymbol{x})=x^3\)

∴ \(p(0)=0^3=1\)

\(\begin{aligned}
& \mathrm{p}(1)=1^3=1 \\
& \mathrm{p}(2)=2^3=8
\end{aligned}\)

4. \(p(x)=(x-1)(x+1)\)

Solution: \(p(x)=(x-1)(x+1)\)

∴\(p(0)=(0-1)(0+1)=-1 \times 1=-1\)

\(\begin{aligned}
& \mathrm{p}(1)=(1-1)(1+1)=0 \times 2=0 \\
& \mathrm{p}(2)=(2-1)(2+1)=1 \times 3=3
\end{aligned}\)

3. Verify whether the following zeroes of the polynomial are indicated against them.

1. \(p(x)=3 x+1, x=-\frac{1}{3}\)

Solution:

\(\begin{aligned}
\mathrm{p}\left(-\frac{1}{3}\right) & =3\left(-\frac{1}{3}\right)+1 \\
& =-1+1 \\
& =0
\end{aligned}\)

∴\(-\frac{1}{3} \text { is a zero of } \mathrm{p}(x)\)

2. \(p(x)=5 x-\pi, \quad x=\frac{4}{5}\)

Solution:

\(\begin{aligned}
p=\left(\frac{4}{5}\right) & =5\left(\frac{4}{5}\right)-\pi \\
& =4-\pi \neq 0
\end{aligned}\)

∴\(\frac{4}{5} \text { is not a zero of } \mathrm{p}(x)\)

3. \(p(x)=x^2-1, \quad x=1,-1\)

Solution:

\(\begin{aligned}
& \mathrm{p}(1)=1^2-1=1-1=0 \\
& \mathrm{p}(-1)=(-1)^2-1=1-1=0
\end{aligned}\)

∴\(1,-1 \text { are zeroes of } \mathrm{p}(x)\)

4. \(p(x)=(x+1)(x-2), x=-1,2\)

Solution:

\(\begin{aligned}
\mathrm{p}(-1) & =(-1+1)(-1-2) \\
& =0(-3) \\
& =0 \\
\mathrm{p}(2) & =(2+1)(2-2) \\
& =(3)(0) \\
& =0
\end{aligned}\)

∴\(-1,2 \text { are zeroes of } \mathrm{p}(x)\)

5. \(p(x)=x^2, \quad x=0\)

Solution:

\(p(0)=0^2=0\)

∴ 0 is a zero of p(x)

6. \(p(x)=I x+m, \quad x=\frac{-m}{l}\)

Solution:

\(\begin{gathered}
p=\left(\frac{-m}{I}\right)=I\left(\frac{-m}{I}\right)+m \\
=-\mathrm{m}+\mathrm{m}=0
\end{gathered}\)

∴\(\frac{-m}{l}\) is a zero of p(x)

7. \(p(x)=3 x^2-1, \quad x=\frac{-1}{\sqrt{3}}, \frac{2}{\sqrt{3}}\)

Solution:

\(\begin{aligned}
p\left(-\frac{1}{\sqrt{3}}\right) & =3\left(-\frac{1}{\sqrt{3}}\right)^2-1 \\
& =3\left(\frac{1}{3}\right)-1=1-1= \\
p\left(\frac{2}{\sqrt{3}}\right) & =3\left(\frac{2}{\sqrt{3}}\right)^2-1 \\
& =3 \times \frac{4}{3}-1 \\
& =4-1 \\
& =3 \neq 0
\end{aligned}\)

∴\(\frac{-1}{\sqrt{3}}\) is a zero of p(x) but \(\frac{2}{\sqrt{3}}\) is not a zero of p(x)

8. \(p(x)=2 x+1, \quad x=\frac{1}{2}\)

Solution:

\(\begin{aligned}
p=\left(\frac{1}{2}\right) & =2 \times \frac{1}{2}+1 \\
& =1+1=2 \neq 0
\end{aligned}\)

∴ \(\frac{1}{2}\) is not a zero of p(x).

4. Find the zero of the polynomial in each of the following cases

1. \(p(x)=x+5\)

Solution:

\(\begin{aligned}
& p(x)=0 \\
& \Rightarrow \quad x+5=0 \\
& \Rightarrow \quad x=-5
\end{aligned}\)

∴-5 is a zero of the polynomial p(x)

2. \(p(x)=x-5\)

Solution:

\(\begin{aligned}
& p(x)=0 \\
& \Rightarrow \quad x-5=0 \\
& \Rightarrow \quad x=5
\end{aligned}\)

∴-5 is a zero of the polynomial p(x)

3. \(p(x)=2 x+5\)

Solution:

\(\begin{aligned}
& \mathrm{p}(x)=0 \\
& \Rightarrow \quad 2 x+5=0 \\
& \Rightarrow \quad 2 x=-5 \\
& \Rightarrow \quad x=\frac{-5}{2}
\end{aligned}\)

∴\(\frac{-5}{2}\) is a zero of the polynomial p(x)

4. \(p(x)=3 x-2\)

Solution:

\(\begin{aligned}
& \mathrm{p}(x)=0 \\
& \Rightarrow \quad 3 x-2=0 \\
& \Rightarrow \quad 3 x=2 \\
& \Rightarrow \quad x=\frac{2}{3}
\end{aligned}\)

∴\(\frac{2}{3}\) is a zero of the polynomial p(x)

5. \(p(x)=3 x\)

Solution:

\(\begin{aligned}
& \mathrm{p}(x)=0 \\
& \Rightarrow \quad 3 x=0 \\
& \Rightarrow \quad x=0
\end{aligned}\)

∴ 0 is a zero of the polynomial p(x)

6. \(p(x)=a x, \quad a \neq 0\)

Solution:

\(\begin{aligned}
& p(x)=0 \\
& \Rightarrow \quad a x=0 \\
& \Rightarrow \quad x=0
\end{aligned}\)

∴ 0 is a zero of the polynomial p(x)

7. \(p(x)=c x+d, \quad c \neq 0\) ,c,d are rael numbers

Solution:

\(\begin{aligned}
& p(x)=0 \\
& \Rightarrow \quad c x+d=0 \\
& \Rightarrow \quad c x=-d \\
& \Rightarrow \quad x=\frac{-d}{c}
\end{aligned}\)

∴ \(-\frac{d}{c}\) is a zero of the polynomial p(x)

Class 9 Maths KSEEB Chapter 2 Polynomials Examples 

Polynomials Exercise 2.3

1. Find the remainder when \(x^3+3 x^2+3 x+1\) is divided by
1) x+1
2)\(x-\frac{1}{2}\)
3)x
4)x+π
5)5+2x

1. Solution:

1) Let \(\mathrm{p}(x)=x^3+3 x^2+3 x+1\)

\(\begin{aligned}
& x+1=0 \\
& \Rightarrow \quad x=-1
\end{aligned}\)

∴Remainder

\(\begin{aligned}
\mathrm{p}(-1) & =(-1)^3+3(-1)^2+3(-1)+1 \\
& =-1+3-3+1 \\
& =0
\end{aligned}\)

2. Solution:

\(\begin{aligned}
& \Rightarrow \quad x-\frac{1}{2}=0 \\
& \Rightarrow \quad x=\frac{1}{2}
\end{aligned}\)

∴ Remainder

\(\begin{aligned}
& =\left(\frac{1}{2}\right)^3+3\left(\frac{1}{2}\right)^2+3\left(\frac{1}{2}\right)+1 \\
& =\frac{1}{8}+3 \times \frac{1}{4}+\frac{3}{2}+1 \\
& =\frac{27}{8}
\end{aligned}\)

3. Solution:

Remainder =\(0^3+3(0)^2+3(0)+1=1\)

4. Solution:

\(\begin{array}{ll}
\Rightarrow & x+\pi=0 \\
\Rightarrow & x=-\pi
\end{array}\)

∴Remainder = \(\begin{array}{r}
(-\pi)^3+3(-\pi)^2+3(-\pi)+1 \\
=-\pi^3+3 \pi^2-3 \pi+1
\end{array}\)

5. Solution:

\(\begin{array}{ll}
\Rightarrow & 5+2 x=0 \\
\Rightarrow & x=-5 / 2
\end{array}\)

∴Remainder

\(\begin{aligned}
& =\left(\frac{-5}{2}\right)^3+3\left(\frac{-5}{2}\right)^2+3\left(\frac{-5}{2}\right)+1 \\
& =\frac{125}{8}+\frac{75}{4}-\frac{15}{2}+1 \\
& =\frac{-27}{8}
\end{aligned}\)

2. Find the remainder when \(x^3-a x^2+6 x-a\) is divided by x-a

Solution:

Let \(\begin{aligned}
& p(x)=x^3-a x^2+6 x-a \\
& \quad x-a=0 \\
& x=a
\end{aligned}\)

∴Remainder

\(\begin{aligned}
& =a^3-a(a)^2+6(a)-a \\
& =a^3-a^3+6 a-a \\
& =5 a
\end{aligned}\)

3.Check whether 7 + 3x is a factor of \(3 x^3+7 x\).

Solution:

7 + 3x will be a factor of \(3 x^3+7 x\) only if 7 +3x divecides \(3 x^3+7 x\) leaving no. remainder

Let \(p(x)=3 x^3+7 x\)

\(\begin{aligned}
& 7+3 x=0 \\
& \Rightarrow \quad 3 x=-7 \\
& \Rightarrow \quad x=-7 / 3
\end{aligned}\)

∴Remainder = \(3\left(\frac{-7}{3}\right)^3+7\left(\frac{-7}{3}\right)\)

\(\begin{gathered}
=-3 \times \frac{343}{27}-\frac{49}{3}=\frac{-343}{9}-\frac{49}{3} \\
=\frac{-490}{9} \neq 0
\end{gathered}\)

7+3x is not a factor of \(3 x^3+7 x\)

Polynomials Exercise 2.4

1. Determine which of the following polynomials has (X+1) a factor.

1. \(x^3+x^2+x+1\)

Solution:

Let \(p(x)=x^3+x^2+x+1\)

The zero of x+1 is -1

\(\begin{aligned}
\mathrm{p}(-1) & =(-1)^3+(-1)^2+(-1)+1 \\
& =-1+1-1+1 \\
& =0
\end{aligned}\)

By factor theorem, x+ 1 is a factor of \(x^3+x^2+x+1\)

2. \(x^4+x^3+x^2+x+1\)

Solution:

Let \(p(x)=x^4+x^3+x^2+x+1\)

The zero of x+1 is -1

\(\begin{aligned}
p(-1) & =(-1)^4+(-1)^3+(-1)^2+(-1)+1 \\
& =1-1+1-1+1=1 \neq 0
\end{aligned}\)

∴By factor theorem, x +1 is not a factor of \(x^4+x^3+x^2+x+1\)

KSEEB Chapter 2 Polynomials Solved Questions 

3. \(x^4+3 x^3+3 x^2+x+1\)

Solution:

Let \(p(x)=x^4+3 x^3+3 x^2+x+1\)

The zero of x+1 is -1

\(\begin{aligned}
\mathrm{p}(-1) & =(-1)^4+3(-1)^3+3(-1)^2+(-1)+1 \\
& =1-1+1-1+1=1 \neq 0
\end{aligned}\)

By factor theorem, x +1 is not a factor of \(x^4+3 x^3+3 x^2+x+1\)

4. \(x^3-x^2-(2+\sqrt{2}) x+\sqrt{2}\)

Solution:

Let \(p(x)=x^3-x^2-(2+\sqrt{2}) x+\sqrt{2}\)

The zero of x+1 is -1

\(\begin{aligned}
\mathrm{p}(-1)= & (-1)^3-(1)^2-(2+\sqrt{2})(-1)+\sqrt{2} \\
& =-1-1+2+\sqrt{2}+\sqrt{2} \\
& =2 \sqrt{2} \neq 0
\end{aligned}\)

By factor theorem, x +1 is not a factor of

\(x^3-x^2-(2+\sqrt{2}) x+\sqrt{2}\)

2.  Use the factor theorem to determine whether g(x) is a factor of p(x) in each of the following cases.

1.\(\mathbf{p}(\boldsymbol{x})=2 x^3+x^2-2 x-1, \quad \mathbf{g}(\boldsymbol{x})=\boldsymbol{x}+\mathbf{1}\)

Solution:

g(x)=0

\(\begin{array}{ll}
\Rightarrow & x+1=0 \\
\Rightarrow & x=-1
\end{array}\)

∴ zero of g(x) is -1,

Now p(-1)

\(\begin{aligned}
& =2(-1)^3+(-1)^2-2(-1)-1 \\
& =-2+1+2-1 \\
& =0
\end{aligned}\)

∴By factor theorem, g(x) is a factor of p(x).

2.\(p(x)=x^3+3 x^2+3 x+1, \quad g(x)=x+2\)

Solution:

\(\begin{aligned}
& g(x)=x+2 \\
& g(x)=0 \\
& \Rightarrow \quad x+2=0 \\
& \Rightarrow \quad x=-2
\end{aligned}\)

∴zero of g(x) is -2

Now, \(\begin{aligned}
p(-2) & =(-2)^3+3(-2)^2+3(-2)+1 \\
& =-8+12-6+1 \\
& =-1 \neq 0
\end{aligned}\)

∴By factor theorem, g(x) is a factor of p(x).

3.\(p(x)=x^3-4 x^2+x+6, g(x)=x-3\)

Solution:

\(\begin{aligned}
& g(x)=0 \\
& \Rightarrow \quad x-3=0 \\
& \Rightarrow \quad x=3
\end{aligned}\)

∴zero of g(x) is 3

Now,p(3) \(\begin{aligned}
& =3^3-4(3)^2+3+6 \\
& =27-36+3+6 \\
& =0
\end{aligned}\)

∴By factor theorem, g(x) is a factor of p(x).

3.Find the value of k, if x-1 is a factor of p(x) in each of the following cases.

1.\(\mathbf{p}(\boldsymbol{x})=x^2+x+\mathbf{k}\)

Solution:

If x-1 is a factor of p(x), then p( 1) = 0.

(By factor theorem)

\(\begin{array}{cc}
\Rightarrow & 1^2+1+k=0 \\
\Rightarrow & 2+k=0 \\
\Rightarrow & k=-2
\end{array}\)

2.\(\mathbf{p}(x)=2 x^2+\mathbf{k} x+\sqrt{2}\)

Solution:

If x-1 is a factor of p(x), then p( 1) = 0.

\(2(1)^2+k(1)+\sqrt{2}=0\) \(\begin{aligned}
& \Rightarrow \quad 2+k+\sqrt{2}=0 \\
& \Rightarrow \quad k=-2-\sqrt{2}=-(2+\sqrt{2})
\end{aligned}\)

3.\(p(x)=k x^2-\sqrt{2} x+1\)

Solution:

If x-1 is a factor of p(x), then p( 1) = 0.

\(\begin{array}{ll}
\Rightarrow & \mathrm{k}(1)^2-\sqrt{2}(1)+1=0 \\
\Rightarrow & \mathrm{k}-\sqrt{2}+1=0 \\
\Rightarrow & \mathrm{k}=\sqrt{2}-1
\end{array}\)

KSEEB Solutions for 9th Standard Maths Chapter 2 Polynomials 

4.\(p(x)=k x^2-3 x+k\)

Solution:

If x-1 is a factor of p(x), then p( 1) = 0.

\(\begin{array}{ll}
\Rightarrow & \mathrm{k}(1)^2-3(1)+\mathrm{k}=0 \\
\Rightarrow & \mathrm{k}-3+\mathrm{k}=0 \\
\Rightarrow & 2 \mathrm{k}=3 \\
\Rightarrow & \mathrm{k}=3 / 2
\end{array}\)

4.Factorise

1.\(12 x^2-7 x+1\)

Solution:

\(\begin{aligned}
& 12 x^2-4 x-3 x+1 \\
& =4 x(3 x-1)-1(3 x-1) \\
& =(3 x-1)(4 x-1)
\end{aligned}\)

2.\(2 x^2+7 x+3\)

Solution:

\(\begin{aligned}
& 2 x^2+6 x+x+3 \\
& 2 x(x+3)+1(x+3) \\
& (x+3)(2 x+1)
\end{aligned}\)

3.\(6 x^2+5 x-6\)

Solution:

\(\begin{aligned}
& 6 x^2+9 x-4 x-6 \\
& 3 x(2 x+3)-2(2 x+3) \\
& (2 x+3)(3 x-2)
\end{aligned}\)

4.\(3 x^2-4 x+3 x-4\)

Solution:

\(\begin{aligned}
& 3 x^2-4 x+3 x-4 \\
& \quad x(3 x-4)+1(3 x-4) \\
& (3 x-4)(x+1)
\end{aligned}\)

5. Factorise

1.\(x^3-2 x^2-x+2\)

Solution:

Let \(p(x)=x^3-2 x^2-x+2\)

By tril, we find that

\(\begin{aligned}
\mathrm{p}(1) & =1^3-2(1)^2-1+2 \\
& =1-2-1+2 \\
& =0
\end{aligned}\)

By factor theorem, (x -1) is a factor of p(x)

Now , \(\begin{aligned}
& x^2(x-1)-x(x-1)-2(x-1) \\
& (x-1)\left(x^2-x-2\right) \\
& (x-1)\left(x^2-2 x+x-2\right) \\
& (x-1)(x(x-2)+1(x-2)) \\
& (x-1)(x-2)(x+1)
\end{aligned}\)

2.\(x^3-3 x^2-9 x-5\)

Solution:

\(x^3-3 x^2-9 x-5\)

Let \(p(x)=x^3-3 x^2-9 x-5\)

By tril, we find that

\(\begin{aligned}
p(-1) & =(-1)^3-3(-1)^2-9(-1)-5 \\
& =-1-3+9-5 \\
& =0
\end{aligned}\)

By factor theorem, x -(-1) i.e. x+1 is a factor of p(x)

Now \(x^3-3 x^2-9 x-5\)

\(\begin{aligned}
& x^2(x+1)-4 x(x+1)-5(x+1) \\
& x^2(x+1)-4 x(x+1)-5(x+1) \\
&(x+1)\left(x^2-4 x-5\right) \\
&(x+1)\left(x^2-5 x+x-5\right) \\
&(x+1)\{x(x-5)+1(x-5)\} \\
&(x+1)(x-5)(x+1)
\end{aligned}\)

3.\(x^3+13 x^2+32 x+20\)

Solution:

Let \(p(x)=x^3+13 x^2+32 x+20\)

By tril, we find that

\(\begin{aligned}
p(-1) & =(-1)^3+13(-1)^2+32(-1)+20 \\
& =-1+13-32+20 \\
& =0
\end{aligned}\)

By factor theorem, x -(-1) i.e. x+1 is a factor of p(x)

Now , \(x^3+13 x^2+32 x+20\)

\(\begin{aligned}
& =x^2(x+1)+12 x(x+1)+20(x+1) \\
& =(x+1)\left(x^2+12 x-20\right)
\end{aligned}\) \(\begin{aligned}
& =(x+1)\left(x^2+10 x+2 x+20\right) \\
& =(x+1)\{x(x+10)+2(x+10) \\
& =(x+1)(x+10)(x+2)
\end{aligned}\)

4.\(2 y^3+y^2-2 y-1\)

Solution:

Let \(p(y)=2 y^3+y^2-2 y-1\)

By tril, we find that

\(\begin{aligned}
p(1) & =2(1)^3+1^2-2(1)-1 \\
& =2+1-2-1 \\
& =0
\end{aligned}\)

By factor theorem, (y-1) is a factor of p(y).

Now ,\(2 y^3+y^2-2 y-1\)

\(\begin{aligned}
& =2 y^2(y-1)+3 y(y-1)+1(y-1) \\
& =(y-1)\left(2 y^2+3 y+1\right) \\
& =(y-1)\left(2 y^2+2 y+y+1\right) \\
& =(y-1)\{(2 y(y+1)+1(y+1)\} \\
& =(y-1)(y+1)(2 y+1)
\end{aligned}\)

 

KSEEB Maths Chapter 2 Polynomials Free Solutions 

Polynomials Exercise 2.5

1. Use suitable identities to find the following products.

1.\((x+4)(x+10)\)

Solution:

\(\begin{aligned}
& (x+a)(x+b)=x^2+(a+b) x+a b \\
& \quad(x+4)(x+10)=x^2+(4+10) x+4 \times 10 \\
& =x^2+14 x+40
\end{aligned}\)

2.\((x+8)(x-10)\)

Solution:

\(\begin{aligned}
& (x+a)(x-b)=x^2+(a-b) x-a b \\
& (x+8)(x-10)=x^2+(8-10) x-8 \times 10 \\
& =x^2-2 x-80
\end{aligned}\)

3.\((3 x+4)(3 x-5)\)

Solution:

\(\begin{aligned}
& (x+a)(x-b)=x^2+(a-b) x-a b \\
& (3 x+4)(3 x-5)=(3 x)^2+(4-5)(3 x)-4 \times 5 \\
& =9 x^2-3 x-20 \\
&
\end{aligned}\)

4.\(\left(y^2+3 / 2\right)\left(y^2-3 / 2\right)\)

Solution:

\(\begin{aligned}
& (a+b)(a-b)=a^2-b^2 \\
& \begin{aligned}
&\left(y^2+3 / 2\right)\left(y^2-3 / 2\right)=\left(y^2\right)^2-(3 / 2)^2 \\
&=y^4-\frac{9}{4}
\end{aligned}
\end{aligned}\)

5.\((3-2 x)(3+2 x)\)

Solution:

\(\begin{aligned}
& (a-b)(a+b)=a^2-b^2 \\
& (3-2 x)(3+2 x)=3^2-(2 x)^2=9-4 x^2
\end{aligned}\)

2.Evaluate the following products without multiplying directly:

1.103 x 107

Solution:

(100 + 3) x (100 + 7)

\((x+a)(x+b)=x^2+(a+b) x+a b\)

(100+ 3) (100+ 7)

= 1002 + (3 + 7) (100) + 3 x7

= 10000+ 1000 + 21

= 11021

2.  95 x 96

Solution:

95 x 96 = (100 -5) (100-4)

= (100 x 100) + {(-5) + (-4)} 100 + (-5) (-4)

= 10000-900 + 20

= 9120.

(OR)

95 x 96 = (90 + 5) (90 + 6)

= 902 + (5 + 6) (90) + (5) (6)

= 8100 + 990 + 30

= 9120

3. 104 x 96

Solution:

104 x 96 = (100 + 4) (100 – 4)

\((a+b)(a-b)=a^2-b^2\)

= (100)² – 4²

= 1000 – 16

= 9984

3.Factorise the following using appropriate identities.

1.\(9 x^2+6 x y+y^2\)

Solution:

\(9 x^2+6 x y+y^2\) \(\begin{aligned}
(3 x)^2 & +2(3 x)(y)+y^2\left\{a^2+2 a b+b^2=(a+b)^2\right\} \\
& =(3 x+y)^2 \\
& =(3 x+y)(3 x+y)
\end{aligned}\)

2.\(4 y^2-4 y+1\)

Solution:

\(\begin{aligned}
& 4 y^2-4 y+1=(2 y)^2-2(2 y)(1)+1^2 \\
& =(2 y-1)^2 \quad\left\{a^2-2 a b+b^2=(a-b)^2\right\} \\
& =(2 y-1)(2 y-1)
\end{aligned}\)

3.\(x^2-y^2 / 100\)

Solution:

\(\begin{aligned}
& x^2-y^2 / 100 \\
& x^2-\frac{y^2}{100}=\left(x^2\right)-\left(\frac{y}{10}\right)^2 \\
& a^2-b^2=(a+b)(a-b) \\
& x^2-\left(\frac{y}{10}\right)^2=\left(x+\frac{y}{10}\right)\left(x-\frac{y}{10}\right)
\end{aligned}\)

4. Expand each of the following using suitable identities.

1.\((x+2 y+4 z)^2\)

Solution:

\((a+b+c)^2=a^2+b^2+c^2+2 a b+2 b c+2 c a\) \(\begin{gathered}
(x+2 y+4 z)^2=x^2+(2 y)^2+(4 z)^2+2 \times x \times 2 y \\
+2 \times 2 y \times 4 z+2 \times 4 z \times x \\
=x^2+4 y^2+16 z^2+4 x y+16 x z+8 x z
\end{gathered}\)

2.\((2 x-y+z)^2\)

Solution:

\((a-b+c)^2=a^2+b^2+c^2-2 a b-2 b c+2 c a\) \(\begin{gathered}
(2 x-y+z)^2=(2 x)^2+(y)^2+(z)^2-2 \times 2 x \times y \\
-2 \times y \times z+2 \times 2 x \times z
\end{gathered}\) \(=4 x^2+y^2+z^2-4 x y-2 y z+4 x z\)

3.\((-2 x+3 y+2 z)^2\)

Solution:

\(\begin{gathered}
(-a+b+c)^2=a^2+b^2+c^2-2 a b+2 b c-2 c a \\
(-2 x+3 y+2 z)^2=(2 x)^2+(3 y)^2+(2 z)^2 \\
-2 \times 2 x \times 3 y+2 \times 3 y \times 2 z-2 \times 2 z \times 2 x \\
=4 x^2+9 y^2+4 z^2-12 x y-12 y z-8 z x
\end{gathered}\)

4.\((3 a-7 b-c)^2\)

Solution:

\((a-b-c)^2=a^2+b^2+c^2-2 a b+2 b c-2 c a\) \(\begin{gathered}
(3 a-7 b-c)^2=(3 a)^2+(7 b)^2+(c)^2-2 \times 3 a \times 7 b \\
+2 \times 7 b \times c-2 \times c \times 3 a \\
=9 a^2+49 b^2+c^2-42 a b+14 b c-6 c a
\end{gathered}\)

5.\((-2 x+5 y-3 z)^2\)

Solution:

\(\begin{aligned}
& (-a+b-c)^2=a^2+b^2+c^2-2 a b-2 b c+2 c a \\
& =(2 x)^2+(5 y)^2+(3 z)^2-2 \times 2 x \times 5 y \\
& -2 \times 5 y \times 3 z+2 \times 3 z \times 2 x \\
& =4 x^2+25 y^2+9 z^2-20 x y-30 y z+12 z x \\
&
\end{aligned}\)

6.\(\left[\frac{1}{4} a-\frac{1}{2} b+1\right]^2\)

Solution:

\((a-b+c)^2=a^2+b^2+c^2-2 a b+2 c a-2 b c\)
\(\begin{gathered}
\left(\frac{1}{4} a-\frac{1}{2} b+1\right)^2=\left(\frac{1}{4} a\right)^2+\left(\frac{1}{2} b\right)^2+(1)^2 \\
-2 \times \frac{1}{4} a \times \frac{1}{2} b+2 \times 1 \times \frac{1}{4} a-2 \times \frac{1}{2} b \times 1 \\
=\frac{1}{16} a^2+\frac{1}{4} b^2+1-\frac{1}{4} a b+\frac{1}{2} a-b
\end{gathered}\)

 

KSEEB Class 9 Chapter 2 Polynomials Revision Notes 

5.  Factorise

1.\(4 x^2+9 y^2+16 z^2+12 x y-24 y z-16 x z\)

Solution:

\(\begin{aligned}
& 4 x^2+9 y^2+16 z^2+12 x y-24 y z-16 x z \\
& \begin{aligned}
(2 x)^2+(3 y)^2+ & +(-4 z)^2+2(2 x)(3 y) \\
& +2(3 y)(-4 z)+2(-4 z)(2 x) \\
= & {[2 x+3 y+(-4 z)]^2 } \\
= & (2 x+3 y-4 z)^2 \\
= & (2 x+3 y-4 z)(2 x+3 y-4 z)
\end{aligned}
\end{aligned}\)

2.\(2 x^2+y^2+8 z^2-2 \sqrt{2} x y+4 \sqrt{2} y z-8 z x\)

Solution:

\(\begin{aligned}
& (-\sqrt{2} x)^2+y^2+(2 \sqrt{2} z)^2+2(-\sqrt{2} x) y+2 y \\
& (2 \sqrt{2}) x+2(2 \sqrt{2} z)(-\sqrt{2} x) \\
& \quad=(-\sqrt{2} x+y+2 \sqrt{2} z)^2 \\
& =(-\sqrt{2} x+y+2 \sqrt{2} z)(-\sqrt{2} x+y+2 \sqrt{2} z)
\end{aligned}\)

6.Write the following cubes in expanded form.

1.\((2 x+1)^3\)

Solution:

\(\begin{aligned}
(a+b)^3=a^3 & +b^3+3 a b(a+b) \\
(2 x+1)^3 & =(2 x)^3+1^3+3 \times 2 x \times 1(2 x+1) \\
& =8 x^3+1+6 x(2 x+1) \\
& =8 x^3+1+12 x^2+6 x
\end{aligned}\)

2.\((2 a-3 b)^3\)

Solution:

\(\begin{aligned}
&(a-b)^3=a^3-b^3-3 a^2 b+3 a b^2 \\
&=(2 a-3 b)^3=(2 a)^3-(3 b)^3 \\
&-3(2 a)^2(3 b)+3(2 a)(3 b)^2 \\
&=8 a^3-27 b^3-36 a^2 b+54 a b^2
\end{aligned}\)

3.\(\left[\frac{3}{2} x+1\right]^3\)

Solution:

\((a+b)^3=a^3+b^3+3 a^2 b+3 a b^2\) \(\begin{aligned}
& =\left(\frac{3}{2} x\right)^3+1^3+3 \times\left(\frac{3}{2} x\right)^2 \times 1+3 \times \frac{3}{2} x \times 1^2 \\
& =\frac{27}{8} x^3+1+\frac{27}{4} x^2+\frac{9 x}{2}
\end{aligned}\)

4.\(\left(x-\frac{2}{3} y\right)^3\)

Solution:

\(\begin{aligned}
& (a-b)^3=a^3-b^3-3 a^2 b+3 a b^2 \\
& \left(x-\frac{2}{3} y\right)^3=x^3-\left(\frac{2}{3} y\right)^3-3(x)^2\left(\frac{2}{3} y\right) \\
& +3 \times x \times\left(\frac{2}{3} y\right)^2 \\
& =x^3-\frac{8}{27} y^3-2 x^2 y+\frac{4 x y^2}{3} \\
&
\end{aligned}\)

7. Evaluate the following using suitable identities.

1.\((99)^3\)

Solution:

\((100-1)^3\) \(\begin{aligned}
& (a-b)^3=a^3-b^3-3 a^2 b+3 a b^2 \\
& (100-1)^3=(100)^3-1^{3-3}(100)^2 \times 1+ \\
& \quad 3 \times 100 \times 1^2 \\
& =100000-1-30000+300 \\
& =970299
\end{aligned}\)

2.\((102)^3\)

Solution:

\((100+2)^3\) \(\begin{aligned}
(a+b)^3= & a^3+b^3+3 a^2 b+3 a b^2 \\
(100+2)^3= & (100)^3+2^3+3(100)^2(2) \\
& +3 \times 100 \times 2^2 \\
= & 1000000+8+60000+1200 \\
= & 1061208
\end{aligned}\)

3.\((998)^3\)

Solution:

\((1000-2)^3\) \(\begin{aligned}
& (a-b)^3=a^3-b^3-3 a^2 b+3 a b^2 \\
& =(1000)^3-2^3-3 \times(1000)^2 \times \\
& \quad 2+3 \times 1000 \times 2^2 \\
& =1000000000-8-6000000+12000 \\
& =994011992
\end{aligned}\)

 

KSEEB Class 9 Maths Chapter 2 Polynomials Exercises 

8.Factorise each of the following

1.\(8 a^3+b^3+12 a^2 b+6 a b^2\)

Solution:

\(\begin{aligned}
8 a^3 & +b^3+12 a^2 b+6 a b^2 \\
& =(2 a)^3+b^3+3(2 a) b(2 a+b) \\
& =(2 a+b)^3 \\
& =(2 a+b)(2 a+b)(2 a+b)
\end{aligned}\)

2.\(8 a^3-b^3-12 a^2 b+6 a b^2\)

Solution:

\(\begin{aligned}
8 a^3 & -b^3-12 a^2 b+6 a b^2 \\
& =(2 a)^3-b^3-3(2 a)(b)(2 a-b) \\
& =(2 a-b)^3 \\
& =(2 a-b)(2 a-b)(2 a-b)
\end{aligned}\)

3.\(27-125 a^3-135 a+225 a^2\)

Solution:

\(\begin{aligned}
27 & -125 a^3-135 a+225 a^2 \\
& =(3)^3-(5 a)^3-3(3)(5 a)(3-5 a) \\
& =(3-5 a)^3 \\
& =(3-5 a)(3-5 a)(3-5 a)
\end{aligned}\)

4.\(64 a^3-27 b^3-144 a^2 b+108 a b^2\)

Solution:

\(\begin{aligned}
& 64 a^3-27 b^3-144 a^2 b+108 a b^2 \\
& \quad=(4 a)^3-(3 b)^3-3 \times 4 a \times 3 b(4 a-3 b) \\
& \quad=(4 a-3 b)^3 \\
& \quad=(4 a-3 b)(4 a-3 b)(4 a-3 b)
\end{aligned}\)

5.\(27 p^3-\frac{1}{216}-\frac{9}{2} p^2+\frac{1}{4} p\)

Solution:

\(\begin{aligned}
27 & p^3-\frac{1}{216}-\frac{9}{2} p^2+\frac{1}{4} p \\
& =(3 p)^3-\left(\frac{1}{6}\right)^3-3 \times 3 p \times \frac{1}{6}\left(3 p-\frac{1}{6}\right) \\
& =\left(3 p-\frac{1}{6}\right)^3 \\
& =\left(3 p-\frac{1}{6}\right)\left(3 p-\frac{1}{6}\right)\left(3 p-\frac{1}{6}\right)
\end{aligned}\)

9.  Verify

1.\(x^3+y^3=(x+y)\left(x^2-x y+y^2\right)\)

Solution:

Consider RHS

\(\begin{aligned}
& (x+y)\left(x^2-x y+y^2\right) \\
& =x\left(x^2-x y+y^2\right)+y\left(x^2-x y+y^2\right)
\end{aligned}\) \(\begin{aligned}
& =x^3-y^2 y+y y+y x-y y+y^3 \\
& =x^3+y^3
\end{aligned}\)

LHS

2.\(x^3-y^3=(x-y)\left(x^2+x y+y^2\right)\)

Solution:

RHS=

\(\begin{aligned}
& (x-y)\left(x^2+x y+y^2\right) \\
& =x\left(x^2+x y+y^2\right)-y\left(x^2+x y+y^2\right) \\
& =x^3+y^2 y+y^2-y x^2-y^2-y^3 \\
& =x^3-y^3
\end{aligned}\)

Hence verified.

10. Factorise each of the following

1.\(27 y^3+125 z^3\)

Solution:

\(\begin{aligned}
& 27 y^3+125 z^3 \\
& =(3 y)^3+(5 z)^3 \\
& a^3+b^3=(a+b)\left(a^2-a b+b^2\right) \\
& (3 y)^3+(5 z)^3=(3 y+5 z)\left[(3 y)^2-3 y \times 5 z+(5 z)^2\right] \\
& =(3 y+5 z)\left(9 y^2-15 y z+25 z^2\right) \\
&
\end{aligned}\)

2.\(64 m^3-343 n^3\)

Solution:

\(\begin{aligned}
& 64 m^3-343 n^3 \\
& =(4 m)^3-(7 n)^3 \\
& a^3-b^3=(a-b)\left(a^2+a b+b^2\right) \\
& (4 m-7 n)\left[(4 m)^2+4 m \times 7 n+(7 n)^2\right] \\
& (4 m-7 n)\left(16 m^2+28 m n+49 n^2\right)
\end{aligned}\)

11. Factorise \(27 x^3+y^3+z^3-9 x y z\)

Solution:

\(27 x^3+y^3+z^3-9 x y z\) \(\begin{aligned}
& a^3+b^3+c^3-3 a b c=(a+b+c)\left(a^2+b^2+c^2-a b-b c-c a\right) \\
&(3 x)^3+y^3+z^3-3(3 x) y z= \\
&=(3 x+y+z)\left[(3 x)^2+y^2+z^2-3 x \times y-y \times z-z \times 3 x\right] \\
&=(3 x+y+z)\left(9 x^2+y^2+z^2-3 x y-y z-3 x z\right)
\end{aligned}\)

12.  Verify that \(x^3+y^3+z^3-3 x y z\)
\(=\frac{1}{2}(x+y+z)\left[(x-y)^2+(y-z)^2+(z-x)^2\right]\)

Solution:

LHS=

\(x^3+y^3+z^3-3 x y z\) \(\begin{aligned}
& =(x+y+z)\left(x^2+y^2+z^2-x y-y z-z x\right) \\
& =\frac{1}{2}(x+y+z) 2\left(x^2+y^2+z^2-x y-y z-z x\right) \\
& =\frac{1}{2}(x+y+z)\left(2 x^2+2 y^2+2 z^2-2 x y-2 y z-2 z x\right) \\
& =\frac{1}{2}(x+y+z)\left\{\left(x^2-2 x y+y^2\right)+\left(y^2-2 y z+z^2\right)\right. \\
& \left.\quad+\left(z^2-2 z x+x^2\right)\right\}
\end{aligned}\)

13.If x+y+z=0, show that \(x^3+y^3+z^3\) = 3xyz

Solution:

We know that

\(\begin{aligned}
& x^3+y^3+z^3-3 x y z \\
& =(x+y+z)\left(x^2+y^2+z^2-x y-y z-z x\right) \\
& =(0)\left(x^2+y^2+z^2-x y-y z-z x\right)
\end{aligned}\)

(x + y + z = 0)

\(\Rightarrow \quad x^3+y^3+z^3=3 x y z\)

 

KSEEB Maths Chapter 2 Polynomials Answers 

14.  Without actually calculating the cubes, find the value of each of the following.

1. \((-12)^3+(7)^3+(5)^3\)

Solution:

\((-12)^3+(7)^3+(5)^3=3(-12)(7)(5)\)

(-12) + (7) + (5) = 0

= -1260

2.\((28)^3+(-15)^3+(-13)^3\)

Solution:

\((28)^3+(-15)^3+(-13)^3=3(28)(-15)(-13)\)

(-12) +(7) + (5) = 0

= -1260

15. Give possible expressions for the length & breadth of each of the following rectangles in which their areas are given:
1. Area = \(25 a^2-35 a+12\)
2. Area = \(35 y^2+13 y-12\)

Solution:
1.
\(\begin{gathered}
25 a^2-35 a+12 \\
=25 a^2-20 a-15 a+12
\end{gathered}\)
\(\begin{aligned}
& =5 a(5 a-4)-3(5 a-4) \\
& =(5 a-4)(5 a-3)
\end{aligned}\)

∴ The possible expressions for the length & breadth of the rectangle are 5a-3 & 5a-4

2. \(\begin{aligned}
& 35 y^2+13 y-12 \\
& =35 y^2+28 y-15 y-12 \\
& =7 y(5 y+4)-3(5 y+4) \\
& =(5 y+4)(7 y-3)
\end{aligned}\)

∴ The possible expressions for the length & breadth of the rectangle are7y – 3 & 5y + 4

16.What are the possible expressions for the dimensions of the cuboids whose volumes are given below?
1. Volume : \(3 x^2-12 x\)
2. Volume : \(12 k y^2+8 k y-20 k\)

Solution:

\(\begin{aligned}
& 3 x^2-12 x \\
& \quad=3 x(x-4)
\end{aligned}\)

∴ The possible expressions for the dimensions of the cuboid are 3, x& x- 4.

2.\(12 k y^2+8 k y-20 k\)

Solution:

\(12 k y^2+8 k y-20 k\) \(\begin{aligned}
& =4 k\left(3 y^2+2 y-5\right) \\
& =4 k\left(3 y^2+5 y-3 y-5\right) \\
& =4 k\{y(3 y+5)-1(3 y+5)\} \\
& =4 k(3 y+5)(y-1)
\end{aligned}\)

∴ The possible expressions for the dimensions of the cuboid are 4k, 3y + 5 &y- 1

Additional Problems

Choose the correct answer from the following:

1. The zeroes of the polynomial \(x^2(x-1)\) are :

1. 0.1
2. 0,0,1
3. 0,1,1
4. 1,1,1

Solution: 2. 0,0,1

2.If p(x) = \(2 x^3+5 x^2-3 x-2\) is divided by (x-1), then, the remainder is

1. 2
2. p(-l)
3. p(0)
4. p(2)

Solution: 1. 2

3.Zero of the zero polynomial is:

1. 0
2. 1
3. any real number
4. not defined

Solution: 3. any real number

4.Which of the following is a polynomial in one variable?

1. \(3-x^2+x\)
2. \(\sqrt{3 x}+4\)
3. \(x^3+y^3+7\)
4. \(x+\frac{1}{x}\)

Solution: 1. \(3-x^2+x\)

5.The value of the polynomial \(x^2-x-1\) at x=-1 is

1. -3
2. 1
3. -1
4. 0

Solution: 2. 1

6.The co-efficient of \(x^2\) in \(\left(3 x+x^3\right)\left(x+\frac{1}{x}\right)\) is

1. 3
2. 1
3. 4
4. 2

Solution: 3. 4

KSEEB Solutions Class 9 Polynomials Practice Problems 

7.If the area of a rectangle is \(4 x^2+4 x-3\), then its possible dimensions are:

1. \(2 x-3,2 x+1\)
2. \(2 x-1,2 x+3\)
3. \(3 x+1,2 x-3\)
4.  \(3 x-1,2 x+3\)

Solution: 2. \(2 x-1,2 x+3\)

8. Product of \(\left(x-\frac{1}{x}\right)\left(x+\frac{1}{x}\right)\left(x^2+\frac{1}{x^2}\right)\) is

1. \(x^4+\frac{1}{x^4}\)
2. \(x^3+\frac{1}{x^3}-2\)
3. \(x^4-\frac{1}{x^4}\)
4. \(x^2+\frac{1}{x^2}+2\)

Solution: 3. \(x^4-\frac{1}{x^4}\)

9. If \(x^2+k x+6=(x+2)(x+3)\) for all x, the value of k is 

1. 1
2. -1
3. 5
4. 3

Solution: 3. 5

10.Apolynomial having one term is called

1. monomial
2. binomial
3. trinomial
4. zero polynomial

Solution: 1. monomial

One Mark Questions

1. What is the degree of the polynomial \(\left(x^3+5\right)\left(4-x^5\right)\) ?

Solution:

Degree of \(x^3+5=3\)

Degree of \(4-x^5=5\)

Degree of \(\left(x^3+5\right)\left(4-x^5\right)=3+5=8\)

2. Find p(o), if \(p(y)=y^2-y+1\)

Solution:

\(p(y)=y^2-y+1\) \(\begin{aligned}
\mathrm{p}(0) & =0^2-0+1 \\
& =1
\end{aligned}\)

3.If \(x^{11}+101\) is divided by x+ 1, then what remainder do we get

Solution:

consider x+1 = 0

x= -1

Then remainder

\(\begin{aligned}
& =x^{11}+101 \\
& =(-1)^{11}+101 \\
& =-1+101 \\
& =100
\end{aligned}\)

4. Factorise : \(x^3-3 x^2\)

Solution: \(x^2(x-3)\)

5. Write the factors of the polynomial \(x^2+5 \sqrt{2} x+12\)

Solution:

\(x^2+5 \sqrt{2} x+12\) \(\begin{aligned}
& =x^2+3 \sqrt{2} x+2 \sqrt{2} x+12 \\
& =x(x+3 \sqrt{2})+2 \sqrt{2}(x+3 \sqrt{2}) \\
& =(x+3 \sqrt{2})(x+2 \sqrt{2})
\end{aligned}\)

6. Write the co-efficient of y in the expansion of \((x+2)^3\)

Solution:

\(\begin{aligned}
& (x+2)^3=x^3+2^3+3 \times x \times 2(x+2) \\
& =x^3+8+6 x(x+2) \\
& =x^3+8+6 x^2+12 x
\end{aligned}\)

∴ co-efficient of y in the expansion of \((x+2)^3\) is 6.

7. Simplify : \(\left(a+\frac{1}{2}\right)\left(a+\frac{3}{2}\right)\)

Solution:

\(\begin{aligned}
\left(a+\frac{1}{2}\right)\left(a+\frac{3}{2}\right) & =a^2+\frac{3}{2} a+\frac{1}{2} a+\frac{3}{4} \\
= & a^2+2 a+\frac{3}{4}
\end{aligned}\)

8. Find the value of k, if x-2 is a factor of p(x)=\(2 x^2+3 x-k\).

Solution:

x-2 is a factor of p(x), then p(2) = \(2(2)^2+3(2)-k=0\)

=8+6-k=0

k= 14

Two Mark Questions

1. If f{x) = 3x+ 5 , evaluate f{l)- f(5)

Solution:

f(x) = 3x+5

then,   f( 7) = 3×7 + 5

= 21+5 =26

f(5) = 15 + 5 = 20

∴ f(7)- f(5) = 26-20 = 6

Class 9 Maths KSEEB Chapter 2 Polynomials Examples 

2. Find the value of the polynomial \(p(x)=x^3-3 x^2-2 x+6 \text { at } x=\sqrt{2}\)

Solution:

\(p(x)=x^3-3 x^2-2 x+6\)

Then

\(\begin{aligned}
p(\sqrt{2}) & =(\sqrt{2})^3-3(\sqrt{2})^2-2(\sqrt{2})+6 \\
& =2 \sqrt{2}-6-2 \sqrt{2}+6 \\
& =0
\end{aligned}\)

3.Find the remainder when \(x^3+x^2+x+1\) is divided by \(x-\frac{1}{2}\) , using remainder theorem.

Solution:

\(p(x)=x^3+x^2+x+1\) \(\text { put } x-\frac{1}{2}=0 \quad \Rightarrow x=\frac{1}{2} \text { in } p(x)\)

Remainder

\(\begin{aligned}
& =p\left(\frac{1}{2}\right) \\
& =\left(\frac{1}{2}\right)^3+\left(\frac{1}{2}\right)^2+\frac{1}{2}+1 \\
& =\frac{1}{8}+\frac{1}{4}+\frac{1}{2}+1
\end{aligned}\) \(=\frac{1+2+4+8}{8}=\frac{15}{8}\)

4. Factorise : \(x^4-125 x y^3\)

Solution: 

\(\begin{aligned}
& x^4-125 x y^3 \\
& =x\left(x^3-125 y^3\right) \\
& =x\left[(x)^3-(5 y)^3\right] \\
& =x(x-5 y)\left(x^2+(5 y)^2+x \times 5 y\right) \\
& =x(x-5 y)\left(x^2+25 y^2+5 x y\right)
\end{aligned}\)

5. Factorise : \((x+2)^2+p^2+2 p(x+2)\)

Solution:

\(\begin{aligned}
& (x+2)^2+p^2+2 p(x+2) \\
& =(x+2)^2+p^2+2 \times(x+2) \times p
\end{aligned}\) \(=(x+2+p)^2\)

6. Factorise : \(x^4-y^4\)

Solution: 

\(\begin{aligned}
& x^4-y^4 \\
& =\left(x^2\right)^2-\left(y^2\right)^2 \\
& {\left[a^2-b^2=(a+b)(a-b)\right]} \\
& =\left(x^2+y^2\right)\left(x^2-y^2\right) \\
& =\left(x^2+y^2\right)(x+y)(x-y)
\end{aligned}\)

7. If a, b, c are all non-zero & a + b + c = 0 prove \(\frac{a^2}{b c}+\frac{b^2}{a c}+\frac{c^2}{a b}=3\)

Solution:

\(\mathrm{LHS}=\frac{a^2}{b c}+\frac{b^2}{a c}+\frac{c^2}{a b}=\frac{a^3+b^3+c^3}{a b c}=\frac{3 a b c}{a b c}\)

=3

=RHS

8. Factorise : \(9 x^2+6 x y+y^2\)

Solution: 

\(\begin{aligned}
9 x^2+6 x y+y^2 & =(3 x)^2+2 \times 3 x+y+y^2 \\
& =(3 x+y)^2
\end{aligned}\)

9. If x & y are two positive real numbers such that \(x^2+4 y^2=17\) & xy = 2, then find the value of (x+2y).

Solution: 

\(\begin{aligned}
& (x+2 y)^2=x^2+4 y^2+2 \times x \times 2 y \\
& \quad=17+4 \times 2 \\
& \quad=25
\end{aligned}\) \(x+2 y=\sqrt{25}=5\)

10. Without actually calculating the cubes, evaluate \(14^3+13^3-27^3\).

Solution:

a= 14, b = 13, c = -27

a+b+c = 14+ 13-27 = 0

∴\(a^3+b^3+c^3=3 a b c∴\)

\(\begin{aligned}
14^3+13^3-27^3 & =3 \times 14 \times 13 \times-27 \\
& =-14742
\end{aligned}\)

Three Mark Questions

1. Polynomial \(3 x^3-5 x^2+k x-2\)& \(-x^3-x^2+7 x+k\) leave the same remainder when divided by x+ 2 . Find the value at k.

Solution:

Let \(p(x)=3 x^3-5 x^2+k x-2\)

\(q(x)=-x^3-x^2+7 x+k\)

put x + 2 = 0

x = -2 in p(x) & q(x)

\(\begin{aligned}
\mathrm{p}(-2) & =3(-2)^3-5(-2)^2+\mathrm{k}(-2)-2 \\
& =-24-20-2 \mathrm{k}-2 \\
& =-2 \mathrm{k}-46 \\
\mathrm{q}(-2) & =-(-2)^3-(-2)^2+7(-2)+\mathrm{k} \\
& =8-4-14+\mathrm{k} \\
& =-10+\mathrm{k}
\end{aligned}\)

∴p (x) & q(x) leave the same remainder when divided by x+ 2

\(\begin{aligned}
& \Rightarrow \quad-2 \mathrm{k}-46=-10+\mathrm{k} \\
& \Rightarrow \quad-46+10=\mathrm{k}+2 \mathrm{k} \\
& \Rightarrow-36=3 \mathrm{k} \\
& \Rightarrow \quad 3 \mathrm{k}=-36
\end{aligned}\) \(\begin{aligned}
& k=\frac{-36}{3}=-12 \\
& ∴k=-12
\end{aligned}\)

 

KSEEB Chapter 2 Polynomials Solved Questions 

2. Factorise : \(9 x^2+y^2+z^2-6 x y+2 y z-6 x z\), Hence find its value when x= 1, y= 2 & z= -1

Solution:

\(9 x^2+y^2+z^2-6 x y+2 y z-6 x z\) \(\begin{aligned}
= & (-3 x)^2+y^2+z^2+2 \times(-3 x)(y) \\
& +2 \times y \times z+2(-3 x)(z) \\
= & (-3 x+y+z)^2
\end{aligned}\)

If x=l, y= 2, z= -1 then

\(\begin{aligned}
(-3 x+y+z)^2 & =[-3 \times 1+2+(-1)]^2 \\
& =(-3+2-1)^2 \\
& =(-2)^2 \\
& =4
\end{aligned}\)

3. If x- a is the factor of \(3 x^2-m x-n x\) then prove that \(a=\frac{m+n}{3}\)

Solution:

\(p(x)=3 x^2-m x-n x\)

If (x- a) is a factor of p(x), then p(a) = 0

ie \(\begin{aligned}
& 3(a)^2-m(a)-n(a)=0 \\
& 3 a^2-m a-n a=0 \\
& a[3 a-m-n]=0, \quad a \neq 0
\end{aligned}\)

Since 3a-m-n = 0

∴ 3a = m+ n

\(a=\frac{m+n}{3}\)

4. If (3x-2)is a factor of \(3 x^2+x^2-20 x+12\) find other factors.

Solution:

Let \(p(x)=3 x^3+x^2-20 x+12\)

Given 3 x – 2 is a factor of p(x)

\(\begin{aligned}
& x^2+x-6 \\
= & x^2+3 x-2 x-6 \\
= & x(x+3)-2(x+3)
\end{aligned}\)

∴The other factors are (x+3)&(x-2)

5. If \(a^2+b^2+c^2=280\) & \(a b+b c+c a=\frac{9}{2}\) then find the value of \((a+b+c)^3\)

Solution:

\(\begin{aligned}
& (a+b+c)^2=a^2+b^2+c^2+2(a b+b c+c a) \\
& =280+2 \times \frac{9}{2} \\
& =280+9 \\
& =289 \\
& a+b+c=\sqrt{289} \\
& =17 \\
& (a+b+c)^3=17^3 \\
& =4913 \\
&
\end{aligned}\)

 

KSEEB Solutions For 9th Standard Maths Chapter 2 Polynomials 

6. 1) using suitable identity, evaluate \((98)^3\)
2) which mathematical concept is used in this problem.
3) What is its value.

Solution :

1) \(\begin{equation}
(98)^3=(100-2)^3
\end{equation}\)

w . k . t \((a-b)^3=a^3-b^3-3 a^2 b+3 a b^2\)

\(\begin{aligned}
(100-2)^3 & =(100)^3-2^3-3(100)^2 x 2 + 3 x\times 2+ \\
100 \times 2^2 & =1000000-8-60000+1200 \\
& =941192
\end{aligned}\)

2)Algebraic identities

3)satisfaction solves the identity crisis among people.

7. If \(x+\frac{1}{x}=3\), then find \(x^3+\frac{1}{x^3}\)

Solution:

Consider \(x+\frac{1}{x}=3\)

Cubing both the sides we get

\(\begin{aligned}
& \left(x+\frac{1}{x}\right)^3=3^3 \\
& x^3+\left(\frac{1}{x}\right)^3+3 \times x \times \frac{1}{x}\left(x+\frac{1}{x}\right)=27 \\
& x^3+\frac{1}{x^3}+3 \times 3=27 \\
& x^3+\frac{1}{x^3}+9=27 \\
& x^3+\frac{1}{x^3}=27-9 \\
& =18
\end{aligned}\)

8. Using remainder theorem factorise  \(6 x^3-25 x^2+32 x-12\)

Solution:

Factors of 12 = (±1, ± 2, ± 3, ± 4, ± 6, ± 12)

\(\begin{aligned}
p(x) & =6 x^3-25 x^2+32 x-12 \\
p(2) & =6(2)^3-25(2)^2+32 \times 2-12 \\
& =48-100+64-12 \\
& =112-112=0
\end{aligned}\)

∴ x – 2 is a zero of p(x), x – 2 is a factor of p(x)

\(\begin{array}{rl}
6 x^3-2 & 5 x^2+32 x-12 \\
& =6 x^2(x-2)-13 x(x-2)+6(x-2) \\
& =(x-2)\left(6 x^2-13 x+6\right) \\
& =(x-2)\left(6 x^2-9 x-4 x+6\right) \\
& =(x-2)[3 x(2 x-3)-2(2 x-3)] \\
& =(x-2)(2 x-3)(3 x-2)
\end{array}\)

Four Mark Questions

1.  If \(f(x)=x^2+5 x+7\), evaluate \(f(2)-f(-1)+f\left(\frac{1}{3}\right)\)

Solution:

\(f(x)=x^2+5 x+7\)

Then

\(\begin{aligned}
f(2) & =2^2+5 \times 2+7 \\
& =4+10+7 \\
& =21
\end{aligned}\) \(\begin{aligned}
f(-1) & =(-1)^2+5(-1)+7 \\
& =1-5+7 \\
& =3 \\
f\left(\frac{1}{3}\right)= & \left(\frac{1}{3}\right)^2+5\left(\frac{1}{3}\right)+7 \\
& =\frac{1}{9}+\frac{5}{3}+7 \\
= & \frac{9+15+63}{9} \\
& =\frac{87}{9}
\end{aligned}\)

∴ \(\begin{aligned}
& f(2)-f(1)+f\left(\frac{1}{3}\right) \\
& =21-3+\frac{87}{9} \\
& =\frac{189-27+87}{9}=\frac{249}{9}
\end{aligned}\)

2. Find the quotient & remainder when\(6 x^4+11 x^3+13 x^2-3 x+27\) is divided by 3 x+ 4 .  Also check the remainder obtained by using remainder theorem

Solution:

Thus quotient = \(2 x^3+x^2+3 x-5\)

and remainder = 47

Let F(x) = \(6 x^4+11 x^3+13 x^2-3 x+27\)

Zero of \(3 x+4 \text { is } \frac{-4}{3}\)

Remainder \(=P\left(\frac{-4}{3}\right)\)

\(\begin{aligned}
& =6\left(\frac{-4}{3}\right)^4+11\left(\frac{-4}{3}\right)^3+13\left(\frac{-4}{3}\right)^2-3\left(\frac{-4}{3}\right)+27 \\
& =\frac{512}{27}-\frac{704}{27}+\frac{208}{9}+4+27 \\
& =\frac{512-704+624}{27}+31 \\
& =\frac{432}{27}+31 \\
& =16+31=47
\end{aligned}\)

3. If x=2& x=0 are zeroes of the polynomial \(2 x^3-5 x^2+p x+b\), then find the value of p & b.

Solution:

\(P(x)=2 x^3-5 x^2+P x+b\)

x= 2 and x= 0 are the zeroes of polynomials

then

=16-20 + 2P + b = 0

= 2P + b = 4 _______(1)

and  \(P(0)=2 \times 0^3-5(0)^2+P(0)+b=0\)

=0-0+0+b=0

b = 0 ________(2)

From (1) & (2), we get

2P + b = 4

2P + 0 = 4

2P = 4

\(\mathrm{P}=\frac{4}{2}=2\)

∴P = 2 and b = 0

4. Find the values of a & b, if \(x^2-4\) is a factor of \(a x^4+2 x^3-3 x^2+b x-4\)

Solution:

Let \(P(x)=a x^4+2 x^3-3 x^2+b x-4\)

\(x^4-4 \text { (or) }(x-2)(x+2)\) is a factor of p (x) then put x -2 in p(x)

\(\begin{array}{rl}
\mathrm{P}(2)= & a(2)^4+2(2)^3-3(2)^2+\mathrm{b}(2)-4=0 \\
= & 16 a+16-12+2 b-4=0 \\
& 16 a+2 b=0 \\
\div 2 & 8 a+b=0 ……………(1)
\end{array}\)

again put x=-2 in p(x)

\(\begin{array}{rl}
\mathrm{P}(-2) & =a(-2)^4+2(-2)^3-3(-2)^2+\mathrm{b}(-2)-4=0 \\
& =16 a-16-12-2 b-4=0 \\
& =16 a-2 b=32 \\
\div 2 & 8 a-b=16 \ldots \ldots \ldots \ldots(2)
\end{array}\)

Adding eqn (1) & (2) we get

\(\begin{aligned}
& 8 a+b=0 \\
& \underline{8 a-b}=16
\end{aligned}\) \(\begin{aligned}
16 a & =16 \\
a & =16 / 16=1
\end{aligned}\)

by eqn(l) we get

\(\begin{aligned}
& 8 \times 1+b=0 \\
& 8+b=0 \\
& b=-8 \\
& ∴ a=1 \text { and } b=-8
\end{aligned}\)

5. Factorise completely : \(x^8-y^8\)

Solution:

\(x^8-y^8\) \(=\left(x^4\right)^2-\left(y^4\right)^2\)

∴\(a^2-b^2=(a+b)(a-b)\)

\(\begin{aligned}
& =\left(x^4+y^4\right)\left(\left(x^2\right)^2-\left(y^2\right)^2\right) \\
& =\left(x^4+y^4\right)\left(x^2+y^2\right)\left(x^2-y^2\right) \\
& =\left(x^4+y^4\right)\left(x^2+y^2\right)(x+y)(x-y)
\end{aligned}\)

6. If a-b = 7& \(a^2+b^2=85\) find \(a^3-b^3\).

Solution:

a-b = 7& \(a^2+b^2=85\)

consider a-b=7

square both side

\(\begin{aligned}
& (a-b)^2=7^2 \\
& a^2-2 a b+b^2=49 \\
& 85-2 a b=49 \\
& 85-49=2 a b \\
& 2 a b=36 \\
& a b=\frac{36}{2}=18
\end{aligned}\)

then,

\(\begin{aligned}
a^3-b^3 & =(a-b)\left(a^2+b^2+a b\right) \\
& =(7)(85+18) \\
& =7 \times 103 \\
a^3-b^3 & =721
\end{aligned}\)

KSEEB Solutions for Class 9 Maths Chapter 1 Number Systems

Number of Systems Points To Remember

Any number that can be expressed in the form p/ q, where p & q are both integers & q * 0 is called a rational number usually, we take q>0, while p may be positive, negative or zero.
Rational numbers do not have a unique representation.

For example \( \frac{1}{3}=\frac{2}{6}=\frac{7}{21}=\frac{30}{90}\)  etc

•  Every rational number can be written in the form p/ q, where p, q are integers, q ≠ 0, p, q have no common factors (except 1). It is called in the lowest terms or simplest form.
• A number that cannot be expressed in the form p/q, where p, q are integers, q ≠ 0, p, q have no common factors (except l)is called an irrational number

For example  \( \sqrt{2}, \sqrt{3}, \sqrt{6},-\sqrt{7}, 2-\sqrt{5}, \pi\) all irrational number.

Read and Learn More KSEEB Solutions for Class 9 Maths 

The decimal expansion of a rational number is either terminating or non-terminating recurring (repeating), conversely, a number whose decimal expansion is terminating or non-terminating recurring is rational.

The decimal expansion of a rational number p/q, where p, q are integers, q>0, p & q have no common factors except 1 is:
1) Terminating if prime factors of q are 2 or 5 or both.
2) Non-terminating recurring if q has a prime factor other than 2 or 5.

The decimal expansion of an irrational number is non-terminating and non-recurring. Conversely, a number whose decimal expansion is non-terminating, and non-recurring is irrational.

• All rational numbers & all irrational numbers are real numbers. The collection of real numbers is denoted by R.
• Every real number (rational or irrational) can be represented by a unique point on the number line. Conversely, every point on the number line represents a unique real number.
• If m is rational & n is irrational, then m+n, m – n & n- mare irrational numbers.
• If m is a nonzero rational number & n is an irrational number, \(\frac{m}{n} \text { and } \frac{n}{m}\) — and — are irrational numbers.
• If a and b are positive real numbers, then the following results hold.

1) \(\sqrt{a b}=\sqrt{a} \sqrt{b} \\\)
2) \( \sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}} \\\)
3) \((\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=a-b \\\)
4) \((\sqrt{a}+\sqrt{b})^2=a+2 \sqrt{a b}+b \\\)
5) \((\sqrt{a}-\sqrt{b})^2=a-2 \sqrt{a b}+b \\\)
6) \((a+\sqrt{b})(a-\sqrt{b})=a^2-b\)

Class 9 Social Science

Class 9 Science

Class 9 Maths

 

• If the product of two irrational numbers is a rational number, then each number is called the rationalising factor of the other number.
• The process of multiplying an irrational number by its rationalising factor is called rationalisation.

KSEEB Class 9 Maths Number Systems Exercises 

Chapter 1 Number Systems Rule to Rationalise The Denominator Of a Fraction

• Multiply & divide the numerator & denominator of the given fraction by the rationalising factor of its denominator & simplify.
•  lf a>0 is areal number &n is a positive integer, then \(\sqrt[n]{a}=b\) if & only if \(\mathrm{b}^{\mathrm{n}}=a, \mathrm{~b}>0, \sqrt[n]{a}\) is also written as \(a^{1 / n}\)
• If a > 0 is a real number & m, n are integers n > o, m, n have no common factors except 1, then

\(\frac{a^m}{a^n}=\left(a^{\frac{1}{n}}\right)^m=(n \sqrt{a})^m=\sqrt[n]{a^m}\)

If a > 0 is a real number & m & n are rational num­bers then

1. \(a^m \cdot a^n=a^{m+n}\)

2. \(\left(a^m\right)^n=a^{m n}\)

3. \(\frac{a^m}{a^n}=a^{m-n}, m>n\)

4. \(\frac{a^m}{a^n}=\frac{1}{a^{n-m}}, \quad n>m\)

5. \(a^m b^m=(a b)^m\)

6. \(\frac{a^m}{b^m}=\left(\frac{a}{b}\right)^m\)

7. \(a^{-n}=\frac{1}{a^n}\)

8. \(a^0=1\)

9. \(a^1=a\)

Chapter 1 Number Systems Exercise 1.1

1. Is zero a rational number? Can you write it in the form\(\frac{p}{q}\), where p & q are integers & q≠0?

Solution: yes! zero is a rational number, we can write zero in the form\(\frac{p}{q}\) , where p & q are integers & \(q \neq 0\)as follows.

\(0=\frac{0}{1}=\frac{0}{2}=\frac{0}{3}\) etc.

2. Find six rational numbers between 3 & 4

Solution: There can be infinitely many rational numbers between 3 & 4.

Method 1:

\(\frac{3+4}{2}=\frac{7}{2}, \quad \frac{3+7 / 2}{2}=\frac{13}{4}\) \(\frac{3+\frac{13}{4}}{2}=\frac{25}{8}\) \(\frac{3+25 / 8}{2}=\frac{49}{16}, \quad \frac{3+\frac{49}{16}}{2}=\frac{97}{32}\) \(\frac{3+\frac{97}{32}}{2}=\frac{193}{64}\)

Thus, six rational numbers between 3 & 4 are

\(\frac{7}{2}, \frac{13}{4}, \frac{25}{8}, \frac{49}{16}, \frac{97}{32} \& \frac{193}{64}\)

Method 2 :

\(\begin{aligned}
& \frac{3}{1}=\frac{3 \times 7}{1 \times 7}=\frac{21}{7} \\
& \frac{4}{1}=\frac{4 \times 7}{1 \times 7}=\frac{28}{7}
\end{aligned} \mid 6+1=7\)

Thus, six rational numbers between 3 & 4 can be taken as \(\frac{22}{7}, \frac{23}{7}, \frac{24}{7}, \frac{25}{7}, \frac{26}{7} \& \frac{27}{7}\)

3. Find five rational numbers between \(\frac{3}{5} \& \frac{4}{5}\)

Solution:  \(\frac{3}{5}=\frac{3 \times 10}{5 \times 10}=\frac{30}{50}\)

\(\frac{4}{5}=\frac{4 \times 10}{5 \times 10}=\frac{40}{50}\)

Thus five rational numbers between \(\frac{3}{4} \& \frac{4}{5}\) can be taken as\(\frac{31}{50}, \frac{32}{50}, \frac{33}{50}, \frac{34}{50}, \frac{35}{50}\)

4. State whether the following statements are true or false. Give reasons for your answers

1. Every natural number is a whole number
   Solution: True, since the collection of whole numbers contains all natural numbers.
2. Every integer is a whole number.
   Solution: False, for example, -2 is an integer but not a whole number.
3. Every rational number is a whole number.
   Solution: False, for example, \(\frac{1}{2}\) is a rational number but not a whole number.

KSEEB Maths Chapter 1 Number Systems Answers 

Chapter 1 Number Systems Exercise 1.2

1. State whether the following statements are true or false. Justify your answers.

1.  Every irrational number is a real number.
   Solution: True, since the collection of real numbers is made up of rational & irrational numbers.
2. Every point on the number line is of the form \(\sqrt{m}\), where m is a natural number.
   Solution: False, because no negative number can be the square root of any natural number.
3. Every real number is an irrational number.
   Solution: False, for example, 2 is real but not irrational.

2. Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.

Solution: No, For example, \(\sqrt{9}\) = 3 is a rational number.

3. Show how \(\sqrt{5}\) can be represented on the number line.

Solution: Consider a unit square OABC & transfer it onto the number line making sure that the vertex O coincides with zero.

Then OB=\(\sqrt{1^2+1^2}=\sqrt{2}\)

Construct BD of unit length perpendicular to OB.

Then OD=\(\sqrt{(\sqrt{2})^2+1^2}=\sqrt{3}\)

construct DE of unit length perpendicular to OE.

Then OF=\(\sqrt{2^2+1^2}=\sqrt{5}\)

using a compass, with centre O & radius OF, draw an arc that intersects the number line in the point R, then R corresponds to \(\sqrt{5}\).

Chapter 1 Number Systems Exercise 1.3

1). Write the following in decimal form & say what kind of decimal expansion each has :

1.1\(\frac{36}{100}\)

1.2 \(\frac{1}{11}\)

1.3 \(4 \frac{1}{8}\)

1.4 \(\frac{3}{13}\)

1.5 \(\frac{2}{11}\)

1.6 \(\frac{329}{400}\)

Solution: 1.1) \(\frac{36}{100}=0.36\)

The decimal expansion is terminating

1.2)

The decimal expansion is non terminating repeating

1.3) \(4 \frac{1}{8}\)

\(4 \frac{1}{8}\) =\(\frac{4 \times 8+1}{8}=\frac{33}{8}\)

∴ \(4 \frac{1}{8}=4.125\)

The decimal expansion is terminating.

1.4) \(\frac{3}{13}\)

\(\frac{3}{13}=0.230769230769 \ldots \ldots=0 . \overline{230769}\)

The decimal expansion is non-terminating repeating.

1.5) \(\frac{2}{11}\)

∴ \(\frac{2}{11}=0.1818\)

The decimal expansion is non terminating repeating.

1.6) \(\frac{329}{400}=0.8225\)

The decimal expansion is terminating g.

2. You know that \(\frac{1}{7}=0 . \overline{142857}\) can you predict
what the decimal expansions of \(\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}\) the long division? If so, how?
[Hint: Study the remainders while finding the value of \(\frac{1}{7}\) carefully] 

Solution: yes! we can predict the decimal expansions of \(\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}\) without actually doing the long division as follows:

To predict the decimal expansion of \(\frac{2}{7}\), locate when the remainder becomes 2 & respective quotient (here it is 2). Then write the new quotient beginning from
there using the repeating digits 1,4,2,8,5,7.

∴ \(\frac{2}{7}=0 . \overline{285714}\)

\(\frac{3}{7}=0 . \overline{428571}\) \(\frac{4}{7}=0 . \overline{571428}\) \(\frac{5}{7}=0 . \overline{714285}\) \(\frac{6}{7}=0 . \overline{857142}\)

KSEEB Solutions Class 9 Number Systems Practice 

3. Express the following in the form \(p / q\) , where p & q are integers & q≠0
1) \(0 . \overline{6}\)
2) \(0.4 \overline{7}\)
3) \(0 . \overline{001}\)

Solution: 1) \(0 . \overline{6}\)  = Let x =  \(0 . \overline{6}=0.6666 \ldots\)

Multiplying both sides by 10 (since one digit is repeating) we get

\(\begin{aligned}
& 10 x=6.666 \ldots \ldots . \\
& \Rightarrow 10 x=6+0.6666 \ldots \ldots \\
& \Rightarrow 10 x=6+x \\
& \Rightarrow 10 x-x=6 \\
& \Rightarrow 9 x=6 \\
& \Rightarrow x=\frac{6}{9} \\
& x=\frac{2}{3}
\end{aligned}\)

Thus, \(0 . \overline{6}=\frac{2}{3}\)

Here, P = 2,  q=3(≠0)

2) \(0.4 \overline{7}\) = Let \(x=0.4 \overline{7}=0.47777 \ldots \ldots\)

Multiplying both sides by 10 (since one digit is repeating), we get

\(\begin{aligned}
& 10 x=4.7777 \ldots \ldots \\
& \Rightarrow 10 x=4.3+0.4777 \ldots \ldots \\
& \Rightarrow 10 x=4.3+x \\
& \Rightarrow 10 x-x=4.3 \\
& \Rightarrow 9 x=4.3 \\
& \Rightarrow x=\frac{4.3}{9}=\frac{43}{90}
\end{aligned}\)

Thus, \(0.4 \overline{7}=\frac{43}{90}\)

Here P = 43 & q = 90 (≠ 0)

3) \(0 . \overline{001}\) =Let \(x=0 . \overline{001}=0.001001001 \ldots \ldots\)

Multiplying both sides by 1000 (since three digits are repeating), we get

\(\begin{aligned}
& 1000 x=1.001001 \ldots . \\
& \Rightarrow 1000 x=1+0.001001001 \ldots \\
& \Rightarrow 1000 x=1+x \\
& \Rightarrow 1000 x-x=1 \\
& \Rightarrow 999 x=1
\end{aligned}\) \(\Rightarrow x=\frac{1}{999}\)

Thus, \(0 . \overline{001}=\frac{1}{999}\)

Here P = 1, q = 999(≠0)

4. Express 0.99999 in the form p/q. Are you surprised by your answer? With your teacher & classmates discuss why the answer makes sense.

Solution: Let x= 0.99999………..

Multiplying both sides by 10 (since one digit is repeating) we get

10x = 9.9999……..

10x =9 + 0.9999……..

10x=9 + x

10x – x = 9

9x = 9

\(x=\frac{9}{9}=1\)

Thus \(0.99999=1=\frac{1}{1}\)

Here P = 1, q = 1

Since 0.99999 goes on forever, so there is no gap between 1 & 0.99999… & hence they are equal.

5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of \(\frac{1}{17}\)? Perform the division to check your answer.

Solution: The Maximum number of digits in the repeating block of digits in the decimal expansion of \(\frac{1}{17}\) can be 16.

Thus \(\frac{1}{17}=0 . \overline{058823529411747}\)

By long division, the number of digits in the repeating block of digits in the decimal expansion of \(\frac{1}{17}=16\)

∴ The answer is verified.

6. Look at several examples of rational numbers in the form \(\frac{p}{q}(q \neq 0)\) where p & q are integers with no common factors other than 1 & having terminating decimal representations (expansions) can you guess what property q must satisfy?

Solution: Examples:

1) \(\frac{1}{2}=\frac{1}{2} \times \frac{5}{5}=\frac{5}{10}=0.5 \quad q=2\)

2) \(\frac{1}{4}=\frac{1}{4} \times \frac{25}{25}=\frac{25}{100}=0.25 \quad q=2^2\)

3) \(\frac{3}{8}=\frac{3}{8} \times \frac{125}{125}=\frac{375}{1000}=0.375 \quad q=2^3\)

4) \(\frac{31}{25}=\frac{31 \times 4}{25 \times 4}=\frac{124}{100}=1.24 \quad q=5^2\)

5) \(\frac{7}{125}=\frac{7 \times 8}{125 \times 8}=\frac{56}{1000}=0.056 \quad q=5^3\)

6) \(\frac{13}{20}=\frac{13 \times 5}{20 \times 5}=\frac{65}{100}=0.65 \quad q=2^2 \times 5\)

7) \(\frac{29}{16}=\frac{29}{16} \times \frac{625}{625}=\frac{18125}{10000}=1.8125 \quad q=2^4\)

7. Write three numbers whose decimal expansions are non-terminating, and nonrecurring.

Solution: 0.01001000100001………………..

0. 20200220002200002……………………

0. 003000300003………….

8. Find three different irrational numbers between the rational numbers \(\frac{5}{7} \& \frac{9}{11}\)

Solution:

Thus, \(\frac{5}{7}=0.714285 \ldots\) \(=0 . \overline{714285}\)

Thus, = \(\frac{9}{11}=0.8181 \ldots\) \(=0 . \overline{81}\)

Three different irrational numbers between the \(\frac{9}{11}=0.8181 \ldots\) rational numbers \(\frac{5}{7} \& \frac{9}{11}\) can be taken as

0. 750750075000 …………………….

0.7670767000767 ……………………

0.808008000800008 …………………

Class 9 Maths KSEEB Chapter 1 Explanations 

9. Classify the following numbers as rational or irrational

1) \(\sqrt{23}\)
2) \(\sqrt{225}\)
3) 0.3796
4) 7.478478
5) 1.101001000100001… 

Solution:

1) \(\sqrt{23}\)

Thus, \(\sqrt{23}=4.795831\)
The decimal expansion is non – terminating nonrecurring
∴ \(\sqrt{23}\) is an irrational number

2) \(\sqrt{225}=15=\frac{15}{1}\)
\(=\left(\frac{p}{q} \text { form }\right)\)

∴ \(\sqrt{225}\)
Here P = 15 & q = 1 (≠0)

3) 0.3796 = The decimal expansion is terminating
∴ 0.3796 is a rational number.

4) 7.478478 ………………..
7.478478 = \(7 . \overline{478}\)
∴ The decimal expansion is a non-terminating recurring
∴ 7.478478 is a rational number.

5) 1.101001000100001 …………………
The decimal expansion is non-terminating nonrecurring
∴ 1.101001000100001 is an irrational number.

Chapter 1 Number Systems Exercise 1.4

1. Visualise 3.765 on the number line using successive magnification.
Solution: 

2. Visualise \(4 . \overline{26}\) on the number line up to 4 decimal places.
Solution:

Chapter 1 Number Systems Exercise 1.5

1. Classify the following numbers as rational or irrational.

1) \(2-\sqrt{5}\)

Solution: 2 is a rational number & \(\sqrt{5}\) is an irrational number

∴ \(2-\sqrt{5}\) is an irrational number

(∵ The difference of a rational number & an irrational number is irrational)

2) \((3+\sqrt{23})-\sqrt{23}\)

Solution: \((3+\sqrt{23})-\sqrt{23}\) =3 which is a rational number.

3) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}=\frac{2}{7}\)

Solution: \(\frac{2 \sqrt{7}}{7 \sqrt{7}}=\frac{2}{7}\) Which is a rational number.

4) \(\frac{1}{\sqrt{2}}\)

Solution: 1 is a rational number & \(\sqrt{2}\) is an irrational number

∴ \(\frac{1}{\sqrt{2}}\) is an irrational number

(The quotient of a non zero rational number with an irrational number is irrational)

5) 2π

Solution: (2 ≠ 0) is a rational number & n is an irratio nal number.

∴2π is an irrational number.

∴ The product of a non-zero rational number with an irrational number is irrational.

2. Simplify each of the following expressions:

1) \((3+\sqrt{3})(2+\sqrt{2})\)

Solution: \((3+\sqrt{3})(2+\sqrt{2})\)

\(\begin{aligned}
& =3(2+\sqrt{2})+\sqrt{3}(2+\sqrt{2}) \\
& =3 \times 2 \times+3 \sqrt{2}+\sqrt{3} \times 2+\sqrt{3} \times \sqrt{2} \\
& =6+3 \sqrt{2}+2 \sqrt{3}+\sqrt{6}(\sqrt{a} \sqrt{b}=\sqrt{a b})
\end{aligned}\)

2) \((3+\sqrt{3})(3-\sqrt{3})\)

Solution: \((3+\sqrt{3})(3-\sqrt{3})=3^2-(\sqrt{3})^2\)

\(\left\{\begin{array}{l}
(a+\sqrt{b})(a-\sqrt{b}) \\
=a^2-b
\end{array}\right\}\)

3) \((\sqrt{5}+\sqrt{2})^2\)

Solution: \((\sqrt{5}+\sqrt{2})^2=(\sqrt{5})^2+2 \sqrt{5} \times \sqrt{2}+(\sqrt{2})^2\)

\(\begin{aligned}
& \left\{\begin{array}{c}
(\sqrt{a}+\sqrt{b})^2=(\sqrt{a})^2+2 \sqrt{a b}+(b)^2 \\
=a^2+2 \sqrt{a b}+b
\end{array}\right\} \\
& =5+2 \sqrt{10}+2 \\
& =7+2 \sqrt{10} \\
&
\end{aligned}\)

4) \((\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})\)

Solution: \((\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})\)

\(\begin{aligned}
& =(\sqrt{5})^2-(\sqrt{2})^2(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=a-b \\
& =5-2 \\
& =3
\end{aligned}\)

3. Recall π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is π=c/d This seems to contradict the fact that π is irrational. How will you resolve this contradiction?

Solution: There is no contradiction as either C or d is irrational & hence π is irrational.

KSEEB Chapter 1 Number Systems Solved Questions 

4. Represent \(\sqrt{9.3}\) on the number line.

Solution: Mark the distance 9.3 from a fixed point A on a given line to obtain a point B such that AB = 9.3 units. From B mark a distance of 1 unit & mark the new point as C. Find the midpoint of AC & mark that point as O. Draw a semi-circle with center O & radius OC.

Draw a line perpendicular to AC passing through B & intersecting the semi-circle at D. Then

BD = \(\sqrt{9.3}\)

5. Rationalise the denominators of the following:

1) \(\frac{1}{\sqrt{7}}\)

\(\frac{1}{\sqrt{7}}=\frac{1}{\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}}\)(multiplying & dividing by)

\(\sqrt{7}=\frac{\sqrt{7}}{7}\)

2) \(\frac{1}{\sqrt{7}-\sqrt{6}}\)

Solution: \(\frac{1}{\sqrt{7}-\sqrt{6}}=\frac{1}{\sqrt{7}-\sqrt{6}} \times \frac{\sqrt{7}+\sqrt{6}}{\sqrt{7}+\sqrt{6}}\)

(multiplying & dividing by \(\sqrt{7}+\sqrt{6}\))

\(\frac{\sqrt{7}+\sqrt{6}}{7-6}=\sqrt{7}+\sqrt{6}\)

3) \(\frac{1}{\sqrt{5}+\sqrt{2}}\)

Solution: \(\frac{1}{\sqrt{5}+\sqrt{2}}=\frac{1}{\sqrt{5}+\sqrt{2}} \times \frac{\sqrt{5}-\sqrt{2}}{\sqrt{5}-\sqrt{2}}\)

(multiplying & dividing by \(\sqrt{5}-\sqrt{2}\))

\(=\frac{\sqrt{5}-\sqrt{2}}{5-2}=\frac{\sqrt{5}-\sqrt{2}}{3}\)

4) \(\frac{1}{\sqrt{7}-2}\)

Solution: \(\frac{1}{\sqrt{7}-2}=\frac{1}{\sqrt{7}-2} \times \frac{\sqrt{7}+2}{\sqrt{7}+2}\)

(multiplying & dividing by \(\sqrt{7}+2)\))

\(=\frac{\sqrt{7}+2}{7-4}=\frac{\sqrt{7}+2}{3}\)

Chapter 1 Number Systems Exercise 1.6

1. Find
1) \(64^{1 / 2}\)
Solution: \(64^{1 / 2}=\left(8^2\right)^{1 / 2}=8^{2 \times 1 / 2}=8^1=8\)

2) \(32^{1 / 5}\)
Solution: \(32^{1 / 5}=\left(2^5\right)^{1 / 5}=2^{5 \times 1 / 5}=2^1=2\)

3) \(125^{1 / 3}\)
Solution: \(125^{1 / 3}=\left(5^3\right)^{1 / 3}=5^{3 \times 1 / 3}=5^1=5\)

2. Find
1) \(9^{3 / 2}\)
Solution: \(9^{3 / 2}=\left(3^2\right)^{3 / 2}=3^{2 \times 3 / 2}=3^3=27\)

2) \(32^{2 / 5}\)
Solution: \(32^{2 / 5}=2^{5 \times 2 / 5}=2^2=4\)

3) \(16^{3 / 4}\)
Solution: \(16^{3 / 4}=2^{4 x^3 / 4}=2^3=8\)

4) \(125^{-1 / 3}\)
Solution: \(125^{-1 / 3}=\left(5^3\right)^{-1 / 3}=5^{3 \times-1 / 3}=5^{-1}=\frac{1}{5}\)

3. Simplify
1) \(2^{2 / 3} \times 2^{1 / 5}\)
solution: \(2^{2 / 3} \times 2^{1 / 5}=2^{\frac{2}{3}+\frac{1}{5}}=2^{\frac{10+3}{15}}=2^{\frac{13}{15}}\)

2) \(\left(\frac{1}{3^3}\right)^7\)
Solution: \(\left(\frac{1}{3^3}\right)^7=\frac{1^7}{\left(3^3\right)^7}=\frac{1}{3^{21}}=3^{-21}\)

3) \(\frac{11^{1 / 2}}{11^{1 / 4}}\)
Solution: \(\frac{11^{1 / 2}}{11^{1 / 4}}=11^{1 / 2-1 / 4}=11^{1 / 4}\)

4) \(7^{1 / 2} \times 8^{1 / 2}\)
Solution: \(7^{1 / 2} \times 8^{1 / 2}=(7 \times 8)^{1 / 2}=56^{1 / 2}\)

Chapter 1 Number Systems Choose the correct answer from the following

1. Which of the following is a rational number?

1. \(\sqrt{5}\)
2. π
3. 0.101001000100001
4. 0.853853853

Solution: 4) 0.853853853

2. π is :

1. a rational number
2. an integer
3. an irrational number
4. a whole number

Solution: 3) an irrational number

3. The value of \(\sqrt[4]{\sqrt[3]{2^2}}\) is equal to

1. \(2^{-1 / 6}\)
2. \(2^{-6}\)
3. \(2^{1 / 6}\)
4. \(2^6\)

Solution: 3) \(2^{1 / 6}\)

KSEEB Maths Solutions Chapter 1 Step-By-Step Guide 

4. Which of the following is irrational number?

1. 0.15
2. \(0.15 \overline{16}\)
3. \(0 . \overline{1516}\)
4. 0.501500150001

Solution: 3) \(0 . \overline{1516}\)

5. The value of \(\frac{2^{\circ} \times 7^{\circ}}{5^{\circ}}\) is

1. 1
2. 0
3. \(\frac{9}{5}\)
4. \(1 / 5\)

Solution: 1) 1

6. Two rational numbers between \(\frac{2}{3} \& \frac{5}{3}\) are

1. \(\frac{1}{6} \& \frac{2}{6}\)
2. \(\frac{1}{2} \& \frac{2}{7}\)
3. \(\frac{5}{6} \& \frac{7}{6}\)
4. \(\frac{2}{3} \& \frac{4}{3}\)

Solution: \(\frac{5}{6} \& \frac{7}{6}\)

7. Every rational number is

1. a natural number
2. an integer
3. a real number
4. a whole number

Solution: 3) a real number

8. If \(x^{1 / 2}=49^{1 / 24}\) then x is equal to :

1. 49
2. 2
3. 12
4. 7

Solution: 4) 7

9. If \(8^x=\frac{64}{2^x}\) then the value of x is

1. 3
2. 1
3. 1/2
4. 3/-2

Solution: 4) 3/-2

10. \((0.001)^{1 / 3}\) is equal to

1. 0.1
2. 0.001
3. 0.01
4. 0.0001

Solution: 1) 0.1

11. If a = 2 & b = 3, then the value of \(b^a\) is

1. 4
2. 9
3. 2
4. 3

Solution: 2) 9

12. The decimal form of \(\frac{1}{500}\) is

1. 0.002
2. 0.02
3. 0.2
4. 0.005

Solution: 1) 0.002

13. The product of any two irrational number is

1. always an irrational number
2. always a rational number
3. always an integer
4. sometimes rational, sometimes irrational.

Solution: 4) sometimes rational, sometimes irrational.

14. The value of \(0 . \overline{25}\) is equal to 

1. \(\frac{65}{99}\)
2. \(\frac{37}{99}\)
3. \(\frac{5}{9}\)
4. \(\frac{25}{99}\)

Solution: 4) \(\frac{25}{99}\)

15. After rationalising the denominator of \(\frac{7}{3 \sqrt{3}-2 \sqrt{3}}\) we get the denominator as.

1. 13
2. 19
3. 5
4. 35

Solution: 2) 19

Chapter 1 Number Systems One Mark Questions

1. Write the simplest form of a rational number \(\frac{177}{413}\)

Solution: \(\frac{177}{413}=\frac{59 \times 3}{59 \times 7}=\frac{3}{7}\)

2. Find two rational numbers between \(\frac{1}{3} \& \frac{4}{5}\)

Solution: \(\frac{1}{3}=\frac{1 \times 5}{3 \times 5}=\frac{5}{15}\)

\(\frac{4}{5}=\frac{4 \times 3}{5 \times 3}=\frac{12}{15}\)

Hence two rational numbers can be taken as \(\frac{6}{15}, \frac{8}{15}\)

3. Find two irrational numbers between 0.1 & 0.12

Solution: The two irrational numbers between 0.1 & 0.12 are

0.101001001 & 0.11010010001.

Class 9 KSEEB Maths Chapter 1 Video Solutions 

4. Write the sum of \(2 \sqrt{5} \& 3 \sqrt{7}\)

Solution: \(2 \sqrt{5}+3 \sqrt{7}\)

5. Write the sum of \(0 . \overline{3}+0 . \overline{4}\)

Solution: \(0 . \overline{3}+0 . \overline{4}=(0.333 \ldots \ldots \ldots)+(0.444 \ldots \ldots . .)\)

= 0.777……….

6. Simplify \((\sqrt{2}+\sqrt{5})^2\)

Solution:

\(\begin{aligned}
(\sqrt{2}+\sqrt{5})^2 & =(\sqrt{2})^2+2 \sqrt{2} \sqrt{5}+(\sqrt{5})^2 \\
= & 2+2 \sqrt{10}+5 \\
= & 7+2 \sqrt{10}
\end{aligned}\)

7. Write the equivalent of \(\sqrt{12} \times \sqrt{8}\)

Solution:

\(\begin{aligned}
\sqrt{12} \times \sqrt{8} & =\sqrt{4 \times 3} \times \sqrt{4 \times 2} \\
& =2 \sqrt{3} \times 2 \sqrt{2} \\
& =4 \sqrt{3 \times 2} \\
& =4 \sqrt{6}
\end{aligned}\)

8. If \(x=\frac{\sqrt{7}}{5} \& \frac{5}{x}=\mathrm{P} \sqrt{7}\) , then find the value of P

Solution:

\(\frac{5}{x}=P \sqrt{7}\) \(\begin{aligned}
& \frac{5}{\sqrt{7}} \times 5=P \sqrt{7} \\
& 25=P \sqrt{7} \times \sqrt{7} \\
& \Rightarrow \quad P=\frac{25}{7}
\end{aligned}\)

9. Calculate the quotient obtained when \(\sqrt{1500}\) is divided by \(2 \sqrt{15}\)

Solution:

\(\begin{aligned}
\frac{\sqrt{1500}}{2 \sqrt{15}} & =\frac{1}{2} \times \sqrt{\frac{1500}{15}} \\
& =\frac{1}{2} \sqrt{100}=\frac{10}{2}=5
\end{aligned}\)

10. Write the rationalising factor of \(\frac{1}{\sqrt{50}}\)

Solution: \(\frac{1}{\sqrt{50}}=\frac{1}{\sqrt{5 \times 5 \times 2}}=\frac{1}{5 \sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{10}\)

∴ \(\sqrt{2}\) is a rationalising factor.

Chapter 1 Number Systems Two Mark Questions

1. Calculate the value of \(2 . \overline{9}\) in the form of \(\frac{p}{q}\) where p & q are integers & q ≠ 0.

Soution: \(\text { Let } x=2 . \overline{9}=2.9999 \text {…………. }\)

\(\begin{aligned}
& \Rightarrow 10 x=29.999 \ldots \ldots \\
& \Rightarrow 10 x=27+2.999 \ldots . \\
& \Rightarrow 10 x=27+x \\
& \Rightarrow 10 x-x=27 \\
& \Rightarrow 9 x=27 \\
& \Rightarrow x=27 / 9 \\
& \Rightarrow x=3
\end{aligned}\)

2. If 7x= 1, then find the decimal expansion of x.

Solution: \(x=\frac{1}{7}\)

∴ \(x=0 . \overline{142857}\)

3. In the following equations, find which variables x, y, z etc., represent rational number & which represent irrational numbers.

1) \(x^2=5\)

Solution: \(x=\sqrt{5}\), which is an irrational number.

2) \(y^2=9\)

Solution: \(y=\sqrt{9}=3\), which is a rational number.

3) \(z^2=0.04\)

Solution: \(z^2=\sqrt{0.04}=0.2=\frac{2}{10}=\frac{1}{5}\) which is a rational number.

4) \(\mathbf{u}^2=\frac{17}{4}\)

Solution: \(u=\sqrt{\frac{17}{4}}=\frac{\sqrt{17}}{\sqrt{4}}=\frac{\sqrt{17}}{2}=\frac{1}{2} \times \sqrt{17}\)

\(\frac{1}{2}\) is a rational number & \(\sqrt{17}\) is an irrational number.

∴ \(\frac{1}{2} \times \sqrt{17}\) is an irrational number.

4. Express the decimal number \(2.2 \overline{18}\) in the form of \(\frac{p}{q}\) where p & q are integers & q ≠ 0

Solution: Let \(x=2.2 \overline{18}=2.2181818\)

\(\begin{aligned}
& 10 x=22.181818 \ldots \ldots \\
& 1000 x=2218.1818 \ldots . \\
& 1000 x=2196+22.181818 \ldots . \\
& 1000 x=2196+10 x \\
& 1000 x-10 x=2196 \\
& 990 x=2196
\end{aligned}\) \(x=\frac{2196}{990}=\frac{2 \times 3 \times 3 \times 122}{2 \times 3 \times 3 \times 55}\)

x = \(\frac{122}{55}\)

KSEEB Solutions for 9th Standard Maths Number Systems 

5. Simplify: \(\sqrt[4]{16}-6 \sqrt[3]{343}+18 \sqrt[5]{243}-\sqrt{196}\)

Solution: \(\sqrt[4]{2^4}-6 \sqrt[3]{7^3}+18 \sqrt[5]{3^5}-\sqrt{14^2}\)

\(\begin{aligned}
& =2-(6 \times 7)+(18 \times 3)-14 \\
& =2-42+54-14 \\
& =56-56 \\
& =0
\end{aligned}\)

6. Simplify the product \((4 \sqrt{3}+3 \sqrt{2})(4 \sqrt{3}-3 \sqrt{2})\)

Solution: \((4 \sqrt{3}+3 \sqrt{2}) \times(4 \sqrt{3}-3 \sqrt{2})\)

\(\begin{aligned}
& =(4 \sqrt{3})^2-(3 \sqrt{2})^2\left\{(a+b)(a-b)=a^2-b^2\right\} \\
& =4^2(\sqrt{3})^2-3^2(\sqrt{2})^2 \\
& =16 \times 3-9 \times 2 \\
& =48-18=30
\end{aligned}\)

7. Calculate the value of \(\left[\left\{(81)^{-1 / 2}\right\}^{-\frac{1}{4}}\right]^2\)

Solution: \(\left[\left\{(81)^{-1 / 2}\right\}^{-\frac{1}{4}}\right]^2\)

\(\begin{aligned}
& =(81)^{-1 / 2 \times \frac{1}{4} \times 2} \\
& =(81)^{\frac{2}{8}} \\
& =(81)^{\frac{1}{4}}=\left(3^4\right)^{1 / 4} \\
& =3^1=3
\end{aligned}\)

8. Find the value of \(\frac{3^{30}+3^{29}+3^{28}}{3^{31}+3^{30}-3^{29}}\)

Solution: \(\frac{3^{30}+3^{29}+3^{28}}{3^{31}+3^{30}-3^{29}}=\frac{3^{28}\left(3^2+3^1+1\right)}{3^{29}\left(3^2+3^1-1\right)}\)

\(=\frac{1}{3} \frac{(9+3+1)}{(9+3-1)}\) \(=\frac{1}{3} \times \frac{13}{11}\) \(=\frac{13}{33}\)

9. If a = 3 & b= 2, then find the value of \(a^b+b^a\)

Solution: Given a = 3 & b = 2

\(\begin{aligned}
a^b+b^a & =3^2+2^3 \\
& =9+8 \\
& =17
\end{aligned}\)

10. Simplify: \(\frac{6-4 \sqrt{3}}{6+4 \sqrt{3}}\) by rationalising the denominator.

Solution: \(\frac{6-4 \sqrt{3}}{6+4 \sqrt{3}}=\frac{6-4 \sqrt{3}}{6+4 \sqrt{3}} \times \frac{6-4 \sqrt{3}}{6-4 \sqrt{3}}\)

\(=\frac{(6-4 \sqrt{3})^2}{6^2-4^2(\sqrt{3})^2}=\frac{36+48-48 \sqrt{3}}{36-48}\) \(\begin{aligned}
& =\frac{84-48 \sqrt{3}}{-12} \\
& =\frac{12(7-4 \sqrt{3})}{-12}
\end{aligned}\) \(\begin{aligned}
& =-(7-4 \sqrt{3}) \\
& =-7+4 \sqrt{3}
\end{aligned}\)

11. If \(\sqrt{2}\) =1.414, find the value of \(\frac{1}{\sqrt{2}+1}\)

Solution: \(\frac{1}{\sqrt{2}+1}=\frac{1}{\sqrt{2}+1} \times \frac{\sqrt{2}-1}{\sqrt{2}-1}\)

\(=\frac{\sqrt{2}-1}{(\sqrt{2})^2-1^2}\) \(=\frac{\sqrt{2}-1}{2-1}=\frac{1.1414-1}{1}=0.414\)

12. Find six rational numbers between 3 & 4

Solution: Let a = 3 & b = 4

Here, we find six rational numbers i.e., n = 6

So, d = \(\frac{b-a}{n+1}=\frac{4-3}{6+1}=\frac{1}{7}\)

1st rational number = \(a+d=3+\frac{1}{7}=\frac{22}{7}\)

2nd rational number = \(a+2 d=3+\frac{2}{7}=\frac{23}{7}\)

3rd rational number = \(a+3 d=3+\frac{3}{7}=\frac{24}{7}\)

4th rational number = \(a+4 d=3+\frac{4}{7}=\frac{25}{7}\)

5th rational number = \(a+5 d=3+\frac{5}{7}=\frac{26}{7}\)

6th rational number = \(a+6 d=3+\frac{6}{7}=\frac{27}{7}\)

So, six rational numbers are \(\frac{22}{7}, \frac{23}{7}, \frac{24}{7}, \frac{25}{7}, \frac{26}{7} \& \frac{27}{7}\)

Chapter 1 Number Systems Three Mark Questions

1. Find three rational numbers between \(\frac{5}{7} \& \frac{9}{11}\)

Solution: Since LCM of 7 & 11 is 77.

∴ \(\frac{9}{11}=\frac{9}{11} \times \frac{7}{7}=\frac{63}{77} \times \frac{3}{3}=\frac{441}{539}\)

\(\frac{5}{7}=\frac{5}{7} \times \frac{11}{11}=\frac{55}{77} \times \frac{3}{3}=\frac{385}{539}\)

Hence, three rational numbers between \(\frac{5}{7}\) & \(\frac{9}{11}\) are \(\frac{386}{539}, \frac{387}{539}, \frac{388}{539}\)

2. Represent \(\sqrt{5}\) on the number line.

Solution: w.k.t. \(\sqrt{5}=\sqrt{4+1}=\sqrt{2^2+1^2}\)

Draw a right angled ΔOBA such that OB = 2 units, AB = 1 unit & [\(\lfloor\mathrm{OBA}\) = 90°

By Pythagora’s theorem, we have

\(\mathrm{OA}^2=\mathrm{OB}^2+\mathrm{AB}^2=2^2+1^2\) \(\mathrm{OA}=\sqrt{4+1}=\sqrt{5}\)

Now, take O as, center, OA= \(=\sqrt{5}\) as radius draw an arc that intersects the line at point C. Hence, the point R represents \(\sqrt{5}\)

KSEEB Maths Chapter 1 Number Systems Free Solutions 

3. Evaluate: \(\sqrt{5+2 \sqrt{6}}+\sqrt{8-2 \sqrt{15}}\)

Solution: \(\sqrt{5+2 \sqrt{6}}=\sqrt{3+2+2 \sqrt{6}}=\sqrt{(\sqrt{3}+\sqrt{2})^2}\)

\(=\sqrt{3}+\sqrt{2}\) \(\begin{aligned}
\sqrt{8-2 \sqrt{15}} & =\sqrt{5+3-2 \sqrt{15}} \\
& =\sqrt{(\sqrt{5}-\sqrt{3})^2} \\
& =\sqrt{5}-\sqrt{3}
\end{aligned}\)

∴ \(\sqrt{5+2 \sqrt{6}}+\sqrt{8-2 \sqrt{5}}=\sqrt{3}+\sqrt{2}+\sqrt{5}-\sqrt{3}\)

\(=\sqrt{2}+\sqrt{5}\)

4. Show that: \(\frac{x^{a(b-c)}}{x^{b(a-c)}} \div\left[\frac{\left(x^b\right)}{\left(x^a\right)}\right]^c=1\)

Solution: LHS: \(\frac{x^{a(b-c)}}{x^{b(a-c)}} \times\left[\frac{\left(x^a\right)}{\left(x^b\right)}\right]^c\)

\(\begin{aligned}
& =\frac{x^{a b-a c}}{x^{b a-b c}} \times \frac{x^{a c}}{x^{b c}} \\
& =\frac{x^{a b-a c+a c}}{x^{a b-b c+b c}} \\
& =\frac{x^{a b}}{x^{a b}} \\
& =x^{a b-a b}
\end{aligned}\)

\(=x^0=1\) = RHS

Hence Proved.

5. Simplify: \(\left(\frac{5^{-1} \times 7^2}{5^2 \times 7^{-4}}\right)^{7 / 2} \times\left(\frac{5^{-2} \times 7^3}{5^3 \times 7^{-5}}\right)^{-5 / 2}\)

Solution: \(\left(\frac{5^{-1} \times 7^2}{5^2 \times 7^{-4}}\right)^{7 / 2} \times\left(\frac{5^{-2} \times 7^3}{5^4 \times 7^{-5}}\right)^{-5 / 2}\)

\(\begin{aligned}
& =\left(\frac{7^4 \times 7^2}{5^2 \times 5^1}\right)^{7 / 2} \times\left(\frac{7^5 \times 7^3}{5^3 \times 5^2}\right)^{-5 / 2} \\
& =\left(\frac{7^6}{5^3}\right)^{7 / 2} \times\left(\frac{7^8}{5^5}\right)^{-5 / 2}
\end{aligned}\) \(=\frac{7^{6 \times 7 / 2}}{5^{3 x^{7 / 2}}} \times\left(\frac{5^5}{7^8}\right)^{5 / 2}\) \(=\frac{7^{21}}{5^{21 / 2}} \times \frac{5^{25 / 2}}{7^{20}}\) \(=7^{21-20} \times 5^{\frac{25}{2}-\frac{21}{2}}\) \(=7^1 \times 5^{\frac{2}{4}}=7^1 \times 5^2=175\)

6. If x= 5 & y= 2, then find the value of
1) \(\left(x^y+y^x\right)^{-1}\)
2) \(\left(x^y+y^y\right)^{-1}\)

Solution: (1) = \(\left(5^2+2^5\right)^{-1}\)

\(\begin{aligned}
& =(25+32)^{-1} \\
& =(57)^{-1}=\frac{1}{57}
\end{aligned}\)

(2) \(=\left(5^2+2^2\right)^{-1}\)

\(\begin{aligned}
& =(25+4)^{-1} \\
& =(29)^{-1} \\
& =\frac{1}{29}
\end{aligned}\)

7. If x= \(x=3-2 \sqrt{2}\), find the value of \(\sqrt{x}+\frac{1}{\sqrt{x}}\)

Solution: \(x=3-2 \sqrt{2}\)

\(\frac{1}{x}=\frac{1}{3-2 \sqrt{2}} \times \frac{3+2 \sqrt{2}}{3+2 \sqrt{2}}\) \(\begin{aligned}
& =\frac{3+2 \sqrt{2}}{3^2-2^2(\sqrt{2})^2} \\
& =\frac{3+2 \sqrt{2}}{9-8}
\end{aligned}\) \(\begin{aligned}
& \frac{1}{x}=3+2 \sqrt{2} \\
& \left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)^2=x+\frac{1}{x}+2 \sqrt{x} \times \frac{1}{\sqrt{x}}
\end{aligned}\) \(=x+\frac{1}{x}+2\) \(=3-2 \sqrt{2}+3+2 \sqrt{2}+2\) \(\begin{aligned}
& \left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)^2=8 \\
& =\sqrt{8}
\end{aligned}\) \(=\pm 2 \sqrt{2}\)

8. Find the values of a & b when \(\frac{5+\sqrt{6}}{5-\sqrt{6}}\)

Solution: \(\frac{5+\sqrt{6}}{5-\sqrt{6}}=\frac{5+\sqrt{6}}{5-\sqrt{6}} \times \frac{5+\sqrt{6}}{5+\sqrt{6}}\)

\(=\frac{(5+\sqrt{6})^2}{5^2-(6)^2}=\frac{25+6+10 \sqrt{6}}{25-6}\) \(=\frac{31+10 \sqrt{6}}{19}\)

∴ \(a+b \sqrt{6}=\frac{31}{19}+\frac{10}{19} \sqrt{6}\)

comparing the powers of both sides, we

\(a=\frac{31}{19}\), \(b=\frac{10}{19}\)

9. Find the value of \(\left(x-\frac{1}{x}\right)^3\), if \(x=1+\sqrt{2}\)

Solution: \(x=1+\sqrt{2}\)

\(\frac{1}{x}=\frac{1}{1+\sqrt{2}} \times \frac{1-\sqrt{2}}{1-\sqrt{2}}\) \(\begin{gathered}
=\frac{1-\sqrt{2}}{1^2-\sqrt{2}} \\
=\frac{1-\sqrt{2}}{-1} \\
=-1+\sqrt{2}
\end{gathered}\) \(\left(x-\frac{1}{x}\right)^3=[(1+\sqrt{2})-(-1+\sqrt{2})]^3\) \(\begin{aligned}
& =(1+\sqrt{2}+1-\sqrt{2})^3 \\
& =(2)^3 \\
& =8
\end{aligned}\)

10. Write \(\sqrt[3]{4}, \sqrt{3}, \sqrt[4]{6}\) in ascending order.

Solution: \(4^{1 / 3}, 3^{1 / 2}, 6^{1 / 4}\), LCM of 3, 2, 4 is 12.

\(4^{1 / 3}=4^{1 / 3^{\times 2} 12}=4^{\frac{4}{12}}=\left(4^4\right)^{1 / 12}=(729)^{1 / 12}\) \(3^{1 / 2}=3^{1 / 2 \times \frac{12}{12}}=3^{\frac{6}{12}}=\left(3^6\right)^{1 / 12}=(256)^{1 / 12}\) \(6^{1 / 4}=6^{1 / 4^{\frac{12}{12}}}=6^{\frac{3}{12}}=\left(6^3\right)^{1 / 12}=(729)^{1 / 12}\)

ascending order =

\((216)^{1 / 12},(256)^{1 / 12},(729)^{1 / 12}\)

i.e; \(\sqrt[4]{6}, \quad \sqrt[3]{4}, \quad \sqrt{3}\)

11. Rationalise the denominator of \(\frac{30}{5 \sqrt{3}-3 \sqrt{5}}\)

Solution: \(\frac{30}{5 \sqrt{3}-3 \sqrt{5}}=\frac{30}{5 \sqrt{3}-3 \sqrt{5}} \times \frac{5 \sqrt{3}+3 \sqrt{5}}{5 \sqrt{3}+3 \sqrt{5}}\)

\(=\frac{30(5 \sqrt{3}+3 \sqrt{5})}{(5 \sqrt{3})^2-(3 \sqrt{5})^2}\)

⇒ \(\begin{aligned}
& =\frac{30(5 \sqrt{3}+3 \sqrt{5})}{75-45} \\
& =\frac{30(5 \sqrt{3}+3 \sqrt{5})}{30} \\
& =5 \sqrt{3}+3 \sqrt{5}
\end{aligned}\)

KSEEB Class 9 Chapter 1 Number Systems Revision Notes 

12. Prove that : \(\frac{a^{-1}}{a^{-1}+b^{-1}}+\frac{a^{-1}}{a^{-1}-b^{-1}}=\frac{-(2 b)^2}{a^2+b^2}\)

Solution: LHS = \(\frac{a^{-1}}{a^{-1}+b^{-1}}+\frac{a^{-1}}{a^{-1}-b^{-1}}\)

\(\begin{aligned}
& =\frac{\frac{1}{a}}{\frac{1}{a}+\frac{1}{b}}+\frac{\frac{1}{a}}{\frac{1}{a}-\frac{1}{b}} \\
& =\frac{\frac{1}{a}}{\frac{b+a}{a b}}+\frac{\frac{1}{a}}{\frac{b-a}{a b}} \\
& =\frac{1}{a} \times \frac{a b}{a+b}+\frac{1}{a} \times \frac{a b}{b-a} \\
& =\frac{b}{a+b}+\frac{b}{b-a} \\
& =\frac{(b-a) b+b(a+b)}{(a+b)(b-a)} \\
& =\frac{b^2-a b+a b+b^2}{b^2-a^2} \\
& =\frac{\left(2 b^2\right)}{b^2-a^2} \\
& =\frac{-\left(2 b^2\right)}{\left(a^2-b^2\right)} \\
&
\end{aligned}\)

13. Simplify: \(\frac{\sqrt{2}}{\sqrt{5}+2}-\frac{2}{\sqrt{10}-2 \sqrt{2}}+\frac{8}{\sqrt{2}}\)

 Solution: \(\left(\frac{\sqrt{2}}{\sqrt{5}+2} \times \frac{\sqrt{5}-2}{\sqrt{5}-2}\right)-\left(\frac{2}{\sqrt{10}-2 \sqrt{2}} \times \frac{\sqrt{10}+2 \sqrt{2}}{\sqrt{10}+2 \sqrt{2}}\right)\) + \(\frac{8}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}\)

\(=\left(\frac{\sqrt{10}-2 \sqrt{2}}{5-4}\right)-\left(\frac{2(\sqrt{10}+2 \sqrt{2})}{10-8}\right)+\frac{8 \sqrt{2}}{2}\) \(=(\sqrt{10}-2 \sqrt{2})-2\left(\frac{\sqrt{10}+2 \sqrt{2}}{2}\right)+4 \sqrt{2}\) \(=\sqrt{10}-2 \sqrt{2}-\sqrt{10}-2 \sqrt{2}+4 \sqrt{2}\)

= 0

Chapter 1 Number Systems Four Mark Questions

1. If a = \(\frac{3-\sqrt{5}}{3+\sqrt{5}}\) & b = \(\frac{3+\sqrt{5}}{3-\sqrt{5}}\) find \(a^2-b^2\)

Solution: \(\mathrm{a}^2-\mathrm{b}^2=(\mathrm{a}+\mathrm{b})(\mathrm{a}-\mathrm{b})\)

\(\begin{aligned}
a+b & =\frac{3-\sqrt{5}}{3+\sqrt{5}}+\frac{3+\sqrt{5}}{3-\sqrt{5}} \\
& =\frac{3-\sqrt{5}}{3+\sqrt{5}} \times \frac{3-\sqrt{5}}{3-\sqrt{5}}+\frac{3+\sqrt{5}}{3-\sqrt{5}} \times \frac{3+\sqrt{5}}{3+\sqrt{5}} \\
& =\frac{(3-\sqrt{5})^2}{9-5}+\frac{(3+\sqrt{5})^2}{9-5} \\
& =\frac{9+5-6 \sqrt{5}}{4}+\frac{9+5+6 \sqrt{5}}{4} \\
& =\frac{14-6 \sqrt{5}+14+6 \sqrt{5}}{4}
\end{aligned}\)

\(a+b=\frac{28}{4}=7\) ……………………..(1)

\(\begin{aligned}
& a-b=\left(\frac{3-\sqrt{5}}{3+\sqrt{5}}\right)-\left(\frac{3+\sqrt{5}}{3-\sqrt{5}}\right) \\
& =\left(\frac{3-\sqrt{5}}{3+\sqrt{5}} \times \frac{3-\sqrt{5}}{3-\sqrt{5}}\right)-\left(\frac{3+\sqrt{5}}{3-\sqrt{5}} \times \frac{3+\sqrt{5}}{3+\sqrt{5}}\right) \\
& =\frac{(3-\sqrt{5})^2}{9-5}-\frac{(3+\sqrt{5})^2}{9-5} \\
& =\frac{9+5-6 \sqrt{5}}{4}-\frac{9+5+6 \sqrt{5}}{4} \\
& =\frac{14-6 \sqrt{5}}{4}-\frac{14+6 \sqrt{5}}{4} \\
& =\frac{14-6 \sqrt{5}-14-6 \sqrt{5}}{4} \\
& =\frac{-12 \sqrt{5}}{4}
\end{aligned}\)

\(a-b=-3 \sqrt{5}\) ……………………(2)

from (1) & (2) we get

\(\begin{aligned}
& a^2-b^2=(a+b)(a-b) \\
& =7 \times(-3 \sqrt{5}) \\
& =-21 \sqrt{5} \\
&
\end{aligned}\)

2. Express \(1.3 \overline{2}+0 . \overline{35}\) in the form \(\frac{p}{q}\), where p & q are integers & q ≠ 0

Solution: Let \(x=1.3 \overline{2}=1.32222 \ldots \ldots\)

\(100 x=132.2222 \ldots \ldots\) \(\begin{aligned}
& 10 x=13.2222 \ldots \ldots . \\
& 100 x-10 x=(132.222 \ldots)-(13.222 \ldots .) \\
& 90 x=119 \\
& x=\frac{119}{90}
\end{aligned}\)

Again let y = \(0.3 \overline{5}=0.353535 \ldots\)

\(\begin{aligned}
& 100 y=35.3535 \ldots . \\
& 100 y-y=(35.3535)-(0.3535 \ldots \ldots)
\end{aligned}\) \(\begin{array}{r}
99 y=35 \\
y=\frac{35}{99}
\end{array}\)

∴ \(1.3 \overline{2}+0.3 \overline{5}=x+y=\frac{119}{90}+\frac{35}{99}\)

\(=\frac{119 \times 11+35 \times 10}{990}=\frac{1309+350}{990}=\frac{1659}{990}\)

3. Show that : \(\frac{1}{1+x^{a-b}}+\frac{1}{1+x^{b-a}}=1\)

Solution: LHS = \(\frac{1}{1+x^{a-b}}+\frac{1}{1+x^{b-a}}\)

\(=\frac{1}{1+\frac{x^a}{x^b}}+\frac{1}{1+\frac{x^b}{x^a}}\) \(=\frac{\frac{1}{x^b+x^a}}{x^b}+\frac{1}{\frac{x^a+x^b}{x^a}}\) \(=\frac{x^b}{x^a+x^b}+\frac{x^a}{x^a+x^b}\) \(=\frac{x^b+x^a}{x^a+x^b}\)

= 1

= RHS

Hence Proved

4. If \(x=\frac{1}{2-\sqrt{3}}\) , find the value of \(2 x^3-2 x^2+7 x+5\)

Solution: Given: \(x=\frac{1}{2-\sqrt{3}}\)

\(x=\frac{1}{2-\sqrt{3}} \times \frac{2+\sqrt{3}}{2+\sqrt{3}}\) \(\begin{array}{r}
=\frac{2+\sqrt{3}}{4-3} \\
x=2+\sqrt{3}
\end{array}\)

Consider \(2 x^3-2 x^2+7 x+5\)

\(=2(2+\sqrt{3})^3-2(2+\sqrt{3})^2+7(2+\sqrt{3})+5\)

\(=2[8+3 \sqrt{3}+12 \sqrt{3}+18]-2(4+3+4 \sqrt{3})\)\(+14+7 \sqrt{3}+5\)

= \(16+6 \sqrt{3}+24 \sqrt{3}+36-8-6-8 \sqrt{3}\)\(+14+7 \sqrt{3}+5=29 \sqrt{3}+57\)

KSEEB Solutions Class 9 Number Systems Practice 

5. Two classmates Salma & Anand simplified two different expressions during the revision hour & explained to each other their simplifications. Salma explains the simplification of \(\frac{\sqrt{2}}{\sqrt{5}+\sqrt{3}}\) &Anand explains the simplification of \(\sqrt{28}+\sqrt{98}+\sqrt{147}\) write both the simplification. What value does it depict?

Solution: Justify:

\(\frac{\sqrt{2}}{\sqrt{5}+\sqrt{3}}=\frac{\sqrt{2}}{\sqrt{5}+\sqrt{3}} \times \frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}-\sqrt{3}}\) \(=\frac{\sqrt{2}(\sqrt{5}-\sqrt{3})}{5-3}\) \(=\frac{\sqrt{10}-\sqrt{6}}{2}\)

Again, \(\sqrt{28}+\sqrt{98}+\sqrt{147}\)

\(\begin{aligned}
& =\sqrt{2 \times 2 \times 7}+\sqrt{2 \times 7 \times 7}+\sqrt{3 \times 7 \times 7} \\
& =2 \sqrt{7}+7 \sqrt{2}+7 \sqrt{3}
\end{aligned}\)

value: cooperative learning among classmates without any gender & religious bias.

6. Simplify: 

1) \(\left\{5\left(8^{1 / 3}+27^{1 / 3}\right)^3\right\}^{1 / 4}\)

Solution: \(\left\{5\left(8^{\frac{1}{3}}+27^{\frac{1}{3}}\right)^3\right\}^{\frac{1}{4}}\)

\(=\left[5\left(2^{3 \times \frac{1}{3}}+3^{3 \times \frac{1}{3}}\right)^3\right]^{\frac{1}{4}}\) \(\begin{aligned}
& =\left\{5(2+3)^3\right\}^{\frac{1}{4}} \\
& =\left(5 \times 5^3\right)^{\frac{1}{4}} \\
& =\left(5^4\right)^{\frac{1}{4}} \\
& =5^1
\end{aligned}\)

=5

2) \(\frac{9^{1 / 3} \times 27^{1 / 2}}{3^{-1 / 6} \times 3^{1 / 3}}\)

Solution: \(\frac{9^{\frac{1}{3}}+27^{\frac{1}{2}}}{3^{\frac{-1}{6}} \times 3^{\frac{1}{3}}}\)

\(=\frac{\left(3^2\right)^{\frac{1}{3}} \times\left(3^3\right)^{\frac{1}{2}}}{3^{-\frac{1}{6}} \times 3^{\frac{1}{3}}}\) \(=3^{\frac{2}{3}} \times 3^{\frac{3}{2}} \times 3^{\frac{1}{6}} \times 3^{-\frac{1}{3}}\) \(=3^{\frac{2}{3}+\frac{3}{2}+\frac{1}{6}-\frac{1}{3}}\) \(=3^{\frac{4+9+1-2}{6}}\) \(\begin{aligned}
& =3^{\frac{12}{6}} \\
& =3^2
\end{aligned}\)

=9