KSEEB Solutions For Class 9 Maths Chapter 13 Surface Areas & Volumes Points to Remember
- Cuboid is a solid figure bounded by six parallel opposite faces, it has length, width (breadth) & height.
- A cuboid whose all edges are equal is called a cube.
- Every cube is a cuboid but every cuboid is not a cube.
- Volume is the capacity or the space occupied by a body.
- A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball.
- A hemisphere is half of a sphere.
- In case of room, lateral surface area means the area of the four walls of the room, where as total surface area means the areas of four walls plus the area of the floor & the ceiling
- The total surface area of any object will be greater than its lateral surface area.
- The unit of measurement of both volume & capacity is cubic unit such as cubic feet, cubic cm & cubic metre.
- When an object of certain volume is recast into a cylinder, the volume of the cylinder formed will always be equal to the volume of the original object.
- The solids having the same curved surface do not necessarily occupy the same volume.
- When an object is dropped into a liquid the volume of the displaced liquid is equal to the volume of the object that is dipped.
- A cylinder is a solid or a hollow object that has a circular base & a circular top of the same size.
- Cone is a pyramid with a circular base.
Cuboid.
LSA (or) area of four walls = 2 h(l + b)
TSA= 2 (lb+bh+hl)
Volume = l x b x h
Length of all 12 edges of the cuboid = 4(l + b+ h)
Diagonal of cuboid = \(\sqrt{\ell^2+b^2+h^2}\)
Cube:
LSA = 4 x (edge)²
TSA = 6 x (edge)²
Volume = (edge)² x (edge)
Length of all 12 edges of the cube = 12 x (edge)
Diagonal of the cube = \(\sqrt{3} \ell\)
Sphere:
Surface area = 4πr²
Volume = \(\frac{4}{3} \pi r^3\)
Hemisphere: curved surface area = 2πr²
Total surface area = 3πr²
Volume =\(\frac{2}{3} \pi r^3\)
Right circular cylinder
Area of each end or base area = πr²
Area of curved surface area or LSA = 2πrh
TSA (including both ends) = 2πrh + 2πr²
=2πr(h + r)
Volume = πr²h
Right circular hollow cylinder
Area of curbed surface
= External surface+Internal surface
= (2πRh+2πrh) + 2(πR² – πr²)
= [2πh(R+ r) + 2π(R² – r²)]
= [2π(R+ r) (h + (R – r)]
Volume = External volume – Internal volume
= [πR²h-πr² h] = πh(R² -r²)
Cone
Right circular cone
Slant height (l) =\(\sqrt{h^2+r^2}\)
Area of curved surface = πrl (or) πr\(\sqrt{h^2+r^2}\)
77Total surface area=Area of curved surface + Area of base
= πrl + πr² = πr(l + r)
Volume = \(\frac{1}{3} \pi r^2 h\)
KSEEB Class 9 Maths Chapter 13 Surface Areas & Volumes Exercises
Surface Areas & Volumes Exercise 13.1
1. A plastic box 1.5m long, 1.25m wide & 65cm deep is to be made. It is opened at the top. Ignoring the thickness of the plastic sheet determined. (1) The area of the sheet required for making the box (2) The cost of sheet for it, if a sheet measuring 1m² costs ₹20.
Solution: 1) l =1.5m, b= 1.25m, h= 65 cm = 0.65m
∴ The area of the sheet required = 0.65m
for making the box = lb+ 2(bh+ hl)
= (1.5X1.25) + 2 {(1.25)(0.65) + (0.65)(1.5)}
= 1.875 + 2 (0.8125 + 0.975)
= 1.875 + 2 (1.7875) = 1.875 + 3.575
= 5.45m²
2) The cost of sheet for it = ₹ 5.45 x 20
= ₹109
2. The length, breadth & height of a room are 5m, 4m & 3m respectively. Find the cost of whitewashing the walls of the room & the ceiling at the rate of ₹7.50perm².
Solution: l = 5m, b = 4m, h = 3m
Area of the walls of the room = 2(l + b)h
= 2 (5 + 4)3= 54m²
∴ Area of the ceiling = lb = (5) (4) = 20m²
∴ Total area of the walls ofthe room & the ceiling = 54m² + 20m² = 74m²
∴ Cost of white washing the walls ofthe room & the ceiling = 74 x 7.50 =₹555
3. The floor of a rectangular hall has a perimeter 250m. If the cost of painting the four walls at the rate of 10perm² is ₹15000. Find the height of the hall.
Solution: Perimeter = 250m
2(l + b) = 250
l+b = 250/2 = 125 ………………….(1)
Area of the four walls
= 15000/10= 1500m²
=> 2(l + b)h = 1500
=> (l + b)h= 750
=> 125h = 750(using (1))
=> h = 750/125
=> h=6m
Hence, the height of the hall is 6m.
4. The paint in a certain container is sufficient to paint an area equal to 9.375m² How many bricks of dimensions 22.5cm x 10cm x 7.5cm can be painted out of this container?
Solution: For a brick
l = 22.5 cm, b=10cm, h=1.5 cm
∴ Total surface area of a brick = 2 (lb+ bh+ hl)
= 2(22.5 x 10 +10 x 7.5 + 7.5 x 22.5)
= 2(225 + 75 + 168.75) = 2(468.75) = 937.5cm²
= 0.09375m²
∴ Number of bricks that can be painted out
\(=\frac{9.375}{0.09375}=100\)
5. A cubical box has each edge 10cm & another cuboidal box is 12.5cm long, 10cm wide & 8cm high (1) Which box has the greater lateral surface area & by how much (2) Which box has the smaller total surface area & by how much
Solution: (1) Each edge of the cubical box (a) = 10cm
∴ LSA of the cubical box
= 4a² = 4(10)² = 400cm²
l = 2.5cm, b=10cm, h = 8cm
∴ LSA of the cuboidal box = 2 (l + b) h
= 2(12.5 + 10) (8) = 360cm²
∴ cubical box has a greater lateral surface area than the cuboidal box by (400 – 360)cm² ie 40cm²
(2) TSA of cubical box =6a² – 6(10)² = 600cm²
TSA of cuboidal box = 2[lb+ bh+ hl)
= 2(12.5 x 10 + (10) (8) + 8x 12.5)
= 2(125+ 80+ 100) = 610cm²
∴ Cubical box has the smaller TSA than the cuboidal box by (610 – 600)cm² i.e. 10cm²
6. A small indoor greenhouse (herbarium) is made entirely of glass panes (including the base) held together with tape. It is 30cm long, 25cm wide & 25cm high, (1) What is the area of the glass? (2) How much of tape is needed for all 12 edges?
Solution: (1) For the herbarium
l = 30 c/77, b = 25 cm, h = 25 cm
∴ Area of the glass = 2(lb+ bh+ hl)
= 2(30×25 + 25×25 + 25×30)
= 2(750 + 625 + 750)
=4250cm²
2) The tape needed for all the 12 edges
= 4(l + b+ h)
= 4(30+25+25) = 320cm
KSEEB Maths Chapter 13 Surface Areas & Volumes Answers
7. Shanti sweets stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25cm x 20cm x 5cm & the smaller of dimensions 15cm x 12cm x 5cm. For all the overlaps 5% of the TSA is required extra. If the cost of the cardboard is ₹4 for 1000cm², find the cost of the cardboard required for supplying 250 boxes of each kind.
Solution: For bigger box
l = 25 cm, b= 20cm, h = 5 cm
TSA of the bigger box = 2(lb+ bh+ hl)
= 2(25×20 + 20×5 + 5×25)
= 2(500 + 100 + 125) = 1450cm²
Cardboard required for all the overlaps
= 1450 x 5/100=72.5cm²
∴ Net surface area of the bigger box
= 1450cm² + 72.5cm² = 1522.5cm²
∴ Net surface area of 250 bigger boxes
= 1522.5×250 = 380625cm²
∴ cost of cardboard = 4/1000 x 380625 = ₹1522.50
For smaller box l = 15cm, b = 12cm, h = 5cm
∴ TSA of the smaller box = 2(lb+ bh+ hl)
= 2(15×12 + 12×5 + 5×15)
= 2(180+ 60+ 75) = 630cm²
Cardboard required for all the overlaps
= 630x 5/100 = 31.5cm²
∴ Net surface area of the smaller box = 630+ 31.5 = 661.5cm²
∴ Net surface area of 250 smaller boxes
= 661.5 x 250 = 165375cm²
Cost of cardboard = 4/1000 x 165375
= ₹661.50
∴ Cost of cardboard required for supplying 250 boxes of each kind
= ₹1522.50 + ₹661.50 = ₹2184
8. Parveen wanted to make a temporary shelter for her car, by making a box-like structure with a tarpaulin that covers all four sides & the top of the car (with the front face as a flap that can be rolled up). Assuming that the stitching margins are very small, & therefore negligible, how many tarpaulins would be required to make the shelter of height 2.5m, with base dimensions 4m x 3m?
Solution: For shelter
l = 4m, b = 3m, h = 2.5m
∴ Total surface area of the shelter =
lb+ 2(bh+ hl)
= 4×3 + 2[3 x 2.5 + 2.5 x 4]
= 12 + 2(7.5 + 10)
= 47m²
Hence, 47m² of tarpaulin will be required.
Surface Areas & Volumes Exercise 13.2
1. The curved surface area of a right circular cylinder of height 14cm is 88cm². Find the diameter of the base of the cylinder.
Solution: Let the radius of the base of the cylinder be ‘r’ cm.
h= 14cm, CSA = 88cm²
=> 2πrh = 88
= > \(2 \times \frac{22}{7} \times r \times 14=88\)
=> \(r=\frac{88 \times 7}{2 \times 22 \times 14}\)
=> r = 1
=> 2r = 2 = d
Hence, the diameter of the base of the cylinder is 2cm.
2. It is required to make a closed cylindrical tank of height lm & base diameter 140cm from a metal sheet. How many square metres of the sheet are required for the same?
Solution: h = 1m = 100cm, 2r = 140cm
=> r = 140/2= 70 cm
∴ Total surface area of the closed cylindrical tank
= 2 πr(h+ r)
= 2×22/7×70(100 + 70) = 74800cm²
= \(\frac{74800}{100 \times 100} m^2\)
= 7.48m²
3. A metal pipe is 77cm long, the inner diameter of the cross-section is 4cm, the outer diameter being 4.4cm. Find its (1) inner curved surface area (2) outer curved surface area (3) Total surface area.
Solution: h = 11 cm, 2r = 4cm, r = 2cm
2R = 4.4cm R = 2.2cm
1) Inner curved surface area = 2 πrh
= 2x 22/7x2x77 = 968cm²
2) Outer curved surface area = 2πRh
= 2 x 22/7 x 2.2 x 77 = 1064.8 cm²
3) Total surface area
= 2πRh+2πrh+2π(R² – r²)
= 1064.8 + 968 + 2×22/7[(2.2)² -2²]
= 1064.8 + 968 + 44/7(4.84 – 4)
= 1064.8 + 968 + 5.28
= 2038.08 cm²
KSEEB Solutions Class 9 Surface Areas & Volumes Problems
4. The diameter of a roller is 84cm & its length is 120cm. It takes 500 complete revolutions to move once over to level a playground. Find the area of the playground in m².
Solution: 2r = 84cm, => r = 42cm, b = 120cm
∴ Area of the playground leveled in taking 1 complete revolution.
=2πrh = 2×22/7x42x120 = 31680cm²
∴ Area of the playground = 31680 x 500
\(\begin{aligned}
& =15840000 \mathrm{~cm}^2=\frac{15840000}{100 \times 100} \mathrm{~m}^2 \\
& =1584 \mathrm{~m}^2
\end{aligned}\)
Hence, the area of the playground is 1584m²
5. A cylindrical pillar is 50cm in diameter & 3.5m in height. Find the cost of painting the curved surface of the pillar at the rate of ₹12.50 perm².
Solution: 2r-50cm
r=50/2 = 25cm= 0.25cm
h = 3.5m
∴ curved surface area of the pillar = 2πrh
= 2x 22/7 x 0.25 x 3.5 = 5.5m²
∴ Cost of painting the curved surface of the pillar at the rate of ₹12.50 per m²
= ₹5.5 x 12.50=₹68.75
6. Curved surface area of a right circular cylinder is 4.4m². If the radius of the base of the cylinder is 0.7m. Find its height
Solution: Let the height of the right circular cylinder be h m.
r= 0.7m
CSA = 4.4m²
2πrh = 4.4
=> 2x 22/7×0.7xh= 4.4
4.4h = 4.4
h x 1m
Hence, the height of the right circular cylinder is 1m.
7. The inner diameter of a circular well is 3.5m it is 10m deep. Find (1) its inner curved surface area (2) The cost of plastering this curved surface at the rate of ₹40 per m².
Solution: (1) 2r = 3.5m => r = 3.5/2m
h= 10m
∴ Inner curved surface area of the circular well= 2πrh = 2x 22/7 x 1.75×10 110m²
2) Cost of plastering the curved surface at the rate of ₹40 per m² = ₹110×40 = ₹4400
8. In a hot water heating system, there is a cylindrical pipe of length 28m & diameter 5cm. Find the total radiating surface in the system.
Solution: h = 28m, 2r= 5cm => r = -cm = 5/2cm = 5/2×100 m = 1/40 m
∴ Total radiating surface in the system
= 2πrh = 2x 22/7 x 1/40 x 28 = 4.4m²
9. (1) The lateral or curved surface area of a closed cylindrical petrol storage tank that is 4.2m in diameter & 4.5m high, (2) How much steel was actually used if 1/12 of the steel actually used was wasted in making the tank?
Solution: (1) 2r = 4.2m => r= 2.1m, h = 4.5m
∴ Lateral (or) CSA = 2πrh
= 2x 22/7 x 2. lx 4.5 = 59.4m²
2) Total surface area =2πr(r+h)
= 2 x 22/7 X2.1 (4.5+ 2.1)
= 2x 22/7 x 2. 1x 6.6 = 87.12m²
Let the actual area of steel used be xm²
since 1/12 of the actual steel used was wasted the area of steel which has gone into the tank = 11/12 of x
∴ 11/12x = 87.12
=> \(x=\frac{87.12 \times 12}{11}=95.04 \mathrm{~m}^2\)
∴ Streel actually used = 95.04m²
10. In figure, you see the frame of a lampshade. It is to be covered with a decorative
cloth. The frame has a base diameter of 20cm & height of 30cm. A margin of 2.5cm is to be given for folding it over the top & bottom of the frame. Find how much cloth is required for covering the lampshade.
Solution:
2r= 20cm => r = 10cm, h = 50cm
cloth required = 2πr(h + 2.5 + 2.5)
= 2πr(h+5)
= 2×22/7×10(30 + 5)
= 2x 22/7 x10x35
=2200cm²
11. The students of a Vidyalaya were asked to participate in a competition for making & decorating penholders in the shape of a cylinder with a base, using cardboard. Each pen holder was to be of radius 3cm & height 10.5cm, the Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors how much cardboard was required to be bought for the competition?
Solution: r = 3cm, h = 10.5cm
∴ Cardboard required for 1 competitor
= 2πrh + πr²
\(=2 \times \frac{22}{7} \times 3 \times 10.5+\frac{22}{7} \times 3^2\)
\(=198+\frac{198}{7}=198\left(1+\frac{1}{7}\right)=\frac{198 \times 8}{7} \mathrm{~cm}^2\)
∴ Cardboard required for 35 competitors
\(=\frac{198 \times 8}{7} \times 35 \mathrm{~cm}^2=7920 \mathrm{~cm}^2\)
Hence, 7920cm2 of cardboard was required to be bought for the competition.
Surface Areas & Volumes Exercise 13.3
1. Diameter of the base of a cone is 10.5cm & its slant height is 10cm. Find its curved surface area.
Solution: Diameter of the base = 10.5cm, r = 10.2/5cm
= 5.25cm
Slant height (l) = 10cm
∴ curved surface area of the cone = πrl
= 22/7 x 5.25 x 10 = 165cm²
2. Find the TSA of a cone, if its slant height is 21m & diameter of its base is 24m.
Solution: Slant height (l) = 21m,
Diameter of base = 24m
Radius of base (r) = 24/2 m = 12m
∴ Total curved surface area of the cone
= πr(l + r)
= 22/7×12(21 + 12)
\(=\frac{22}{7} \times 12 \times 33=\frac{8712}{7}\)
\(=1244 \frac{4}{7} m^2\)
3. Curved surface area of a cone is 308cm² & its slant height is 14cm. Find (1) radius of the base & (2) Total surface area of the cone.
Solution: (1) Slant height (l) = 14cm
curved surface area = 308cm2
=> πrl = 308
=> 22/7xrx14 = 308
=> \(r=\frac{308 \times 7}{22 \times 14}\)
=> r = 7cm
Hence, the radius of the base is 7cm
2) Total surface area of the cone = πr(l + r)
\(\begin{aligned}
& =\frac{22}{7} \times 7 \times(14+7) \\
& =\frac{22}{7} \times 7 \times 21=462 \mathrm{~cm}^2
\end{aligned}\)
Hence the total surface area of the cone is 462cm².
Class 9 Maths KSEEB Chapter 13 Surface Areas & Volumes Examples
4. A conical tent is 10m high & the radius of its base is 24m, Find (1) the slant height of the tent (2) cost of the canvas required to make the tent, if the cost of 1m² canvas is ₹70.
Solution: 1) h=10m, r= 24m
\(\begin{aligned}
\ell & =\sqrt{(r)^2+(h)^2}=\sqrt{(24)^2+(10)^2} \\
& =\sqrt{576+100}=\sqrt{676}=26 \mathrm{~m}
\end{aligned}\)
Hence, the slant height of the tent is 26m
2) curved surface area of the tent = πrl
= \(\frac{22}{7} \times 24 \times 26 m^2\)
∴ cost of the canvas required to make the tent, if the cost of 1m² canvas is ₹70.
=\(\frac{22}{7} \times 24 \times 26 \times 70=₹ 137280\)
Hence, the cost of the canvas is ₹137280
5. What length of tarpaulin 3m wide will be required to make conical tent of height 8m and base radius 6m? Assume that the extra length of material that will be required for stitching margins & wastage in cutting is approximately 20cm (use π=3.14)
Solution: For conical tent
h = 8m, r = 6m
∴ \(\begin{aligned}
\ell & =\sqrt{h^2+r^2}=\sqrt{8^2+6^2} \\
& =\sqrt{64+36}=\sqrt{100}=10 m
\end{aligned}\)
∴ curved surface area
= πrl = 3.14x6x10 = 188.4m²
width of tarpaulin = 3m
∴ length of tarpaulin = 188.4/3 = 62.8 m
Extra length of the material required = 20cm
= 0.2m
∴ Actual legnth of tarpaulin required = 62.8 + 0.2m
= 63m
6. The slant height & base diameter of a conical tomb are 25m & 14m respectively. Find the cost of whitewashing its curved surface at the rate of ₹210 per 100m²
Solution: l = 25m, Base diameter (d) = 14m
(r) = 7m
The curved surface area of the tomb = πrl
= 22/7 x 7 x 25 = 550m²
∴ Cost of white-washing the curved surface of the tomb at the rate of ₹210 per 100m²
\(=₹ \frac{210}{100} \times 550=₹1155\)
7. A Joker’s cap is in the form of a right circular cone with a base radius of 7cm & height of 24cm. Find the area of the sheet required to make 10 such caps.
Solution: Base radius (r) = 7cm
Height (h) = 24cm
∴ Slant height
\(\begin{aligned}
(\ell) & =\sqrt{r^2+h^2}=\sqrt{7^2+24^2} \\
& =\sqrt{49+576}=\sqrt{625}=25 \mathrm{~cm}
\end{aligned}\)
∴ curved surface area of a cap = πrl
=\(\frac{22}{7} \times 7 \times 25=550 \mathrm{~cm}^2\)
∴ curved surface area of 10 caps = 550 x 10 = 5500cm²
Hence, the area of the sheet required to make 10 such caps is 5500cm².
8. A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40cm & height 1m, if the outer side of each of the cone is to be painted & the cost of painting is ₹12 perm², what will be the cost of painting all these cones? (use π=3.14 & take \(\sqrt{1.04}\)=1.02)
Solution: Base diameter = 40cm
Base radius = r= 20cm = 20/100 m = 0.2m
Height (h) = 1m
\(\begin{aligned}
\ell & =\sqrt{r^2+h^2}=\sqrt{(0.2)^2+1} \\
& =\sqrt{1.04}=1.02 \mathrm{~m}
\end{aligned}\)
∴ Curved surface area = πrl
= 3.14 x 0.2 x 1.02 = 0.64056m²
∴ Curved surface area of 50 cones
= 0.64056 x 50m² = 32.028m²
∴ Cost of painting all these cones = 32.028 x 12
= 384.336 x ₹384.34 (approx.)
Surface Areas & Volumes Exercise 13.4
1. Find the surface area of a sphere of radius
(1) 10.5cm (2) 5.6cm (3) 14cm
Solution: (1) r= 10.5cm
surface area= 4πr²
\(=4 \times \frac{22}{7} \times(10.5)^2\)
= 1386cm²
(2) r= 5.6cm
S.A. = 4πr² = \(4 \times \frac{22}{7} \times(5.6)^2\)
=394.24cm²
(3) r= 14cm
S.A. = 4πr² = \(4 \times \frac{22}{7} \times(14)^2\) = 2464cm²
2. Find the surface area of a sphere of diameter (1) 14cm (2) 21cm (3) 3.5m
Solution: d= 14cm
1) r = 7cm
S.A. = 4πr²
= \(4 \times \frac{22}{7} \times 7^2\)
= 616cm²
2) d = 21 cm
r = 21/2 cm
S.A. = 4πr²
\(=4 \times \frac{22}{7} \times\left(\frac{21}{2}\right)^2\)
= 1386cm²
3) d = 3.5m
r=3.5/2m
S.A. = 4 πr²
\(=4 \times \frac{22}{7} \times\left(\frac{3.5}{2}\right)^2\)
= 38.5m²
KSEEB Chapter 13 Surface Areas & Volumes Solved Questions
3. Find the TSA of a hemisphere of radius 10cm (use π=3.14)
Solution: r = 10cm,
TSA of the hemisphere = 3πr²
= 3 x 3.14 x (10)² = 942cm²
4. The radius of a spherical balloon increases from 7cm to 14cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Solution: Case 1
r= 7cm
surface area = 4πr²
=\(=4 \times \frac{22}{7} \times 7^2=616 \mathrm{~cm}^2\)
Case 2
r = 14cm
S.A = 4πr²
=\(4 \times \frac{22}{7} \times 14^2=2464 \mathrm{~cm}^2\)
∴ Ratio of surface areas of the balloon
= 616:2464 = 1/4 = 1:4
5. A hemispherical bowl made of brass has inner diameter 10.5cm. Fnd the cost of tinplating it on inside at the rate of ₹16 per 100cm²
Solution: Inner diameter = 10.5cm
Inner radius (r) = 10.5/2 = 5.25cm
Inner surface area = \(2 \pi r^2=2 \times \frac{22}{7} \times(5.25)^2\)
= 173.25cm²
∴ Cost of tin-plating at the rate of ₹16 per
100cm²=\(₹ \frac{16}{100} \times 173.25=₹ 27.72\)
6. Find the radius of a sphere whose surface area is 154cm²
Solution: Let the radius of the sphere be r cm
Surface area = 154cm²
=> 4πr² = 154
4x 22/7 xr² =154
\(\begin{aligned}
& r^2=\frac{154 \times 7}{4 \times 22} \\
& r^2=\frac{49}{4} \Rightarrow r=\sqrt{\frac{49}{4}}=\frac{7}{2}=3.5 \mathrm{~cm}
\end{aligned}\)
Hence the radius of the sphere is 3.5cm
7. The diameter of the moon is approximately one-fourth of the diameter of the earth. Find the ratio of their surface areas.
Solution: Let the diameter of the earth be 2 r
Then the diameter of the moon
\(=\frac{1}{4}(2 r)=\frac{r}{2}\)
Radius of the earth = 2r/2 = 2
& Radius of the moon = \(\frac{1}{2}\left(\frac{r}{2}\right)=\frac{r}{4}\)
& Surface area of the earth = =4πr²
f& Surface area of the moon = \(4 \pi\left(\frac{r}{4}\right)^2=\frac{1}{4} \pi r^2\)
∴ Ratio of their surface areas
\(\begin{aligned}
& =\frac{\text { Surface area of the moon }}{\text { Surface area of the earth }} \\
& =\frac{\frac{1}{4} \pi r^2}{4 \pi r^2}=\frac{1}{16}=1: 16
\end{aligned}\)
8. A hemispherical bowl is made of steel 0.25cm thick. The inner radius of the bowl is 5cm. Find the outer curved surface area of the bowl.
Solution: Inner radius of the bowl = 5cm
the thickness of steel = 0.25cm
∴ outer radius of the bowl
= 5 +0.25 = 5.25cm Outer curved surface of the bowl = 2πr²
\(\begin{aligned}
& =2 \times \frac{22}{7} \times(5.25)^2=1212.75 / 7 \\
& =173.25 \mathrm{~cm}^2
\end{aligned}\)
9. A right circular cylinder just encloses a sphere of radius r. Find (1) surface area of the sphere (2) curved surface area of the cylinder, (3) Ratio of the areas obtained in (1) & (2)
Solution:
(1) Surface area of the sphere = 4πr²
(2) For cylinder Radius of the base = r
Height =2 r
∴ Curved surface area of the cylinder = 2π(r)x2r
4/rr2
(3) Ratio of the areas obtained in (1) & (2)
\(\begin{aligned}
& =\frac{\text { surface area of the sphere }}{\text { curved surface area of the cylinder }} \\
& =\frac{4 \pi r^2}{4 \pi r^2}=\frac{1}{1}=1: 1
\end{aligned}\)
Surface Areas & Volumes Exercise 13.5
1. A matchbox measures 4cm x 2.5cm x 1.5cm. What will be the volume of a packet containing 12 such boxes?
Solution: Volume of a matchbox = 4 x 2.5 x 1.5cm3
= 15cm3
∴ Volume of a packet containing 12 such boxes = 15 x 12cm3 = 180cm3
2. A cuboidal water tank is 6m long, 5m wide & 4.5m deep. How many litres of water can it hold? (1m3 = 1000l)
Solution: capacity of the tank = 6×5 x 4.5 m3= 135m3
∴ volume of water it can hold =13 5m3
=135 x 1000l = 135000l.
3. A cuboidal vessel is 10m long & 8m wide. How high must it be made to hold 380 cubic metres of a liquid?
Solution: Let the height of the cuboidal vessel be ‘h’m.
l = 10m, b = 8m capacity of the cuboidal vessel = 380m3
=> lbh = 380
=> 10 x 8 x h=380
=> \(h=\frac{380}{10 \times 8}=\frac{19}{4}=4.75 \mathrm{~m}\)
Hence, the cuboidal vessel must be made 4.7m high.
KSEEB Maths Solutions Chapter 13 Practical Problems
4. Find the cost of digging a cuboidal pit 8m long, 6m board & 3m deep at the rate of ₹30 per m3.
Solution: l = 8m, b= 6m, h = 3m
∴ Volume of the cuboidal pit = lbh
= 8 x 6X 3m3 = 144m3
∴ Cost of digging the cuboidal pit at ₹30
perm3 = ₹144x 30 = ₹4320.
5. The capacity of a cuboidal tank is 5000 litres of water. Find the breadth of the tank if its length & depth are respectively 2.5m & 10m.
Solution: Let the breadth of the cuboidal tank be ‘b’m
l = 2.5m, h = 10m
The capacity of the cuboidal tank = 50000 litres
\(\begin{aligned}
& =\frac{50000}{1000} m^3=50 m^3 \\
& \Rightarrow \quad \ell b h=50 \\
& \Rightarrow 2.5 \times b \times 10=50 \Rightarrow 25 b=50 \\
& \Rightarrow b=\frac{50}{25}=2 m \\
&
\end{aligned}\)
Hence, the breadth of the cuboidal tank is 2m.
6. A village, having a population of4000, requires 150 litres of water per head per day. It has a tank measuring 20m x 15m x 6m. For how many days will the water of this tank last?
Solution: Requirement of water per head per day
= 150 litres
∴ Requirement of water for the total population of the village per day = 150 x 4000 litre
= \(600000 \text { litres }=\frac{600000}{1000} m^3=600 m^3\)
For tank, l = 20 m, b = 15 m, h = 6m
∴ Capacity of the tank = 20 x 15 x 6m3 = 1800m3
Number of days for which the water of the tank last
\(=\frac{\text { capacity of the tank }}{\text { Requirement of water for the total population of the village for the day }}\)
\(=\frac{1800}{600}=3\)
Hence, the water of this tank will last for 3 days.
7. A godown measures 40m x 25m x 10m. Find the maximum number of wooden crates each measuring 1.5m x 1.25m x 0.5m that can be stored in the godown.
Solution: For godown, l = 40m, b = 25m, h = 10m
Capacity of the godown = lbh =40 x 25 x 10 = 10000m3
For a wooden crate
l = 1.5m, b = 1.25, h = 0.5m
∴ capacity of a wooden crate = lbh
= 1.5 x 1.25 x 0.5m3 = 0.9375 m3
we have = \(\frac{10000}{0.9375}=10666.66\)
Hence, the maximum number of wooden crate that can be stored in the godown is 10666.
8. A solid cube of side 12cm is cut into eight cubes of equal volume. What will be the side of the new cube? Also, find the ratio between their surface areas.
Solution: Side of the solid cube (a) = 12cm
∴ Volume of the solid cube = a3 =123 = 1728cm3
It is cut into eight cubes of equal volume
∴ Volume of a new cube
\(=\frac{1728}{8} \mathrm{~cm}^3=216 \mathrm{~cm}^3\)
Let the side of the new cube be x cm
Then, volume of the new cube = x3 cm3
According to the question, x3 = 216
=> \(x=(216)^{1 / 3}=(6 \times 6 \times 6)^{1 / 3}=6 \mathrm{~cm}\)
Hence, the side of the new cube will be 6cm
Surface area of the original cube = 6a² = 6(12)²
∴ Ratio between their surface areas
\(\begin{aligned}
& =\frac{\text { surface area of the original cube }}{\text { surface area of the new cube }} \\
& =\frac{6(12)^2}{6(6)^2}=\frac{4}{1}=4: 1
\end{aligned}\)
Hence, the ratio between their surface area is 4:1
9. A river 3m deep & 40m wide is flowing at the rate of 2km per hour. How much water will fall into the sea in a minute?
Solution: In one hour
l = 2km = 2 x 1000m = 2000m, b = 40m, h = 3m
∴ Water fell into the sea in one hour = lbh
= 2000 x 40 x 3m3
∴ Water fell into the sea in a minute 2000 x 40 x 3m3
\(=\frac{2000 \times 40 \times 3 m^3}{60}=4000 \mathrm{~m}^3\)
Hence, 4000m3 of water will fall into the sea in a minute
Surface Areas & Volumes Exercise 13.6
1. The circumference of the base of a cylindrical vessel is 132cm & its height is 25cm. How many litres of water can it hold (1000cm3 = 1l)
Solution: Let the base radius of the cylindrical vessel be r cm.
Then, the circumference of the base of the cylindrical vessel = 2πrcm
According to the question, 2πr = 132
\(\begin{aligned}
& \Rightarrow \quad 2 \times \frac{22}{7} \times r=132 \\
& \Rightarrow \quad r=\frac{132 \times 7}{2 \times 22}=21 \mathrm{~cm} \\
& \quad h=25 \mathrm{~cm}
\end{aligned}\)
∴ Capacity of the cylindrical vessel = πr²h
\(\begin{aligned}
& =\frac{22}{7} \times(21)^2(25) \mathrm{cm}^3=34650 \mathrm{~cm}^3 \\
& =\frac{34650}{1000} \ell=34.65 \ell
\end{aligned}\)
Hence, the cylindrical vessel can hold 34.65l of water.
2. The inner diameter of a cylindrical wooden pipe is 24cm & its outer diameter is 28cm. The length of the pipe is 35cm. Find the mass of the pipe, if 1cm3 of wood has a mass of 0.6g
Solution: Inner diameter=24cm
∴ Inner radius (r) = 12cm
outer diameter = 28 cm
∴ Outer radius (R) = 14cm
Length of the pipe (h) = 35cm
Outer volume = πR²h
\(=\frac{22}{7} \times(14)^2 \times 35=21560 \mathrm{~cm}^3\)
Inner volume = πr²h
\(\begin{aligned}
& =\frac{22}{7} \times(12)^2 \times 35 \\
& =15840 \mathrm{~cm}^3
\end{aligned}\)
Volume of the wood used
= Outer volume – Inner Volume
= 21560- 15840 = 5720cm3
Mass of the pipe = 5720 x 0.6g = 3432g
= 3.432kg
3. A soft drink is available in two packs (1) a tin can with a rectangular base of length 5cm & width 4cm, having a height of 15cm? & (2) a plastic cylinder with a circular base of diameter 7cm & height 10cm, which container has greater capacity & by how much.
Solution: (1) For tin can
l = 5cm, b = 4cm, h = 15cm
∴ Capacity = l x b x h = 5x4x15 = 300cm3
(2) For plastic cylinder
Diameter = 7cm, r= 7/2 cm, h= 10cm
Capacity \(=\pi r^2 h=\frac{22}{7} \times\left(\frac{7}{2}\right)^2 \times 10\)
= 385cm3
clearly the second container, i.e. a plastic cylinder has greater capacity than the first container, i.e., a tin can by 385-300 = 85cm3.
4. If the Lateral surface of a cylinder is 94.2cm² & its height is 5cm, then find (1) radius of its base (2) its volume (use π=3.14)
Solution: (1) Let the radius of the base of the cylinder be mm, h = 5cm
Lateral surface = 94.2cm²
=> 2πrh = 94.2
=> 2×3.14xrx5 =94.2
\(\Rightarrow \quad r=\frac{94.2}{2 \times 3.14 \times 5}=\frac{94.2}{31.4}=3 \mathrm{~cm}\)
Hence, the radius of the base is 3 cm.
(2) r = 3cm, h = 5cm
∴ Volume of the cylinder = πr² h
= 3.14×3²x5 = 141.3cm3
KSEEB Solutions for 9th Standard Maths Chapter 13 Surface Areas & Volumes
5. It costs ₹2200 to paint the inner curved surface of a cylindrical vessel 10m deep. If the cost of painting is at the rate of ₹20 per m², find (1) Inner curved surface area of the vessel (2) radius of the base (3) capacity of the vessel.
Solution: (1) Inner curved surface area of the vessel =
\(=\frac{2200}{20}=110 \mathrm{~m}^2\)
(2) Let the radius of the base be r m
h = 10m
Inner curved surface area = 110m²
\(\begin{aligned}
& \Rightarrow \quad 2 \pi r h=110 \\
& \Rightarrow \quad 2 \times \frac{22}{7} \times r \times 10=110 \\
& \Rightarrow \quad r=\frac{110 \times 7}{2 \times 22 \times 10}=\frac{7}{4}=1.75 \mathrm{~m}
\end{aligned}\)
Hence, the radius of the base is 1.75m
(3) r= 1.75m, h= 10m
∴ Capacity of the vessel =
\(=\pi r^2 h=\frac{22}{7} \times(1.75)^2 \times 10=96.25 \mathrm{~m}^3\)
Hence, the capacity of the vessel is 96.25m3
6. The capacity of a closed cylindrical vessel of height lm is 15.4 litres. How many square metres of metal sheet would be needed to make it?
Solution: h= 1m, capacity = 15.4 litres = 15.4/1000m3
= 0.0154m3
Let the radius of the base be r m
Capacity = 0.0154m3
\(\begin{aligned}
& \Rightarrow \quad \pi r^2 h=0.0154 \\
& \Rightarrow \quad \frac{22}{7} \times r^2 \times 1=0.0154 \\
& \Rightarrow \quad r^2=\frac{0.0154 \times 7}{22}=0.0049 \\
& \Rightarrow \quad r=\sqrt{0.0049}=0.07 \mathrm{~m}
\end{aligned}\)
∴ CSA = 2πrh+2πr²
\(\begin{aligned}
& =2 \times \frac{22}{7} \times 0.07 \times 1+2 \times \frac{22}{7} \times(0.07)^2 \\
& =0.44+0.0308=0.4708 \mathrm{~m}^2
\end{aligned}\)
Hence 0.47m² of metal sheet should be needed.
7. A lead pencil consists of a cylinder of wood with a solid cylinder of graphite filled in the interior. The diameter of the pencil is 7mm & the diameter of the graphite is 1mm. If the length of the pencil is 14cm, find the volume of the wood & that of the graphite.
Solution: For solid cylinder of graphite Diameter = 1mm
∴ radius (r) = 1/2 mm
Length of the pencil (h) = 14cm= 140mm
∴ Volume of the graphite = πr²h
\(\begin{aligned}
& =\frac{22}{7} \times\left(\frac{1}{2}\right)^2 \times 140=110 \mathrm{~mm}^3 \\
& =\frac{110}{10 \times 10 \times 10} \mathrm{~cm}^3=0.11 \mathrm{~cm}^3
\end{aligned}\)
For cylinder of wood
Diameter = 7mm
Radius (R) = 7/2 mm
Length of the pencil (h) = 14cm = 140mm
∴ Volume of the wood
\(\begin{aligned}
& =\pi\left(R^2-r^2\right) h=\frac{22}{7}\left\{\left(\frac{7}{2}\right)^2-\left(\frac{1}{2}\right)^2\right\} 140 \\
& =\frac{22}{7} \times\left(\frac{49}{4}-\frac{1}{4}\right) 140=\frac{22}{7} \times \frac{48}{4} \times 140 \\
& =5280 \mathrm{~mm}^3=\frac{5280}{10 \times 10 \times 10}=5.28 \mathrm{~cm}^3
\end{aligned}\)
8. A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7cm. If the bowl is filled with soup to a height of 4cm, how much soup the hospital has to prepare daily to serve 250 patients?
Solution: Diameter = 7cm
Radius (r)= 7/2cm,
height (h) = 4cm
Volume of soup in the cylindrical bowl
\(=\pi r^2 h=\frac{22}{7} \times\left(\frac{7}{2}\right)^2 \times 4 \mathrm{~cm}^3=154 \mathrm{~cm}^3\)
∴ Volume of soup to be prepared daily to serve 250 patients = 154 x 250 cm3
= 38500cm3 (or 38.50l)
Hence, the hospital has to prepare 38500cm3 of soup daily to serve 250 patients.
Surface Areas & Volumes Exercise 13.7
1. Find the volume of the right circular cone with (1) radius 6cm, height 7cm (2) radius 3.5cm, height 12cm.
Solution: (1) r =6cm, h = 7cm
∴ Volume of the right circular cone =\(\frac{1}{3} \pi r^2 h\)
\(=\frac{1}{3} \times \frac{22}{7} \times 6^2 \times 7=264 \mathrm{~cm}^3\)
(2) r = 3.5cm, h= 12cm
Volume of the right circular cone = \(\frac{1}{3} \pi r^2 h\)
= \(=\frac{1}{3} \times \frac{22}{7} \times(3.5)^2 \times 12=154 \mathrm{~cm}^3\)
2. Find the capacity in litres of a conical vessel with (1) radius 7cm, slant height 25cm (2) height 12cm, slant height 13cm.
Solution: (1) r= 7 cm, l = 25cm
\(\begin{aligned}
& r^2+h^2=\ell^2 \\
& \Rightarrow \quad(7)^2+h^2=(25)^2 \\
& \begin{aligned}
h^2 & =(25)^2-7^2 \\
& =625-49=576 \\
\mathrm{~h} & =\sqrt{576} \\
\Rightarrow & h=24 \mathrm{~cm}
\end{aligned}
\end{aligned}\)
∴ capacity = \(\frac{1}{3} \pi r^2 h\)
\(=\frac{1}{3} \times \frac{22}{7} \times 7^2 \times 24=1232 \mathrm{~cm}^3=1.232 \ell\)
(2) h=12cm, l = 13cm
\(\begin{aligned}
& \Rightarrow r^2+h^2=\ell^2 \\
& \Rightarrow \quad r^2+12^2=13^2 \\
& \Rightarrow \quad r^2+144=169 \\
& \Rightarrow r^2=169-144 \\
& \Rightarrow r^2=25 \\
& \Rightarrow r=5 \mathrm{~cm}
\end{aligned}\)
∴ capacity = \(\frac{1}{3} \pi r^2 h\)
\(=\frac{1}{3} \times \frac{22}{7} \times 5^2 \times 12\)
= \(\frac{2200}{7} \mathrm{~cm}^3=\frac{2200}{7000} \ell=\frac{11}{35} \ell\)
KSEEB Maths Chapter 13 Surface Areas & Volumes Free solutions
3. The height of a cone is 15cm. If its volume is 1570cm3, find the radius of the base.(π = 3.14)
Solution: Let the radius of the base of the cone be r cm.
h= 15cm
Volume = 1570cm3
\(\begin{aligned}
& \Rightarrow \quad \frac{1}{3} \pi r^2 h=48 \pi \\
& \Rightarrow \quad r^2=\frac{1570 \times 3}{\pi h}=\frac{1570 \times 3}{3.14 \times 15} \\
& \Rightarrow \quad r^2=100 \\
& \Rightarrow \quad r=\sqrt{100}=10 \mathrm{~cm}
\end{aligned}\)
Hence, the radius of the base of the cone is 10cm
4. If the volume of a right circular cone of height 9cm is 48πcm3, find the diameter of its base.
Solution: Let the radius of the base of the right circular
cone be r cm.
h = 9cm,
Volume = 48πcm3
\(\begin{aligned}
& \Rightarrow \quad \frac{1}{3} \pi r^2 h=1570 \\
& \Rightarrow \quad \frac{1}{3} \times r^2 h=48 \\
& \Rightarrow \quad r^2=\frac{48 \times 3}{9} \\
& \Rightarrow \quad r^2=16 \\
& r=\sqrt{16}=4 \mathrm{~cm} \\
& \Rightarrow \quad 2 r=2(4)=8 \mathrm{~cm}
\end{aligned}\)
Hence, the diameter of the base of the right circular cone is 8cm.
5. A conical pit of top diameter 3.5m is 12m deep. What is its capacity in kilolitres?
Solution: For conical pit Depth (h)= 12m
Diameter = 3.5cm
∴ Radius (r) = \(\frac{3.5}{2} m=1.75 m\)
The capacity of the conical pit = \(\frac{1}{3} \pi r^2 h\)
\(\begin{aligned}
& =\frac{1}{3} \times \frac{22}{7} \times(1.75)^2 \times 12=38.5 \mathrm{~m}^3 \\
& =38.5 \times 1000 \ell \\
& =38.5 \mathrm{k} \ell
\end{aligned}\)
6. The volume of a right circular cone is 9856cm3. If the diameter of the base is 28cm, find
(1) height of the cone
(2) slant height of the cone
(3) curved surface area of the cone.
Solution: Let the radius of the base of the cone be r cm
1) Diameter of the base = 28cm
∴ Radius of the base (r) = 14cm
Let the height of the cone be h cm Volume = 9856cm3
\(\begin{aligned}
& \Rightarrow \frac{1}{3} \pi r^2 h=9856 \\
& \Rightarrow \frac{1}{3} \times \frac{22}{7} \times(14)^2 \times h=9856 \\
& \Rightarrow h=\frac{9856 \times 3 \times 7}{22 \times 142}=48 \mathrm{~cm}
\end{aligned}\)
Hence, the height of the cone is 48cm.
2) r= 14cm, h = 48cm
∴ \(\begin{array}{r}
\ell=\sqrt{r^2+h^2}=\sqrt{14^2+48^2} \\
=\sqrt{196+2304} \\
\ell=\sqrt{2500}=50 \mathrm{~cm}
\end{array}\)
Hence, the slant height of the cone is 50cm
3) r= 14cm, l = 50 cm
∴ Curved surface area =
\(\pi r \ell=\frac{22}{7} \times 14 \times 50=2200 \mathrm{~cm}^2\)
Hence, the curved surface area of the cone is 2200cm²
7. Aright Δle ABC with sides 5cm, 12cm & 13cm is revolved about the side 12cm. Find the volume of the solid so obtained.
Solution:
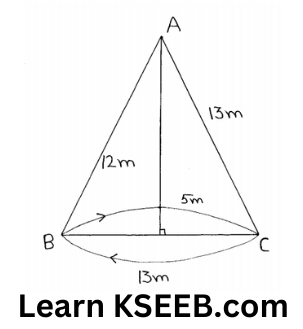
The solid obtained will be a right circular cone whose radius of the base is 5 cm & height is 12cm.
∴ r = 5cm, h =12cm
∴ \(\begin{aligned}
\text { Volume } & =\frac{1}{3} \pi r^2 h=\frac{1}{3} \times \pi \times 5^2 \times 12 \\
& =100 \pi \mathrm{cm}^3
\end{aligned}\)
Hence, the volume of the solid so obtained is 100π cm3
8. If the Δle ABC in question 7 above is revolved around the side 5cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in questions 7 & 8.
Solution:
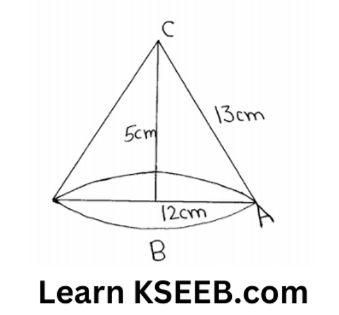
The solid obtained will be a right circular cone whose radius of the base is 12cm & height is 5 cm.
∴ r= 12cm, h = 5cm
Volume \(\begin{aligned}
& =\frac{1}{3} \pi r^2 h=\frac{1}{3} \times \pi \times 12^2 \times 5 \mathrm{~cm}^3 \\
& =240 \pi \mathrm{cm}^3
\end{aligned}\)
Ratio of the volumes of the two solids obtained 100π: 240π = 5: 12
9. A heap of wheat is in the form of a cone whose diameter is 10.5m & height is 3m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
Solution: For a heap of wheat Diameter = 10.5m
Radius
\(\begin{aligned}
& (r)=\frac{10.5}{2}=5.25 m \\
& h=3 m
\end{aligned}\)
Volume =
\(\begin{aligned}
& \frac{1}{3} \pi r^2 h \\
& =\frac{1}{3} \times \frac{22}{7} \times(5.25)^2 \times 3=86.625 \mathrm{~m}^3
\end{aligned}\)
Slant height
\(\begin{aligned}
(\ell) & =\sqrt{r^2+h^2} \\
& =\sqrt{(5.25)^2+3^2} \\
& =\sqrt{27.5625+9} \\
& =\sqrt{36.5625} \\
& =6.05 \mathrm{~m} \text { (approx.) }
\end{aligned}\)
∴ CSA
\(\begin{aligned}
& =\pi r \ell \\
& =\frac{22}{7} \times 5.25 \times 6.05=99.825 \mathrm{~m}^2
\end{aligned}\)
Hence, the area of the canvas required is 99.825m²
KSEEB Class 9 Chapter 13 Surface Areas & Volumes Revision Notes
Surface Areas & Volumes Exercise 13.8
1. Find the volume of a sphere whose radius is (1) 7cm (2) 0.63m
Solution: (1) r= 7cm
∴ Volume= \(\frac{4}{3} \pi r^3\)
\(=\frac{4}{3} \times \frac{22}{7} \times 7^3=\frac{4312}{3}=1437 \frac{1}{3} \mathrm{~cm}^3\)
2)r= 0.63m
∴ Volume = \(\frac{4}{3} \pi r^3\)
\(=\frac{4}{3} \times \frac{22}{7} \times(0.63)^3=1.05 m^3 \text { (approx.) }\)
2. Find the amount of water displayed by a solid spherical ball of diameter (1)28cm (2)0.21cm
Solution: Diameter = 28cm Radius(r)= 14cm
Amount of water displayed \(=\frac{4}{3} \times \frac{22}{7} \times 14^3=\frac{34496}{3} \mathrm{~cm}^3\)
\(=11498 \frac{2}{3} \mathrm{~cm}^3\)
(2) Diameter = 0.21m
Radius(r)=\(\frac{0.21}{2} m=0.105 m\)
∴ Amount of water displayed \(=\frac{4}{3} \pi r^3\)
\(=\frac{4}{3} \times \frac{22}{7} \times(0.105)^3=0.004851 \mathrm{~m}^3\)
3. The diameter of a metallic ball is 4.2cm, what is the mass of the ball, if the density of the metal is 8.9g per cm3?
Solution: Diameter 4.2cm, Radius (r) = 4.2/2 = 2.1 cm
∴ Volume = \(\begin{gathered}
\frac{4}{3} \pi r^3=\frac{4}{3} \times \frac{22}{7} \times(2.1)^3 \\
=38.808 \mathrm{~cm}^3
\end{gathered}\)
Density = 8.9 g per cm3
∴ Mass of the ball = Volume x Density
= 38.808 + 8.9 = 345.39g(approx.)
4. The diameter of the moon is approximately one-fourth of the diameter of the earth, what fraction of the volume of the earth is the volume of the moon?
Solution: Let the radius of the earth be r.
Then, diameter of the earth = 2 r
∴ Diameter of the moon = \(\frac{1}{4}(2 r)=\frac{r}{2}\)
∴ Radius of the moon = \(\frac{1}{2}\left(\frac{r}{2}\right)=\frac{r}{4}\)
Volume of the earth ( v1) = \(\frac{4}{3} \pi r^3\)
Volume of the moon (v2) \(\begin{aligned}
& =\frac{4}{3} \pi\left(\frac{r}{4}\right)^3 \\
& =\frac{1}{64}\left(\frac{4}{3} \pi r^3\right)
\end{aligned}\)
= 1/64 volume of earth.
Hence, the volume of the moon is\(\frac{1}{64^{t h}}\) fraction of the volume of the earth.
5. How many litres of milk can a hemispherical bowl of diameter 10.5cm hold?
Solution: Diameter = 10.5cm
Radius (r) = \(\frac{10.5}{2}=5.25 \mathrm{~cm}\)
Amount of milk \(=\frac{2}{3} \pi r^3=\frac{2}{3} \times \frac{22}{7} \times(5.25)^3 \mathrm{~cm}^3\)
= \(303 \mathrm{~cm}^3 \text { (approx.) }=0.303 \ell \text { (approx.) }\)
6. A hemispherical tank is made up of an iron sheet 1cm thick. If the inner radius is 1m, then find the volume of the iron used to make the tank.
Solution: Inner radius (r) = 1m
Thickness of iron sheet = lcm=0.01m
∴ Outer radius (R) = Inner radius (r) + thickness of iron sheet
= 1m + 0.01m= 1.01m
∴ Volume of the iron used to make the tank
\(\begin{aligned}
& =\frac{2}{3} \pi r^3\left(R^3-r^3\right) \\
& =\frac{2}{3} \times \frac{22}{7} \times\left[(1.01)^3-1^3\right] \\
& =0.06348 \mathrm{~m}^3 \text { approx. }
\end{aligned}\)
7. Find the volume of a sphere whose surface area is 154cm²
Solution: Let the radius of the sphere be r cm
surface area = 154cm²
4πr² = 154
\(\Rightarrow 4 \times \frac{22}{7} \times r^2=154\)
\(\begin{aligned}
& \Rightarrow r^2=\frac{154 \times 7}{4 \times 22} \\
& \Rightarrow r^2=\frac{49}{4} \\
& r=\sqrt{\frac{49}{4}} \\
& \Rightarrow r=7 / 2 \mathrm{~cm}
\end{aligned}\)
∴ Volume of the sphere
\(\begin{aligned}
& \frac{4}{3} \pi r^3=\frac{4}{3} \times \frac{22}{7} \times\left(\frac{7}{2}\right)^3 \\
& =\frac{539}{3} \mathrm{~cm}^2=179 \frac{2}{3} \mathrm{~cm}^3
\end{aligned}\)
8. A dome of a building is in the form of a hemisphere. From inside, it was whitewashed at the cost of ₹498.96. If the cost of whitewashing is ₹2.00 per square metre, find the
1) inside surface area of the dome
2) volume of the air inside the dome
Solution: (1) Inside the surface area of the dome
\(=\frac{498.96}{2}=249.48 \mathrm{~m}^2\)
(2) Let the radius of the hemisphere be rm Inside surface area = 249.48m²
\(\begin{aligned}
& \Rightarrow \quad 2 \pi r^2=249.48 \\
& \Rightarrow \quad 2 \times \frac{22}{7} \times r^2=249.48 \\
& \Rightarrow \quad r^2=\frac{249.48 \times 7}{2 \times 22} \\
& \Rightarrow \quad r^2=39.69 \\
& \Rightarrow \quad r=\sqrt{39.69} \\
& \Rightarrow \quad r=6.3 \mathrm{~m}
\end{aligned}\)
∴ Volume of the air inside the dome =\(\frac{2}{3} \pi r^3\)
\(=\frac{2}{3} \times \frac{22}{7} \times(6.3)^3=523.9 \mathrm{~m}^3 \text { (approx.) }\)
9. Twenty-seven solid Iron spheres each of radius r & surface area S are melted to form a sphere with surface area S1, Find the
1) radius r1 of the new sphere,
2) ratio of S & S1.
Solution: (1) Volume of a solid iron sphere = \(\frac{4}{3} \pi r^3\)
∴ Volume of 27 solid iron spheres \(=27\left(\frac{4}{3} \pi r^3\right)=36 \pi r^3\)
Volume of the new sphere = 36πr3
∴ Let the radius of the new sphere be r1.
then, volume of the new sphere = \(\frac{4}{3} \pi r^3\)
According to the question,
\(\begin{aligned}
& \frac{4}{3} \pi\left(r^3\right)^3=36 \pi r^3 \Rightarrow\left(r^1\right)^3=\frac{\left(36 \pi r^3\right) \times 3}{4 \pi}=27 r^3 \\
& \Rightarrow\left(r^1\right)^3=27 r^3 \Rightarrow r^3=3 r
\end{aligned}\)
Hence, the radius r of the new sphere is 3r
2) S = 4πr²
S1 = 4π(3r)²
∴ \(\frac{S}{S1}=\frac{4 \pi r^2}{4 \pi(3 r)^2}=\frac{1}{9}=1: 9\)
Hence, the ratio of S & S1 is 1: 9
10. A capsule of medicine is in the shape of a sphere of diameter 3.5mm. How much medicine (in mm3) is needed to fill this capsule?
Solution: Diameter of the capsule = 3.5mm
Radius of the capsule(r) \(=\frac{3.5}{2}=1.75 \mathrm{~mm}\)
∴ Capacity of the capsule \(=\frac{4}{3} \pi r^3\)
\(\begin{aligned}
& =\frac{4}{3} \times \frac{22}{7} \times(1.75)^3 \mathrm{~mm}^3 \\
& =22.46 \mathrm{~mm}^3 \text { (approx.) }
\end{aligned}\)
Hence, 22.46 mm3 (approx.) of medicine is needed to fill this capsule.
KSEEB Class 9 Maths Chapter 13 Surface Areas & Volumes Exercises
Surface Areas & Volumes Exercise 13.9
1. A wooden bookshelf has external dimensions as follows: Height = 110cm, Depth = 25cm, and breadth = 85cm (see fig). The thickness of the plank is 5cm everywhere. The external faces are to be polished & the inner faces are to be painted. If the rate of polishing is 20 paise per cm² & the rate of painting is 10 paise per cm² Find the total expenses required for polishing & painting the surface of the bookshelf.
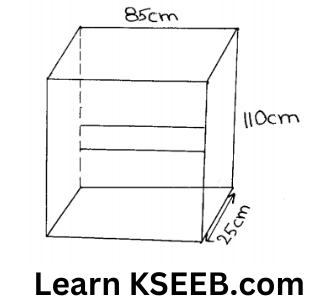
Solution:
Surface area to be polished
=[(110 + 85) + 2(110×25)+ 2(85×25)+ (110×5)+ 4(75+5)]
= (9350 + 5500 + 4250+ 1100+ 1500) cm²
= 21700 cm²
∴ Expenses required for polishing at 20 paise per cm²
₹21700 x 20 paise
\(=₹ \frac{21700 \times 20}{100}=₹ 4340\)
Surface area to be painted
= [2(20 x 90) + 6 (75 x 20) + (75 x 90)]
= (3600 + 9000 + 6750) cm²
= 19350 cm²
∴ Expenses required for painting at 10 paise
percm²= 19350x 10 paise
\(=₹ \frac{19350 \times 10}{100}=₹ 1935\)
∴ Total expenses required for painting and polishing the surface of the bookshelf
= ₹4340+ ₹1935 = ₹6275
2. The front compound wall of a house is decorated by wooden spheres of diameters 21cm, placed on small supports as shown in the figure. Eight such spheres are used for this purpose and are to be painted silver. Each support is a cylinder of radius 1.5cm and height 7cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm² and black paint costs 5 paise per cm².
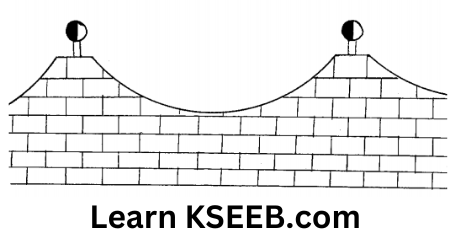
Solution: For a wooden sphere Diameter = 21 cm
∴ Radius(r) = 21/2 cm
Surface area of a wooden sphere = 4πr²
\(=4 \times \frac{22}{7} \times\left(\frac{21}{2}\right)^2=1386 \mathrm{~cm}^2\)
∴ Surface area of a wooden sphere to be painted = 1386 – π(1.5)²
\(\begin{aligned}
& =1386-\frac{22}{7}(1.5)^2 \\
& =1378.93
\end{aligned}\)
∴ Surface area of eight wooden spheres =\(=1378.93 \times 8=11031.44 \mathrm{~cm}^2\)
∴ Cost of painting silver at 25 paise per cm² = 11031.44 x 25 paise
\(\begin{aligned}
& =₹ \frac{11031.44 \times 25}{100} \\
& =₹ 2757.86
\end{aligned}\)
For a cylindrical support
Radius (r) = 1.5 cm
Height (h) = 7 cm
∴ Surface area of a cylindrical support
\(\begin{aligned}
& =2 \pi \mathrm{rh} \\
& =2 \times \frac{22}{7} \times 1.5 \times 7=66 \mathrm{~cm}^2
\end{aligned}\)
∴ Surface area of eight cylindrical supports = 66 x 8
= 528cm²
∴ Cost of painting black at 5 paise per cm² = 528 x 5 paise
\(=₹ \frac{528 \times 5}{100}=₹ 26.40\)
∴ Cost of paint required = 2757.86+26.40
= ₹2784.26(approx.)
3. The diameter of a sphere is decreased by 25%. By what percent does its curved surface area decrease?
Solution: Let the radius of the sphere be r/2 cm,
then its Diameter \(=2\left(\frac{r}{2}\right)=\mathrm{rcm}\)
Curved surface area of the original sphere = \(4 \pi\left(\frac{\mathrm{r}}{2}\right)^2=\pi \mathrm{r}^2 \mathrm{~cm}^2\)
New diameter (decreased) of the sphere
\(\begin{aligned}
& =r-r \times \frac{25}{100} \\
& =r-\frac{r}{4}=\frac{3 r}{4} \mathrm{~cm}
\end{aligned}\)
∴ Radius of the new sphere = \(\frac{1}{2}\left(\frac{3 r}{4}\right)=\frac{3 r}{8} \mathrm{~cm}\)
∴ New curved surface area of the sphere
= \(4 \pi\left(\frac{3 r}{8}\right)^2=\frac{9 \pi r^2}{16} \mathrm{~cm}^2\)
∴ Decrease in the original curved surface area
\(\begin{aligned}
& =\pi \mathrm{r}^2-\frac{9 \pi \mathrm{r}^2}{16} \\
& =\frac{16 \pi \mathrm{r}^2-9 \pi \mathrm{r}^2}{16}=\frac{7 \pi \mathrm{r}^2}{16}
\end{aligned}\)
Percentage of decrease in the original curved surface area
\(=\frac{\frac{7 \pi r^2}{16}}{\pi r^2} \times 100 \%\)
\(=\frac{700 \%}{16}=\frac{175 \%}{4}=43 \frac{3}{4} \% \text { or } 43.75 \%\)
Hence the original curved surface area decreases by 43.75%.
Multiple Choice Questions
1. A tank is 6mx 5m x 4m. Its 2/3rd portion is filled with water. Volume of the water is
- 80m3
- 60m3
- 50m3
- 40m3
Solution: 1. 80m3
2. The base radius and height of a cylinder are 7cm and 14cm respectively. Its total surface area is
- 462cm3
- 462 cm²
- 924cm3
- 924cm²
Solution: 4. 924cm²
3. How many times will the surface area of a sphere become if its radius is doubled?
- 2 times
- 4 times
- 8 times
- 16 times
Solution: 2. 4 times
4. The radius of a sphere is 3cm. It is melted and recast into small spheres of radii 1cm each. Find the number of small spheres
- 1
- 3
- 9
- 27
Solution: 4. 27
5. The area of the four walls of a room is 80cm² and its height is 4m. Then, the perimeter of the floor of the room is
- 16m
- 5m
- 20m
- 10m
Solution: 3. 20m
6. The diameter of a sphere is d, and its volume is
- \(\frac{1}{3} \pi \mathrm{d}^3\)
- \(\frac{1}{24} \pi \mathrm{d}^3\)
- \(\frac{4}{3} \pi \mathrm{d}^3\)
- \(\frac{1}{6} \pi \mathrm{d}^3\)
Solution: 4. \(\frac{1}{6} \pi \mathrm{d}^3\)
7. The volume and curved surface area of a sphere are numerically equal. The radius of the sphere is
- 1/3cm
- 3cm
- 4cm
- 7cm
Solution: 2. 3cm
KSEEB Maths Chapter 13 Surface Areas & Volumes Answers
8. A cone and a hemisphere have equal bases and equal volumes. The ratio of their heights is
- 2:1
- 1:2
- 2:3
- 3:2
Solution: 1. 2:1
9. If the dimensions of a cuboid are a, b and c respectively, then the volume of the cuboid is _
- abc
- (ab + bc + ca)
- a3
- a²b²c²
Solution: 1. abc
10. If the sum of all the edges of a cube is 36cm, then the volume of the cube is
- 9cm3
- 27cm3
- 216cm3
- 1728cm3
Solution: 2. 27cm3
EXTRA SUMS
1. Find the volume of a cube of side \(3 \sqrt{3 a}\) .
Solution: Volume of Cube = (edge)3 = \((3 \sqrt{3 a})^3\) = \(81 \sqrt{3} a^3\)
2. The diameter of a football is five times the diameter of a cricket ball. Find the ratio of surface areas of football and cricket ball.
Solution: Diameter of football = 5 x diameter of a cricket ball.
If r denotes the radius of a football and r that of a cricket ball, then we have
\(\begin{aligned}
& 2 r=5 \times\left(2 r^1\right) \\
& =\frac{2 r}{2 r^1}=5 \text { (or) } \frac{r}{r^1}=5
\end{aligned}\)
Now, the ratio of surface area
\(=\frac{4 \pi r^2}{4 \pi\left(r^1\right)^2}=\left(\frac{r}{r^1}\right)^2=\frac{25}{1}=25: 1\)
3. A cuboidal block of wood is of dimensions 5m x 2m x lm, find the number of cubes of dimensions 1m x 1m x 1m which can be cut from it.
Solution:
\(\begin{aligned}
& \mathrm{n}=\frac{\mathrm{V} \text { cuboid }}{\mathrm{V} \text { cube }} \\
& =\frac{5 \times 2 \times 1}{1 \times 1 \times 1}=10 \text { cubes }
\end{aligned}\)
4. There are two cones. The ratio of their radii is 4:1. Also the slant height of the second cone is twice that of the first. Find the relationship between their curved surface area.
Solution:
\(\begin{aligned}
& r_1: r_2=4: 1 \\
& \Rightarrow \frac{r_1}{r_2}=\frac{4}{1} \\
& \Rightarrow \frac{1_1}{1_2}=\frac{1}{2}
\end{aligned}\)
∴ \(\frac{\mathrm{CSA}_1}{\mathrm{CSA}_2}=\frac{\pi r_1 l_1}{\pi r_2 l_2}=\left(\frac{r_1}{r_2}\right)\left(\frac{1_1}{1_2}\right)\)
\(=\frac{4}{1} \times \frac{1}{2}=\frac{2}{1}\)
∴ \(\mathrm{CSA}_1=2 \mathrm{CSA}_2\)
5. The total cost of making a solid spherical ball is ₹33957 at the rate of ₹7 per cubic meter. Find the radius of this ball.
Solution:
\(\begin{aligned}
& \frac{\text { Total Cost }}{\text { Cost } / \mathrm{m}^3}=\text { Volume of sphere } \\
& =\frac{33957}{7}=\frac{4}{3} \pi \mathrm{r}^3 \\
& \Rightarrow \mathrm{r}^3=\frac{33957 \times 3}{7 \times 4 \times \pi} \\
& =\frac{33957 \times 3 \times 7}{7 \times 4 \times 22}=1157.625 \\
& \Rightarrow \mathrm{r}=10.5 \mathrm{~cm}
\end{aligned}\)
6. The volumes of two spheres are in the ratio of 64:27. Find their radii if the sum of their radii is 21cm.
Solution: Let the radii of two spheres be r1 r2.
∴ r1 + r2 = 21
=> r1 = 21 b- r2
Volume of I sphere = \(\frac{4}{3} \pi \mathrm{r}_1^3 \mathrm{~cm}^3\)
Volume of II sphere = \(\frac{4}{3} \pi r_2^3 \mathrm{~cm}^3\)
\(\begin{aligned}
& \frac{\text { Volume of I sphere }}{\text { Volume of II sphere }}=\frac{\frac{4}{3} \pi\left(21-r_2\right)^3}{\frac{4}{3} \pi r_2^3}=\frac{64}{27} \\
& \Rightarrow \frac{\left(21-r_2\right)^3}{r_2^3}=\frac{64}{27}
\end{aligned}\)
\(\begin{aligned}
& \Rightarrow \frac{21-r_2}{r_2}=\frac{4}{3} \\
& \Rightarrow 63-3 r_2=4 r_2 \\
& \Rightarrow 63=4 r_2+3 r_2 \\
& \Rightarrow 7 r_2=63 \\
& \Rightarrow r_2=\frac{63}{7}=9 \mathrm{~cm}
\end{aligned}\)
∴ \(r_1=21-r_2\)
= 21 – 9
∴ \(r_1=12 \mathrm{~cm}\)
7. A teak wood log is in the form of cuboid of length 2.3m, width 75cm and of certain thickness. Its volume is 1.104m3. How many rectangular planks of size 2.3m x 72cm x 4cm can be cut from the cuboid?
Solution:
\(\text { Thickness }=\frac{\text { Volume }}{1 \times \mathrm{b}}=\frac{1.104}{2.3 \times 0.75}=0.64 \mathrm{~m}\)
\(\text { Number of planks }=\frac{1.104}{2.3 \times 0.75 \times 0.04}=16\)
8. Lead spheres of diameter 6cm each are dropped into a cylindrical beaker containing some water and are fully submerged. If the diameter of the beaker is 18cm and the water level rises by 40cm, find the number of lead spheres dropped in the water.
Solution: Volume of water = πr²h
= π x 9 x 9 x 40
Volume of sphere = \(\frac{4}{3} \pi \mathrm{r}^3\)
\(\begin{aligned}
& =\frac{4}{3} \pi \times 3 \times 3 \times 3 \\
& =4 \pi \times 9
\end{aligned}\)
Number of Spheres = \(\frac{\pi \times 9 \times 9 \times 40}{4 \pi \times 9}\)
= 90
9. A rectangular piece of paper is 22cm long and 10cm wide. A cylinder is formed by rolling the paper along its length. Find the volume of the cylinder.
Solution:
h = 10cm
\(\begin{aligned}
& 2 \pi r=22 \\
& \Rightarrow 2 \times \frac{22}{7} \times r=22 \\
& \Rightarrow r=\frac{22 \times 7}{2 \times 22}=\frac{7}{2} \\
& V=\pi r^2 \mathrm{~h} \\
& =\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 10 \\
& =385 \mathrm{~cm}^2
\end{aligned}\)
10. What is the radius and curved surface area of a cone made from a quadrant of a circle of radius 28cm?
Solution: l = 28cm
l = Radius of quadrant of cone = R
Area of quadrant = Area of cone
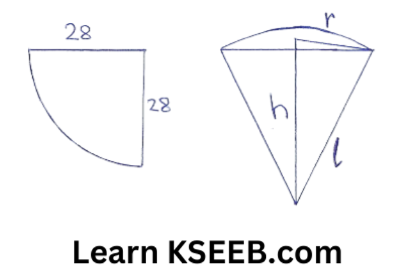
\(\frac{1}{4} \pi R^2=\pi r l\)
\(\Rightarrow \frac{1}{4} \times \pi \times(28)^2=\pi r l\)
\(\begin{aligned}
& \Rightarrow \frac{28 \times 28}{4}=\mathrm{r} \times 28 \\
& \Rightarrow \mathrm{r}=\frac{28 \times 28}{4 \times 28}=7 \mathrm{~cm} \\
& \text { C.S.A of come }=\pi \mathrm{rl}=\frac{22}{7} \times 7 \times 28 \\
& =22 \times 28=616 \mathrm{~cm}^2
\end{aligned}\)
11. Bhavya has a piece of canvas whose area is 552m². She uses it to make a conical tent with a base radius of 7m. Assuming that all the stitching margins and the wastage incurred while cutting amounts to approximately 2m². Find the volume of the tent that can be made with it.
Solution:
CSA of the tent = 552 – 2 = 550 m²
Radius (r) = 7 m
∴ πx7x1 = 550
\(\Rightarrow l=\frac{550 \times 7}{22 \times 7}=25 \mathrm{~m}\)
∴ \(h=\sqrt{l^2-r^2}=\sqrt{25^2-7^2}=\sqrt{625-49}\)
\(\begin{aligned}
& =\sqrt{576} \\
& =24 \mathrm{~m}
\end{aligned}\)
Volume of the tent = \(\frac{1}{3} \times \frac{22}{7} \times 7 \times 7 \times 24\)
= 1232 m3
12. The height, curved surface area and volume of a cone are h, c and v respectively. Prove that 3πrh3 -c²h² +9v² = 0.
Solution: If r be the radius of cone, then slant height
l = \(\sqrt{\mathrm{h}^2+\mathrm{r}^2}\)
∴ c = πrl
V = \(\frac{1}{3} \pi r^2 h\)
LHS = 3πrh3 -c²h² +9v²
\(\begin{aligned}
& =3 \pi\left(\frac{1}{3} \pi r^2 h\right) h^3-(\pi r l)^2 h^2+9\left(\frac{1}{3} \pi r^2 h\right)^2 \\
& =\pi^2 r^2 h^4-\pi^2 r^2 l^2 h^2+\pi^2 r^4 h^2 \\
& =\pi^2 r^2 h^4-\pi^2 r^2\left(h^2+r^2\right) h^2+\pi^2 r^4 h^2 \\
& =\pi^2 r^2 h^4-\pi^2 r^2 h^4-\pi^2 r^4 h^2+\pi^2 r^4 h^2 \\
& =0=\text { RHS }
\end{aligned}\)
13. A cylindrical container of base radius 6 cm, has water up to a height of 5 cm. Find
1. Volume of water
2. A metal sphere of radius 2 cm is totally submerged in the water. Find a rise in the water level.
Solution: For cylinder
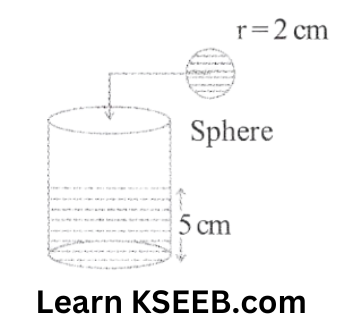
H = 5 cm and R = 6 cm
For sphere r = 2 cm
Volume of water in cylinder
\(\begin{aligned}
& \Rightarrow \pi \mathrm{R}^2 \mathrm{H}=\frac{22}{7} \times 6 \times 6 \times 5 \\
& =\frac{110 \times 36}{7}=565.71 \mathrm{~cm}^3
\end{aligned}\)
Let rise in water level in cylinder be ‘h’ units
=> Volume of sphere = Volume of water displaced in cylinder
\(\begin{aligned}
& \frac{4}{3} \pi \mathrm{r}^3=\pi \mathrm{r}^2 h \\
& \mathrm{~h}=\frac{4 \mathrm{r}^3}{3 \mathrm{R}^2}=\frac{4 \times 2 \times 2 \times 2}{3 \times 6 \times 6}=0.29 \mathrm{~cm}
\end{aligned}\)
KSEEB Chapter 13 Surface Areas & Volumes Solved Questions
14. The teacher asked students to prepare project related to Diwali. Likitha prepared 12 cylindrical candles each having radius of base 2 cm and a height 7 cm. Himanshu prepared 14 firecrackers each of spherical shape of radius 1.50 cm.
1. Find the volume of candles and firecrackers
2. According to you which has better project work and why?
Solution: 1. Radius of a cylindrical candle(r) = 2 cm
Height of a cylindrical candle(h) = 7 cm
∴ Volume of a cylindrical candle = πr²h
= \(\frac{22}{7} \times 2 \times 2 \times 7=88 \mathrm{~cm}^3\)
∴ Volume of 12 cylindrical candles
= 12 x 88
= 1056cm3
Also, radius of a spherical firecracker 3
r = 1.5 cm=3/2 cm
∴ Volume of a spherical firecracker = \(\frac{4}{3} \pi r^3\)
\(\begin{aligned}
& =\frac{4}{3} \times \frac{22}{7} \times \frac{3}{2} \times \frac{3}{2} \times \frac{3}{2} \\
& =\frac{99}{7} \mathrm{~cm}^3
\end{aligned}\)
Volume of 14 spherical firecrackers
\(=\frac{99}{7} \times 14=198 \mathrm{~cm}^3\)
2. Likitha has a better project because candles do not pollute the environment.
15. Naresh, a juice seller has set up his Juice shop. He has three types of glasses (see figure) of inner diameter 5 cm to serve the customers. The height of the glasses is 10 cm.
Type A Type B Type C
Type A: A glass with a plane bottom.
Type B: A glass with the hemispherical raised bottom.
Type C: A glass with the conical raised bottom of height 1.5 cm.
He decided to serve the customers in ’A’ type of glasses (π =3.14)
1. Find the volume of each type of glass.
2. Which glass has the minimum capacity?
Solution: 1. Volume of glass A = πr²h
= 3.14x(2.5)² x 10
= 196.25 cm3
Volume of the hemisphere in glass B
\(\begin{aligned}
& =\frac{2}{3} \pi \mathrm{r}^3=\frac{2}{3} \times 3.14 \times(2.5)^3 \\
& =32.71 \mathrm{~cm}^3
\end{aligned}\)
Volume of glass B = Volume of glass A – Volume of hemisphere.
= 196.25-32.71 = 163.54cm3
Volume of cone of glass C
= \(\frac{1}{3} \pi \mathrm{r}^2 \mathrm{~h}=\frac{1}{3} \times 3.14 \times(2.5)^2 \times 1.5=9.81 \mathrm{~cm}^3\)
Volume of glass C = 196.25-9.81 = 186.44 cm3
The glass of type B has minimum capacity of 163.54 cm3
16. A table cover 4m x 2m is spread on the table. Find the cost of polishing the top of the table at ₹40 per square metre of 25 cm table cover is hanging all around the table.
Solution: For table cover
l = 4 – (0.25 + 0.25) (∵ 25 cm = 0.25 m)
= 3.5 m
b = 2-(0.25+ 0.25)= 1.5 m
∴ Area of cover = l x b = 3.5x 1.5 = 5.25 m²
∴ Cost of polishing the top of the table at ₹40 per square metre = 5.25 x 40 = ₹210
17. Two cubes of side 6 cm each, are joined end to end. Find the surface area of the resulting cuboid.
Solution: For resulting cuboid
Length(l) = 6+6 = 12 cm
Breadth(b) = 6 cm
Height(h) = 6 cm
Surface area = 2(lb+bh+hl)
= 2(12 x 6 + 6 x 6 + 6 x 12)
= 360 cm²
18. A cylinder 3m high, is open at the top. The circumference of its base is 22 cm. Find its total surface area.(π=22/7)
Solution: Let the base radius of the cylinder be r cm. then, 2πr = 22
\(\begin{aligned}
& \Rightarrow 2 \times \frac{22}{7} \times \mathrm{r}=22 \\
& \Rightarrow \mathrm{r}=\frac{22 \times 7}{2 \times 22}=\frac{7}{2}
\end{aligned}\)
h = 3 m
∴ Total surface area= 2πrh +πr²
\(\begin{aligned}
& =2 \times \frac{22}{7} \times \frac{7}{2} \times 3+\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \\
& =66+38.5 \\
& =104.5 \mathrm{~m}^2
\end{aligned}\)
19. Find the area of the metal sheet required to make two closed hollow cones each of height 24 cm and slant height 25 cm.
Solution: h = 24 cm, l = 25 cm
\(\begin{aligned}
& \Rightarrow \mathrm{l}^2=\mathrm{r}^2+\mathrm{h}^2 \\
& \Rightarrow(25)^2=\mathrm{r}^2+(24)^2 \\
& \Rightarrow \mathrm{r}^2=(25)^2-(24)^2 \\
& =(25+24)(25-24) \\
& =49 \times 1 \\
& \Rightarrow r=\sqrt{49}=7 \mathrm{~cm}
\end{aligned}\)
∴ Area of the metal sheet required = 2(πrl)
\(=2 \times \frac{22}{7} \times 7 \times 25=600 \mathrm{~cm}^2\)
20. If the radius of a sphere is halved then what is the decrease in its surface area?
Solution: Let the radius of the sphere be r.
Then surface area of the sphere = 4πr²
New radius of the sphere = r/2
∴ New surface area of the sphere = \(4 \pi\left(\frac{r}{2}\right)^2=\pi r^2\)
∴ Decrease in the surface area = 4πr² – πr²
\(=3 \pi r^2=\frac{3}{4}\left(4 \pi r^2\right)\)
=3/4(Surface area of the Original Sphere)
21. If V is the volume of a cuboid of dimensions a, b and c and s is its surface area, then prove that:
\(\frac{1}{v}=\frac{2}{s}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
Solution:
\(\text { LHS }=\frac{1}{v}=\frac{1}{a b c}\)……………………(1)
\(\mathrm{RHS}=\frac{2}{\mathrm{~s}}\left(\frac{1}{\mathrm{a}}+\frac{1}{\mathrm{~b}}+\frac{1}{\mathrm{c}}\right)\)
\(=\frac{2}{2(a b+b c+c a)}\left(\frac{b c+c a+a b}{a b c}\right)\)
\(=\frac{1}{a b c}\)………………….(2)
from (1) and (2) we get,
\(\frac{1}{v}=\frac{2}{s}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
22. Coins of the same size are placed one above the other and a cylindrical solid block is formed. The volume of this block is 49.28 cm3. The diameter of each coin is 2.8 cm and the thickness is 0.2 cm. Find the number of coins arranged in the block.(π = 22/7)
Solution: Let n be the number of coins.
For block, r = 2.8/2 cm = 1.4 cm
\(\begin{aligned}
& \mathrm{h}=(0.2) \mathrm{ncm}, \mathrm{v}=49.28 \mathrm{~cm}^3 \\
& \mathrm{v}=\pi \mathrm{r}^2 \mathrm{~h} \\
& \Rightarrow 49.28=\frac{22}{7} \times(1.4)^2 \times(0.2) \mathrm{n}
\end{aligned}\)
\(\begin{aligned}
& \mathrm{h}=(0.2) \mathrm{n} \mathrm{cm}, \mathrm{v}=49.28 \mathrm{~cm}^3 \\
& \mathrm{v}=\pi \mathrm{r}^2 \mathrm{~h} \\
& \Rightarrow 49.28=\frac{22}{7} \times(1.4)^2 \times(0.2) \mathrm{n} \\
& \Rightarrow \mathrm{n}=\frac{49.28 \times 7}{22 \times 0.2 \times(1.4)^2} \\
& \Rightarrow \mathrm{n}=40
\end{aligned}\)
23. If the radius of the base of a right circular cone is halved keeping the height same, what is the ratio of the volume of the reduced cone to that of the original one?
Solution: Let the radius of the base and the height of the original cone be r and h respectively.
Volume of the original cone\(\left(\mathrm{V}_1\right)=\frac{1}{3} \pi \mathrm{r}^2 \mathrm{~h}\)……………..(1)
For the reduced cone
Radius = r/2
Height = h
∴ Volume of the reduced cone (V2)
\(\begin{aligned}
& =\frac{1}{3} \pi\left(\frac{\mathrm{r}}{2}\right)^2 \mathrm{~h} \\
& \left(\mathrm{~V}_2\right)=\frac{1}{4} \times \frac{1}{3} \pi \mathrm{r}^2 \mathrm{~h}=\frac{1}{4} \mathrm{~V}_1(\text { from (1)) }
\end{aligned}\)
∴ \(\frac{\mathrm{V}_2}{\mathrm{~V}_1}=\frac{1}{4}=1: 4\)
Hence, the ratio of the volume of the reduced cone to that of the original one is 1: 4.
24. A spherical ball of lead 3 cm in radius is melted and recast into three spherical balls. If the radii of two balls are 3/2 cm and 2 cm, find the diameter of the third ball.
Solution: Let the radius of the third ball be r cm, then according to the question
\(\begin{aligned}
& \frac{4}{3} \pi(3)^3=\frac{4}{3} \pi\left(\frac{3}{2}\right)^3+\frac{4}{3} \pi(2)^3+\frac{4}{3} \pi(\mathrm{r})^3 \\
& \Rightarrow \frac{4}{3} \pi \times 27=\frac{4}{3} \pi\left(\frac{27}{8}+8+\mathrm{r}^3\right) \\
& \Rightarrow 27=\frac{27}{8}+8+\mathrm{r}^3 \\
& \Rightarrow \mathrm{r}^3=27-\frac{27}{8}-8 \\
& \Rightarrow \mathrm{r}^3=\frac{155}{8} \\
& \Rightarrow \mathrm{r}=\sqrt[3]{\frac{155}{8}} \\
& \Rightarrow \mathrm{r}=\frac{\sqrt[3]{155}}{2} \mathrm{~cm} \\
& \Rightarrow 2 \mathrm{r}=\sqrt[3]{155} \mathrm{~cm}
\end{aligned}\)
Hence, the diameter of the third ball is \(\sqrt[3]{155}\) cm
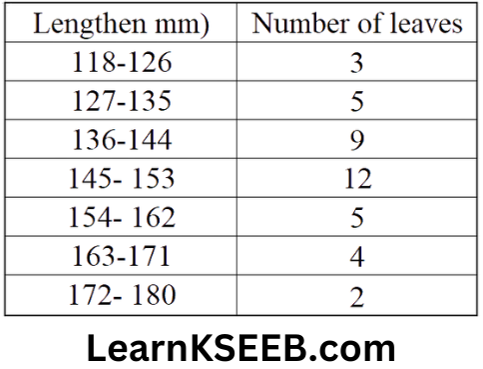
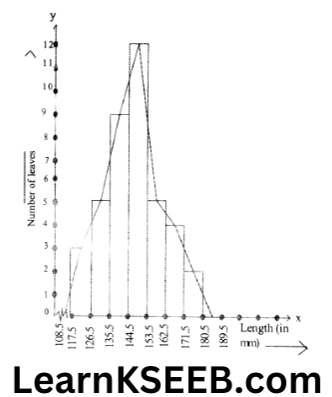
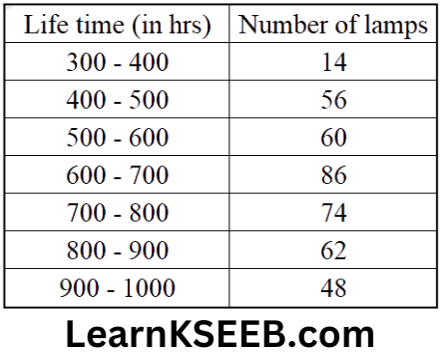
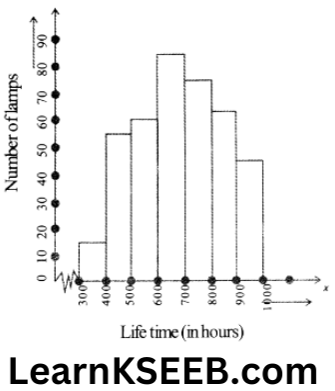
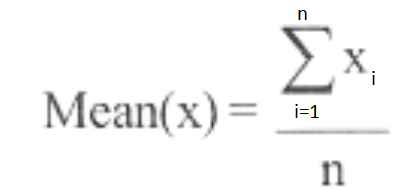where n is the number of observations.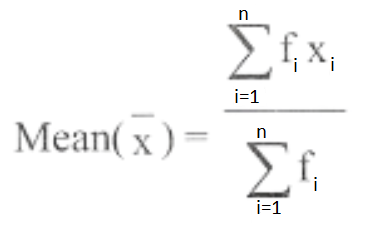
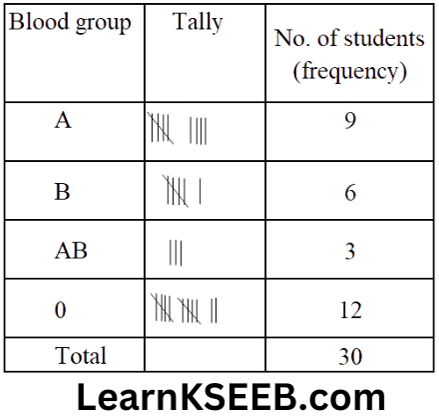
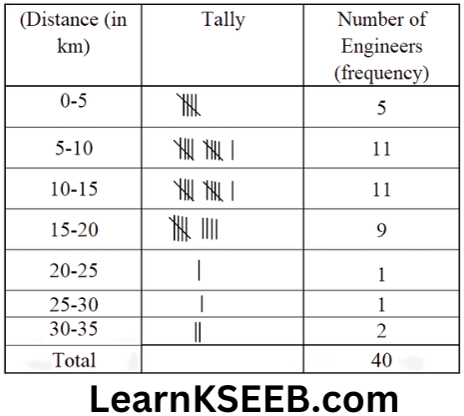
(Hint: Draw perpendicular (normals) at B & C to the two plane mirrors. Recall that angle of incidence is equal to angle of reflection)
