Pressure-Volume Work
A chemical reaction, is generally, associated with an absorption or evolution of heat However, many reactions also involve mechanical work along with the absorption or evolution of heat.
This work is done either by the system on its surroundings or by the surroundings of the system. The mechanical work associated with a chemical reaction is due to the change in the volume ofthe reaction system.
If the volume of a system increases against an external pressure or decreases by an external pressure, then some amount of mechanical work is performed because of the change in the volume of the system. This work is called pressure-volume work (or P-Vwork).
Read and Learn More KSEEB Class 11 Chemistry Notes
In a reaction, if one or more gaseous products are formed [example Zn(s) + 2HCl(aq)→ZnCl2(aq) + H2(g) ] or the number of moles of gaseous substances increases [example PCl5(g)→PCl3(g) + Cl2(g) ], then the volume of the system increases against external pressure (usually against atmospheric pressure). The work is thus performed by the system on the surroundings.
On the other hand, in a reaction, if the gaseous reactants are consumed [example 2H2(g) + O2(g) 2H2O(1) ] or the number of moles of gaseous substances decreases [example N2(g) + 3H2(g) 2NH3(g) ], then work is performed on the system! by the surroundings under the influence of external pressure.

KSEEB Class 11 Chemistry Notes For Pressure Volume Work
Calculation of pressure-volume (P-V) work:
According to mechanics, if dx is the displacement of the point of application of force F acting on a particular body, then [ work done = Fcost? dx [where 6 is the angle between the direction of applied F and the direction of displacement (dx) of the point, FcosB is the component of force along the direction ofdisplacement] If the applied force (F) and f . the displacement (dx) be in the same direction, then. 9 = 0 and cos# = 1 . Hence, in this case, we can write,
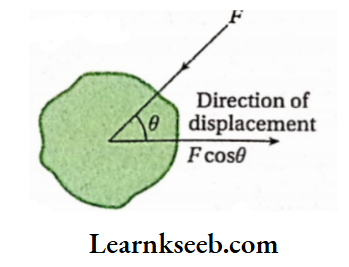
- Again, when (lie applied force (P) and displacement are In the opposite direction, then and COHO m In this case, work done = Pdx.
- Force And displacement are both vector quantities, but their product (work) Is a scalar quantity.
The equation for pressure-volume work:
Let us consider, that a gas is kept In a cylinder fitted with a weightless and frictionless piston. The piston Is held up by the stops (s,s).
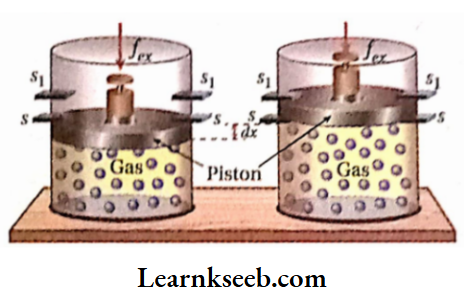
Suppose, an external force is applied to the piston. If the cross-sectional area of the piston is A then external pressure, Pex \(=\frac{f_{e x}}{A}\) Suppose, Pex is less than the pressure of the gas.
Now, if stops (s, s) are removed, the gas will expand against external pressure till the piston is again held up by the stops (s1, S1). The piston moves a distance of dx, then work is done by the system on the surroundings
⇒ \(\delta w=-f_{e x} d x=-P_{e x} A d x\) [since \(f_{e x}=P_{e x} A\)
[According to the convention, work done by the system is -ve ] Now, A dx – dV = increase in volume ofthe gas (system) due to the displacement of the piston. So, \(\delta w=-P_{e x} d V\) Let us consider the gas is expanded from its initial volume K1 to final volume V2. If this expansion is carried out in several steps, then the total work done by the gas.
⇒ \(w=-\int_{V_1}^{V_2} P_{e x} d V\)
[since Since work is not a state function, the value of \(\int_1^2 \delta w\) cannot be expressed as (u/2- u/1, instead we represent it as w .] Equation [1] is the general expression of P-Vwork. Work done by the gas and work done on the gas both can be calculated by using equation [1].
Expansion work of a gat:
If a gas expands from iu initial volume V1 to final volume V2 against a constant eternal pressure of V2, then work done
⇒ \(w=-\int_{V_1}^{V_2} p_{e x} d V=p_{e x}\left(V_2-V_1\right)\left\{p_{s x}=\text { constant }\right]\)
⇒ \(=-P_{e x} \Delta V\)
⇒ \(w=-P_{e x} \Delta V=-v e\)
Since \(V_2>V_1, \Delta V=V_2-V_1=+v e j\)
Conventionally, the Work done by the system is negative.
Pressure-Volume Work Explained In KSEEB Class 11 Chemistry
Compression work of a gas:
If a gas is compressed from its initial volume V1 to final volume V2 where a constant external pressure is Pex, then work done, \(w=-\int_{V_1}^{V_2} P_{e x} d V=-P_{e x}\left(V_2-V_1\right)\)
since Pex constant
⇒ \(=-P_{e x} \Delta V\)
∴ \(w=-P_{e x} \Delta V=+v e\)
Since \(V_2<V_1 \text { and } \Delta V=V_2-V_1=-v e\)
Conventionally, work done on the die system is positive.
Pressure-volume work in a reversible process
A reversible process is completed by an infinite number of small steps. In each step of this process, the driving force is infinitesimally greater than the opposing force.
Let V1 be the volume of a certain amount of a gas confined in a cylinder fitted with a weightless & frictionless piston. The gas is expanded reversibly from volume V1 to V2.
If the external pressure (Pex) on the gas is equal to the pressure ofthe gas (P), then there will be no displacement ofthe piston. Consequently, the volume ofthe gas does not change and the system remains in equilibrium.
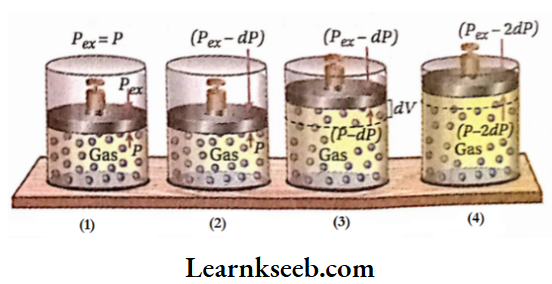
Now, external pressure is diminished by an infinitesimal amount of DP. As a result, the gas will start to expand against pressure (Pex- dP) until the pressure of the gas equals the pressure (Pgx- dP). Suppose the volume is increased by an amount of dV. At the end of this expansion, the system regains its equilibrium state.
Again, external pressure is further decreased by an amount of DP. Consequently, the volume ofthe gas also increases by an infinitesimal amount of dV, and at the end of the expansion, the equilibrium of the system is restored. In this way, the gas is made to expand in an infinite number of small steps until the volume ofthe gas reaches V2.
Expression of pressure-volume work in a reversible process: In a reversible expansion of a gas, in each step, external pressure (Pex) is infinitesimally smaller than the pressure of the gas (P). Thus, in each step, Pgx is considered to be almost equal to P. So, in each step work done, 8wrgv = -PgxdV =-PdV [P = pressure ofthe gas at respective step, dV= infinitesimal increase in volume due to infinitesimal decrease in pressure & ‘rev’ = reversible]. If in a reversible expansion, the volume ofa gas is increased from V1 to V2, then-
⇒ \(w_{r e v}=-\int_{V_1}^{V_2} P d V\)
Equation [1] can be used to calculate the work done by a gas in its reversible expansion. To integrate equation [1], it is necessary to know the variation of pressure of the gas with volume. Work done on the gas in a reversible compression can also be calculated using equation [1], in this case, V2 < V1.
KSEEB Chemistry Notes On Pressure-Volume Work Class 11
Work done by an ideal gas in its isothermal reversible expansion
Let us consider that n mol of an ideal gas is enclosed in a cylinder fitted with a weightless and frictionless piston. The initial pressure, temperature, and volume of the gas are P1, T, and V1 respectively. Now the gas is expanded reversibly from volume V1 to V2 under isothermal conditions. Suppose, due to this expansion, the pressure of the gas decreases from P1 to P2.

Calculation of work done: Work done due to isothermal reversible expansion,
⇒ \(w_{r e v}=-\int_{V_1}^{V_2} P d V=-\int_{V_1}^{V_2} \frac{n R T}{V} d V\)
∴ \(P=\frac{n R T}{V}\)
As the process is isothermal, so Tremains constant
∴ \(w_{r e v}=-n R T \int_{V_1}^{V_2} \frac{d V}{V}\)
∴ \(w_{r e v}=-n R T \ln \frac{V_2}{V_1}=-2.303 n R T \log \frac{V_2}{V_1}\)
At constant temperature for an ideal gas \(\frac{V_2}{V_1}=\frac{P_1}{P_2}\)
In equations [1] and [2], wrong is negative because during expansion V2 > & P1 > P2. This conforms with the convention because the sign of work done by the system is negative. Therefore, applying equations [1] and [2], it is possible to calculate the amount of work done by an ideal gas (system) in an isothermal reversible expansion.
Work done on an ideal gas in its isothermal reversible compression
Let us consider that n mol of an ideal gas is enclosed in a cylinder fitted with a weightless and frictionless piston. The initial pressure, temperature, and volume (before compression) are Px, T, and V respectively. Now the gas is compressed reversibly from volume V1 to V2 under isothermal conditions.
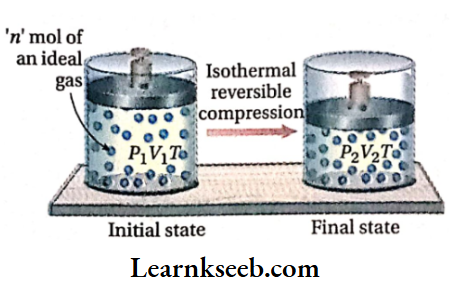
Suppose, the pressure of the gas increases from P1 to P2 because of this compression.
Calculation of work done: Work done in the isothermal reversible compression,
⇒ \(w_{r e v}=-n R T \ln \frac{V_2}{v_1}\) …………………………….(1)
= \(w_{r e v}=-n R T \ln \frac{P_1}{P_2}=-2.303 n R T \log \frac{P_1}{P_2}\) …………………………….(2)
In equations (1) and (2), the sign is positive because V2 < V1 and P2 > P1. This conforms with the convention because the sign of work done on the system is positive. Therefore, applying equations (1) and (2), it is possible to calculate the amount of work done on an ideal gas (system) in its isothermal reversible compression.
Work done by a gas in its irreversible expansion
Let us assume that a certain amount of gas is kept in a cylinder fitted with a weightless and frictionless piston. Suppose, the initial volume and pressure of the gas are V1 and P1 respectively

If the external pressure is suddenly reduced to P2 (where P2 is much less than P1 ), the gas will go on expanding till the internal pressure becomes equal to P2. Let the volume of the gas increase from V1 to V2 due to the lowering of pressure from P1 to P2.
Calculation of Work done: Work done by the gas
⇒ \(w_{i r r}=-\int_{V_1}^{V_2} P_{e x} d V=-\int_{V_1}^{V_2} P_2 d V\)
[External pressure Pex= P2Irr = irreversible]
∴ \(w_{i r r}=-P_2\left(V_2-V_1\right)\) ……………..(1)
As \(v_2>v_1, w_{i r r}\) = negative. This agrees with the convention as the sign of work done by the system is negative. The amount of work done by the gas in its irreversible expansion against a constant external pressure can be calculated by using the above equation (1),
KSEEB Class 11 Chemistry Pressure-Volume Work Solutions
Work done by n mol of an Ideal gas in Its isothermal irreversible expansion:
From equation [1] we obtain
⇒ \(w_{i r r}=-P_2\left(V_2-V_1\right) \text {; where, } V_2>V_1 \text {. For } n \mathrm{~mol} \text { of an }\)
⇒ \(\text { ideal gas, } V=\frac{n R T}{P} \text {. At the initial state, } V_1=\frac{n R T}{P_1} \text { and at }\) \(\text { final state, } V_2=\frac{n R T}{P_2}\)
Therefore ⇒ \(w_{i r r}=-P_2\left(\frac{n R T}{P_2}-\frac{n R T}{P_1}\right)\)
∴ \(w_{i r r}=-n R T\left(1-\frac{P_2}{P_1}\right)\left[P_2<P_1\right]\)
The amount of work done by n mol of an ideal gas is due to its isothermal irreversible expansion can be calculated by using equation (1) or (2)
Work done on a gas in its irreversible compression
Let us consider a gas kept in a cylinder fitted with a frictionless and weightless piston is in thermodynamic equilibrium. Suppose, the initial pressure and volume of the gas are P1 and V1 respectively.
As the gas is in the state of thermodynamic equilibrium, the internal and external pressures are equal. If the external pressure is suddenly increased from (P1 to P2 (where P2 is much greater than P1 ), the volume of the gas will keep on decreasing until the internal pressure becomes equal to the external pressure P2. Suppose the volume of the gas decreases from V1 to V2 due to an increase in pressure from P1 to P2.

Calculation of work done:
⇒ \(w_{i r r}=-\int_{V_1}^{V_2} P_{e x} d V=-\int_{V_1}^{V_2} P_2 d V\)
External pressure Pex = P2
∴ \(w_{i r r}=-P_2\left(V_2-V_1\right)\) ……………………..(1)
∴ \(w_{i r r}=\text { positive }\left[V_2<V_1\right]\)
This agrees with the convention because the sign of work done on the system is positive.
The amount of work done on the gas (by the surroundings) in an isothermal irreversible compression can be calculated try the equation 11 {. Work done by n mol of an Ideal gnu In Its Isothermal Irreversible compression: Prom the equation |1| we obtain
⇒ \(w_{i r r}=-P_2\left(V_2-V_1\right) \quad\left|V_2<V_1\right|\)
⇒ \(\text { Initial volume, } V_1=\frac{n R T}{P_1} \text { and the final volume } V_2=\frac{n R T}{P_2}\)
Therefore \(w_{i r}=-P_2\left(\frac{n n T}{P_2}-\frac{n R T}{P_1}\right) .\)
∴ \(w_{i r r}=-n R T\left(1-\frac{P_2}{P_1}\right)\left[P_2>P_1\right]\)
The amount of work done on n mol of an ideal gas in its isothermal irreversible compression can be calculated by the equation [1] or [2].
The magnitude of work done by a gas in its reversible expansion is always greater than that in its irreversible expansion provided the initial and final states of the system arc are identical in hodi die cases.
Fit tu on Reversible expansion of gas occurs through a large number of infinitesimal steps, and in each step, the external pressure differs from the pressure of the gas by an infinitesimal amount. Therefore, in each step of a reversible expansion, the gas is expanded against the maximum possible pressure. As a result, The work obtained in a reversible expansion is maximum.
On die other hand, in an irreversible expansion of a gas, the external pressure differs from the pressure of the gas by a finite amount. In this expansion, since the gas expands against an external pressure fairly less than the pressure of the gas, the work obtained is always less than the reversible expansion.
Work done by a gas in its free expansion
In free expansion, the gas expands against zero external pressure. The work done
⇒ \(\boldsymbol{w}=-\int_{V_1}^{V_2} \boldsymbol{P}_{e x} d V=-\int_{V_1}^{V_2} 0 \times d V=0\)
[Since the gas expands against zero pressure, Pex = 0] Therefore, the work done by a gas in its free expansion is zero.
Pressure-volume work in a chemical reaction
At a particular temperature and pressure, the change in volume of a reaction system is considered to be made up of reactants and products involved in the reaction depending primarily on the change in the number of moles of gaseous substances that participated in the reaction.
This is because the change in the number of moles of solid or liquid substances that participated in a reaction has a negligible effect on the volume of the reaction system.
Pressure-volume work in a chemical reaction Example:
When I mol of Zn reacts completely with dilute HCl, 1 mol of H2 gas is produced. In this reaction, the change in volume of the reaction system will be approximately equal to the volume of 1 mol of H2 since the contribution of other constituents towards the volume change is negligible.
Suppose, at constant temperature ( T) and pressure, the difference in volume between the gaseous products and reactants in a reaction is AV’. So. work done, w = -PΔV. If the difference in the number of moles between the gaseous products and the gaseous reactants Is An and these gases behave like an ideal gas, then work done
⇒ \(w=-P \Delta V=-\Delta n R T\)
If Δn > 0, (Example \(\left.\mathrm{Zn}(s)+2 \mathrm{HCl}(a q) \rightarrow \mathrm{ZnCl}_2(a q)+\mathrm{H}_2(g)\right) .\). then w is negative. In this case, work is done by the system on die surroundings.
If Δn < 0 , [Example \(2 \mathrm{H}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{H}_2 \mathrm{O}(l)\). then w is positive, in this case, work is done on the system by the surroundings.
