KSEEB Solutions For Class 11 Physics Chapter 8 Gravitation

KSEEB Solutions For Class 11 Physics Chapter 8 Gravitation Important Points

Kepler’s Laws:

Law Of Orbits (1st Law): All planets move in an elliptical orbit with the sun at one of its foci.

Law Of Areas (2nd Law): The line joining the planet to the sun sweeps equal areas in equal intervals of time, i.e., \(\frac{\Delta \mathrm{A}}{\Delta \mathrm{T}}\) = constant.

i.e., planets will appear to move slowly when they are away from the sun, and they will move fast when they are nearer to the sun.

Law Of Periods (3rd Law): The square of time period of revolution of a planet is proportional to the cube of the semi-major axis of the ellipse traced out by the planet.

i.e., \(T^2 \propto R^3 \Rightarrow \frac{T^2}{R^3}=\text { constant }\)

Read and Learn More KSEEB Class 11 Physics Solutions

Newton’s Law Of Gravitation (Or) Universal Law Of Gravitation: Everybody in the universe attracts other bodies with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

F \(\propto m_1 m_2, F \propto \frac{1}{r^2} \Rightarrow F=G \frac{m_1 m_2}{r^2}\)

Central Force: A central force is a force which acts along the line joining the sun and the planet or along the line joining the two mass particles.

KSEEB Class 11 Physics Chapter 8 Solutions PDF

Conservative Force: For a conservative force work done is independent of the path. Work done depends only on initial and final positions. Gravitational force is a conservative force.

Gravitational Potential Energy: Potential energy arising out of gravitational force is called gravitational potential energy.

Since gravitational force is a conservative force gravitational potential depends on the position of the object.

V = –\(\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{r}}\)

Gravitational Potential: Gravitational potential due to the gravitational force of the earth is defined as the “potential energy of a par tide of unit mass at that point”.

Gravitational potential V = \(\frac{GM}{r}\)

(r = distance from the centre of the earth)

Acceleration Due To Gravity (g): \(\frac{G N}{R^2}\)

Acceleration Due To Gravity Below And Above Surface Of Earth:

For points above the earth, the total mass of the earth seems to be concentrated at the centre of the earth.

For a height ‘h’ above the earth \(g(h)=\frac{G M_E}{\left(R_E+h\right)^2}\)

When h<<\(R^E\)

g(h) = \(g\left(1+\frac{h}{R_E}\right)^{-2} \simeq g\left(1-\frac{2 h}{R_E}\right)\)

For a point inside the earth at a depth ‘d’ below the groundmass of the earth (M_s) with radius (R_E– d) Is considered. That mass seems to be at the centre of the earth.

g’ = \(g\left(1-\frac{d}{R}\right)\)

Escape speed (v)_min: The minimum initial velocity on the surface of the earth to overcome gravitational potential energy is defined as “escape speed v_e.”

∴ \(\mathrm{v}_{\mathrm{e}}=\sqrt{2 \mathrm{gR}}=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}\)

Orbital Velocity: The velocity of a body revolving in the orbit is called orbital velocity.

∴ Orbital velocity \(V_0=\sqrt{\frac{\mathrm{GM}}{R}} \Rightarrow V_0=\sqrt{g R}\)

1. Relation between orbital velocity V and escape speed v_e = √2 V₀
2. If the velocity of a satellite in the orbit is increased by √2 times or more it will go to infinite distance.

Time Period Of The Orbit (T): The time taken by a satellite to complete one rotation in the orbit is called “time period of rotation”.

T = \(2 \pi \frac{\left(\mathrm{R}_{\mathrm{E}}+\mathrm{h}\right)^{3 / 2}}{\sqrt{\mathrm{GM}_{\mathrm{E}}}}\)

Geostationary Orbit: For a geostationary orbit in the equatorial plane its time period of rotation is 24 hours, i.e., the angular velocity of the satellite in that orbit is equal to the angular velocity of the rotation of the earth. Geostationary orbit is at a height of 35800 km from Earth.

Geostationary Satellite: A Geostationary satellite will revolve above the earth in a geostationary orbit along the direction of rotation of the earth. So it always seems to be stationary w.r.t earth.

The period of geostationary satellites is 24 hours. It rotates in an equatorial plane in the west-to-east direction.

Polar Satellites: Polar satellites are low-attitude satellites with an altitude of 500 km to 800 km. They will revolve in the north-south direction of the earth. Time period of polar satellites is nearly 100 minutes.

Weightlessness: For a freely falling body its weight seems to be zero. The weight of a body falling downwards with acceleration ‘a’ is w’ = mg’ = m(g-a). When a = g the body is said to be under free fall and it seems to be weightless.

Chapter 8 Gravitation Solutions KSEEB Class 11 Physics Important Formulae

Force between two mass particles, \(\mathrm{F}=\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{r}^2}\)

Universal gravitational constant, \(\mathrm{G}=\frac{\mathrm{Fr}^2}{\mathrm{~m}_1 \mathrm{~m}_2}\)

G = \(6.67 \times 10^{-11} \mathrm{Nm}^2 / \mathrm{Kg}^2\)

D.F.: \(\mathrm{M}^{-1} \mathrm{~L}^3 \mathrm{~T}^{-2}\)

Relation between g and G is, \(\mathrm{g}=\frac{\mathrm{GM}}{\mathrm{R}^2}=\frac{4}{3} \pi \rho \mathrm{G} \cdot \mathrm{R}\)

Variation of g with depth, \(g_d=g\left(1-\frac{d}{R}\right)\)

Variation of g with height, \(g_h=g\left(1-\frac{2 h}{R}\right)\)

For small values of h i.e., h < < R then \(g_h=g\left(1-\frac{2 h}{R}\right)\)

1. Gravitational potential, U = \(-\frac{\mathrm{GMm}}{\mathrm{R}}\)
2. If a body is taken to a height ‘h’ above the ground then

Gravitational potential, \(U_h=-\frac{G M m}{(R+h)}\)

Orbital velocity, \(V_0=\sqrt{\frac{G M}{R}}=\sqrt{g R}\)

Orbital angular velocity, \(\omega_0=\sqrt{\frac{G M}{R^3}}=\sqrt{\frac{g}{R}}\)

Escape velocity, \(\mathrm{V}_{\mathrm{e}}=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}=\sqrt{2 \mathrm{gR}}\)

Time period of geostationary orbit = 24 hours.

Angular velocity of earth’s rotation \((\omega)=\frac{2 \pi}{24 \times 60 \times 60}=0.072 \times 10^{-3} \mathrm{rad} / \mathrm{sec} \text {. }\)

KSEEB Class 11 Physics Chapter 8 Gravitation Very Short Answer Questions

Question 1. State the unit and dimension of the universal gravitational constant (G).
Answer:

Units of G = N-m²/ kg².

Dimensional formula = M^-1 L³ T^-2.

Question 2. State the vector form of Newton’s law of gravitation.
Answer:

Vector form of Newton’s Law of gravitation \(\overline{\mathrm{F}}=\frac{\mathrm{Gm}_1 \mathrm{~m}_2 \overline{\mathrm{r}}}{\overline{\mathrm{r}}^3}\)

Karnataka 1st PUC Physics Chapter 8 Notes

Question 3. If the gravitational force of the Earth on the Moon is F. What is the gravitational force of the Moon on the Earth? Do these forces form an action-reaction pair?
Answer:

The gravitational force between the earth and moon and moon and earth are the same i.e., F_EM = – F_ME

The gravitational force between the bodies is treated as an action-reaction pair.

KSEEB Class 11 Physics Gravitation

Question 4. What would be the change in acceleration due to gravity (g) at the surface, if the radius of Earth decreases by 2% keeping the mass of Earth constant?
Answer:

Acceleration due to gravity, g = \(\frac{GM}{R^2}\)

When the mass is kept constant and the radius is decreased by 2% then \(\frac{\Delta R}{R} \times 100=2\)

From the distribution of errors in multiplications and divisions \(\frac{\Delta g}{g}\) x 100 = -2 \(\frac{\Delta R}{R}/100\)

% Change in g = – 2 x 2 = – 4% – ve sign indicates that when R decreases ‘g’ increases.

Question 5. As we go from one planet to another, how will

1. The mass and
2. Does the weight of the body change?

Answer:

1. As we go from one planet to another planet mass of the body does not change. The mass of a body is always constant.
2. As we move from one planet to another planet weight of the body gradually decreases. It becomes weightless. When we approach the other planet the weight will gradually increase.

Question 6. Keeping the length of a simple pendulum constant, will the time period be the same on all planets?
Answer:

Even though the length of pendulum l is the same T the time period of oscillation T value changes from planet to planet.

Time period of pendulum, \(\mathrm{T}=2 \pi \sqrt{\frac{l}{g}}\)

i.e., T depends on l and g.

Acceleration due to gravity, \(\left(g=\frac{G M}{R^2}\right)\) changes from planet to planet.

Hence Time period of the pendulum changes even though the length ‘l’ is the same.

Question 7. Give the equation for the value of g at a depth ’d’ from the surface of Earth. What is the value of ‘g’ at the centre of Earth?
Answer:

Acceleration due to gravity at a depth d’ below the ground is, g_d = g\(\left(1-\frac{D}{R}\right)\)

Acceleration due to gravity at the centre of the earth is zero. (Since D = R)

Question 8. What are the factors that make ‘g’ the least al the equator amt maximum at the poles?
Answer:

‘g’ Is Least At Equator Due To

The equatorial radius of Earth is the maximum

∴ g = \(\frac{G M}{R^2}\) (R = maximum)

Due to the rotation of the earth, centrifugal force will act on the bodies. It opposes the gravitational pull of the earth on the bodies. At the equator centrifugal force is maximum. So the ’g’ value is least at the equator.

The ’g’ ⇒ Maximum At Poles Due To

The polar radius of the earth is minimum (because \(g=\frac{G M}{R^2}\))

Centrifugal force due to the rotation of the earth is zero at the poles. This centrifugal force reduces Earth’s gravitational pull.

Since the Centrifugal force is zero, the ‘g’ value is maximum at the poles.

KSEEB Class 11 Physics Gravitation Solutions

Question 9. “Hydrogen is in abundance around the sun but not around the earth”. Explain.
Answer:

The escape velocity of the sun is very high compared to that of the Earth. The gravitational pull of the sun is very large because of its larger mass compared to that of the Earth.

So it is very difficult for hydrogen to escape from the Sun’s atmosphere. Hence hydrogen is abundant in the sun.

Question 10. What is the time period of revolution of a geostationary satellite? Does it rotate from West to East or from East to West?
Answer:

Time period of a geostationary satellite is equal to time period of rotation of the earth.

Time period of geostationary orbit T = 24 hours. Satellites in geostationary orbit will revolve around the earth in west to east direction in an equatorial plane.

Question 11. What are polar satellites?
Answer:

Polar Satellite: Polar satellites are low-altitude satellites. They will revolve around the poles of the earth in a north-south direction. Time period of polar satellites is nearly 100 minutes.

KSEEB Class 11 Physics Solutions For Chapter 8 Gravitation Short Answer Questions

Question 1. State Kepler’s Laws of planetary motion
Answer:

Kepler’s Laws:

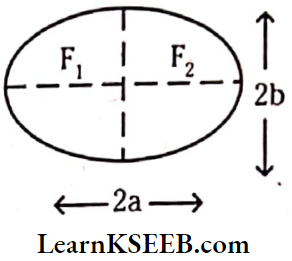
Law Of Orbits (1st Law): All planets will move in elliptical orbits with the sun lying al one of its foci.

‘a’ and ‘b’ are lengths of semi-major axis and semi-minor axis.

Law Of Areas (2nd Law): The line that joins any planet to the sun sweeps equal areas in equal intervals of time, i.e., \(\frac{\Delta \mathrm{A}}{\Delta T}\) = constant

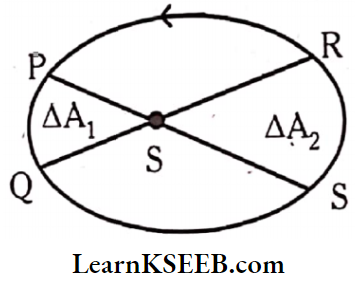
i.e., planets will appear to move slowly when they are away from the sun, and they will move fast when they are nearer to the sun.

Law Of Periods (3rd Law): The square of time period of revolution of a planet is proportional to the cube of the semi-major axis of the ellipse traced out by the planet.

i.e., \(\mathrm{T}^2 \propto \mathrm{a}^3 \text { or } \frac{\mathrm{T}^2}{\mathrm{a}^3}=\text { constant }\)

where T = time period of revolution a = semi-major axis (length)

Question 2. Derive the relation between acceleration due to gravity (g) at the surface of a planet and Gravitational constant (G).
Answer:

Relation Between g and G: Each and everybody was attracted towards the centre of the earth with some force. This is called the weight of the body, W = mg…..(1)

This force is due to the gravitational pull on the body by the Earth.

For small distances above the earth from the centre of the earth Is equal to the radius of the earth ‘R’.

According to Newton’s law of gravitation, w = mg

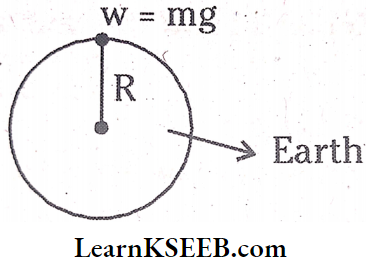
Force between two bodies, \(F=\frac{G M m}{R^2} \text {. }\)…..(2)

From equations, (1) and (2)

∴ \(\mathrm{mg}=\frac{\mathrm{GMm}}{\mathrm{R}^2} \Rightarrow \mathrm{g}=\frac{\mathrm{GM}}{\mathrm{R}^2}\)

∴ Relation between \(\mathrm{g}\) and G is \(\mathrm{g}=\frac{\mathrm{GM}}{\mathrm{R}^2}\)

Question 3. How does the acceleration due to gravity change for the same values of height (h) and depth(d)?
Answer:

Variation Of ‘g’ With Altitude: When we go to a height ‘h’ above the ground ‘g’ value decreases.

On surface of earth (g) = \(\frac{GM}{R^2}\)

At an altitude ‘h’ \(g(h)=\frac{G M}{(R+h)^2}\) because R + h is the distance from the centre of the earth to the given point at ‘h

h <<R ⇒ g(h) = \(g\left(1-\frac{2 h}{R}\right)\)

So acceleration due to gravity decreases with height above the ground.

Variation of ‘g’ With Depth: When we go deep into the ground ‘g’ value decreases.

At a depth ’d’ inside the groundmass of the earth up to point d from the centre will exhibit force of attraction on the body.

The remaining mass does not exhibit any influence. So effective radius is (R – d) only. Acceleration due to gravity ’g’ at a depth ’d’ is given by

∴ \(\mathrm{g}_{\mathrm{d}}=\frac{4}{3} \pi \rho \mathrm{G}(\mathrm{R}-\mathrm{d})\) (because \(\mathrm{g}=\frac{4}{3} \pi \rho \mathrm{GR}\))

(or) \(\mathrm{g}_{\mathrm{d}}=\frac{4}{3} \pi \rho \mathrm{GR}\left(1-\frac{\mathrm{d}}{\mathrm{R}}\right)\)

(or) \(g_d=g\left(1-\frac{d}{R}\right)\)

So, the ‘g’ value decreases with depth below the ground.

Question 4. What is orbital velocity? Obtain an expression for it.
Answer:

Orbital Velocity (V₀): The velocity of a satellite moving in the .orbit is called orbital velocity (V₀).

Let a satellite of mass m is revolving around the earth in a circular orbit at a height ‘h’ above the ground.

The radius of the orbit = R + h where R is the radius of the earth.

In orbital motion is “The centrifugal and centripetal forces acting on the satellite”.

Centrifugal force = \(\frac{m V^2}{r}=\frac{m V_0^2}{R+h}\)…..(1)

(In this case \(V=V_0\) and r=R+h)

Centripetal force is the force acting towards the centre of the circle it is provided by the gravitational force between the planet and the satellite.

∴ F = \(\frac{G M \cdot m}{(R+h)^2}\)….(2)

(1)=(2) \(\frac{m V_0^2}{(R+h)}=\frac{G M \cdot m}{(R+h)^2}\)

∴ \(V_0^2=\frac{G M}{R+h}\) or \(V_0=\sqrt{\frac{G M}{R+h}}\)

When h<<R then orbital velocity,

∴ \(V_0=\sqrt{\frac{G m}{R}}\), But \(g=\frac{G m}{R^2}, V_0=\sqrt{g R}\)

V₀ = \(\sqrt{gR}\) is called orbital velocity. Its value Is 7.92 km/sec.

Question 5. What Is escape velocity? Obtain an expression for It
Answer:

Escape Speed (V₁)_min: ft is defined as the minimum velocity required by a body to overcome the gravitational field of the earth is known as escape velocity.

For a body of mass ‘m’ gravitational potential energy on the surface of the earth

PE = \(-\frac{G \cdot m \cdot M_E}{R_E}\)

For a body to escape from the gravitational field of the earth its kinetic energy must be equal to or more than gravitational potential energy.

KE = \(\frac{1}{2} \mathrm{mv}^2\)

For minimum velocity \(\mathrm{KE}=\mathrm{PE}\)

∴ \(\frac{1}{2} m v^2=-\frac{G m \cdot M_E}{R_E} \cdot O R \quad v=\sqrt{\frac{2 G M_E}{R_E}}\)

∴ The minimum initial speed on the surface of the earth \(\left[v_i\right]_{\min }=\sqrt{\frac{2 G M_E}{R_E}}\) is called escape speed. (or) \(V=\sqrt{2 \mathrm{gR}_{\mathrm{E}}}\)

∴ \(\mathrm{g}=\frac{\mathrm{GM}}{\mathrm{R}^2}\)

Question 6. What is a geostationary satellite? State its uses.
Answer:

A geostationary satellite will always appear to be stationary relative to Earth.

The time period of a geostationary satellite is equal to time period of rotation of the earth.

∴ Time period of geostationary orbit t = 24 hours. Satellites in geostationary orbit will revolve around the earth in the west to the east direction in an equatorial plane.

Uses Of Geostationary Satellites:

1. For the study of the upper layers of the atmosphere.
2. For forecasting the changes in atmosphere and weather.
3. To find the size and shape of the earth.
4. For investigating minerals and ores present in the earth’s crust.
5. For transmission of TV signals.
6. For the study of the transmission of radio waves.
7. For space research.

Question 7. If two places are at the same height from the mean sea level; One is a mountain and the other is in the air. At which place will ‘g’ be greater? State the reason for your answer.
Answer:

The ’g’ value on the mountain is greater than the ‘g’ value in the air even though both are at the same height.

For a point on a mountain, while deciding the ‘g’ value, the mass of the mountain is also considered which leads to change in the ‘g’ value depending on local conditions such as the concentration of huge mass at a particular place.

Whereas for a point in the air, no such effect is considered. Hence ‘g’ on the top of the mountain is more.

Question 8. The weight of an object is more at the poles than at the equator. At which of these can we get more sugar for the same weight? State the reason for your answer.
Answer:

If we are using common balance to measure sugar we will get some quantity of sugar both at the equator and at the poles.

Whereas if we are using spring balance to weigh sugar then the weight of sugar at poles is more. So we will get less quantity.

The weight of sugar at the equator is less. So we will get more quantity of sugar at the equator.

Question 9. If a nut becomes loose and gets detached from a satellite revolving around the Earth, will it fall down to Earth or will it revolve around Earth? Give reasons for your answer.
Answer:

If a nut is detached from a satellite revolving in the orbit then its velocity is equal to orbital velocity. So it continues to revolve in the same orbit. It does not fall to earth.

Question 10. An object projected with n velocity greater than or equal to 11.2 km s^-1 will not return to Earth. Explain the reason.
Answer:

The escape velocity of the earth Is 11.2 km/sec. If any body acquires a velocity of 11.2 km/ sec. or more its kinetic energy is more than gravitational potential energy.

So earth is not able to stop the motion of that body. So anybody with a velocity of 11.2 km/s or more will escape from the gravitational field of Earth and never come back to Earth.

Gravitation Solutions KSEEB Class 11 Physics Long Answer Questions

Question 1. Define gravitational potential energy and derive an expression for it associated with two particles of masses m₁ and m₂.
Answer:

The gravitational potential energy of a body at a point in the gravitational field of another. It is defined as the amount of work done in bringing the given body from infinity to that point in the field is called Gravitational potential energy.

Expression For Gravitational Potential Energy: Consider two particles of masses m₁ and m₂ placed at the points, ‘O’ and p respectively. Let the distance between the two particles be V i.e., OP = r.

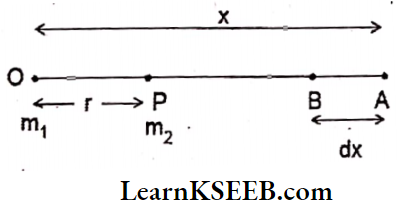
Let us calculate the gravitational potential energy of the particle of mass m₂ placed at point p in the gravitational field of m₁ Join OP and extend it in the forward direction.

Consider two points A and B on this line such that OA = x and AB = dx.

The gravitational force of attraction on the particle at A is, \(\mathrm{F}=\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{x}^2}\)

A small amount of work done In bringing the particle without acceleration through a very small distance AB is, dW = F dx

= \(\mathrm{F}=\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{x}^2}\) dx

Total work done In bringing the particle from infinity to point P is,

N = \(\int_{\infty}^G \frac{G m_1 m_2}{x^2} d x=G m_1 m_2 \int_{\infty}^r x^{-2} d x\)

= \(-G m_1 m_2\left[\frac{1}{x}\right]_{\infty}^r=-G m_1 m_2\left[\frac{1}{r}-\frac{1}{\infty}\right]\)

= \(\frac{-G m_1 m_2}{r}\)

Since this work done is stored in the particle as its gravitational potential energy (U).

Therefore, the gravitational potential energy of the particle of mass m₂ placed at point ‘p’, in the gravitational field of a particle of mass m at distance r is \(\mathrm{U}=\frac{-G \mathrm{~m}_1 \mathrm{~m}_2}{} \text {. }\)

Here, a negative sign shows that the potential energy is due to an attractive gravitational force between two particles.

Question 2. Derive an expression for the variation of acceleration due to gravity

1. Above and
2. Below the surface of the Earth.

Answer:

Variation Of Acceleration Due To Gravity Above The Surface Of Earth: We know ‘g’ on the planet, g = \(\frac{G M}{R^2}\). But on earth ‘g’ value changes with height above the ground ‘h’

Variation Of ’g’ With Altitude: For a point ‘h’ above the earth, the total mass of the earth seems to be concentrated at the centre of the earth. Now the distance from the centre of the earth is (R + h).

Acceleration due to gravity at ‘h’ = g(h) = \(\frac{G M_E}{\left(R_E+h\right)^2}\)

For small values of ‘h’ l.e., h << R then \(g(h)=g\left(1-\frac{2 h}{R_E}\right)\)

Proof: \(g(h)=\frac{G M}{(R+h)^2}=\frac{G M}{R^2\left(1+\frac{h}{R}\right)^2}\) or

⇒ \(\mathrm{g}(\mathrm{h})=\frac{\mathrm{GM}}{\mathrm{R}^2}\left(1+\frac{\mathrm{h}}{\mathrm{R}}\right)^{-2}\)

(or) \(\mathrm{g}(\mathrm{h})=\mathrm{g}\left(1+\frac{\mathrm{h}}{\mathrm{R}}\right)^{-2}\)

on Binomial expansion \(g(h)=g\left(1-\frac{2 h}{R}+\frac{4 h^2}{R^2} \ldots . . \text { etc. }\right)\).

By neglecting higher order terms, g(h) = \(g\left(1-\frac{2 h}{R}\right)\)

Variation Of Acceleration Due To Gravity Below The Surface Of Earth: At a depth d inside the groundmass of the earth up to point d from the centre will exhibit the force of attraction on the body. The remaining mass does not exhibit any influence.

Mass of spherical body M ∝ R³

∴ \(M_{/} / M_E=\left(R_E-d\right)^3 / R_E^3\) where \(M_s\) is mass of earth ‘s’ shell up to a depth ‘d’ from the centre. Gravitational force at depth ‘d’ is

F(d) = \(G M_s m /\left(R_E-d\right)^2=G M_E m\left(R_E-d\right) / R_E^2\)

∴ g(d) = \(\frac{F(d)}{m}=\frac{G M_E}{R_E^3}\left(R_E-d\right)=g\left(R_E-d\right)\)

= \(g\left(1-\frac{d}{R_E}\right)\)

So ‘g’ value decreases with depth below the ground.

Question 3. State Newton’s Universal Law of Gravitation. Explain how the value of the Gravitational constant (G) can be determined by the Cavendish method.
Answer:

Newton’s Law Of Gravitation: Everybody in the universe attracts every other body with a force which is directly proportional to the product of their maw”, and Inversely proportional to the square of the distance between them.

∴ \(F \propto m_1 m_2 \text { and } F \propto \frac{1}{d^2}\) or \(F \propto \frac{m_1 m_2}{d^2}\)

or \(F=\frac{G m_1 m_2}{d^2}\)

This is always a force of attraction and acts along the line joining the two bodies.

Cavendish Experiment To Find Gravitational Constant ‘G’: The Cavendish experiment consists of a long metallic rod AB to which two small lead spheres of mass ’m’ are attached.

This rod is suspended from a rigid support with the help of a thin wire. Two heavy spheres of mass M are brought near to these small spheres in opposite directions. Then gravitational force will act between the spheres.

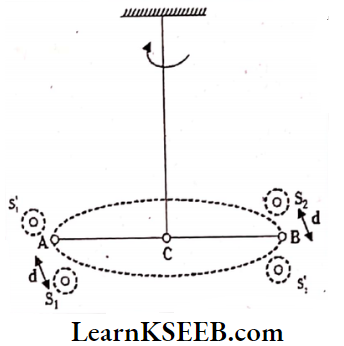
Force between the spheres, \(\mathrm{F}=\frac{\mathrm{GMm}}{\mathrm{d}^2}\)

Two equal and opposite forces acting at the two ends of the rod AB will develop a force couple and the rod will rotate through an angle ‘θ’.

∴ Torque on the rod \(\mathrm{F} \times \mathrm{L}=\frac{\mathrm{GM} \cdot \mathrm{m}}{\mathrm{d}^2} \mathrm{~L}\)….(1)

Restoring force couple = τθ…(2)

Where τ = Restoring couple per unit twist

∴ \(\tau \theta=\frac{\mathrm{GMm}}{\mathrm{d}^2} \mathrm{~L}\)

or \(\mathrm{G}=\frac{\tau \cdot \theta \mathrm{d}^2}{\mathrm{MmL}}\)

By measuring we can calculate the “G” value when other parameters are shown.

The particle value of G is 6.67 x 10^-11 Nm²/kg²

KSEEB Class 11 Physics Chapter 8 Gravitation Problems

(Gravitational Constant ‘G’ = 6.67 x 10^-11 Nm²kg^-2, Radius of earth ‘R’ = 6400 km; Mass of earth M_E= x 10²⁴ kg)

Question 1. Two spherical halls each of mass 1 kg are placed 1 cm apart, a kind the gravitational force of attraction between them.
Solution:

Mass of each ball, m = 1 kg;

Separation, r = 1 cm = 10^-2 m

The gravitational force of attraction,

F = \(\frac{\mathrm{Gmm}}{\mathrm{r}^2}=\frac{6.67 \times 10^{-11} \times 1 \times 1}{\left(10^{-2}\right)^2}\)

= \(6.67 \times 10^{-11} \times 10^4=6.67 \times 10^{-7} \mathrm{~N}\)

Question 2. The mass of a ball is four times the mass of another ball. When these balls are separated by a distance of 10 cm, the gravitational force between them is 6.67 x 10^-7 N. Find the masses of the two balls.
Solution:

Mass of 1st ball = m;

Mass of 2nd ball = 4m.

Separation, r = 10 cm = 0.1 m;

Mass of the 1st ball = m =?

Gravitational force, F = 6.67 x 10^-7 N

Gravitational force, \(F=\frac{\mathrm{G} \cdot \mathrm{m} \cdot 4 \mathrm{~m}}{\mathrm{r}^2}\)

6.67 \(\times 10^{-7}=\frac{6.67 \times 10^{-11} 4 \mathrm{~m}^2}{0.1 \times 0.1}\)

∴ \(10^{-7}=10^{-9} .4 \mathrm{~m}^2\)

∴ \(\mathrm{m}^2=\frac{10^{-7}}{4 \times 10^{-9}}=\frac{100}{4}=25 \Rightarrow \mathrm{m}=5\)

∴ Mass of the balls is \(5 \mathrm{~kg}, 20 \mathrm{~kg}\).

Question 3. Three spherical balls of masses 1 kg, 2 kg and 3 kg are placed at the corners of an equilateral triangle of side 1 m. Find the magnitude of the gravitational force exerted by the 2 kg and 3 kg masses on the 1 kg mass.
Solution:

Side of an equilateral triangle, a = 1 m.

Masses at corners = 1 kg, 2 kg, 3 kg.

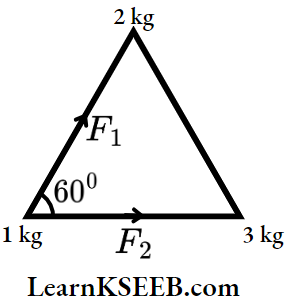
Force between 1 kg, 2g = \(F_1=G \frac{2 \times 1}{1^2}=2 G\).

Force between 1 kg, 3kg = \(F_2= G\frac{3 \times 1}{1^2}=3 \mathrm{G}\)

Now F₁ and F₂ act with an angle of 60″

∴ Resultant force \(F_K=\sqrt{F_1^2+F_2^2+2 F_1 F_2 \cos \theta}\)

= \(\sqrt{4 G^2+9 G^2+2 \times 2 \times 3 G^2 \times \frac{1}{2}}\)

= \(G \sqrt{4+9+6}=\sqrt{19} G\)

Question 4. At a certain height above the earth’s surface, the acceleration due to gravity is 4% of its value at the surface of the earth. Determine the height.
Solution:

Acceleration due to gravity at a height, h = 4% of g.

Radius of earth, R = 6400 K.M. = 6.4 x 10⁶ m

∴ \(g_h=\frac{4}{100} g . \quad B u t g_h=\frac{g \cdot R^2}{\left(1+\frac{h}{R}\right)^2}\)

∴ \(\frac{4}{100} g=\frac{g}{\left(1+h / R^2\right)} \Rightarrow\left(1+\frac{h}{R}\right)^2=\frac{100}{4}\)

Take roots on both sides then, \(+\frac{h}{R}=\frac{10}{2}\)

= \(5 \Rightarrow 1+\frac{\dot{h}}{R}=5 \Rightarrow \frac{h}{R}=5 .-1=4\)

∴ h = \(4 R=6400 \times 4=25,600 \mathrm{k} \cdot \mathrm{m}\)

Question 5. A satellite orbits the earth at a height of 1000 km. Find its orbital speed.
Solution:

Radius of earth, R = 6,400 km = 6.4 x 10⁶ m;

Mass of earth, M = 6 x 10²⁴

Height of satellite, h = 1000 km; G = 6.67 x 10¹¹ N-m²/kg²

Orbital velocity \(V_0=\sqrt{\frac{G M}{R+h}}\)

∴ \(\mathrm{V}_{\mathrm{o}}=\sqrt{\frac{6.67 \times 10^{-11} \times 6 \times 10^{24}}{6400+1000}}\)

= \(\sqrt{\frac{6.67 \times 6 \times 10^{13}}{7.4 \times 10^6}}=\sqrt{\frac{40.02 \times 10^7}{7.4}}\)

= 7354 m

KSEEB 1st PUC Physics Chapter 8 Important Questions

Question 6. A satellite orbits the Earth at a height equal to the radius of Earth. Find it’s

1. Orbital speed and
2. Period of revolution.

Solution:

Radius of earth, R = 6400 k.m.;

height above the earth, h = R.

Mass of earth, M = 6 x 10²⁴;

G = 6.67 x 10^-11 N – m²/kg²

1. Orbital velocity, \(\mathrm{V}_0=\sqrt{\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})}}=\sqrt{\frac{\mathrm{GM}}{2 \mathrm{R}}}\)

∴ \(\mathrm{V}_0=\sqrt{\frac{6.67 \times 10^{-11} \times 6 \times 10^{24}}{2 \times 6.4 \times 10^6}}\)

= \(\sqrt{\frac{40.02 \times 10^{13}}{12.8 \times 10^6}}=\sqrt{\frac{40.02 \times 10^7}{12.8}}\)

= \(5592 \mathrm{~m} / \mathrm{s}=5.592 \mathrm{~km} / \mathrm{sec}\)

2. Time period, \(\mathrm{T}=\frac{2 \pi(2 \mathrm{R})}{\mathrm{V}}\)

= \(\frac{2 \times 3.142 \times 6.4 \times 10^6 \times 2}{5592}=14,380 \mathrm{sec}\)

= \(3.994 \mathrm{~h} \approx 4 \text { hours. }\)

Question 7. The gravitational force of attraction between two objects decreases by 36% when the distance between them is increased by 4 m. Find the original distance between them.
Solution:

Let force between the objects = F;

Distance between them = r.

For Case II distance, r₁ = (r + 4);

The new force, F₁ = 36% less than F

∴ \(F_1=F\left(1-\frac{36}{100}\right)=\frac{64}{100} F\)

⇒ \(\frac{\text { G.m.m. }}{(r+4)^2}=\frac{64}{100} \frac{\text { G.m.m }}{r^2}\)

⇒ \(100 r^2=64(r+4)^2\) Take square roots on both sides

⇒ \(10 \mathrm{r}=8(\mathrm{r}+4) \Rightarrow 10 \mathrm{r}=8 \mathrm{r}+32\)

∴ (10-8)r = 32

∴ \(\mathrm{r}=16 \dot{\mathrm{m}} \text {. }\)

Question 8. Four identical masses m are kept at the corners of a square of side a. Find the gravitational force exerted on one of the masses by the other masses.
Solution:

Given all masses are equal m₁ = m₂ = m₃ = m₄

Force between \(m_1, m_4=F_1=\frac{G \cdot m^2}{a^2}\)….(1)

Force between \(m_4, m_3=F_2=\frac{G \cdot m^2}{a^2}\)…….(2)

Forces F₁ and F₂ act perpendicularly.

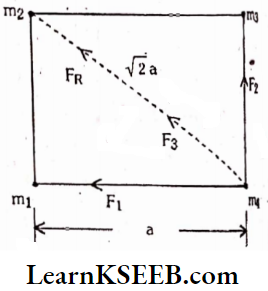
Their magnitudes are equal.

∴ \(F_R=\sqrt{2 F}=\sqrt{2} \cdot \frac{\mathrm{Gm}^2}{\mathrm{a}^2}\)…..(3) (From Parallelogram Law)

Force between \(m_4, m_2=\frac{G m^2}{(\sqrt{2 a})^2}=\frac{G m^2}{2 a^2}\)

(say \(\mathrm{F}_3\)) ….. (4)

Now forces \(F_R\) and \(F_3\) are like parallel. So resultant is the sum of these forces.

Total force at \(\mathrm{m}_4\) due to other masses

= \(\sqrt{2} \frac{G m^2}{a^2}+\frac{G m^2}{2 a^2}=\frac{G m^2}{a^2}\left(\sqrt{2}+\frac{1}{2}\right)\)

Karnataka Board Class 11 Physics Chapter 8 MCQs

Question 9. Two spherical balls of 1 kg and 4 kg are separated by a distance of 12 cm. Find the distance of a point from the 1 kg mass at which the gravitational force on any mass becomes zero.
Solution:

Mass, m₁ = 1 kg ;

Mass, m₂ = 4 kg ;

Separation, d = 12 cm

Mass of 3rd body m₃ =?

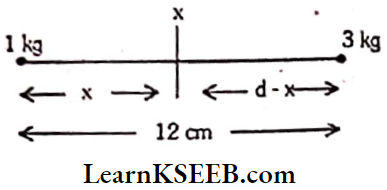
For m₃ not to experience any force the condition is

Force between m₁, m₃ = Force between

∴ \(\frac{G_1 \times m_3}{x^2}=\frac{G \times 4 m_3}{(d-x)^2} \Rightarrow(d-x)^2=4 x^2\)

Take square roots on both sides,

d-x = \(2 x \Rightarrow d=3 x \text { or } x=\frac{12}{3}=4 \mathrm{~cm}\)

∴ Distance from 1 kg mass = 4 cm

Question 10. Three uniform spheres each of mass m and radius R are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any one of the spheres due to the other two.
Solution:

Mass m and radius R are the same for all spheres.

Force between 1, 3 spheres = \(F_1=\frac{G \cdot m^2}{(2 R)^2}\)

Force between 1, 2 spheres = \(F_2=\frac{G \cdot m^2}{(2 R)^2}\)

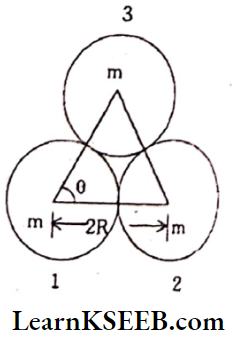
Now F₁ and F₂ will act with an angle θ = 60° between them so from Parallelogram law

Resultant force F = \(\sqrt{F_1^2+F_2^2+2 F_1 F_2 \cos \theta}\)

= \(\sqrt{F^2+F^2+2 F^2 \frac{1}{2}}=\sqrt{3} F\)

∴ Force on 1st sphere due to other two spheres \(=\frac{\sqrt{3} \cdot \mathrm{Gm}^2}{4 \mathrm{R}^2}\)

Force on 1st sphere due to other two spheres = \(\frac{\sqrt{3} \cdot \mathrm{Gm}^2}{4 \mathrm{R}^2}\)

KSEEB Class 11 Physics Gravitation Numericals

Question 11. Two satellites are revolving around the earth at different heights. The ratio of their orbital speeds is 2:1. If one of them is at a height of 100 km what is the height of the other satellite?
Solution:

Mass of the earth, m = 6 x 10²⁰ kg

G = 6.67x 10^-11N-m²/kg²

The ratio of orbital velocities V₀₁: V₀₂ = 2:1;

Height of one satellite, h = 100 k.m

But \(\mathrm{V}_0=\sqrt{\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}}}\)

∴ \(\sqrt{\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}_1}}=\frac{1}{2} \sqrt{\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}_2}}\)

By squaring on both sides \(\frac{\mathrm{Gm}}{\mathrm{R}+\mathrm{h}_1}=\frac{1}{4} \frac{\mathrm{Gm}}{\mathrm{R}+\mathrm{h}_2}\)

⇒ \(4\left(R+h_2\right)=R+h_1\)

⇒ \(4 R+4 h_2=R+h_1 \Rightarrow h_1=3 R+4 h_2\)

Put \(\mathrm{h}_2=100 \mathrm{~km}\)

∴ \(\mathrm{h}_1=3 \times 6400+400=19600 \mathrm{~km} \text {. }\)

Question 12. A satellite revolves around in a circular orbit with a speed of 8 km/s^-1 at a height where the value of acceleration due to gravity is 8 m/s^-2. How high is the satellite from the Earth’s surface? (Radius of the planet 6000 km.).
Solution:

Orbital velocity of satellite, V₀ =8km/s. = 8 x 10³ m/s.

Acceleration due to gravity in the orbit = g = 8 m/s²

Orbital Velocity \(V=\sqrt{g R}\)

Where R is the radius of the orbit and g is the acceleration due to gravity In the orbit.

∴ \(R=V^2 / g=\frac{8 \times 8 \times 10^6}{8}=8 \times 10^6 \mathrm{~m}\)

= \(8000 \mathrm{~km}\)

Height of satellite = 8000 – radius of earth; Radius of earth = 6000 km.

∴ Height above earth = 8000 – 6000 = 2000 km.

Question 13.

1. Calculate the escape velocity of a body from the Earth’s surface,
2. If the Earth were made of wood, its mass would be 10% of its current mass. What would be the escape velocity, if the Earth were made of wood?

Solution:

The radius of the earth, R = 6400 km = 6.4 x 10⁶ m.

Mass of earth, M = 6 x 1024 kg; g = 9.8 ms^-2.

1. Escape velocity, \(\mathrm{V}_{\mathrm{e}}=\sqrt{2 \mathrm{gR}}\)

∴ \(\mathrm{V}_{\mathrm{e}}=\sqrt{2 \times 9.8 \times 6.4 \times 10^6}=11.2 \mathrm{~km} / \mathrm{s}\)

2. If the earth is made of wood mass, \(M_1=10 \% \text { of } M=6 \times 10^{23}\)

Escape velocity, \(V_e=\sqrt{\frac{2 G m}{R}}\)

= \(\sqrt{\frac{2 \times 6.67 \times 10^{-11} \times 6 \times 10^{23}}{6.4 \times 10^6}}\)

= \(\sqrt{\frac{2 \times 40.02 \times 10^{12}}{6.4 \times 10^6}}\)

∴ \(\mathrm{V}_{\mathrm{e}} =\sqrt{12.51 \times 10^6}=3.537 \mathrm{~km} / \mathrm{s}\)

Question 14. A comet orbits the Sun in a highly elliptical orbit. Does the comet have a constant

1. Linear speed
2. Angular speed
3. Angular momentum
4. Kinetic energy
5. Potential energy
6. Total energy throughout its orbit?

Neglect any mass loss of the comet when it comes very close to the Sun.

Solution:

A comet while going on elliptical orbit around the Sun has constant angular momentum and total energy at all locations but other quantities vary with locations.

Question 15. A Saturn year is 29.5 times the Earth year. How far is Saturn from the sun if the Earth is 1.5 x 10⁸ km away from the sun?
Solution:

Here, T_s = 29.5 T_e; R_e = 1.5 x 10⁸ km; R_s = ?

Using the relation, \(\frac{T_{\mathrm{s}}^2}{\mathrm{R}_{\mathrm{s}}^3}=\frac{\mathrm{T}_{\mathrm{e}}^2}{\mathrm{R}_{\mathrm{e}}^3}\)

or \(\mathrm{R}_{\mathrm{s}}=\mathrm{R}_{\mathrm{e}}\left(\frac{\mathrm{T}_{\mathrm{s}}}{\mathrm{T}_{\mathrm{e}}}\right)^{2 / 3}\) = \(1.5 \times 10^8\left(\frac{29.5 \mathrm{~T}_{\mathrm{e}}}{\mathrm{T}_{\mathrm{e}}}\right)^{2 / 3}\)

= \(1.43 \times 10^9 \mathrm{~km}\)

Class 11 Physics Gravitation KSEEB Guide

Question 16. A body weighs 63 N on the surface of Earth. What is the gravitational force on it due to the Earth at a height equal to half the radius of the Earth?
Solution:

Weight of body = mg = 63 N

At height h, the value of ‘g’ is given by, \(g^{\prime}=\frac{g R^2}{(R+h)^2}=\frac{g R^2}{(R+R / 2)^2}=\frac{4}{9} g\)

The gravitational force on the body at a height of h is

⇒ \(\mathrm{F}=\mathrm{mg}^{\prime}=\mathrm{m} \times \frac{4}{9} \mathrm{~g}=\frac{4}{9} \mathrm{mg}=\frac{4}{9} \times 63=28 \mathrm{~N}\)

Question 17. Assuming the earth to be a sphere of uniform mass density, how much would the body weigh halfway down to the centre of the earth if it weighed 250 N on the surface?
Solution:

Weight of body at a depth, d = mg’

= \(m \times g\left(1-\frac{d}{R}\right)=250\left(1-\frac{\frac{R}{2}}{R}\right)=125 \mathrm{~N}\)