KSEEB Solutions For Class 11 Physics Chapter 14 Oscillations

KSEEB Solutions For Class 11 Physics Chapter 14 Oscillations Important Points

Periodic Motion: A motion that replies itself at regular intervals of time is called periodic motion.

Oscillations Or Vibrations: When a small displacement is given to a body at rest position (i.e. its mean position) then a force will come into play and try to bring back the body to its rest position or equilibrium position by executing and ho motion about a mean position. These are called vibrations or oscillations.

Time period (T): In periodic motion, the smallest time interval after which the motion is repeated is called its time period.

Displacement: For a body in periodic motion the displacement changes with time, so displacement is given by x(t) (or) f(t) = A cos ωt

Frequency: The reciprocal of time period (T) gives the number of repetitions that occur for unit time. It is called frequency υ).

υ = \(\frac{1}{T}\) = 1/Time period

Read and Learn More KSEEB Class 11 Physics Solutions

Fourier Theory: According to Fourier “any periodic function can be expressed as a superposition of sine and cosine functions of different time periods with suitable coefficients.”

KSEEB Class 11 Physics Chapter 14 Solutions PDF

Simple Harmonic Motion (Explanation Of Equation): In simple harmonic motion displacement is a sinusoidal function of time. i.e. x(t) = Acos(ωt±ø)

The particle will oscillate back and forth about the origin on the X-axis within the limits +A and -A where A is amplitude, ω and ø are constants.

1. Amplitude A of simple harmonic motion (S.H.M.) is the magnitude of the maximum displacement of the particle. Displacement of particles varies from +A to -A.
2. Phase Of Motion (Or) Argument: For a body in S.H.M the position of a particle or state of motion of a particle at any time V is determined by the argument (wt + ø). The term (wt + ø) is called argument or phase of motion.
3. Phase Constant (Or) Phase Angle: The value of the phase of motion at time t=0 is called “phase constant ø” or “phase angle”.
4. Simple harmonic motion is represented with a cosine function. It has a periodicity of 2π. The function repeats after a time period T.

Reference Circle: Let a particle ’p’ move uniformly on a circle. The projection of p on any diameter of the circle will execute S.H.M.

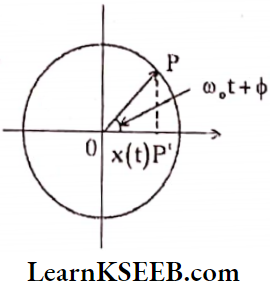
The particle ‘p’ is called a “reference particle” and the circle on which the particle moves is called a “reference circle”.

Velocity Of A Body On S.H.M.: For a body in uniform circular motion speed v = ωA. The direction of velocity \(\bar{V}\), at any time is along the tangent to the circle at that instantaneous point.

Mathematically velocity of the body \(\bar{V}\)(t) = — ωAsin(ωt + ø)

Or, \(v(t)=\frac{d}{d t} x(t)=\frac{d}{d t} A \cos (\omega t+\phi)\)

= \(-\omega \mathrm{A} \sin (\omega t+\phi)\)

Acceleration (a): For a body In S.H.M the Instantaneous acceleration of the particle is a(t) = -ω² A cos(wt + ø) = -ω²x(t)

or \(a(t)=\frac{d}{d t} v(t)=\frac{d}{d t}[-A \omega \sin (\omega t+\phi)]\)

= \(-A \omega^2 \cos (\omega t+\phi)\)

a(t) implies the acceleration of the body is a function of time.

Maximum acceleration of the body a_max = -ωA.

The -ve sign indicates that acceleration and displacement are in opposite directions.

Force On A Body In S.H.M: Acceleration a(t) = – ²x(t)

Force F = m a

∴ Force on a body in S.H.M

F(t) = ma = m(-ω²xt) = – K x(t)

Where K = mω² and m = mass of the body

Energy Of A Body In S.H.M: For a body in S.H.M both kinetic energy and potential energy will change with time. These values will vary between zero and their maximum value.

Kinetic energy K  = \(\frac{1}{2} \mathrm{mv}^2\)

= \(\frac{1}{2} \mathrm{m \omega}^2 \mathrm{~A}^2 \sin ^2(\omega t+\phi)\)

= \(\frac{1}{2} \mathrm{kA}^2 \sin ^2(\omega t+\phi)\)

Potential energy U = \(\frac{1}{2} \mathrm{kx}^2\)

= \(\frac{1}{2} \mathrm{kA}^2 \cos ^2(\omega t+\phi)\)

Potential energy \(\mathrm{U}=\frac{1}{2} \mathrm{kx}^2\)

Springs:

1. In the case of springs for smaller displacements when compared with the length of the spring Hooke’s law will hold good.
2. The small oscillations of a block of mass ‘m’ connected to a spring can be taken as simple harmonic.
3. In the case of springs the restoring force acting on the block of mass m is F(x) = -k(x)
4. Spring constant k is defined as the force required for unit elongation. Unit: newton/meter, K= force/displacement ⇒ K = \(\frac{-F}{x}\) -ve sign indicates that x force and displacement are opposite in direction. For a stiff spring, k is high. For a soft spring, k is less.
5. Angular frequency of a loaded spring \(\omega=\sqrt{\frac{K}{m}}\)

Time period of pendulum = \(\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{K}}}\)

Where m is the load attached and k is the constant of spring.

Simple Pendulum: Time period of oscillation \(\mathrm{T}=2 \pi \sqrt{l / g}\)

Damped Oscillations: In damped oscillations, the energy of the system is dissipated continuously.

When damping is very small the oscillations will remain approximately periodic.

Damped Oscillations Example: Oscillations of a simple pendulum.

Damping force depends on the nature of the medium.

Free Oscillations: When a system is displaced from its equilibrium position and allowed free to oscillate then oscillations made by the body are known as free oscillations.

The frequency of vibration is known as the natural frequency of that body.

Forced Or Driven Oscillations: If a body is made to oscillate under the influence of an external periodic force (say ω₀) then those oscillations are called forced oscillations.

Resonance: The phenomenon of an increase in the amplitude of the vibrating body when driving force frequency ‘ω₀‘ is equal to or very close to the natural frequency ‘ω’ of the oscillator is called resonance.

When the driving frequency is very close to the natural frequency of the vibrating body then also resonance will occur. Due to this reason damage to buildings is caused in earthquake-affected areas.

KSEEB Class 11 Physics Chapter 14 Oscillations Important Formulae

Displacement of a body in S.H.M Y = A sin (ωt ± ø)

The velocity of a body in S.H.M is

V = \(\frac{d y}{d t}=\frac{d}{d t}(A \sin \omega t)\)

V = \(A \omega \cos \omega t\) where \(Y=A \sin \omega t\)

or \(V=\omega \sqrt{A^2-Y^2}\)

Maximum velocity, \(\mathrm{V}_{\max }=\mathrm{A} \omega\)

Acceleration of a body in S.H.M a = – ω² A sin ωt or a = – ω²Y (where Y = A sin ωt)

(The -ve sign shows that acceleration and displacement are opposite to each other)

Maximum acceleration, a_max = ω²A

Angular Velocity ‘ω’ Of A Body In S.H.M: a ∝ -Y or a = -ω²Y (-ve sign for opposite direction only)

∴ \(\omega^2=\frac{a}{Y}\) or \(\omega=\sqrt{\frac{a}{Y}}\)

∴ Angular velocity of a body in S.H.M, \(\omega=\sqrt{\frac{\text { acceleration }}{\text { displacement }}}\)

Time Period Of A Body In S.H.M: The time taken for one complete oscillation is called the “time period”.

Time period, (T) = \(\frac{\text { Angular displacement for one rotation }}{\text { Angular velocity }}=\frac{2 \pi}{\omega}\)

∴ T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{Y}}{\mathrm{a}}}=2 \pi \sqrt{\frac{\text { displacement }}{\text { acceleration }}}\)

Frequency (ν) is the number of vibrations (or) rotations per second.

Frequency, v = \(\frac{1}{T}=\frac{1}{2 \pi} \sqrt{\frac{a}{Y}}\)

⇒ v = \(\frac{\omega}{2 \pi}\) or \(\omega=2 \pi v\)

Springs:

1. In springs force constant is defined as the ratio of Force to displacement.

Spring constant, (K) = \(\frac{F}{Y}\)

2. Time period, \(\mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{K}}}\)

3. If the mass of the spring m₁ is also taken into account, then the time period, \(T_1=2 \pi \frac{\sqrt{\left(m+\frac{m_1}{3}\right)}}{K}\) (For real spring )

4. Frequency of vibration, n = \(\frac{1}{2 \pi} \sqrt{\frac{K}{m}}\)

For real spring, n = \(\frac{1}{2 \pi} \sqrt{\frac{K}{\left(m+\frac{m_1}{3}\right)}}\)

When a spring is divided into ‘n’ parts then its force constant (k) will increase.

New force constant k₁ = nk

where n = number of parts and k = original spring constant.

Simple Pendulum:

1. In a simple pendulum component of the weight of the bob useful for to and motion is F = mg sin θ
2. Time period, \(\mathrm{T}=2 \pi \sqrt{\frac{l}{\mathrm{~g}}} \Rightarrow \mathrm{g}=4 \pi^2 \frac{l}{\mathrm{~T}^2}\)
3. When a simple pendulum is placed in a lift moving with some acceleration then its time period chants.
4. When lift moves up with an acceleration its time period decreases, \(T=2 \pi \sqrt{\frac{1}{g+a}}\)
5. When lift moves down with an acceleration ‘a’ its lime period increases, \(\mathrm{T}=2 \pi \sqrt{\frac{l}{g-\mathrm{a}}}\)
6. For a seconds pendulum time period, T = 2 sec
7. Length of seconds pendulum on earth = 100 cm = 1 m ( nearly )
8. In a simple pendulum L – T² graph is a straight line passing through the origin.

KSEEB Physics Class 11 Oscillations Very Short Answer Questions

Question 1. Give two examples of periodic motion which are not oscillatory.
Answer:

1. Motion of seconds hand of a watch.
2. Motion of fan blades which are rotating with constant angular velocity ‘w’.

For these two cases, they have constant centrifugal acceleration which does not change with rotation so it is not considered as S.H.M.

Karnataka 1st PUC Physics Chapter 14 Notes

Question 2. The displacement in S.H.M. is given by y = a sin (20t + 4). What is the displacement when it is increased by 2π/ω?
Answer:

Displacement: Displacement remains constant; \(\frac{2 \pi}{\omega}\) = time period T.

After a time period of T, there is no change in the equation of S.H.M

i.e. Y = A sin (20t + 4) = Y  = A sin (20 t + 4 + T)

∴ There is no change in displacement.

Question 3. A girl is swimming seated in a swing. What is the effect on the frequency of oscillation if statement?
Answer:

The frequency of oscillation (n) will Increase because, in the standing position, the location of the center of mass of the girl shifts upwards. Due to this, the effective length of the swing decreases.

As increases \(\mathrm{n} \propto \frac{1}{\sqrt{1}}\), therefore, n increases.

Question 4. The bob of a simple pendulum is a hollow sphere filled with water. How will the period of oscillation change, if the water begins to drain out of the hollow sphere?
Answer:

When water begins to drain out of the sphere, the center of mass of the system will first move down and then will come up to the initial position. Due to this the equivalent length of the pendulum and hence time period first increases, reaches a maximum value, and then decreases till it becomes equal to its initial value.

Question 5. The bob of a simple pendulum is made of wood. What will be the effect on the time period if the wooden bob is replaced by an identical bob of aluminum?
Answer:

The time period of a simple pendulum does not change if the wooden bob is replaced by an identical bob of aluminum because the time period of a simple pendulum is independent of the material of the bob.

Question 6. Will a pendulum clock gain or lose time when taken to the top of a mountain?
Answer:

At higher altitudes i.e., on mountains, the acceleration due to gravity is less as compared to the surface of the earth. Since the period is inversely proportional to the square root of the acceleration due to gravity, the time period increases. The pendulum clock loses time on the top of a mountain.

Question 7. What is the length of a simple pendulum which ticks seconds? (g = 9.8 ms^-2)
Answer:

In simple pendulum \(\mathrm{T}=2 \pi \sqrt{\frac{l}{\mathrm{~g}}} \text { or } l=\frac{\mathrm{gt}^2}{4 \pi^2}\)

For seconds pendulum T = 2s

⇒ t² = 4

∴ l = \(\frac{9.8 \times 4}{4 \pi^2}=1 \mathrm{~m}\) (π² nearly 9.8)

Question 8. Wind happens to The time period of n simple pendulum If Its length is increased up to four times.
Answer:

In a simple pendulum Time period T ∝ √l

∴ \(\frac{T_1}{T}=\sqrt{\frac{l_1}{l}}\) given \(l_1=4 l\)

∴ \(T_1=T \sqrt{\frac{4 l}{l}}=2 \mathrm{~T}\)

From the above equation, the period is doubled.

Question 9. A pendulum clock gives the correct time at the equator. Will it gain or lose time if it is taken to the poles? If so, why?
Answer:

When a pendulum clock showing the correct time at the equator is taken to poles then it will gain time.

Acceleration due to gravity at the poles is high. Time period of pendulum \(\mathrm{T}=2 \pi \sqrt{\frac{l}{\mathrm{~g}}}\)

When g increases T decreases. So several oscillations made in the given time increase hence clock gains time.

Question 10. What fraction of the total energy is K.E when the displacement is one-half of the amplitude of a particle executing S.H.M?
Answer:

Kinetic energy is equal to the fourth (i.e., \(\frac{3}{4}\)) of the total energy when the displacement is one-half of its amplitude.

Question 11. What happens to the energy of a simple harmonic oscillator if its amplitude is doubled?
Answer:

The energy of a simple harmonic oscillator,

E = \(\frac{1}{2} m \omega^2 A^2\)

E \(\propto A^2 \Rightarrow \frac{E_1}{E_2}=\frac{A_1^2}{A_2^2} ; E_2=\frac{A_2^2}{A_1^2} \times E_1\);

⇒ \(E_2=\frac{4 A^2}{A^2} \times E_1 \Rightarrow E_2=4 E_1\)

From the above equation energy increases by four lines.

Question 12. Can a simple pendulum be used In an artificial satellite? Give the reason.
Answer:

No, this Is because, Inside the satellite, there is no gravity, i.e., g = 0. As \(\mathrm{T}=2 \pi \sqrt{\frac{l}{g}}\), where T = ∞ for g = 0. Thus, the simple pendulum will not oscillate.

KSEEB Class 11 Physics Chapter 14 Oscillations Short Answer Questions

Question 1. Define simple harmonic motion. Give two examples.
Answer:

Simple Harmonic Motion: A body is said to be in S.H.M. if its acceleration is directly proportional to its displacement, and acts opposite in direction towards a faced point.

Examples:

1. Projection of uniform circular motion on a diameter.
2. Oscillations of a simple pendulum with| small amplitude.
3. Oscillations of a loaded spring.
4. Vibrations of a liquid column in a U-tube.

KSEEB Class 11 Physics Oscillations Solutions

Question 2. Present graphically the variations of displacement, velocity, and acceleration with time for a particle in S.H.M.
Answer:

The variations of displacement, velocity, and acceleration with time for a particle in S.H.M can be represented graphically as shown) in the figure.

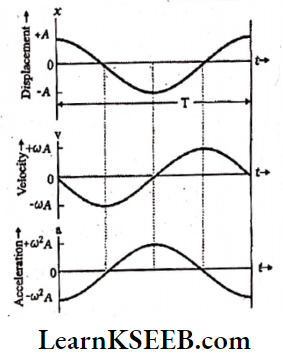
From The Graph

1. All quantities vary sinusoidally with time.
2. Only their maxima differ and the different plots differ in phase.
3. Displacement x varies between – A to A; v(t) varies from -ωA to ωA and a(t) varies from – ω²A to ω²A.
4. With respect to the displacement plot, the velocity plot has a phase difference of \({\pi}{2}\), and the acceleration plot has a phase difference of π.

KSEEB Class 11 Physics Oscillations Solutions

Question 3. What is phase? Discuss the phase relations between displacement, velocity, and acceleration in simple harmonic motion.
Answer:

Phase (θ): Phase is defined as its state or condition as regards its position and direction of motion at that instant.

In S.H.M phase angle, \(\theta=\omega t=2 \pi\left(\frac{t}{T}\right)\)

1. Phase Between Velocity And Displacement: In S.H.M, displacement,

y = \(A \sin (\omega t-\phi)\)

Velocity, \(V=A \omega \cos (\omega t-\phi)\)

So phase difference between displacement and velocity is 90°.

2. Phase Between Displacement And Acceleration:

In S.H.M, acceleration ‘a’ = – ω² y

or y = A sin ωt and a = – ω²A sin ωt

The -ve sign indicates that acceleration and displacement are opposite.

So phase difference between displacement and acceleration is 180°.

Question 4. Obtain an equation for the frequency of oscillation of spring of force constant k to which a mass m is attached.
Answer:

Let a spring of negligible mass is suspended from a fixed point and mass m is attached as shown. It is pulled down by a small distance x and allowed free it will execute simple harmonic oscillations.

Displacement from mean position = x

The restoring forces developed are opposite to displacement and proportional to ‘x’.

∴ F ∝ -x or F = -kx where k is constant of spring, (-ve sign for opposite direction)

Acceleration \(\mathrm{a}=\frac{\mathrm{F}}{\mathrm{m}}=\frac{\mathrm{Kx}}{\mathrm{m}} \Rightarrow \frac{\mathrm{x}}{\mathrm{a}}=\frac{\mathrm{m}}{\mathrm{K}}\)

Time period \(\mathrm{T}=2 \pi \sqrt{\frac{\text { displacement }}{\text { acceleration }}}=2 \pi \sqrt{\frac{\mathrm{x}}{\mathrm{a}}}\)

For spring \(\frac{\mathrm{x}}{\mathrm{a}}=\frac{\mathrm{m}}{\mathrm{K}}\)

∴ \(\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{K}}}\)

Time period of loaded spring \(\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{K}}}\)

Question 5. Derive expressions for the kinetic energy and potential energy of a simple harmonic oscillator.
Answer:

Expression For K.E Of A Simple Harmonic Oscillator: The displacement of the body in S.H.M., X = A sin ωt

where A = amplitude, ωt = Angular displacement.

Velocity at any instant, v = \(\frac{d x}{d t}\) Aω cos ωt

∴ K.E = \(\frac{1}{2} m v^2=\frac{1}{2} m A^2 \omega^2 \cos ^2 \omega t\)

∴ \(K \cdot E=\frac{1}{2} m A^2 \omega^2\left(1-\sin ^2 \omega t\right)\)

= \(\frac{1}{2} m A^2 \omega^2\left[1-\frac{x^2}{\mathrm{~A}^2}\right]\)

= \(\frac{1}{2} m \omega^2\left[\mathrm{~A}^2-\mathrm{x}^2\right]\)

∴ \(K. E=\frac{1}{2} m \omega^2\left[\mathrm{~A}^2-\mathrm{x}^2\right]\)

At mean position, velocity is maximum, and displacement x=0

∴ \(\mathrm{K}_{\mathrm{max}}=\frac{1}{2} \mathrm{~mA}^2 \omega^2\)

Expression For P.E Of A Simple Harmonic Oscillator: Let a body of mass ‘m’ be in S.H.M with an amplitude A.

Let O be the mean position.

The equation of a body in S.H.M is given by, x = A sin ωt

For a body in S.H.M acceleration, a = – ω²Y

Force, F = ma = – mω²x

∴ Restoring force, F = mω² x

Potential Energy Of The Body At Any Point Say ‘x’: Let the body be displaced through a small distance dx

Work done, dW = F • dx = P.E.

This work is done.

∴ P.E = mω²x • dx(where x is its displacement)

Total work done, \(\mathrm{W}=\int \mathrm{dW}=\int_0^{\mathrm{x}} \mathrm{m} \omega^2 \mathrm{x} \cdot \mathrm{dx}\)

⇒ Work done, \(\mathrm{W}=\frac{\mathrm{m} \omega^2 \mathrm{x}^2}{2}\)

This work is stored as potential energy.

∴ P.E at any point = \(\frac{1}{2} m \omega^2 x^2\)

Question 6. How does the energy of a simple pendulum vary as it moves from one extreme position to the other during its oscillations?
Answer:

The total energy of a simple pendulum is, \(\mathrm{E}=\frac{1}{2} \mathrm{~mA}^2 \frac{(\mathrm{g})}{l}\) (or) \(\mathrm{E}=\frac{1}{2} \frac{\mathrm{mg}}{l} \mathrm{~A}^2\)

The above equation shows that the total energy of a simple pendulum remains constant irrespective of the position at any time during the oscillation i.e., the law of conservation of energy is valid in the case of a simple pendulum.

At the extreme positions, P and Q the energy is completely in the form of potential energy, and at the mean position O it is totally converted as kinetic energy.

At any other point, the sum of the potential and kinetic energies is equal to the maximum kinetic energy at the mean position or maximum potential energy at the extreme position.

As the bob of the pendulum moves from P to O, the potential energy decreases but appears in the same magnitude as kinetic energy.

Similarly, as the bob of the pendulum moves from O to P or Q, the kinetic energy decreases to the extent it is converted into potential energy, as shown in the figure.

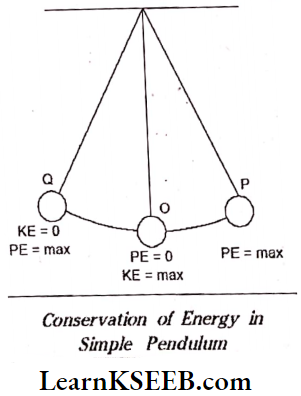
Question 7. Derive the expressions for displacement, velocity, and acceleration of a particle executes S.H.M.
Answer:

Displacement of a body in S.H.M.

X = A cos (ωt + ø).

Displacement (x): At t = 0 displacement x = A i.e., at the extreme position when ωt + ø = 90° displacement x = 0 at a mean position at any point x = A cos (ωt + ø).

Velocity (V): Velocity of a body in S.H.M. is V = \(\frac{d x}{d t}=\frac{d}{d t}\{A \omega \cos (\omega t+\phi)\}\)

V = \(-A \omega \sin (\omega t+\phi)\) or

∴ V = \(-\omega \sqrt{A^2-x^2}\)

When (ωt + ø) = 0 then velocity v = 0. For points where (ωt + ø) = 90°

Velocity V = – Aω i.e., velocity is maximum

Acceleration (a): Acceleration of a body in S.H.M. is a = \(\frac{dv}{dx}\)

= \(\frac{d}{d t}(-A \omega \sin (\omega t+\phi)\)

= \(-A \omega^2 \cos (\omega t+\phi)=-\omega^2 x\)

∴ \(a_{\max }=-\omega^2 A\)

Chapter 14 Oscillations Long Questions And answers KSEEB Physics

Question 1. Define simple harmonic motion. Show that the motion of projection of a particle performing uniform circular motion, on any diameter is simple harmonic.
Answer:

Simple Harmonic Motion: A body is said to be in S.H.M. if its acceleration is directly proportional to its displacement, and acts opposite in the direction towards a fixed point.

Relation between uniform circular motion and S.H.M.: Let a particle ‘P’ rotate in a circular path of radius ‘r’ with a uniform angular velocity ‘ω’. After time’ it goes to a new position ‘P’.

Draw normals from ‘P’ onto the X-axis and onto the Y-axis. Let ON and OM be the projections on the X and Y axes respectively.

As the particle Is In motion it will subtend an angle θ = ωt at the centre.

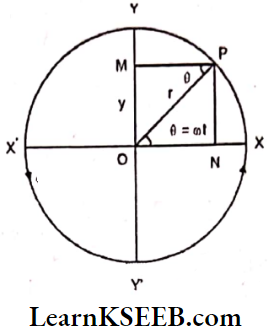
From triangle OPN

ON = OP cos θ

But OP = r and θ = ωt

∴ Displacement of particle P on X – axis at any time t is X = r cos ωt…..(1)

From triangle OPM

OM = Y = OP sin θ

But OP = r and θ = ωt

∴ Displacement of particle P on Y- axis is Y = r sin ωt……(2)

As the particle rotates in a circular path the foot of the perpendiculars OM and ON will oscillate within the limits X to X¹ and Y to Y¹.

At any point, the displacement of particle P is given by OP² = OM² + ON²

Since OM = X = r cos ωt and ON = Y = r sin ωt.

So a uniform circular motion can be treated as a combination of two mutually perpendicular simple harmonic motions.

KSEEB 1st PUC Physics Chapter 14 Important Questions

Question 2. Show that the motion of a simple pendulum is simple harmonic and hence derive an equation for its time period. What is a second pendulum?
Answer:

Simple Pendulum: A massive metallic bob is suspended from a rigid support with the help of an inextensible thread. This arrangement is known as a simple pendulum.

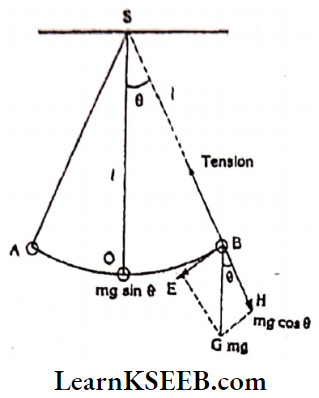
So the length of a simple pendulum is T. Let the pendulum be pulled to a side by a small angle ‘θ’ and released it oscillate about the mean position.

Let the bob be at one extreme position B. The weight (W = mg) of the body acts vertically downwards.

By resolving the weight into two perpendicular components:

One component mg sin θ is responsible for the to and fro motion of the pendulum.

Other components mg cos θ will balance the tension in the string.

Force useful for motion F = mg sin θ = ma (From Newton’s 2nd Law)

From the above equations a = g sin θ

When is small \(\sin \theta \approx \theta=\frac{\text { arc }}{\text { radius }}=\frac{x}{l}\)

∴ a = \(g \frac{x}{l} \ldots \ldots \ldots \ldots . .(1) \Rightarrow a \propto x\)

Since acceleration is proportional to displacement and acceleration is always directed towards a fixed point the motion of the simple pendulum is “simple harmonic”. Period of the simple pendulum:

Time period of pendulum = \(2 \pi \sqrt{\frac{Y}{a}}\)

= \(2 \pi \sqrt{\frac{\text { displacement }}{\text { acceleration }}}\)

From equation (1) \(\mathrm{a}=\frac{\mathrm{g}}{l} \mathrm{x}\)

or \(\frac{\mathrm{x}}{\mathrm{a}}=\frac{\text { displacement }(\mathrm{y})}{\text { acceleration }(\mathrm{a})}=\frac{l}{\mathrm{~g}}\)

∴ Time period of simple pendulum, \(\mathrm{T}=2 \pi \sqrt{\frac{l}{g}}\)

Seconds Pendulum: A pendulum whose time period is 2 seconds is called “seconds pendulum.”

Question 3. Derive the equation for the kinetic energy and potential energy of a simple harmonic oscillator and show that the total energy of a particle in simple harmonic motion is constant at any point on its path.
Answer:

Expression for K.E of a simple harmonic oscillator: The displacement of the body in S.H.M, X = A sin ωt

where A = amplitude and ωt = Angular displacement.

Velocity at any instant, v = \(\frac{dx}{dt}\) = Aω cos ωt

So its K.E = \(\frac{1}{2} m v^2=\frac{1}{2} m A^2 \omega^2 \cos ^2 \omega \mathrm{t}\)

But \(\cos ^2 \omega t=\left(1-\sin ^2 \omega t\right)\)

∴ \(\mathrm{K} . E=\frac{1}{2} \mathrm{~mA}^2 \omega^2\left(1-\sin ^2 \omega \mathrm{t}\right)\)

= \(\frac{1}{2} m A^2 \omega^2\left[1-\frac{\mathrm{x}^2}{\mathrm{~A}^2}\right]\)

= \(\frac{1}{2} m \omega^2\left[A^2-x^2\right]\)

∴ \(\mathrm{K} . \mathrm{E}=\frac{1}{2} \mathrm{~m} \omega^2\left[\mathrm{~A}^2-\mathrm{x}^2\right]\)

At mean position, velocity is maximum, and displacement x=0

∴ \(\mathrm{K} \cdot \mathrm{E}_{\max }=\frac{1}{2} \mathrm{~mA}^2 \omega^2\)

Expression for P.E Of A Simple Harmonic Oscillator: Let a body of mass ‘m’ be in S.H.M with an amplitude A.

Let O be the mean position.

The equation of a body in S.H.M is given by, x = A sin ωt

For a body in S.H.M acceleration, a = – ω²Y

Force, F = ma = – mω²x

∴ Restoring force, F = mω²x

Potential Energy Of The Body At Any Point Say ‘x’: Let the body be displaced through a small distance dx

⇒ Work done, dW = F • dx

This work done = P.E. in the body

∴ P.E = mω²x • dx(where x is its displacement)

Total work done, \(\mathrm{W}=\int \mathrm{dW}=\int_0^{\mathrm{x}} \mathrm{m} \omega^2 \mathrm{x} \cdot \mathrm{dx}\)

work done, \(\mathrm{W}=\frac{\mathrm{m} \omega^2 \mathrm{x}^2}{2}\).

This work is stored as potential energy.

∴ P.E at any point \(=\frac{1}{2} \mathrm{~m} \omega^2 \mathrm{x}^2\)

This work is stored as potential energy.

P.E at any point = \(\frac{1}{2} m \omega^2 x^2\)

For conservative force total Mechanical Energy at any point = E= P.E + K.E

∴ Total energy,

E = \(\frac{1}{2} m \omega^2\left(A^2-x^2\right)+\frac{1}{2} m \omega^2 x^2\)

∴ E = \(\frac{1}{2} m \omega^2\left\{A^2-x^2+x^2\right\}=\frac{1}{2} m \omega^2 A^2\)

So for a body in S.H.M total energy at any point of its motion is constant and equals to \(\frac{1}{2} m \omega^2 x^2\)

KSEEB Class 11 Physics Chapter 14 Oscillations Problems

Question 1. The bob of a pendulum is made of a hollow brass sphere. What happens to the time period of the pendulum, if the bob is filled with water completely? Why?
Solution:

If the hollow brass sphere is completely filled with water, then time period of the simple pendulum does not change. This is because time period of a pendulum is independent of the mass of the bob.

Question 2. Two identical springs of force constant “k” are joined one at the end of the other (in series). Find the effective force constant of the combination.
Solution:

When two springs of constant k each are joined together with end to end in series then effective spring constant \(\mathrm{k}=\frac{\mathrm{k}_1 \mathrm{k}_2}{\mathrm{k}_1+\mathrm{k}_2}\)

In this case \(k_{e q}=\frac{k \cdot k}{k+k}=\frac{k}{2}\)

In a series combination, the force constant of springs decreases.

Question 3. What are the physical quantities having maximum value at the mean position in SHM?
Solution:

In S.H.M at mean position velocity and kinetic energy will have maximum values.

KSEEB 1st PUC Physics Chapter 14 Important Questions

Question 4. A particle executes SHM such that, the maximum velocity during the oscillation is numerically equal to half the maximum acceleration. What is the time period?
Solution:

Given maximum velocity, \(\mathrm{V}_{\max }=\frac{1}{2}\) maximum acceleration \(\left(a_{\max }\right)\)

But \(V_{\max }=A \omega\) and \(\mathrm{a}_{\max }=\omega^2 \mathrm{~A}\)

∴ \(A \omega=\frac{1}{2} \cdot A \omega^2 \Rightarrow \omega=2\)

Time period of the body, \(\mathrm{T}=\frac{2 \pi}{\omega}=\frac{2 \pi}{2}\)

= \(\pi \mathrm{sec}\)

Question 5. An amass of 2 kg attached to a spring of force constant 200 Nm^-1 makes 100 oscillations. What Is the time taken?
Solution:

Mass attached, m = 2 kg; Force constant, k = 260 N/m

∴ Time period of loaded spring, \(\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\)

= \(2 \pi \sqrt{\frac{2}{260}}=0.5509 \mathrm{sec}\)

∴ Time for 100 oscillations = 100 x 0.551 = 55.1 sec

Question 6. A simple pendulum in a stationary lift has time period of T. What would be the effect on the time period when the lift

1. Moves up with uniform velocity
2. Moves down with uniform velocity
3. Moves up with uniform acceleration ‘a’
4. Moves down with uniform acceleration ‘a’
5. Begin to fall freely under gravity?

Solution:

1. When the lift moves up with uniform velocity i.e., a = 0, there would be no change in the time period of a simple pendulum.

2. When the lift moves down with uniform velocity i.e., a = 0, there would be no change in the time period of a simple pendulum.

3. When the lift is moving up with acceleration ‘a’ then relative acceleration = g + a

∴ Time period, \(\mathrm{T}=2 \pi \sqrt{\frac{l}{\mathrm{~g}+\mathrm{a}}}\) so when the lift is moving up with uniform acceleration time period of the pendulum in it decreases.

4. When lift is moving down with acceleration ‘a’ time period, \(\mathrm{T}=2 \pi \sqrt{\frac{l}{\mathrm{~g}-\mathrm{a}}}\)

(g – a = relative acceleration of pendulum)

So time period of the pendulum in the lift decreases:

5. If the lift falls freely, a = g then the time period of a simple pendulum becomes infinite.

Question 7. A particle executing SHM has an amplitude of 4cm, and its acceleration at a distance of 1cm from the mean position is 3 cm s^-2. What will its velocity be when it is at a distance of 2cm from its mean position?
Solution:

Amplitude, A = 4cm =4×10^-2 m

Acceleration, a = 3cm/s² = 3 x 10^-2 m/s²

Displacement, y = 1cm = 10^-2 m

∴ Angular velocity, \(\omega=\sqrt{\frac{a}{y}}=\sqrt{\frac{3}{1}}=\sqrt{3}\)

To find the velocity at a displacement of 2 cm use \(\mathrm{v}=\omega \sqrt{\mathrm{A}^2-\mathrm{y}^2} \text { given } \mathrm{y}=2 \mathrm{~cm}\)

∴ V = \(\sqrt{3} \sqrt{(16-4) 10^{-4}}\)

= \(\sqrt{3} \times \sqrt{12} \cdot 10^{-2}=\sqrt{3} \times 2 \sqrt{3} \times 10^{-2}\)

= \(6 \times 10^{-2} \mathrm{~m} / \mathrm{sec} \approx 6 \mathrm{~cm} / \mathrm{sec}\)

Question 8. A simple harmonic oscillator has a time period of 2s. What will be the change in the phase after 0.25 s after leaving the mean position?
Solution:

Time period, T = 2 sec; time, t = 0.25 sec

Phase difference after t sec = \(\phi=\frac{t}{\mathrm{~T}} \times 2 \pi\)

= \(\frac{0.25}{2} \times 2 \pi=\frac{\pi}{4}=90^{\circ}\)

For a phase of \(\frac{\pi}{4}\) starting from the mean position the body will be at an extreme position. (Phase difference between mean position and extreme position is \(\frac{\pi}{4}\) Rad or 90°)

Question 9. A body describes simple harmonic motion with an amplitude of 5 cm and a period of  0.2 s. Find the acceleration and velocity of the body when the displacement is

1. 5 cm
2. 3 cm
3. 0 cm.

Solution:

Given that, A = 5 cm = 5 x 10^-2 m and T = 0.2 s

Angular velocity, ω = \(\frac{2 \pi}{\mathrm{T}}=\frac{2 \pi}{0.2}=10 \pi \mathrm{rads}^{-1}\)

1. Displacement, \(y=5 \mathrm{~cm}=5 \times 10^{-2} \mathrm{~m}\)

Acceleration of the body, a = \(-\omega^2 y\) = \(-(10 \pi)^2 \times 5 \times 10^{-2}=-5 \pi^2 \mathrm{~ms}^{-2}\)

Velocity of the body, v = \({ }_{10} \sqrt{\mathrm{A}^2-\mathrm{y}^2}\)

= \(10 \pi \sqrt{\left(5 \times 10^{-2}\right)^2-\left(5 \times 10^{-2}\right)^2}=0\)

2. Displacement, \(y=3 \mathrm{~cm}=3 \times 10^{-2} \mathrm{~m}\)

Acceleration of the body, \(a=-\omega^2 y\)

= \(-(10 \pi)^2 \times 3 \times 10^{-2}=-3 \pi^2 \mathrm{~ms}^{-2}\)

Velocity of the body, \(v=\omega \sqrt{A^2-y^2}\)

= \(10 \pi \sqrt{\left(5 \times 10^{-2}\right)^2-\left(3 \times 10^{-2}\right)^2}\)

= \(10 \pi \times 4 \times 10^{-2}=0.4 \pi \mathrm{ms}^{-1}\)

3. Displacement, \(\mathrm{y}=0 \mathrm{~cm}\)

Acceleration of the body, \(a=-\omega^2 y=0\)

Velocity of the body, \(v=\omega \sqrt{\mathrm{A}^2-\mathrm{y}^2}\)

= \(10 \pi \sqrt{\left(5 \times 10^{-2}\right)^2-(0)^2}\)

= \(10 \pi \times 5 \times 10^{-2},=0.5 \pi \mathrm{ms}^{-1}\)

Question 10. The mass and radius of a planet are double that of the Earth. If the time period of a simple pendulum on the earth is T, find the time period on the planet.
Solution:

Mass of planet, \(\mathrm{M}_{\mathrm{p}}=2 \mathrm{M}_{\mathrm{e}}\);

The radius of the planet, \(R_p=2 R_e\)

The time period of the pendulum on earth =T;

Time period on planet \(=\mathrm{T}^{\prime}\)

∴ \(\mathrm{g}_{\mathrm{e}}=\frac{\mathrm{GM}}{\mathrm{R}^2} ; \mathrm{g}_{\mathrm{p}}=\frac{\mathrm{G} \cdot 2 \mathrm{M}}{(2 R)^2}=\frac{\mathrm{GM}}{2 \mathrm{R}^2}=\frac{\mathrm{g}_{\mathrm{e}}}{2}\)

T = \(2 \pi \sqrt{\frac{l}{\mathrm{~g}_e}}\), on the earth;- \(\mathrm{T}^{\prime}=2 \pi \sqrt{\frac{l}{\mathrm{~g}_{\mathrm{p}}}}\), on the planet

∴ \(\frac{\mathrm{T}^{\prime}}{\mathrm{T}}=\sqrt{\frac{\mathrm{g}_e}{\mathrm{~g}_{\mathrm{p}}}}=\sqrt{2}\) or \(\mathrm{T}^{\prime}=\sqrt{2} \mathrm{~T}\)

Question 11. Calculate the change in the length of a simple pendulum of length 1, when its period of oscillation changes from 2 s to 1.5 s.
Solution:

For seconds pendulum \(T_1=2 \mathrm{sec}\);

Length \(l_1=1 \mathrm{~m}\).

New time period \(\mathrm{T}_2=1.5 \mathrm{sec}\); Length \(l_2=\)?

In Pendulum \(T=2 \pi \sqrt{\frac{l}{g}}\);

For second’s pendulum, \(2=2 \pi \sqrt{\frac{l}{g}}=2 \pi \sqrt{\frac{l}{g}}\)

On planet, \(1.5=2 \pi \sqrt{\frac{l}{\mathrm{~g}}} \Rightarrow \frac{2}{1.5}=\frac{1}{\sqrt{l}}=\frac{4}{3}\)

l = \(\frac{9}{16} \mathrm{~m}\)

∴ Decrease in length \(=1-\frac{9}{16}=\frac{7}{16} \mathrm{~m}\)

= \(0.4375 \mathrm{~m}\)

Karnataka Board Class 11 Physics Chapter 14 MCQs

Question 12. A freely falling body takes 2 seconds to reach the ground on a plane when it is dropped from a height of 8m. If the period of a simple pendulum is seconds on the planet. Calculate the length of the pendulum.
Solution:

Height, \(\mathbf{h}=8 \mathrm{~m}\);

Time taken to reach the ground, \(\mathrm{t}=2 \mathrm{sec}\)

But for a body dropped, \(t=\sqrt{\frac{2 h}{g}}\)

⇒ 2 = \(\sqrt{\frac{16}{g}} \Rightarrow \mathrm{g}=\frac{16}{4}=4 \mathrm{~m} / \mathrm{s}^2\) on that planet Time period of pendulum, \(T=2 \pi \sqrt{\frac{l}{g}}=\pi\)

∴ \(2 \sqrt{\frac{l}{\mathrm{~g}}}=1\)

or \(\frac{l}{\mathrm{~g}}=\frac{1}{4} \Rightarrow l=\frac{\mathrm{g}}{4}\)

Length of pendulum \(=\frac{4}{4}=1 \mathrm{~m}=100 \mathrm{~cm}\) on that planet

Question 13. The period of a simple pendulum Is found to Increase by 50% when the length of the pendulum Is Increased by 0.6 m. Calculate the Initial length and the initial period of oscillation at a place where g = 9.8 m/s².
Solution:

1. Increase In length of pendulum = 0.6m;

Increase in time period = 50% = 1.5T

Let the original length of the pendulum = 1

Original time period = T; g = 9.8 m/s²

For 1st case \(9.8=4 \pi^2 \frac{l}{\mathrm{~T}^2} \rightarrow 1\);

For 2nd case \(l_1=(l+0.6), \mathrm{T}_1=.1 .5 \mathrm{~T}\)

9\(\times 8=4 \pi^2 \frac{l_1}{T_1^2} \rightarrow(2)\)

divide eq. (2) with eq. (1)

1 = \(\frac{l_1}{l} \cdot \frac{\mathrm{T}^2}{\mathrm{~T}_1^2} \Rightarrow \frac{l_1}{l}=\frac{\mathrm{T}_1^2}{\mathrm{~T}^2}=2.25 \Rightarrow l_1=2.25 l\)

But \(l_1=l+0.6\);

∴ \(l+0.6=2.25 l \Rightarrow 0.6=1.25 l\)

∴ Length of pendulum \(l=\frac{0.6}{1.25}=0.48 \mathrm{~m}\)

2. Time period \(\mathrm{T}=2 \pi \sqrt{\frac{l}{\mathrm{~g}}}\)

= \(2 \times 3.142 \sqrt{\frac{0.48}{9.8}}\)

= \(6.284 \times 0.2213\)

= \(1.391 \mathrm{sec}\)

Class 11 Physics Oscillations KSEEB Guide

Question 14. A clock regulated by a second pendulum keeps the correct time. During summer the length of the pendulum increases to 1.02m. How much will the clock gain or lose in one day?
Solution:

The time period of the seconds’ pendulum, T = 2 sec

Length of seconds pendulum, \(\mathrm{L}=\mathrm{gT}^2 / 4 \pi^2=0.9927 \mathrm{~m}\)

Length of seconds pendulum during summer \(=1.02 \mathrm{~m}\)

∴ Error in length, \(\Delta l=1.02-1=0.0273\)

In pendulum \(\mathrm{T} \propto \sqrt{l}\).

From principles of error \(\frac{\Delta \mathrm{T}}{\mathrm{T}}=\frac{1}{2} \frac{\Delta l}{l}=\frac{1}{2} \frac{0.0273}{0.9927}\)

∴ Error in time per day

= \(86,400 \times \frac{1}{2} \frac{0.0273}{0.9927}=1188 \mathrm{sec} \text {. }\)

KSEEB Class 11 Physics Oscillations Numericals

Question 15. The time period of a body suspended from a spring is T. What will be the new time period if the spring is cut into two equal parts and

1. The mass is suspended from one part?
2. The mass is suspended simultaneously from both the parts?

Solution:

Time period of spring, \(\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{K}}}\)

When a spring is cut into two equal parts force constant of each part K = 2K

1. For one piece, \(T=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{K}_1}}\)

= \(2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{K}}} \frac{1}{\sqrt{2}}=\frac{\mathrm{T}}{\sqrt{2}}\)

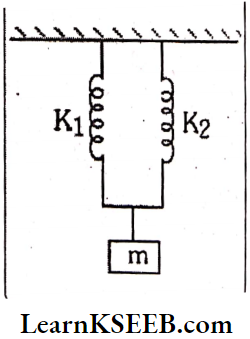
2. When mass is suspended simultaneously from two parts ⇒ they are connected in parallel. For springs in parallel \(\mathrm{K}_{\mathrm{p}}=\mathrm{K}_1+\mathrm{K}_2=4 \mathrm{~K}\)

Time period, \(\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{K}_{\mathrm{p}}}}\)

= \(2 \pi \sqrt{\frac{\mathrm{m}}{4 \cdot \mathrm{K}}}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{K}}} \cdot \frac{1}{2}=\frac{\mathrm{T}}{2}\)

Question 16. What is the length of a second pendulum on the earth?
Solution:

g = \(4 \pi^2 \frac{l}{\mathrm{~T}^2}, l=\frac{\mathrm{gT}^2}{4 \pi^2}\)

= \(\frac{9.8 \times 2^2}{4 \times(3.14)^2}=\frac{9.8}{9.86}\)

= \(0.99=1 \mathrm{~m}=100 \mathrm{~cm}\)