KSEEB Solutions For Class 11 Physics Chapter 7 Systems Of Particles And Rotational Motion

KSEEB Solutions For Class 11 Physics Chapter 7 Systems Of Particles And Rotational Motion Important Points

Rigid Body: A rigid body is a body with a perfectly definite and unchanging shape. The distance between all the pairs of particles of such a body does not change.

There is no real body that is truly rigid. All real bodies deform under the influence of forces., But in many cases this deformation is negligible.

Translational Motion: In translational motion, the body will move as a whole from one place to another place.

KSEEB Class 11 Physics Chapter 7 Solutions PDF

In pure translational motion, all the particles of the body will have the same velocity at any instant in time.

Axis Of Rotation: To prevent translational motion a rigid body has to be fixed along a straight line. Then the only possible motion is rotation about that fixed line. This fixed line is called the axis of rotation.

Read and Learn More KSEEB Class 11 Physics Solutions

Rotation: In rotation, every particle of a rigid body moves in a circle which lies in a plane perpendicular to the axis of rotation. The rotating body has a centre on the axis.

Centre Of Mass: For a rigid body or system of particles the total mass seems to be concentrated at a particular point is called the centre of mass. Such a point will behave as if it represents the whole translational motion of that body.

Centre Of Gravity: It is a point in the body where the body’s total weight seems to be concentrated.

If we apply an equal and opposite force to the body’s weight (W = mg) the body will be in mechanical equilibrium (i.e. both in translational and rotational equilibrium).

Co-ordinates Of The Centre Of Mass:

1. For symmetric bodies when the origin is taken at the geometric centre then the centre of mass is also at the geometric centre. Example: Thin rod, disc, sphere etc.
2. Let two bodies of masses say m₁ and m₂ are at distances say x₁ and x₂ from origin then centre of mass \(x_c=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\)

So we can assume that the position centre of mass is the ratio of the sum of the moment of masses and the total mass of the body.

1. Let two bodies of equal masses m and I m are separated by a distance x then the centre of mass of that system is at \(\frac{x}{2}\).
2. If three equal masses are at the corners of a triangle then centre of mass is at  centroid of that triangle.
3. Let a system of particles say m₁, m₂, m₃ …. m_n are in a plane or in space then co-ordinates of centre of mass will have x, y for the plane and X, Y and Z for space where

⇒ \(X_c =\frac{m_1 x_1+m_2 x_2+\ldots \ldots \ldots .+m_n x_n}{m_1+m_2+\ldots \ldots \ldots .+m_n}\)

⇒ \(Y_c=\frac{m_1 y_1+m_2 y_2+\ldots \ldots \ldots . .+m_n y_n}{m_1+m_2+\ldots \ldots \ldots . .+m_n}\)

⇒ \(Z_c=\frac{m_1 z_1+m_2 z_2+\ldots \ldots \ldots .+m_n z_n}{m_1+m_2+\ldots \ldots \ldots .+m_n}\)

Characteristics Of Centre Of Mass:

1. The total mass of the body seems to be concentrated at the centre of mass.
2. The total external force (F_ext) applied on a body seems to be applied at the centre of mass. F_ext = M a_c where ‘a_c‘ is the acceleration of the centre of mass.
3. Internal forces can’t change the motion of center of mass.
4. A complex motion Is a combination of translational and rotational motions. In complex motion centre of mass represents the entire translational motion of the whole body.
5. The momentum of a body is the product of the mass of the body and velocity of the centre of mass \(\overline{\mathrm{P}}=\mathrm{MV}_{\mathrm{c}}\)
6. The coordinates of the centre of mass do not depend on the coordinate system chosen.

Motion Of Centre Of Mass:

1. The motion of the centre of mass represents the translational motion of the whole body.

2. Velocity of centre of mass \(\mathrm{V}_{\mathrm{c}}=\frac{\mathrm{m}_1 \mathrm{v}_1+\mathrm{m}_2 \mathrm{v}_2+\ldots \ldots \ldots+\mathrm{m}_{\mathrm{n}} \mathrm{v}_{\mathrm{n}}}{\Sigma \mathrm{m}_{\mathrm{i}}}\)

i.e., the velocity of the centre of mass is the ratio of the sum of the momentum of all particles to the total mass of the body.

3. The momentum of the centre of mass \(\overline{\mathrm{P}}_{\mathrm{c}}\) is the sum of the momentum of all the particles of the body.

⇒ \(\bar{P}_c=M \bar{V}_c=m_1 v_1+m_2 v_2+\ldots \ldots \ldots . .+m_n v_n\)

4. The external force acting on the centre of mass \(F_{e t t}=M A_c=m_1 a_1+m_2 a_2 \ldots \ldots+m_n a_n\) or \(F_{e x t}=M A_c=F_1+F_2+\ldots \ldots. .+F_n\)

Where a₁, a₂, a_n are accelerations of individual particles of masses m₁, m₂…. m_n

Explosion Of A Shell In Mid-Air: Let a shell move along a parabolic trajectory explode in mid-air and divide into a number of fragments. Still, the centre of mass of that system of fragments will follow “the same parabolic path”.

Explanation: Explosion is due to internal forces. Internal forces cannot change the momentum of a body. So algebraic sum of the momentum of all fragments is constant. So the velocity of the centre of mass is constant. Hence centre of mass will follow the same parabolic path.

Crow Product Or Vector Product Of Vectors: If the multiplication of two vectors generates a vector then that vector multiplication is called cross product. Mathematically \(\bar{A} \times \bar{B}=|\bar{A}||\bar{B}| \sin \theta \hat{n}\)

Where \(\hat{n}\) is a unit vector perpendicular to the plane of \(\bar{A}\) and \(\bar{B}\).

The new vector generated is always perpendicular to both \(\bar{A}\) and \(\bar{B}\) i.e., perpendicular to the plane containing \(\bar{A}\) and\(\bar{B}\)

Karnataka 1st PUC Physics Chapter 7 Notes

Properties Of Cross Product:

1. Cross product is not commutative i.e., \(\overline{\mathrm{A}} \times \overline{\mathrm{B}} \neq \overline{\mathrm{B}} \times \overline{\mathrm{A}} \text { But } \overline{\mathrm{A}} \times \overline{\mathrm{B}}=-\overline{\mathrm{B}} \times \overline{\mathrm{A}}\)
2. Cross product obeys distributive law i.e. \(\overline{\mathrm{A}} \times(\overline{\mathrm{B}}+\overline{\mathrm{C}})=(\overline{\overline{\mathrm{A}}} \times \overline{\mathrm{B}})+(\overline{\mathrm{A}} \times \overline{\mathrm{C}})\)
3. If any vector is represented by the combination of \(\bar{i}\), \(\bar{j}\) and \(\bar{k}\) then cross product will obey right-hand screw rule.
4. The product of two coplanar perpendicular unit vectors will generate a unit vector perpendicular to that plane i.e. \(\overline{\mathrm{i}} \times \overline{\mathrm{j}}=\overline{\mathrm{k}}\), \(\overline{\mathrm{j}} \times \overline{\mathrm{k}}=\overline{\mathrm{i}}\) and \(\cdot \overline{\mathrm{k}} \times \overline{\mathrm{i}}=\overline{\mathrm{j}}\)
5. Cross product of parallel vectors is zero i.e. \(\overline{\mathrm{i}} \times \overline{\mathrm{i}}=\overline{\mathrm{j}} \times \overline{\mathrm{j}}=\overline{\mathrm{k}} \times \overline{\mathrm{k}}=0\)

Angular Displacement (θ): The angle subtended by a body at the centre when it is in angular motion is called angular displacement. Unit: Radian.

Angular Velocity (ω): The rate of change in angular displacement is called angular velocity.

Let angular displacement be Δθ over a  time interval Δt then average angular velocity \(\omega=\frac{\Delta \theta}{\Delta \mathrm{t}}\), Unit = Radian/sec

1. The relation between angular velocity and| linear velocity is v = rω
2. For a body in rotatory motion, all the particles will have the same angular velocity ‘ω’. But linear velocity ‘v’ changes.

Angular Acceleration(α): The rate of change in angular velocity is defined as angular acceleration.

Angular acceleration \(\alpha=\frac{\mathrm{d} \omega}{\mathrm{dt}}\).

Unit: Radian /sec²

Moment Of Force Couple Or Torque (τ): The moment of force is called torque or moment of force couple.

Let a force \(\overrightarrow{\mathrm{F}}\) be applied on a point ‘P’.

The position vector of P from the origin is \(\overrightarrow{\mathrm{r}}\) then

Torque \(\tau=\overline{\mathrm{r}} \times \overline{\mathrm{F}}=|\overline{\mathrm{r}}| \times|\overline{\mathrm{F}}| \sin \theta \cdot \overrightarrow{\mathrm{n}}\)

It is a vector. Its direction is perpendicular to both \(\overrightarrow{\mathrm{r}}\) and \(\overrightarrow{\mathrm{F}}\) (or) it is perpendicular to the plane containing \(\overrightarrow{\mathrm{r}}\) and \(\overrightarrow{\mathrm{F}}\).

Unit: Newton metre (N – m); D.F: ML² T^-2

1. Torque is the product of force \(\vec{F}\) and the perpendicular distance between force (F) and point of application (i.e. r sin θ).
2. Torque represents the energy with which a body is rotated. So units of torque and energy are the same.

Angular Momentum (L): Let a particle of mass ‘m’ has a linear momentum \(\overrightarrow{\mathrm{p}}\) and its position vector is \(\overrightarrow{\mathrm{r}}\) from origin then angular momentum of that particle is defined as \(\overline{\mathrm{L}}=\overline{\mathrm{r}} \times \overline{\mathrm{p}}=|\overline{\mathrm{r}} \| \overline{\mathrm{p}}| \sin \theta \cdot \hat{\mathrm{n}}\)

Angular momentum is a vector. \(\overrightarrow{\mathrm{L}}\) is perpendicular to the plane containing \(\overrightarrow{\mathrm{r}}\) and \(\overrightarrow{\mathrm{p}}\)

Unit: Kg – metre² and D.F.: ML²

Angular momentum is the product of momentum \(\bar{P}\) and perpendicular distance (r sin θ) from the origin. It is also written as L = Iω

Torque And Angular Momentum: The time rate of change of the angular momentum of a particle is equal to the torque acting on it.

Torque \(\tau=\frac{\mathrm{d} \overline{\mathrm{L}}}{\mathrm{dt}}=\overline{\mathrm{r}} \cdot \frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{dt}}\)

The time rate of change of the angular momentum of a system of particles about a point is equal to the sum of external torque i.e., \(\frac{\mathrm{d} \overline{\mathrm{L}}}{\mathrm{dt}}=\tau_{\text {ext }}\) just like \(\frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{dt}}=\mathrm{F}_{\text {ext }}\)

Law Of Conservation Of Angular Momentum: When external torque (τ_ext) is zero, the total angular momentum of a system is conserved i.e., it remains constant.

When \(\tau_{\text {ext }}=0\) then \(\frac{d \overline{\mathrm{L}}}{d t}=0\) i.e. angular momentum \(\bar{L}\) is constant, i.e. \(\mathrm{I}_1 \omega_1+\mathrm{I}_2 \omega_2=\) constant

1. For a system of particles when \(\tau_{\text {ext }}=0\) then \(\mathrm{d} \overline{\mathrm{L}}_1+\mathrm{d} \overline{\mathrm{L}}_2+\ldots \ldots+\mathrm{d} \overline{\mathrm{L}}_{\mathrm{n}}=\sum_{\mathrm{i}=1}^{\mathrm{n}} \mathrm{d} \overline{\mathrm{L}}_{\mathrm{i}}=0\)
2. The law of conservation of angular momentum is similar to the law of conservation of linear momentum in linear motion.

Equilibrium Of A Rigid Body: A rigid body is said to be in mechanical equilibrium if both its linear momentum and angular momentum are not changing with time. Then the body has neither linear acceleration nor angular acceleration.

(or),

1. The vector sum of all the forces acting on a rigid body must be zero.

i.e. \(F_1+F_2+\ldots \ldots \ldots+F_n=\sum_{i=1}^n F_i=0 \text {. }\)

This condition provides translational equilibrium of the body.

The vector sum of all the torques acting on a rigid body must be zero i.e., \(\tau_1+\tau_2 \ldots \ldots \ldots .+\tau_n=\sum_{i=1}^n \tau_i=0\)

This condition provides the rotational equilibrium of the body.

Couple (Or) Force Couple: A pair of equal and opposite forces with different lines of action is known as a couple. A couple produces rotation without translation.

KSEEB Class 11 Physics Systems of Particles and Rotational Motion Solutions

Moments Or Moment Of Force: It is defined as the product of force and the perpendicular distance between the force and its point of application

Principles Of Moments: For a lever to be in mechanical equilibrium let R be the reaction of the support at the fulcrum. It is directed upwards and F₁ and F₂ are the forces then

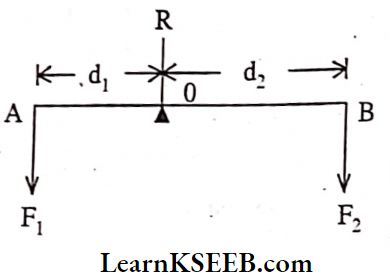
For translational equilibrium R – F₁ – F₂ = 0 i.e. algebraic sum of forces must be zero.

For rotational equilibrium d₁F₁ – d₂F₂ = 0. i.e. algebraic sum of moments must be zero.

Lever: An ideal lever is a light rod pivoted at a point along its length. This point is called “fulcrum”. In levers d₁F₁ = d₂F₂ i.e. Load arm x load = Force arm x Force

Mechanical advantage (M.A) = \(\frac{F_1}{F_2}=\frac{d_2}{d_2}\)

If effort arm d₂ is larger than the load arm then M.A > 1 i.e. we can lift greater loads with less effort.

Moment Of Inertia(I): The inertia of a rotating body is called moment of inertia.

Mathematically, Moment of Inertia, \(I=\sum_{i=1}^n m_1 r_1^2=M R^2\)

Radius Of Gyration (k): The radium of gyration of a body about an axis may be defined as the distance from the axis of a mass point whose mass is equal to the whole mass of the body and whose moment of inertia is equal to the moment of inertia of the whole body about that axis.

Fly Wheel: Flywheel is a metallic body with large moments of inertia.

It is used in the rotational motion of engines like automobiles. It allows a gradual change in speed and prevents jerky motion.

Perpendicular Axis Theorem: The moment of inertia of a plane body (lamina) about an axis perpendicular to its plane is equal to the sum of its moment of inertia about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body, i.e., l_z =I_x+ I_y

Parallel Axis Theorem: The moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through the centre of mass and the product of its mass and the square of the distance between the two parallel axes, i.e., I = I_G + MR²

Rolling Motion: Rolling motion is a combination of translational motion and mandatory motion.

Kinetic Energy Of A Rolling Body: When a body is rolling on a body without slipping then it will have translational kinetic energy \(\left(\frac{1}{2} m v^2\right)\) and rotational kinetic energy \(\left(\frac{1}{2} I \omega^2\right)\).

∴ Total kinetic energy of rolling body \(\mathrm{K} \cdot \mathrm{E}_{\mathrm{R}}=\frac{1}{2} \mathrm{mv}^2+\frac{1}{2} \mathrm{I} \omega^2\)

Systems Of Particles And Rotational Motion Important Formulae

For a two-particle system of masses m₁ and m₂ with positions x₁ and x₂.

1. Coordinates of centre of mass, \(x_c=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\)
2. If coordinate system coincides with m then \(x_c=\frac{m_2 x_2}{m_1+m_2} \text { or } x_c=\frac{m_2 d}{m_1+m_2}\) where d is distance between m₁ and m₂.
3. Ratio of distances from centre of mass is \(\frac{d_1}{d_2}=\frac{m_2}{m_1}\)

For Many-Particle System

1. \(x_{c . m}=\frac{m_1 x_1+m_2 x_2+m_3 x_3+\ldots .+m_n x_n}{m_1+m_2+m_3+\ldots .+m_n}\)

= \(\frac{1}{M} \sum_{i=1}^n m_1 x_1\)

2. \(Y_{c. m}=\frac{m_1 y_1+m_2 y_2+m_3 y_3+\ldots+m_n y_n}{m_1+m_2+m_3+\ldots .+m_n}\)

= \(\frac{1}{\mathrm{M}} \sum_{\mathrm{i}=1}^{\mathrm{n}} \mathrm{m}_{\mathrm{i}} \mathrm{y}_{\mathrm{i}}\)

\(z_{c. m}=\frac{m_1 z_1+m_2 z_2+m_3 z_3+\ldots .+m_n z_n}{m_1+m_2+m_3+\ldots .+m_n}\)

= \(\frac{1}{M} \sum_{i=1}^n \mathrm{~m}_i z_i\)

4. Position vector of the centre of mass \(\overline{\mathrm{r}}_{\mathrm{C}. \mathrm{M}}=\frac{\mathrm{m}_1 \overline{\mathrm{r}}_1+\mathrm{m}_2 \overline{\mathrm{r}}_2+\mathrm{m}_3 \overline{\mathrm{r}}_3+\ldots+m_n \overline{\mathrm{r}}_{\mathrm{n}}}{m_1+m_2+m_3+\ldots+m_n}\)

= \(\frac{1}{M} \sum_{\mathrm{i}=1}^n m_i r_i\)

5. Momentum of centre of mass, \(P_c=m v_c\)

= \(\sum_{i=1}^n \mathrm{~m}_1 v_i \text { or } \overline{\mathrm{P}}_{\mathrm{C}}=\overline{\mathrm{P}}_1+\overline{\mathrm{P}}_2+\ldots . . \overline{\mathrm{P}}_{\mathrm{n}}\) or \(\mathrm{m}_1 \overline{\mathrm{v}}_1+\mathrm{m}_2 \overline{\mathrm{v}}_2+\ldots . .+\mathrm{m}_{\mathrm{n}} \overline{\mathrm{v}}_{\mathrm{n}}\)

The velocity of the centre of mass \(V_{c m}=\frac{m_1 v_1+m_2 v_2+\ldots .+m_n v_n}{m_1+m_2+\ldots. .+m_n}\)

6. Acceleration of centre of mass, a = \(\frac{F_C}{M}=\sum_{i=1}^n a_i m_1\)

∴ a = \(\frac{m_1 a_1+m_2 a_2+m_3 a_3+\ldots .+m_n a_n}{m_1+m_2+m_3+\ldots .+m_n}\)

Cross Product: \(\bar{A}\) x \(\bar{B}\) is defined as |\(\bar{A}\)| |\(\bar{A}\)| sin G. \(\bar{n}\) where \(\bar{n}\) is a unit vector perpendicular to the plane of \(\bar{A}\) and \(\bar{B}\).

In cross product \(\overline{\mathrm{i}} \times \overline{\mathrm{i}}=\overline{\mathrm{j}} \times \overline{\mathrm{j}}=\overline{\mathrm{k}} \times \overline{\mathrm{k}}=0\) i.e., cross product of parallel vectors is zero.

In cross product \(\overline{\mathrm{i}} \times \overline{\mathrm{j}}=\overline{\mathrm{k}}, \overline{\mathrm{j}} \times \overline{\mathrm{k}}=\overline{\mathrm{i}}\) and \(\overline{\mathrm{k}} \times \overline{\mathrm{i}}=\overline{\mathrm{j}}\) cross product of two heterogeneous unit vectors will generate third unit vector) taken in a clockwise direction.

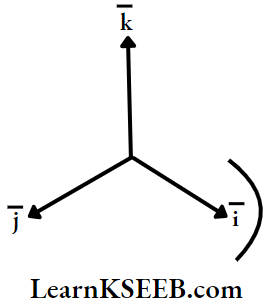
If \(\bar{A}=x_1 \bar{i}+y_1 \bar{j}+z_1 \bar{k}\) and \(\bar{B}=x_2 \bar{i}+y_2 \bar{j}\) + \(z_2 \bar{k}\) then

⇒ \(\bar{A} \times \bar{B}\) = \(\left|\begin{array}{rrr}
i & j & k \\
x_1 & y_1 & z_1 \\
x_2 & y_2 & z_2
\end{array}\right|\)

= \(\left(y_1 z_2-y_2 z_1\right) \bar{i}-\left(x_1 z_2-x_2 z_1\right) \bar{j}+\left(x_1 y_2-x_2 y_1\right) \bar{k}\)

Angular velocity, \(\omega=\frac{\text { angular displacement }}{\text { time }}=\frac{\theta}{t}\)

∴ \(\omega=\frac{\theta}{t}\)

For small quantities, \(\omega=\frac{\mathrm{d} \theta}{\mathrm{dt}}\);

Unit: Radian/sec.

∴ \(\omega=\frac{\theta}{\mathrm{t}}\) or \(\omega=\frac{\mathrm{d} \theta}{\mathrm{dt}}\) or \(\omega=\frac{2 \pi \mathrm{n}}{\mathrm{t}}(\mathrm{n}=\) number of rotations)

Angular acceleration, \(\alpha=\frac{\text { change in angular velocity }}{\text { time }}\)

∴ \(\alpha=\frac{\omega_2-\omega_1}{\mathrm{t}}\) or

∴ \(\alpha=\frac{\mathrm{d} \omega}{\mathrm{dt}}\) Unit : Radian \(\mathrm{sec}^2\)

The relation between v and ro is v = rω

The relation between a and α is a = rα

Centripetal acceleration, \(a_c=r w^2=v \omega=\frac{v^2}{r}\)

Centrifugal force = \(\frac{m v^2}{r}=m r \omega^2\)

When a coin is placed on a gramophone disc or on a circular turn table or for a vehicle is moving in a curved path limiting friction, \(\mu_s=\frac{f_s}{N}=\frac{r \omega^2}{g}\)

When a vertically hanging body ‘M’ is balanced by a rotating body m in the horizontal plane then at equilibrium

Mg = mrω² or Angular velocity required for balance is \(\omega=\sqrt{\frac{\mathrm{Mg}}{\mathrm{mr}}}\)

Torque, \(\tau=\overline{\mathrm{r}} \times \overline{\mathrm{F}}=|\overline{\mathrm{r}}||\overline{\mathrm{F}}| \sin \theta\). It represents the energy with which a body is turned.

Moment of force couple = one of the forces in couple x distance between the directions of forces.

Moment of inertia, \(I=\sum_{i=1}^n m_i r_1^2 \text { or } I=M R^2\)

If the moment of inertia, I = MR² = MK² then K is called radius of gyration.

From the parallel axis theorem moment of inertia about any parallel axis to the axis passing through the centre of mass is, I = I_G + MR².

From perpendicular axis theorem M.O.I. about a perpendicular axis to the plane I_z = I_x+ I_y

KSEEB 1st PUC Physics Chapter 7 Important Questions

Moment Of Inertia Of A Thin Rod Of Length l

1. M.O.I of the thin rod about its axis and perpendicular to the length, \(\mathrm{I}=\frac{\mathrm{M} l^2}{12}; \mathrm{K}=\frac{l}{\sqrt{12}}\)

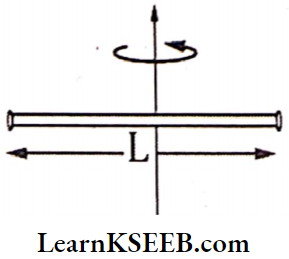
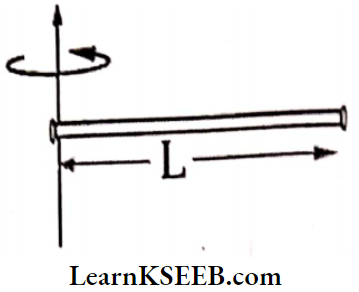
2. M.O.I of the thin rod about the end of the rod and perpendicular to the length.

Moment Of Inertia Of A Circular Ring Of Radius R

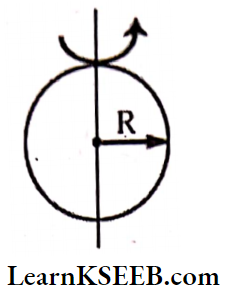
1. M.O.I of a circular ring about an axis passing through the centre and perpendicular to its plane I = MR², K = R

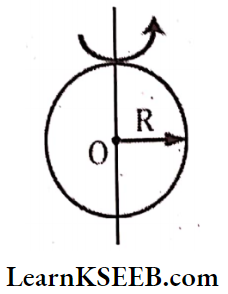
2. M.O.I. of a circular ring about any diameter, \(\mathrm{I}=\frac{\mathrm{MR}^2}{2}; \mathrm{K}=\frac{\mathrm{R}}{\sqrt{2}}\)

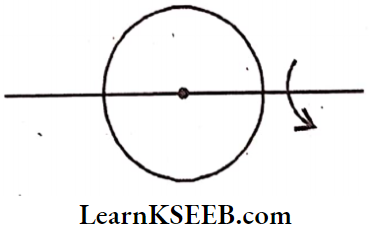
3. M.O.I. about any tangent and parallel to the diameter \(\mathrm{I}=\frac{3}{2} \mathrm{MR}^2; \mathrm{K}=\sqrt{\frac{3}{2}} \mathrm{R}\)

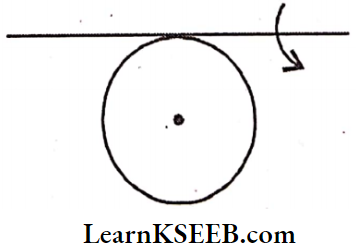
Moment Of Inertia Of A Disc Of Radius R

1. M.O.I about an axis passing through the centre and perpendicular to the plane, \(\mathrm{I}=\frac{\mathrm{MR}^2}{2}; \mathrm{K}=\frac{\mathrm{R}}{\sqrt{2}}\)

2.  M.O.I. about any diameter, \(\mathrm{I}=\frac{\mathrm{MR}^2}{4} ; \mathrm{K}=\frac{\mathrm{R}}{2}\)

3. M.O.I. about any tangent \(\mathrm{I}=\frac{5}{4} \mathrm{MR}^2 ; \mathrm{K}=\frac{\sqrt{5}}{2} \mathrm{R}\)

Moment Of Inertia Of A Rectangular Plane Lamina

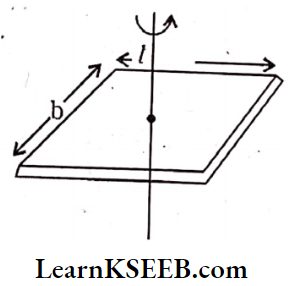
1. About the centre and perpendicular to the plane \(\mathrm{I}=\mathrm{M} \frac{\left(l^2+\mathrm{b}^2\right)}{12}; \mathrm{K}=\sqrt{\frac{l^2+\mathrm{b}^2}{12}}\)

2. About the axis parallel to length, \(\mathrm{I}=\frac{\mathrm{Mb}^2}{12}; K=\frac{\mathrm{b}}{\sqrt{12}}\)

3. About any axis parallel to breadth, \(\mathrm{I}=\frac{\mathrm{M} l^2}{12}; \mathrm{K}=\frac{l}{\sqrt{12}}\)

Moment Of Inertia Of A Solid Sphere

1. About an axis passing through diameter \(\mathrm{I}=\frac{2}{5} \mathrm{MR}^2; \mathrm{K}=\sqrt{\frac{2}{5}} \mathrm{R}\)

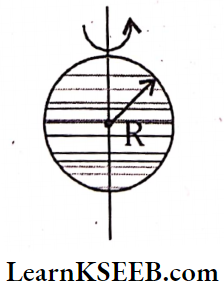
2. About any tangent, \(I=\frac{7}{5} M R^2 ; K=\sqrt{\frac{7}{5}} R\)

Moment Of Inertia Of A Hollow Sphere

1. About any diameter, \(\mathrm{I}=\frac{2}{3} \mathrm{MR}^2 ; \mathrm{K}=\sqrt{\frac{2}{3}} \mathrm{R}\)

2. About any tangent, \(\mathrm{I}=\frac{5}{3} \mathrm{MR}^2 ; \mathrm{K}=\sqrt{\frac{5}{3}} \mathrm{R}\)

Moment Of Inertia Of A Solid Cylinder Of Length L And Radius R

1. M.O.I. about natural axis of cylinder, \(\mathrm{I}=\frac{\mathrm{MR}^2}{2} ; \mathrm{K}=\frac{\mathrm{R}}{\sqrt{2}}\)

2. M.O.I. about an axis perpendicular to length and passing through centre, \(\mathrm{I}=\mathrm{M}\left(\frac{l^2}{12}+\frac{\mathrm{R}^2}{4}\right); \mathrm{K}=\sqrt{\frac{l^2}{12}+\frac{\mathrm{R}^2}{4}}\)

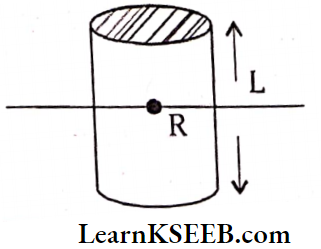
M.O.I Of A Hollow Cylinder Ol Length L And Radius R

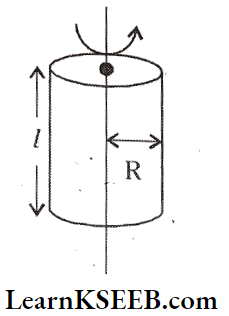
1. About The natural axis, I = MR²; K = R

2. About an axis perpendicular to length and passing through centre \(\mathrm{I}=\mathrm{M}\left(\frac{l^2}{12}+\frac{\mathrm{R}^2}{2}\right); \mathrm{K}=\sqrt{\frac{l^2}{12}+\frac{\mathrm{R}^2}{2}}\)

Angular momentum, L = Iω

Relation between angular momentum (L) and torque \((\tau)\) is, \(\tau=\frac{d \overline{\mathrm{L}}}{d \mathrm{It}}=\frac{\mathrm{L}_2-\mathrm{L}_1}{1}\)

Relation between τ and α Is τ = lα

From the law of conservation of angular momentum I₁ω₁ + I₂ω₂ = constant (When no external torque on the body)

Systems Of Particles And Rotational Motion Solutions KSEEB Class 11 Physics Very Short Answer Questions

Question 1. Is it necessary that a mass should be pre¬sent at the centre of mass of any system?
Answer:

No. It is not necessary to present some mass at the centre of mass of the system.

Example: At the centre of the ring (or) bangle, there is no mass present at the centre of mass.

Question 2. What is the difference in the positions of a girl carrying a hag in one of her hands and another girl carrying a hag in each of her two hands?
Answer:

1. When she carries a bag in one hand her centre of mass will shift to the side of the hand that carries the bag.
2. When a bag is in one hand some un-balanced force will act on her and it is difficult to carry.
3. If she carries two bags in two hands then her centre of mass remains unchanged Force on the two hands is equal, and balanced so it Is easy to carry the bags.

Question 3. Two rigid bodies have the same moment of inertia about their axes of symmetry. Of the two, which body will have greater kinetic energy?
Answer:

The relation between angular momentum and kinetic energy is, \(K E = \frac{L^2}{21}\)

Because the moment, of inertia, is the same the body with large angular momentum will have larger kinetic energy.

Question 4. Why are spokes provided in a bicycle wheel?
Answer:

The spokes of the cycle wheel increase its moment of inertia. The greater the moment of inertia, the greater the opposition to any change in uniform rotational motion

. As a result, the cycle runs smoother and speeder. If the cycle wheel had no spokes, the cycle would be driven in jerks and hence unsafe.

Question 5. We cannot open or close the door by applying force to the hinges. Why?
Answer:

To open or close a door, we apply a force normal to the door. If the force is applied at the hinges the perpendicular distance of force is zero. Hence, there will be no turning effect however large force is applied.

Question 6. Why do we prefer a spanner of the longer arm as compared to the spanner of the shorter arm?
Answer:

The turning effect of force, \(\tau=\vec{r} \times \vec{F}\). When the arm of the spanner is long, r is larger. Therefore, a smaller force (F) will produce the same turning effect. Hence, the spanner of a longer arm is preferred as compared to the spanner of a shorter arm.

Question 7. By spinning eggs on a tabletop, how will you distinguish a hard-boiled egg from a raw egg?
Answer:

To distinguish between a hard-boiled egg and a raw egg, we spin each on a tabletop. The egg which spins at a slower rate shall be a raw egg. This is because, in a raw egg, liquid matter inside tries to get away from the axis of rotation.

Therefore, its moment of inertia ‘I’ increases. As τ = lα = constant, therefore, α decreased i.e., raw egg will spin With smaller angular acceleration.

Question 8. Why should a helicopter necessarily have two propellers?
Answer:

If the helicopter had only one propeller, then due to the conservation of angular momentum, the helicopter itself would turn in the opposite direction. Hence, the helicopter should necessarily have two propellers.

Question 9. If the polar ice caps of the earth were to melt, what would the effect of the length of the day be?
Answer:

Earth rotates about its polar axis. When the ice of the polar caps of the earth melts, mass concentrated near the axis of rotation spreads out. Therefore, a moment of inertia ‘I’ increases.

As no external torque acts, \(\mathrm{L}=\mathrm{I} \omega=\mathrm{I}\left(\frac{2 \pi}{\mathrm{T}}\right)\) = constant with the increase of I, T will increase i.e., the length of the day will increase.

Question 10. Why is it easier to balance a bicycle in motion?
Answer:

A bicycle in motion is in rotational equilibrium. From the principles of the Dynamics of rotational bodies is that the forces that are perpendicular to the axis of rotation will try to turn the axis of rotation. Still, necessary forces will arise cancelling these forces due to the inertia of rotation and the fixed position of the axis is maintained. So it is easy to balance a rotating body.

KSEEB Class 11 Physics Chapter 7 Systems Of Particles And Rotational Motion Short Answer Questions

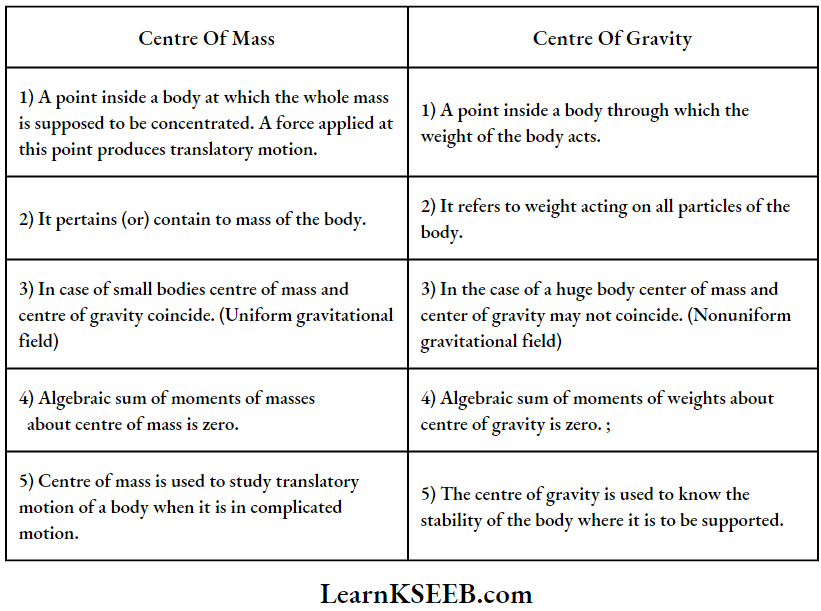
Question 1. Distinguish between the centre of mass and the centre of gravity.
Answer:

Question 2. Show that a system of particles moving under the influence of external force moves as if the force is applied at a centre of mass.
Answer:

Consider a system of particles of masses \(\mathrm{m}_1, \mathrm{~m}_2, \ldots \ldots \mathrm{m}_{\mathrm{n}}\) moves with velocity

vectors \(\overrightarrow{v_1}, \overrightarrow{v_2}, \overrightarrow{v_3} \ldots ., \overline{v_n}\)

∴ Velocity of the centre of mass

⇒ \(\overrightarrow{\mathrm{V}}_{\mathrm{CM}}=\frac{1}{M}\left\{m_1 \overline{\mathrm{v}_1}+m_2 \overrightarrow{\mathrm{v}_2}+\ldots+m_n \overline{v_n}\right\}\)

∴ \(m_1+m_2+\ldots \ldots+m_n=M\)

We know

∴ \(\overline{\mathrm{a}}=\frac{\mathrm{d}}{\mathrm{dt}}(\overline{\mathrm{V}}) \text {. }\)

∴ Acceleration of centre of mass  \(\mathrm{a}_{\mathrm{CM}}=\frac{\mathrm{d}}{\mathrm{dt}}\left(\overrightarrow{\mathrm{v}}_{\mathrm{CM}}\right)\)

∴ \(\mathrm{a}_{\mathrm{CM}}=\frac{1}{\mathrm{M}}\left\{\mathrm{m}_1 \frac{\mathrm{d}}{\mathrm{dt}} \vec{v}_1+\mathrm{m}_2 \frac{\mathrm{d}}{\mathrm{dt}} \overrightarrow{\mathrm{v}_2}+\ldots .+\mathrm{m}_{\mathrm{n}} \frac{\mathrm{d}}{\mathrm{dt}} \overrightarrow{\mathrm{v}_{\mathrm{n}}}\right\}\)

But Force (F)=m a, so the total force on the body is

⇒ \(\mathrm{F}=\mathrm{Ma}_{\mathrm{C} . \mathrm{M}}=\mathrm{m}_1 \mathrm{a}_1+\mathrm{m}_2 \mathrm{a}_2+\mathrm{m}_3 \mathrm{a}_3+\ldots \ldots+\mathrm{m}_{\mathrm{n}} \mathrm{a}_{\mathrm{n}}\)

or Total Force \(\mathrm{F}=\mathrm{Ma}_{\mathrm{C} . \mathrm{M}}\).

= \(\mathrm{F}_1+\mathrm{F}_2+\mathrm{F}_3\) + \(\ldots \ldots . .+\mathrm{F}_{\mathrm{n}}\)

Hence, the total force on the body is the sum of forces on individual particles and it is equal to the force on the centre of mass of the body.

Karnataka Board Class 11 Physics Chapter 7 MCQs

Question 3. Explain the centre of mass of the earth-moon system and its rotation around the sun.
Answer:

The interaction of the earth and moon does not affect the motion of the centre of mass of the earth and moon system around the sun.

• The gravitational force between the earth and the moon is the internal force. Internal forces cannot change the position of the centre of mass.
• The external force acting on the centre of mass of the Earth and Moon system is the force between the sun and C.M. of the Earth and Moon system.
• The motion of the centre of mass depends on external force. Hence, the moon system continues to move in an elliptical path around the sun. It is irrespective of the rotation of the moon around Earth.

Question 4. Define vector product. Explain the properties of a vector product with two examples.
Answer:

Vector Product (Or) Cross Product: If the product of two vectors (say \(\bar{A}\) and \(\bar{B}\)) gives a vector then that multiplication of vectors is called cross product or vector product of vectors.

Mathematically \(\bar{A}\) x \(\bar{A}\) = |\(\bar{A}\)| |\(\bar{B}\)|sinθ-\(\hat{n}\)

where \(\hat{n}\) = a unit vector perpendicular to both \(\bar{A}\) and \(\bar{B}\) (or) perpendicular to the plane of \(\bar{A}\) and \(\bar{B}\).

Properties Of Cross Product:

1. Cross product is not commutative i.e. \(\bar{A} \times \bar{B} \neq \bar{B} \times \bar{A} \text { But } \bar{A} \times \bar{B}=-\bar{B} \times \bar{A}\)
2. Cross product obeys distributive law i.e., \(\bar{A} \times(\bar{B}+\bar{C})=(\bar{A} \times \bar{B})+(\bar{A} \times \bar{C})\)
3. If any vector is represented by the combination of \(\bar{i}\), \(\bar{j}\) and \(\bar{k}\) then cross product will obey right-hand screw rule.
4. The product of two coplanar perpendicular unit vectors will generate a unit, vector perpendicular to that plane i.e., \(\overline{\mathrm{i}} \times \overline{\mathrm{j}}=\overline{\mathrm{k}}, \overline{\mathrm{j}} \times \overline{\mathrm{k}}=\overline{\mathrm{i}}\) and \(\overline{\mathrm{k}} \times \overline{\mathrm{i}}=\overline{\mathrm{j}}\)
5. The cross product of parallel vectors is zero i.e., \(\overline{\mathrm{i}} \times \overline{\mathrm{i}}=\overline{\mathrm{j}} \times \overline{\mathrm{j}}=\overline{\mathrm{k}} \times \overline{\mathrm{k}}=0\)

Examples Of Cross Product:

1. Torque (Or) Moment Of Force (\((\bar{\tau})\)): It is defined as the product of force and perpendicular distance from the point of application.

∴ Torque \(\tau=\overline{\mathrm{r}} \times \overline{\mathrm{F}}\)

2. Angular Momentum And Angular Velocity: For a rigid body in motion, Angular momentum \((\overline{\mathrm{L}})\) = radius \((\overline{\mathrm{r}})\) x momen- turn \((\overline{\mathrm{p}})\)

∴ Angular momentum \((\overline{\mathrm{L}})\)

= \(\overline{\mathrm{r}} \times(\mathrm{m} \overline{\mathrm{v}})=\mathrm{m}(\overline{\mathrm{r}} \times \overline{\mathrm{v}})\)

Question 5. Define angular velocity. Derive v = rω.
Answer:

Angular Velocity (ω): The rate of change of angular displacement is called angular velocity.

Relation Between Linear Velocity (V) And Angular Velocity (ω): Let a particle P is moving along the circumference of a circle of radius V with uniform speed v.

Let it be initially at position A, during a small time Δt it goes to a new position say C from B. The Angle subtended during this small interval is say dθ.

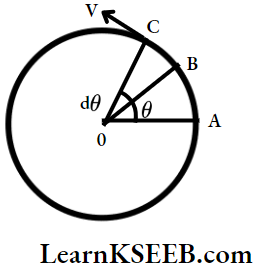
By definition angular velocity, \(\omega=\mathrm{Lt}_{\Delta t \rightarrow 0} \frac{\Delta \theta}{\Delta \mathrm{t}}=\frac{\mathrm{d} \theta}{\mathrm{dt}}\)

But linear velocity \(v=\underset{\Delta t \rightarrow 0}{\mathrm{Lt}} \frac{\mathrm{BC}}{\delta \mathrm{t}}\)

When \(\theta\) is small \(\text{arc} B C=r dθ \theta\)

⇒ v = \(\mathrm{r} \cdot \frac{\mathrm{d} \theta}{\mathrm{dt}}\)

∴ \(\mathrm{v}=\mathrm{r} \cdot \omega\) (because \(\frac{\mathrm{d} \theta}{\mathrm{dt}}=\omega\))

Question 6. State the principle of conservation of angular momentum. Give two examples.
Answer:

Law Of Conservation Of Angular Momentum:

When no external torque is acting on a body then the angular momentum of that rotating body is constant.

i.e., \(\mathrm{I}_1 \omega_1=\mathrm{I}_2 \omega_2(\text { when } \tau=0)\)

Example 1: A boy stands over the centre of a horizontal platform which is rotating freely with a speed ω₁ (n₁ revolutions/sec.)  about a vertical axis passing through the centre of the platform and straight up through the boy.

He holds two bricks in each of his hands close to his body. The combined moment of inertia of the system is said l₁. Let the boy stretch his arms to hold the masses far away from his body. In this position, the moment of inertia increases to I₂ and lets ω₂ be his angular speed.

Here ω₂ <ω₁ because the moment of inertia increases.

∴ \(\mathrm{I}_1 \omega_1=\mathrm{I}_2 \omega_2 \Rightarrow \mathrm{I}_1 \frac{2 \pi}{\mathrm{T}_1}=\mathrm{I}_2 \frac{2 \pi}{\mathrm{T}_2} \Rightarrow \mathrm{I}_1 \mathrm{n}_1=\mathrm{I}_2 \mathrm{n}_2\)

Example 2: An athlete diving off a high springboard can bring his legs and hands close to the body and perform a Somersault about a horizontal axis passing through his body in the air before reaching the water below it. During the fall his angular momentum remains constant.

Question 7. Define angular acceleration and torque. Establish the relation between angular acceleration and torque.
Answer:

Angular acceleration (α): The rate of change of angular velocity is called angular acceleration.

Torque: It is defined as the product of the force and the perpendicular distance of the point of application of the force from that point.

Relation Between Angular Acceleration And Torque:

We know that, L = Iω

On differentiating the above expression with respect to time ‘t’ \(\frac{\mathrm{dL}}{\mathrm{dt}}=\frac{\mathrm{d}}{\mathrm{dt}}(\mathrm{I} \omega) \Rightarrow \frac{\mathrm{dL}}{\mathrm{dt}}=I \frac{\mathrm{d} \omega}{\mathrm{dt}}\)

But \(\frac{dL}{dt}\) is the rate of change of angular momentum called “Torque(τ)”.

and \(\frac{d \omega}{d t}\) is the rate of change of angular velocity called “angular acceleration (α)”

∴ The relation between Torque and angular acceleration is τ = Iα,

Question 8. Write the equations of motion for a particle rotating about a fixed axis.
Answer:

Equations Of Rotational Kinematics: If ‘θ’ is the angular displacement, ω₁ is the initial angular velocity, ω_f is the final angular velocity after a time ‘t’ seconds and ‘α’ is the angular acceleration, then the equations of rotational kinematics can be written as,

⇒ \(\omega_{\mathrm{f}}=\omega_{\mathrm{i}}+\alpha \mathrm{t}\)

⇒ \(\theta=\omega_{\mathrm{i}} t+\frac{1}{2} \alpha \mathrm{t}^2\)

∴ \(\omega_i^2-\omega_{\mathrm{i}}^2=2 \alpha \theta\)

Question 9. Derive expressions for the final velocity and total energy of a body rolling without slipping.
Answer:

A rolling body has both translational kinetic energy and rotational kinetic energy. So the total K.E energy of a rolling body is,

⇒ \(\mathrm{K} \cdot \mathrm{E}_{\mathrm{T}}=\mathrm{K} \cdot \mathrm{E}_{\text {(Translational) }}+\mathrm{K} \cdot \mathrm{E}_{\text {(Rotational) }}\)

⇒ \(K \cdot E_T=\frac{1}{2} m v^2+\frac{1}{2} l_{\omega^2} \text {. }\)

⇒ \(K. E_T=\frac{1}{2} m v^2+\frac{1}{2} m k^2 \frac{v^2}{r^2}\)

(because \(\mathrm{I}=\mathrm{mk}^2\) and \(\mathrm{v}=\mathrm{r} \omega\))

Total energy \(\mathrm{E}=\frac{1}{2} m v^2\left[1+\frac{\mathrm{k}^2}{\mathrm{r}^2}\right]\)

⇒ \(v^2=\frac{2 E}{m\left[1+\frac{k^2}{r^2}\right]}\)

∴ Velocity of the body, v = \(\sqrt{\frac{2 E}{m\left[1+\frac{k^2}{r^2}\right]}}\)

Chapter 7 Systems Of Particles And Rotational Motion Long Answer Type Question

Question 1.

1. State and prove the parallel axis theorem.
2. For a thin flat circular disk, the radius of gyration about a diameter as axis is k. If the disk is cut along a diameter AB as shown into two equal pieces, then find the radius of gyration of each piece about AB.

Answer:

1. Parallel Axis Theorem: The moment of inertia of a rigid body about an axis passing through a point is the sum of the moment of inertia about a parallel axis passing through the centre of mass (I_G) and the mass of the body multiplied by the square of the distance (MR²) between the axes i.e., I = I_G + MR²

Proof: Consider a rigid body of mass M with ‘G’ as its centre of mass. I_G is the moment of inertia about an axis passing through the centre of mass. I = The moment of inertia about an axis passing through the point ‘O’ in that plane.

Let the perpendicular distance between the axes be OG = R (say)

Consider point P in the given plane. Join OP and GP. Extend the line OG and drop a normal from ‘P’ onto it as shown.

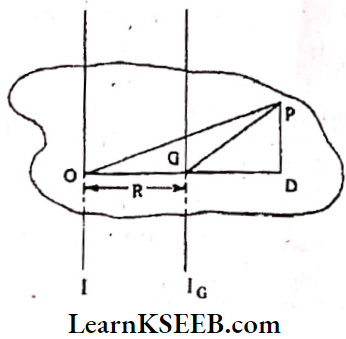
The moment of inertia about the axis passing through the centre of mass G. \(\left(\mathrm{I}_{\mathrm{G}}\right)=\Sigma \mathrm{mGP}^2 \quad \ldots. .(1)\)….(1)

M.O.I. of (he body about an axis passing through ‘O’ (I) = ∑mOP²…..(2)

From triangle O P D \(O P^2=O D^2+D P^2\)

⇒ OD = OG + GD

∴ \(O D^2=(O G+G D)^2=O G^2+G D^2+2 O G . G D\)…..(3)

From Equations (2) and (3)

I = \(\Sigma \mathrm{mOP} \mathrm{P}^2=\Sigma \mathrm{m}\left[\left(\mathrm{OG}^2+\mathrm{GD}^2\right.\right.\)

+ \(20 G . G D)+D^2 \text { ] }\)

∴ I\(=\Sigma \mathrm{m}\left\{\mathrm{GD}^2+\mathrm{DP}^2+\mathrm{OG}^2+20 \mathrm{G} . \mathrm{GN}\right\}\)…..(4)

But \(\mathrm{GD}^2+\mathrm{DP}^2=\mathrm{GP}^2\)

∴ \(\mathrm{I}=\Sigma \mathrm{m}\left\{\mathrm{GP}^2+\mathrm{OG}^2+20 \mathrm{OG} . \mathrm{GD}\right\}\)

∴ \(\mathrm{I}=\Sigma \mathrm{m} \mathrm{GP}^2+\Sigma \mathrm{mOG}^2+20 \mathrm{G} \mathrm{mGD} \text {. }\)

But the terms \(\Sigma m \mathrm{mP}^2=\mathrm{I}_{\mathrm{G}}\)

∴ \(\Sigma \mathrm{mOG}^2=\mathrm{MR}^2\) (because \(\Sigma \mathrm{m}=\mathrm{M}\) and \(O G=\mathrm{R}\))

The term 2OG ∑mGD = 0. Because it represents the sum of the moment of masses about the centre of mass. Hence its value is zero.

∴ I = I_G+ MR²

Hence parallel axis theorem is proved,

2. Moment of inertia of a disc of mass ‘M’ and radius ‘R’ about its diameter is, \(\mathrm{I}=\frac{\mathrm{MR}^2}{4}\)

If ‘k’ is the radius of the gyration of the disc then, I = Mk²∴

∴ \(\mathrm{Mk}^2=\frac{\mathrm{MR}^2}{4} \Rightarrow \mathrm{k}=\mathrm{R} / 2\)

After cutting along the diameter, the mass of each piece \(=\frac{\mathrm{M}}{2}\)

Moment of inertia of each piece, \(I^{\prime}=\frac{1}{4} \times \frac{M}{2} \times R^2\)

If \(\mathrm{k}^{\prime}\) is the radius of gyration of each piece then, \(\mathrm{I}^{\prime}=\frac{\mathrm{M}}{2}\left(\mathrm{k}^{\prime}\right)^2\)

∴ \(\frac{M}{2}\left(k^{\prime}\right)^2=\frac{1}{4} \times \frac{M}{2} \times R^2 \Rightarrow k^{\prime}=\frac{R}{2}=k\)

Question 2.

1. State and prove the perpendicular axis theorem.
2. If a thin circular ring and a thin flat circular disk of the same mass have the same moment of inertia about their respective diameters as the axis. Then find the ratio of their radii.

Answer:

1. Perpendicular Axis Theorem: The I moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of the moment of inertia about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body.

∴ \(\mathrm{I}_z=\mathrm{I}_{\mathrm{x}}+\mathrm{I}_{\mathrm{y}}\)

Proof: Consider a rectangular plane lamina. X and Y are two mutually perpendicular axes in the plane. Choose another perpendicular axis Z passing through the point ‘O’.

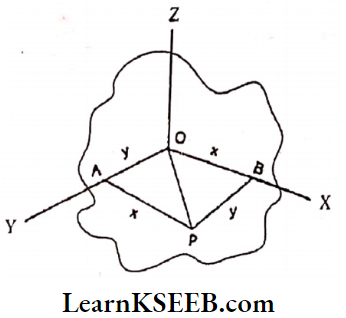
Consider a particle P in the XOY plane.

Its coordinates are (x, y).

The moment of inertia of the particle about the X-axis is I_X = ∑my².

M.O.I about Y-axis is I_Y = ∑mx²

M.O.I about the Z axis is I_Z = ∑ m. OP²

From triangle OAP, \(\mathrm{OP}^2=\mathrm{OA}^2+\mathrm{AP}^2=\mathrm{y}^2+\mathrm{x}^2\)

∴ \(\mathrm{I}_{\mathrm{Z}}=\Sigma \mathrm{mOP} \mathrm{P}^2=\Sigma \mathrm{m}\left(\mathrm{y}^2+\mathrm{x}^2\right)\)

∴ \(\mathrm{I}_{\mathrm{Z}}=\Sigma \mathrm{my}^2+\Sigma \mathrm{mx}^2\)

But \(\Sigma m y^2=I_x\) and \(\Sigma m x^2=I_y\)

∴ Moment of Inertia about a perpendicular axis passing through ‘O’ is \(\mathrm{I}_z=\mathrm{I}_{\mathrm{x}}+\mathrm{I}_{\mathrm{y}}\)

Hence perpendicular axis theorem is proved.

2. Moment of inertia of a thin circular ring about its diameter is, \(I_1=m_1 R_1^2\)

The moment of inertia of a flat circular disc about its diameter is; \(\mathrm{I}_2=\frac{\mathrm{m}_2 \mathrm{R}_2^2}{2}\)

Given that two Objects have the same moment of inertia i.e., I₁ = I₂

⇒ \(m_1 R_1^2=\frac{m_2 R_2^2}{2}\)

Given that \(m_1=m_2\) hence \(R_1^2=\frac{R_2^2}{2}\)

⇒ \(\frac{R_1^2}{R_2^2}=\frac{1}{2}\) or \(\frac{R_1}{R_2}=\frac{1}{\sqrt{2}}\)

∴ Ratio of radii, \(R_1: R_2=1: \sqrt{2}\)

Question 3. State and prove the principle of conservation of angular momentum. Explain the principle of conservation of angular momentum with examples.
Answer:

Law Of Conservation Of Angular Momentum: When no external torque is acting on a body then the angular momentum of that rotating body is constant.

i.e., \(\left.\mathrm{I}_1 \omega_1=\mathrm{I}_2 \omega_2 \text { (when } \tau=0\right)\)

Explanation: Here I₁ and I₂ are the moment of inertia of rotating bodies and ω₁ and ω₂ are their initial and final angular velocities. If external torque \(\tau=0\) then \(\frac{\mathrm{d} \overline{\mathrm{L}}}{\mathrm{dt}}=\tau=0\)

∴ Change in angular momentum is also zero

⇒ \(\mathrm{d} \overrightarrow{\mathrm{L}}_2-\mathrm{d} \overrightarrow{\mathrm{L}}_1=0\)

i.e., \(\mathrm{I}_2 \omega_2-\mathrm{I}_1 \omega_1=0\) or \(\mathrm{I}_1 \omega_1=\mathrm{I}_2 \omega_2\)

Example 1: A boy stands over the centre of a horizontal platform which is rotating freely with a speed ω₁ (n₁ revolutions/sec.) about a vertical axis passing through the centre of the platform and straight up through the boy.

He holds two bricks in each of his hands close to his body. The combined moment of inertia of the system is say I₁. Let the boy stretch his arms to hold the masses far away from his body. In this position, the moment of inertia increases to I₂ and lets ω₂ be his angular speed.

Here ω₂ < ω₁ because the moment of inertia increases.

∴ \(I_1 \omega_1=I_2 \omega_2 \Rightarrow I_1 \frac{2 \pi}{T_1}=I_2 \frac{2 \pi}{T_2} \Rightarrow I_1 n_1=I_2 n_2\)

Example 2: An athlete diving off a high springboard can bring his legs and hands close to the body and perform a Somersault about a horizontal axis passing through his body in the air before reaching the water | below it. During the fall his angular momentum remains constant.

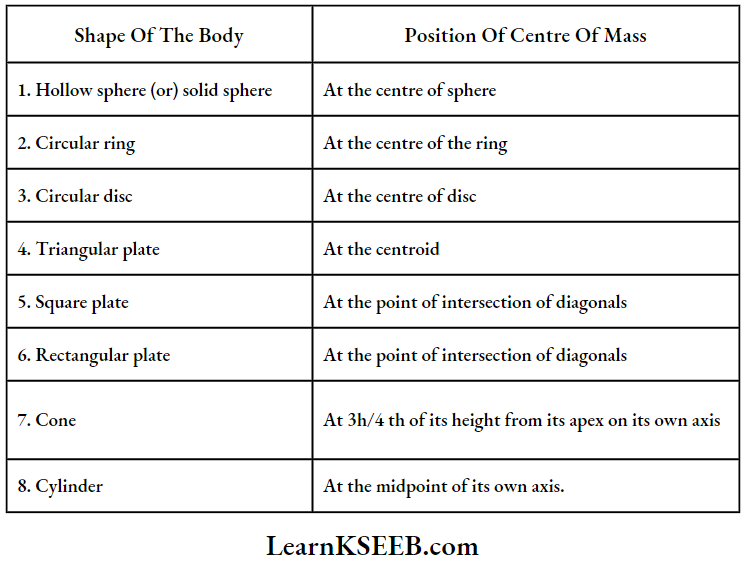
Position Of Centre Of Mass Of Some Symmetrical Bodies:

Comparison Of Translatory And Rotatory Motions:

KSEEB Class 11 Physics Systems Of Particles And Rotational Motion Problems

Question 1. Show that a (b x c) is equal in magnitude to the volume of the parallelopiped formed on the three vectors a, b and c.
Solution:

Let a parallelopiped be formed on three vectors \(\overrightarrow{O A}=\vec{a}, \overrightarrow{O B}=\vec{b}, \overrightarrow{O C}=\vec{c}\)

Now, \(\vec{b} \times \vec{c}\)= bc \(\sin 90^{\circ} \hat{n}\) = bc \(\hat{n}\)

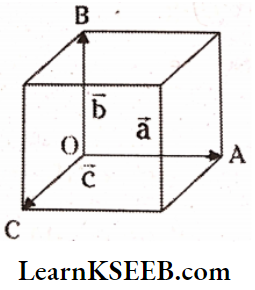
where \(\hat{n}\) is the unit vector along \(\overrightarrow{O A}\) perpendicular to the plane containing \(\vec{b}\) and \(\vec{c}\)

Now \(\vec{a} \cdot(\vec{b} \times \vec{c})\) = \(\vec{a} \cdot b c \hat{n}\) =(a)(b c) \(\cos 0^°=a b c\)

Which is equal in magnitude to the volume of parallelopiped.

Question 2. A rope of negligible mass is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N ? What is the linear acceleration of the rope? Assume that there is no slipping.
Solution:

Here M = 3 kg ; R = 40 cm = 0.4 m

Moment of inertia of the hollow cylinder about its axis, I = MR² = 3(0.4)² = 0.48 kg m²

Force applied, F = 30 N

∴ Torque, τ = F x R =30×0.4 =12N-m

If α is angular acceleration produced, then from τ = Iα

⇒ \(\alpha=\frac{\tau}{1}=\frac{12}{0.48}=25 \mathrm{rad} \mathrm{s}^{-2}\)

Linear acceleration, a = Rα = 0.4 x 25 = 10 ms^-2.

Question 3. A coin is kept at a distance of 10 cm from the centre of a circular turn table. If the coefficient of static friction between the table and the coin is 0.8. Find the frequency or rotation of the disc at which the coin will just begin to slip.
Solution:

Distance of coin = r = 10 cm = 0.1 m.

Coefficient of friction μ = 0.8.

Frequency of rotation = number of rotations per second.

For coin not to slip \(\mu \mathrm{mg}=\mathrm{mr} \omega^2 \Rightarrow \omega=\sqrt{\frac{\mu g}{\mathrm{r}}}\)

∴ \(\omega=\sqrt{\frac{0.8 \times 9.8}{1}}=\sqrt{78.4}=8.854 \mathrm{rad} / \mathrm{sec} \text {. }\)

Number of rotations per \(\mathrm{sec}=\)

Rotational frequency \(=\frac{\omega}{2 \pi}=\frac{8.854}{2 \pi}=1.409 \text{Rot} / \mathrm{sec}\) or 84.54 r.p.m.

Question 4. Find the torque of a force \(7 \overrightarrow{\mathrm{i}}+3 \overrightarrow{\mathrm{j}}-5 \overrightarrow{\mathrm{k}}\) about the origin. The force acts on a particle whose position vector is \(\overrightarrow{\mathbf{i}}-\overrightarrow{\mathbf{j}}+\overrightarrow{\mathbf{k}}.\).
Solution:

Force \(\overrightarrow{\mathrm{F}}=7 \overrightarrow{\mathrm{i}}+3 \overrightarrow{\mathrm{j}}-5 \overrightarrow{\mathrm{k}}\);

Position of particle \(\vec{r}=\vec{i}-\vec{j}+\vec{k}\)

Torque \(\mathrm{t}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{F}}\)

∴ \(\tau=\left|\begin{array}{rrr}
\overrightarrow{\mathrm{i}} & \vec{j} & \vec{k} \\
1 & -1 & 1 \\
7 & 3 & -5
\end{array}\right|\)

∴ \(\tau= \overrightarrow{\mathrm{i}}[(-1)(-5)-(3 \times 1)]\)–\(\overrightarrow{\mathrm{j}}[1 \times(-5)-(7 \times 1)]\)

+ \(\overrightarrow{\mathrm{k}}[(1 \times 3)-(-1) \times 7]\)

⇒ \(\tau=\vec{i}(5-3)-\vec{j}(-5-7)+\vec{k}(3+7)\)

= \(2 \overrightarrow{\mathrm{i}}+12 \overrightarrow{\mathrm{j}}+10 \overrightarrow{\mathrm{k}}\)

Magnitude of torque \(\tau=\sqrt{2^2+12^2+10^2}\)

= \(\sqrt{4+144+100}=\sqrt{248}\) units

Question 5. Particles of masses 1g, 2g, 3g…, and 100g are kept at the marks 1 cm, 2 cm, 3 cm…, and 100 cm respectively on a meter scale. Find the moment of inertia of the system of particles about a perpendicular bisector of the meter scale.
Solution:

Given Masses of lg, 2g, 3g 100 g are 1, 2, 3…….100 cm on a scale.

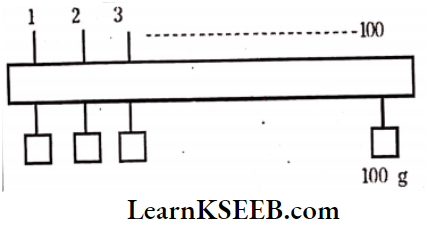
1. Sum of masses \(\Sigma m=\sum_{i=1}^n n i\)

The sum of n natural numbers S = \(\frac{\mathrm{n}(\mathrm{n}+1)}{2}=\frac{100 \times 101}{.2}=5051\)

∴ Total mass \(\mathrm{M}=5051 \mathrm{gr}=5.051 \mathrm{~kg} \rightarrow\) (1)

2. The centre of mass of all these masses is given by

⇒ \(X_{C. M}=\frac{\left(m_1 x_1+m_2 x_2+\ldots . .\right)}{\Sigma m}\)

= \(\frac{1 \times 1+2 \times 2+3 \times 3+\ldots .+100 \times 100}{M}\)

= \(\frac{1^2+2^2+3^2+\ldots .+100^2}{M}\)

But sum of squares of 1st n natural numbers is S = \(\frac{n(n+1)(2 n+1)}{6}\)

∴ CM = \(\frac{n(n+1)(2 n+1)}{6 \times n(n+1)}\) use \(M=\frac{n(n+1)}{2}\)

∴ CM = \(\frac{201}{3}=67 C M \quad \rightarrow \text { (2) }\)

3. M . O .1 .=1

= \(m_1 r_1^2+m_2 r_2^2+m_3 r_3^2+\ldots . .+m_{100} r_{100}^2\)

∴ I = \(1 \times 1 \times 1+2 \times 2^2+3 \times 3^2+\ldots \ldots \ldots\) + \(100 \times 100^2\)

= \(1+2^3+3^3+\ldots \ldots+100^3 \times 10^{-7} \mathrm{Kg} \cdot \mathrm{m}^2\)

(because 1g = \(10^{-3} \mathrm{~kg} \ 1 . C M=10^{-2} \mathrm{~m}\))

Sum of cubes of 1st n natural numbers is S = \(\frac{\mathrm{n}^2(\mathrm{n}+1)^2}{4}\)

I = \(\frac{100^2 \times(101)^2}{4} \mathrm{~g} \cdot \mathrm{cm}^2\)

= \(2.550 \times 10^7 \mathrm{~g} \cdot \mathrm{cm}^2=2.550 \mathrm{Kg} \cdot \mathrm{m}^2\) (From one end of scale).

M.O.I. about C.M. = \(I_G=I-\mathrm{MR}^2\)

= \(2.550-5.05 \times 0.67 \times 0.67\)

= \(2.550-2.267=0.283 \mathrm{~kg} \cdot \mathrm{m}^2\)

4. Perpendicular bisector is at 50 CM.

So shift M.O.I from centre of mass to x₁ = 50cm point from x = 67 CM

∴ Distance between the axis R = 67 – 50 = 17cm = 0.17M

M.O.I. about this axis I = I_G + MR²

= 0.283 + 5.05 x 0.17 x 0.17 = 0.283 + 0.146 = 0.429 kgm²

M.O.I. about perpendicular bisector of scale = 0.429 kg – m_²

Question 6. Calculate the moment of inertia of a flywheel, if its angular velocity is increased from 60 r.p.m. to 180 r.p.m. when 100 J of work is done on it.
Solution:

W=\(100 \mathrm{~J}, \omega_1=60 \text { RPM }=1 \text { R.P.S }=2 \pi \text { Rad. } \\\), \(\omega_2=180 \text { R.P.M. }=3 \text { R.P.S }=6 \pi \text { Rad. }\)

Work done, \(\mathrm{W}=100 \mathrm{~J}=\frac{1}{2} \mathrm{I} \omega_2^2-\frac{1}{2} \mathrm{I} \omega_1^2\)

∴ 100 = \(\frac{1}{2} I\left(36 \pi^2\right. \left.-4 \pi^2\right) \Rightarrow I=\frac{200}{32 \pi^2}\)

= \(0.6332 \mathrm{kgm} \mathrm{m}^2=0.63 \mathrm{~kg} \cdot \mathrm{m}^2\)

Question 7. Three particles each of mass 100 g are placed at the vertices of an equilateral triangle of side length 10 cm. Find the moment of inertia of the system about an axis passing through the centroid of the triangle and perpendicular to its plane.
Solution:

Mass of each particle m = 100 g; side of equilateral triangle = 10 cm.

In equilateral triangle height of angular bisector \(\mathrm{CD}=\frac{\sqrt{3}}{2} l\)

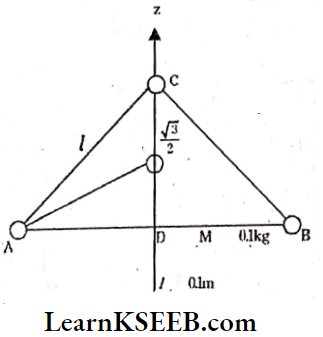
Centroid will divide the angular bisector in a ratio 2 :1 So X distance of each mass from vertex to centroid is \(\text { 2. } \frac{\sqrt{3}}{3} l=\frac{1}{\sqrt{3}} l\)

Moment of Inertia of the system

I = \(m_1 r_1^2+m_2 r_2^2+m_3 r_3^2\)

∴ I = \(0.1 \times\left(\frac{\sqrt{3}}{3} \times 0.1\right)^2+0.1 \times\left(\frac{\sqrt{3}}{3} \times 0.1\right)^2\)

+ \(0.1 \times\left(\frac{\sqrt{3}}{3} \times 0.1\right)^2\)

= \(3 \times \frac{3}{9} \times 0.1^3=1 \times 10^{-3} \mathrm{kg.} \mathrm{m}\)

Question 8. Four particles each of mass 100g are placed at the corners of a square of side 10 cm. Find the moment of inertia of the system about an axis passing through the centre of the square and perpendicular to its plane. Find also the radius of gyration of the system.
Solution:

Mass of each particle, m = 100 g = 0.1 kg.

Length of side of square, a = 10 cm = 0.1 m

In square distance of corner from centre of square = – diagonal = \(\frac{\sqrt{2} a}{2}=\frac{a}{\sqrt{2}}\)

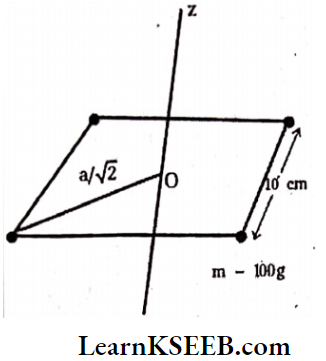
∴ Total moment of Inertia

1. I = \(m_1 r_1^2+m_2 r_2^2+m_3 r_3^2+m_4 r_4^2=4 \mathrm{mr}^2\)

I = \(4 \times 0.1\left(\frac{1}{\sqrt{2}} \times 0.1\right)^2=4 \times \frac{1}{2} \times 0.1^3\)

= \(2 \times 10^{-3} \mathrm{Kg} \cdot \mathrm{m}^2\)

2. Radius of gyration \(\mathrm{k}=\sqrt{\frac{1}{\mathrm{~m}}}=\sqrt{\frac{2 \times 10^{-3}}{4 \times 10^{-1}}}\)

= \(\frac{1}{\sqrt{2}} \times 10^{-1}\)

= \(0.7071 \times 10^{-1} \mathrm{~m} \text { or } 7.071 \mathrm{~cm} .\)

Class 11 Physics Systems of Particles and Rotational Motion KSEEB Guide

Question 9. Two uniform circular discs, each of mass 1 kg and radius 20 cm, are kept in contact about the tangent passing through the point of contact. Find the moment of inertia of the system about the tangent passing through the point of contact.
Solution:

Mass of disc = M = 1 kg.

Radius of disc = 20 cm = 0.2 m

They are in contact as shown.

M.O.I of a circular disc about a tangent parallel to its plane = \(\frac{5}{9}\) MR²

Total M.O.I of the system

I = \(\frac{5}{4} M R^2+\frac{5}{4} M R^2=\frac{5}{2} M R^2\)

∴ \(\mathrm{I}=\frac{5}{2} \times 1 \times 0.2 \times 0.2=5 \times 1 \times 0.1 \times 0.2\)

= \(0.1 \mathrm{kgm}^2\)

Question 10. Four spheres each diameter 2a and mass ‘m’ are placed with their centres on the four corners of a square of the side b. Calculate the moment of inertia of the system about any side of the square.
Solution:

Diameter of sphere = 2a ⇒ radius = a.

Side of square = b.

For spheres 1 and 2 axis of rotation is the same and passes through diameters.

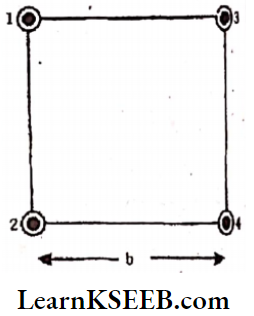
∴ M.O.I. of spheres \(1 \ 2=\mathrm{I}_1+\mathrm{I}_2=\frac{2}{5} \mathrm{ma}^2\)

+ \(\frac{2}{5} m a^2=\frac{2}{5} m a^2 \rightarrow 1\)

For spheres 3,4 M.O.L about diameters

= \(\frac{2}{5} \mathrm{ma}^2+\frac{2}{5} \mathrm{ma}^2=\frac{2}{5} \mathrm{ma}^2\)

Transfer this M.O.I. onto the axis using the Parallel axis theorem.

∴ \(\mathrm{I}_3+\mathrm{I}_4=\frac{2}{5} m a^2+m b^2+\frac{2}{5} m a^2+m b^2\)

= \(\frac{4}{5} m a^2+2 m b^2\)

Total M.O.I. of the system

= \(\frac{4}{5} m a^2+\frac{4}{5} m a^2+2 m b^2\)

∴ I = \(\left[\frac{8}{5} m a^2+2 m b^2\right]\)

Question 11. To maintain a rotor at a uniform angular speed or 200 rad s^-1, an engine needs to transmit a torque of 180 Nm. What is the power required by the engine? (Note: uniform angular velocity in the absence of friction implies zero torque. In practice, applied torque is needed to counter frictional torque). Assume that the engine is 100% efficient.
Solution:

Given uniform angular speed (ω) = 200 rad s^-1

Torque, τ = 180 N-m;

But power p = τω =

∴ P = 180 x 200 = 36000 watt = 36 kW

Question 12. A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5g are put on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick?
Solution:

Let m be the mass of the stick concentrated at C, the 50 cm mark

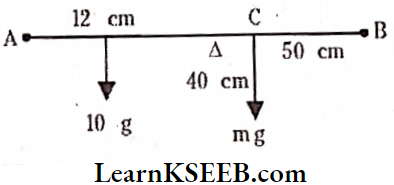
For equilibrium about C’, i.e. at the 45 cm mark, 10g (45-12) = mg (50-45)10g x 33 = mg x 5

m = \(\frac{10 \times 33}{5}\) = 66 grams

Question 13. Determine the kinetic energy of a circular disc rotating with a speed of 60 rpm about an axis passing through a point on its circumference and perpendicular to its plane.
The circular disc has a mass of 5 kg and a radius of 1 m. 
Solution:

Mass of disc, M = 5 kg; Radius R = 1 m.

Angular velocity, \(\omega=60 \mathrm{RPM}=\frac{60 \times 2 \pi}{60}\)

= \(2 \pi \mathrm{Rad} / \mathrm{sec}\).

M.O.I. of the disc about a point passing through the circumference and perpendicular to the plane. \(I^{\prime}=I_G+M R^2\)

But \(\mathrm{I}_{\mathrm{G}}=\frac{\mathrm{MR}^2}{2}\) (for above case)

∴ \(\mathrm{I}^{\prime}=\frac{\mathrm{MR}^2}{2}+\mathrm{MR}^2=\frac{3}{2} \mathrm{MR}^2\)

Rotational Kinetic Energy = \(\frac{1}{2} I \omega^2\)

= \(\frac{1}{2} \cdot \frac{3}{2} \mathrm{MR}^2 \times(2 \pi)^2\)

∴ R.K.E. = \(\frac{3}{4} \times 5 \times 1 \times 1 \times 2 \times 3.142 \times 2 \times 3.142\)

= \(15 \times 3.142 \times 3.142=148.1 \mathrm{~J} \text {. }\)

Question 14. Two particles, each of mass m and speed u, travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of the two-particle system is the same whatever the point about which the angular momentum is taken.
Solution:

Angular momentum, L = mvr

Choose any axis say ‘A’

Let at any given time distance between m₁ and m₂ = L = L₁ + L₂

About the axis ‘A’ both will rotate in the same direction.

∴ Total angular momentum \(\mathrm{L}=\mathrm{L}_1+\mathrm{L}_2=m u L_1+m u L_2=m u\left(L_1+L_2\right)\) = muL

about any new axis say B distance of m₁ and m₂, are say \(\mathrm{L}_1^{\prime} \text { and } \mathrm{L}_2^{\prime}\)

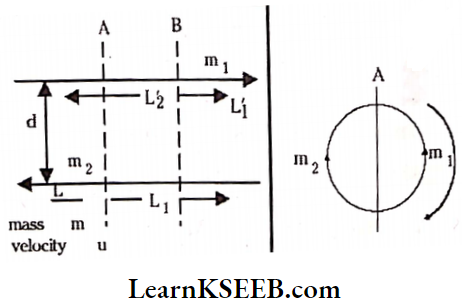
Total angular momentum, \(L=m u L_1^{\prime}+m u L_2^{\prime}\)

or \(L=m u\left(L_1^{\prime}+L_2^{\prime}\right)=m u L\)

(because \(L_1^{\prime}+L_2^{\prime}=L\))

Hence, the total angular momentum of the system is always constant.

Question 15. The moment of inertia of a flywheel making 300 revolutions per minute is 0.3 kgm². Find the torque required to bring it to rest in the 20s.
Solution:

M.O.I, I = 0.3 kg. ; time, t = 20 sec.,

ω₁ = 300 R.P.M. = \(\frac{300}{60}\) = 5. R.P.S.; ω₂ = 0

Torque, \(\tau=\mathrm{l} \alpha=0.3 \times \frac{5 \times 2 \pi}{20}=0.471 \mathrm{~N}-\mathrm{m}\)

Question 16. When 100J of work is done on a flywheel, its angular velocity is increased from 60 rpm to 180 rpm. What is the moment of inertia of the wheel?
Solution:

W = 100J, ω₁ = 60 RPM = 1 R.P.S = 2π Rad.

ω₂ = 180 R.P.M. = 3 R.P.S = 6π Rad.

Work done, \(W=100 \mathrm{~J}=\frac{1}{2} \mathrm{I} \omega_2^2-\frac{1}{2} \mathrm{I} \omega_1^2\)

∴ 100 = \(\frac{1}{2} \mathrm{I}\left(36 \pi^2-4 \pi^2\right) \Rightarrow I=\frac{200}{32 \pi^2}\)

= \(0.6332 \mathrm{kgm} \mathrm{m}^2=0.63 \mathrm{~kg} \cdot \mathrm{m}^2\)

KSEEB Class 11 Physics Rotational Motion Numericals

Question 17. Find the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are 100g, 150g and 200g respectively. Each side of the equilateral triangle is 0.5 m long, 100g mass is at the origin and 150g mass is on the X-axis.
Solution:

Mass at A = 100g ; Coordinates = 0, 0

Mass at B = 150 g; Coordinates = (0.5, 0)

Mass at C = 200g; Coordinates (0.25,0.25 √3)

Coordinates \(x_{c m}=\frac{m_A x_A+m_B x_B+m_C x_C}{m_A+m_B+m_C}\)

= \(\frac{(100 \times 0)+(150 \times 0.5)+(200 \times 0.25)}{100+150+200}\)

= \(\frac{75+50}{450}=\frac{125}{450}=\frac{5}{18} \mathrm{~m}\)

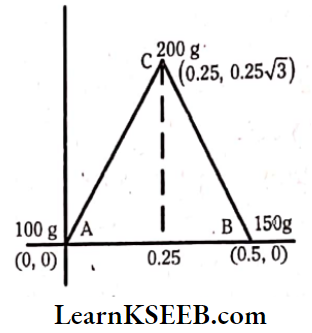
∴ \(Y_{c m}=\frac{m_A y_A+m_B y_B+m_C y_C}{m_A+m_B+m_C}\)

= \(\frac{(100 \times 0)+(150 \times 0)+(200 \times 0.25 \sqrt{3})}{100+150+200}\)

= \(\frac{50 \sqrt{3}}{450}=\frac{\sqrt{3}}{9}=\frac{1}{3 \sqrt{3}} \mathrm{~m}\)

Question 18. Find the scalar and vector product of two vectors \(\vec{a}=(3 \hat{i}-4 \hat{j}+5 \hat{k})\) and \(\overrightarrow{\mathbf{b}}=(-2 \hat{\mathbf{i}}+\hat{\mathbf{j}}-3 \hat{\mathbf{k}}) \text {. }\)
Solution:

⇒ \(a \cdot b=(3 \hat{i}-4 \hat{j}+5 \hat{k}) \cdot(-2 \hat{i}+\hat{j}-3 \hat{k})\)

= -6-4-15=-25

⇒ \(\mathbf{a} \times \mathbf{b}\) = \(\left|\begin{array}{ccc}
\hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\
3 & -4 & 5 \\
-2 & 1 & -3
\end{array}\right|\)

= \(7 \hat{\mathbf{i}}-\hat{\mathbf{j}}-5 \hat{\mathbf{k}}\)

∴ \(\mathrm{b} \times \mathrm{a}=-7 \hat{\mathrm{i}}+\hat{\mathrm{j}}+5 \hat{\mathrm{k}} \) (Recognise.)