KSEEB Solutions For Class 11 Physics Chapter 6 Work Energy And Power

KSEEB Class 11 Physics Solutions For Chapter 6 Work, Energy, and Power Important Points

Dot Product (Or) Scalar Product: The scalar product (or) dot product of any two vectors A and B is \(\bar{A} \text { and } \bar{B} \text { is } \bar{A} \cdot \bar{B}=|\bar{A}||\bar{B}| \cos \theta\)

where θ is the angle between them.

Dot Product (Or) Scalar Product Example: Work W = \(\bar{F} \cdot \bar{S}\)

Read and Learn More KSEEB Class 11 Physics Solutions

Properties Of Dot Product:

1. Scalar product obeys “commutative law” i. e., \(\overline{\mathrm{A}} \cdot \overline{\mathrm{B}}=\overline{\mathrm{B}} \cdot \overline{\mathrm{A}}\)
2. Scalar product obeys “distributive law” \(\overline{\mathrm{A}} \cdot(\overline{\mathrm{B}}+\overline{\mathrm{C}})=\overline{\mathrm{A}} \cdot \overline{\mathrm{B}}+\overline{\mathrm{A}} \cdot \overline{\mathrm{C}}\)
3. In unit vector i, j, k system \(\overline{\mathrm{i}} \cdot \overline{\mathrm{i}}=\overline{\mathrm{j}} \cdot \overline{\mathrm{j}}=\overline{\mathrm{k}} \cdot \overline{\mathrm{k}}=1\) i.e., the dot product of like unit vectors is unity.
   1. \(\overline{\mathrm{i}} \cdot \overline{\mathrm{j}}=\overline{\mathrm{j}} \cdot \overline{\mathrm{k}}=\overline{\mathrm{k}} \cdot \overline{\mathrm{i}}=0\) i.e., dot product of perpendicular vectors is zero.

Example: If \(\overline{\mathrm{A}} \cdot \overline{\mathrm{B}}=0 \Rightarrow \overline{\mathrm{A}} \text { and } \overline{\mathrm{B}}\) are pendicular.

Work: Work done by a force is defined as the product of a component of force in the direction of displacement and the magnitude of displacement.

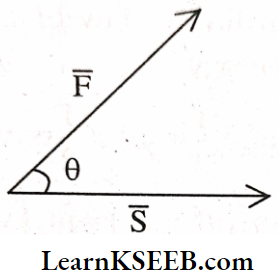
W = \(\overline{\mathrm{F}} \cdot \overline{\mathrm{S}} \text { (or) } \mathrm{W}=\overline{\mathrm{F}} \cdot \overline{\mathrm{S}} \cos \theta\)

Work is a scalar, unit kg² /sec² called joule (J), D.F = ML²T^-2

Energy: The ability (or) capacity of a body to do work is called energy.

KSEEB Class 11 Physics Chapter 6 Solutions PDF

Note: Energy can be termed as stored work in the body.

Kinetic Energy: Energy possessed by a moving body is called kinetic energy (k).

KE = \(\frac{1}{2}\) mv²

Kinetic Energy Example: All moving bodies contain kinetic energy.

Relation Between Kinetic Energy And Momentum: Kinetic energy KE = \(\frac{1}{2}\) mv  momentum \(\overline{\mathrm{p}}=\mathrm{mv}\)

∴ E = \(\frac{P^2}{2 m}\)

Work Energy Theorem (For Variable Force): Work done by a variable force is always equal to the change in kinetic energy of the body.

Work done \(\mathrm{W}=\frac{1}{2} \mathrm{mV}^2-\frac{1}{2} \mathrm{mV}_0^2=\mathrm{K}_{\mathrm{f}}-\mathrm{K}_{\mathrm{i}}\)

Potential Energy (V): It is the energy possessed by virtue of the position (or) configuration of a body.

Law Of Conservation Of Mechanical Energy: The total mechanical energy of a system is conserved if the forces doing work on it are conservative.

Spring Constant (k): It is defined as the ratio of force applied to the displacement produced in the spring.

k = \(-\frac{\mathrm{F}_{\mathrm{s}}}{\mathrm{x}}\) unit: Newton/metre, D.F = MT^-2

Note: A spring is said to be stiff if k is large. A spring is said to be soft if k is small.

Law Of Conservation Of Energy: When forces doing work on a system are conservative then the total energy of the system is constant i. e. energy can neither be created nor destroyed.

Law Of Conservation Of Energy Explanation: When conservative forces are applied to a system then the total mechanical energy is

1. As kinetic energy which depends on motion OR
2. As potential energy which depends on the position of the body.

Collisions: In collisions, a moving body collides with another body. During collision, the two colliding bodies are in contact for a very small period. During time of contact the two bodies will exchange the momentum and kinetic energy.

Collisions Are Two Types:

1. Elastic collision
2. Inelastic collision.

1. Elastic collisions: Elastic collisions will obey
   • Law of conservation of momentum and
   • Law of conservation of energy.
2. Inelastic Collisions: Inelastic collisions will follow, the law of conservation of momentum only.

In these collisions, a part of energy is lost in the form of heat, sound etc.

Coefficient Of Restitution (e): The coefficient of restitution is the ratio or relative velocity of separation (v₂– v₁) to the relative velocity of approach (u₁-u₂).

Coefficient of restitution e = \(\frac{v_2-v_1}{u_1-u_2}\)

1. For Perfect elastic collisions e = 1
2. For Perfect inelastic collisions e = 0
3. For collisions ’e’ lies between ’0’ and ‘1’.

One-Dimensional Collision (Or) Head-On Collisions: If the two colliding bodies are moving along the same straight line they are called dimensional collisions or hear-on collisions.

For these collisions, the initial and final velocities of the two colliding bodies are along the same straight line.

Two-Dimensional Collisions: If the two bodies moving in a plane collide and even after collision they are moving in the same plane, then such collisions are called two-dimensional collisions.

Power (P): It is the rate of doing work.

Power (P) = \(\frac{\text { work }}{\text { time }}\), Unit: Watt

Dimensional formula \(\mathrm{ML}^2 \mathrm{~T}^{-3}\)

Power can also be expressed as \(\mathrm{P}=\frac{\mathrm{dw}}{\mathrm{dt}}=\overline{\mathrm{F}} \cdot \frac{\mathrm{d} \overline{\mathrm{r}}}{\mathrm{dt}}=\overline{\mathrm{F}} \cdot \overline{\mathrm{V}}\)

Kilo Watt Hour (K.W.H): If work done is at a rate of 1000joules/sec continuously for a period of one hour then that amount of work is defined as K.W.H.

K.W.H is taken as 1 unit for supplying electrical energy.

Horse Power(H.P): 746 watts is called one horsepower.

∴ 1 H.P = 746 Watt.

Work, Energy, And Power Solutions KSEEB Class 11 Physics Important Formulae

Work is the product of force and displacement in the same direction.

1. When force and displacement are in same direction work, W = F.S.; Unit: joule; D.F. = ML²T^-2
2. When a force (\(\bar{F}\)) is applied with some angle ‘0’ with displacement vector (s) then work W = F • S cos θ or W = F • S
3. When a variable force is applied to a body, W = ∫F • dx

Power (P) is defined as the rate of doing work. It is a scalar.

Power, (P) = \(\frac{\text { work }}{\text { time }}=\frac{W}{t}\); Unit : watt; D.F. \(=\mathrm{ML}^2 \mathrm{~T}^{-3}\).

Work and energy can be interchanged. In machine gun problems work done = kinetic energy stored in bullets

i.e. W = \(\frac{1}{2}\) mv²

In motor and lift problems work done = change in potential energy (mgh)

Potential energy, (PE) = mgh;

Kinetic energy, KE = \(\frac{1}{2}\) mv²

Note: Work, P.E and K.E are scalars. Their units and Dimensional formulae are the same.

Relation Between KE And Momentum Are:

1. Kinetic energy, KE = \(\frac{p^2}{2m}\)
2. Momentum, \(p=\sqrt{2 m \cdot K E}\)

For a conservative force total work done in a closed path is zero. Example: Gravitational force.

For a non – conservative force work done in a closed path is not equal to zero. Example: Frictional force.

Work Energy Theorem: Work done by an unbalanced force is equal to the difference in kinetic energy.

W = \(\frac{1}{2}\) mv² – \(\frac{1}{2}\) mu²

From the Law of conservation of energy change in potential energy is equal to work done.

∴ W = mgh₂ – mgh₁

1. In elastic collisions Relative Velocity of approach = relative velocity of separation ⇒ u₁ – u₂ = v₂ — v₁
2. In the case of elastic collision, the Law of conservation of momentum and the Law of conservation of Energy are conserved. ⇒ \(m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2\)

∴ \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2\)

In elastic collisions final velocities after collisions are

⇒ \(v_1=\left[\frac{m_1-m_2}{m_1+m_2}\right] u_{1^{+}}\left[\frac{2 m_2}{m_1+m_2}\right] u_2\)

⇒ \(v_2=\left[\frac{2 m_1}{m_1+m_2}\right] u_{1^{+}}\left[\frac{m_2-m_1}{m_1+m_2}\right] u_2\)

In perfectly Inelastic collision common velocity of the bodies, (v) = \(\frac{m_1 u_1+m_2 u_2}{m_1+m_2}\)

Coefficient of restitution, \(\mathrm{e}=\frac{\mathrm{v}_2-\mathrm{v}_1}{\mathrm{u}_1-\mathrm{u}_2}=\frac{\text { Velocity of separation }}{\text { Velocity of approach }}\)

For a body dropped from a height ‘h’

1. Velocity of approach, \(\mathrm{u}=\sqrt{2 \mathrm{gh}}\)
2. Coefficient of restitution, e = \(\sqrt{\frac{h_2}{h_1}}\)
3. Velocity of separation, v₁ = – e \(\mathrm{u}=\sqrt{2 \mathrm{gh}}\)
4. The height attained after the nth bounce, h_n = e²ⁿ h

KSEEB Class 11 Physics Chapter 6 Work Energy And Power Very Short Answer Questions

Question 1. If a bomb at rest explodes Into two pieces, the pieces must travel In opposite directions. Explain.
Answer:

Explosion is due to internal forces. In the law of conservation of linear, momentum internal forces cannot change the momentum of the system. So after explosion m₁v₁ + m₂v₂ = 0 or m₁v₁ = – m₂v₂. ⇒ they will fly in opposite directions.

Question 2. State the conditions under which a force does no work.
Answer:

When a force (F) and displacement (S) are mutually perpendicular then work done is zero.

∴ \(\mathrm{W}=\overline{\mathrm{F}} \cdot \overline{\mathrm{S}}=|\mathrm{F}||\mathrm{S}| \cos \theta \text { when } \theta=90^{\circ}\) work W = 0

Even though force is applied if displacement is zero then work done W = 0.

Karnataka 1st PUC Physics Chapter 6 Notes

Question 3. Define Work, Power and Energy. State their S.I. units.
Answer:

Work: The product of force and displacement along the direction of force is called work.

Work done \(\mathrm{W} =\overline{\mathrm{F}} \cdot \overline{\mathrm{S}}\)

= \(|\overline{\mathrm{F}}||\overline{\mathrm{S}}| \cos \theta\)

S.I.’s unit of work is Joule.

Dimensional formula: ML²T^-2.

Power: The rate of doing work is called power.

Power = \(\frac{\text { Work done }}{\text { time }}=\frac{W}{t}\)

S.I. unit: Watt

D.F.: \(\mathrm{ML}^2 \mathrm{~T}^{-3}\)

Energy: It is the capacity or ability of the body to do work. By spending energy we can do work or by doing work energy content of the body will increase.

S.I. unit: Joule;

D.F.: ML²T^-2

Question 4. Slate the relation between the kinetic energy and momentum of a body.
Answer:

Kinetic Energy, Momentum Relation:

Kinetic energy K.E = \(\frac{1}{2}\) mv²……..(1)

Momentum \(\bar{p}\) = mv…..(2)

from equation K.E = \(\frac{1}{2}\) mv²

multiply with \(\frac{m}{m}\)

K.E = \(\frac{1}{2} m v^2 \times \frac{\mathrm{m}}{\mathrm{m}}\)

= \(\frac{1}{2} \frac{\left(m^2 v^2\right)}{m}\) from equation (2) \(\bar{p}=m v\)

K.E = \(\frac{1}{2} \cdot \frac{\mathrm{p}^2}{\mathrm{~m}}\)

∴ K.E. = \(\frac{p^2}{2 m} \text { (Or) } p=\sqrt{(\text { K.E.) } 2 m}\)

Question 5. State the sign of work done by a force in the following.

1. Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
2. Work done by the gravitational force in the above case.

Answer:

1. When a bucket is lifted out of the well work is done against gravity so work done is negative.
2. Work done by the gravitational force is positive.

Question 6. State the sign of work done by a force in the following.

1. Work done by friction on a body sliding down an inclined plane.
2. Work done gravitational force in the above case.

Answer:

1. Work done by friction while sliding down is negative because it opposes the downward motion of the body.
2. Work done by gravitational force when a body is sliding down is positive.

Question 7. State the sign of work done by a force in the following.

1. Work done by an applied force on a body moving on a rough horizontal plane with uniform velocity.
2. Work done by the resistive force of air on a vibrating pendulum In bringing It to rest.

Answer:

1. Work done against the direction of motion of a body moving on a horizontal plane is negative.
2. In pendulum a ∝ -y. So work done by air resistance to bring it to rest is considered as positive.

Question 8. State if each of the following statements is true or false. Give reasons for your answer.

1. The total energy of a system is always con¬served, no matter what internal and external forces on the body are present.
2. The work done by Earth’s gravitational force in keeping the moon in its orbit for its one revolution is zero.

Answer:

1. The law of conservation of energy states that energy can be neither created nor destroyed. This rule is applicable to internal forces and also to external forces when they are conservative forces,
2. Gravitational forces are conservative forces. Work done by conservative force around a closed path is zero.

Question 9. Which physical quantity remains constant

1. In an elastic collision
2. In an inelastic collision?

Answer:

1. In Elastic Collision: Momentum (P) and Energy (K.E.) are conserved, (remain constant)
2. In Inelastic Collision: only momentum is conserved, (remains constant)

Question 10. A body freely falling from a certain height h, after striking a smooth floor rebounds and h rises to a height h/2. What is the coefficient of restitution between the floor and the body?
Answer:

Given that, h₁ = h and h₂ = \(\frac{h_2}{2}\)

We know that the coefficient of restitution

e  \(=\sqrt{\frac{h_2}{h_1}}=\sqrt{\frac{\left(\frac{h}{2}\right)}{h}}=\frac{1}{\sqrt{2}}\)

∴ Coefficient of restitution, \(e=\frac{1}{\sqrt{2}}\)

Question 11. What is the total displacement of a freely falling body, after successive rebounds from the same place of ground, before it comes to a stop? Assume that ‘e’ is the coefficient of restitution between the body and the ground.
Answer:

The total displacement of a freely falling body, after successive rebounds from the same place of ground, before it comes to a stop is equal to the height (h) from which the body is dropped.

KSEEB Physics Class 11 Work Energy And Power Short Answer Questions

Question 1. What is potential energy? Derive an expression for the gravitational potential energy.
Answer:

Potential Energy: It is the energy possessed by a body by virtue of its position.

Example: Energy stored in water an overhead tank, wound spring

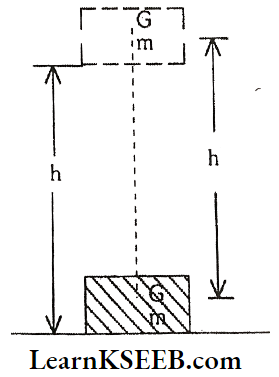
Equation For Potential Energy: Let a body of mass m be lifted through a height h’ above the ground. Where the ground is taken as a reference. In this process, we are doing some work.

Work done against gravity W = m.g.h.

i.e. Force x displacement along the direction of force applied. This work is stored in the body in the form of potential energy because work and energy can be interchanged.

Potential Energy P.E. = mgh.

Question 2. A lorry and a car moving with the same momentum are brought to rest by the application of brakes, which provide equal retarding forces. Which of them will come to rest in a shorter time? Which will come to rest in less distance?
Answer:

Momentum (\(\bar{p}\) = mv) is the same for both lorry and car.

Work done to stop a body = Kinetic energy stored

∴ W = F. S = \(\frac{1}{2}\) mv² = K.E.

But the force applied by brakes is the same for lorry and car.

Relation between \(\bar{P}\) on K.E. is \(\frac{p^2}{2m}\) = F.S

or stopping distance S = \(\frac{\overline{\mathrm{p}^2}}{2 \mathrm{mF}}\)

∴ \(\overline{\mathrm{P}}\) and \(\overline{\mathrm{F}}\) are same \(\mathrm{S} \propto \frac{1}{\mathrm{~m}}\)

So lighter body (car) will travel longer distances when P and F are the same.

Then mS = constant.

∴ So a car travels a longer distance than a lorry before it is stopped.

Question 3. Distinguish between conservative and non-conservative forces with one example each.
Answer:

Conservative Forces: If work done by the force around a closed path is zero and is independent of the path, then such forces are called conservative forces.

Conservative Forces Example:

1. Work done in lifting a body In gravitational Held. When the body returns to Its original position work done on it is zero. So gravitational forces are conservative forces.
2. Let a charge ‘q’ be moved in an electric field on a closed path then change in its electric potential i.e., static forces are conservative forces.

Non-Conservative Forces: For non-con-servative forces work done by a force1 around a closed path is not equal to zero j and it is dependent on the path.

Non-Conservative Forces Example:

1. Work done to move a body against friction. While taking a body between two points say A and B. We have to do work to move the body from A to B and also work is done to move the body from B to A.
2. As a result, the work done in moving the body in a closed path is not equal to zero. So frictional forces are non-conservative forces.

KSEEB Class 11 Physics Work, Energy, and Power Solutions

Question 4. Show that in the case of one-dimensional elastic collision, the relative velocity of approach of two colliding bodies before collision is equal to the relative velocity of separation after collision.
Answer:

To show the relative velocity of approach of two colliding bodies before the collision is equal to the relative velocity of separation after the collision.

Let two bodies of masses m₁, and m₂ move with velocities u₁, and u₂ along the straight line in the same direction and collide elastically.

Let their velocities after collision be v₁ and v₂.

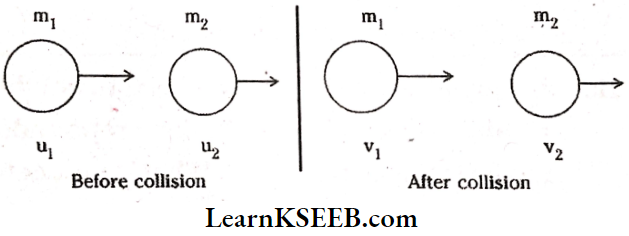
According to the law of conservation of linear momentum \(m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2 \)

or \(m_1\left(u_1-v_1\right)=m_2\left(v_2-u_2\right) \ldots \text { (1) }\)…..(1)

According to the law of conservation of kinetic energy \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2\)

∴ \(m_1\left(u_1^2-v_1^2\right)=m_2\left(v_2^2-u_2^2\right) \ldots\)…..(2)

Dividing equation (2) by (1) \(\frac{u_1^2-v_1^2}{u_1-v_1}=\frac{v_2^2-u_2^2}{v_2-u_2}\)

(or) \(u_1+v_1=v_2+u_2 \Rightarrow u_1-u_2=v_2-v_1 \ldots\)……(3)

i.e., relative velocity of approach of the two bodies before collision = relative velocity of separation of the two bodies after collision. So the coefficient of restitution is equal to T.

Question 5. Show that two equal masses undergoing oblique elastic collision will move at right angles after the collision if the second body is initially at rest.
Answer:

Consider two bodies possess equal mass (m) and they undergo oblique elastic collision.

Let the first body moving with initial velocity ‘u’ collide with the second body at rest.

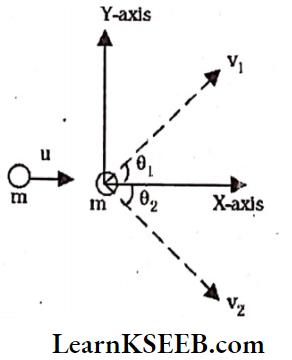
In elastic collision, momentum is conserved. So, conservation of momentum along the X-axis yields.

mu \(=m v_1 \cos \theta_1+m v_2 \cos \theta_2\)

(i.e.) \(u=v_1 \cos \theta_1+v_2 \cos \theta_2\)…..(1)

along Y-axis

0 = \(\mathrm{v}_1 \sin \theta_1-\mathrm{v}_2 \sin \theta_2\)…..(2)

squaring and adding equations (1) and (2) we get \(u^2=v_1^2+v_2^2+2 v_1 v_2 \cos \left(\theta_1+\theta_2\right)\)…..(3)

As the collision is elastic,

Kinetic Energy (K.E.) is also conserved.

(i.e.) \(\frac{1}{2} m u^2=\frac{1}{2} m v_1^2+\frac{1}{2} m v_2^2\)

⇒ \(u^2=v_1^2+v_2^2\)……(4)

From equations (3) and (4) \(2 v_1 v_2 \cos \left(\theta_1+\theta_2\right)=0\)

As it is given that \(v_1 \neq 0\) and \(v_2 \neq 0\)

∴ \(\cos \left(\theta_1+\theta_2\right)=0 \text { or } \theta_1+\theta_2=90^{\circ}\)

The two equal masses undergoing oblique elastic collision will move at right! angles after collision, if the second body is initially at rest.

Question 6. Derive an expression for the height attained by a freely falling body after the ‘n’ number of rebounds from the floor.
Answer:

Let a small ball be dropped from a height ’h’ on a horizontal smooth plate. Let it rebound to a height of ’h₁’.

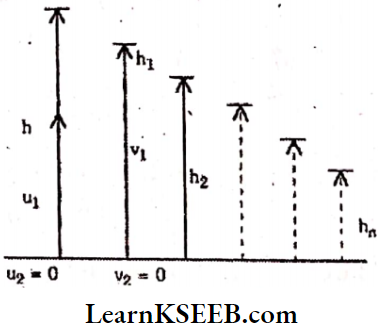
The velocity with which it strikes the plate \(u_1=\sqrt{2 g h}\)

The velocity with which it leaves the plate \(v_1=\sqrt{2 g h_1}\)

The velocity of the plate before and after the collision is zero i.e., u₂ = 0, v₂ = 0

Coefficient of restitution, \(\mathrm{e}=\frac{\text { relative velocity of separation }}{\text { relative velocity of approach }}\)

= \(\frac{\sqrt{2 \mathrm{gh}_2-0}}{\sqrt{2 \mathrm{gh}_1-0}}\)

∴ \(\mathrm{e}=\sqrt{\frac{\mathrm{h}_1}{h}} \text { or } \mathrm{h}_1=\mathrm{e}^2 \mathrm{~h}\)

For 2nd rebound it goes to a height \(h_2=e^2 h_1=e^2 e^2 h=e^4 h\)

For 3rd rebound it goes to a height \(h_3=e^2 h_2=e^2 e^4 h=e^6 h\)

For nth rebound height attained \(h_n=e^{2 n} h\)

Question 7. Explain the law of conservation of energy.
Answer:

Law Conservation Of Energy: When forces doing work on a system are conservative then the total energy of the system is constant i.e., energy can neither be created nor destroyed.

i.e. Total energy = (K + u) = constant form.

Explanation: Consider a body that undergoes small displacement Δx under the action of the conservative force F. According to the work-energy theorem.

Change in K.E = work done

ΔK = F(x)Δx ………(1)

but Potential energy Δu = -F(x) Δx……(2)

from (1) and (2) = ΔK = – Δu

⇒ Δ(K + u) = 0

Hence (K + u) = constant

i.e., the sum of the kinetic energy and potential energy of the body is a constant

Since the universe may be considered as an isolated system, the total energy of the universe is constant.

KSEEB Class 11 Physics Work Energy And Power Long Answer Questions

Question 1. Develop the notions of work and kinetic energy and show that it leads to work- energy theorem. State the conditions under which a force does no work.
Answer:

Work: The product of the component of force in the direction of displacement and the magnitude of displacement is called work

W = \(\overline{\mathrm{F}} \cdot \overline{\mathrm{S}}\)

When \(\overline{\mathrm{F}}\) and \(\overline{\mathrm{S}}\) are parallel W = |\(\overline{\mathrm{F}}\)| x |\(\overline{\mathrm{S}}\)|

When \(\overline{\mathrm{F}}\) and \(\overline{\mathrm{S}}\) has some angle θ between them

W = \(\overline{\mathrm{F}}\).\(\overline{\mathrm{S}}\) cos θ

Kinetic Energy: Energy possessed by a moving body is called kinetic energy (k)

The kinetic energy of an object is a measure of the work that an object can do by virtue of its motion.

Kinetic energy can be measured with equation K = \(\frac{1}{2}\)mv²

Example: All moving bodies contain kinetic energy.

Work Energy Theorem (For Variable Force): Work done by a variable force is always equal to the change in kinetic energy of the body

Work done \(\mathrm{W}=\frac{1}{2} \mathrm{mV}^2-\frac{1}{2} m V_0^2=\mathrm{K}_{\mathrm{f}}-\mathrm{K}_{\mathrm{i}}\)

Proof: Kinetic energy of a body K = \(\frac{1}{2}\)mv2

The time rate of change of kinetic energy is \(\frac{\mathrm{dk}}{\mathrm{dt}}=\frac{\mathrm{d}}{\mathrm{dt}}\left(\frac{1}{2} \mathrm{mv}^2\right)=\frac{1}{2} \mathrm{~m} \cdot 2 \mathrm{v} \cdot \frac{\mathrm{dv}}{\mathrm{dt}}=\mathrm{mv} \cdot \frac{\mathrm{dv}}{\mathrm{dt}} \cdot\)

But \(\frac{\mathrm{dv}}{\mathrm{dt}}=\mathrm{a}\)

∴ \(\frac{\mathrm{dk}}{\mathrm{dt}}\) = m a v but ma = Force {F}

∴ \(\frac{\mathrm{dk}}{\mathrm{dt}}=\mathrm{Fv}=\mathrm{F} \cdot \frac{\mathrm{dx}}{\mathrm{dt}}\)

∴ \(\frac{\mathrm{dk}}{\mathrm{dt}}=\mathrm{F} \cdot \frac{\mathrm{dx}}{\mathrm{dt}}\)

Or, \(\mathrm{dk}=\mathrm{F} \cdot \mathrm{dx}\)

When force is conservative force F = F(x)

∴ On integration over initial position (x,) and final position x₂

\(\int_i^f d k=\int_{x_1}^{x_2} F(x) d x\) but \(\int_{x_1}^{x_2} F(x) d x=\) work done

By variable force W

∴ \(\mathrm{W}=\int_{\mathrm{i}}^{\mathrm{t}} \mathrm{dk} \Rightarrow W=\mathrm{K}_{\mathrm{f}}-\mathrm{K}_{\mathrm{i}}\)

i.e., work done by a conservative force is equal to a change in the kinetic energy of the body.

Condition for Force not to do any work.

When force (\(\bar{F}\)) and displacement (\(\bar{S}\)) are perpendicular work done is zero. i.e., when 0 = 90 then W = \(\bar{F}\) \(\bar{S}\) = 0

KSEEB Physics Class 11 Work, Energy, and Power 

Question 2. What are collisions? Explain the possible types of collisions. Develop the theory of one-dimensional elastic collision.

(OR)

What arc collisions? Explain the possible types of collisions. Show that in the case of one-dimensional elastic collision, the relative velocity of approach of two colliding bodies before collision is equal to the relative velocity of separation after collision.

Answer:

A process in which the motion of a system of particles changes but keeps the total momentum conserved is called a collision.

Collisions are two types:

1. Elastic
2. In-elastic.

To show the relative velocity of the approach before the collision is equal to the relative velocity of separation after the collision.

Let two bodies of masses m₁, and m₂ moving with velocities u₁, and u₂ along the same line, in the same direction collide elastically.

Let their velocities after collision are v₁ and v₂

According to the law of conservation of linear momentum \(m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2 \)

or \(m_1\left(u_1-v_1\right)=m_2\left(v_2-u_2\right)\)……(1)

According to the law of conservation of kinetic energy \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2\)

∴ \(m_1\left(u_1^2-v_1^2\right)=m_2\left(v_2^2-u_2^2\right)\)…….(2)

Dividing equation (2) by (1)

⇒ \(\frac{u_1^2-v_1^2}{u_1-v_1}=\frac{v_2^2-u_2^2}{v_2-u_2}\)

or \(u_1+v_1=v_2+u_2 \Rightarrow u_1-u_2=v_2-v_1 \ldots \ldots\)(3)

i.e., In clastic collisions relative velocity of approach of the two bodies before collision = relative velocity of separation of the two bodies after collision.

Velocities Of Two Bodies After Elastic Collision:

To find \(v_1\), put \(v_2=u_1-u_2+v_1\) in eqn. (1)

⇒ \(m_1 u_1+m_2 u_2=m_1 v_1+m_2\left(u_1-u_2+v_1\right)\)

⇒ \(m_1 u_1+m_2 u_2=m_1 v_1+m_2 u_1-m_2 u_2+m_2 v_1\)

⇒ \(m_1 u_1+m_2 u_2-m_2 u_1+m_2 u_2=v_1\left(m_1+m_2\right)\)

⇒ \(u_1\left(m_1-m_2\right)+2 m_2 u_2=v_1\left(m_1+m_2\right)\)

∴ \(v_1=\frac{m_1-m_2}{m_1+m_2} u_1+\frac{2 m_2}{m_1+m_2} u_2 \ldots . . \text { (4) }\)

Similarly, \(v_2=\frac{u_2\left(m_2-m_1\right)}{m_1+m_2}+\frac{2 m_1 u_1}{m_1+m_2} . . \text { (5) }\)

Question 3. State and prove the law of conservation of energy in the case of a freely falling body.
Answer:

Law Of Conservation Of Energy: Energy can neither be created nor destroyed. But it can be converted from one form into another form so that the total energy will remain constant in a closed system.

Proof: In case of a freely falling body: Let a body of mass be dropped from a height ‘H’ at point A.

Forces due to the gravitational field are conservative forces, so total mechanical energy (E=P.E + K.E.) is constant i.e., neither destroyed nor created.

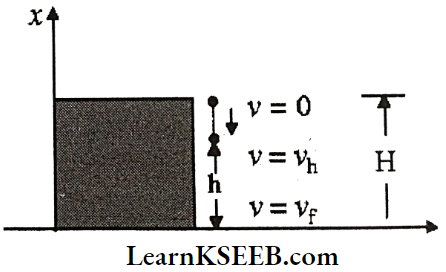
The conservation of potential energy to kinetic energy  for a ball of mass m dropped from a height H

KSEEB Class 11 Physics Work, Energy, and Power key concepts

1. At point H: Velocity of body v = 0 ⇒ K = 0

Potential energy (u) = mgH where H=height above the ground

T.E = u + K = mgH….(1)

2. At point 0: i.e., just before touching the ground

A constant force is a special case of specifically dependent force F(x) so mechanical energy is conserved.

So energy at H = Energy at 0 = mgH

Proof: At point ‘0’ height h = 0

⇒ v = \(\sqrt{2 \mathrm{gH}} \text {; }\); u = 0

⇒ \(\mathrm{K}_0=\frac{1}{2} \mathrm{mv}^2=\frac{1}{2} \mathrm{~m} 2 \mathrm{gH}=\mathrm{mgH}\)

Total energy E = mgH + 0 = mgH …….(2)

3. At Any Point h: Let height above ground = h

u = mgh, Kh = \(\frac{1}{2}\) mv²

where = \(V=\sqrt{2 g(h-x)}\)

∴ The velocity of the body when it falls through a height (h-x) is \(\sqrt{2 g(h-x)}\)

∴ Total energy = mgh = \(\frac{1}{2}\) m2g(H-h)

⇒  E = mgh + mgH – mgh = mgH…….(3)

From equations 1, 2 and 3 total energy at any point is constant.

Hence, the law of conservation of energy is proved.

Conditions To Apply The Law Of Conservation Of Energy:

1. Work done by internal forces is conservative.
2. No work is done by an external force.

When the above two conditions are satisfied then the total mechanical energy of a system will remain constant.

Problems For Work, Energy, And Power KSEEB Physics Chapter 6

Question 1. A test tube of mass 10 grnniH closed with a cork of mass 1 gram contains some ether. When the test tube is heated the cork flics out under the pressure of the ether gas. The test tube is suspended horizontally by a weightless rigid bar of length 5 cm. What is the minimum velocity with which the cork should fly out of the tube, so that the test tube describes a full vertical circle about the point O. Neglect the mass of the ether.
Solution:

Length of bar, L = 5 cm, = \(\frac{5}{100}\), g = 10m/s²

For the cork not to come out minimum, the velocity at the lowest point is, v = \(\sqrt{5 \mathrm{gL}}\).

At this condition centrifugal and centripetal forces are balanced.

∴ \(\mathrm{V}_{\min }=\sqrt{5 \times \frac{5}{100} \times 10}=\frac{5}{10} \sqrt{10} \mathrm{~m} / \mathrm{s}\) or \(0.5 \sqrt{10} \mathrm{~m} / \mathrm{s}\)

Question 2. A machine gun fires 360 bullets per minute and each bullet travels with a velocity of 600 ms^-1. If the mass of each bullet is 5 gm, find the power of the machine gun.
Solution:

Number of bullets, n = 360

Time, t = 1 minute = 60s

The velocity of the bullet, v = 600 ms^-1;

Mass  of each bullet, m = 5gm = 5 x 10^-3 kg

Power of the machine gun, \(P=\frac{n\left(\frac{1}{2} m v^2\right)}{t}\)

= \(\frac{360\left(\frac{1}{2} \times 5 \times 10^{-3} \times(600)^2\right)}{60}\)

P = \(5400 \mathrm{~W}=5.4 \mathrm{KW}\)

KSEEB Class 11 Physics Chapter 6 Work, Energy, and Power 

Question 3. Find the useful power used in pumping 3425 m³ of water per hour from a well 8 in deep to the surface, supposing 40% of the horsepower during pumping is wasted. What is the horsepower of the engine?
Solution:

Mass of water pumped, m = 3425 m³ = 3425 x 10‚ kg.

Mass of 1 m³ water = 1000 kg

Depth of well d = 8 m.,

Power wasted = 40%

∴ efficiency, η = 60%

time, t = 1 hour = 3600 sec.

Useful power = \(\frac{\text { Actual work done }}{\text { time } \times \text { efficiency }}=\frac{\mathrm{mgd}}{\mathrm{t} \cdot \eta}\)

Useful power = \(\frac{3425 \times 10 \times 9.8 \times 8 \times 100}{3600 \times 60}\)

= \(124315 \text { watt, But } 1 \mathrm{H} . \mathrm{P}=746 \mathrm{~W}\)

∴ Useful power in H.P = \(\frac{124315}{746}=166.6 \text { H.P }\)

Question 4. A pump is required to lift 600 kg of water per minute from a well 25m deep and to eject it with a speed of 50 ms^-1. Calculate the power required to perform the above task. (g = 10 m sec^-2)
Solution:

Mass of water m = 600 kg; depth = h = 25 m

Speed of water v = 25 m/s; g = 10 m/s², time t = 1 min = 60 sec.

Power of motor P = Power to lift water (P₁) + Kinetic energy of water (K.E) per second.

Power to lift water \(P_1=\frac{\mathrm{mgh}}{\mathrm{t}}=\frac{600 \times 10 \times 25}{60}=2500 \mathrm{watt}\)

K.E. of water per second = \(\frac{1}{2} \frac{\mathrm{mv}^2}{\mathrm{t}}\)

= \(\frac{1}{2} \frac{600 \times 25 \times 25}{60}=\frac{6250}{2}\)

= 3125 watts.

∴ Power of motor P = 2500 + 3125 = 5625 watt = 5.625 K.W.

Question 5. A block of mass 5 kg initially at rest at the origin is acted on by a force along the X-positive direction represented by F = (20 + 5x)N Calculate the work done by the force during the displacement of the block from x = 0 to x = 4m.
Solution:

Mass of block, m = 5 kg

Force acting on the block, F = (20 + 5x) N

If ‘w’ is the total amount of work done to displace the block from x = 0 to x = 4m then

W = \(\int \mathrm{dW}=\int_{x=0}^{x=4} F d x=\int_{x=0}^{x=4}(20+5 x) d x\)

= \(\left[20 x+\frac{5 x^2}{2}\right]_0^4=\left[20 \times 4-0+\frac{5}{2} \times(4)^2-0\right]\)

⇒ W=80+40=120 J

Question 6. A block of mass 5 kg is sliding down a smooth inclined plane as shown. The spring arranged near the bottom of the inclined plane has a force constant of 600 N/m. Find the compression in the spring at the moment the velocity of the block is maximum.

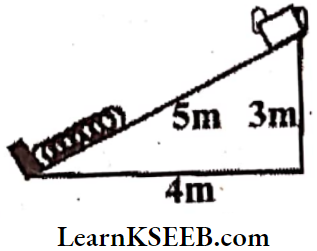
Solution:

Mass of the block, m = 5kg

Force constant, K = 600 N m_^-1.

From sin = \(\frac{3}{5}\)

The force produced by the motion in the block,

F = mg sin θ

⇒ F = 5 x 9.8 x \(\frac{3}{5}\) = 29.4 N

But force constant K = \(\frac{F}{x}\)

∴ x = \(\frac{\mathrm{F}}{\mathrm{K}}=\frac{29.4}{600}=0.05 \mathrm{~m}=5 \mathrm{~cm}\)

Question 7. A force F = –\(\frac{K}{x^2}\) (x ≠ 0) nets on a particle along the X-axis. Find the work done by the force in displacing the particle from x = + a to x = + 2a. Take K as a positive constant.
Solution:

Force acting on the particle, F = –\(\frac{K}{x^2}\)

The total amount of work done to displace the particle from x = + a to x = + 2a is,

W = \(\int d W=\int_{x=a}^{x=2 a} F d x\)

⇒ W = \(\int_{x=a}^{2 a} \frac{-K}{x^2} d x=-K \int_{x=a}^{x=2 a} \frac{1}{x^2} d x\)

= \(-K \int_{x=a}^{x=2 a} x^{-2} d x=K\left[x^{-1}\right]_{x=a}^{x=2 a}\)

= \(K\left[\frac{1}{2 a}-\frac{1}{a^{\prime}}\right]=K\left[\frac{-1}{2 a}\right]=\frac{-K}{2 a}\)

Question 8. A force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x = -a to x = + 2a.

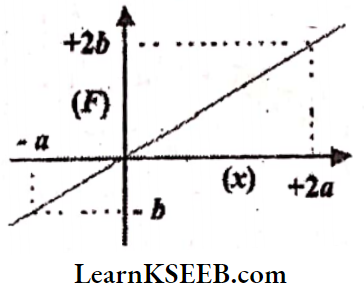
Solution:

Average force acting on the particle, \(\mathrm{F}=\frac{-\mathrm{b}+2 \mathrm{~b}}{2}=\frac{\mathrm{b}}{2}\)

The amount of work done by the force to displace the particle from x = -a to x = +2a is,

W = \(\int F d x \Rightarrow W=\int_{x=-a}^{x=2 a} F d x=\int_{x=-a}^{x=2 a} \frac{b}{2} d x\)

= \(\frac{b}{2} \int_{x=-a}^{x-2 a} d x=\frac{b}{2}[x]_{x=-a}^{x=2 a}=\frac{b}{2}[2 a+a]=\frac{3 a b}{2}\)

Question 9. From a height of 20 in above a horizontal floor, a ball is thrown down with an initial velocity of 20 m/s. After striking the floor, the ball bounces to the same height from which it was thrown. Find the coefficient of restitution for the collision between the ball and the floor. (g = 10 m/s²)
Solution:

Initial velocity = u¹ = 20 m/s, h = 20 m, g = 10 m/s²

Velocity of approach, \(u^2=u^{1^2}=u^{1^2}+2 a s=400+2 \times 10 \times 20\)

⇒ \(u^2=400+400=800 \Rightarrow u=20 \sqrt{2}\)

Height of rebounce = h = 20 m.

∴ Velocity of separation \(v=\sqrt{2 g h}=\sqrt{2 \times 10 \times 20}=\sqrt{400}=20\)

Coefficient of restitution, \(\mathrm{e}=\frac{\text { Velocity of separation }}{\text { Velocity of approach }}=\frac{20}{20 \sqrt{2}}=\frac{1}{\sqrt{2}}\)

Work, Energy, And Power Questions And Answers KSEEB Physics 

Question 10. A ball falls from a height of 10 m onto a hard horizontal floor and repeatedly bounces. If the coefficient of restitution is \(\frac{1}{\sqrt{2}}\), then what is the total distance travelled by the ball before it ceases to rebound?
Solution:

Height from which the ball is allowed to fall, h = 10 m

Coefficient of restitution between the hard horizontal floor and the ball, e = \(\frac{1}{\sqrt{2}}\)

∴ Total distance travelled by the ball before it ceases to rebound, \(\mathrm{d}=\mathrm{h}\left[\frac{1+\mathrm{e}^2}{1-\mathrm{e}^2}\right]=10\left[\frac{1+(1 / \sqrt{2})^2}{1-(1 / \sqrt{2})^2}\right]=30 \mathrm{r}\)

Question 11. In a ballistics demonstration, a police officer fires a bullet of mass 50g with a speed of 200 ms^-1 on soft plywood of thickness 2 cm. The bullet emerges with only 10% of its initial kinetic energy. What is the emergent speed of the bullet?
Answer:

Mass of bullet m = 50g = 0.05 kg

Initial Velocity V₀ = 200 m/s

Initial K.E. = \(\frac{1}{2} \mathrm{mv}_0{ }^2=\frac{1}{2} \times \frac{50}{1000} \times 200 \times 200\)

Final K.E. = 10% of \(1000 \mathrm{~J}=100 \mathrm{~J}\)

But K.E. = \(\frac{1}{2} \mathrm{mv}_1{ }^2 \Rightarrow \mathrm{v}_1=\sqrt{\frac{2 \mathrm{KE}}{\mathrm{m}}}\)

∴ \(\mathrm{v}_1=\sqrt{\frac{2 \times 100}{0.05}}=\sqrt{4000}=20 \sqrt{10}=63.2 \mathrm{~m} / \mathrm{s}\)

Question 12. Find the total energy of a body of 5 kg mass, which is at a height of 10 m from the earth and falling downwards straightly with a velocity of 20 m/s. (Take the acceleration due to gravity as 10 m/s²)
Answer:

Mass m = 5 kg;

Height h = 10 m; g = 10 m/s²

Velocity v = 20 m/s.

Total energy = PE + KE = mgh + \(\frac{1}{2}\) mv²

= \((5 \times 10 \times 10)+\frac{1}{\not 2} \times 5 \times 20^{10} \times 20\)

= \(500+1000=1500 \mathrm{~J}\)