KSEEB Solutions For Class 9 Maths Chapter 9 Areas of Parallelogram and Triangles Points to Remember
Figure on the same base & between the same parallels
- Two figures are said to be on the same base & between the same parallels, if they have a common base & the vertices (or the vertex) opposite to the common base of each figure lie on a line ||le to the base.
- Parallelograms on the same base & between the same parallels are equal in area.
- The area of a ||gm is the product of its side which is known as the base & the corresponding altitude.
- ||gm on the same base (or equal bases) & having equal areas lie between the same parallels.
Area of triangles
- Two triangles on the same base (or equal base) & between the same parallels are equal in area.
- The area of Δle is half the product of its base (or any side) & the corresponding altitude (or height).
- Two triangles with the same base (or equal bases) and equal areas will have equal corresponding altitudes.
- Two triangles having the same base (or equal bases) & equal areas lie between the same parallels.
- A median of a Δle divides it into triangles of equal areas.
| Class 9 Social Science | Class 9 Science | Class 9 Maths |
Read and Learn More KSEEB Solutions for Class 9 Maths

Areas of Parallelogram and Triangles EXERCISES 9.1
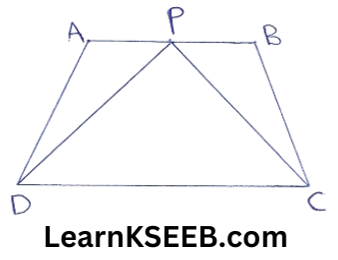
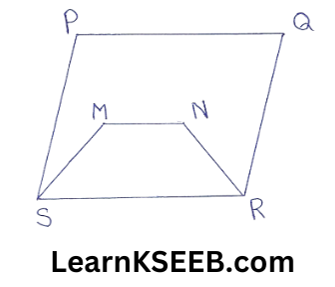
1. Which of the following figures lie on the same base & between the same parallels? In such a case, write the common base & the two ||les.
1)
2)
KSEEB Class 9 Maths Chapter 9 Solutions PDF
3)
4)
5)
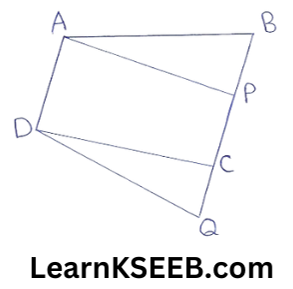
6)
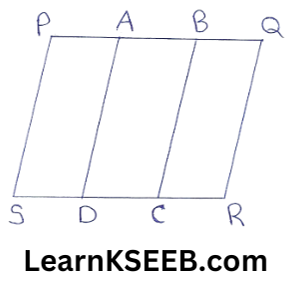
Solution:
(1) ΔPDC & Quadrilateral ABCD lie on the same base DC & between the same ||les DC & AB.
(3) ΔTRQ & ||gm SRQP lie on the same base RQ & between the same ||les RQ & SP.
(5) Quadrilateral APCD & ABQD lie on the same base HD & between the same ||les AD & BQ.
Karnataka 9th Standard Maths Chapter 9 Notes
Areas of Parallelogram and Triangles Exercise 9.2
1. In figure, ABCD is a ||gm, AE ⊥ DC & CF ⊥ AD. If AB = 16cm, AE = 8cm & CF = 10cm, find AD.
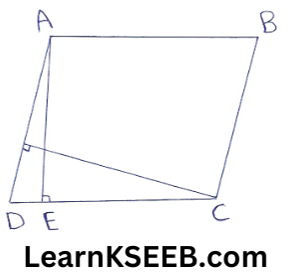
Solution: ar of ||gm ABCD = AB x AE
= 16 x \(8 \mathrm{~cm}^2\)
= \(128 \mathrm{~cm}^2\) …………….(1)
ar of ||gm ABCD = AD x CF
= AD x \(10 \mathrm{~cm}^2\) ………………(2)
from (1) & (2), we get
AD x 10=128
=> AD = 128/10
=> AD = 12.8cm
2. If E, F, G & H are respectively the mid-points of the sides of a ||gm ABCD, show that ar (EFGH) = 1/2 ar (ABCD).
Solution:
Given: E, F, G & H are respectively the mid-points of the sides of a ||gm ABCD.
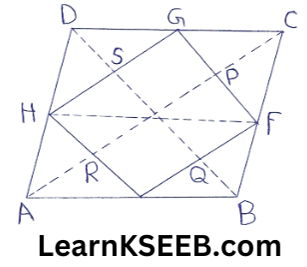
To prove: ar(EFGH) = 1/2ar(ABCD)
Contraction: Join OF, OG, OH & OE. Also, join AC & BD.
Proof: In Δ BCD.
F & G are the mid-points of BC & DC respectively FG || BD ……………..(1)
(In a ΔIe, the line segment joining the mid-points of any two sides is ||le to the third side)
In ΔBAD
E & H are the mid-points of AB & AD respectively.
EH || BD ………………(2)
(In a Δle, the line segment joining the mid-points of any two sides is ||le to the third side) from(1) &(2)
EH || FG ……………….(3)
||ly we can prove that
EF || HG ……………….(4)
from (3) & (4)
Quadrilateral EFGH is a ||gm (a quadrilateral is a ||gm if its opposite sides are equal)
∴ F is the mid-point of CD & O is the mid-point of CA.
∴ FO||BA (In a Δle, the line segment joining the mid-points of any two sides joining the mid-points of any two sides is ||le to the third side & is half of it)
=> FO || CG ………………..(5)
(∵ BA || CD)
∴ BA || CG
& FO = 1/2BA = 1/2CD
(opp. sides of a ||gm are equal)
= CG ………………(6)
(∵ G is the mid-point of CD)
In view of (5) & (6)
Quadrilateral OFCG is a ||gm ( ∵ A quadrilateral is a ||gm if a pair of opposite sides are ||le & are of equal length)
∴ OP = PC (Diagonals of a ||gm bisect each other)
∴ ΔOPF & ΔCPF have equal bases.
(∵ OP = PC) & have a common vertex P.
Their altitudes are also the same.
∴ ar(ΔOPF) = ar(ΔCPF)
||ly ar(ΔOQF) = ar(ΔBQF)
adding we get
ar(ΔOPF) +ar(ΔOQF) = ar(ΔCPF)+ (ΔBQF)
=> ar(||gm OQPF) = ar(ΔCPF)
+ ar(ΔBQF) …………….(7)
||ly ar( ||gm OPGS) = ar(ΔGPC)
+ar(ΔDSG) ………………(8)
ar(||gm OSHR) = ar(ΔDSH)
+ar(ΔHAR) ……………….(9)
ar(||gm OREQ) = ar(ΔARE)
+ ar(ΔEQB) ………………..(10)
adding (7), (8), (9) & (10) we get
ar(||gm EFGH) {(ar(ΔCPF) +ar(ΔGPC)}
+ {ar(ΔDSG) + ar(ΔDSH)}
+ {ar(ΔHAR) + ar(ΔARE)}
+ {ar(ΔBQF) + ar(ΔEQB)}
= ar(ΔFCG) + ar(ΔGDH) + ar(ΔHAE) + ar(AEBF)
= 1/2ar(||gm ABCD)
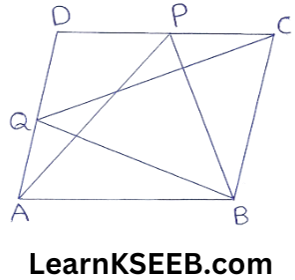
3. P & Q are any two points lying on the sides DC & AD respectively of a ||gm ABCD. Show that ar(ΔAPB) = ar(ΔBQC)
Solution:
Given: P & Q are any two points lying on the sides DC & AD respectively of a ||gm ABCD.
To prove: ar(ΔAPB) =ar(ΔBQC)
Proof: ΔAPB & ||gm ABCD are on the same base AB & between the same ||gm AB & DC.
∴ ar(ΔAPB) = 1/2ar(||gm ABCD) …………………(1)
ΔBQC & ||gm ABCD are on the same base BC & between the same ||le BC & AD.
∴ ar(ΔBQC) = 1/2ar(||gm ABCD) ………………….(2)
from(1) & (2)
∴ ar(ΔAPB) = ar(ΔBQC)
4. In the figure, P is the point in the interior of a ||gm ABCD. Show that.
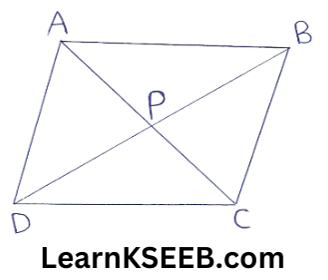
1) ar(ΔAPB) +ar(ΔPCD) = 1/2 ar(||gm ABCD)
2) ar(ΔAPD) + ar(ΔPBC)
= ar(ΔAPB) +ar(ΔPCD)
(Hint: Through P, draw a line ||le to AB)
Solution:
Given: P is a point in the interior of a ||gm ABCD
To Prove: (1) ar(ΔAPB) + ar(ΔPCD)= 1/2 ar (||gm ABCD)
(2)ar(ΔAPD) +ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD).
Construction: Throughout P, draw a line EF ||le to AB.

Proof: (1) EF || AB ……………….(1) (by Construction)
∴ AD || BC (opp sides of a ||gm are ||le)
∴ AE || BF ………………(2)
from (1) & (2)
Quadrilateral ABFE is a ||gm
(A quadrilateral is a |p if its opp sides are ||le)
||ly, quadrilateral CDEF is a ||gm
ΔAPB & ||gm ABFE is on the same base AB & between the same ||les AB & EF.
(∴ ar(ΔAPB) = 1/2 ar(||gm ABFE) …………………..(3)
ΔPCD& ||gm CDEF
KSEEB Class 9 Maths Areas of Parallelogram and Triangles Solutions
5. In the figure, PQRS & ABRS are ||gms & X is any point on side BR. Show that
1) ar(||gm PQRS) = ar(||gm ABRS)
2) ar(ΔAXS) =1/2 ar(||gm PQRS)
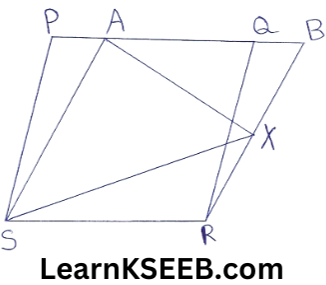
Solution: (1) In ΔPSA& ΔQRB
\(\lfloor\mathrm{SPA}\) = \(\lfloor\mathrm{RQB}\) ………………..(1)
(Corresponding angles from PS || QR & transversal PS)
\(\lfloor\mathrm{PAS}\) = \(\lfloor\mathrm{QBR}\) ………………….( 2)
(Corresponding angles from AS || BR& transversal PB)
∴ \(\lfloor\mathrm{PSA}\) = \(\lfloor\mathrm{QRB}\) …………………(3)
(Angle sum property of a Δle)
Also, PS = QR …………………(4)
(Opposite sides of ||gm PQRS)
In view of (1), (3)&(4)
ΔPSA ≅ ΔQRB …………………(5)
(by ASA rule)
∴ ar(ΔPSA) ≅ ar(ΔQRB) ……………….(6)
(Congruent figures have equal areas)
Now, ar(||gm PQRS) = ar(ΔPSA) + ar(||gm AQRS)
= ar(ΔQRB) +ar(||gm AQRS) (using (6))
= ar(||gm ABRS)
2) ΔAXS & ||gm ABRS are on the same base AS & between the same ||gm AS & BR.
∴ ar(ΔAXS) = 1/2(||gm ABRS)
=1/2 {ar(||gm AQRS) +ar(ΔQRB)}
= 1/2{ar(||gm AQRS) +ar(ΔPSA)} (using (6))
= 1/2ar(||gm PQRS)
6. A farmer was having a field in the form of a ||gm PQRS. She took any point A on RS & joined it to points P & Q. In how many parts the fields are divided? What are the shapes of these parts? The farmer wants to sow wheat & pulses in equal portions of the field separately. How should she do it?
Solution: ΔAPQ, ΔAPS & ΔAQR lie between the same parallels.
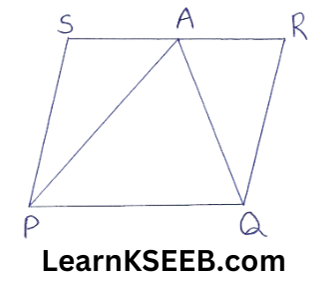
∴ Their altitudes are same
Let it be x, then
ar(ΔAPQ) = \(\frac{(\mathrm{PQ})(x)}{2}\) …………………..(1)
ar(ΔAPS) +ar(ΔAQR)
= \(\frac{(\mathrm{AS})(x)}{2}+\frac{(\mathrm{AR})(x)}{2}\)
= \(\frac{(\mathrm{AS}+\mathrm{AR}) x}{2}\)
= \(\frac{\mathrm{SR} \times \mathrm{x}}{2}\)
= \(\frac{(\mathrm{PQ})(\mathrm{x})}{2}\)
(∵ SR = PQ, opp sides of ||gm are equal)
∴ Either the farmer shouted sow wheat in ΔAPQ & pulses in the other two Δles APS & AQR (or) pulses in ΔAPQ & wheat in the other two Δles APS & AQR.
Areas of Parallelogram and Triangles Exercise 9.3
1. In figure, E is any point on median AD of a ΔABC • Show that ar(ΔABE) = ar (ΔACE).
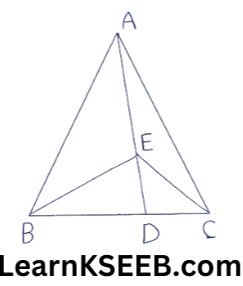
Solution: In ΔABC AD is a median

ar(ΔABD) = ar(ΔACD) ………………….(1)
(∵ A median of a Δle divides it into two Δles of equal areas)
In ΔEBC
ED is a median.
ar(ΔEBD) =ar(ΔECD) ……………….(2)
( ∵ A median of a Δle divides it into two A/es of equal areas)
Subtracting (2) from(1), we get
ar(ΔABD)= ar(ΔEBD) = ar(ΔACD)
= ar(ΔECD)
=> ar(ΔABE) = ar(ΔACE)
2. In a Δle ABC, E is the mid-point of median AD, show that ar(ΔBED) = 1/4 ar(ΔABC)
Solution: In ΔABC , AD is a median

ar(ΔABD) = ar(ΔACD)
= 1/2ar(ΔABC) ……………….(1)
(A median of a Δle divides it into two A/es of equal areas)
In ΔABD,
BE is a median.
∴ ar(ΔBED) = ar(ΔBEA)
= 1/2 ar(AABD)
(A median of a Δle divides it into two Δlesof equal areas)
=> ar(ΔBED) = 1/2 ar(ΔABD)
= 1/2 x 1/2 x ar(ΔABC) from(1)
= 1/2 ar(ΔABC)
3. Show that the diagonals of a ||gm divides it into four Δles of equal area.
Solution:

Given: ABCD is a ||gm whose diagonals AC & BD intersecting at O.
Divide it into four Δles of ΔOAB, ΔOBC, ΔOCD& ΔODA.
To prove: ar(ΔOAB) = ar(ΔOBC)
= ar(ΔOCD) = ar(ΔODA)
Construction: Draw BE ⊥ AC
Proof: ABCD is a ||gm
∴ OA=OC & OB = OD (Diagonals of a ||gm bisect each other)
Now, as (ΔOAB)
\(=\frac{\text { Base } \times \text { Corresponding altitude }}{2}\) \(=\frac{(\mathrm{OA})(\mathrm{BE})}{2}\)& ar(ΔOBC)\(=\frac{\mathrm{B} \times \mathrm{h}}{2}\)
\(=\frac{(\mathrm{OC})(\mathrm{BE})}{2}\)But OA = OC
∴ ar(AOAB) = ar(ΔOBC) …………………(1)
||ly ar(ΔOBC) = ar(ΔOCD) ………………….(2)
&ar(ΔOCD) = ar(ΔODA) …………………(3)
from (1), (2) & (3) we get
ar(ΔOAB) =ar(ΔOBC) =ar(ΔOCD)
= ar(ΔODA)
KSEEB 9th Standard Maths Chapter 9 Important Questions
4. In figure, ABC & ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O. Show that ar(ΔABC) = ar(ΔABD).
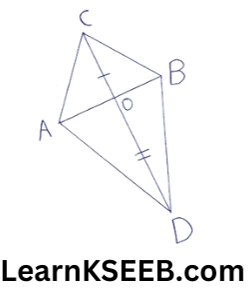
Solution: Line Segment CD is bisected by AB at O.

∴ OC = OD
∴ BO is a median of ABCD & AO is a median of ΔACD
∴ ar(ΔOBC) = ar(ΔOBD) …………………(1)
(A median of a Δle divides it into two Δles of equal areas)
AO is a median of ΔACD
ar(ΔOAC) = ar(ΔOAD) ……………….(2)
(A median of a Δle divides it into two Δles of equal areas)
adding (1) & (2), we get
ar(ΔOBC) +ar(ΔOAC) = ar(ΔOBD)
= ar(ΔOAD)
=>ar(ΔABC) = ar(ΔABD)
5. D, E & F are respectively the mid-points of the sides BC, CA & AB of a ΔABC, show that.
(1)BDEF is a ||gm
(2)ar(ΔDEF) \(=\frac{1}{4}\)ar(ΔABC)
(3)ar(||gm BDEF) \(=\frac{1}{2}\)ar(ΔABC)
Solution:
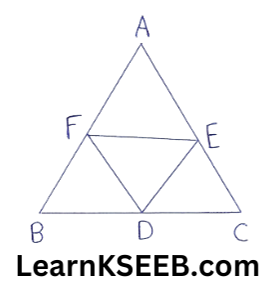
(1) In ΔABC
F is the mid-point of side AB & E is the mid-point of side AC.
EF || BC
(∵ In a Δle, the line segment joining the mid-points of any two sides is ||le to the third sides)
=> EF || BD …………….(1)
||ly, ED || BF ……………….(2)
In view of (1) & (2)
||gm BDEF is a ||gm
(A quadrilateral is a ||gm if it opposite sides are ||le)
(2) As in (1), we can prove that.
AFDE & FDCE are ||gm
FD is a diagonal of 1||gm BDEF
ar(ΔFBD) =ar(ΔDEF) ……………….(3)
||ly ar(ΔDEF) =ar(ΔFAE) ………………(4)
ar(ΔDEF) = ar(ΔDCE) …………………(5)
from (3), (4) & (5), we have
ar(ΔFBD) = ar(ΔDEF) = ar(ΔFAE)
= ar(ΔDCE) …………………(6)
(ΔABC is divided into four non-overlapping Δles ΔFBD, ΔDEF , ΔFAE, & ΔDCE)
∴ ar(ΔABC) = ar(ΔFBD) +ar(ΔDEF)
+ ar(AFAE) + ar(ADCE)
= 4 ar(ADEF) (from (6))
=> ar(ΔDEF) = 1/4ar(AABC) …………………..(7)
(3) ar(BDEF) = ar(ΔFBD) + ar(ΔDEF)
= ar(ΔDEF) +ar(ΔDEF) from(3)
= 2 ar(ΔDEF)
= 2 x 1/4ar(ΔABC) (from (7))
= 1/2ar(ΔABC)
6. In figure diagonal AC & BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that
1) ar(ΔDOC) = ar(ΔAOB)
2) ar(ΔDCB) =ar(ΔACB)
3) DA || CB (or) ABCD is a ||gm
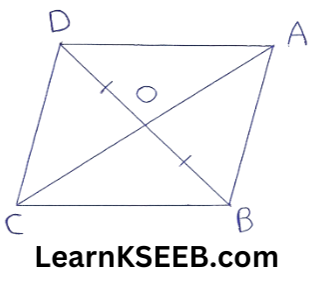
(Hint: from D&B, draw ⊥lar to AC)
Solution:
Given: Diagonals AC & BD of a quadrilateral ABCD intersect at O such that OB = OD
To Prove: If AB = CD,
1) ar(ΔDOC) =ar(ΔAOB)
2) ar(ΔDCB) =ar(ΔACB)
3) DA || CB (or) ABCD is a ||gm
Construction: Draw DE ⊥ AC & BF ⊥ AC
Proof: 3) In ΔADB
AO is median
ar(ΔAOD) = ar(ΔAOB) ………………..(1)
(A median of a Δle divides it into two Δles of equal areas)
In ΔCBD
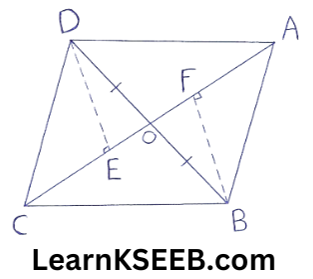
CO is a median
∴ ar(ΔCOD) =ar(ΔCOB) ………………(2)
(A median of a Δle divides it into two Δles of equal areas)
adding (1) & (2) we get
ar(ΔAOD) +ar(ΔCOD) = ar(ΔAOB) + ar(ΔCOB)
=> ar(ΔACD) =ar(ΔACB)
=> \(\frac{(\mathrm{AC})(\mathrm{DE})}{2}\) = \(\frac{(\mathrm{AC})(\mathrm{BF})}{2}\)
(∵ Area of Δle= 1/2 x b x h)
=> DE = BF ………………..(3)
In right ΔleDEC & BFA
Hyp. DC = Hyp. BA (given)
DE = BF (from (3))
∴ ΔDEC = ΔBFA (RHS rule)
∴ \(\lfloor\mathrm{DCE}\) = \(\lfloor\mathrm{BAF}\) (C.P.C.T)
But these angles form a pair of equal alternate interior angles.
∴ DC || AB ………………….(4)
∴ DC = AB & DC || AB
∴ ABCD is a ||gm
(or) DA || CB
(opp. sides of a ||gm are ||le)
1) ABCD is a ||gm
OC = OA (Diagonals of ||gm bisect each other)
(ΔDOC) \(=\frac{\mathrm{OC} \times \mathrm{DE}}{2}\)
(ΔAOB) \(=\frac{\mathrm{OA} \times \mathrm{BF}}{2}\)
DE = BF & OC = OA (from (3) & (5))
ar(ΔDOC) = ar(ΔAOB)
=> ar(ΔDOC) +ar(ΔAOB) = ar(ΔAOB) + ar(ΔOCB)
(Adding equal areas on both sides)
=> ar(ΔDCB) = ar(ΔACB)
Class 9 Maths KSEEB Chapter 9 Areas of Parallelogram And Triangles Examples
Karnataka Board Class 9 Maths Chapter 9 MCQs
7. D & E are points on sides AB & AC respectively of ΔABC such that as (ΔDBC) =as (ΔEBC) Prove thatDE || BC
Solution:
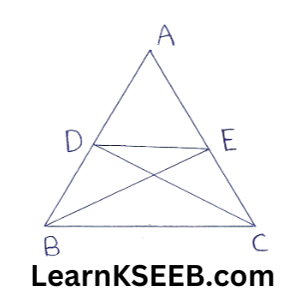
ΔDBC & ΔEBC are on the same base BC & have equal areas.
∴ Their altitudes must be the same.
∴ DE || BC
8. XY is a line ||le to side BC of a Δle ABC. If BE || AC and CF || AB meet XY at E and F respectively. Show that ar(ΔABE)=ar(ΔACF).
Solution:
XY || BC (given)
and CF || BX(∵ CF || AB(given))
∴ BCFX is a ||gm.
(a quadrilateral is a ||gm if its opposite sides are ||le)
∴ BC = XF (opp sides of a ||gm are equal)
=>BC=XY+YF ……………..(1)
again XY || BC (given)
and BE || CY(∵ BE || AC)
∴ BCYE is a ||gm
(A quadrilateral is a ||gm if its opposite sides are ||le)
∴ BC=YE (opp. sides of a ||gm are equal)
=> BC = XY + XE ……………….(2)
from (1) and (2)
XY + YF = XY + XE
=> YF = XE
XE = YF ……………….(3)
∵ ΔAEX and ΔAFY have equal bases
(∵ XE=YF) on the same line EF and have a common vertex A.
∴ Their altitudes are also the same.
∴ ar(ΔAEX) = ar(ΔAFY) ……………….(4)
ΔBEX and ΔCFY have equal bases (XE=YF) on the same line EF and are between the same ||les EF and BC (∵ XY || BC)
∴ ar(ΔBEX) = ar(ΔCFY) ………………..(5)
(Two Δles on the same base (equal base and between the same parallels are equal in area) Adding the corresponding sides of (4) and (5) we get ar(ΔAEX)+ar(ΔBEX) = ar(ΔAFY)+ar(ΔCFY)
∴ ar(ΔABE)=ar(ΔACF)
9. The side AB of a ||gm ABCD is produced to any point P. A line through A and ||le to CP meets CB produced at Q and then ||gm PBQR is completed. Show that ar(||gm,ABCD) = ar(||gm PBQR).
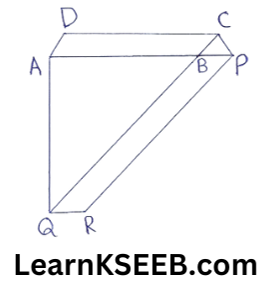
Solution:
Given: The side AB of a ||gm ABCD is produced to any point P. A line through A and ||le to CP meets CB produced at Q and then ||gm PBQR is completed.
To prove: ar(||gm ABCD)=ar(||gm PBQR)
Construction: Join AC and PQ Proof: AC is a diagonal of ||gm ABCD
∴ ar(ΔABC) = 1/2 ar(||gm ABCD) ……………..(1)
PQ is a diagonal of ||gm BQRP
∴ ar(ΔBPQ) = 1/2ar(||gm BQRP) ……………….(2)
(ΔACQ and ΔAPQ are on the same base AQ and between the same parallels AQ and CP)
ar(ΔACQ) = ar(ΔAPQ)
(Two Δles on the same base and between the same ||les are equal in areas)
ar(ΔACQ) – ar(ΔABQ) = ar (ΔAPQ) – ar (ΔABQ)
(Subtracting the same areas from both sides)
=> ar(ΔABC) = ar(ΔBPQ)
1/2ar(||gm ABCD) =1/2ar(||gm PBQR) (from(1) and (2))
=> ar(||gm ABCD) = ar(||gm PBQR)
10. Diagonals AC and BD of a trapezium ABCD with AB||DC intersect each other at O. Prove that ar(ΔAOD) = ar(ΔBOC) .
Solution:
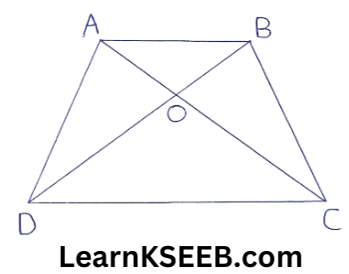
ΔABD and ΔABC are on the same base AB and between the same ||les AB and DC.
∴ ar(ΔABD) = ar(ΔABC)
(Two Δles on the same base (equal bases) and between the same parallels are equal in area)
=> ar(ΔABD) – ar(ΔAOB) = ar(ΔABC) – ar(ΔAOB) (Subtracting the same areas from both sides)
=> ar(ΔAOD) = ar(ΔBOC)
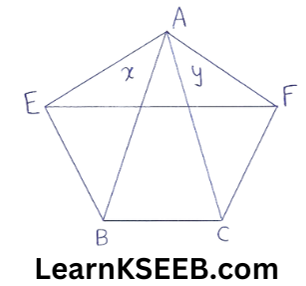
11. In figure, ABCDE is a pentagon. A line through g BE || AC meets DC produced at F. Show that
1. ar(ΔACB) = ar(ΔACF)
2. ar(AEDF) = ar(ABCDE)
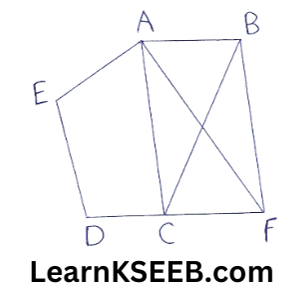
Solution:
Given: ABODE is a pentagon, A line through B parallel to AC meets DC produced at F.
To prove: 1. ar(ΔACB) = ar(ΔACF)
2. ar( AEDF)=ar(ABODE)
Proof: 1. ΔACB and ΔACF are on the same base AC and between the same ||les AC and BF.
[ ∵ AC || BF (given)]
∴ ar(ΔACB) = ar(ΔACF)
(Two Δles on the same base (or equal bases) and between the same parallels are equal in area) 2. From 1
ar(ΔACB) = ar(ΔACF)
=> ar (ΔACB) + ar ( AEDC) = ar(ΔACF) + ar( AEDC)
(adding the same area on both sides)
=> ar(ABCDE) = ar( AEDF)
=>ar( AEDF) = ar(ABCDE)
12. A villager Itwaari has a plot land of in the shape of a quadrilateral. The Gram panchayat of the village decided to take over a portion of his plot from one of the corners to construct the Health Centre. Itwaari agrees to the above proposal with the condition that he should be given an equal amount of land in lieu of the land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Solution: Let ABCD be the plot, of the land in the shape of a quadrilateral. Let the portion ADE be taken over by the Gram panchayat of the village from one corner D to construct a Health Centre.
Join AC. Draw a line through D ||le to AC to meet BC produced in P. Then Itwaari must be given the land ECP adjoining his plot so as to form a triangular plot ABP as then
ar(ΔADE) = ar(ΔPEC)
Proof: ADAP and ADCP are on the same base DP & between the same parallels DP and AC.
∴ ar(DAP) = ar(ΔDEP)
(Two Δles on the same base and between the same ||les are equal in area)
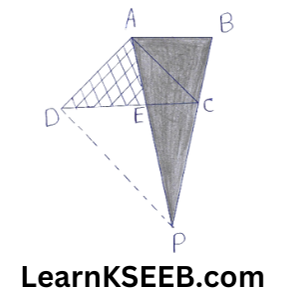
=> ar(DAP) – ar(ΔDCP) = ar(DCP) – ar(ΔDEP) (Subtracting the same areas from both sides)
=> ar(ADE) = ar(ΔPCE)
=> ar(ΔDAE)+ar( ABCE) = ar(ΔPCE) + ar( ABCE)
(adding the same areas to both sides)
=> ar( ABCD) = ar(ΔABP)
KSEEB Chapter 9 Areas of Parallelogram and Triangles Solved Questions
13. ABCD is a trapezium with AB || DC. A line ||le to AC intersects AB at X and BC at Y. Prove that ar (ΔADX) = ar ΔACY
Solution:
Given : ABCD is a trapezium, AB || DC A line parallel to AC intersects AB at x & BC at y.
To prove: ar(ΔADX) = ar(ΔACY)
Construction: Join CX
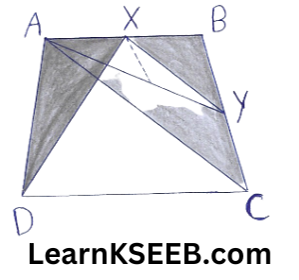
Proof: ΔADX and ΔACX are on the same base AX and between the same ||les AB and DC.
∴ar(ΔADX) = ar(ΔACX) …………………..(1)
ΔACX and ΔACY are on the same base AC and between the same parallels AC and XY.
∴ ar(ΔACX) = ar(ΔACY) ……………….(2)
(Two Δle on the same base (or) equal bases and between the same ||les are equal in area)
From (1) and (2), we get
ar(ΔADX) = ar(ΔACY)
14. In fig. AP|jBQ||CR. Prove that ar(ΔAQC) = ar(ΔPBR)
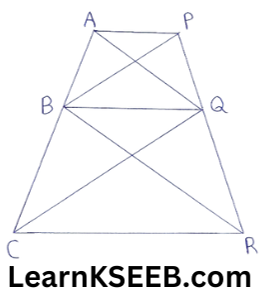
Solution:
Given: AP || BQ || CR
Proof: ABAQ and ABPQ are on the same base BQ and between the same parallels BQ and AP.
∴ ar(ΔBAQ) = ar(ΔBPQ) …………………(1)
ΔBCQ and ΔBQR are on the same base BQ and between the same ||les BQ and CR.
∴ ar(ΔBCQ) = ar(ΔBQR) …………………(2)
(Two triangles on the same base (or) equal bases and between the same parallels are equal in the area)
Adding the corresponding sides of(1) and (2)
ar(ΔBAQ)+ar(ΔBCQ) = ar(ΔBPQ)+ar(ΔBQR)
=> ar(ΔAQC)=ar(ΔPBR)
15. Diagonals AC and BD of a quadrilateral ABCD Intersect at O in such a way that ar(ΔAOD) = ar(ΔBOC). Prove that ABCD is a trapezium.
Solution:
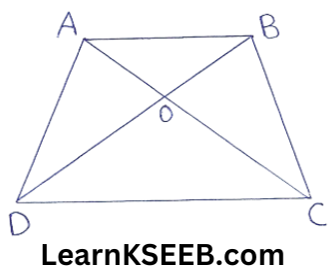
ar(ΔAOD) = ar(ΔBOC) (given)
ar(ΔAOD) = ar(ΔBOC) (given)
=> ar(ΔAOD)+ar(ΔAOB) = ar(ΔBOC) + ar(ΔAOB)
(Adding the same areas on both sides)
=> ar(ΔABD)=ar(ΔABC)
But ΔABD and ΔABC are on the same base AB
∴ ΔABD and ΔABC will have equal and corresponding altitudes.
∴ ΔABD and ΔABC will lie between the same parallels.
∴ AB || DC
∴ ABCD is a trapezium.
16. In fig, ar(ΔDRC) = ar(ΔDPC) and ar(ΔBDP) =ar(ΔARC). Show that both the quadrilaterals ABCD and DC PR are trapezium.
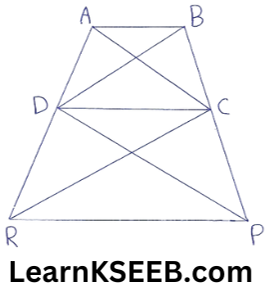
Soution:
Given: ar(ΔDRC) = ar(ΔDPC) and
ar(ΔBDP) = ar(ΔARC)
To prove: Both the quadrilaterals ABCD and DCPR are trapezium.
Proof: ar(ΔDRC) = ar(ΔDPC) ………………..(1)
But ΔDRC and ΔDPC are on the same base DC.
∴ ΔDRC and ΔDPC will have equal corresponding altitudes.
∴ ΔDRC and ΔDPC will lie between the same parallels.
∴ DC || RP
∴ DCPR is a trapezium
(A quadrilateral is a trapezium if exactly one pair of opp sides are ||le)
Again ar(ΔBDP) = ar(ΔARC)
=> ar(ΔBDC)+ar(ΔDPC)=ar(ΔADC) +ar(ΔDRC)
=> ar(ΔBDC)=ar(ΔADC) (using (1))
But ΔBDC and ΔADC are on the same base DC.
∴ ΔBDC and ΔADC will have equal corresponding altitudes.
ΔBDC and ΔADC will lie between the same lies
∴ AB || DC
∴ ABCD is a trapezium
(A quadrilateral is a trapezium if exactly one pair of opposite sides are ||le)
Choose the correct answer from the following.
1. In the following figure, ABCD Is a ||gm DE ⊥ AB and BF ⊥ AD. If AB=12cm, DE=6cm, and AD=8cm. Find BF.
- 8cm
- 6cm
- 12cm
- 9cm
Solution: 4. 9cm
2. In ΔABC, E is the mid-point of median AD. Then the ratio of areas of ΔBED to area of ΔABC is
- 1:2
- 2:1
- 4:1
- 1:4
Solution: 4. 1:4
3. In ΔABC, D,E, and F are the mid-points of BC, CA, and AB respectively. If ar(AABC)=56cm². Then ar(AEDF) is
- 21cm²
- 28cm²
- 16cm²
- 14cm²
Solution: 2. 28cm²
4. In the fig, BE=2EC and ar(ΔABC)=60cm², then ar(ΔAEC) is
- 15cm²
- 20cm²
- 30cm²
- 40cm²
Solution: 2. 20cm²
5. In the fig, the area of ||gm PQRS is
- PQ x QB
- QR x QC
- SR x QC
- PS x SA
Solution: 3. SR x QC
6. The mid-points of the sides of a Δle ABC along with any of the vertices as the fourth point make a ||gm of area equal to
- ar(ΔABC)
- 1/2ar(ΔABC)
- 1/3ar(ΔABC)
- 1/4ar(ΔABC)
Solution: 2. 1/2ar(ΔABC)
7. ABCD is a trapezium w ith parallel sides AB = a & DC = b. If E & F are mid-points of non-parallel sides AD & BC respectively then the ratio of areas of quadrilaterals ABFE & EFCD is
- a:b
- (a + 3b) : (3a + b)
- (3a+b):(a + 3b)
- (2a + b) : (3a + b)
Solution: 3. (3a+b):(a+3b)
Class 9 Maths Areas of Parallelogram and Triangles KSEEB Guide
8. ABCD is a rectangle with O as any point in its interior. If ar (AOD) = 3cm² & ar(ABOC) = 6cm², there area of rectangle ABCD is
- 9cm²
- 12cm²
- 15cm²
- 18cm²
Solution: 4. 18cm²
9. If AD is median of ΔABC & Pis a point on AC such that ar(ΔADP) : ar(ΔABD) = 2:3 then ar(ΔPDC) : ar(ΔABC) is
- 1:5
- 5 :1
- l:6
- 3:5
Solution: 3. 1:6
10. Diagonal AC & BD of trapezium ABCD in which AB || DC, intersect each other at O. The triangle which is equal in area of ΔAOD is
- ΔAOB
- ΔBOC
- ΔDOC
- ΔADC
Solution: 2. ΔBOC
One Mark Questions
1. If a Δle & a ||gm are on same base & between same ||les, then the ratio of the area of the Δle to the area of a ||gm is
Solution: 1:2
2. In the figure, PQ || RS, ABCD is a ||gm & AEB is a Δle. Area of the ||gm ABCD is twice the area of
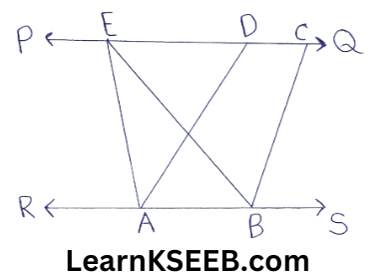
Solution: ar(ΔAEB) = 1/2 ar(||gm ABCD)
=> ar(||gm ABCD) = 2ar(ΔAEB)
Hence area of ||gm ABCD is twice area of ΔAEB
3. In ΔABC, E is the mid-point of median AD, then the ratio of area of ΔBED to the area ΔABC is
Solution: The required ratio is 1:4
4. In the fig, BE-2E C & ar (ΔABC) = 60cm² then find ar(ΔAEC).
Solution:
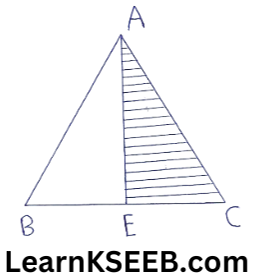
BE = 2EC
\(\Rightarrow \frac{\mathrm{BE}}{\mathrm{EC}}=2\)& ar(ΔABC) = 60cm²
∴ ar(ΔAEC) = 20cm²
5. In the fig, ||gm ABCD & ΔBCP are on the same base BC & between the same ||les. If as (ΔBCP) = 15cm2, Then ar(ΔBCD) is
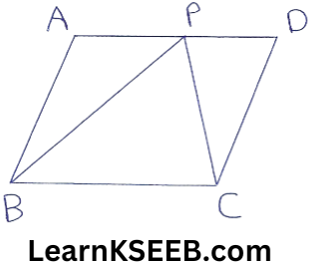
Solution:
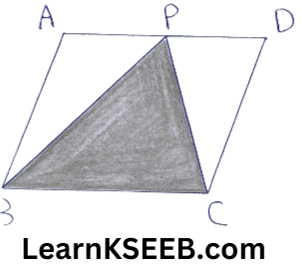
ar(ΔBCP) = 15cm²
∴ ar(ΔBCD) = ar(ΔBCP)
= 2 x 15
= 30cm²
Two Mark Questions
1. In ||gm ABCD, AB = 10cm, The altitudes corresponding to the sides AB & AD are respectively 7cm & 8cm, find AD.
Solution:
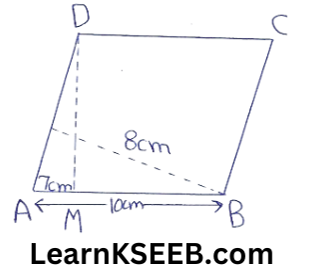
Area of a ||gm = Base x height
ar(||gm ABCD) = AB x DM
= 10 x 7
= 70cm²
also as (||gm ABCD) = AD x BN
70= AD x 8
=> AD = 70/8
= 8.75cm
2. ABCD is aquadrialteral. A line through D, ||le to AC meets BC produced in P as shown in fig. Prove that ar(ΔABP) = ar(quadrilateral ABCD).
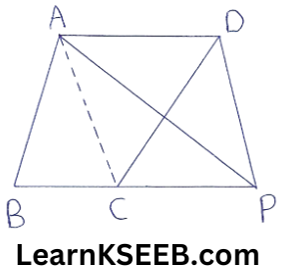
Solution: Since ΔACP & ΔACD are on the base AC & between the same ||les AC & DP.

∴ ar(ΔACP) = ar(ΔACD)
=> ar(ΔACP) + ar(ΔABC)
= ar(ΔACD) + ar(ΔABC)
(adding equal areas both sides)
=> ar(ΔABP) = ar(quadrilateral ABCD)
3. BD is one of the diagonals of a quadrilateral ABCD. AM & CN are perpendiculars from A & C respectively on BD. Show that ar(quadrilateralABCD) = 1/2 BDx(AM+CN)
Solution: We have
ar(quad ABCD) = ar(ΔABD) + ar(ΔBCD)
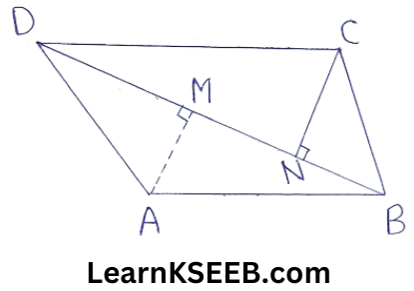
=> ar(quadrilateral ABCD) = 1/2 (BD x AM)
+ 1/2(BD x CN)
=> ar(quadrilateral ABCD)= 1/2BD x (AM + CN)
4. In figure, it is given that AD || BC, prove that ar(ΔCGD) = ar(ΔABG).
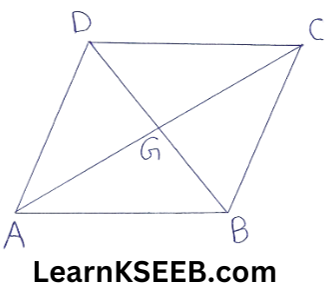
Solution: Since ΔADC & ΔADB are on the same base AD & between the same parallels AD & BC.
ar(ΔADC) =ar(AADB)
=> ar(ΔADC) = ar(ΔADG) = ar(ΔADB) = ar(ΔADG)
=> ar(ΔCGD) = ar(ΔABG)
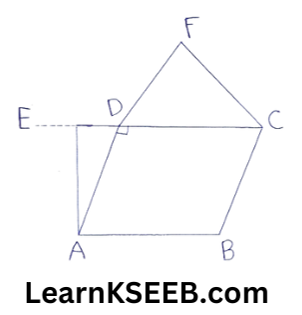
5. ABCD is a ||gm, AE ⊥ DC & CF ⊥ AD. If AB = 16cm, AE= 8cm, CF = 10cm, find AD.
Solution: Area of parallelogram
= AD x CF
= CD x AE
= AD x 10
=> AD x 10 = 16 x 8 (∵ CD = AB)
= > AD \(=\frac{16 \times 8}{10}\)
=> AD= 12.8cm
6. ABCD is a ||gm with area 80 sq.cm The diagonals AC & BD intersect at O. Pis the midpoint of OA. calculate ar (ΔBOP).
Solution: Area of ||gm is divided into four equal parts by the diagonals.
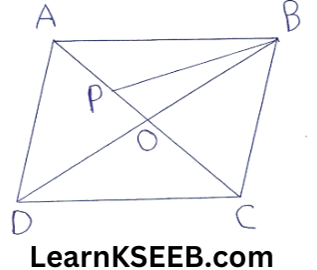
ar(ΔBOP) \(=\frac{1}{4}\) ar(ABCD)
ar(ΔBOP) \(\frac{1}{2}\) ar(AOB) = \(\frac{1}{8}\) ar(ABCD)
\(=\frac{1}{8} \times 80\)= 10cm²
7. In given fig. ABCD is a ||gm, BE ⊥ AD. If BE = 14cm & AD = 8cm, find the area of ΔDBC.
Solution: BE = 14cm, AD = 8 cm.
∴ Area of (ΔABD)
=1/2 x 8 x 14
= 56cm²
( ∵ ABCD is a ||gm)
∴ ar(ΔDBC) = ar(ΔADB) = 56cm².
8. In the given fig, T is the mid-point of PS. Find ar(QTR).
Solution: Median QT & RT divide
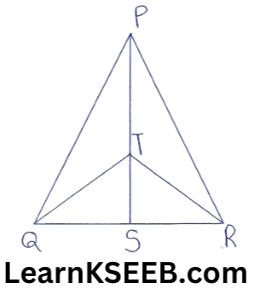
ΔPQS & ΔPRS in two Δles of equal areas.
ar(QTS) = 1/2ar(PQS)
ar(RTS) = 1/2ar(RPS)
ar(QTS + RTS) = 1/2 [ar(PQS) + ar(PRS)]
∴ ar(QTR)=1/2ar(PQR)
9. ΔABC & ΔABD are two Δles on the same base AB. If the line segment CD is bisected by AB at O. Show that ar(ABC) = ar(ABD).
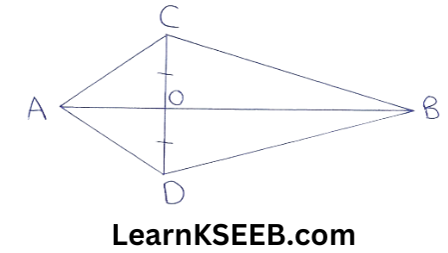
Solution: Since CD is bisected at O.
=> CO = OD
In ΔADC, AO is the median
∴ ar(ΔAOC) = ar(ΔAOD) ………………(1)
In ΔCDB, BO is the median
ar(ΔBOC) = ar(ΔBOD) ……………….(2)
adding (1) & (2) we get
as (AOC) + as (BOC) = as (AOD) + as (BOD)
ar(ABC) = ar(ABD)
10. Show that a median divides a Δle into two Δles of equal areas.
Solution: AD is a median & AE ⊥ BC
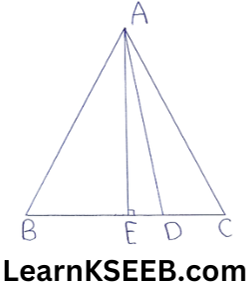
Area of ΔABD = 1/2 x BD x AE
Area of ΔADC = 1/2 x DC x AE
but BD = DC ( ∵ AD is a mediam)
∴ Area of (ΔABD) = area of (ΔADC)
Three Mark Questions
1. Prove that the area of an equilateral Δle is equal to \(\frac{\sqrt{3} a^2}{4}\), where a is the side of the Δle.
Solution:
Given: ABC is an equilateral Δle such that AB = BC = CA = a.
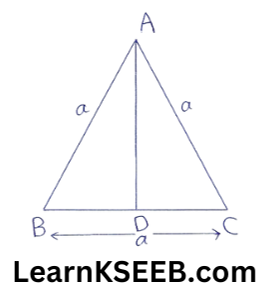
To Prove: ar(ΔABC) = \(\frac{\sqrt{3} a^2}{4}\).
Construction: Draw AD ⊥ BC.
Proof: In ΔABD & ΔACD, we have
AB = AC (∵ ΔABC is equilateral)
lADB = 1 ADC = 90°
& AD = AD (Common)
∴ ΔABD ≅ ΔACD (by RHS rule)
=> BD = DC (CPCT)
but BD + DC = a
BD = DC = a/2
Now, in right ΔABD, we have
AB² =AD²+BD² (using pythagoras theorem)
=> a² = AD² + \(\left(\frac{a}{2}\right)^2\)
=> AD² =\(a^2-\frac{a^2}{4}\)
AD² = \(\frac{3 a^2}{4}\)
AD = \(\frac{\sqrt{3 a}}{2}\)
∴ (ΔABC) = \(=\frac{1}{2}(\mathrm{BC} \times \mathrm{AD})\)
= \(\frac{1}{2}\left(\frac{a \times \sqrt{3} a}{2}\right)\)
= \(\frac{\sqrt{3} a^2}{4}[latex]
KSEEB Class 9 Maths Chapter 9 Exercise Solutions
2. The medians of ΔABC intersect at G Prove that ar(ΔAGB) =ar(ΔAGC) =ar(ΔBGC) = 1/3ar(ΔABC)
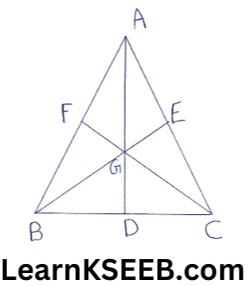
Solution:
AD is the median of ΔABC
∴ ar(ΔABD) =ar(ΔACD) …………………(1)
In ΔGBC, GD is the median
∴ ar(GBD) = ar(GCD) ……………….(2)
subtracting (1)&(2), we get
ar( ABD) – ar(GBD) = ar(ACD) – ar(GCD)
=> ar(AGB) = ar(AGC) ………………(3)
||ly we can prove that
∴ ar(AGB)=ar(BGC) …………………(4)
from (3) (4), we get
ar (AGB)=ar(BGC) = ar(AGC) …………………(5)
Now, ar(ΔABC) = ar(AGB) + ar(BGC) + ar(AGC).
= ar(AGB)+ar( AGB) + ar(AGB)
= 3ar(AGB)
Hence ar (AGB) = 1/3 ar (ΔABC)
Hence ar(ΔAGB) = ar (ΔAGC) = ar (ΔBGC)
= 1/3 ar(ABC)
3. In ΔGHK, D, E & F are the mid-point of sides HK, KG & GH respectively. Show that EFHK is trapezium & ar(EFHK)= 3/4 ar(AGHK).
Solution: In ΔGHK, F & E are the mid-points of HG & GK respectively.
∴ By mid-point theorem
FE=-1/2KH & FE || KH …………………(1)
In quadrilateral EFHK, EF || HK(by (1))
∴ EFHK is a trapezium
also, ar (EFHK) = ar(FHD) + ar (DEF) + ar(DEK) ………………..(2)
we have, FE || HD &FE = HD.
∴ FEDH is a ||gm
so, ar(FHD) = ar(DEF) …………………(3)
||ly, DFGE, is a ||gm
ar(DEF) = ar(GEF) ………………..(4)
also, DEFK is a ||gm
ar(DEF) = ar(DEK) ………………..(5)
using (3), (4) & (5) we get.
ar(GEF) = ar(FHD) = ar(DEK) = ar(DEF)
= 1/4as (GHK) ………………(6)
using (6) & (2) we get
ar(EFHK) = 3/4 ar(GHK)
4. Two brothers have a triangular plot. They decided to distribute it equally amongst themselves but also want to give away a triangular part of it for charity to a school which is attached on the base side of 12cm of the triangular plot.
(1) What is the area of the triangualar plot if its height is 90m?
(2) Explain with the help of figure how could this be possible & what type of parts do the brothers get.
Solution: (1) Area of triangular plot
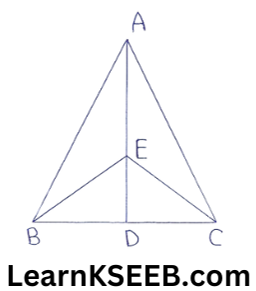
= 1/2 x b x h
= 1/2 x 120 x 90
= 5400cm²
2) In ΔABC they draw medium Ad on base BC & divide it into two equal areas ABD & ACD.
Take any point E on AD & join BE & CE.
The brothers get areas
ar(ΔABE) & ar(ΔACE)
ar(ΔBCE) is donated to school.
5. In the given figure, ABC & DBC are triangles on the same base & between the ||le lines l & m, If AB = 3cm, BC = 5cm and [A = 90° find the area of ΔDBC.
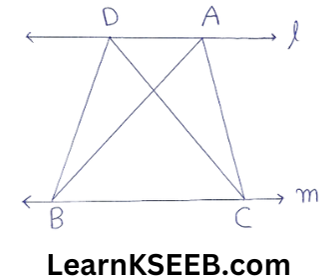
Solution: In ΔABC, AC =[latex]\begin{equation}
\sqrt{\mathrm{BC}^2-\mathrm{AB}^2}\end{equation}\)
= \(\sqrt{5^2-3^2}\)
= \(\sqrt{25-9}\)
=\(\sqrt{16}\)
AC= 4cm
ar(ΔABC) = 1/2xABxAC
= 1/2 x 3 x 4 = 6cm²
ar(ΔDBC) = ar(ΔABC) =6cm² (Δles on the same base & between the same ||ls)
