Karnataka Class 9 Maths Model Question Papers 2023 Set 5

Class 9 Maths Karnataka Model Papers Set 5 With Solutions

Choose the correct alternative and Write the complete answer along with its alphabet in the sheet provided:

Question 1. Recurring decimal 0.68686868……is also represented as

1. \(0. \overline{6}\)
2. \(\overline{0.68}\)
3. \(\overline{0.68}\)
4. \(0.6 \overline{8}\)

Solution: 3.  \(\overline{0.68}\)

Question 2. An example of a rational number is

1. 4.795831
2. 0.3796
3. 1.1012001…..
4. 0.6868…..

Solution: 2. 0.3796

Karnataka 9th Standard Maths Model Paper 2023 Set 5 Free PDF with Answer Key

Question 3. The expansion form of(a + b)² is

1. a²+2ab +b²
2. a²-2ab + b²
3. a² – 2ab – b²
4. a² +ab + b²

Solution: 1. a²+2ab +b²

Question 5. If a ray stands on a line, then the sum of two adjacent angles is

1. 60°
2. 180°
3. 360°
4. 90°

Solution: 2. 180°

Question 5. In the fig, APAB is congruent to

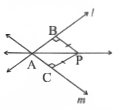
1. △PAC
2. ∠PAC
3. ∠PAB
4. △PAB

Solution: 1. △PAC

Question 6.Write any two solutions for x + 4y = 0

Solution:

x + 4y = 0

4 y = -x

y = -x/4

when x = 0, y = 0 (0, 0)

∴ Two solutions are when x=l, y = -1/4 (0, -1/4 ) (0,0)(0, -1/4)

Question 7. In the fig, AB AC then

1. OB =___________
2. AO bisects_________

Solution:

1. OB = OC
2. AO bisects ∠A

Question 8. Write any two properties of a rhombus.
Solution:

1. The sides of a rhombus are equal.
2. The diagonals bisect each other at right angles.

Answer the following:

Question 1. Represent \(\sqrt{5}\) on the number line.
Solution:

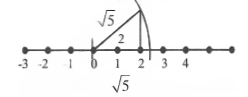
Question 2.Express \(0.4 \overline{7}\) in the form of p/q where p and q interfere and q ≠ 0

Solution:

Let x = 0.477……………..

10x = 4.7777……………

⇒10x = 4.3 + 0.4777….

⇒10x = 4.3 + x

⇒ l0x-x = 4.3

⇒ 9x = 4.3

⇒x = 4.3/9 = 43/90

Thus, \(0.4 \overline{7}=\frac{43}{90}\)

Question 3.use the factor theorem to determine whether g(x) = x +1 is a factor of p(x) = 2x³+x²– 2x -1

Solution:

If g(x) =x + 1 is a factor of the given polynomial p(x), then p(-1) must be zero.

P(x) = 2x³+x²+(-1)²– 2 (-1) -1

P(-1) = 0

Hence g(x) =x+ 1 is a factor of the given polynomial.

Class 9 Karnataka Maths Model Paper 2023 Set 5 Solved Questions PDF

Question 4. Evaluate 95 x 96 using the suitable identity.

Solution:

95 x 96 = (100 – 5) (100 -4)

(x+ a) (x + b) = x² + (a + b)x + ab

=(100)²+ { (-5) + (-4) } 100 + (-5) (-4)

= 10000 – 900 + 20

= 9120

Question 5. Take any three consecutive even numbers and find their product: for example, 2 x 41 6 = 48,4x6x8 = 192 and so on. Make two conjectures about these products.
Solution:

Three possible conjectures are:

1. The product of any three consecutive even nos. is even.
2. The product of any three consecutive even numbers is divisible by 4.

Question 6. Restate the following statements with appropriate conditions, so that they become true statements.

1. All prime numbers are odd.
2. Two times a real number is always even.
3. For any x, 3x +1 > 4
4. For any x, x³≥0

Solution:

1. All prime numbers greater than 2 are odd.
2. Two times a natural number is always even.
3. For any x > 1, 3x + 1 > 4
4. For any x > 0, x³ > 0

Question 7. ABCD is a cyclic quadrilateral whose diagonals intersect at point E. If ∠DBC = 70°, ∠BAC = 30° find ∠BCD.

Solution:

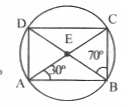
∠BAC = ∠BDC

[∵ angles in the same D. segment]

∴∠BAC = ∠BDC =30°

In ABCD,

∠BDC +∠DBC +∠BCD = 180°

30° +70° + ∠BCD = 180°

∠BCD = 180° – 100°

∴∠BCD =80°

Question 8. Diagonals AC and BD of an A trapezium ABCD with AB || DC intersect each other at O. Prove that ar (△AOD) = ar (△BOC)

Solution: △DAC and △DBC lie on the same base DC and between the same parallels AB and CD.

∴ Area ( △DAC) = Area (△DBC )

Area (△DAC) – Area (△DOC) = Area (△DBC)-ar△DOC

∴ Area (△AOD)= Area (△BOC)

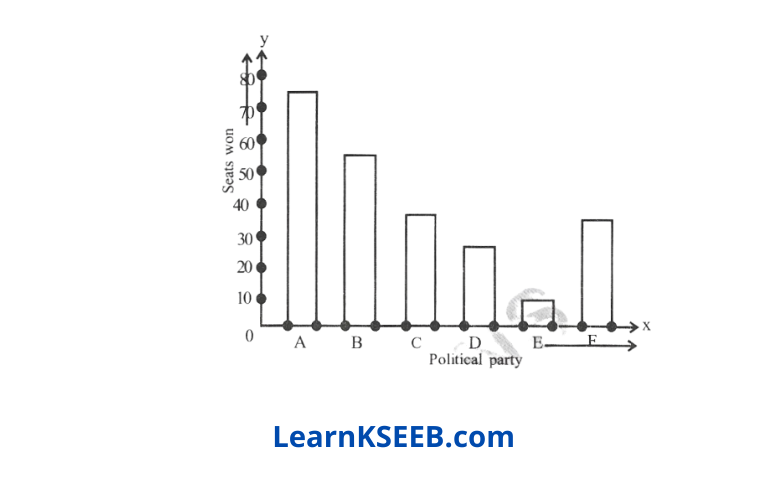
Question 9. Represent the following data with a bar graph
Political party Seats won.

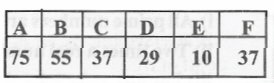
Solution:

Question 10. A river 3m deep and 40m wide is flowing at the rate of 2km per hour. How much water will fall into the sea in a minute?

Solution:

The breadth of the river = 40m

Depth of the river = 3 m

flowing speed of the river per hour = 2km

or length per minute of the river = 2000/60 m

∴ water flowing per minute

\(=\frac{2000}{6 \emptyset} \times{ }^2-4 \emptyset \times \not^1\)

=4000m³

Question 11. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively. S.T. these altitudes are equal.

Solution:

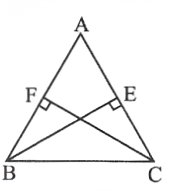
In △AEB and △AFC

∠AEB =∠AFC (each 90°)

∠A = ∠A (common)

AB = AC (given)

∴ △AEB = △AFC (AAA congruence rule)

∴ BE = CF(CPCT)

Karnataka Board 9th Maths Model Paper 2023 Set 5 Latest Exam Pattern

Question 12. Give a possible expression for the length and breadth of the rectangle whose area is 25a²-35a+ 12

Solution:

Area of the rectangle = length x breadth

25a² – -35a + 12 *= length x breadth

25a² -15a – 20a +12 = length x breadth

5a(5a – 3) – 4(5a – 3) = length x breadth

(5a – 3) (5a – 4) = length x breadth

∴ length = (5a – 3)

breadth = (5a – 4)

Solved Karnataka Class 9 Maths Papers Set 5 

Question 13. Find the area of a triangle two sides of which are 18cm and 10cm and the perimeter is 42cm.

Solution:

Let a, b and c be the sides of the triangle.

∴ a = 18cm, b = 10cm and c = x

∴a + b + c=18+ 10+ x

42 — 28 + x

x = 42 – 28

x = 14cm

S = perimeter/2

S = 42/2

S = 21cm

Area of a triangle = \( \sqrt{s(s-a)(s-b)(s-c)}\)

\(=\sqrt{21(21-18)(21-10)(21-14)}\) \(\begin{aligned}
& =\sqrt{21 \times 3 \times 11 \times 7} \\
& =\sqrt{21 \times 21 \times 11} \\
& =\sqrt{(21)^2 \times 11} \\
& =21 \sqrt{11} \mathrm{~cm}^2
\end{aligned}\)

Question 14.Write four solutions for 2x + y = 7

Solution:

2x + y – 7

⇒ y = 7-2x

when x = 0,    2 (0) + y = 7

0 + y = 7

y =7

x = 1,    2(1) + y = 7

2 + y = 7

y = 7-2

y=5

x = 2,  2(2)+y =7

6 + y = 7

y = 7- 6

y= 1

x = 3, 2 (3) + y = 7

6 + y = 7

y = 7 – 6

y=1

∴ four solutions are (0, 7) (1, 5) (2,3) (3,1)

Question 15. In the fig, if AB || DE, ∠BAC = 35° and ∠CDE-53°, find ∠DCE.

Solution:

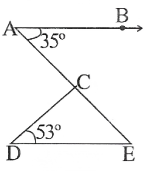
In the fig AB || DE

BAC = 35° and CDE = 530

∴ ∠BAE = ∠DEC (altemater angles)

∴ ∠DEC = 35°

In ADCE,

∠DCE + ∠CDE + ∠DEC = 180°

∠DCE + 53° +35° = 180°

∠DCE =180°—88°

∠DCE = 92°

Question 16. ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F. S.T. F is the midpoint of BC.

Solution:

Let EF intersect BD and G

In △ABD,

E is the midpoint of

AD and EF || AB.

∴ G is the midpoint of BD

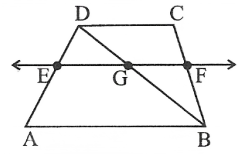
[∵ converse of the midpoint of theorem]

DC || AB and EF || AB

DC || EF

In △BDC

GF || DC and G is the midpoint of BD

∴ ‘F’ is the midpoint of BC [By converse of midpoint theorem]

Question 17. If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.

Solution:
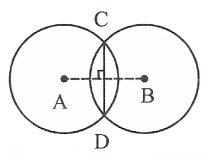Two circles with centres A and B intersect at C and D to join CD.

CD is the chord to a circle with centre ‘A’.

∴ The perpendicular bisector drawn from the centre ‘O’ of a chord passes through the centre ‘B’ of the circle. Similarly, Cd is also the chord to the circle with centre B.

∴ The perpendicular bisector drawn from the centre ‘O’ of the chord passes the centre B of the circle.

∴ centres of the circles lie on the perpendicular bisector of the common chord.

9th Standard Karnataka Maths Sample Paper 2023 Set 5 Important Questions

Question 18. △ABC and △DBG are two isosceles triangles on the same base BC. S.T.
∠ABD = ∠ACD A

Solution: In △ABC , AB = AC (given)

∴ ∠ABC = ∠ACB.-(1)

[Angles opp. to equal sides are equal]

 

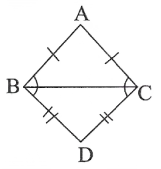
In ADBC,

DB = DC (given)

∴ ∠DBC = ∠DCB……..(2) [Angles opposite to equal sides are equal]

By adding (1) and (2)

∠ABC + ∠DBC = ∠ACB + ∠DCB

∴ ∠ABD = ∠ACD

Answer the following:

Question 1. In △ABC and △DEF, AB = DE, AB || DE,
BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively S. T.

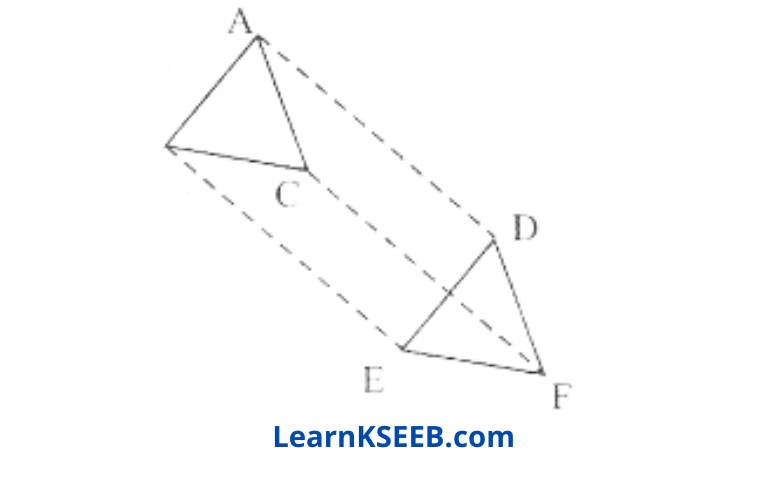
1. Quadrilateral ABED is a parallelogram B
2. Quadrilateral BEFC A is a parallelogram
3. AD || CF and AD = CF

Solution:

1. AB = DE [Given]
   AB || DE [Given]
   If two opposite sides of a quadrilateral are equal and parallel to each other. Then it will be a parallelogram
   ∴ Quadrilateral ABED is a parallelogram.
2. Again BC = EF and BC || EF
   ∴ Quadrilateral BCEF is a parallelogram.
3. As we know that ABED and BEFC are parallelograms
   ∴ AD = BE and AD || BE
   and BE = CF and BE || CF
   ∴ AD = CF and AD || CF

Question 2. XY is a line parallel to the side BC of a triangle ABC. If BE || AC and CF 11 AB meet XY at E and F respectively, S.T. ar(ABE) = ar (ACE)

Solution:

XY || BC(given)

and CF||BX  (∵ CF || AB(given))

∴ BCFX is a ||^gm

(a quadrilateral is a ||^gm if its opposite sides are ||le) A

∴ BC=XF (opposite sides of ||^gmare equal)

⇒ BC-XY+YF……….. (1)

again XY || BC (given)

and BE || CY(∵ BE || AC)

∴ BCYE is a ||^gm

(A quadrilateral is a ||^gm if its opposite sides are ||^gm)

∴ BC=YE (opp. sides of a ||^gm are equal)

⇒ BC=XY+XE…………… (2)

from (1) and (2)

XY+YF = XY+XE

⇒ YF = XE

XE = YF

∴ △AEX and △AFY have equal bases

(∵ XE=YF) on the same line, EF and have a common vertex A.

∴ Their altitudes are also the same.

∴ ar(△AEX)=ar(△AFY)…………. (4)

△BEX and △CFY have equal bases (XE=YF) on the same line, EF and are between the same ||les

EF and BC (∵ XY||BC)

ar(△BEX)=ar(△CFY)………….(5)

Two Triangles on the same base (equal and between the same parallels are equal in the area)

Adding the corresponding sides of(4) and (5) we get

ar(△EX)+ar(△BEX) = ar(△AFY)+ar(△CFY)

∴ ar(△ABE)=ar(△ACF)

Question 3. In a city, the weekly observations made in a study on the cost of a living index are given in the following table.

 

Draw a frequency polygon for the above data. 

Solution:

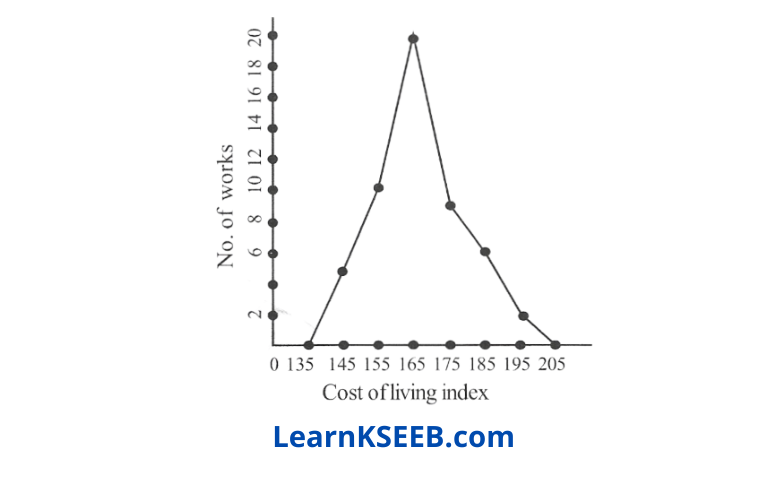
Karnataka Board 9th Class Maths Model Question Paper 2023 Set 5 with Answer Key

Question 4. Construct a triangle PQR in which QR =6cm, ∠Q = 60° and PR – PQ = 2cm.

Solution:

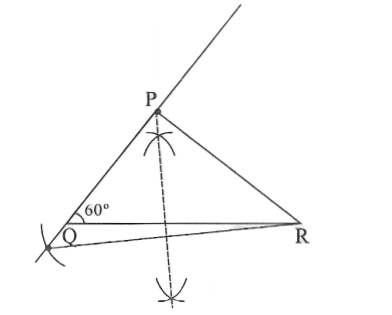
Question 5. S.T. a median of a triangle divides it into two triangles of equal areas.

Solution: Let ABC be a triangle and AD be one of its medians

ar (△ABD) = 1/2 x base x altitude

=1/2 x BD x AN

= 1/2  x CD x AN (BD = CD)

= 1/2 x base x altitude(of △ACD)

ar(△ABD) = ar(△ACD)

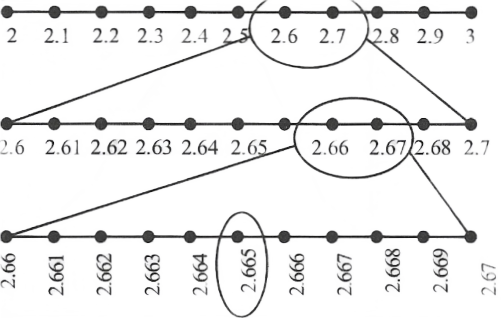
Question 6.Represent 2.665 on the number line

Solution:

Answer the following:

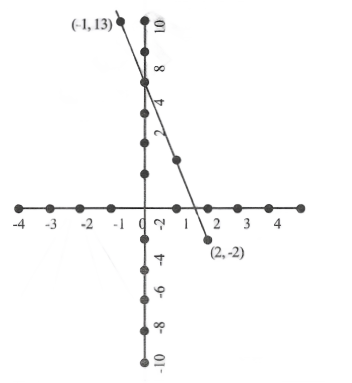
Question 1. Draw the graph 5x + y = 8

Solution:

Scale: x-axis ; 1cm = limit y-axis ; 1cm= 1unit

Karnataka 9th Maths Sample Paper 2023 Set 5 for Board Exam Preparation

Question 2. Two parallel lines % and m are intersected by a transversal P. Show that the quadrilateral formed by the bisectors of interior angles is a rectangle

Solution: PS || QR and transversal p intersect them at points A and C respectively.

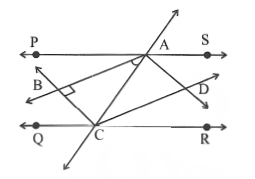
The bisectors of ∠PAC and ∠ACQ intersect at B and bisectors of ∠ACR and ∠SAC intersect at D.

Now, ∠PAC = ∠ACR

∴ 1/2 ∠PAC = 1/2 ∠ACR

∠BAC = ∠ACD

Alternate angles

∴ AB || DC

Similarly, BC || AD

∴ quadrilateral ABCD is a parallelogram

∠PAC + ∠CAS = 180° (linear pair)

1/2 ∠PAC +1/2 ∠CAS = 1/2 x180°

∠BAC + ∠CAD = 90°

∠BAD = 90°

So, ABCD is a parallelogram in which one angle is 90°

∴ ABCD is a rectangle.

Question 3. There is a slide in the park. One of its side walls has been painted in some colour with a message “keep the park green and clean”. If the sides of the wall are 15m, 11m and 6 m, find the area painted in colour.

Solution: The side is in the form of a triangle.

Let the sides be a = 15m, b= 11m, c = 6m

∴ \(\mathrm{S}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}\)

\(\mathrm{S}=\frac{15+11+6}{2}\) \(S=\frac{32}{2}\)

S = 16m

Area of the triangular area =

\(\sqrt{s(s-a)(s-b)(s-c)}\) \(\begin{aligned}
& =\sqrt{16(16-15)(16-11)(16-6)} \\
& =\sqrt{16 \times 1 \times 5 \times 10} \\
& =20 \sqrt{2} \mathrm{~m}^2
\end{aligned}\)

Karnataka State Board Class 9 Maths Model Paper 2023 Set 5 with Step-by-Step Solutions

Question 4. Find the capacity in litres of a conical vessel with

1. Radius 7cm, slant height 25cm
2. Height 12cm, slant height 13cm.

Solution:

1. Radius 7cm (r) slant height 25cm(l)

\(\mathrm{h}=\sqrt{\ell^2-\mathrm{r}^2}=\sqrt{25^2=7^2}=24 \mathrm{~cm}\)The volume of the conical vessel = \(\frac{1}{3} \pi r^2 h\)

\(=\frac{1}{\not \beta} \times \frac{22}{\not x} \times 7 \times 7 \times 24^8\)

= 1232cm3

∴ The capacity of the vessel in litres = 1232/1000

= 1.232 litres

2. h= 12cm, l = 13cm

∴ \(\mathrm{r}=\sqrt{\ell^2-\mathrm{h}^2}\)

\(\begin{aligned}
& r=\sqrt{13^2-12^2} \\
& r=\sqrt{169-144} \\
& r=\sqrt{25} \\
& r=5 \mathrm{~cm}
\end{aligned}\)

volume of the conical vessel =\(\frac{1}{3} \pi r^2 h\)

\(=\frac{1}{\not p} \times \frac{22}{7} \times 5 \times 5 \times 12^4\) \(=\frac{22 \times 25 \times 4}{7}\)

=2200/7

= 314.28cm3

∴The capacity of the vessel in litres =314.285/1000

= 0.314281itres