Karnataka Class 9 Maths Model Question Papers 2023 Set 4

Karnataka Class 9 Maths Model Question Papers Set 4

Choose the correct alternative and Write the complete answer along with its alphabet in the sheet provided:

Question 1. Which of the following is an irrational number

1. \(\sqrt{5}\)
2. \(\sqrt{4}\)
3. 9
4. \(\sqrt{16}\)

Solution: 1. \(\sqrt{5}\)

Question 2.The zero of the polynomial p(x)= x + 6 is

1. 0
2. 6
3. -6
4. 7

Solution: 3. – 6

Karnataka 9th Standard Maths Model Question Paper 2023 Set 4 Free PDF

Question 3. Which of the following are the coordinates of the point lying on the x-axis is

1. (0, 3)
2. (5,0)
3. (-3, -1)
4. (0,2)

Solution: 2. (5, 0)

Question 4. If the diagonals of a quadrilateral bisect each other, then it is a

1. Parallelogram
2. Trapezium
3. Rectangle
4. Square

Solution: 1. Parallelologram

Question 5. The angle in a semicircle is

1. An acute angle
2. An obtuse angle
3. Right angle
4. A reflect angle.

Solution: 3. A right angle

Question 6. The total surface area of a cone is

1. πr (l- r)
2. 2πr(r + h)
3. 3πr²
4. l x b x h

Solution: 1. πr (l- r)

Class 9 Karnataka Maths Model Question Paper 2023 Set 4 with Answer Key

Question 7. In the adjoining fig. the value of ‘x’ is

1. 30°
2. 60°
3. 90°
4. 40°

Solution: 1. 30°

Question 8. If n is an even number, median = mean of the values of the and \(\left(\frac{n}{2}\right)^{t h}\) and

1. \(\left(\frac{n}{2}+3\right)^{t h}\)
2. \(\left(\frac{n+1}{2}\right)^{t h}\)
3. \(\left(\frac{n}{2}+1\right)^{t h}\)
4. \(\left(\frac{n}{2+n}\right)^{t h}\)

Solution: 3. \(\left(\frac{n}{2}+1\right)^{t h}\)

Question 9. x³+y³=(x + y)

1. (x²+ 2xy +y³)
2. (x²+2xy +y²)
3. (x²+)
4. (x²+xy +y²)

Solution: 4. (x²+xy +y²)

Question 10. Only one pair of opposing sides of a quadrilateral are parallel, then it is a

1. Square
2. Rhombus
3. Trapezium
4. Rectangle

Solution: 3. Trapezium

Answer the following :

Question 1.Express x+5y = 0.7 in the form of ax + by + c = 0

Solution: x +5y – 0.7 =0

Question 2. Find the value of \(32^{\frac{1}{5}}\)

Solution: \(32^{\frac{1}{5}}=\left(2^5\right)^{\frac{1}{5}}\)

\(2^{8 \times \frac{1}{8}}=2\)

Question 3. If \(\frac{1}{7}=0 . \overline{142857}\) then find the value of 5/7

Solution: 5/7 \(=0. \overline{714285}\)

Question 4. Find the remainder when p(x) = x³ — 4x²+ x+ 6 is divided by g (x) =x- 3

Solution:

p(x) = x³ -4x² +x+6

p (3) =3³-4(3)²+ 3 + 6

= 27-36 + 3 + 6

p(3) = 0

∴The remainder is ‘ 0 ’

Question 5.Find two solutions for πx + y = 9

Solution: πx+y = 9

x = 0, π(0) + y = 9  (0,9)

y = 9 (0,9)

x = 1, π(1) + y = 9

π + y = 9

y = 9 – π (1,9-π )

∴The two solutions are (0, 9) (1,9 –π)

Karnataka Board 9th Class Maths Model Paper 2023 Set 4 Latest Pattern

Question 6. Define perpendicular lines.

Solution: If two lines intersect each other at 90° then these are called perpendicular lines.

Question 7. In the fig, ∠1+∠2 is

Solution: ∠1 +∠2 <180°

Question 8. State whether the following statements are always true, always false, or ambiguous.

1. The temperature in Bangalore is 30°C
2. The earth has one moon.

Solution:

1. Ambiguous
2. Always true

Question 9. Name any two Quadrilaterals from fig.

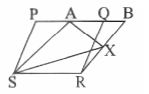
Solution: PQRS and SRBA are two quadrilaterals

Question 10. In the given figure, if AB = PQ and PQ = XY then AB =

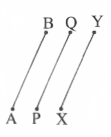
Solution: XY

Answer the following:

Question 1. Express \(0. \overline{6}\) the form of, where p and q are integers and q ≠ 0

Solution:

\(0. \overline{6}\) – 0-666………..

Let x = 0.6666………

10x = 6.666………

10x = 6 + 0.6666…….

⇒ 10x = 6 + x

⇒ lOx – x= 6

⇒ 9x = 6/9

⇒ x = 2/3

Question 2. Simplify: \((3+\sqrt{3})(2+\sqrt{2})\)

Solution:

\((3+\sqrt{3})(2+\sqrt{2})\) \(\begin{aligned}
& =3(2+\sqrt{2})+\sqrt{3}(2+\sqrt{2}) \\
& =6+3 \sqrt{2}+2 \sqrt{3}+\sqrt{6}
\end{aligned}\)

Question 3. Find the remainder when x³+3x²+3x + 1 divided by \(x-\frac{1}{2}\)

Solution:

Let p (x) = x³+3x²+3x + 1    g (x) = \(x-\frac{1}{2}\)

\(\mathrm{p}\left(\frac{1}{2}\right)=\left(\frac{1}{2}\right)^3+3\left(\frac{1}{2}\right)^2+3\left(\frac{1}{2}\right)+1\) \(\mathrm{p}\left(\frac{1}{2}\right)=\frac{1}{8}+\frac{3}{4}+\frac{3}{2}+1\) \(x=\frac{1}{2}\) \(\mathrm{p}\left(\frac{1}{2}\right)=\frac{27}{8}\)

Question 4. Evaluate(99)³ using the suitable identity.

Solution:

(100-1)³

(a-b)³=a³-b³-3a²b + 3ab²

(100-1)³ -(100)³-(1)³3(100)²x 1 +3 x 100 x (1)²

(100-1)³ = 100000 – 1 – 30000 + 300

(100-1)³  = 970299

Question 5. Find the value of k, if x – 1 is a factor of p(x) = 2x²+ kx + \(\sqrt{2}\)

Solution:

If x -1 is a factor of p(x), then p(1) = 0

⇒2(1)²+ k(1) + \(\sqrt{2}\) = 0

⇒ 2 + k + \(\sqrt{2}\) = 0

⇒ k = – 2 – \(\sqrt{2}\)

∴k = – 2 – \(\sqrt{2}\)

Question 6. Express -2x + 3y = 6 in the form of ax + by + c = 0 and indicate the values of a, b and c.

Solution:

a – 2x + 3y = 6

– 2x + 3y-6 = 0

ax + by – c = 0

∴a = -2,b = 3.c = -6

Question 7. In the figure, lines XY and MN intersect at ‘o’. If
∠poy = 90° and a : b = 2 : 3  find c

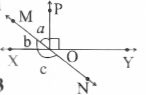
Solution:

Let the common ratio between a and b be ‘x’

∴ xy is a straight line and rays OM and OP stand on it.

∠XQM + ∠MOP + ∠POY = 180°

⇒b + a + ∠POY = 180°

3x + 2x + 90° = 180°

5x + 90° = 180°

5x =180°-90°

x = 90°/5

x = 18°

∴ a = 2x = 2x 18° = 36°

b = 3x = 3×18°=54°

we know that, b + c = 180°

54° + c = 180°

∴ c = 126°

9th Standard Karnataka Maths Practice Papers Set 4

Question 8. ABCD is a parallelogram and AP and CQ are perpendicular from vertices A and C on diagonal a BD S.T AAPB ≅ ACQD

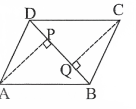
Solution: ABCD is a parallelogram,

In △APB and △CQD

∠APB = ∠CQD = 90°[ ∵ AP ⊥ DB and CQ ⊥ DB ]

AB = CD (opp. sides of a parallelogram)

∠ABP = ∠CDQ (Alternate interior angles)

∴ △APB ≅ △CQD (By AS A congruency)

Question 9. In the fig, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠ BCD

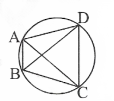
Solution:

∠CAD = ∠DBC =55° (Angles in the same segment)

∴∠DAB = ∠CAD + ∠BAC

= 55° + 45“

= 100°

But ∠DAB +∠BCD = 180° (opposite angles of a cyclic quadrilateral)

so, ∠BCD = 180°-100°

∠BCD = 80°

Question 10. Construct an angle of 22 1/2° at the initial point of a given ray.
Solution:

Question 11. The diameter of the base of a cone is 10.5cm and its slant height is 10cm. Find its curved surface area.

Solution:

The curved surface area of a cone = πrl

= 22/7 x 5.25 x 10

r = d/2

r = 10.5/2

=  5.25cm CSA of a cone = 165cm² h= 10cm

Question 12. What are primary and secondary data?
Solution:

1. Primary Data: When the information was collected by the investigator herself or himself with a definite objective in her or his mind, the data obtained is called primary data.
2. Secondary data: When the information was gathered from a source that already had the information stored, the data obtained is called secondary data.

Question 13. Find the mean for the following goals scored by a team in a series of 10 matches. 2, 3, 4, 5, 0,1, 3,3, 4, 3.
Solution:
The No. of goals scored by the team is 2, 3, 4, 5, 0,1, 3, 3, 4, 3

\(\text { Mean }=\frac{\text { sum of all observations }}{\text { Total Nos. of observations }}\) \(\text { Mean }=\frac{28}{10}\)

Mean=2.8 goals

9th Standard Karnataka Maths Sample Paper 2023 Set 4 with Solutions PDF

 

Question 14. Two coins are tossed simultaneously 500 times, and we get two heads; 105 times, and no heads; 120 times, one head; 275 times. Find the probability of occurrence of each of these events.

Solution: Let us denote the events of getting two heads,

no head and one had byE₁, E₂&E₃ respectively.

∴ P(E₁) = 105/500 = 0.21, P(E₂) = 120/500 = 0.24

P(E₃) = 275/500 = 0.55

P(E₁) + P(E₂) + P(E₃)

= 0.21 + 0.24+0.55

= 1

Ep E2 and E3 cover all the outcomes of a trial.

Question 15. ABCD is a rhombus S.T. diagonal AC bisects ∠C as well as ∠A.

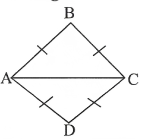
Solution:

ABCD is a rhombus,

AC is diagonal.

In △ABC, AB=AC

∴ ∠BAC

∴ ∠BCA (Angles opp. to equal sides are equal)

But ∴ ∠BAC = ∠DCA (Alternate angles)

∴ ∠BCA= ∠DCA (Axiom- 1)

∴ AC bisects ∠C

Now ∠BCA =∠DAC (Alternate angles)

and ∠BAC- ∠DAC

∴ AC bisects ∠A

Question 16. Prove that “If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram”.

Solution:

Let the sides AB and CD of the quadrilateral ABCD  be equal and also AD = BC

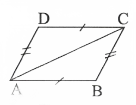
Draw diagonal AC.

∴ △ABC ≅ △CDA

So, ∠BAC = ∠DCA [Alternate angles]

∠BCA = ∠DAC

then AD || BC       AD =BC [given]

and AB || CD         AB = CD

Question 17. State whether the following statements are always true, always false, or ambiguous. Justify your answers.

1. There are 8 days a week
2. Gauri is a kind girl.

Solution:

1. This statement is always false since there are 7 days in a week.
2. This statement is ambiguous since it is subjective-Gauri may be kind to some and not to others

Question 18. Find counterexamples to disprove the following statements.

1. If the corresponding angles in two triangles are equal, then the triangles are congruent.
2. A quadrilateral with all sides equal is a square.

Solution:

1. You can give any two triangles with the same angles but of different sides.
2. A rhombus has equal sides but may not be a square.

Answer the following:

Question 1. Find the value of

1. \(64^{1 / 2}\)
2. \(125^{-1 / 3}\)

Solution:

1. \(64^{1 / 2}=\left(2^6\right)^{1 / 2}\)
   \(=2^{6^3 \times 1 / 2}=2^3=8\)
2. \(125^{-1 / 3}=\left(5^3\right)^{-1 / 3}\)
   \(=5^{\not x \times 1 / 8}=5^{-1}=\frac{1}{5}\)

Question 2. Factorise using suitable identity :

8x³+125y³-64z³+120xyz

Solution:

8x³+125y³-64z³+120xyz

a³+b³+c³-3abc = (a + b + c) (a²+b²+c²-ab-bc-ca)

(2x)³+(5y)³+(4y)³-3(2x)(5y)(-4z)

= (2x + 5y – 4z) (4x²+ 25y²+16z²-10xy+ 20yz + 8zx)

Question 3. Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Solution: yes, consider the following figures

In the above fig. line, ‘n’ falls online l, and when ∠l + ∠4 < 180°, then ∠2 + ∠3 > 180°. When l and m are produced on the side of ∠1 and ∠4 they meet.

In the above fig. if ∠l+∠4 = 180°, then the lines l and m do not meet at the side of ∠1 and ∠4 or at the side of ∠2 and ∠3. This means the lines are parallel.

Question 4. In fig. AB || CD and CD|| EF, Also EA ⊥ AB If ∠BEF = 55°, find the values of x, y, and z.

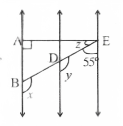
Solution:

y+ 55° = 180° (Interior angles on the same side of the transversal ED)

∴ y = 180 – 55°

y= 125°

Again x = y (AB || CD)

∴ x = 125°

∠EAB = ∠FEA = 180° [Interior angles on the same side of the transversal EA]

90° + (z + 55°) = 180°

90° + z + 55° = 180°

z+ 145°= 180°

z = 180°- 145°

z = 35°

Karnataka Class 9 Maths Previous Year Model Paper 2023 Set 4 Solved PDF

Question 5. The angles of the quadrilateral are in the ratio 3 : 5: 9:13. Find all the angles of the quadrilateral

Solution:

The four angles of the quadrilateral are 3x, 5x, 9x and 13x

∴ 3x + 5x + 9x + 11x = 360°

30x = 360°

x = 360/60

x = 12

∴ The four angle are 3x = 3 x 12 = 36°

5x = 5 x 12 = 60°

9x = 9 x 12= 108°

13x = 13 x 12= 156°

Question 6. Hameed has built a cubical water tank with a lid for his house, with each outer edge 1.5m long. He gets the outer surface of the tank excluding the base, covered with square tiles of side 25cm. Find how much he would spend for the tiles if the cost of the tiles is ₹ 360 per dozen

Solution:

Edge of the cubical tank = 1.5m= 150cm (a)

surface area of the tank = 5 x 150x 1 50cm²

Area of each square tile = side x side

= 25 x 25 cm²

∴ the no. of tiles required

\(=\frac{\text { surface area of the tank }}{\text { area of each tile }}\)

\(=\frac{5 \times 150^{30} \times 150^{30^6}}{25_{\beta_1} \times 25^6}\) = 180

cost of 1 dozen tiles, i.e., cost of12 tiles =₹360

∴ cost of one tile =₹ 360/12 = ₹30

∴ The cost of 180 tiles = 180 x ₹30= ₹5400

Answer the following:

Question 1. Factorise: x³– 23x²+142x-120

Solution:

x³– 23x²+142x-120

= x³– x²– 22×2 + 22x +120x-120

= x²(x-1)- 22x(x-1) +120(x-1)

= (x-1) (x²– 22x +120)

= (x-1) [x²-12x-10x +120]

= (x-1)[x(x-12)-10(x-12)]

= (x-1) (x-12) (x-10)

9th Class Karnataka Maths Model Paper 2023 Set 4 Important Questions PDF

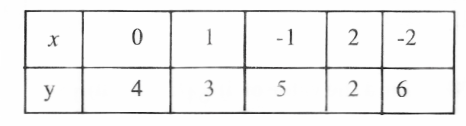
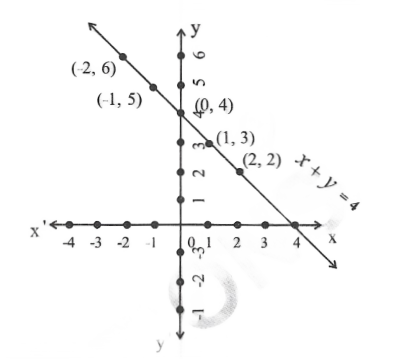
Question 2. Draw the graph of x + y = 4

Solution:

Scale: x-axis ; 1 cm = 1 unit

y-axis ; lcm= 1 unit

Question 3. In the fig, PQRS and ABRS are parallelograms and X is any point on side BR. S.T.

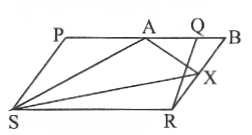
1. ar (PQRS) = ar (ABRS)
2. ar (AX S) = — ar (PQRS)

Solution:

1. PQRS and ABRS are parallelograms, stand on the same base SR and between the same parallels PB and SR.
   ∴ar(▱PQRS) = ar(▱ABRS)……….. (1)
2. ▱ABRS and ▱AXS stand on the same base As and between the same parallels BR and AS
   ∴ar (△AXS) =1/2 ar(▱ABRS)…………(2)
   From(l)and(2)
   ar (△AXS) = 1/2 ar(▱PQRS)

Karnataka 9th Maths Sample Paper 2023 Set 4 for Exam Preparation

Question 4. Prove that “The line segment joining the midpoints of two sides of a triangle is parallel to the third side and half of it?

Solution:

Given: △ABC in which D is the midpoint of AB, and E is the midpoint of AC. Draw DE.

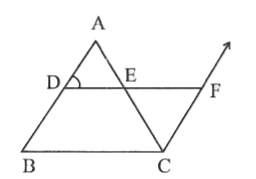
To prove DE || BC and DE = 1/2 BC.

construction: produce DE to F such that DE = EF and draw CF

Proof: In triangles ADE and CFE

AE = EC (E is the midpoint of AC)

DE = EF (by construction)

∠PEA = ∠CEF (V. O.A)

∴ △ADE ≅ △CFE (SAS congruence rule)

∠ADE = ∠CFE [CPCT]

AD = CF

considering AC as transversal between AB and CF,

∠ADE = ∠CFE

∴AB || CF

we also have CF = AD = BD

In the quadrilateral BCFD,

BD || CF and BD = CF

∴BCFD is a parallelogram

∴DF || BC (DE = EF)

BC = 2DE

∴DE || BC

DE = 1/2 BC

Hence it is proven.