KSEEB Solutions For Class 9 Maths Chapter 8 Quadrilaterals

KSEEB Solutions For Class 9 Maths Chapter 8 Quadrilaterals Points to Remember

• A quadrilateral is a closed figure obtained by joining four points (with no three points collinear) in an order.

• A diagonal is a line segment obtained on joining the opposite vertices.
• Two sides of a quadrilateral having no common endpoint are called opposite sides.
• Two angles of a quadrilateral having a common arm are called its adjacent angles.
• Two angles of a quadrilateral not having a common arm are called its opposite angles.
• A trapezium is a quadrilateral in which one pair of opposite sides are parallel.

Class 9 Social Science

Class 9 Science

Class 9 Maths

 

Read and Learn More KSEEB Solutions for Class 9 Maths 

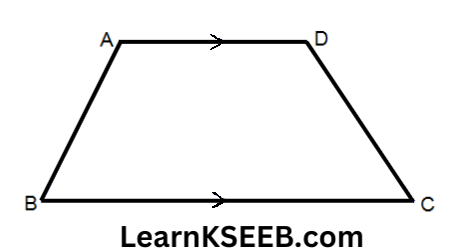
• If the non parallel sides of a trapezium are equal, then it is known as isosceles trapezium.

• A parallelogram is a quadrilateral in which both the pairs of opposite sides are parallel.

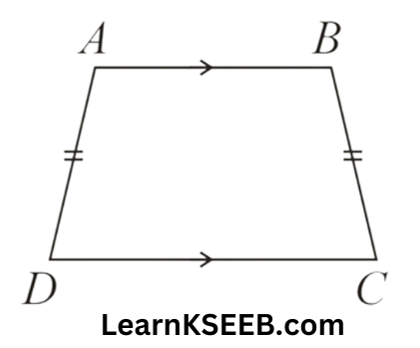
• A rectangle is a quadrilateral each of whose angle is 90°

KSEEB Class 9 Maths Chapter 8 Solutions PDF

• A Rhombus is a parallelogram all the sides of whose are equal.

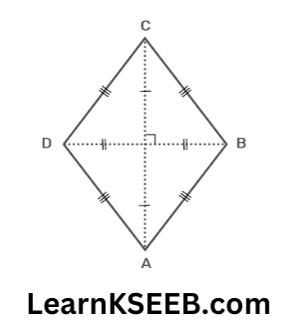
• A square is parallelogram all sides are equal & each angle is 90°

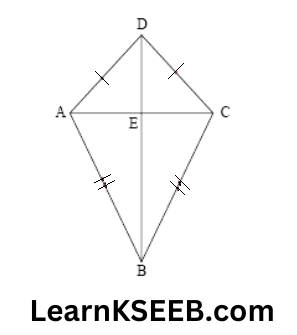
• A kite is a quadrilateral in which two pairs of adjacent sides are equal.

KSEEB Class 9 Maths Chapter 8 Quadrilaterals Exercises 

Properties of parallelogram

• Opposite sides of a parallelogram are parallel
• A diagronal of a parallelogram divides it into two congruent triangles.
• Opposite sides of a parallelogram are equal.
• Opposite angles of a parallelogram are equal.
• Consecutive angles (conjoined angles) of a parallelogram are supplementary.
• Diagonals of a parallelogram bisect each other.
• If each pair of opposite sides of a quadrilateral is equal., then it is a parallelogram.
• If in a quadrilateral each pair of opposite angles is equal, then it is a parallelogram.
• If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
• If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
• A quadrilateral is a parallelogram , if a pair of opposite sides is equal & parallel.
• Square, rectangle & rhombus are all parallelograms.
• Kite & trapezium are not parallelogram.
• A square is a rectangle
• A square is a rhombus
• A parallelogram is a trapezium.
• Every rectangle is a parallelogram.
• It has all the properties of a parallelogram
  -> All the interior angles of a rectangle are right angles.
  -> The diagonals of a rectangle are equal.
• Every rhombus is a parallelogram, it has all the properties of a parallelogram.
  -> All the sides of a rhombus are equal.
  -> Diagonals of a rhombus intersect at right angles.
  -> Diagonals of a rhombus bisects its angles.
• Every square is a parallelogram, it has all the properties of a parallelogram.
  -> All sides are equal
  -> All angles are equal to 90°
  -> Diagonals are equal
  -> Diagonals bisect each other at right angle.
  -> Diagonals bisect the angles of vertex
• The mid-point theorem.
• The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
• Conversely the line drawn through the midpoint of one side of a triangle, parallel to another side bisects the third side.

Quadrilaterals Exercise 8.1

1. The angles of a quadrilateral are in the ratio 3:5:9:13. Find all the angles of the quadrilateral.

Solution: Let ABCD be a quadrilateral in which

\(\lfloor A\):\(\lfloor B\):\(\lfloor C\):\(\lfloor D\) = 3:5:9:13

Sum of the ratios = 3 + 5 + 9+ 13 = 30

Also \(\lfloor A\) + \(\lfloor B\)+ \(\lfloor C\)+ \(\lfloor D\)= 360°

(sum of all the angles of a quadrilateral is 360°)

\(\lfloor A\) = 3/30×360 = 36°

\(\lfloor B\) = 5/30 x 360 = 60°

\(\lfloor C\)= 9/30×360 = 108°

\(\lfloor D\) = 13/30x 360 = 150°

2. If the diagonals of a parallelogram are equal, then show that it is a rectangle

Solution:

Given: In parallelogram ABCD

AC = BD

To prove : ||gm ABCD is a rectangle

Proof: In ΔABC and ABDA

AC = BD (given)

AB = BA (common)

BC = AD (oppsite sides of || gm ABCD)

∴ ΔACB ≅ ΔBDA (SSS rule)

\(\lfloor\mathrm{ABC}\) = \(\lfloor\mathrm{BAD}\) (cpct) …………………(1)

again AD || BC (opp. sides of ||gm ABCD & transversal AB intersects them)

∴ \(\lfloor\mathrm{BAD}\) + \(\lfloor\mathrm{ABC}\) = 180° ………………(2)

(sum of consecutive interior angles on the same side of a transversal is 180°)

from(1) &(2)

\(\lfloor\mathrm{BAD}\) = \(\lfloor\mathrm{ABC}\) = 90°

∴ \(\lfloor A\) = 90°

∴ ||gm ABCD is a rectangle.

3. Show that if the diagonals of a quadrilateral bisect each other at right angles then it is a rhombus.

Solution:

Given: ABCD is a quadrilateral whose diagonals AC & BD intersect each other at right angles at O.

To prove: Quadrilateral ABCD is a rhombus.

Proof: In ΔAOB = ΔAOD

AO = AO (common)

OB = AD (given)

\(\lfloor\mathrm{AOB}\) = \(\lfloor\mathrm{AOD}\) = 90°

ΔAOB = ΔAOD (SAS rule)

=> AB=AD ……………..(1)(cpct)

|||/y we can prove that

AB = BC …………….(2)

BC = CD ……………..(3)

CD =AD ………………(4)

from (1), (2), (3) & (4) we get

AB = BC = CD = DA

∴ Quadrilateral ABCD is a rhombus.

4. Show that the diagonals of a square are equal & bisect each other at right angles.

Solution:

Given: ABCD is a square

To prove: 1) AC = BD

2) AC & BD bisect each other at right angles.

Proof: 1) In AABC & ABAD AB = BA (common)

BC = AD (opp. sides of square)

\(\lfloor\mathrm{ABC}\) = \(\lfloor\mathrm{BAD}\)= 90°

∴ ΔABC ≅ ΔBAD (by SAS rule)

∴ AC = BD (cpct)

2) In ΔOAD and ΔOCB

AD = CB (Opp. sides of square ABCD)

\(\lfloor\mathrm{OAD}\) = \(\lfloor\mathrm{OCB}\)

(AD || BD & transversal AC intersects them)

\(\lfloor\mathrm{ODA}\) = \(\lfloor\mathrm{OBC}\)

(AD || BD & transversal BD intersects them)

∴ ΔOAD ≅ ΔOCB (ASA rule)

∴ OA = OC …………….(1)

|| ly we can prove that OB = OD ……………..(2)

from (1) & (2) we can say

AC & BD bisect each other

Again, in ΔOBA and ΔODA OB = OD (from (2))

BA=DA (opp. sides of square ABCD)

OA = OA (common)

∴ ΔOBA ≅ ΔODA (SSS rule)

=> \(\lfloor\mathrm{AOB}\) = \(\lfloor\mathrm{AOD}\) (cpct)

but \(\lfloor\mathrm{AOB}\) +\(\lfloor\mathrm{AOD}\) = 180° (linear pair)

∴ \(\lfloor\mathrm{AOB}\)=\(\lfloor\mathrm{AOD}\) = 90°

∴ AC & BD bisect each other at right angles.

5. Show that if the diagonals of a quadrilateral are equal & bisect each other at right angles, then it is square

Solution:

Given: The diagonals AC & BD of a quarilateralABCD are equal & bisect each other at right angles. A B

To prove: Quadrilateral ABCD is a square

Proof: In ΔOAD and ΔOCB

OA = OC (given)

OD = OB (given)

\(\lfloor\mathrm{AOD}\) =\(\lfloor\mathrm{COB}\) (vertically opp. angles)

∴ ΔOAD ≅ ΔOCB (SAS rule)

∴ AD= CB{CPCT)

∴ \(\lfloor\mathrm{ODA}\) = \(\lfloor\mathrm{OBC}\) (CPCT)

=>\(\lfloor\mathrm{BDA}\) = \(\lfloor\mathrm{DBC}\)

∴ AD || BC

Now, AD = CB & AD || CB

∴ Quadrilateral ABCD is a ||gm

In ΔAOB and ΔAOD

AO = AO (common)

OB = OD (given)

\(\lfloor\mathrm{AOB}\) = \(\lfloor\mathrm{AOD}\) = 90°

∴ ΔAOB ≅ ΔAOD (SAS rule)

∴ AB= AD (CPCT)

∴ ABCD is a ||gm &AB=AD

∴ ABCD is a rhombus.

Again in ΔABC and ΔBAD AC = BD (given)

BC = AD (ABCD is a rhombus)

AB = BA

∴ ΔABC ≅ ΔBAD (SSS rule)

\(\lfloor\mathrm{ABC}\) = \(\lfloor\mathrm{BAD}\) (CPCT)

AD || BC (opp. sides of ||gm ABCD & transversal AB intersects them)

∴ \(\lfloor\mathrm{ABC}\) + \(\lfloor\mathrm{BAD}\) = 180°

∴ \(\lfloor\mathrm{ABC}\) = \(\lfloor\mathrm{BAD}\) = 90°

|| ly \(\lfloor\mathrm{BCD}\) = \(\lfloor\mathrm{ADC}\) = 90°

∴ ABCD is a square

6. Diagonals AC of a parallelogram ABCD bisects \(\lfloor A\) (see figure) show that
1) it bisects \(\lfloor C\) also
2) ABCD is a rohmbous

Solution:

Given: Diagonal AC of a parallelogram ABCD bisects \(\lfloor A\).

To prove: 1) it bisects \(\lfloor C\) also

2) ABCD is a rhombus

Proof: 1) In ΔADC and ΔCBA

AD = CB (opp. sides of ||gm ABCD)

CA = CA (common

DC = BA (opp. sides of ||gm ABCD)

∴ ΔADC ≅ ΔCBA (SSS congruence rule)

\(\lfloor\mathrm{ACD}\) = \(\lfloor\mathrm{CAB}\) (C.P.C.T.)

& \(\lfloor\mathrm{DAC}\) = \(\lfloor\mathrm{BCA}\) (C.P.C.T.)

but \(\lfloor\mathrm{CAB}\) = \(\lfloor\mathrm{DAC}\) (given)

∴ \(\lfloor\mathrm{ACD}\) = \(\lfloor\mathrm{BCA}\)

AC bisects \(\lfloor C\) also

2) from above \(\lfloor\mathrm{ACD}\) – \(\lfloor\mathrm{CAD}\)

AD = CD (sides opp. to equal angles of a Δle are equal)

∴ AB = BC = CD = DA(∵ ABCD is a ||gm)

∴ ABCD is a rhombus.

7. ABCD is a rhombus. Show that diagonal AC bisects \(\lfloor A\) as well as \(\lfloor C\) & diagonal BD bisects \(\lfloor B\) as well as \(\lfloor D\)

Solution:

Given: ABCD is a rhombus

To prove: 1) Diagonal AC

bisects \(\lfloor A\)as well as \(\lfloor C\)

2) Diagonal BD bisects \(\lfloor B\) as well as \(\lfloor D\)

Proof: 1) ABCD is a rhombus.

AD = CD

\(\lfloor\mathrm{DAC}\) = \(\lfloor\mathrm{DCA}\) (angles opp. to equal sides of a Δle are equal)

from(1) &(2)

\(\lfloor\mathrm{DCA}\) = \(\lfloor\mathrm{BCA}\)

=> AC bisects \(\lfloor C\)

|| ly AC bisects \(\lfloor A\)

2) Proceeding || ly as in(1) above, we can prove that BD bisects \(\lfloor B\) as well as \(\lfloor D\)

Karnataka 9th Standard Maths Chapter 8 Notes

8. ABCD is a rectangle in which diagonal AC bisects \(\lfloor A\) as well as \(\lfloor C\). Show that
1) ABCD is a square
2) diagonal BD bisects \(\lfloor B\) as well as [\(\lfloor D\)

Solution:

Given: ABCD is a rectangle in which diagonal AC bisects \(\lfloor A\)as well as \(\lfloor C\)

2) diagonal BD bisects \(\lfloor B\) as well as \(\lfloor D\)

Proof: 1) AB || DC & transversal AC intersects them

∴ \(\lfloor\mathrm{ACD}\) = \(\lfloor\mathrm{CAB}\) (alternate interior angle)

but \(\lfloor\mathrm{CAB}\) = \(\lfloor\mathrm{CAD}\)

∴ \(\lfloor\mathrm{ACD}\) = \(\lfloor\mathrm{CAD}\)

∴ AD = CD (sides opp. to equal angles of a Δle are equal)

ABCD is a square

2) In ΔBDA and ΔDBC

BD = DB (common)

DA=BC (sides of a square ABCD)

AB = DC (sides of a square ABCD)

ΔBDA ≅ ΔDBC (SSS rule)

∴ \(\lfloor\mathrm{ABD}\) = \(\lfloor\mathrm{CDB}\) (CPCT)

but \(\lfloor\mathrm{CDB}\) = \(\lfloor\mathrm{CBD}\) (∵ CB=CD)

∴ \(\lfloor\mathrm{ABD}\) = \(\lfloor\mathrm{CBD}\)

BD bisects \(\lfloor B\)

Now \(\lfloor\mathrm{ABD}\) =\(\lfloor\mathrm{CBD}\)

\(\lfloor\mathrm{ABD}\) = \(\lfloor\mathrm{ADB}\) (∵ AB=AD)

\(\lfloor\mathrm{CBD}\) = \(\lfloor\mathrm{CDB}\) (∵ CB=CD)

∴ \(\lfloor\mathrm{ADB}\) = \(\lfloor\mathrm{CDB}\)

=> BD bisects \(\lfloor D\)

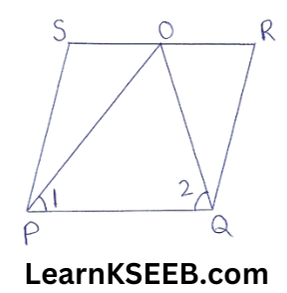
9. In parallelogram ABCD, two points P& Q are taken on diagonal BD such that DP = BQ (see fig) show that

1) ΔAPD ≅ ΔCQB
2) AP=CQ
3) ΔAQB = ΔCPD
4) AQ = CP
5) APCQ is a parallelogram

Solution:

Given: In parallelogram ABCD, two points P & Q are taken on diagonal BD such that DP = BQ

To prove: 1) ΔAPD ≅ ΔCQB

2) AP = CQ

3) ΔAQB = ΔCPD

4) AQ = CP

5) APCQ is a parallelogram

Construction: Join AC to intersect BD at O.

Proof: 1) In ΔAPD and ΔCQB

AD || BC

( ∵ opp. sides of ||gm ABCD & a transversal BD intersects them)

∴ \(\lfloor\mathrm{ADB}\) = \(\lfloor\mathrm{CDB}\) (alternate interior angles)

=>\(\lfloor\mathrm{ADP}\)=\(\lfloor\mathrm{CBQ}\) ……………….(1)

DP = BQ …………………(2) (given)

AD = CB …………………(3) (opp. sides of ||gm ABCD)

ΔAPD ≅ ΔCQB (SAS rule)

2) ΔAPD ≅ ΔCQB (proved in (1) above)

∴ AP = CQ (C.P.C.T.)

3) In ΔAQB and ΔCPD

AB || CD (opp. sides of ||gm ABCD & a transversal BD intersects them)

\(\lfloor\mathrm{ABD}\) = \(\lfloor\mathrm{CDB}\) (alternate interior angles)

=> \(\lfloor\mathrm{ABQ}\) = \(\lfloor\mathrm{CDP}\)

QB = PD (given)

AB = CD (opp. sides of ||gm ABCD)

∴ ΔAQB ≅ ΔCPD (SAS rule)

4) ΔAQB ≅ ΔCPD (proved in 3 above)

AQ = CP (CPCT)

5) The diagonals of a ||gm bisect each other

∴ OB = OD

OB – BQ = OD – DP (∵ BQ = DP given)

∴ OQ = OP …………..(1)

Also OA = OC …………….(2)

(∵ diagonals of a ||gm bisect each other)

In view of(1)&(2)

APCQ is a ||gm

10. ABCD is a ||gm & AP& CQ are perpendiculars from vertices A & C on diagonal BD respectively show that
1) ΔAPB ≅ ΔCQD
2) AP=CQ

Solution:

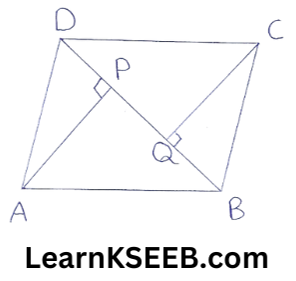
Given: ABCD is a ||gm & AP & CQ are perpendicular from vertices A & C on diagonal BD respectively

To prove : 1) ΔAPB ≅ ΔCQD

2) AP = CQ

Proof: 1) In ΔAPB & ΔCQD

AB = CD (opp. sides of ||gm ABCD)

\(\lfloor\mathrm{ABP}\) = \(\lfloor\mathrm{CQD}\) (∵ AB || DC & transversal BD intersects them)

\(\lfloor\mathrm{APB}\) = \(\lfloor\mathrm{CQD}\) = 90°

∴ ΔAPB ≅ ΔCQD (AAS rule)

2) ΔAPB ≅ ΔCQD (proved above)

∴ AP = CQ (CPCT)

11. In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF & BC || EF. Vertices A, B & C are joined to vertices D, E & F respectively. Show that
1) Quadrilateral ABED is a ||gm
2) Quadrilateral BEFC is a ||gm
3) AD || CF & AD = CF
4) Quadrilateral ACFD is a ||gm
5) AC = DF
6) ΔABC ≅ ΔDEF

Solution:

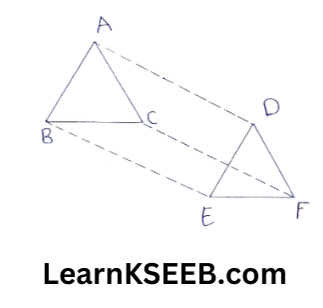
1) In Quadrilateral ABED

AB = DE & AB|| DE (given)

∴ Quadrilateral ABED is a ||gm

( ∵ A quadrilateral is a ||gm if a pair of opposite sides are parallel & are of equal length)

2) In quadrilateral BEFC

BC = EF & BC || EF (given)

∴ Quadrilateral BEFC is a ||gm (∵ A quadrilateral is a ||gm if a pair of opposite sides are parallel & are of equal length)

3) ABED is a ||gm (proved in (1))

∴ AD || BE &AD = BE ………….(1)

(opp. sides of a  ||gm are parallel & equal) BEFC is a | p (proved in (2))

∴ BE || CF & BE = CF ……………..(2)

(∵ opp. sides of a |p are parallel & equal)

from (1) & (2) we obtain

AD || CF & AD = CF

4) In Quadrilateral ACFD

AD || CF & AD = CF (from 3)

∴ QuadrilateralACFD is a ||gm

( ∵ A quadrilateral is a ||gm a pair of opp. sides are parallel & are of equal length)

5) ACFD is a ||gm (proved in (4))

∴ AC || DF & AC = DF

(In a ||gm opp. sides are || le & of equal length)

6) In ΔABC and ΔDEF

AB = DE (∵ ABCDisa ||gm)

BC = EF (∵ BEFC is a ||gm)

AC = DF (proved in 5)

∴ ΔABC ≅ ΔDEF (SSS rule)

KSEEB Class 9 Maths Quadrilaterals Solutions

12. ABCD is a trapezium in which AB || CD & AD = BC show that

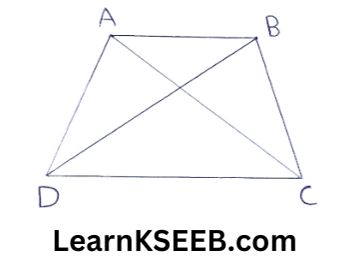
1) \(\lfloor A\)=\(\lfloor B\)
2) \(\lfloor C\)= \(\lfloor D\)
3) ΔABC ≅ ΔBAD
4) diagonal AC = diagonal BD
(Hint: Extend AB & draw a line through C parallel to DA intersecting AB produced at E)

Solution:

Given: ABCD is a trapezium in which AB || CD & AD = BC

To prove: 1) \(\lfloor A\) = \(\lfloor B\)

2) \(\lfloor C\)=\(\lfloor D\)

3) ΔABC ≅ ΔBAD

4) diagonal AC = diagonal BD.

Construction: Extend AB & draw a line through C parallel to DA intersecting AB produced at E.

Proof: 1) AB || CD(given)

& AD || EC (by construction)

∴ AECD is a (a quadrilateral is a ||gm if a pair of opposite sides are parallel & are of equal length)

∴ AD = EC (opp. sides of a ||gm are equal)

But AD = BC (given)

∴ EC = BC

\(\lfloor\mathrm{CBE}\) = \(\lfloor\mathrm{CEB}\) ……………..(1)

(angles opp. to equal sides of a Δle are equal)

\(\lfloor B\) + \(\lfloor\mathrm{CBE}\) = 180° (linear pair) ………………….(2)

AD || EC & transversal AE intersects them

(by construction)

∴ \(\lfloor A\) + \(\lfloor\mathrm{CEB}\) = 180° …………………..(3)

(The sum of consecutive interior angles on the same side of a transversal is 180°)

from (2) & (3)

\(\lfloor B\) + \(\lfloor\mathrm{CBE}\) = \(\lfloor A\) + \(\lfloor\mathrm{CEB}\)

but \(\lfloor\mathrm{CBE}\) = \(\lfloor\mathrm{CEB}\) from (1)

∴ \(\lfloor B\) = \(\lfloor A\)

(or) \(\lfloor A\) = \(\lfloor B\)

2) AB || CD

\(\lfloor A\) + \(\lfloor D\) = 180° (The sum of consecutive interior angles on the same side of a transversal is 180°)

& \(\lfloor B\) + \(\lfloor C\) = 180°

∴ \(\lfloor A\) + \(\lfloor D\) = \(\lfloor B\) + \(\lfloor C\) but \(\lfloor A\) = \(\lfloor B\) (proved in (1))

∴ \(\lfloor D\)=\(\lfloor C\)

or \(\lfloor C\)= \(\lfloor D\)

3) In ΔABC and ΔBAD

AB = BA (common)

BC = AD (given)

\(\lfloor\mathrm{ABC}\) = \(\lfloor\mathrm{BAD}\) (from(1))

∴ ΔABC ≅ ΔBAD (SAS rule)

4) ΔABC ≅ ΔBAD

AC = BD (CPCT)

or diagonal AC = diagonal BD

Quadrilaterals Exercise 8.2

1. ABCD is a quadrilateral in which P, Q, R & S are mid-points of the sides AB, BC, CD & DA, AC is a diagonal show that

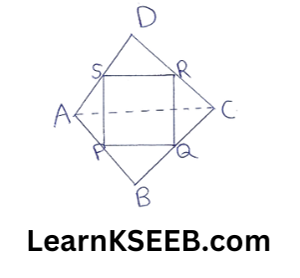
1) SR || AC & SR=1/2AC
2) PQ = SR
3) PQRS is a ||gm

Solution: 1) InADAC

5 is the mid-point of DA & R is the mid-point of DC

∴ SR || AC and SR= 1/2AC (midpoint theorem)

2) In ABAC

P is the midpoint of AB & Q is the mid-point of BC

∴ PQ || AC & PQ = 1/2AC (midpoint theorem)

but from(1) SR = 1/2AC

∴ PQ=SR

3) PQ ||AC(from 2)

SR || AC (from 1)

∴ PQ || SR (Two lines parallel to the same line are parallel to each other)

Also PQ = SR

∴ PQRS is a ||gm

(a quadrilateral is a ||gm if a pair of opp. sides are parallel & are of equal length)

2. ABCD is a rhombus & P, Q, R & S are the mid-points of the sides AB, BC, CD & DA respectively, show that the quadrilateral PQRS is a rectangle.

Solution:

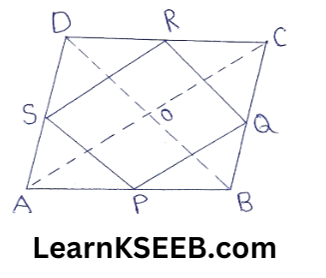
Given: ABCD is a rhombus. P, Q, R, S, are the mid-points of AB, BC, CD &DA respectively. PQ, QR, RS & SP are joined.

To prove: PQRS is a rectangle.

Construction: Join AC & BD

Proof: In triangle RDS & PBQ

DS = QB (Halves of opp. sides of ||gm ABCD which are equal)

DR = PB (Halves of opp. sides of ||gm ABCD which are equal)

\(\lfloor\mathrm{SDR}\) = \(\lfloor\mathrm{QBP}\)

(opp. angle of ||m ABCD which are equal)

∴ ΔRDS ≅ ΔPBQ (SAS rule)

∴ SR = PQ (CPCT)

In Δle RCQ & PAS

RC=AP (Halves of opp. sides of ||m ABCD which are equal)

CQ = AS (Halves of opp. sides of ||gm ABCD which are equal)

\(\lfloor\mathrm{RCQ}\) = \(\lfloor\mathrm{PAS}\) (opp. angle of ||gm ABCD which are equal)

∴ ΔRCQ ≅ ΔPAS (SAS rule)

∴ RQ=SP (CPCT)

In PQRS

SR = PQ & RQ = SP

∴ PQRS is a parallelogram

In ACDB

R & Q are the mid-points of DC & CB respectively.

∴ RQ || DB

RF || EO, ||ly RE || FO

OFRE is a ||gm

∴ \(\lfloor R\) = \(\lfloor\mathrm{EOF}\) = 90°

(∵ opp. angle of a | \m are equal & diagonals of a rhombus intersect at 90°)

Thus PQRS is a rectangle

3. ABCD is a rectangle & P, Q, R & S are mid-points of the sides AB, BC, CD & DA respectively. Show that the quadrilateral PQRS is a rhombus.

Solution:

Given: ABCD is a rectangle P, Q , R & S are mid-points of AB, BC, CD & DA respectively. PQ, QR, RS & SP are joined.

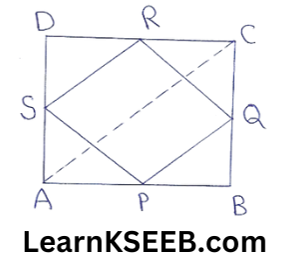
To prove: Quadrilateral PQRS is a rhombus.

Construction: Join AC

Proof: In ΔABC

P & Q are the mid-points of AB & BC respectively.

∴ PQ || AC and PQ=1/2AC …………..(1)

In ΔADC

S & R are the mid-points of AD & DC respectively.

∴ SR || AC & SR= 1/2AC ………………(2)

from(1) &(2)

PQ || SR & PQ = SR ………………….(3)

∴ Quadrilateral PQRS is a ||gm

In rectangle ABCD

AD = BC (opp. sides)

=> 1/2AD = 1/2BC (Halves of equals are equal)

=> AS = BQ

In ΔAPS and ΔBPQ

AP = BP (∵ P is the midpoint of AB)

AS = BQ (proved above)

\(\lfloor\mathrm{PAS}\) = \(\lfloor\mathrm{PBQ}\) = 90°

∴ ΔAPS ≅ ΔBPQ (SAS rule)

∴ PS = PQ ……………..(4) (CPCT)

In view of (3) & (4)

PQRS is a rhombus.

4. ABCD is a trapezium in which AB || DC, BD is a diagonal & E is the midpoint of AD. A line is drawn through E parallel to AB intersecting BC at F. Show that F is the midpoint of BC.

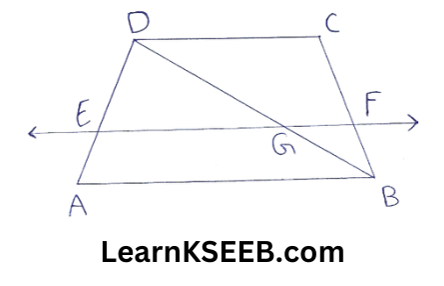
Solution:

Let DB intersect EF at G

In ADAB

E is the midpoint of DA & EG || AB

∴ G is the midpoint of DB (by converse of mid-point theorem)

Again, in ΔBDC

G is the midpoint of BD & GF || AB || DC

∴ F is the midpoint of BC (By converse of midpoint theorem)

5. In a parallelogram ABCD, E & F are the mid-points of sides AB & CD respectively. Show that the line segments AF & EC trisect the diagonal BD.

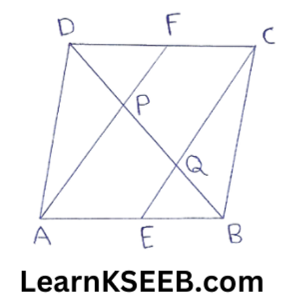
Solution:

AB || DC (Opp. sides of ||gm ABCD)

∴ AE || FC ……………..(1)

AB = DC (opp. sides of ||gm ABCD)

∴ 1/2AB=1/2DC (Halves of equals are equal)

=> AE=CF ……………..(2)

In view of (1)&(2)

AECF is a ||gm

(A quadrilateral is a ||gm, if a pair of opposite sides are parallel & are of equal length)

∵ EC || AF …………….(3) (opp. sides of ||gm AECF)

In ADQC

F is the midpoint of DC

& FP || CO (∴ EC || AF)

∴ P is the mid-point of DQ (By converse of mid-point theorem)

=> DP=PQ …………….(4)

|| ly ln ΔBAP

BQ = PQ ………………..(5)

from (4) & (5) we get

DP = PQ = BQ

=> line segments AF & EC trisect the diagonal BD.

6. Show that the line segments joining the midpoints of the opposite sides of a quadrilateral bisect each other.

Solution:

Given: ABCD is a quadrilateral, P, Q, R & S are the mid-points of the sides DC, CB, BA & AD respectively.

To prove: PR & QS bisect each other.

Construction: Join PQ, QR, RS, SP, AC & BD

Proof: In ΔABC

R & Q are the midpoints of AB & BC respectively

∴ RQ || AC and RQ=1/2AC

|| ly, we can show that

PS || AC &PS=1/2AC

∴ RQ || PS and RQ = PS

Thus a pair of opposite sides of a quadrilateral PQRS are parallel & equal.

∴ PQRS is a ||gm

Since the diagonals of a ||gm bisect each other.

∴ PR & QS bisect each other

7. ABC is a Δle right angled at C. A line through the midpoint M of hypotenuse AB & parallel to BC intersects AC at D. Show that
1) D is the midpoint of AC
2) MD ⊥ AC
3) CM = MA = 1/2AB

Solution:

Given : ABC is a Δle right angled at C. A line through the midpoint M of hypotenuse AB & parallel to BC intersects AC at D.

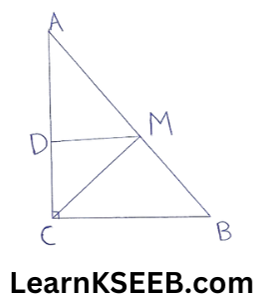
To prove : 1) D is the midpoint of AC

2) MD⊥AC

3) CM = MA = 1/2 AB

Proof: 1) In ΔACB

M is the midpoint of AB & MD || BC

∴ D is the midpoint of AC

(By converse of mid-point theorem)

2) MD || BC & AC intersects them

\(\lfloor\mathrm{ADM}\) = \(\lfloor\mathrm{ACM}\) (corresponding angles) But \(\lfloor\mathrm{ACB}\) = 90° (given)

∴ \(\lfloor\mathrm{ADM}\) = 90°

=> MD ⊥ AC

3) Now, \(\lfloor\mathrm{ADM}\) + \(\lfloor\mathrm{CDM}\) = 180° (linear pair)

\(\lfloor\mathrm{ADM}\) = \(\lfloor\mathrm{CDM}\) = 90°

In ΔADM & ΔCDM

AD = CD (∴ D is the midpoint of AC)

DM = DM (common)

\(\lfloor\mathrm{ADM}\) = \(\lfloor\mathrm{CDM}\) = 90°

∴ ΔADM ≅ ΔCDM (by SAS rule)

∴ MA = MC (CPCT)

But M is the midpoint of AB

∴ MA=MB= 1/2AB

∴ MA=MC= 1/2AB

=> CM = MA = 1/2AB

KSEEB 9th Standard Maths Chapter 8 Important Questions

Additional Questions

Choose the correct answer from the following

1. ABCD is a ||gm & X & Y are the midpoints of sides AB &CD respectively. Then the quadrilateral AXCYis

1. a parallelogram
2. a rectangle
3. a rhombus
4. a square
5. Solution: 1. a parallelogram

2. In a quadrilateral three angles are in the ratio 3:3:1 & one of the angles is 80°, then other angles are

1. 120°, 120°, 40°
2. 100°, 100°, 80°
3. 110°, 110°, 60°
4. 100°, 100°, 90°

Solution: 1. 120°, 120°, 40°

3. If one angle of a ||gm is 90°, then the ||gm is called a

1. kite
2. rectangle
3. rhombus
4. Kite

Solution: 2. rectangle

4. The angle between the diagonals of a rhombus is

1. 45°
2. 90°
3. 30°
4. 60°

Solution: 2. 90°

5. In the following figure, ABCD is a ||gm. The value of x is

1. 25°
2. 60°
3. 75°
4. 45°

Solution: 4. 45°

6. In the following figure D, E & F are the midpoints of sides BC, CA & AB of ΔABC. If AB = 3cm, BC = 4cm & CA = 4cm, then the perimeter of ΔDEF is A

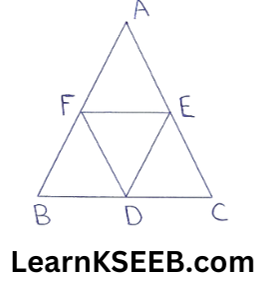
1. 11cm
2. 8cm
3. 7cm
4. 5.5.cm

Solution: 4. 5.5.cm

7. In figure, ABCD is a ||gm. The bisectors of angles A & B intersect at O. Then the angle AOB is

1. a right angle
2. an acute angle
3. an obtuse angle
4. a straight angle

Solution: 1. a right angle

8. In the given figure, ABCD &AEFG are two ||gm, If \(\lfloor C\) = 60°, then \(\lfloor\mathrm{GFE}\) is

1. 60°
2. 120°
3. 30°
4. 45°

Solution: 1. 60°

Fill in the blanks :

1. A quadrilateral whose diagonals are equal & bisect each other at right angles is called a square.
2. The angles of a quadrilateral are in the ratio 2:3:6:7. The largest angle of the quadrilateral is 140°
3. Two consecutive angles of a ||gm are in the ratio 1:3, then the smaller angles is 45°
4. In an equilateral Δle ABC, D & E are the mid-points of sides AB & AC respectively, Then length of DE is 1/2BC.
5. D, E, F are the midpoints of sides BC, CA&AB of ΔABC. If perimeter of AABC is 12.8cm then perimeter of ADEF is 6.4cm

Two Mark Questions

1. The angles of a quadrilateral are 4x°, 7x°, 15×0 & 10×0. Find the smallest & largest angles of the quadrilateral.

Solution: Sum of the angles of a quadrilateral is 360°.

4x+7x+15x+10x=360°

x=360/36=10°

∴ smallest angle = 4x°=40°

largest angle = 15x° = 150°

2. Two opposite angles of a ||gm are (3x-2)° & (63-2x)°. Find all the angles of a ||gm.

Solution: Since opposite angles of a ||gm are equal (3x-2)° = (63-2x)°

=> x=13°

Angles of a parallelogram are (39-2)°, (180-37), (63-26), (180-36)°

ie, 37°, 143°, 37°, 143°

3. Two parallel lines l & m are intersected by a transversal ‘l’ .Show that the quadrilateral formed by bisectors of interior angles is a rectangle.

Solution:

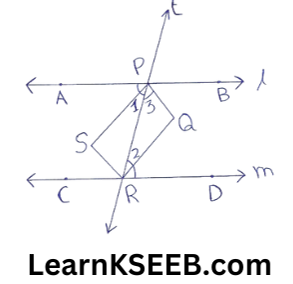
\(\lfloor\mathrm{APR}\) – \(\lfloor\mathrm{DRP}\) (alternate interior angles)

or \(\lfloor 1\) = \(\lfloor 2\)

But these are alternate interior angles.

SP || RQ, SR || PQ

PQRS is a ||gm

\(\lfloor\mathrm{APR}\) +\(\lfloor\mathrm{BPR}\) =180° (linear pair)

=> 1/2\(\lfloor\mathrm{APR}\) + 1/2\(\lfloor\mathrm{BPR}\) =90°

\(\lfloor 1\) + \(\lfloor 3\) = 90°

=> \(\lfloor\mathrm{SPQ}\) = 90°

∴ PQRS is a rectangle

4. In a ||gm, show that the angle bisectors of two adjacent angles intersect at right angle.

Solution:

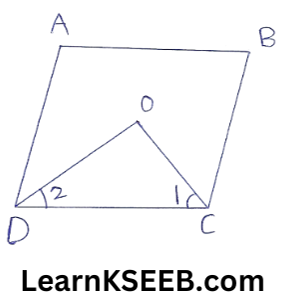
\(\lfloor\mathrm{ADC}\) +\(\lfloor\mathrm{BCD}\) = 180°

=>1/2\(\lfloor\mathrm{ADC}\) + 1/2\(\lfloor\mathrm{BCD}\) = 90°

OR \(\lfloor 1\)+\(\lfloor 2\) = 90°

In ΔODC,

\(\lfloor 1\)+\(\lfloor 2\) + \(\lfloor\mathrm{DOC}\) = 180°

90°+ \(\lfloor\mathrm{DOC}\) = 180°

=> \(\lfloor\mathrm{DOC}\) = 180°-90°

∴ \(\lfloor\mathrm{DOC}\) = 90°

5. The angle between the two altitudes of a ||gm through the vertex of an obtuse angle is 50°. Find the angles of a ||gm.

Solution:

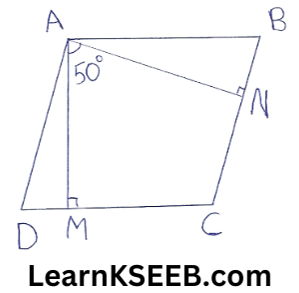
AM ⊥ DC, AN ⊥ BC

In Quadrilateral AMCN

\(\lfloor A\) + \(\lfloor M\)+ \(\lfloor C\) + \(\lfloor N\) = 360°

∴ \(\lfloor A\) + \(\lfloor C\) = 360° -90° -90°

∴ \(\lfloor A\) + \(\lfloor C\) = 180°

=>50°+\(\lfloor C\) = 180°

=>\(\lfloor C\) = 180°-50°

\(\lfloor C\) = 130°

In ||gm, [A = \(\lfloor C\) = 130°

\(\lfloor D\) = \(\lfloor B\) = 180° -130° = 50°

6. ABCD is a ||gm. If E is the midpoint of BC & AE is the bisector of \(\lfloor A\). Prove that AB = 1/2AD

Solution:

Here \(\lfloor 1\) = \(\lfloor 2\)

(AE is the angle bisector) \(\lfloor 1\) = \(\lfloor 3\) (alternate angles as AD || BC)

\(\lfloor 3\) = \(\lfloor 2\)

Hence BE =AB

(sides opp. to equal angles)

but BE =1/2BC (E is the midpoint of BC)

∴ AB = 1/2BC

& BC = AD (opp. sides of a ||gm)

∴ AB = 1/2AD

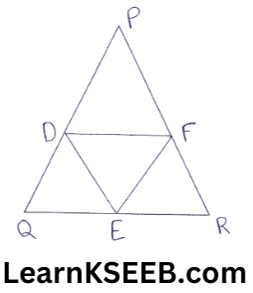
7. D, E & F are the midpoints of sides PQ, QR & RP respectively of an equilateral ΔPQR. Show that ΔDEF is also an equilateral Δle.

Solution:

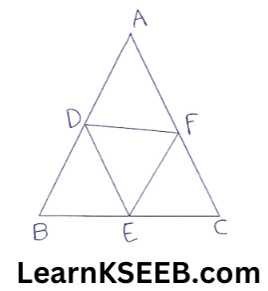
DE || PR & DE = 1/2PR (midpoint theorem)

EF || PQ & EF = 1/2PQ (midpoint theorem)

DF || QR & DF = 1/2QR (mid-point theorem)

also PQ = QR = PR (∵ PQR is an equilateral Δle)

=> DE = EF = DF

=> ADEF is an equilateral Δle.

8. In ΔABC, D, E & F are the midpoints of sides AB, BC & CA. If AB = 6cm, BC = 7.2cm & AC = 7.8cm, find the perimeter of ΔDEF

Solution:

DE = 1/2AC

EF = 1/2AB {Midpoint theorem}

DF = 1/2BC

Perimeter of DEF = DE + EF + DF

= 1/2(AC + AB + BC)

= 1/2(7.8 + 6 + 7.2)

= 1/2×21 = 10.5cm

Three Mark Questions

1. In a ||gm PQRS of the given s figure, the bisectors of \(\lfloor P\) & \(\lfloor Q\) meet SR at O. Show that \(\lfloor\mathrm{POQ}\) = 90°

Solution: PQRS is a ||gm

=> PS || QR

PS || QR & transversal

PQ intersects them.

∴ \(\lfloor P\) + \(\lfloor Q\) = 180°

(sum of consecutive interior angles is 180°)

1/2\(\lfloor P\) + 1/2\(\lfloor Q\) = 90°

=> \(\lfloor 1\)+\(\lfloor 2\) = 90° (∵ OP is bisector of \(\lfloor P\) & OQ is bisector of \(\lfloor Q\))

∴ \(\lfloor 1\) = 1/2\(\lfloor P\) & 1/2\(\lfloor Q\)

Now, in APOQ

\(\lfloor 1\)+ \(\lfloor 2\) + \(\lfloor\mathrm{POQ}\) = 180°

90°+ \(\lfloor\mathrm{POQ}\) = 180°

=> \(\lfloor\mathrm{POQ}\) = 90°

2. In a quadrilateral ABCD, the line segment bisecting \(\lfloor C\) & \(\lfloor D\) meet at E. Prove that \(\lfloor A\) + \(\lfloor B\) = 2\(\lfloor\mathrm{CED}\)

Solution:

Given: In a quadrilateral ABCD, the line segments bisecting \(\lfloor C\), & \(\lfloor D\) meet

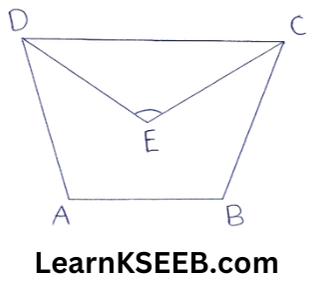
To prove: \(\lfloor A\)+\(\lfloor B\) = 2\(\lfloor\mathrm{CED}\)

Proof: In quadrilateral ABCD,

\(\lfloor A\) + \(\lfloor B\) + \(\lfloor C\)+ \(\lfloor D\) = 360° ………………….(1)

In ACED,

\(\lfloor\mathrm{CED}\) + \(\lfloor\mathrm{EDC}\) + \(\lfloor\mathrm{ECD}\) = 180° (angle sum property)

=> \(\lfloor\mathrm{CED}\) + 1/2 \(\lfloor D\)+ 1/2\(\lfloor C\) = 180°

=> 2\(\lfloor\mathrm{CED}\) + \(\lfloor D\)+ \(\lfloor C\) = 360° ………………..(2)

from(1) &(2)

2\(\lfloor\mathrm{CED}\) + \(\lfloor D\) + \(\lfloor C\) = \(\lfloor A\) + \(\lfloor D\) + \(\lfloor C\) + \(\lfloor D\)

=> 2\(\lfloor\mathrm{CED}\) = \(\lfloor A\) + \(\lfloor B\)

=> \(\lfloor A\) + \(\lfloor B\) = 2\(\lfloor\mathrm{CED}\)

Karnataka Board Class 9 Maths Chapter 8 MCQs

3. Prove that A diagonal of a ||gm divides it into two congruent triangles.
Solution:

ABCD is a ||gm. AC is a diagonal of ABCD which divides it into two Δles,

ie, ΔABC & ΔCDA.

To prove: ΔABC ≅ ΔCDA

Proof: BC || DA & AC is a transversal

∴ \(\lfloor\mathrm{BCA}\) = \(\lfloor\mathrm{DAC}\) …………………….(1) (alternate angles)

also AB || DC & AC is transversal

∴ \(\lfloor\mathrm{BAC}\) = \(\lfloor\mathrm{DCA}\) (alternate angles)

AC = CA = (3) (common)

∴ ΔABC ≅ ΔCDA

4. ABC is an isosceles Δle in which AB = AC. AD bisects \(\lfloor\mathrm{PAC}\) and CD ||AB Show that
1) \(\lfloor\mathrm{DAC}\) = \(\lfloor\mathrm{BCA}\)
2) ABCD is a ||gm

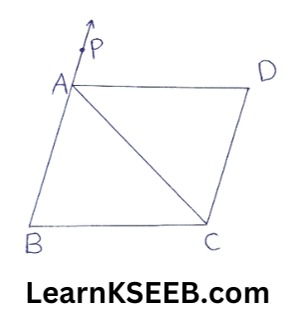
Solution:

Given: ABC is an isosceles Δle in which AB = AC.

AD bisects |PAC &CD || AB

To prove: 1) \(\lfloor\mathrm{DAC}\) = \(\lfloor\mathrm{BCA}\) 2) ABCD is a ||gm

Proof: (1) In ΔABC

AB = AC

=> \(\lfloor B\) = \(\lfloor C\) (Angles opp to equal sides of a Δle are equal)

Also exterior \(\lfloor\mathrm{PAC}\) + \(\lfloor B\) + \(\lfloor C\)

=> \(\lfloor\mathrm{PAC}\) = \(\lfloor C\) + \(\lfloor C\)

=> \(\lfloor\mathrm{PAC}\) = \(\lfloor C\) + \(\lfloor C\)

=> 2\(\lfloor\mathrm{CAD}\) = 2\(\lfloor C\) (∵ AD bisects |PAC)

=> \(\lfloor\mathrm{CAD}\) = \(\lfloor C\)

=>\(\lfloor\mathrm{DAC}\) = \(\lfloor\mathrm{BCA}\)

2) But these angles form a pair of equal alternate interior angles.

∴ AD || BC

also CD || AB

ABCD is a ||gm

(a quadrilateral is a Is ||gm if its both the pairs of opposite sides are parallel)

5. In Δle ABC points M &N on sides AB & AC respectively are taken so that AM = 1/4AB & AN = 1/4AC. Prove that MN = 1/4BC.

Solution:

E is the mid-point of AB &F is the mid-point of AC.

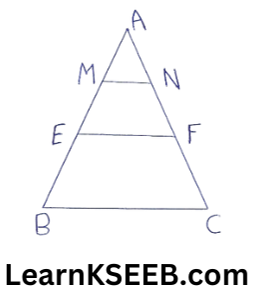
∴ EF || BC & EF = 1/2BC ………………..(1)

Now, AE = 1/2 AB

and AM = 1/4 AB

AM = 1/2AE

||ly AN= 1/2 AF

=> M & N are the mid-points of AE & AF respectively.

∴ MN || EF &

MN= 1/2 EF = 1/2×1/2BC (from(1))

=> MN = 1/4BC

6. In given fig, AD is the median of ΔABC, E is the mid-point of AD, DG || BE. Prove that AC = 3 A F.

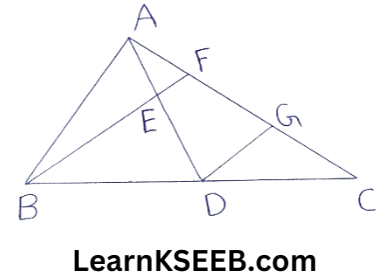
Solution:

In ΔADG, E is the mid-point of AD & EF || DG

=> F is the mid-point of AG (Converse of midpoint theorem)

AF = FG ……………………..(1)

In ΔCBF, BF || DG, D is the mid-point of BC

=> G is the mid-point of FC.

=> FG=GC ………………….(2)

from(1)&(2)

AF = FG = GC

AC = AF + FG + GC

AC = AF + AF + AF

=>AC = 3 AF

Four Mark Questions

1.ABCD is a ||gm & line segments AX, CY bisects the angles A & C respectively. Show that AX || CY

Solution:

ABCD is a ||gm

=>\(\lfloor A\)=\(\lfloor C\) (opp angle)

=> 1/2\(\lfloor A\)=1/2\(\lfloor C\) (Halves of equals are equal)

=> \(\lfloor 1\)=\(\lfloor 2\) (∵ AX is the bisector of A & CY is the bisector of C)

Now, AB || DC & CY intersects them

∴ \(\lfloor 2\)–\(\lfloor 3\) ……………….(2) (alternate interior angle)

from (1) & (2) we get \(\lfloor 1\)–\(\lfloor 3\)

But these form a pair of equal corresponding angles.

∴  AX || CY

Class 9 Maths Quadrilaterals KSEEB Guide

2. Vicky has a photo-frame without a photo in the shape of a Δle with sides a, b, c, in length. He wants to find the perimeter of a Δle formed by joining the mid-points of the sides of the photo frame. He could not understand how to over come this problem. He shares this problem with his classmate Somu. Somu helps him & the required perimeter is computed.
1) Find the perimeter of the Δle formed by joining the mid-points of the frame.
2) Which value is depicted between Vicky & Somu.

Solution:

1) Let the photo frame be ABC such that BC=a, CA=b & AB=c & the mid-points of AB, BC & CA are respectively D, E & F.

We have to determine the perimeter of A DEF.

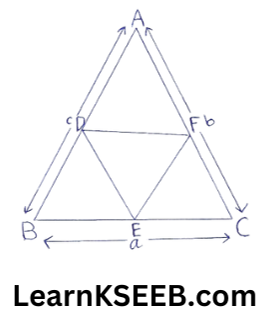
In ΔABC, DF is the line segment joining the mid-points of sides AB & AC.

So, DF is ||le to BC & half of it

i.e \(\mathrm{DF}=\frac{\mathrm{BC}}{2}=\frac{a}{2}\)

|| ly \(\mathrm{DE}=\frac{\mathrm{AC}}{2}=\frac{\mathrm{b}}{2}\)

& \(\mathrm{EF}=\frac{\mathrm{AB}}{2}=\frac{\mathrm{c}}{2}\)

∴ \(\mathrm{DF}+\mathrm{DE}+\mathrm{EF}=\frac{\mathrm{a}}{2}+\frac{\mathrm{b}}{2}+\frac{\mathrm{c}}{2}\)

\(=\frac{a+b+c}{2}\)

Hence required perimeter \(=\frac{a+b+c}{2}\)

2) Unity & cooperation or Mutual understanding.

3. ABCD is a square & on the side DC, an equilateral Δle is constructed. Prove that
1) AE = BE
2) \(\lfloor\mathrm{DAE}\) =15°

Solution: 1) Since ABCD is a square & ΔDCE is an equilateral Δle.

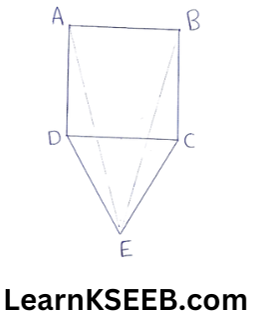
∴ \(\lfloor\mathrm{ADC}\) = 90°

∴ \(\lfloor\mathrm{EDC}\) = 60°

=> \(\lfloor\mathrm{ADC}\) + \(\lfloor\mathrm{EDC}\) = 90 + 60°

=> \(\lfloor\mathrm{APE}\) = 150°

|| Iy we have \(\lfloor\mathrm{BCE}\) = 150°

Thus in ΔADE & ΔBCE, we have

AD = BC

\(\lfloor\mathrm{DAE}\) = \(\lfloor\mathrm{BCE}\) = 150°

DE = CE

=> ΔADE ≅ ΔBCE (bySAS sule)

=> AE = BE (C.P.C.T)2) In AEAD , we have AD = DE

\(\lfloor\mathrm{EAD}\) = \(\lfloor\mathrm{AED}\) = x

Now \(\lfloor\mathrm{APE}\) + \(\lfloor\mathrm{AED}\) + \(\lfloor\mathrm{DAE}\) = 180°

150° + x + x= 180°

2x = 180°-150°

2x = 30°

=> x= 15°

=> \(\lfloor\mathrm{DAE}\) = 15°

4. There was four plants in Suraj’s fields. Suraj named their bases of P,Q, R & S. He joined PQ, QR, RS & SP. His teacher told him that the quadrilateral PQRS is ||gra. He asked him to find the measure of all the angles of the ||gm, provided that the measure of any one interior angle of PQRS. To obtain a technique & hence to solve the problem, he worked hard & spent much time.
1) Obtain all the angles of the ||gm PQRS if [R = 55°.
2) Which mathematical concept is used in the above problem?
3) Which value was depicted by Suraj on such a problem?

Solution:

1) \(\lfloor R\) = 55° (given)

SR || PQ & RQ is a transversal

∴ \(\lfloor R\) + \(\lfloor Q\) = 180°

55° + \(\lfloor Q\) = 180° (Co-interior angles)

\(\lfloor Q\) = 180° -55°

= 125°

\(\lfloor R\) = \(\lfloor P\) = 55°

\(\lfloor Q\) = \(\lfloor S\) = 125° (opp angles of a \\m are equal)

∴ \(\lfloor P\) = 55°, \(\lfloor Q\) = 125°, \(\lfloor R\) = 55° & \(\lfloor S\) = 125°

2) Property of Co-interior angles when a pair of straight lines intersected by another straight line.

3) Dedication, determination & Hard work.

5. ABCD is a rhombus & AB is produced to E & F such that AE = AB = BF. Prove that ED & FC are perpendicular to each other.

Solution:

Given: ABCD is a rhombus AB produced to E & F, such that AE = AB = BF

To prove: ED ⊥ FC

Construction: Join ED & CF & produce it to meet at G

Proof: AB is produced to point G & F

such that AE = AB = BF ………………..(1)

ABCD is a Rhombus

=> AB = BC = CD=AD …………………(2)

In ABCF

BC = BF (from (1) & (2))

=> \(\lfloor 1\)= \(\lfloor 2\)

\(\lfloor 3\) = \(\lfloor 1\) + \(\lfloor 2\) (exterior angle) …………………(3)

|| ly AE = AD

\(\lfloor 5\)= \(\lfloor 6\)

=> \(\lfloor 4\)= \(\lfloor 5\)+ \(\lfloor 6\) = 2\(\lfloor 5\) ………………..(4)

adding (3) & (4) we get

\(\lfloor 4\) + \(\lfloor 3\) = 2\(\lfloor 2\) + 2\(\lfloor 5\)

=> 180° = 2 (\(\lfloor 2\) + \(\lfloor 5\))

(∵ \(\lfloor 4\) & \(\lfloor 3\) are consecutive interior angles)

=> \(\lfloor 5\) + \(\lfloor 2\) = 90°

In ΔEGF

EG ⊥ FC

\(\lfloor 5\) +\(\lfloor 2\) + \(\lfloor\mathrm{EGF}\) = 180°

\(\lfloor 5\) + \(\lfloor 2\) =90°

=> 90° \(\lfloor\mathrm{EGF}\) = 180°

=> \(\lfloor\mathrm{EGF}\) = 90°

=> ED ⊥ FC

Hence proved

KSEEB Class 9 Maths Chapter 8 Exercise Solutions

6. In the given figure, bisectors of [B & [D 0f quadrilateral ABCD meet CD & AB produced at P & Q respectively. Prove that: \(\lfloor P\) + \(\lfloor Q\) =\(\frac{1}{2}(\lfloor\mathrm{ABC}+\lfloor\mathrm{ADC})\)

Solution:

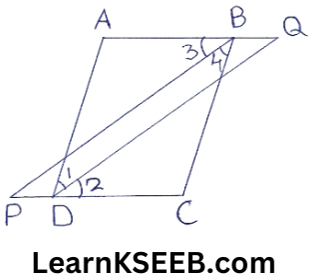
In ΔPBC, we have

\(\lfloor P\) + \(\lfloor 4\) + \(\lfloor C\) = 180°

=> \(\lfloor P\) + 1/2 \(\lfloor B\) + \(\lfloor C\) =180° ……………..(1)

In, ΔQAD, we have \(\lfloor Q\) + \(\lfloor A\) + \(\lfloor 1\) = 180°

=> \(\lfloor Q\) + \(\lfloor A\)+1/2\(\lfloor D\) = 180° ………………..(2)

adding (1) & (2) we get

\(\lfloor P\) + \(\lfloor Q\) + \(\lfloor A\) + \(\lfloor C\) + 1/2\(\lfloor B\)+1/2\(\lfloor D\) = 180 + 180

=>\(\lfloor P\) + \(\lfloor Q\) + \(\lfloor A\) + \(\lfloor C\)+1/2(\(\lfloor B\) + \(\lfloor D\)) = 360°

But \(\lfloor A\) + \(\lfloor B\) + \(\lfloor C\) + \(\lfloor D\) = 360°

(Sum of the angles of a quadrilateral)

∵ \(\lfloor P\) + \(\lfloor Q\) + \(\lfloor A\) + \(\lfloor C\)+1/2 (\(\lfloor B\) + \(\lfloor D\))

= \(\lfloor A\) + \(\lfloor B\) + \(\lfloor C\) + \(\lfloor D\)

=>\(\lfloor P\) + \(\lfloor Q\) = 1/2(\(\lfloor B\) + \(\lfloor D\))

=> \(\lfloor P\) + \(\lfloor Q\) = 1/2 (\(\lfloor\mathrm{ABC}\) + \(\lfloor\mathrm{ADC}\))

7. In the figure, ABCD is a ||gm & | DAB =60°. If the bisectors AP & BP of angles A & B respectively meet at P on CD. Prove that P is the mid-point of CD.

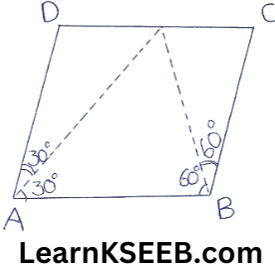
Solution: We have \(\lfloor\mathrm{DAB}\) = 60°

\(\lfloor A\) + \(\lfloor B\) = 180°

=> 60 + \(\lfloor B\) = 180°

=> \(\lfloor B\) = 180° – 60° = 120°

Now, AB || BC & transversal AP intersects them

\(\lfloor\mathrm{PAB}\) = \(\lfloor\mathrm{APD}\)

=> \(\lfloor\mathrm{APD}\) 30° (∵ \(\lfloor\mathrm{PAB}\) = 30°)

Thus in ΔAPD, we have

\(\lfloor\mathrm{PAD}\) = \(\lfloor\mathrm{APD}\)

=> AD = PD …………….(1)

(Angles opp to equal sides are equal)

Since BP is the bisector of \(\lfloor B\)

∴ \(\lfloor\mathrm{ABP}\) = \(\lfloor\mathrm{PBC}\) = 60°

Now, AB || DC & transversal BP intersects them

∴ \(\lfloor\mathrm{CPB}\) – \(\lfloor\mathrm{ABP}\)

=> \(\lfloor\mathrm{CPB}\) = 60°

Thus in ΔCBP, we have

\(\lfloor\mathrm{CBP}\) = \(\lfloor\mathrm{CPB}\) (each equal to 60°)

=> CP = BC (Sides opp. to equal angles are equal)

=> CP = AD ………………..(2)

(ABCD is a || gm , AD = BC)

from (1) & (2) we get

PD = CP

P is the mid-point of CD.