Karnataka Class 9 Maths Model Question Papers Set 3
Choose the correct alternative and Write the complete answer along with its alphabet in the sheet provided:
Question 1. Which of the following is an irrational number
- \(\sqrt{9}\)
- \(\sqrt{4}\)
- \(\sqrt[3]{27}\)
- \(\sqrt{10}\)
Solution: 4. \(\sqrt{10}\)
Question 2. The zero of the polynomial p(x) = x3 +1 is
- \(\sqrt{7}\)
- – 1
- 2
- 1
Solution: 2. – 1
Question 3. The expansion form of (x+ a)(x+ 6) is
- x2-ab-a
- x2 -(a-b)x-ab
- x2+(a+b)x+ab
- x2+2ab
Solution: 3. x2+(a+b)x+ab
Question 4.y = 3x+ 5 has
- A unique solution
- Only two solutions
- No solutions
- Infinitely many solutions
Solution: 4. Infinitely many solutions
Karnataka 9th Standard Maths Model Question Paper 2023 Set 3 Free PDF
Question 5. A sum of the angles of a quadrilateral is
- 180°
- 270°
- 360°
- 400°
Solution: 3.360°

Question 6. In a triangle ABC, E is the midpoint of median AD. Then ar (ABED) =
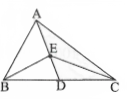
- 1/4 ar(ΔABC)
- 1/3 ar(ΔABC)
- ar(ΔABC)
- 1/6 ar(ΔABC)
Solution: 1. 1/4 ar(ΔABC)
Question 7. The total surface area of a hemisphere is
- 4πr2
- 2πr2
- 3πr2
- πr2
Solution: 3. 3πr2
Question 8. Heron’s formula –
- \(\sqrt{s(s-a)(s-b)}\)
- \(\sqrt{s(s-a)(s-c)}\)
- \(\sqrt{s(s-a)}\)
- \(\sqrt{s(s-a)(s-b)(s-c)}\)
Solution: 4. \(\sqrt{s(s-a)(s-b)(s-c)}\)
Class 9 Karnataka Maths Model Question Paper 2023 Set 3 with Answer Key
Question 9. The mode of the following score is 4, 6, 5, 9, 3, 2, 7, 7, 6, 5, 4
- 5
- 7
- 6
- 4
Solution: 2. 7
Question 10. In which quadrant does (-2, 4) lie?
- I
- II
- III
- IV
Solution: 2. II
Answer the following:
Question 1. Define a rational number
Solution: A number that can be expressed in the form of p/q, where ‘p’ and ‘q’ are integers and (q ≠0)
Example: 1/2,-7/5 ……..
Question 2. Is zero a rational number? can you write it in the form of p/q, where p and q are integers and q ≠ 0
Solution: yes, zero is a rational number as it can be represented as (0/1) or (0/2)…………….
Question 3. Write 36/100 in decimal form.
Solution = 36/100 = 0.36, terminating………..
Question 4. Simplify \((\sqrt{5}+\sqrt{2})^2\)
Solution:
& (\sqrt{5}+\sqrt{2})^2 \\
& (a+b)^2=a^2+2 a b+b^2 \\
& (\sqrt{5}+\sqrt{2})^2=(\not \sqrt{5})^2+2(\sqrt{5})(\sqrt{2})+(\sqrt{2})^2 \\
& (\sqrt{5}+\sqrt{2})^2=7+2 \sqrt{10}
\end{aligned}\)
Question 5. Write the general form of linear equation in two variable
Solution: ax + by + c = 0, where a, b and c are real numbers.
Question 6. Find the value of ‘x’ in the figure,
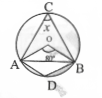
Solution: x = 1/2 x 80°
Question 7. The diameter of the base of a cone is 10cm and its slant height is 10cm. Find the curved surface area
Solution:
CSA of cone =πrl
= 22/7 x 5 x 5
= 7805cm2
Question 8. Find the value of (125)1/3
Solution:
\((125)^{\frac{1}{3}}=\left(125^3\right)^{\frac{1}{3}}=5^{\not p \times \frac{1}{3}}=5\)Question 9. Write any two polynomials whose degree is 2.
Solution: 2X2 +X= 0 , 3 y2+l = 0
Question 10. Name the quadrants in which the following points lie:
- P(4,4)
- Q (-4, 4)
- R(-4,4)
- S(-4,8)
Solution:
- P(4,4) = I
- Q(-4,4) = II
- R(-4,-4) = III
- S(-4,8) =II
Karnataka Board 9th Class Maths Model Paper 2023 Set 3 Latest Pattern
Answer the following :
Question 1. Express locate \(\sqrt{2}\) on the number line.
Solution:
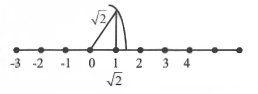
Question 2. Express \(0 \ overlines {99}\) in the form of p/q, where p and q are integers and 0.
Solution:
\(0 \ overlines {99}\)= 0.99999……..
Let x = 0.99999…………
100x= 100 x 0.9999…………..
100x=99.9999…………..
100x=99+0.9999……………
100x = 99 + x 1
100x-x = 99
99x=9
x = 99/99 = 1
Thus 0.99999 = 1 = 1/1
1 Here P = 1, q = 1
Question 3. Simplify: \((\sqrt{5}+\sqrt{3})(2+\sqrt{3})\)
Solution:
\(\begin{aligned}& (5+\sqrt{3})(2+\sqrt{3}) \\
& =5(2+\sqrt{3})+\sqrt{3}(2+\sqrt{3}) \\
& =10+5 \sqrt{3}+2 \sqrt{3}+(\sqrt{3})^2 \\
& =10+5 \sqrt{3}+2 \sqrt{3}+(\sqrt{3})^2 \\
& =10+5 \sqrt{3}+2 \sqrt{3}+3 \\
& =13+5 \sqrt{3}+2 \sqrt{3} \\
& =13+7 \sqrt{3}
\end{aligned}\)
Question 4. Find the value of k, if (x-l) is a factor of
\(p(x)=k x^2-\sqrt{2} x+1\)
Solution:
\(\begin{aligned}& p(x)=k x^2-\sqrt{2} x+1 \\
& x=1, k(1)^2-\sqrt{2}(1)+1 \\
& p(1)=k-\sqrt{2}+1 \\
& 0=k-\sqrt{2}+1 \\
& k=\sqrt{2}-1
\end{aligned}\)
Question 5.Factorise : 6X2 + 5x – 6
Solution:
6X2 +5x-6
= 6X2 +9x—4x — 6
= 3x(2x + 3) — 2(2x + 3)
= (2x + 3)(3x-2)
Question 6. Expand \(\left(x+\frac{2}{3} y\right)^3 \)using a suitable identity.
Solution:
\(\left(x+\frac{2}{3} y\right)^3\)(a + b)3=a3+b3 + 3ab(a + b)
\(\begin{gathered}\left(x+\frac{2}{3} y\right)^3=(x)^3\left(\frac{2}{3} y\right)^3+\not \beta(x)\left(\frac{2}{\not p} y\right)\left(x+\frac{2}{3} y\right) \\
\left(x+\frac{2}{3} y\right)^3=x^3+\frac{8}{27} y^3+2 x y\left(x+\frac{2}{3} y\right)
\end{gathered}\)
Question 7.Which of the following options is true and why?
y = 3xr + 5
- a unique solution
- only two solutions
- infinitely many solutions.
Solution: 3. infinitely many solutions.
As for every value of x, there will be a value for satisfying the above equation and vice-versa.
Question 8.Find the value of k, if x = 2,y = 1 is a solution of the equation 2x + 3y=k
Solution:
2x + 3y = k
2(2) + 3(1) = k
4 + 3 = k
∴ k = l
9th Standard Karnataka Maths Sample Paper 2023 Set 3 with Solutions PDF
Question 9. In AABC 5 AD is the perpendicular bisector of BC. S.T. ΔABCis an isosceles triangle in which AB = AC.
Solution:
ΔABC, AD ⊥ BC,
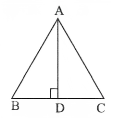
In ΔADB and ΔADC
∠APB = ∠ADC = 90°
DB = DC
∴ AD is the perpendicular bisector of BC
AD =AD (common)
∴ AADB ≅ AADC (SAS)
∴ AB = AC (CPCT)
Question 10. Find the volume of a sphere whose 7cm radius is
Solution:
The volume of the sphere = 4/3πr3
\(=\frac{4}{3} \times \frac{22}{7} \times(7)^{\frac{2}{z}}\)
& =\frac{4}{3} \times \frac{22}{7} \times 7 \times 7 \\
& =\frac{4312}{3} \\
& =1437.33 \mathrm{~cm}^3
\end{aligned}\)
Question 11. Define a line segment.
Solution: A straight line joining any two distinct points is called a line segment.
![]()
Question 12. In the fig, sides QP and RQ of APQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ
Solution: ∠SPR + ∠QPR = 180° (linear pair)
135° + ∠QPR = 180°
∠QPR = 45°
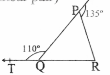
∠PQT + ∠PQR = 180° (linear pair)
110″+ ∠PQR =180°
∠PQR = 70°
In APQR, ∠PQR + ∠QPR + ∠PRQ = 180°
70° + 45° + ∠PRQ = 180°
∴∠PRQ = 65°
Question 13. In fig, if x + y = w + z, then prove that AOB is a line.
Solution:
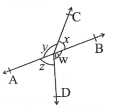
Let x + y — w + z = k
∴ x + y + w + z = 360°
k + k = 360°
2k = 360°
k = 360°/2
k= 180°
∴ x + y = w + z = k
x + y = w + z = 180°
Question 14.ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal S.T.
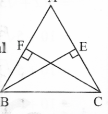
- ΔABE ≅ΔACF
- AB = AC
Solution:
In ΔABE and ΔACF
∠AEB = ∠AFC = 90° (given)
altitude BE = altitude CF (given)
∠A is common
∴ΔABE = ΔACF
AB = AC (CPCT)
∴AB is an isosceles triangle
Question 15.ABCD is a quadrilateral in which P, Q, R, and S are midpoints of the sides AB, BC, CD, and DA. AC diagonal S.T. SR || AC and SR= 1/2 AC
Solution:
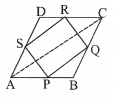
In A ADC, S, and R are the midpoints of the sides AD and CD respectively.
∴By the midpoint theorem, the line joining the midpoints of any two sides of a triangle is parallel to the third side and half of the third side.
∴SR || AC
and SR 1/2 AC
Question 16. The following table gives the lifetimes of 400 neon lamps.
Solution:
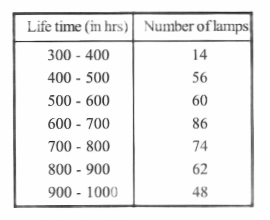
Represent the given information with the help of a histogram.
Scale : x-axis ; 1cm- limit y-axis; lcm = limit

Question 17. In a cricket match, a batswoman hits a boundary 6 times out of 30 balls she plays. Find the probability that she did not hit a boundary.
Solution:
Total number of balls played = 30
Number of boundaries hit = 6
Number of balls in which she has not hit the boundary =30-6 = 24 ∴Probability=
(No. of times she does not hit the boundary)/
(Total number of balls played)
p= 24/30 = 4/5
Question 18. Use deductive reasoning to answer the following.
- Martians have red tongues. Gulag is a Martian. Based on these two statements, what can you conclude about Gulag?
- If it rains for more than four hours on a particular day, the gutters will have to be cleaned the next day. It has rained for 6 hours today. What can we conclude about the condition of the gutters tomorrow?
Solution:
- Gulag his red tongue.
- we conclude that the gutters will have to be cleaned tomorrow.
Answer the following :
Question 1.Check whether 7 + 3x is a factor of 3x3+ 7x
Solution:
consider p (x) = 3x3 + 7x
\(\begin{gathered}\mathrm{P}\left(-\frac{7}{3}\right)=3\left(-\frac{7}{3}\right)^3+7\left(-\frac{7}{3}\right) \\
={ }^1 \not \beta\left(-\frac{343}{27}\right)^3+7\left(-\frac{7}{3}\right) \\
=\frac{-343}{9}-\frac{49}{3} \\
=\frac{-343-147}{9} \\
\mathrm{P}\left(-\frac{7}{3}\right)=\frac{-490}{9}
\end{gathered}\)
Karnataka Class 9 Maths Previous Year Model Paper 2023 Set 3 Solved PDF
Question 2. Visualize \(4. \overline{26}\) on the number line up to 4 decimal places.
Solution: \(4. \overline{26}\)= 4.2626

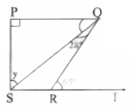
Question 3. In fig, if PQ ⊥PS. PQ || SR, ∠SQR = 28° and ∠QRT = 65°, then find the values of x and y
Solution:
PQ || SR and QR is a transversal line
∴ ∠PQR = ∠QRT (Alternate interior angles)
x + 28° = 65°
x = 65°- 28°
x = 37°
By using the angle sum property in ΔSPQ
∠SPQ + x + y = 180°
90°+37° +y = 180°
y = 53°
∴ x = 37°
y = 53°
Karnataka 9th Maths Sample Paper 2023 Set 3 for Exam Preparation
Question 4.In fig. AC =AE, AB = AD, and ∠BAD = ∠EAC S.T. BC = DE
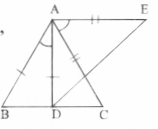
Solution:
∠BAD = ∠EAC (given)
Adding ∠DAC on both sides,
∠BAD + ∠DAC = ∠EAC + ∠DAC
∴∠BAC-∠DAE
In ΔBAC and ΔDAE
AB =AD (given)
∠BAC = ∠DAE
AC = AE (given)
∴ ΔBAC ≅ ΔDAE (SAS)
∴ BC=DE (CPCT)
Question 4. S.T. the diagonals of a parallelogram divide it into four triangles of equal area.
Solution:
We know that the diagonals A and B of a parallelogram bisect, each other.
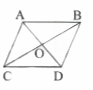
∴‘O’ is the midpoint of AC and BD.
BO is the median in ΔABC.
∴It will divide it into two triangles of equal areas.
∴Area (ΔAOB) =Area (ΔBOC)…………………..(1)
In ΔBCD, CO is the median
∴Area (ΔBOC) =Area (ΔCOD)……………………. (2)
similarly, Area(ΔCOD)=Area (ΔAOD) …(3)
From (1) (2) & (3)
Area (ΔAOB) = Area (ΔBOC)
= Area (ΔCOD) = Area (ΔAOD)
The diagonals of a parallelogram divide it into four triangles of equal area.
Question 5. Construct a triangle ABC in which Be = 8cm,
∠B = 45° and AB – AC = 3.5cm
Solution:
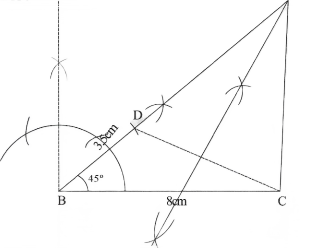
Answer the following:
Question 1. The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
Solution:
The volume of the moon = 4/3 πr3
\(\begin{aligned}
& =\frac{4}{3} \pi r^3\left(\frac{d}{8}\right)^3 \\
& =\frac{4}{3} \times \frac{\pi d^3}{512}
\end{aligned}\)
The volume of the earth = 4/3 πr3
\(\begin{aligned}& =\frac{4}{3} \pi\left(\frac{d}{2}\right)^3 \\
& =\frac{4}{3} \times \frac{\pi d^3}{8}
\end{aligned}\) \(\frac{\text { volume of the moon }}{\text { volume of the earth }}=\frac{\frac{4}{3} \times \frac{\pi d^3}{512}}{\frac{4}{3} \times \frac{\pi d^3}{8}}\) \(\frac{\text { volume of the moon }}{\text { volume of the earth }}=\frac{1}{64}\)
The volume of the moon=1/64 volume of the earth.
Question 2. Find the area of a triangle with two sides which are 18cm and 10cm and the perimeter is 42cm.
Solution:
Let the third side of the triangle 42cm
perimeter = 42cm
18 + 10 + x = 42
28 + x = 42
x = 42 – 28
x = 14
x = perimeter/2 =42/2 = 21cm
By Heron’s formula
Area of a triangle= \(\sqrt{s(s-a)(s-b)(s-c)}\)
\(\begin{aligned}& =\sqrt{21(21-18)(21-10)(21-14)} \\
& =\sqrt{21 \times 3 \times 11 \times 7} \\
& =21 \sqrt{11} \mathrm{~cm}^2
\end{aligned}\)
Question 3. Prove that equal chords in a circle are equidistant from the center.
Solution:
Data: A circle with center‘ O’, chords AB and CD such that AB = CD. Draw OP ⊥ AB and OQ ⊥ CD.
To prove: OP = OQ
Construction: Join OB and OD
Proof: AP = PB
CQ = QD
PB = 1/2 AB and QD = 1/2 CD.
In ΔOPB and ΔOQD
∠OPB= ∠OQD (both equal to 90°)
OB = OD (radii of the circle)
PB = QD
∴ ![]() OPB≅
OPB≅ ![]() QQD
QQD
OB= OD (radii of the circle)
PB = QD
∴![]() OPB≅
OPB≅ ![]() OQD (RHS theorem)
OQD (RHS theorem)
OP = OQ (CPCT)
9th Class Karnataka Maths Model Paper 2023 Set 3 Important Questions PDF
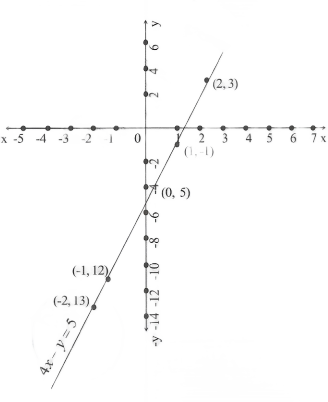
Question 4. Draw the graph of 4x-y = 5
Solution:
Scale : x-axis ; 1cm = 1unit y-axis ; 1cm = 1unit