KSEEB Class 8 Maths Solutions For Chapter 4 Understanding Quadrilaterals Points To Remember
Polygons: A simple closed curve made up of only line segments.
A line segment connecting two non-consecutive vertices of a polygon is called a diagonal.
Convex Polygon: The measure of each angle is less than 180°.
Concave Polygon: The measure of at least one angle is more than 180°.
Read and Learn More KSEEB Solutions for Class 8 Maths
For a regular polygon of n sides (n≥3)
Each exterior angle=[360/n]°
Each interior angle = [2n-4/n x 90]°
Interior angle+exterior angle = 180°.
For a convex polygon of n sides
| Class 10 Science | Class 11 Chemistry |
| Class 11 Chemistry | Transformation of Sentences |
| Class 8 Maths | Class 8 Science |
Sum of all exterior angles=360°
Sum of all interior angles =(2n-4)x90°
Number of diagonals of n sides (n>3)
= n(n-3)/2
A triangle has no diagonals
Quadrilaterals: Polygon having four sides
Kseeb Solutions For 8th Class Maths Chapter 4
Element of Quadrilateral:
Sides: Lined segments joining the points.
Vertices: Point of intersection of two consecutive sides.
Opposite sides: Two sides of a quadrilateral having no common end point.
Opposite angles: Two angles of a quadrilateral not having a common area.
Diagonals: Line segment obtained by joining the opposite vertices.
Adjacent angles: Two angles of a quadrilateral having a common arm
Adjacent sides: Two sides of a quadrilateral having a common end point.
Parallelogram: A quadrilateral with each pair of opposite sides parallel.
1) Opposite sides are equal
2) Opposite angles are equal
3) Diagonals bisect one another
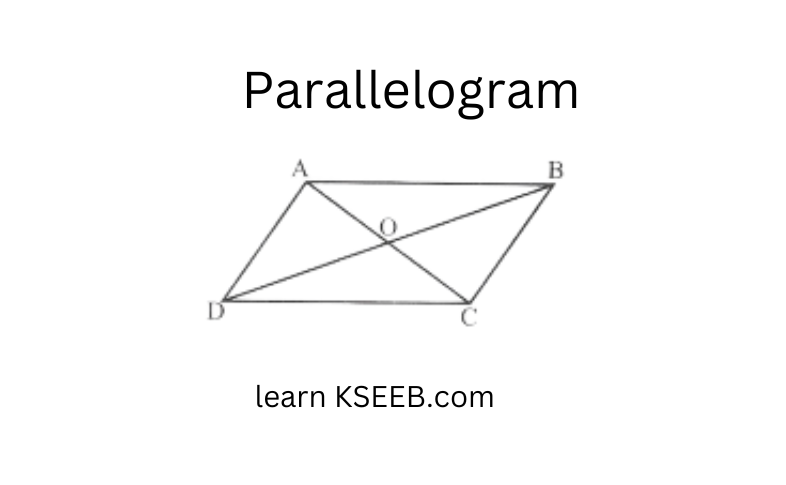
Karnataka Board 8th Maths Chapter 4 Understanding Quadrilaterals Solutions
Rhombus: A parallelogram with sides of equal length
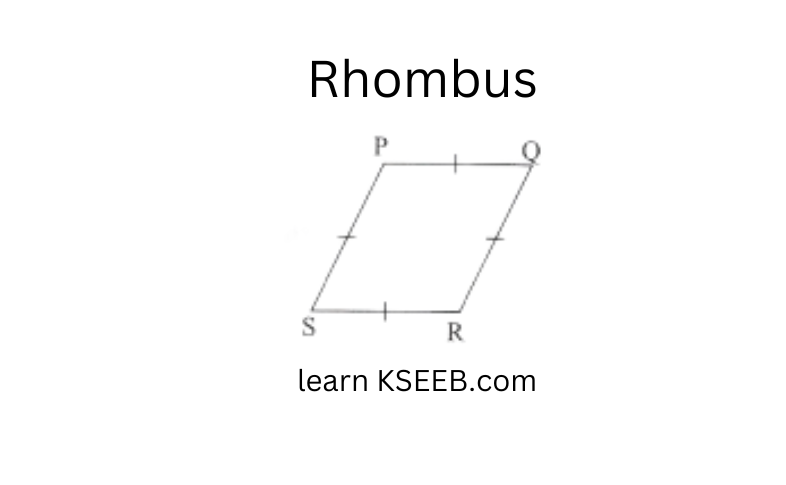
1) All the properties of a parallelogram
2) Diaganols are perpendicular to each other.
Rectangle: a parallelogram with a right angle
1) All the properties of a parallelogram.
2) Each of the angles is a right angle.
3) Diagonals are equal.
Kseeb 8th Standard Maths Chapter 4 Textbook Solutions
Square: A rectangle with sides of equal length,
1) All the properties of a parallelogram, rhombus and a rectangle.
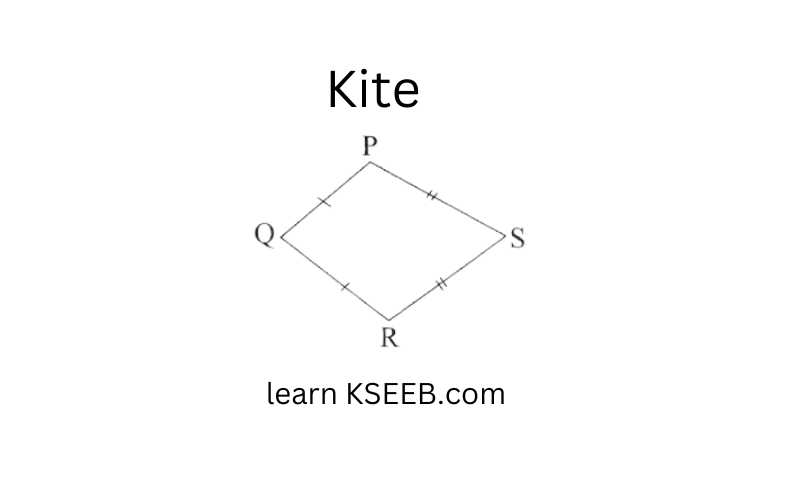
Kite: A quadrilateral with exactly two pairs of equal consecutive sides.
Class 8 Maths Chapter 4 Kseeb Important Questions And Answers
1) The diagonals are perpendicular to one antoher
2) One of the diagonals bisects the other
3) In the figure m∠R=m∠P
but m∠Q = = m∠S
KSEEB Class 8 Maths Chapter 4 Understanding Quadrilaterals Solutions
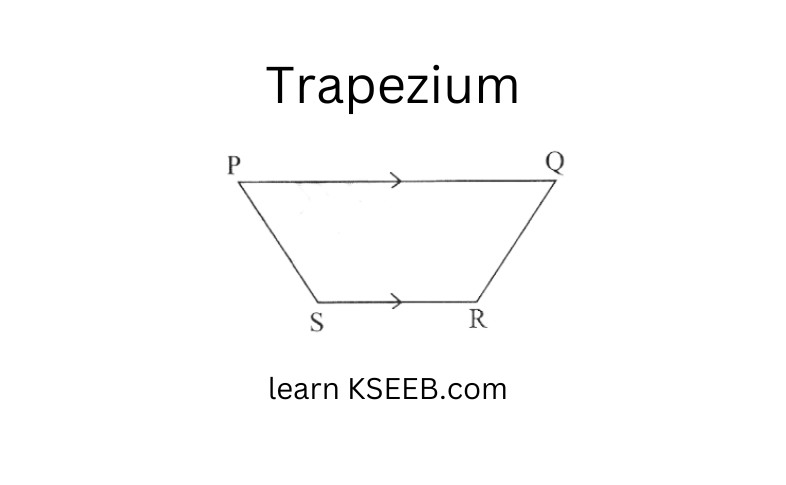
Trapezium: A quadrilateral having exactly one pair of parallel sides.
Understanding Quadrilaterals Solutions KSEEB Class 8 Maths Exercise 4.1
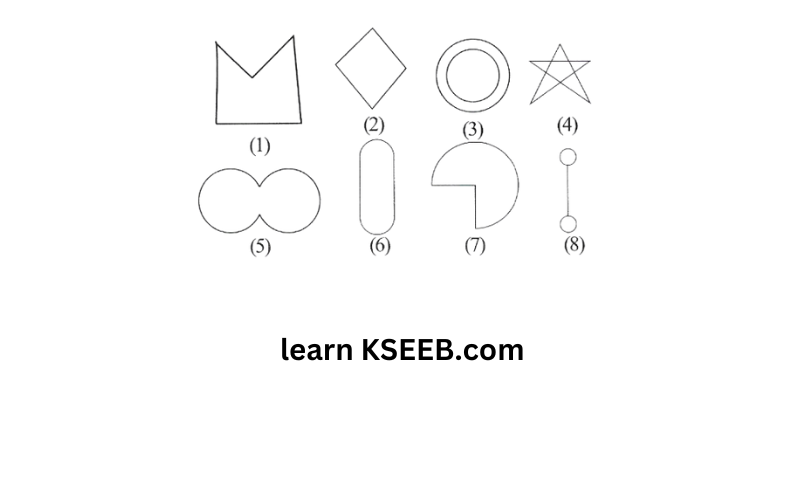
1) Given here are some figures
Understanding Quadrilaterals Class 8 Kseeb Notes
Classify each of them on the basis of the following.
a) Simple curve
b) Simple closed curve
c) polygon
d) Convex polygon
e) Concave polygon
Solution:
a) Simple curve – 1, 2, 5, 6, 7
b) Simple closed curve – 1, 2, 5, 6, 7
c) Polygon – 1,2
d) Convex polygon-2
e) Concave polygon-1
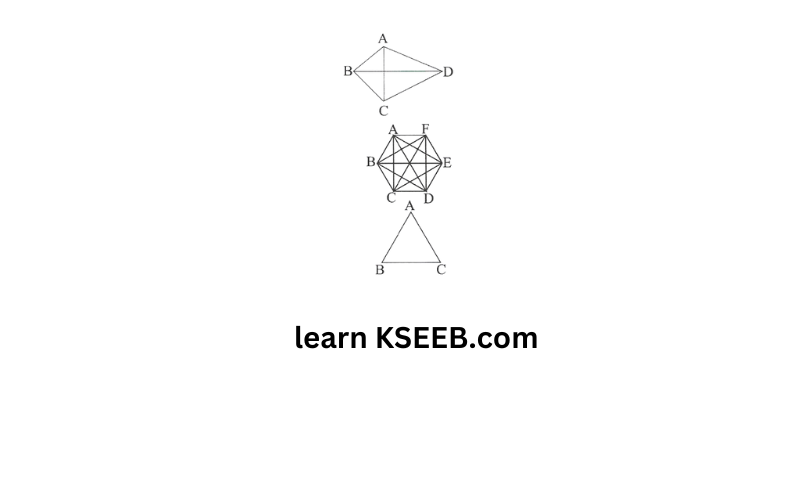
2) How many diagonals does each of the following have?
a) Convex quadrilateral
Solution: There are 2 diagonals in a convex quadrilateral
b) A regular hexagon
Solution: There are 9 diagonals in a regular hexagon
c) A triangle
Solution: A triangle does not have any diagonal in it.|
3)What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)
Solution: The sum of the measure of the angles of a convex quadrilateral is 360° as a convex quadrilateral is made of two triangles.
Here ABCD is a convex quadrilateral made of two triangles △ABD and △BCD
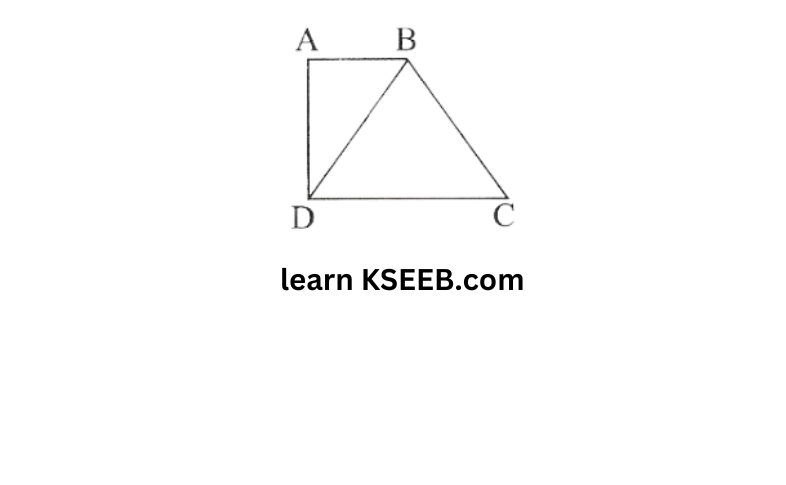
∴ The sum of all the interior angles of this quadrilateral will be same as the sum of all the interior angles of these two triangles ie 180° +180° 360°
Yes, this property also holds true for a quadrilateral which is not convex, this is because any quadrilateral can be divided into two triangles.
Here, again, ABCD is a concave quadrilateral, made of two triangles
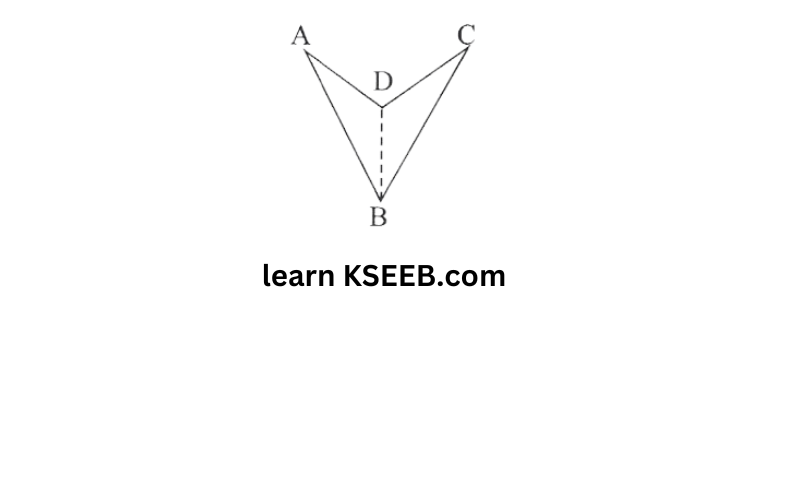
△ABD and △BCD
∴ sum of all the interior angles of this quadrilateral will also be 180° +180°= 360°
4. Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that)
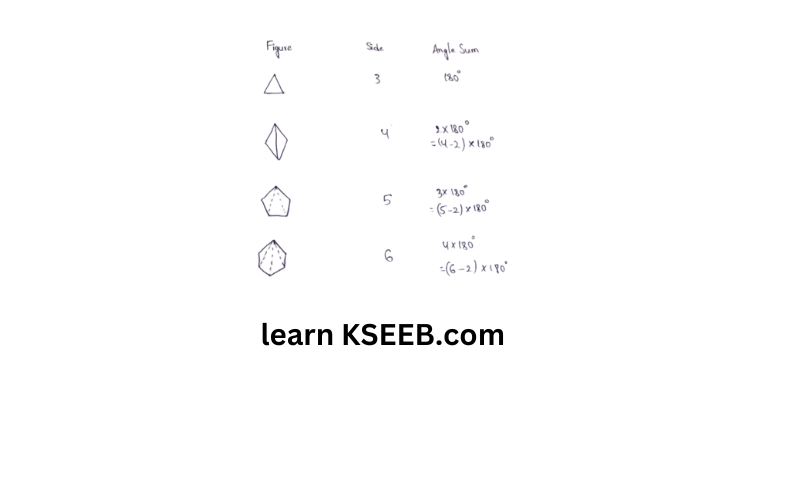
What can you say about the angle sum of a convex polygon with number of sides?
a) 7
b) 8
c) 10
d) n
Solution: From the table, it can be observed that the angle sum of a convex polygon of n sides is (n-2)x180°. Hence, the angle sum of the convex polygons having number of sides as
above will be as follows:
a) (7-2)x180°=900°
b) (8-2)x180°=1080°
c) (10-2)x180°=1440°
d) (n-2)x180°
5) What is a regular polygon? State the name of a regular polygon of
1080°
1) 3 sides
2) 4 sides
3) 6 sides
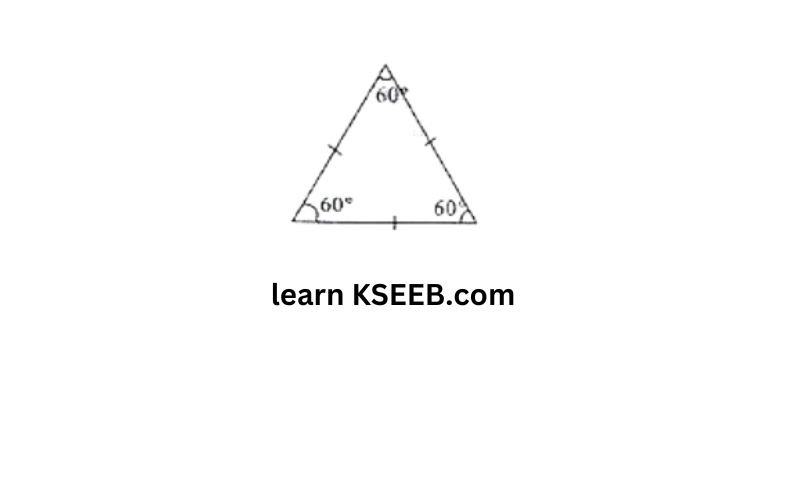
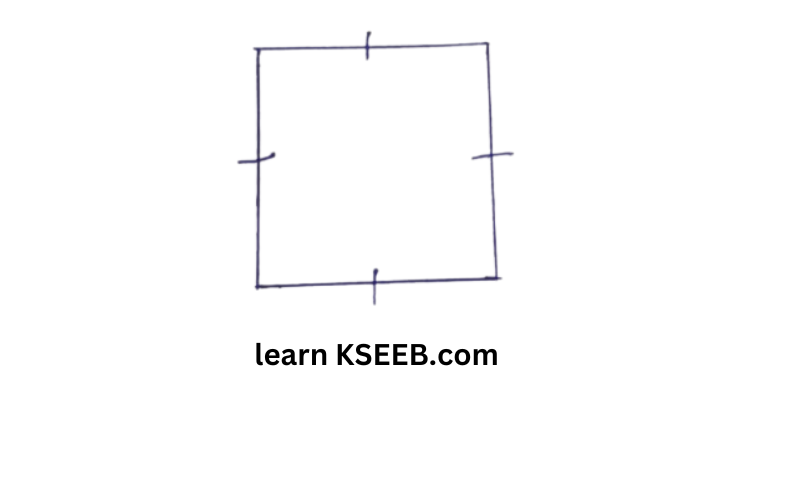
Solution: A polygon with equal sides and equal angles is called a regular polygon.
i) Equilateral triangle
ii) Square
iii)Regular Hexagon
6) Find the angle measure x in the following figures.
a)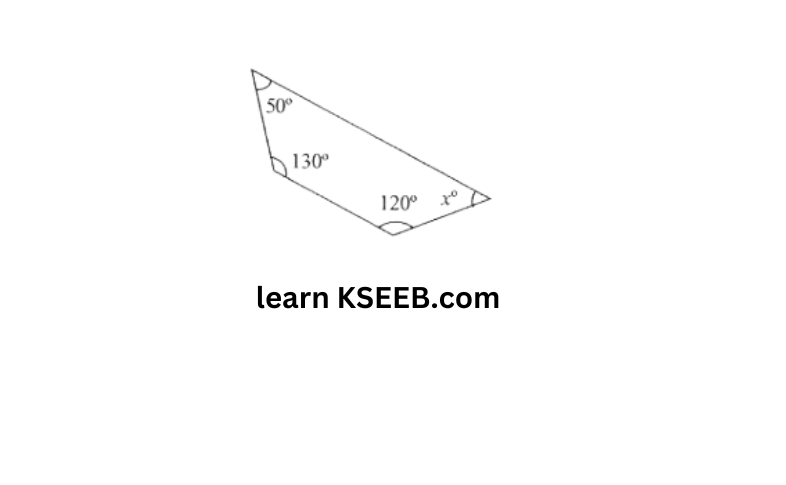 
Sum of the measures of all interior angles of a quadrilateral is 360°.
∴ In the given quadrilateral
50°+130°+120°+x=360°
300°+x=360°
x=360°-300=60°
b)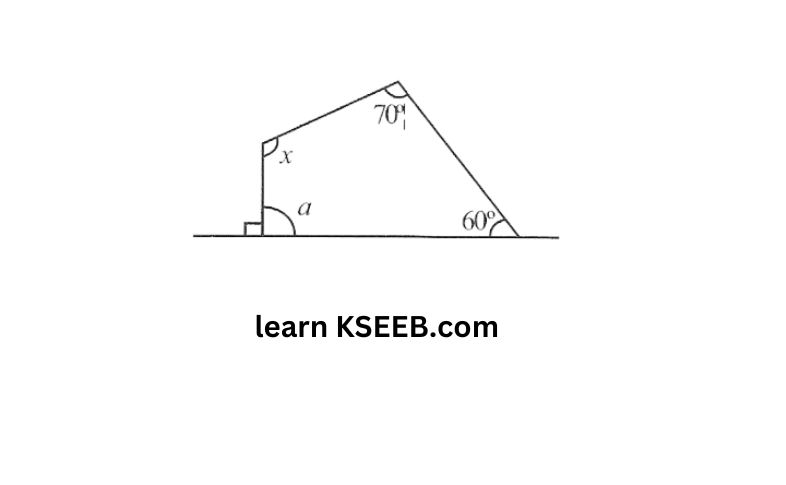 
From the figure, it can be concluded that,
90° +a 180° (linear pair)
a=180°-90=90°
Sum of the measures of all interior angles of a quadrilateral is 360°.
∴ In the given quadrilateral
60° +70°+x+90°= 360°
220°+x=360°
x=360°-220=140°
c)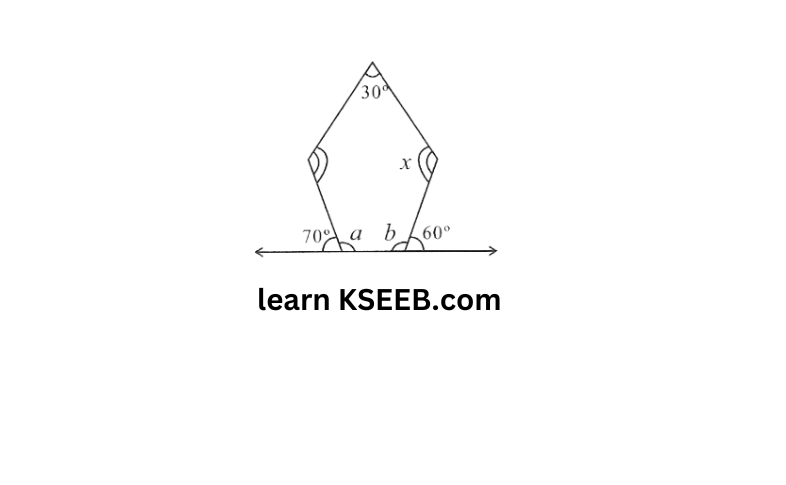 
Solution: From the figure, it can be concluded that
70°+a=180° (linear pair)
a=110°
60° +b=180° (linear pair)
b=120°
Sum of the measures of all interior angles of a pentagon is 540°
∴In the given pentagon
120°+110°+30°+x+x=540°
260°+2x = 540°
2x=540°-260°-280°
x=280/2=140°
d) 
sum of the measure of all interior angles of a pentagon is 540°
5x=540°
x=108°
7) Find x+y+z
a)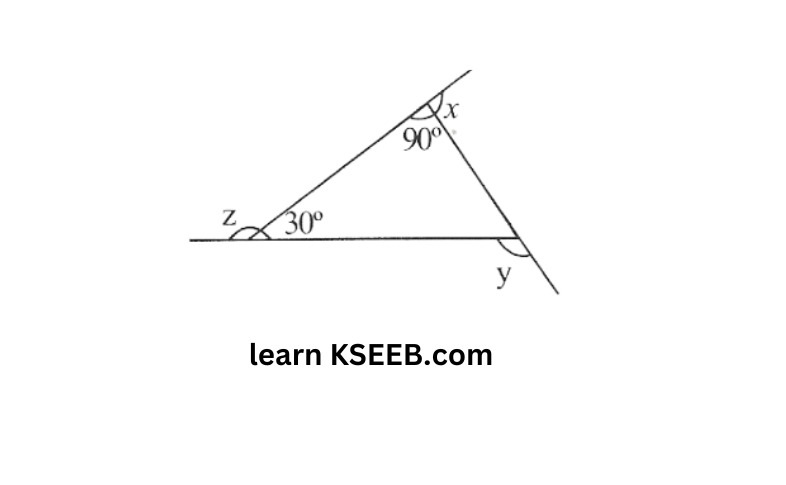 
Solution:
x+90°= 180° (linear pair)
x=90°
z+30=180° (linear pair)
z=150°
y=90°+30° (Exterior angle theorem)
y =120°
∴ x+y+z 90+150+120=360°
b)Find x+y+z+w
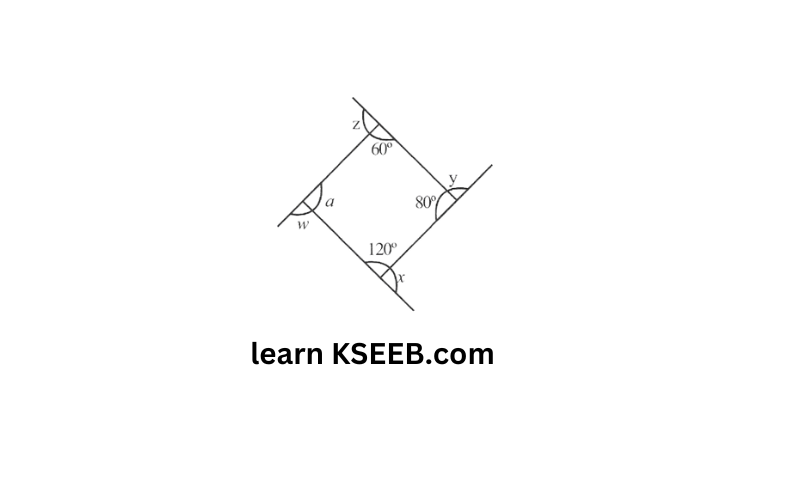
Solution: Sum of the measures of all interior angles of a quadrilateral is 360°
∴In the given quadrilateral
a+60° +80°+120°=360°
a=360-260=100°
x+120° 180° (linear pair)
x = 60°
y+80°=180°
∴ y=100°
z+60°=180°
∴ z=120°
w+100°=180°
∴ w=80°
sum of the measures of all interior angles
= x+y+z+w
=60°+100+120°+80°
x+y+z+w = 360°
KSEEB Class 8 Maths Chapter 4 Understanding Quadrilaterals Exercise 4.2
1) Find x in the following figures.
a)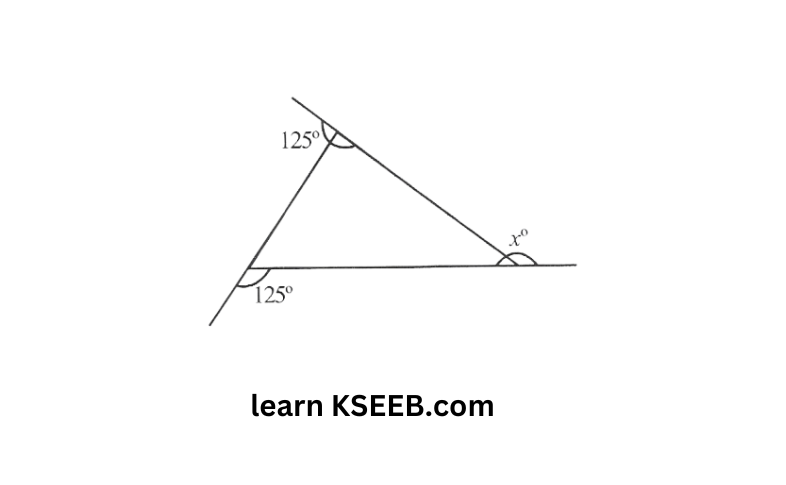 
Solution: W.K.T. the sum of all exterior angles of any polygon is 360°
125°+125°+x = 360°
x+250°= 360°
⇒ x=360°-250°=110°
⇒ x=110°
b)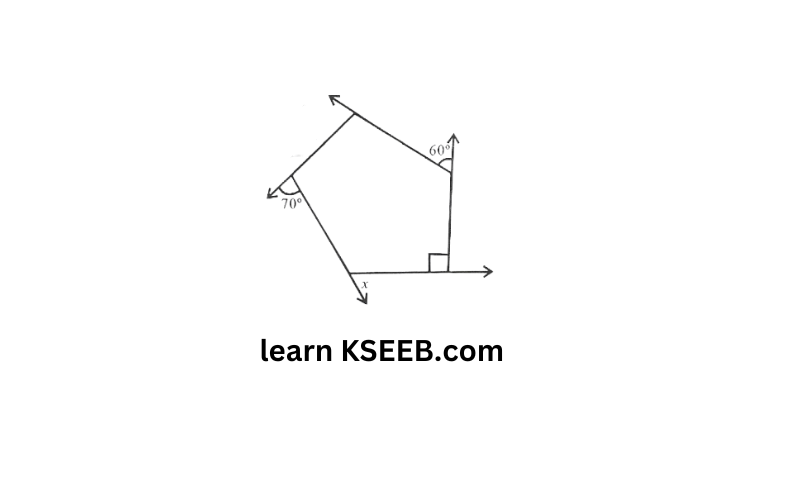 
Solution:
60°+90°+70°+x+90° = 360°
310°+x = 360°
x=360-310 = 50°
KSEEB Class 8 Maths Chapter 4 Solved Problems
2) Find the measure of each exterior angle of a regular polygon of
1) 9 sides
2) 15 sides
Solution:
i) Sum of all exterior angles of the given polygon = 360°
Each exterior angle of a regular polygon has the same measure.
Thus, measure of each exterior angle of a regular polygon of 9 sides = 360°/9 =40°
ii) Sum of all exterior angles of the given polygon=360°
Each exterior angle of a regular polygon has the same measure.
Thus, measure of each exterior angle of a regular polygon of 15 sides = 360°/15 = 24°
3)How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Solution: Sum of all exterior angles of the given polygon=360º.
Measure of each exterior angle = 24°
Thus, number of sides of the regular polygon
= 360°/24 = 15°
4) How many sides does a regular polygon have if each of its interior angles is 165°?
Solution: Measure of each interior angle = 165°
Measure of each exterior angles = 180° – 165° = 15°
The sum of all exterior angles of any polygon is 360º.
Thus, number of sides of the polygon
= 360º/15 = 24
5) a) Is it possible to have a regular polygon with measure of each exterior angle is 22º?
b) Can it be an interior angle of a regular polygon? Why?
Solution:
The sum of all exterior angles of all polygon is 360°. Also in a regular polygon each exterior angle is of the same measure. Hence, if 360° is a perfect multiple of the given exterior angle, then the given polygon will be possible.
a) Exterior angle = 22°
360° is not a perfect multiple of 22º. Hence such polygon is not possible.
b) Interior angle = 22°
Exterior angle = 180-22=158°
Such a polygon is not possible as 360° is not a perfect multiple of 158°.
6) a) What is the minimum interior angle possible for a regular polygon?
b) What is the maximum exterior angle possible for a regular polygon?
Solution: Consider a regular polygon having the lowest possible number of sides (ie, an equilateral triangle). The exterior angle of this triangle will be the maximum exterior angle possible for any regular polygon.
Exterior angle of an equilateral triangle = 360°/3 = 120°
Hence maximum possible measure of exterior
angle for any polygon is 120°. Also, we know
that an exterior angle and an interior angle are always in a linear pair. Hence, minimum interior angle.
= 180°-120° = 60°
Understanding Quadrilaterals KSEEB Maths Exercise 4.3
1. Given a parallelogram ABCD, complete each statement along with the definition or property used
1) AD=—–
2)∠DCB=——
3) OC= —-
4) m∠DAB+M∠CDA
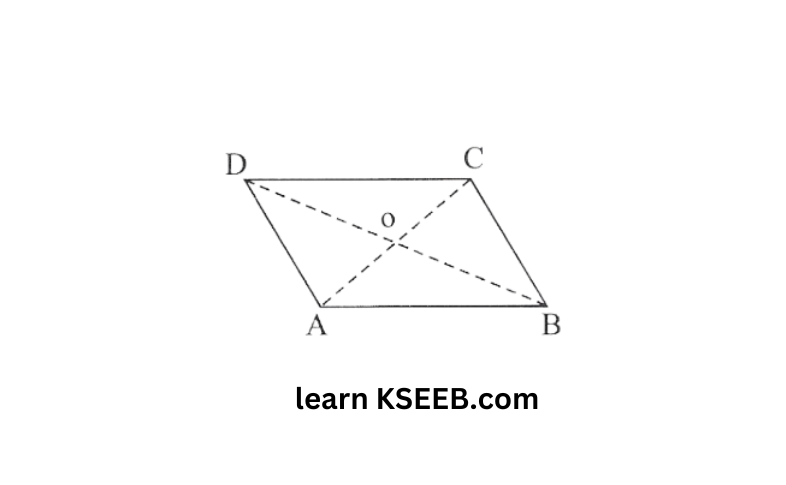
Solution:
i) In a parallelogram, opposite sides are equal in length.
∴ AD = BC
ii) In a parallelogram, opposite angles are equal in measure
∴ ∠DCB = ∠DAB
iii) In a parallelogram, diagonals bisect each other
Hence OC = OA
iv) In a parallelogram, adjacent angles are supplementary to each other
Hence m∠DAB+m∠CDA = 180º.
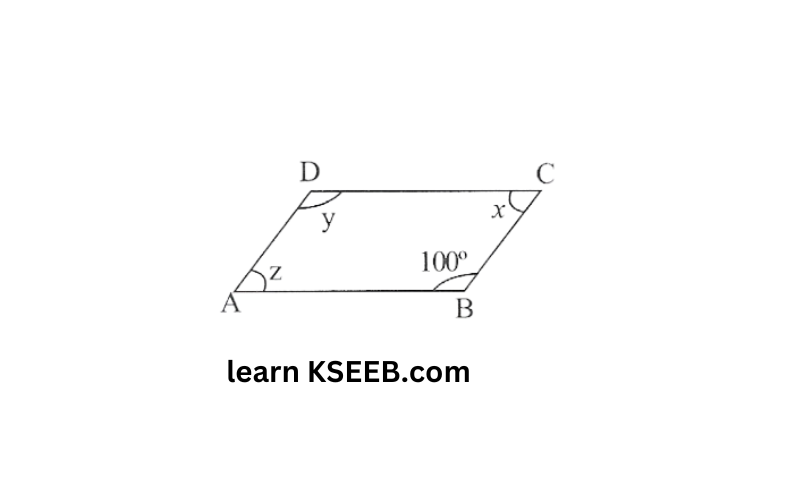
2)Consider the following parallelogram. Find the values of the unknown .x, y, z
1. 
Solution:
x+100° 180° (adjacent angles are supplementary)
x=80°
z = x = 80° (opposite angles are equal)
y = 100° (opposite angles are equal)
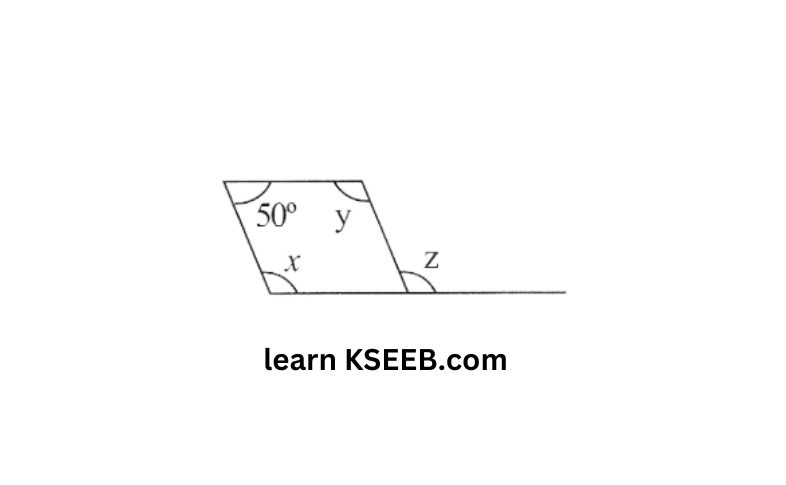
2. 50 + y —180° (Adjacent angles are supplementary)
Solution:
⇒ y = 130°
x = y = 130° (opposite angles are equal)
z = x = 130° (corresponding angles)
x = y = z = 130°
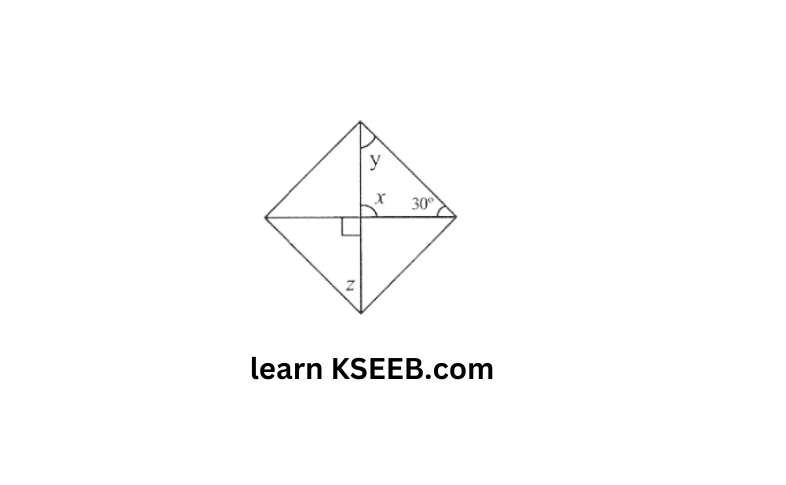
3. 
Solution:
x = 90° (vertically opposite angles)
x + y + 30°=180° (angle sum property of triangle)
90 + y + 30 = 180°
⇒ y = 180 – 120 = 60°
z = y -60° (Alternate interior angles)
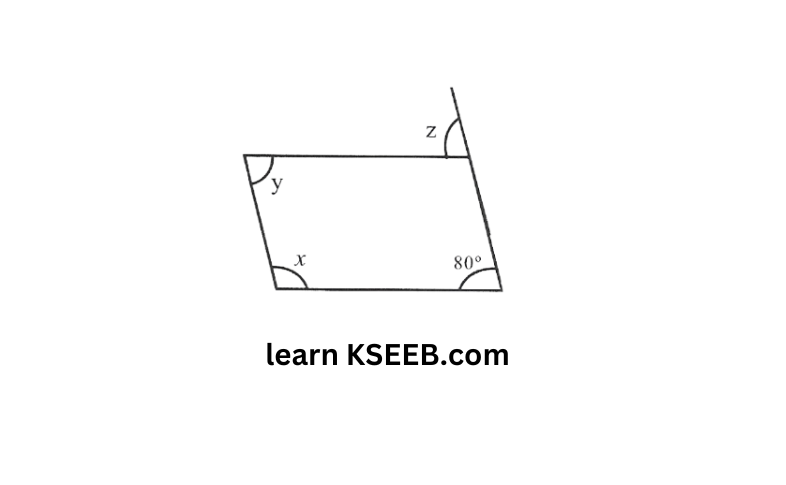
4. 
Solution:
z = 80° (corresponding angles)
y = 80° (opposite angles are equal)
x + y = 180° (adjacent angles are supplementary)
x = 180-y = 180°-80°= 100°
∴ x = 100, y = z = 80°
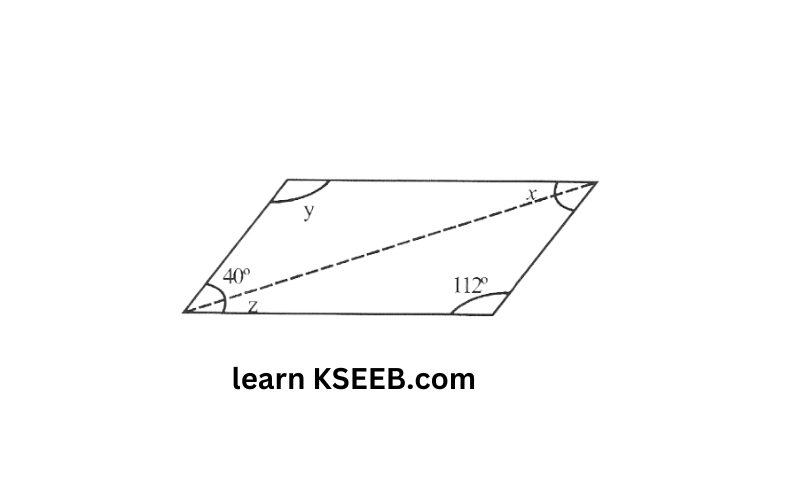
5. 
Solution:
y = 112° (opposite angles are equal)
x + y + 40° = 180° (Angle sum property of triangles)
x + 112 + 40°= 180°
x = 180 —152°= 28°
x = z = 28° (Alternate interior angles)
x = 28°,y = 112°, z = 28°
KSEEB Maths Class 8 Understanding Quadrilaterals Notes
3) Can a quadrilateral ABCD be a parallelogram if
1) ∠D + ∠B = 180°
2) AB = DC = 8cm, AD = 4cm and BC = 4.4cm
3) ∠A = 70° and ∠C = 65° ?
Solution: 1) For ∠D + ∠B = 180° , quadrilateral ABCD may or may not be a parallelogram. Along with this condition, the following conditions should also be fulfilled.
The sum of the measures of adjacent angles should be 180°.
Opposite angles should also be of same measures
2) No. opposite sides AD and BC are of different lengths.
3) No. opposite angles A and C have different measures.
4. Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
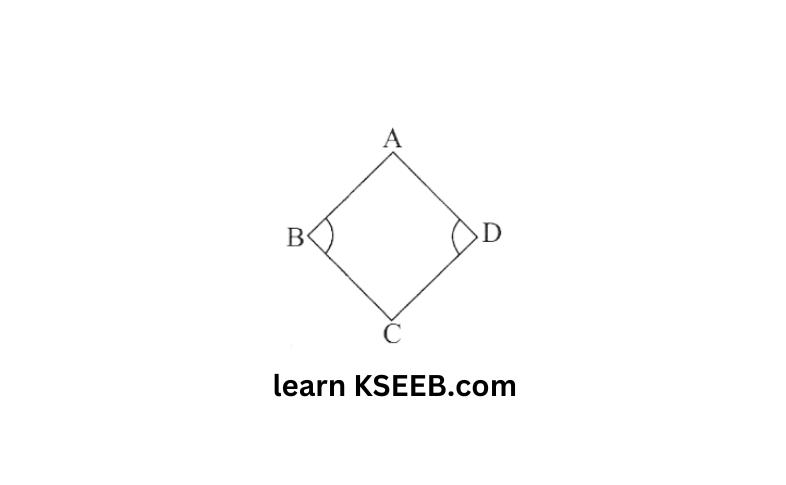
Solution: Here, quadrilateral ABCD (kite) has two of its interior angles
∠B and ∠D of same measures.
However, still the quadrilateral
ABCD is not a parallelogram as the measures of the remaining pair of opposite angles ∠A and ∠C are not equal.
5.The measures of two adjacent angles of a parallelogram are in the ratio 3 :2. Find the measure of each of the angles of the parallelogram.
Solution: Let the measures of two adjacent angles [A and [B of parallelogram ABCD are in the ratio of3 : 2. Let ∠A = 3X and ∠B = 2x
w.k.t The sum of the measures of adjacent angles is 180° for a parallelogram
A+B= 180°
3x+2x=180°
5x=180°
x=180°/5 = 36°
∠A = ∠C = 3x = 108° (opposite angles)
∠B = ∠D = 2x = 72° (opposite angles)
Thus, the measures of the angles of the parallelogram are 108°, 72°, 108° and 72°.
6. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
Solution: Sum of adjacent angles = 180°
∠A + ∠B = 180°
2 ∠A = 180° (∴ ∠A = ∠B)
∠A = 90°
∠B = [A = 90°
∠C = ∠A = 90° (opposite angles)
∠D = ∠B = 90° (opposite angles)
Thus, each angle of the parallelogram measures 90°.
7. The adjacent figure HOPE is a parallelogram. Find the angle measures x, y & z, State the properties you use to find them.
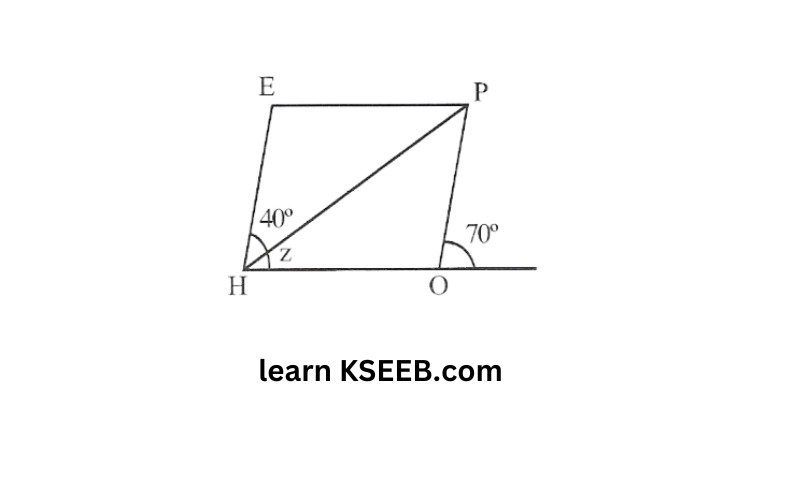
Solution: y = 40° (alternate interior angles)
70° = z + 40° (corresponding angles)
z = 70°-40°
z = 30°
x + (z + 40°) = 180
(Adjacent pair of angles)
x+70° = 180°
x= 180°-70°
x=110°
8) The following figures GUNS and RUNS are parallelogram. Find x and y (lengths are in cm)
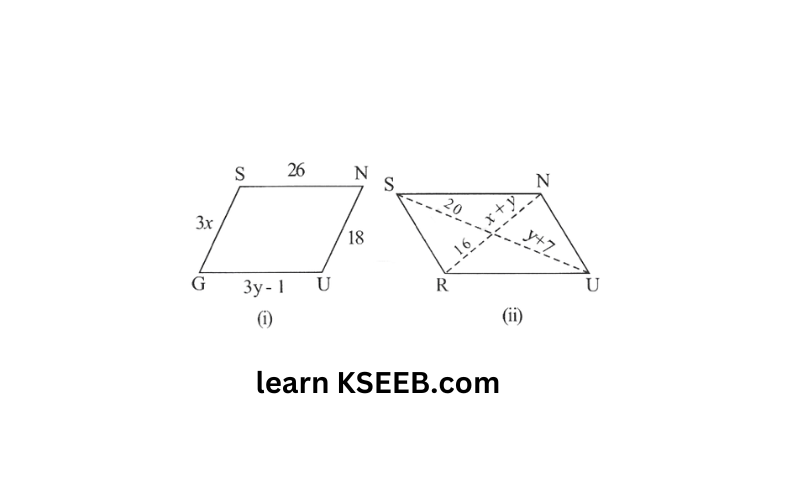
Solution: 1) WKT The length of opposite sides of a parallelogram are equal to each other
GU = SN SG = NU
3y – 1 = 26 3x=18
3y = 26 + 1 = 27 x=18/3=6
y = 9
Hence, the measure of x and y are 6cm and 9cm respectively.
2) WKT the diagonals of a parallelogram bisect each other
y + 7 = 20
y = 13
x+y=16
x+13=16
∴ x=3
Hence, the measures of x and y are 3cm and 13cm respectively
9) 
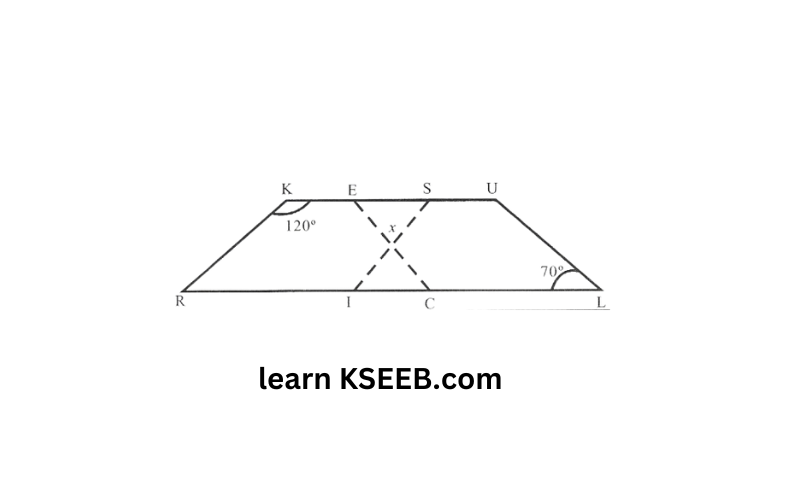
Solution:
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
Adjacent angles of a parallelogram are supplementary
In parallelogram RISK,
∠20°+ ∠ISK = 180°
∠ISK=180°-120°=60°
Also, opposite angles of a parallelogram are equal
In parallelogram CLUE,∠ULE=∠CEU=70°
The sum of the measures of all interior angles of a traingle is 180°.
x+60°+70° = 180°
x = 50°
10) Explain how this figure is a trapezium which of its two sides are parallel?
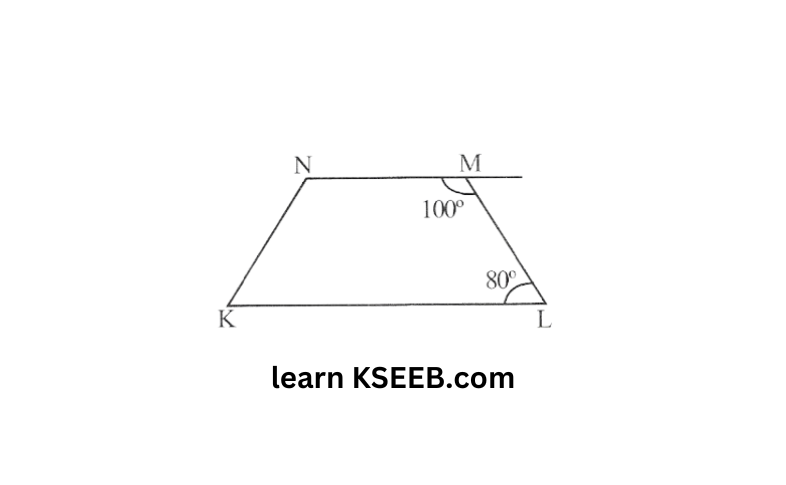
Solution: If a transversal line is intersecting two given lines such that the sum of the measures of the angles on the same side of transversal is 180°, then each other.
Here, LNML+LMLK = 180°
Hence, NM ∥ LK
As quadrilateral KLMN has a pair of parrallel lines, ∴ it is a trapezium
11) Find c in the following figure if AB∥DC
Solution: Given that, Given that, \(\overline{\mathrm{AB}} \| \overline{\mathrm{DC}}\)
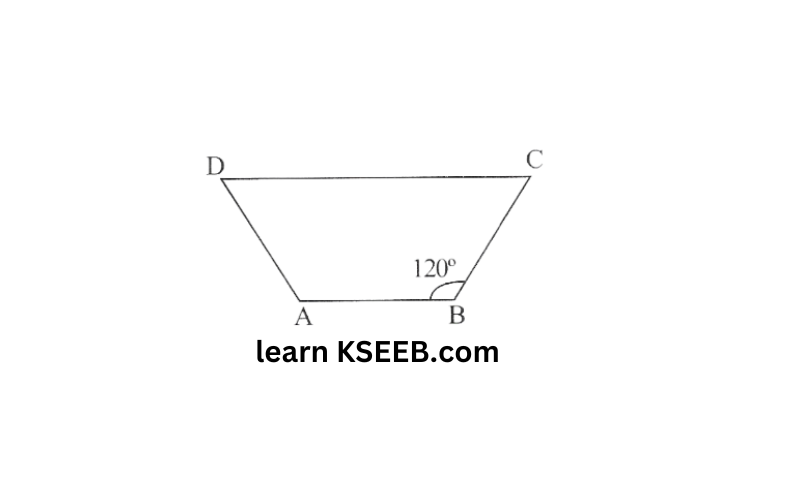
∠B + ∠C = 180° (Angles on the same side of transversal)
120°+∠C = 180°
∠C = 60°
KSEEB Class 8 Maths key concepts of Understanding Quadrilaterals
12) Find the measure of p and s, if \(\overline{\mathrm{SP}} \| \overline{\mathrm{RQ}}\) in the following figure, (If you find m R is there more than one method to find m P?)
Solution: \(\left\lfloor\mathrm{P}+\left\lfloor\mathrm{Q}=180^{\circ}\right.\right.\)(angles on the same side4 of transversal)
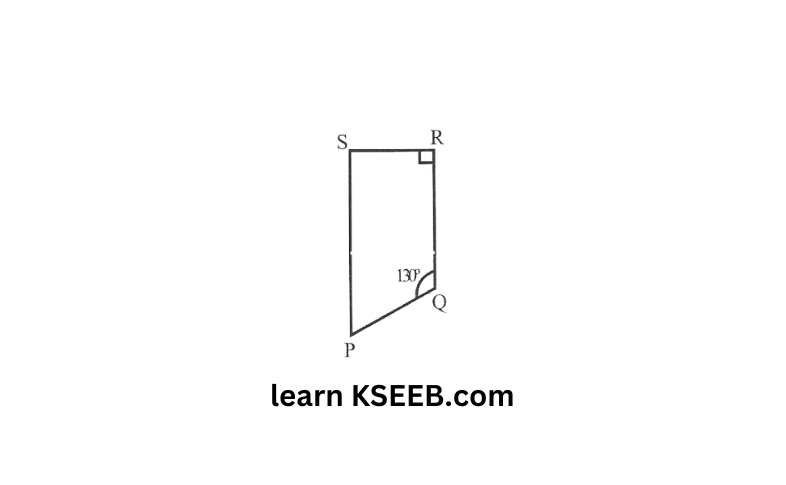\(\left\lfloor\mathrm{P}+130^{\circ}=180^{\circ}\right.\)
(angles on the same side of transversal)
\(90^{\circ}+\left\lfloor\mathrm{S}=180^{\circ}\right.\) \(\mathrm{S}=180^{\circ}-90^{\circ}=90^{\circ}\)Yes, there is one more method to find the measure of \(\mathrm{m} \mid \mathrm{P}\)
m R and m Q are given, after finding m S the angle sum property of a quadrilateral can be applied to find m P.
KSEEB Maths Class 8 Chapter 4 Understanding Quadrilaterals Exercise 4.4
1. state whether True or False.
1) All rectangles are squares
Solution: False, All squares are rectangles but all rectangles are not square.
2) All rhombuses are parallelograms
Solution: True, opposite sides of a rhombus are equal and parallel to each other.
3) All squares are rhombuses and also rectangles.
Solution: True, all squares are rhombuses as all sides of a square are of equal lengths.
All squares are also rectangles as each internal angle measure 90°
4) all squares are not parallelograms.
Solution: False, All squares are parallelograms as opposite sides are equal and parallel.
5) All kites are rhombuses.
Solution: False, A kite does not have all sides of the same length.
6) All rhombuses are kites
Solution: True, A rhombus also has two distinct consecutive pairs of sides of equal length.
How To Solve Quadrilateral Problems In Class 8 Kseeb Maths
7) All parallelograms are trapeziums
Solution: True, All parallelograms have a pair of parallel sides.
8) All squares are trapezium.
Solution: True, All squares have a pair of parallel sides
2. Identify all the quadrilaterals that have
1) Four sides of equal length.
Solution: Rhombus and square are the quadrilaterals that have 4 sides of equal length.
2) Four right angles
Solution: Square and rectangle are the quadrilaterals that have 4 right angles.
3) Explain how a square is
1) a quadrilateral
Solution: A square is a quadrilateral since it has four sides
2) a parallelogram
Solution: A square is a parallelogram since its opposite sides are parallel to each other
3) a rhombus
Solution: A square is a rhombus since its four sides are of the same length.
4) a rectangle
Solution: A square is a rectangle since each interior angle measures 90°
4. Name the quadrilaterals whose diagonals
1) bisect each other
Solution: The diagonals of a parallelogram, rhombus, square and rectangle bisect each other.
2) are perpendicular bisectors of each other
Solution: The diagonals of a rhombus and square act as perpendicular bisectors
3) are equal
Solution: The diagonals of a rectangle and square are equal.
5. Explain why a rectangle is a convex quadrilateral
Solution: In a rectangle, there are two diagonals both lying in the interior of the rectangle. Hence it is a convex quadrilateral.
6. ABC is a right angled triangle and O is the mid-point of the side opposite to the right angle. Explain why O is equidistant from A, B and C (The dotted lines are drawn additionally to help you)
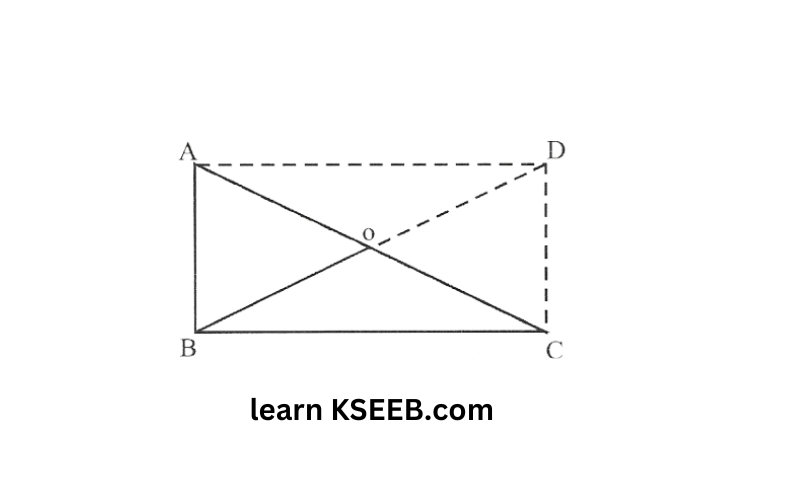
Solution: Draw lines AD and DC such that AD ∥ BC
AB ∥ DC
AD = BC, AB = DC
ABCD is a rectangle as opposite sides are equal and parallel to each other and all the interior angles are of 90°.
In a rectangle diagonals are of equal length and also these bisect each other.
Hence AO = OC = BO = OD
Thus, O is equidistant from A, B and C.
KSEEB Class 8 Maths Key Concepts of Understanding Quadrilaterals Additional Problems
1. Two adjacent angles of a parallelogram are in the ratio 1: 3. Find its angles
Solution: Let the angles be x and 3x
then x + 3x = 180°
4x= 180°
⇒ x = 45° (so angles are 45° and 135°)
2. A photo frame is in the shape of a quadrilateral with one diagonal longer than the other. Is it a rectangle? Why or Why not?
Solution: No, it is not a rectangle. In a rectangle diagonals are equal.
3. A playground in the town is in the form of a kite. The perimeter is 106 metres. If one of its sides is 23 metres what are the lengths of other three sides?
Solution: A kite has two pairs of equal consecutive sides.
∴ one side = 23m
other side = 23m
Sum of rest two sides = 106- (23 + 23)
Length of other two = 60m
Sides are 30m and 30 m
Hence, the length of other three sides are 23m, 30m and 30m.
Karnataka Board Class 8 Maths Quadrilateral Problems And Answers
4. Find the measure of an exterior angle of a regular pentagon and an exterior angle of a regular decagon. What is the ratio between these two angles?
Solution: The measure of each exterior angle of n sided regular polygon= (360/n)°
Measure of exterior angle of a regular pentagon (360/5)° = 72°
Measure of exterior angle of a regular decagon =(360/10)° = 36°.
Ratio = 72°/36° =2/1
5. In rhombus BEAM, find ∠AME and ∠AEM
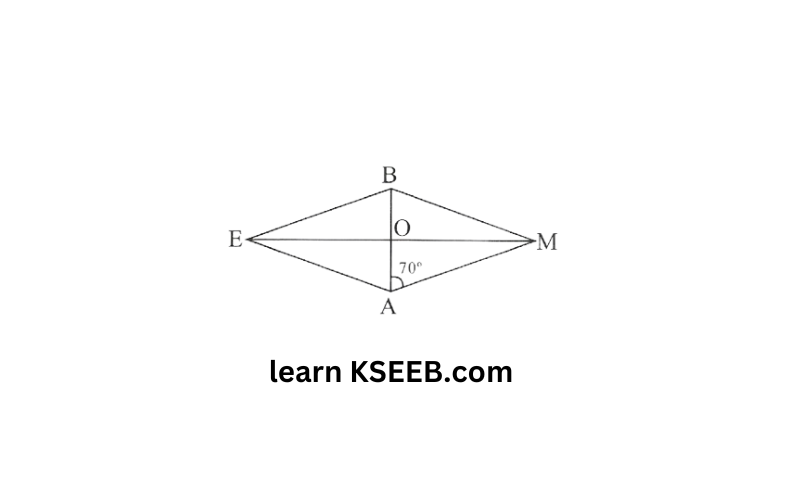
Solution: Since diagonals of rhombus bisect each other at right angles.
∴ ∠AOM = 90°
∠AOM+∠OAM+∠AMO=180°
90°+70°+∠AMO=180°
160°+∠AMO=180°
∠AMO=180°-160° ⇒ ∠AMO=20°
∠AME=∠AMO=20°
In △AEM
AE=AM (sides of rhombus are equal)
∠AME=∠AEM (Angles opposite to equal sides)
∴ ∠AEM =20°
6. In the given parallelogram YOUR, ∠RUO=120° and OY is extended to point S such that ∠SRY=50°, Find ∠YSR.
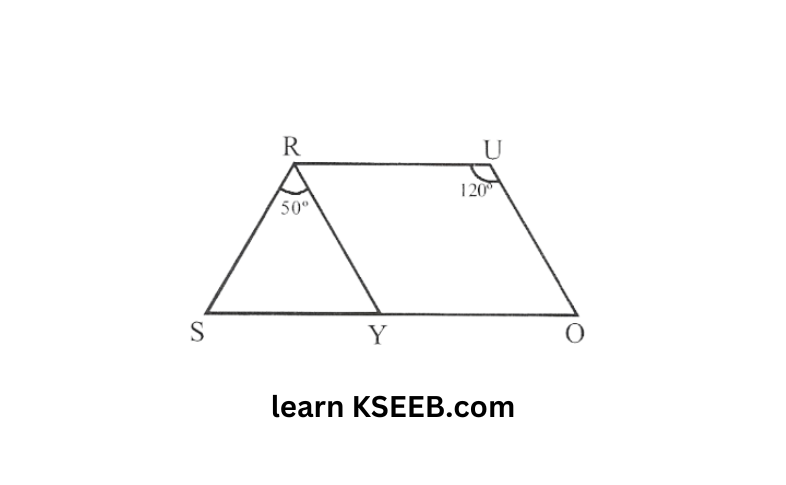
Solution: ∠RYO=∠RUO=120° (opposite angles are equal)
\(\left\lfloor\mathrm{RYS}+\left\lfloor\mathrm{RYO}=180^{\circ}\right. \text { (linear pair) }\right.\) \(\left\lfloor\text { RYS }+120^{\circ}=180^{\circ}\right.\)⇒ ∠RYS=60°
In △RSY
∠YSR+∠RYS+∠SRY=180°
∠YSR+60°+50°=180°
∠YSR=180°-110°=70°
7. Two angles of a quadrilateral measures 75° each and the other two angles are equal. What is the measure of these two angles? Name the possible figure so formed
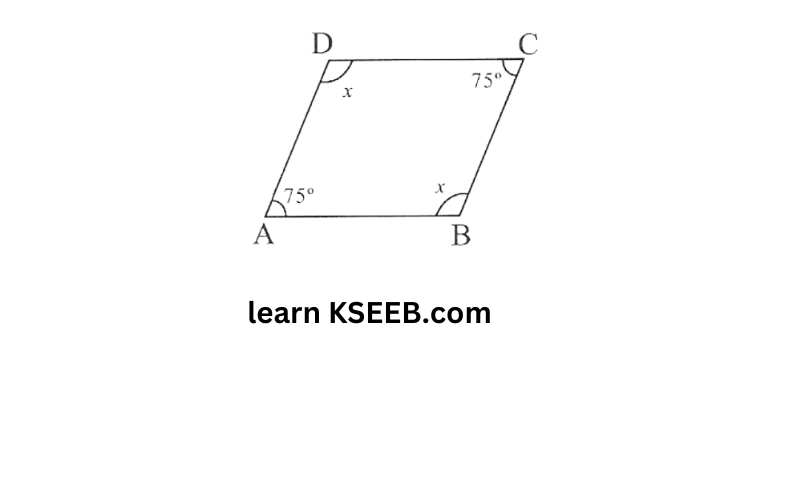
Solution: Let equal angles be x.
∴\(x+x+75^{\circ}+75^{\circ}=360^{\circ}\)
2x+150°=360°
2x=360°-150°=210°
⇒ x=105°
Each equal angle is 105°, the possible figure so formed is parallelogram.
Kseeb 8th Maths Chapter 4 Exercise Solutions Step By Step
8. ABCD is a parallelogram. The bisector of angle of A intersects CD at x and bisector of angle C intersects AB at Y. Is AXCY a parallelogram? Give reason
Solution:
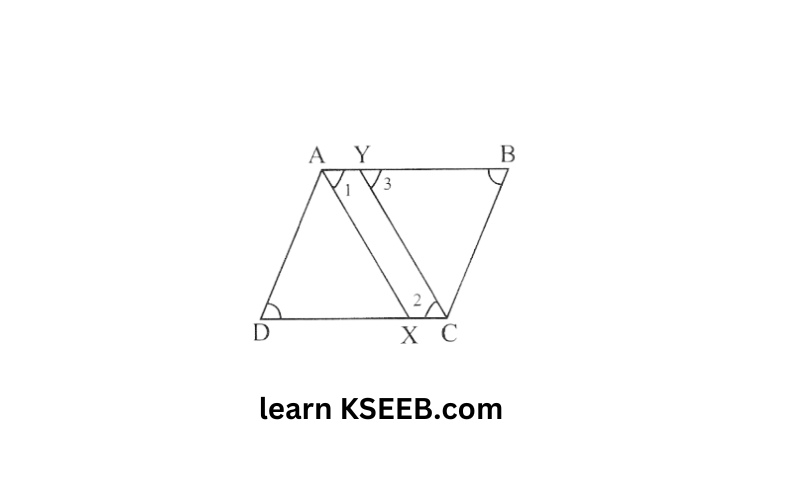
∠A=∠C (opposite angles of parallelogram)
or \(\frac{\lfloor\mathrm{A}}{2}=\frac{\lfloor\mathrm{C}}{2} \text { or }\lfloor 1=\lfloor 2\)
but 2=3 (alternate angles)
∴ ∠1=∠3
But they are a pair of corresponding angles
∴ AX ∥ YC…….(1)
AY ∥ XC…….(2) (∵ AB ∥ DC)
from (1)and(2)
AXCY is a ∥gm
9. A diagonal of an parallelogram bisects an angle.
(1)Will it also bisect the other angle?
(2)It is a rhombus? Give reason.
Solution: Let ABCD is a ∥gm 1=2
1) ∠1=∠4 (alternate angles)
& ∠2=∠3 (alternate angles)
but ∠3=∠4
so, the diagonal will bisect the other angle.
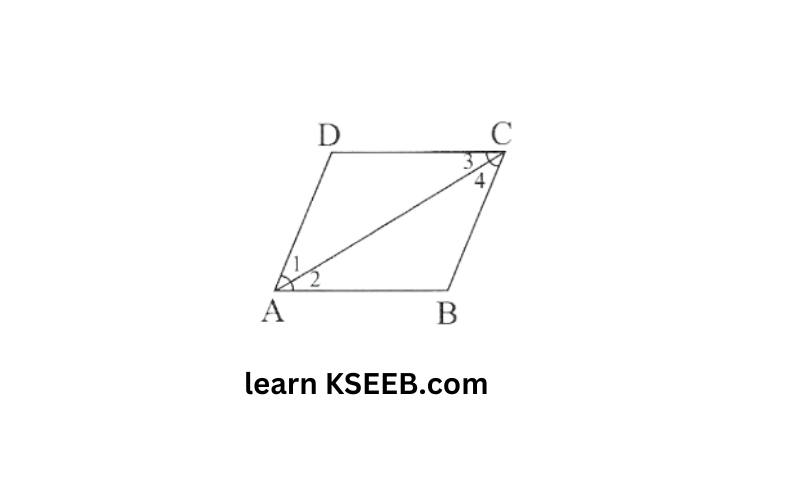
2) ∠1=∠2 (Given)
∠2=∠3 (Alternate angles)
∴ ∠1=∠3
Hence CD=DA (sides opposite to equal angles are equal)
∴ ABCD is a rhombus.
10. In rectangle PQRS, ∠OPQ=48°, find ∠RSQ
Solution:
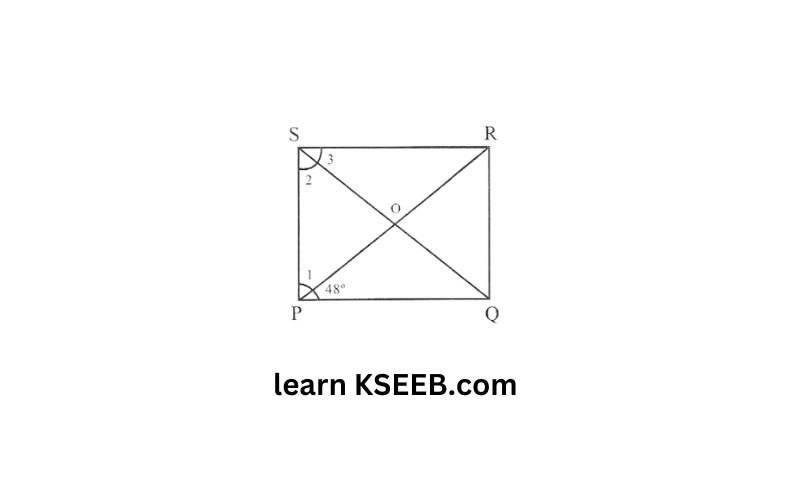
∠QPS = 90°
(As each angle of a rectangle is a right angle)
∠1 + 48°= 90°
⇒∠1 = 90°-48°
∠1 = 42°
Since in a rectangle diagonals are equal and bisect each other.
OS = OP = OQ = OR
⇒∠1 = ∠2 = 42°
Also ∠2 + ∠3 = 90° (each angle of a rectangle is a right angle)
⇒ 42°+∠3 = 90°
∠3 = 90°-42°= 48°
thus ∠RSQ = 48°
11. The angles of a quadrilateral are in the ratio 1 : 2 : 2 : 4. Find the measure of each angle.
Solution: Let the ratio constant hex, thus the measure of the given angles will be (lx)°, (2x)° (2x)° and (4x)°.
w.k.T, The sum of the angles of a quadrilateral is 360°.
1x°+ 2x°+2x° + 4x°= 360°
9x = 360°
x=360°/9 =40°
∴ The angles are
1x = 1×40 = 40°, 2x= 2x 40° = 80°
2x = 2×40 = 80° and 4x = 4×40 = 160°
Hence the angles are 40°, 80°, 80° and 160°.
12. In fig, ABCD is a quadrilateral with ∠B = 56° and ∠D = 104°. If ∠BAD and ∠BCD are in the ratio, 2 : 3, find the values of ∠1 and ∠2.
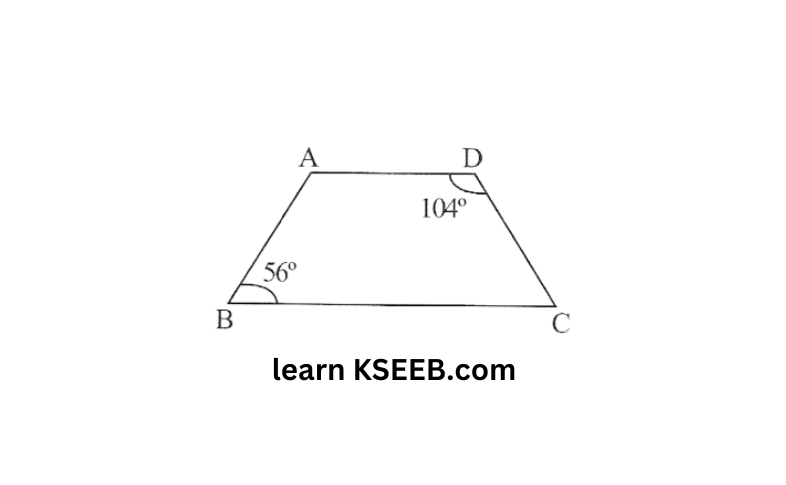
Solution: wkT, The sum of the angles of a quadrilateral is 360°
∴∠BAD + ∠56° + ∠BCD + 104°= 360°
(or) ∠BAD+ ∠BCD+ 160° = 360°
⇒ ∠BAD + ∠BCD = 200°
∴∠BAD +∠BCD = 2:3
Let the ratio constant be x.
∠BAD = 2x and ∠BCD = 3x
∴ 2x + 3x = 200
⇒ 5x = 200
x = 200/5 = 40°
∠BAD = 2x = 2 x 40 = 80°
∠BCD = 3x = 3 x 40 = 120°
but ∠BAD + 1 = 180°(linear pair)
80°+∠1 = 180°
∠1 = 180°-80°= 100°
and ∠BCD + ∠2 = 180°(linear pair)
120°+∠2 = 180°
∠2 = 180° -120°= 60°
13. In a parallelogram PQRS, the bisectors of ∠P & ∠Q meet at O. Find ∠POQ. P Q
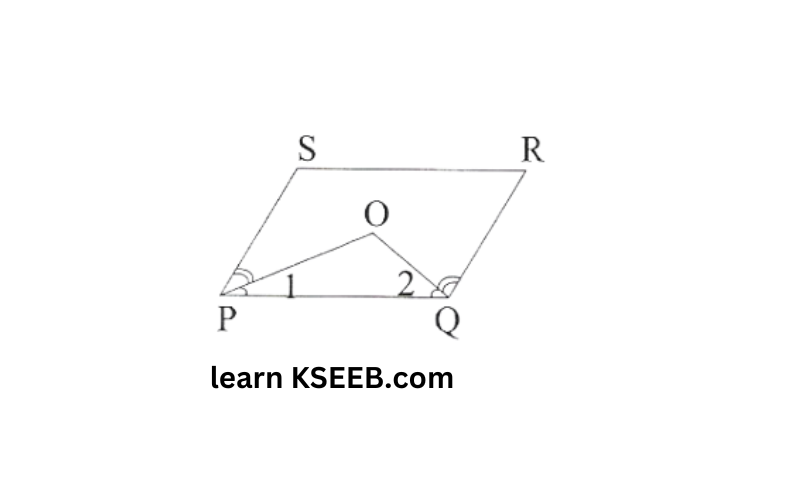
Solution: Since PO and QO are the bisectors of P&[Q respectively.
∴ \(\left\lfloor 1=\frac{1}{2}\left\lfloor\mathrm { P } \& \left\lfloor 2=\frac{1}{2}\lfloor\mathrm{Q}\right.\right.\right.\)
but ∠P + ∠Q = 180°
\(\frac{1}{2}\left\lfloor\mathrm{P}+\frac{1}{2}\left\lfloor\mathrm{Q}=90^{\circ}\right.\right.\)
∠1+ ∠2 = 90°
but ∠1 + ∠2 + ∠POQ = 180°
90°+ ∠POQ = 180°
∠POQ = 180°-90° -90°
⇒ ∠POQ = 90°
14. The diagonals of a rhombus ABCD intersect at O, If AC = 8cm and BD = 6cm, find the length of its sides.
Solution: Since diagonals of a rhombus bisect each other at right angle.
AC=8cm ⇒ OA = OC = 4cm
and BD = 6cm
⇒ OB = 3cm
Also ∠BOC = 90°
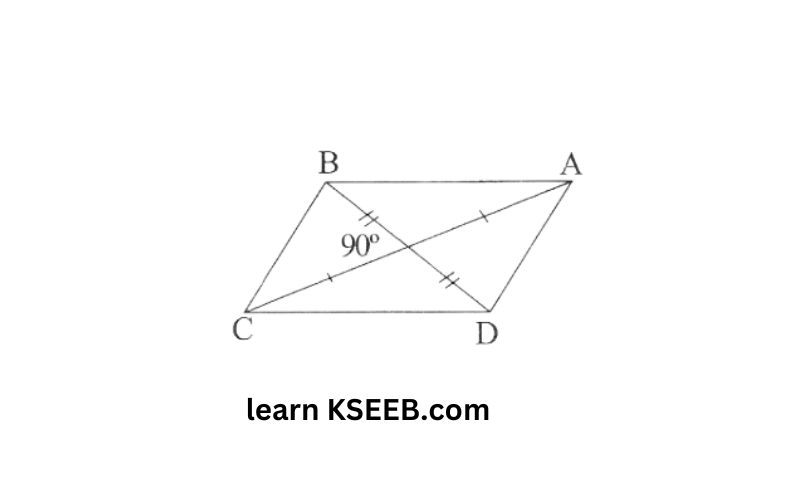
Hence △BOC is a right angled triangle.
∴ \(B C^2=O B^2+O C^2\)
(using pythagoras theorem)
⇒\(\mathrm{BC}^2=4^2+3^2=16+9\)
\(\mathrm{BC}^2=25\) \(\mathrm{BC}=5 \mathrm{~cm}\)Length of each side of the rhombus is 5cm.
15. Both the pairs of opposite angles of a quadrilateral are equal and supplementary.
Solution: Since pairs opposite angles of a quadrilateral are equal and supplementary.
∴ x+x=180°
2x=180°
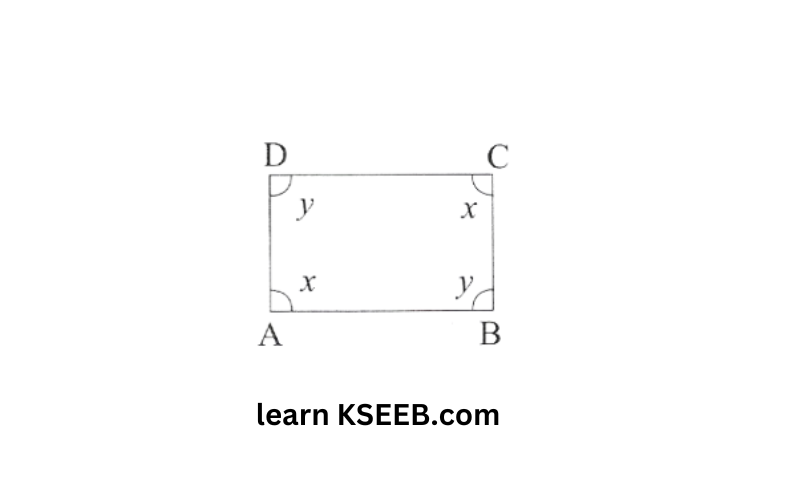
⇒ x=90°
Also, y+y=180°
2y=180°⇒ y=90°
Each angle =90°
16. Length and breadth of a rectangular wire are 9cm and 7cm respectively. If the wire is bent into a square, find the length of its side.
Solution: Perimeter of the rectangle
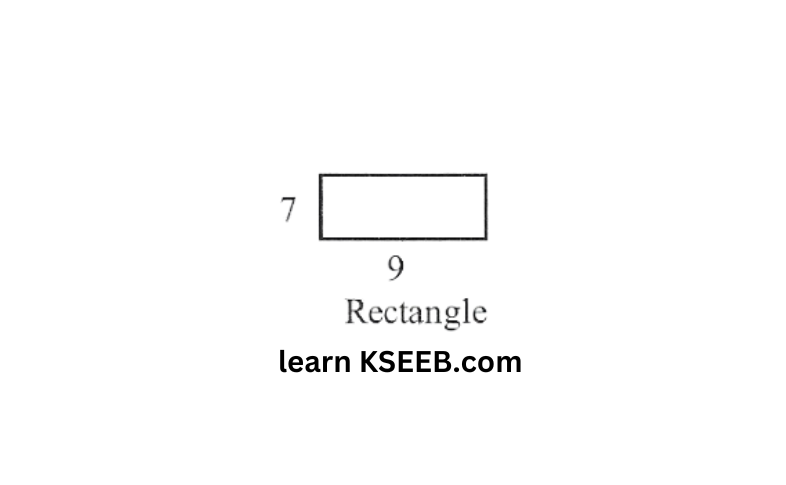
= 2 (l + b)
= 2 (9 + 7) = 2 x 16 = 32cm
Now perimeter of the square
= perimeter of rectangle = 32cm
side of the square = 32/4 = 8cm
Hence, the length of the side of square = 8cm.
17. The sides AB & CD of a quadrilateral ABCD are extended to points P & Q respectively. Is ∠ADQ + ∠CBP =∠A + ∠C? Give reason.
Solution: Join AC, then
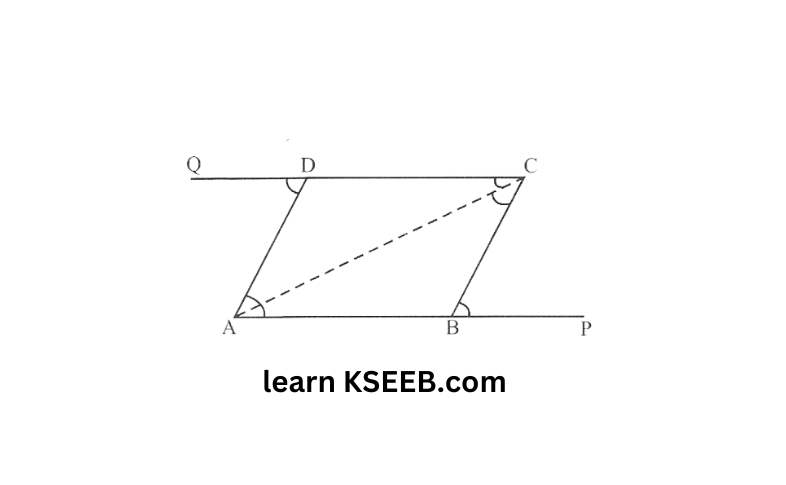
∠CBP = ∠BCA + ∠BAC &
∠ADQ = ∠ACD + ∠DAC
(Exterior angles of △le )
∠CBP +∠ADQ = ∠BCA + ∠BAC + ∠ACD + ∠DAC
= (∠BCA + ∠ACD) + (∠BAC + ∠DAC)
= ∠C + ∠A
18. ABCD is a parallelogram with ∠A = 80°. The internal bisectors of ∠B & ∠C meet at O. Find the measure of the three angles of △BCO•
Solution: ∠C = ∠A
(opposite angles of a parallelogram are equal)
∠C = 800 (Given ∠C = 80°)
OCB = 1/2 ∠C =1/2×80 = 40°
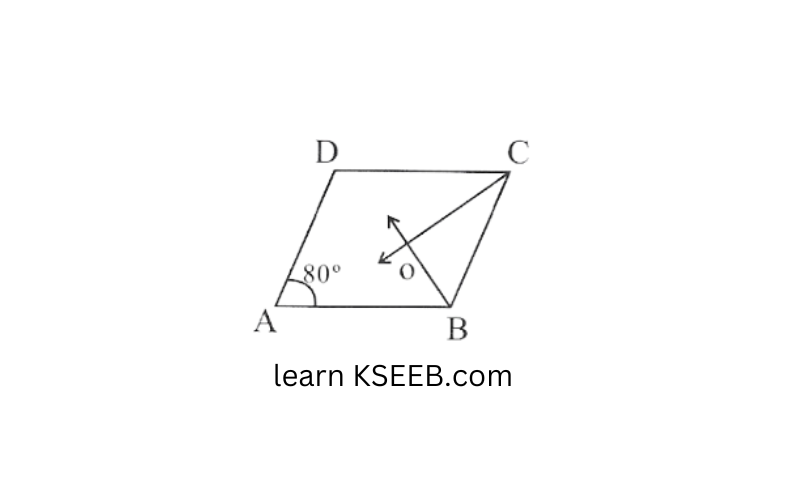
∠B = 180° – ∠A (sum of interior angles on the same side of the transversal is 180°)
= 180° – 80° = 100°
∠CBO = 1/2B =1/2xl00°
= 50° ∠BOC = 180°- ( ∠OBC + ∠CBO)
(angle sum of a △le )
= 180° – 40° + 50° = 180° – 90° = 90°
∴The three angles of the △le BCO namely ∠OCB, ∠CBO, ∠BCO are 40°, 50° and 90° respectively.
19. The ratio of two sides of a parallelogram is 4:3. If its perimeter is 56cm, find the lengths of its sides.
Solution: Let the lengths of two sides of parallelogram be 4x cm and 3x cm respectively.
Then, its perimeter
= 2(4x + 3x)cm = 14x cm
∴ 14x = 56 ⇒ x = 56/14 = 4
∴ one side = (4 x 4)cm= 16cm & other side
= (3 x 4cm) = 12cm