KSEEB Solutions For Class 9 Maths Chapter 5 Introduction to Euclid’s geometry

KSEEB Solutions For Class 9 Maths Chapter 5 Introduction To Euclid’s Geometry

Introduction to Euclid’s Geometry Points to Remember

• Point: A point is that which has no part.
  A point is dimensionless but it has position. In the given figure P is a point.
  • P
•  Ray: A line segment AB when extended indefinitely in one direction is the ray
  \(\overrightarrow{\mathrm{AB}}\)

•  Line: A line has no end points. A line is breadtheless length.
  A line segment AB when extended indefinitely in both directions is called the line AB.

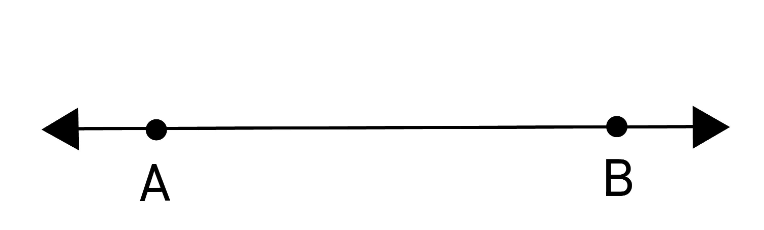
•  Line segment: The straight path between two points A & B is called line segment AB.

The points A & B are called the end points of the line segment AB. A line segment has a definite length.

Class 9 Social Science

Class 9 Science

Class 9 Maths

 

Read and Learn More KSEEB Solutions for Class 9 Maths 

• Axioms : The basic facts which are taken for granted, without proof & which are used throughout mathematics are called axioms.
• Statement: A sentence which can be judged to be true or false is called a statement.
•  Theorem: The conclusion obtained through logi¬cal reasoning based on previously proved results & some axioms constitute a statement which is known as a theorem or a proposition.
• Corollary: A statement whose truthfulness can easily be deduced from a theorem is called its corollary.

Euclid’s definitions. Axioms & Postulates

1. A solid has shape, size position & can be moved from one place to another, its boundaries are called surfaces. The boundaries of surfaces are curves or straight lines.

2. A solid has three dimensions, a surface has two, a line has one & a point has none.

3. Definitions given by Euclid

1. A point is that which has no part.
2. A line is breadthless length
3. The ends of a line are points.
4. A straight line is a line which lies evenly with the points on itself.
5. A surface is that which has length & breadth only.
6. The edges of a surface are lines.
7. A plane surface is a surface which lies with the straight lines on itself.

4. A point, a line & a plane (surface) are undefined terms.

5. Axioms or postulates are the assumptions which are ‘obvious universal truths’ they need not be proved.

6. Euclid’s Axioms

1. Things which are equal to the same thing are equal to one another.
2. If equals are added to equals, the wholes are equal.
3. If equals are subtracted from equals the remainders are equal.
4. Thing which coincide with one another are equal to one another.
5. The whole is greater than the part.
6. Things which are double of the same things are equal to one another.
7. Things which are halves of the same things are equal to one another.

KSEEB Class 9 Maths Chapter 5 Solutions PDF

Euclid’s Five postulates

1) A straight line can be drawn from only one point to any other point.

2) A terminated line can be produced indefinitely

3) A circle can be drawn with any centre & any
radius.

4) All right angles are equal to one another.

\(\angle \mathrm{XYZ}=90^{\circ}, \angle \mathrm{PQR}=90^{\circ} \text {, then }\lfloor\mathrm{XYZ}=\angle \mathrm{PQR}\)

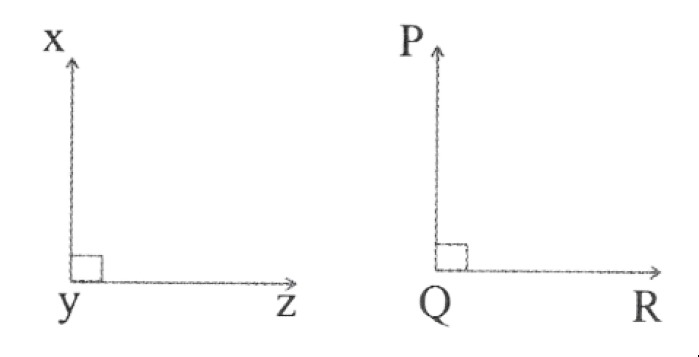
5) If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely meet on that side on which the sum of angles is less than

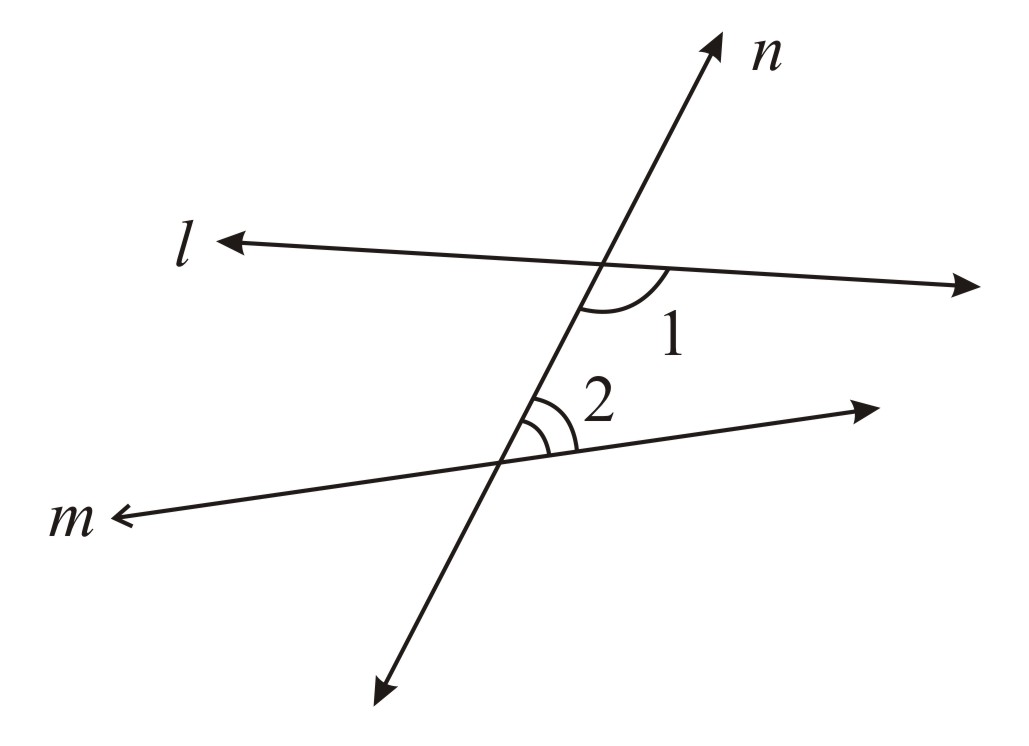
• Two equivalent versions of Euclid’s 5th postulate.
  1) For every line l & for every point n not lying on l , there exist a unique line m passing through n and parallel to l.
  2) Two distinct intersecting lines cannot be parallel to the same line.

Introduction to Euclid’s geometry Exercise 5.1

1. Which of the following statements are true & which are false? Give reasons for your ansewers
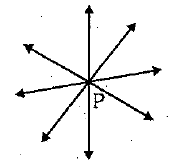
1) Only one line can pass through a single point

Solution:

False, since through a unique point infinite number of lines can pass. In the following figure, it can be seen that there are infinite numbers of lines passing through a single point P.

2) There are an infinite number of lines which pass through two distinct points.

Solution:

False, since through two distinct points only one line can pass. In the following figure, it can be seen that there is only one single line that can pass through two distinct points P & Q

3) A terminated line can be produced indefinitely on both the sides.

Solution:

True, A terminated line can be produced on both the sides. Let AB be a terminated line.

It can be seen that it can be produced indefinitely on both the sides.

4) If two circles are equal, then their radii are equal.

Solution:

True, if two circles are equal, then their centre & circumference will coincide & hence, the radii will also be equal

5) In the following figure, if AB = PQ & PQ = XY, then AB = XY.

Solution:

True, It is given that AB & XY are two terminated lines & both are equal to a third line PQ. Euclid’s first axiom states that things which are equal to the same thing are equal to one
another.

∴ The lines AB & XY will be equal to each other.

Karnataka 9th Standard Maths Chapter 5 Notes

2. Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they & how might you define them?
1) parallel lines

Solution :

If the perpendicular distance between two lines is always constant, then these are called parallel lines. In other words, the lines which never inter¬sect each other are called parallel lines.

To defined parallel lines, we must know about point, lines, & distance between the lines & the point of intersection.

2) perpendicular lines

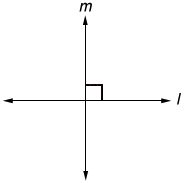
If two lines intersect each other at 90°, then these are called perpendicular lines. We are required to define line & the angle before defining perpendicular lines.

3) line segment

A straight line drawn from any point to any other point is called as line segment. To define line segment, we must know about point & line segment.

4) radius of a circle
Solution:

It is the distance between the centres of a circle to any point lying on the circle, to define the radius of a circle we must know about point & circle.

5) square

Solution:

A square is a quadrilateral having all sides of equal length & all angles of same measure, i.e.90°.

To define a square, we must know about quadrilateral, side & angle.

3. Consider two ‘postulates’ given below.
1) Given any two distinct points A & B there exists a third point C which is in between A & B.
2) There exist at least three points that are not on the same line.
Do, these postulates contain any undefined terms. Are these postulates consistent?
Do they follow from Euclid’s postulates? Explain?

Solution:

Yes, these postulates contain two undefined terms: point & line.

Yes, these postulates are consistent because they deal with two different situations.

1) Say that given two points A & B, there is a point C lying on the line in between them.

2) Say that given A & B, can take C not lying on the line through A & B.

These ‘postulates ’ do not follow from Euclid’s postulates however, they follow fromAxiom.

4. If a point C lies between two points A & B such that AC = BC, then prove that AC =1/2AB. Explain by drawing the figure.
Solution:

 

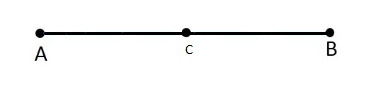
AC = BC

AC + AC = BC + AC

(equals are added to equals)

=> 2AC = AB

(BC + AC coincides with AB)

=> AC=1/2AB

=> AC =BC = 1/2 AB

(Things which are equal to the same point are equal to one another)

KSEEB Class 9 Maths Introduction to Euclid’s Geometry Solutions

5. In question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one & only one midpoint.

Solution:

Let a line AB have two mid-points say C & D.

Then.

AC =1/2 AB……….. (1)

AD = 1/2AB………… (2)

from(1) &(2)

AC = AD (things which are equal to the same thing are equal to one another)

6. In figure, if AC = BD, then prove that AB =CD.

Solution:

AC = BD (given)………………. (1)

AC = AB + BC

(point B lies between A & C)……………….. (2)

BD = BC + CD

(point C lies between B & D)……………… (3)

By substituting (2) & (3) in (1) we get

AB + BC = BC + CD

=> AB = CD (subtracting equals from equals).

7. Why is Axiom 5, in the list of Euclid’s axioms, considered a universal truth’?

Solution:

This is true for anything in any part of the world, this is a universal truth.

Introduction to Euclid’s geometry Exercise 5.2

1. How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?

Solution:

Two distinct intersecting lines cannot be parallel to the same line.

2. Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.

Solution:

If a straight line l falls on two straight lines m & n such that sum of the interior angles on one side of / is two right angles, then by Euclid’s fifth pos¬tulate the lines m& n will not meet on this side of l. Next, we know that the sum of the interior angles on the other side of line l will also be two right angles.

∴ They will not meet on the other side also, so, the lines m & n never meet & are therefore parallel.

Additional Problems

1. How many number of lines does pass through two distinct points?

1. 1
2. 4
3. 3
4. 2

Solution: 1. 1

2. If the point P lies in between M & N & C is mid-point of MP then

1. MC + PN = MN
2. MP + CP = MN
3. MC + CN = MN
4. CP + CN = MN

Solution: 3. MC + CN = MN

3. The number of line segments determined by three collinear points is

1. three
2. two
3. four
4. only one

Solution: 1. three

4. The things which are double of same thing are

1. equal
2. halves of same thing
3. unequal
4. double of the same thing

Solution: 1. equal

KSEEB 9th Standard Maths Chapter 5 Important Questions

5. Euclid stated that all right angles are equal to each other in the form of:

1. an axiom
2. a definition
3. a postulate
4. a proof

Solution: 3. a postulate

Class 9 Maths KSEEB Chapter 5 Euclid’s Geometry Examples 

One Mark Question

1. If AB = x+ 3, BC = 2x & AC = 4x-5 , then for what value of ‘x’ B lies on AC?

Solution:

AB + BC = AC

x+3+2x=4x-5

3x+3 = 4x-5

4x – 3x= 3 + 5

x=8

2. Express in variables the things which are double of the same thing.
Solution:
Let First thing = m
Second thing = n
Then m=2n

3. What is a straight line?
Solution:
Two planes intersect each other to form a straight line.

4. If the point P lies between M & N & C is the mid-point of MP, then what is the value of MN?
Solution:

MN=MC+CN

5. How many lines can be passed through two distinct points?
Solution:

Only one line passes through two distinct points

Two Mark Questions

1. State any two Euclid’s axioms

Solution:

Things which are equal to the same thing are equal to one another. If equals are added to equal, the wholes are equal.

2. In the given figure, if AB = CD, then prove that AC = BD, also write the Euclid’s axiom used for proving it.

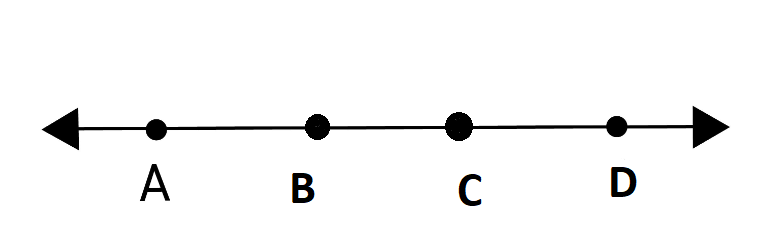
Solution:

AB = CD (given)

AB + BC = BC + CD

AC = BD

Euclid’s axiom used: If equals are added to equals the wholes are equal.

3. In the given figure, we have\(\lfloor 1=\lfloor 2,\lfloor 3=\lfloor 4\).
show that \(\lfloor\mathrm{ABC}=\lfloor\mathrm{DBC}\) State the Euclid’s axiom used.

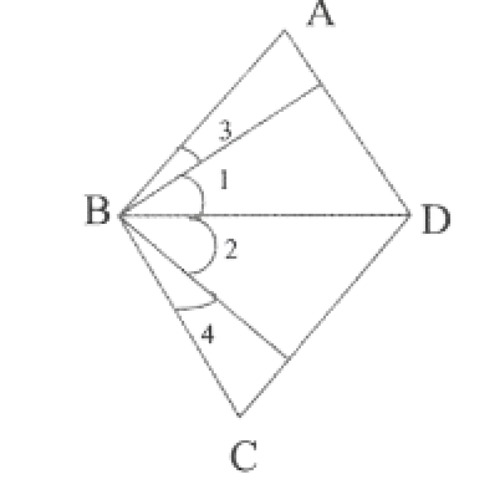
Solution:

\(\lfloor 1=\lfloor 2\)………..(1)

\(\lfloor 3=\lfloor 4\)………..(2)

Adding 1 & 2 we get

\(\lfloor 1+\lfloor 3=\lfloor 2+\lfloor 4\) \(\lfloor\mathrm{ABC}=\lfloor\mathrm{DBC}\)

Euclid’s axiom used: If equals are added to equals, wholes are equal.

Karnataka Board Class 9 Maths Chapter 5 MCQs

4. Solve the equation x-10 = 15 & state Euclid’s axiom used here.

Solution:

x-10 = 15

x-10+10 = 15 + 10

x=25

If equals are added to equals, the wholes are equal.

KSEEB Chapter 5 Euclid’s Geometry Solved Questions 

5. In the given figure, it is given that \(\lfloor 1=\lfloor 4\) &\(\lfloor 3=\lfloor 2\), By which Euclid’s axiom, it can be shown that if \(\lfloor 2=\lfloor 4\) then \(\lfloor 1=\lfloor 3\).

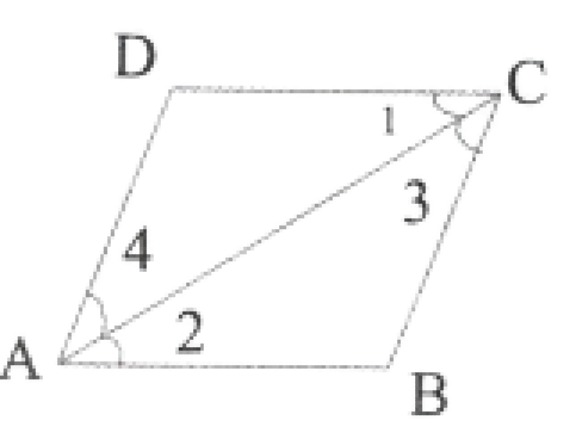
Solution:

Given,

\(\lfloor 1=\lfloor 4\) &\(\lfloor 3=\lfloor 2\) again. \(\lfloor 2=\lfloor 4\)

Axiom: Things which are equal to the same things are equal to one another

∴ \(\lfloor 1=\lfloor 3\)

6. In figure, C is the midpoint of AB & D is the midpoint of AC. Prove that AD =1/4 AB

Solution:

Euclid’s axiom:

If C be the midpoint of a line segment AB, then AC = AB

AC = 1/2 AB

AD = 1/2 AC

\(\mathrm{AD}=\frac{1}{2}\left(\frac{1}{2} \mathrm{AB}\right)\)

AD=1/4AB

7. In figure, AE = DF, E is the midpoint of AB & F is the midpoint of DC using an Euclid’s axiom, show that AB = DC.

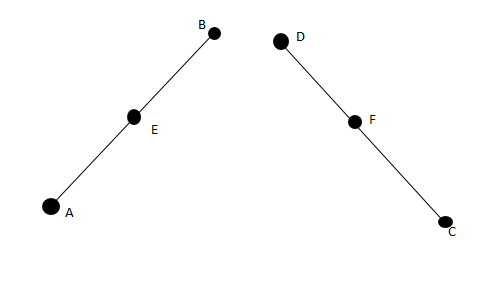
Solution:

AB = 2AE

(E is the midpoint of AB)

CD = 2DF

(F is the midpoint of CD)

Also AE = DF (given)

∴ AB = CD

(Things which are double of the same thing are equal to one another)

8. It is known that x+ y = 10 & that x = z, show that z+ y = 10

Solution:

since x+ y = 10 &

x= z

∴ x + y = z + y

=> 10 = z+ y

=> z+y= 10

9. In the given figure, we have \(\lfloor\mathrm{ABC}=\lfloor\mathrm{ACB}\),
\(\lfloor 3=\lfloor 4\), show that \(\lfloor 1=\lfloor 2\).

Solution:

Given, \(\lfloor\mathrm{ABC}=\lfloor\mathrm{ACB}\)

\(\Rightarrow \quad\lfloor 1+\lfloor 4=\lfloor 2+\lfloor 3\) \(\begin{aligned}
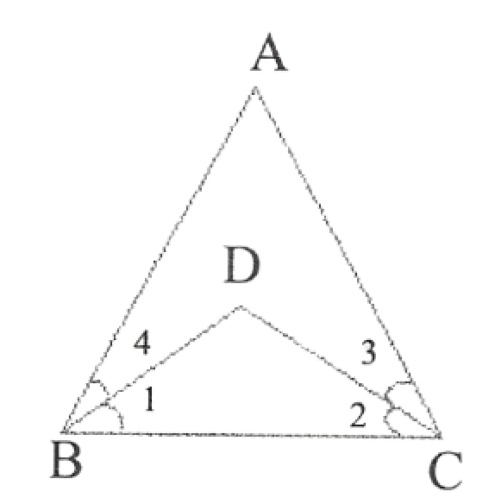
& \Rightarrow \quad\lfloor 1+\lfloor 4-\lfloor 4=\lfloor 2+\lfloor 3-\lfloor 3 \\
& (\operatorname{As}\lfloor 3=\lfloor 4) \\
& \Rightarrow \quad\lfloor 1=\lfloor 2
\end{aligned}\)

Hence Proved

Class 9 Maths Euclid’s Geometry KSEEB Guide

10. In the given figure, we have \(\lfloor 1=\lfloor 3\)& \(\lfloor 2=\lfloor 4\), show that \(\lfloor A=\lfloor C\)

Solution:

Given \(\lfloor 1=\lfloor 3\) & …………..(1)

\(\lfloor 2=\lfloor 4\)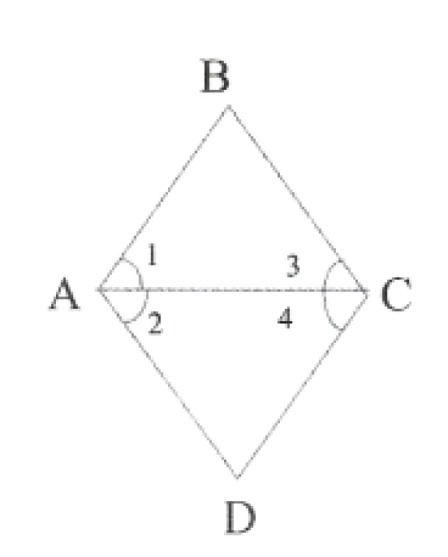

Adding 1 & 2 we get

\(\begin{aligned}
& \lfloor 1+\lfloor 2=\lfloor 3+\lfloor 4 \\
& \Rightarrow\lfloor\mathrm{BAD}=\lfloor\mathrm{BCD} \\
& \Rightarrow\lfloor\mathrm{A}=\lfloor\mathrm{C}
\end{aligned}\)

Three Mark Questions

1. In the given figure, we have AB = BC, BX = BY, show that AX = CY. State the axiom used.

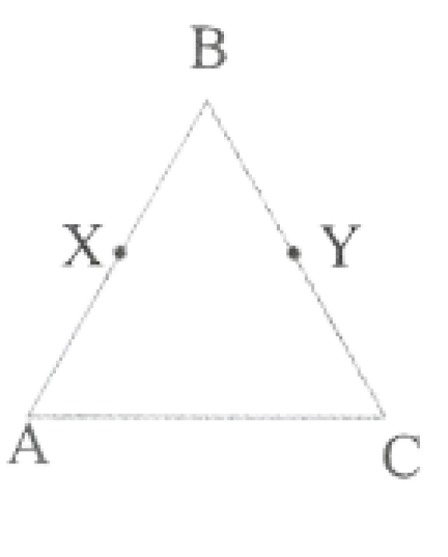
Solution:

Given AB = BC

AX + BX = BY + CY Since BX = BY

AX + BX – BX = BY + CY – BY

=> AX = CY

Axiom: If equals are subtracted from the equals the remainder are equal.

2. Prove that the two lines which are both parallel to the same line are parallel to each other.

Solution:

Given : Three lines /, m & n in a plane such that

l || m&m|| n

To prove: l || n

Proof: If possible, let l be not parallel to n, then l& n should intersect in a unique point, say A.

Thus, through a point A, outside m, there are two lines l & n, both parallel to m.

This contradicts the parallel line axiom, so our assumption is wrong. Hence l || n

3. In the given figure, if OX= 1/2XY, PX= 1/2XZ  &OX = PX, show that XY=YZ

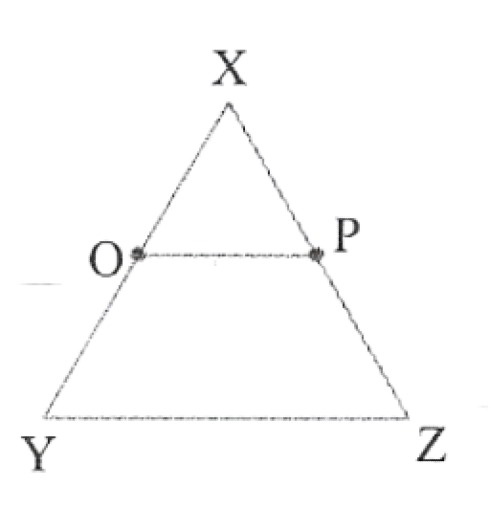
Solution:

Here, OX=1/2XY

=> XY = 2(OX) (given)

=> XY = XZ

(Because things which are double of the same things are equal to one another)

KSEEB Class 9 Maths Chapter 5 Exercise Solutions

4. P & Q are the centres of two intersecting circles. Prove that PQ = QR = PR

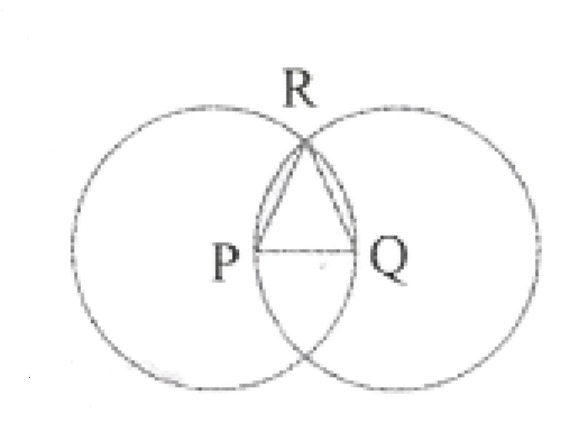
Solution:

In a circle having centre at P,

we have PR = PQ = radius.

In a circle having centre at Q,

we have QR = QP = radius.

Things which are equal to the same thing are equal to one another)

PR = PQ = QR.

5. Read the following statement:
‘’A square is a polygon made up of four line segments, out of which, length of three line segments are equal to the length of fourth one & all its angles are right angles.”
Define the terms used in this definition which you feel necessary, are there any undefined terms in this? Can you justify that all angles & sides of a square are equal?

Solution:

The terms need to be defined are

Polygon: A simple closed figure made up of three or more line segments.

Line segment: Part of a line with two endpoints.

Line: Undefined term.

Point: Undefined term.

Angle: A figure formed by two rays with a common initial point.

Ray: Part of a line with one endpoint

Right angle: Angle whose measure is 90°.

Undefined terms used are: Line, point.

Euclid’s fourth postulate says that “all right angles are equal to one another”.

In a square all angles are right angles

∴ all angles are equal

Three line segments are equal to fourth line segment (given)