KSEEB Class 8 Maths Solutions For Chapter 2 Rational Numbers Points To Remember
Rational nos. are closed under the operations of addition, subtraction and multiplication.
The operations addition and multiplication are
1)commutative for rational numbers.
2)associative for rational numbers.
The rational no. ‘0’ is the additive identity for rational nos.
The rational no.’1′ is the multiplicative identity for rational numbers.
The additive inverse of the rational number [a/b is -a/b] and vice- versa.
Read and Learn More KSEEB Solutions for Class 8 Maths
The reciprocal or multiplicative inverse of the rational numbers. a/b is c/d if a/b x c/d =1
Distributivity of rational nos. For all rational numbers a, b and c,
a(b + c) = ab + ac and a(b-c) =ab-ac
Rational numbers can be represented on a number line.
Between any two given rational numbers there are countless rational numbers. The idea of mean helps us to find rational numbers between two rational numbers.
Positive Rationals: Numerator and denominator both are either opposite or negative.
Example: 4/3,-3/-5
| Class 10 Science | Class 11 Chemistry |
| Class 11 Chemistry | Transformation of Sentences |
| Class 8 Maths | Class 8 Science |
Negative Rationals: Numerator and denominator
both are of opposite signs.
Example: -2/11, 4/-9
Additive inverse: Additive inverse (negative)
(a/b)+(-a/b) = (-a/b)+(a/b)=0
-a/b is the additive inverse of -a/b and a/b is the additive inverse of -a/b
Multiplicative inverse (reciprocal):
a/b x c/d=1=c/d x a/b where c/d is the reciprocal of a/b.
0 has no reciprocal
The reciprocal of 1 is 1 and of -1 is -1.

Kseeb Solutions For Class 8 Maths Chapter 2 Rational Numbers
Rational Numbers Solutions KSEEB Class 8 Maths Exercise 2.1
1. Using appropriate properties find.
1. \(\frac{-2}{3} \times \frac{3}{5}+\frac{5}{2}-\frac{3}{5} \times \frac{1}{6}\)
Solution: \( \frac{-2}{3} \times \frac{3}{5}+\frac{5}{2}-\frac{3}{5} \times \frac{1}{6}\)
= \( \frac{-2}{3} \times \frac{3}{5}-\frac{3}{5} \times \frac{1}{6}+\frac{5}{2}\)(Using commutativity of rational numbers)
= \( \left(-\frac{3}{5}\right) \times\left(\frac{2}{3}+\frac{1}{6}\right)+\frac{5}{2}\)(Distributivity)
= \( \left(-\frac{3}{5}\right) \times\left(\frac{2 \times 2+1}{6}\right)+\frac{5}{2}\)
= \(\left(-\frac{3}{5}\right)\left(\frac{5}{6}\right)+\frac{5}{2}=\left(\frac{-3}{6}\right)+\frac{5}{2}\)
=\(\left(\frac{-3+5 \times 3}{6}\right)=\frac{-3+15}{6}=\frac{12}{6}=2\)
2. \(\frac{2}{5} \times\left(\frac{-3}{7}\right)-\frac{1}{6} \times \frac{3}{2}+\frac{1}{14} \times \frac{2}{5}\)
Solution: =\(\frac{2}{5} \times\left(\frac{-3}{7}\right)+\frac{1}{14} \times \frac{2}{5}-\frac{1}{6} \times \frac{3}{2}\) (By
(By commutativity)
= \(\frac{2}{5} \times\left(\frac{-3}{7}+\frac{1}{14}\right)-\frac{1}{4}\) (By distributivity)
= \(\frac{2}{5}\left(\frac{-3 \times 2+1}{14}\right)-\frac{1}{4}\)
= \(\frac{2}{5}\left(\frac{-5}{14}\right)-\frac{1}{4}\)
= \(\frac{-1}{7}-\frac{1}{4}=\frac{-4-7}{28}=\frac{-11}{28}\)
Rational Numbers Class 8 Kseeb Solutions Pdf
2. Write the additive inverse of each of the following.
1) 2/8
2)-5/9
3)-6/-5
4)2/-9
5)19/-6
Solution:
1) -2/8
2)5/9
3)-6/5
4)2/9
5)19/6
3. Verify that -(-x)=x for
1) x=11/15
2) x=-13/17
Solution: 1) x=11/15 The additive inverse of x=11/15 is
This equality (11/15)+(-11/15)=0 represents that the additive inverse of -11/15 is 11/15 (or) it can be said that -(-11/15)=11/15
i.e., -(-x)=x
2) x=-13/17
The additive inverse of x=13/17 is
-x=13/17 as -13/17+13/17=0
This equality -13/17+13/17=0 represents that the additive inverse of 13/17 is 13/-17 i.e., -(-x)=x.
Class 8 Maths Chapter 2 Kseeb Solutions Karnataka Board
4. Find the multiplicative inverse of the following.
1) -13
Solution: Multiplicative inverse = 1/-13
2) -13/19
Solution: -19/13
3) 1/5
Solution: 5
4)-5/8 x-3/7
Solution: -5/8 x -3/7 = 15/56 multiplicative inverse = 56/15
5) -1 x -2/5
Solution: -1 x -2/5 = 2/5 multiplicative inverse = 5/2
6) -1
Solution: Multiplicative inverse = -1
5. Name the property under multiplication used in each of the following
1)-4/5×1=1x-4/5=-4/5
Solution: 1 is the multiplicative identity
2)-13/17x-2/7=-2/7x-13/17
Solution: Commutativity
3)-19/29×29/-19=1
Solution: Multiplicative inverse
Rational Numbers Solutions KSEEB Class 8 Maths
6. Multiply 6/13 by the reciprocal of -7/16
Solution: 6/13x[Reciprocal of -7/16]
=6/13x-16/7=-96/91
7. Tell what property allows you to compute
1/3 x (6 x 4/3) as (1/3 x 6)x4/3
Solution: Associativity
8. Is 8/9 the multiplicative inverse of -1 1/8 ? Why or Why not?
Solution: If it is the multiplicative inverse, then the product should be 1. However, here, the product is not 1 as 8/9 x(-1 1/8)=8/9 x (-9/8) = -1≠1
Solution: 3 1/3 = 10/3
Here, the product is 1.
Hence, 0.3 is the multiplicative inverse of 3 1/3.
Kseeb Solutions For Class 8 Maths Chapter 2 Important Questions
10. Write.
(1) The rational number that does not have a reciprocal.
Solution: 0 is a rational number but its reciprocal is not defined.
2) The rational numbers that are equal to their reciprocals.Solution: 1 and -1 are the rational numbers that are equal to their reciprocals.
3) The rational number that is equal to its negative.
Solution: 0 is the rational number that is equal to its negative.
11. Fill in the blanks:
1) Zero has No reciprocal.
2) The numbers 1 and -1 are their own reciprocals.
3) The reciprocal of-5 is -1/5
4) Reciprocal of 1/x, where x ≠ 0 is x.5) The product of two rational numbers is always
a Rational Number.
6) The reciprocal of a positive rational number is positive rational number.
KSEEB Class 8 Maths Chapter 2 Rational Numbers Exercise 2.2
1. Represent these numbers on the number line.
1) 7/4
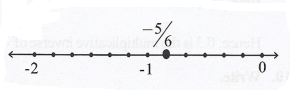
2)-5/6
Solution:1) 7/4cann be represented on the number line as follows

2) -5/6
Solution:
2. Represent-2/11, -5/11, -9/11 on the number line.
Solution:

3. Write five rational numbers which are smaller than 2.
Solution: 2 can be represented as 14/7
∴ five rational numbers smaller than 2 are 13/7, 12/7, 11/7, 10/7, 9/7
4. Find ten rational numbers between -2/5 and 1/2.
Solution: -2/5 and 1/2 can be represented as -8/20 and 10/20 respectively
∴ Ten rational numbers between-2/5 and 1/2 are
-7/20, -6/20, -5/20, -4/20, -3/20, -1/20, 0, 1/20, 2/20
Karnataka Board Class 8 Maths Chapter 2 Textbook Solutions
5. Find five rational numbers between
1) 2/3 and 4/5 2) -3/2 and 5/3
3) 1/4 and 1/2
Solution: l)2/3 and 4/5 can be represented as 30/45 and 30/45 and 36/45 respectively.
∴ 5 rational numbers between 2/3 and 4/5 are
31/45, 32/45, 33/45, 34/45, 35/45
2) -3/2 and 5/3 can be represented as -9/6 and 10/6 respectively.
∴ 5 rational number between -3/2 and 5/3 are
-8/6, -7/6, -1, -5/6, -4/6
3) 1/4 and 1/2 can be represented as 8/32 and 16/32 respectively
∴ 5 rational numbers between 1/4 and 1/2 are
9/32, 10/32, 11/32, 12/32, 13/32
Kseeb Solutions For Class 8 Maths Rational Numbers Exercises
6. Write five rational numbers greater than -2.
Solution: -2 can be represented as -14/7
∴ 5 rational numbers greater than -2 are
-13/7, -12/7, -11/7, -10/7, -9/7
7. Find ten rational numbers between 3/5 and 3/4
Solution: 3/5 and 3/4 can be represented as 48/80 and 60/80 respectively.
∴ 10 rational numbers between 3/2 and 3/4 are
49/80, 50/80, 51/80, 52/80, 53/80, 54/80, 55/80, 56/80, 57/80, 58/80
KSEEB Maths Class 8 Rational numbers Additional Problems
1. The product of two rational numbers is -14/27.
If one of the numbers be 7/9, find the other.
Solution: Product of two rational numbers =-14/27
one number =7/9
∴ other number = -14/27 ÷ 7/9
= -14/27 x 9/7 = -2/3
2. Find three rational numbers between -2 and 7
Solution: A rational number lying between -2 and 7
= (-2+7)÷2
=5÷2=5/2
∴ -2<5/2<7
Now a rational number lying between -2 and 5/2
-2 and 5/2=(-2+5/2)÷2
= \( \left(\frac{-4+5}{2}\right) \div 2=\frac{1}{2} \times \frac{1}{2}=\frac{1}{4} \)
∴ -2<1/4<5/2<7
A rational number lying between 5/2 and 7
=\(\left(\frac{5}{2}+7\right) \div 2=\left(\frac{5+14}{2}\right) \div=\frac{19}{2} \times \frac{1}{2}=\frac{19}{4}\)
∴ -2<1/4<5/2<19/4<7
Hence 1/4, 5/2 and 19/4 are three rational numbers between -2 and 7.
3. Arrange the following numbers in ascending order 4/5, -2/3, 1/-2, -4/7
Solution: Rewrite each rational number with a positive denominator so 4/5, -2/3, 1/-2, -4/7 is same as 4/5, -2/3, 1/-2, -4/7
LCM of 5,3,2 and 7 =210
Now \(\frac{4}{5}=\frac{4 \times 42}{5 \times 42}=\frac{168}{210}\)
\(\frac{-2}{3} \times \frac{70}{70}=\frac{-140}{210}, \frac{-1 \times 105}{2 \times 105}=\frac{-105}{210} \text { and }\)\(\frac{-4}{7}=\frac{-4 \times 30}{7 \times 30}=\frac{-120}{210}\)
∵ -140<-120<-105<168
∴ -140/210<-120/210<-105/210<168/210
∴ -2/3<-4/7<-1/2<4/5
4. What should be added to 2/3 so as to get 1/15?
Solution: Let us suppose that the required number to be added be x, then
2/3 + x =1/15
\(x=\frac{1}{15}-\frac{2}{3}=\frac{1-2 \times 5}{15}=\frac{1-10}{15}=\frac{-9}{15}\)x=-3/5 (reducing to lowest terms)
Hence, the required number is -3/5.
Class 8 Maths Rational Numbers Kseeb Solved Examples
5. Using the rearrangement property find the sum of 4/3+3/5+ -2+3+ -11/5
Solution: Using commutative and Associative property, we can rearrange terms in any suitable order, using this rearrangement property, we have
4/3+3/5+ -2+3+ -11/5
=\(\left(\frac{4}{3}+\frac{-2}{3}\right)+\left(\frac{3}{5}+\frac{-11}{5}\right)\)
=\(\left\{\frac{4+(-2)}{3}\right\}+\left\{\frac{3+(-11)}{5}\right\}\)
=\(\left(\frac{4-2}{3}\right)+\left(\frac{3-11}{5}\right)=\frac{2}{3}+\frac{(-8)}{5}\)
= \(\frac{10+(-24)}{15}=\frac{10-24}{15}=\frac{-14}{15}\)
6. Find the rational number between 1/4 and 1/3
Solution: A rational number between 1/4 and 1/3 is
7. Verify that
a) 2 x (-3/5)=(-3/5) x 2
b) \(\frac{-2}{7} \times\left(\frac{-3}{7} \times \frac{(-9)}{14}\right)=\left(\frac{-2}{7} \times \frac{-3}{7}\right) \times \frac{(-9)}{14}\)
Solution: a) 2 x (-3/5)=(-3/5) x 2
LHS =\( 2 \times\left(\frac{-3}{5}\right)=\frac{2}{1} \times \frac{-3}{5}=\frac{2 \times(-3)}{1 \times 5}=\frac{-6}{5}\)
RHS = \( \left(\frac{-3}{5}\right) \times 2=\frac{-3 \times 2}{5 \times 1}=\frac{-6}{5}\)
LHS=RHS
Hence verified that 2 x (-3/5)=(-3/5) x 2
b) \(\frac{-2}{7} \times\left(\frac{-3}{7} \times \frac{(-9)}{14}\right)=\left(\frac{-2}{7} \times \frac{-3}{7}\right) \times \frac{(-9)}{14}\)
LHS = \(\frac{-2}{7} \times\left(\frac{-3}{7} \times \frac{(-9)}{14}\right)\)
= \(\frac{-2}{7} \times\left\{\frac{(-3) \times(-9)}{7 \times 14}\right\}\)
=\(\frac{-2}{7} \times\left\{\frac{(-3) \times(-9)}{7 \times 14}\right\}\)
RHS = \(\left(\frac{-2}{7} \times \frac{-3}{7}\right) \times\left(\frac{-9}{14}\right)\)
=\(\left(\frac{6}{49}\right) \times \frac{-9}{14}=\frac{-54}{686}=\frac{-27}{343}\)
Hence verified, LHS=RHS
8. A farmer has a field of area 49 4/5 ha. He wants to divide it equally among his one son and two daughters. Find the area of each one’s share.
(ha means hectare: 1 hectare = 10000m2)
Solution:
49 4/5 ha =249/5 ha
Each share = 1/3 x 249/5 ha
= 83/5 ha
= 16 3/5 ha
Karnataka Board Class 8 Maths Solutions For Rational Numbers
9. Let O, P and Z represent the numbers 0, 3 and -5 respectively on the number line. Points Q, R and S are between O and P such that OQ = QR = RS = SP. What are the rational numbers represented by the point Q, R and S Next Choose a point T between Z and O so that ZT = TO, which rational number does T represent?
Solution:
![]()
As OQ=QR=RS=SP
and OQ+QR+RS+SP=OP
∴ Q,R and S divide OP into four equal parts.
so, R is the mid-point of OP.
i.e., R = \(\frac{0+3}{2}=\frac{3}{2}\)
⇒ i.e., Q=\(\frac{1}{2}\left(\frac{0+3}{2}\right)=\frac{3}{4}\) and S is the midpoint of RP.
i.e., s =\(\frac{1}{2}\left(\frac{3}{2}+3\right)=\frac{9}{4}\)
∴ Q=3/4, R=3/2 and S=9/4
also ZT=TO
So T is the mid-point of OZ
i.e., T=\(\frac{0+(-5)}{2}=\frac{-5}{2}\)
10. From a rope 40m long, pieces of equal size are cut, if the length of one piece is 10/3m, find the number of such pieces.
Solution: Total length of rope =40m
Length of one piece =10/3m
Let the number of pieces be x
Then, according to be the question 10x/3=40
⇒ x=\(\frac{40 \times 3}{10}=12\)
Hence, number of pieces cut from the rope are 12.
Practice Questions For Rational Numbers KSEEB Maths
11. Find the sum of 1/2 and 5/-6.
Solution: \(\frac{1}{2}+\left(\frac{5}{-6}\right)=\frac{1}{2}-\frac{5}{6}\)
L.C.M. of 2 and 6 is 6.
\(\frac{1}{2}-\frac{5}{6}=\frac{1 \times 3-5 \times 1}{6}=\frac{3-5}{6}=\frac{-2}{6}=\frac{-1}{3}\)12. The sum of two rational numbers is -2. If one of the number is -14/5, find the other
Solution: Let the other number be x, then
⇒ \(x-\frac{14}{5}=-2\)
⇒ \(x=\frac{14}{5}-2\)
⇒ \(x=\frac{14-2 \times 5}{5}\)
\(x=\frac{14-10}{5}\)=4/5
Hence, the required number is 4/5.
Kseeb Solutions For Class 8 Maths Pdf
13. If the product of two numbers is -5/8 and one of them is -3/4. Find the other.
Solution: Let the other number be 3 x.
then -3/4 x X=-5/8
⇒ \(x=\frac{-5}{8} \div \frac{-3}{4}=\frac{-5}{8} \times \frac{-4}{3}\)
= 20/24 = 5/6
Hence, the other number is 5/6
14. Find three rational number between -3 and -2.
Solution: A rational numbers between -3 and -2 is
A rational number between -3 and -5/2 is
=\(\frac{1}{2}\left\{-3+\left(\frac{-5}{2}\right)\right\}=\frac{1}{2}\left(-3-\frac{5}{2}\right)=\frac{1}{2}\left(\frac{-11}{2}\right)=\frac{-11}{4}\)
A rational number between -5/2 and -2 is
=\(\frac{1}{2}\left\{\frac{-5}{2}+(-2)\right\}\)
=\(\frac{1}{2}\left\{\frac{-5-4}{2}\right\}=\frac{1}{2}\left(\frac{-9}{2}\right)=\frac{-9}{4}\)
∴ -11/4, -5/2, -9/4 are three rational numbers between -3 and -2.
15. One fruit salad receipe requires 1/2 cup of sugar. Another receipe for the same fruit salad requires 2 tablespoons of sugar. If 1 tablespoon is equivalent to 1/16 cup, how much more sugar does the first receipe require?
Solution: 1 tablespoon =1/16 cup
2 tablespoon= 1/16×2 cup =1/8 cup
The quantity of more sugar the first receipe requires
=\(\frac{1}{2}-\frac{1}{8}=\frac{4-1}{8}=\frac{3}{8} \text { cup. }\)
KSEEB Class 8 Maths key concepts of Rational Numbers
16. Tarun purchased 15 3/4m of cloth from the market and gave 7 1/3m of cloth to his sister. How much cloth is left with him?
Solution: Total cloth purchased =15 3/4m =63/4m
Cloth given to his sister =7 1/3m =22/3m
∴ cloth left with Tarun = \(\frac{63}{4}-\frac{22}{3}=\frac{189-88}{12}\)
101/12m or 8 5/12m
17. Roller coaster at an amusment park is 2/3m high. If a new roller coaster is built that is 3/5 times the height of the existing coaster, what will be the height of the new roller coaster?
Solution: Height of roller coaster =2/3m
New roller coaster =3/5 x2/3m =2/5m
Hence, height of the new roller coaster is 2/5m
18. The product of two rational numbers is -14/27, If one of the numbers be 7/9, find the other.
Solution: Product of two rational numbers = -14/27
one number = 7/9
∴ Other number= \(\frac{-14}{27} \div \frac{7}{9}=\frac{-14}{27} \times \frac{9}{7}=\frac{-2}{3}\)
Kseeb Class 8 Rational Numbers Solutions Step By Step
19. Rajini had a certain amount of money in her purse. She spent ₹10 1/4 in the school canteen, bought a gift worth ₹25 3/4 and gave ₹16 1/2 to her friend. How much she have to begin with?
Solution: Amount give to school canteen= ₹10 1/4
Amount given to buy gift= ₹25 3/4
Amount given to her friend= ₹16 1/2
To begin with Rajni had
=₹\(10 \frac{1}{4}+₹ 25 \frac{3}{4}+₹ 16 \frac{1}{2}=₹\left(\frac{41}{4}+\frac{103}{4}+\frac{33}{2}\right)\)
=₹\(\left(\frac{41+103+66}{4}\right)=₹ \frac{210}{4}=₹ 52 \frac{2}{4}\)
=₹52 1/2.
20. One third of a group of people are men. If the nuimber of women is 200 more than the men, find the total number of people.
Solution: Number of men in the group =1/3 of the group.
Number of women = 1-1/3 = 2/3
Difference between the number of men and women = 2/3-1/3 = 1/3
If difference is 200, then total lnumber of people
= \(200 \div \frac{1}{3}=200 \times 3=600\)
Hence, the total number of people= 600.
